DOI:
10.1039/C7RA07387A
(Paper)
RSC Adv., 2017,
7, 41512-41519
Construction and evaluation of chemical structure model of Huolinhe lignite using molecular modeling†
Received
4th July 2017
, Accepted 19th August 2017
First published on 25th August 2017
Abstract
Molecular model construction plays an important role in gaining insight into the thermal conversion process and reaction mechanism of lignite. Based on element analysis, solid-state 13C nuclear magnetic resonance (13C NMR), X-ray photoelectron spectroscopy (XPS), and Fourier transform infrared (FTIR), a Huolinhe (HLH) lignite two dimensional (2D) molecular model was initially constructed. Concentrations of main covalent bonds were employed to adjust and examine the molecular model. The advantage of this approach is not only that it can solve the problem of selecting a representative isomer in constructing the model but also that it considers the essence of chemical reaction. The three dimensional (3D) minimum energy configuration was obtained by molecular mechanics (MM) and molecular dynamics (MD) calculation in Materials Studio package (Accelrys). Finally, the sequence of bond-cleavage from DTG analysis and molecular simulations were used to verify the rationality of proposed model. In general, this work has opened pathways in studying the lignite thermal reaction process at the molecular scale.
1. Introduction
Lignite storage in China reaches 130 billion tons, accounting for approximately 13% of global coal storage.1,2 With the high-ranking coal being gradually exhausted, the utilization of lignite has great potential in energy conversion processes.3 Because of its low mining cost, large amounts of volatiles as well as high chemical reactivity, lignite is being applied to a wide range of applications in the energy sector, such as pyrolysis, combustion, gasification, and liquefaction.4 However, because these coal utilization processes involve a myriad of coupled reaction pathways, it is difficult to explore these reaction mechanism just by experimental methods.5 Molecular simulation, recognized as ‘the third way to explore real matter’ provides a new approach to research these reaction processes.6 It should be pointed out that a rational lignite molecular model is supposed to be the key role in studying lignite conversion processes by molecular simulation.7
The first model of coal was proposed by Fuchs in 1942.8 Over the past 75 years, large number (>134) of coal molecular models have progressively appeared in the literature.9–12 However, the studies of lignite molecular models lag far behind. The first model of lignite was generated by Wender in 1976.10 The proposed structure model only included 92 atoms with an average structural unit (C42H40O10). Even so, Wender's model is the scientific foundation of lignite molecular model, which captures amount of important features of lignite structure. After that, Philip et al.11 published a model of lignite (C115H125O17NS) based on liquefaction products of lignite. It is worthwhile mentioning that a variety of further significant structural features (heteroatoms N and S, esterified aliphatic side chain, and H-bonding) exist in lignite molecular model for the first time. Wolfrum et al.12 reported a brown coal molecular model (C227H183O35N4S3CaFeAl) by detailed analyzing its chemical structure features. It contains more structural heterogeneity and metal cations.
The development of numerical simulations and computer technologies are aiding demystification of the 3D models of coal.13 3D structural model cannot only characterize the detailed structural information but also shine a light on thermal reaction process.14 A brown coal 3D structure unit (C21H20O7) was created by Kumagai et al.,15 who first obtained lignite model by taking advantage of computational chemistry to create a 3D periodic cell with one tetramer plus one pentamer. It is worth to note that the validity of the model is extremely significant. Considering that carbon content (C%) and aromaticity (fa) have always been utilized as the key parameters to characterize chemical structures of coal, researchers widely used 13C NMR spectra to check and adjust the model.16,17 However, owing to the presence of amounts of isomers, structure model obtained by 13C NMR spectra verification is only one conceptual image among a large number of graphical models.18 Furthermore, it is difficult to make use of conceptual images to correlate structures with reactivity.
It is generally agreed that the essence of chemical reaction is the breakage and rearrangement of chemical bonds. Guo et al.19 described that the complicated behavior of lignin pyrolysis could be simplified by only considering the changes in main covalent bonds. This idea was also practiced by Liu et al.,20 they analyzed the peak temperature of DTG sub-curves which greatly matches with the cleavage of major covalent bonds during pyrolysis. Consequently, concentrations of main covalent bonds are thought to be more suitable to examine and adjust the model. Nevertheless, very little information is available for adjustment of coal molecular model by concentrations of main covalent bonds.21
For the purpose of filling the above knowledge gap, the initial 2D molecular model for HLH lignite was constructed according to chemical structure characteristics of coal. The main covalent bond concentrations of coal can be obtained by the information of 13C NMR and ultimate analysis, while the bond concentrations of model can be determined using the number of bonds dividing the molecular weight of the model. The final 2D model can be generated by adjusting the covalent bond concentrations of the model to get close to experimental values. In the end, the correctness of the model is verified by comparing the results of experiments and simulations during the thermal reaction process. Compared to the real coal structure, the model is only an ‘average structural unit’22 of coal, but it can give a reasonable representation of HLH lignite in terms of energy conversion process.
2. Experimental and computational details
2.1 Sample
HLH lignite samples used in this work were obtained from Inner Mongolia. They were crushed and grounded to 109–180 μm, and then were dried under vacuum at 40 °C for 24 h before used. The proximate and ultimate analyses results are shown in Table 1.
Table 1 Proximate and ultimate analyses of HLH lignite and elemental portion of the model (wt%)a
| Sample |
Proximate analysis |
Ultimate analysis |
| Mad |
Aad |
FCad |
Vdaf |
Cdaf |
Hdaf |
Odafa |
Ndaf |
Sdaf |
| ad: air-dried base; daf: dry and ash-free base; a: by difference. |
| HLH lignite |
7.30 |
7.78 |
45.13 |
47.23 |
75.40 |
6.14 |
16.00 |
1.46 |
1.00 |
| Model |
|
|
|
|
75.52 |
6.15 |
16.02 |
1.31 |
1.00 |
2.2 Structural characteristic analysis
2.2.1 13C NMR spectra analysis. 13C NMR spectroscopic measurement for HLH lignite was conducted at 100.64 MHz by using a Bruker Avance III 400 MHz spectrometer, which was equipped with a 4 mm cross polarization magic angle spinning double-resonance probe head. The contact time, recycle delay time, and accumulative number of collected data were set to 2 ms, 6 s, and 9000 respectively. MestReNova software was used to analyze 13C NMR spectra of coal, amounts of carbon skeleton structural parameters were got by integration of the different chemical shifts.23 The results are shown in Table 2.
Table 2 Assignments for peaks in 13C NMR spectra and relative content
| Carbon distribution |
Chemical shift (ppm) |
Structural fragments |
Symbols |
Relative content (%) |
| Aliphatic carbon 34.32% |
14–16 |
Aliphatic CH3 |
fMal |
1.24 |
| 16–22 |
Aromatic CH3 |
fAal |
4.89 |
| 22–36 |
Methylene |
fHal |
17.60 |
| 36–50 |
Methine quaternary |
fDal |
8.74 |
| 50–90 |
Oxy-aliphatic carbon |
fOal |
1.85 |
| Aromatic carbon 61.25% |
100–129 |
Aromatic protonated |
fHar |
27.83 |
| 129–137 |
Aromatic bridgehead |
fBar |
10.64 |
| 137–148 |
Aromatic branched |
fCar |
12.61 |
| 148–165 |
Oxy-aromatic carbon |
fOar |
10.17 |
| Carbonyl carbon 4.43% |
165–180 |
Carboxyl carbon |
fCa |
2.44 |
| 180–220 |
Carbonyl carbon |
fOa |
1.99 |
2.2.2 XPS spectra analysis. To obtain the surface composition of HLH lignite, C 1s, N 1s and S 2p spectrum were determined using a Thermo VG Scientific ESCALAB 250Xi spectrometer and curve-resolved with Casa XPS processing software.24 In addition, all corrections for binding energies were carried out in reference the principal C 1s peak at 284.8 eV.25 The data about carbon, oxygen, nitrogen and sulfur forms are listed in Table 3.
Table 3 Distributions of carbon, oxygen, nitrogen, and sulfur forms in HLH lignite from XPS analysis
| Elemental peak |
Functionality |
Binding energy (eV) |
Molar content (%) |
| C 1s |
C–C |
284.8 |
82.00 |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
287.5 |
1.67 |
| C–O |
286.3 |
13.86 |
O–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
289.0 |
2.48 |
| N 1s |
Pyridinic |
398.7 |
18.07 |
| Pyrrolic |
400.1 |
54.58 |
| Quaternary nitrogen |
401.3 |
15.25 |
| Nitrogen oxide |
402.8 |
12.1 |
| S 2p |
Aliphatic sulfur |
163.5 & 164.7 |
29.15 |
| Aromatic sulfur |
164.2 & 165.4 |
35.6 |
| Sulfoxide |
165.4 & 166.6 |
4.53 |
| Sulfone |
169.4 & 170.6 |
30.72 |
2.2.3 FTIR analysis. The characteristics of functional groups for HLH lignite were measured by Nicolet-6700 FTIR spectrometer. The spectra was recorded in the range of 4000 to 400 cm−1 with a resolution of 4 cm−1. The sample (1 mg) with KBr (150 mg) were powered for 2 min and pressed into a pellet, after that dried in a vacuum oven under 60 °C for 12 h. The infrared spectra of HLH lignite are shown in Fig. 1.
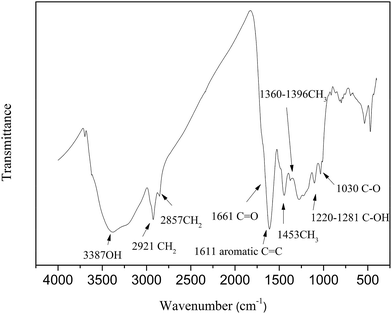 |
| | Fig. 1 FTIR spectra of HLH lignite. | |
2.2.4 DTG analysis. The pyrolysis behavior of HLH lignite was studied by a thermogravimetric analyzer (TGA) from Metter-Toledo. The experiments were performed from 30 °C to 110 °C at 10 °C min−1 and maintain 30 min at 110 °C, then from 110 °C to 900 °C with the same heating rate. High purity helium (99.999%) was utilized at 50 mL min−1 to make sure an inert atmosphere.26 The differential thermogravimetric (DTG) curve was fitted by 6 sub-curves with a high correlation coefficient (R2 = 0.9919). Liu et al.20 suggested a series of sub-curves can represent a group of covalent bonds. Therefore, the sequence of bond-cleavage can be obtained by DTG analysis.
2.3 Computational methods and model construction
2.3.1 Computational methods. The optimal geometry structure was obtained by MM and MD calculations in Materials Studio package (Accelrys). MM calculations were performed using Forcite module. Calculation details: task, geometry optimization; minimization algorithm, smart minimizer; quality, fine; max iterations, 5000; energy differences, 0.0001 kcal mol−1; RMS force, 0.005 kcal mol−1 A−1; charge equilibration method, QEq; the calculated electrostatic energy and van der Waals energy was based on atoms; force field, Dreiding.27 And then, MD calculations were carried out by the anneal dynamics in the same module. Calculation details: initial temperature, 300 K; mid-cycle temperature, 600 K; heating ramps per cycle, 5; dynamics steps per ramp, 100; annealing cycles, 10; ensemble, NVT; thermostat, Nosé. Simulation time, 200 ps. For the purpose of getting a low energy state, geometry optimization with above parameters was carried out on the output configuration after each cycle.The structure was further refined by using DFT method at the B3LYP/3-21g basis set. Natural bond orbital (NBO) analysis28 was performed to assign the atomic charges and Wiberg bond indices (WBI) at the same levels with the Gaussian 09 package.29 NBO analysis is a good tool for getting bond length and bond order, which can analyze the bond-cleavage behavior of the model.
2.3.2 Model construction. The construction procedure of HLH lignite model is shown in Fig. 2. The initial 2D model can be constructed based on elemental analysis, spectra of 13C NMR, XPS, and FTIR.30,31 Concentrations of main covalent bonds have been used to adjust the molecular model. And then, optimal geometry 3D structure was obtained by MM and MD calculations in Materials Studio package (Accelrys). Finally, the model was evaluated by comparing the bond-cleavage sequence from DTG analysis and molecular simulations.
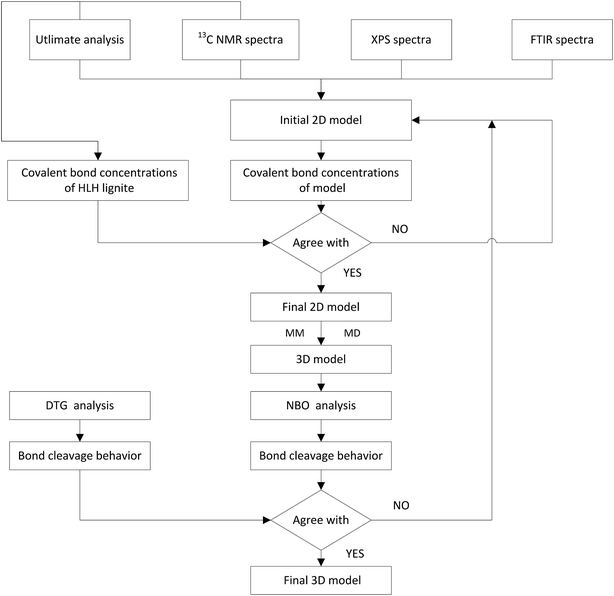 |
| | Fig. 2 Schematic diagram for the construction of HLH lignite structural model. | |
2.4 Calculation of covalent bond concentrations of model and HLH lignite
It is generally accepted that coal mainly involves 11 types of covalent bonds. Since the contents of S and N in coal are usually very low, only 9 types of bonds have been considered in the study including Car–Car, Car–Cal, Cal–Cal, Car–H, Cal–H, Car–O, Cal–O, Cal![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, and O–H. These bond concentrations of model can be determined by eqn (1).21
O, and O–H. These bond concentrations of model can be determined by eqn (1).21| |
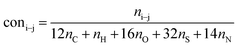 | (1) |
here coni–j denotes the concentration of bond i–j; ni–j is the amount of bond i–j in a molecule; i represents Car, Cal, and O, while j represents Car, Cal or H; the denominator is the molecular weight of the model.
The concentrations of 9 types covalent bonds in coal can be determined by eqn (2)–(10),21 which can calculate the quantity of the single bond, double bonds, and quasi-double bonds. This method was modified from the work of Gyul'maliev et al.,32 who reported the quantity of the bonds could be determined by half of the unpaired electrons in the system only considering the single bond.
| |
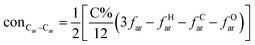 | (2) |
| |
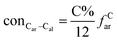 | (3) |
| |
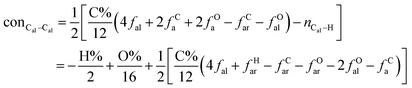 | (4) |
| |
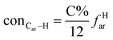 | (5) |
| |
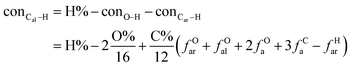 | (6) |
| |
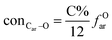 | (7) |
| |
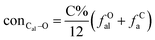 | (8) |
| |
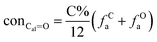 | (9) |
| |
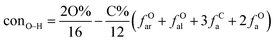 | (10) |
here
far represents aromaticity;
fHar represents the fraction of protonated aromatic carbons;
fCar is the ratio of alkylated aromatic carbons;
fOar is the ratio of aromatic carbons bonded to oxygen;
fal is the ratio of aliphatic carbons;
fCa denotes the fraction of carboxyl carbon;
fOa denotes the ratio of carbonyl carbon;
fOal is the ratio of aliphatic carbons bonded to oxygen.
3. Results and discussion
3.1 HLH lignite molecular model construction
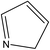
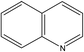
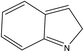
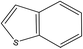
A formula of C200H195N3S1O32 can be determined for HLH lignite from elemental analysis, whose magnitude is consistent with Yuzhou lignite (molecular formula of C240H211N3SO76).33 According to the aforementioned results of XPS analysis and the number of S and N in the formula, thiophene, pyridine, and two pyrrole were selected as representative heterocycles in the model. After that, we began to determine the type of aromatic structures. Aromatic carbon, accounting for 61.25%, constitute the skeletal structure of molecular model. The number and type of aromatic unit structures can be determined by Xb (the molar fraction of aromatic bridgehead carbon), the number of aromatic carbon, and aromatic bridgehead carbon. Xb determined by eqn (11) is a significant parameter that can be employed to analyze the aromatic cluster size.34 The Xb calculated for HLHM is 0.17, which gets closer to naphthalene (Xb = 0.2), suggesting that the amount of aromatic rings in aromatic clusters is rarely greater than two.35 Hence, we choose benzene and naphthalene as the main aromatic structural units. The type and quantity of aromatic structures in the model are listed in Table 4.
Table 4 The type and quantity of aromatic unit structures
| Type |
Quantity |
Type |
Quantity |
 |
1 |
 |
1 |
 |
1 |
 |
1 |
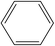 |
4 |
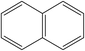 |
6 |
 |
1 |
|
|
For additions of aliphatic side chains, there is no way knowing how these aliphatic carbons are linked to each other or other structural units.36 We can only know aliphatic carbon structural parameters: the average methylene chain length Cn = 1.4, branched degree of aliphatic chain BI = 25.47%. Cn and BI were determined by eqn (12) and (13).37 On the basis of these results, it can be concluded that aliphatic structural units mainly exist in the form of short chain and branch structure.
As shown in Fig. 1, the oxygen functional group in HLH lignite exist in different forms, such as carboxyl, carbonyl, hydroxyl, and ether. Oxygen forms can be also determined by analyzing oxygen's influence on the XPS carbon (1s) signal of adjacent carbon atoms.38 Table 3 shows the proportion of carbon bound to oxygen by two oxygen bonds (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) and carbon bound to oxygen by three bonds (O
O) and carbon bound to oxygen by three bonds (O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–O) are much smaller, which agrees with the results of FTIR and 13C NMR spectra analysis. The carbon bound to one oxygen by a single bond (e.g., C–O, C–OH, etc.) is the main existence of oxygen. However, little information regarding the distribution of ether (C–O) and hydroxyl (C–OH) can be obtained by XPS and 13C NMR spectra analysis. The final forms of oxygen in molecular structure can be achieved through model adjustment. At last, 2D molecular model was initially constructed according to chemical structural characteristics getting by experimental methods.
C–O) are much smaller, which agrees with the results of FTIR and 13C NMR spectra analysis. The carbon bound to one oxygen by a single bond (e.g., C–O, C–OH, etc.) is the main existence of oxygen. However, little information regarding the distribution of ether (C–O) and hydroxyl (C–OH) can be obtained by XPS and 13C NMR spectra analysis. The final forms of oxygen in molecular structure can be achieved through model adjustment. At last, 2D molecular model was initially constructed according to chemical structural characteristics getting by experimental methods.
3.2 Adjustment of HLH lignite molecular model
Simulated 13C NMR spectra has always been taken so as to ‘adjust’ model structures to get close to experimental data. Although the carbon skeleton structure of model can be identical with the experimental value, it cannot avoid the problem of choosing representative isomer. Isomers with the same molecular formula have a great difference in reactivity, more often than not the reason might be found in the form of chemical bond connection. Meanwhile, the model got by this method is only a conceptual image, which cannot reflect the nature of the chemical reaction. The reactivity of models was often obviously lower than the actual values.16,39 Concentrations of main covalent bonds instead of simulated 13C NMR spectra can be employed to check and adjust molecular model. Nine bonds concentrations of HLH lignite can be got according to 13C NMR data and the ultimate analysis data. Eqn (2)–(10) contain nearly all carbon structural parameters structural features (far, fHar, fCar, fOar, fal, fCa, fOa, and fOal) determined by 13C NMR. It can be speculated that the method of covalent concentrations embodies the essence of simulated 13C NMR spectra method. The preliminary 2D molecular model was modified by the comparison between the simulated concentrations of main covalent bonds and the experimental results. The final 2D molecular model is shown in Fig. 3. Table 5 lists 9 main covalent bond concentrations of HLH lignite and model. Geometry optimization 3D configuration of HLH lignite was produced by MM and MD calculations in Materials Studio package (Accelrys) and the structures before and after optimization are shown in Fig. 4(a and b). The detailed structural information of optimal geometry configuration is shown in Table S1 of the ESI.† The changes of energy are listed in Table 6. It can be seen the total energy of optimized structure decreased sharply, only accounting for approximately 5% of initial structure. And more, optimized structure becomes much more compact with excellent spatial structure.
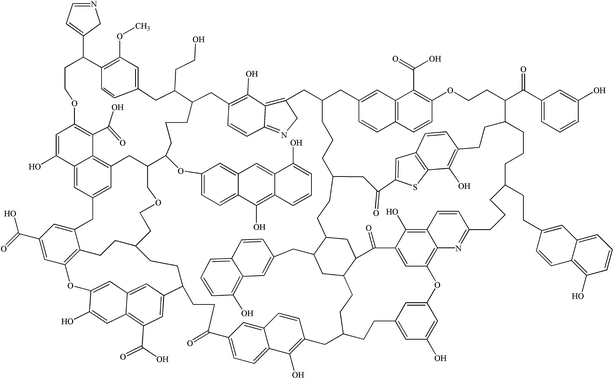 |
| | Fig. 3 The final 2D molecular model of HLH lignite. | |
Table 5 Main covalent bond concentrations of HLH lignite and model (mmol g−1)
| Sample |
conCar–Car |
conCar–Cal |
conCal–Cal |
conCar–H |
conCal–H |
conCar–O |
conCal–O |
conCal![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
conO–H |
| HLH lignite |
41.83 |
7.92 |
22.09 |
17.94 |
38.56 |
6.39 |
2.70 |
2.78 |
5.35 |
| Model |
41.97 |
7.51 |
20.02 |
18.76 |
36.91 |
6.26 |
2.19 |
2.50 |
5.32 |
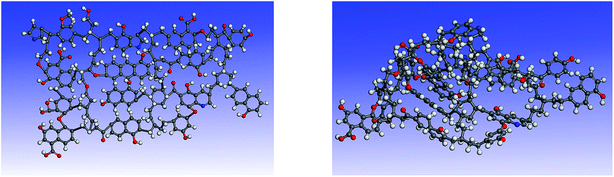 |
| | Fig. 4 The 3D structures of HLH lignite model before and after geometry optimization. (a) The initial 3D structural model of HLH lignite (b) the optimal geometry structure obtained by MM and MD calculation. | |
Table 6 Energy changes of HLH lignite model before and after geometry optimization (kcal mol−1)
| Conformer |
Valence energy |
Non-bond energy |
Total energy |
| Bond |
Angle |
Torsion |
Inversion |
Hydrogen bond |
van der Waals |
Electrostatic |
| Initial structure |
2984.94 |
149.53 |
280.36 |
5.05 |
−0.02 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 856.73 856.73 |
−35.87 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 240.72 240.72 |
| Final structure |
96.24 |
146.18 |
119.45 |
4.00 |
−7.26 |
403.72 |
−52.64 |
709.67 |
3.3 Model evaluation
The purpose of constructing lignite molecular model is mainly to research the thermal reaction process by molecular simulation. Therefore, the sequence of bond-cleavage reactions is more reasonable for evaluation of model.
3.3.1 Sub-curves of DTG analysis. TG analysis is a technique that used to study the relationship between the sample mass and reaction temperature in control process.40 The changes of mass during reaction are mainly caused by the breakage of bonds. Therefore, TG analysis can be employed to obtain the sequence of bond cleavage. Liu et al.20 demonstrated that DTG curve of coal pyrolysis could be fitted by a series of sub-curves which can represent a number of covalent bonds in coal. In this study DTG peaks were fitted by using 6 sub-curves (R2 = 0.9919; see Fig. 5). As shown in Table 7, 6 peaks were detected at 190, 350, 428, 510, 614, and 727 °C. According to the studies proposed by He et al.,3 Liu et al.,20 and Li et al.,26 peak 1 at temperature of 190 °C may be ascribed to the release of H2O and CO2. The assignment of peak 2 at 350 °C is likely to Cal–O, Cal–S, or Cal–N. Peak 3 at 428 °C corresponds to Cal–Cal, Cal–H, or Car–N. Peak 4 detected at 510 °C can be attributed to Car–Cal, Car–O, or Car–S. Peak 5 at 614 °C is related to decomposition of carbonates to generate CO2. Peak 6 at 727 °C is thought to be the condensation of aromatic rings. It is concluded that the breakage of the weakest bonds (such as Cal–O, Cal–S, and Cal–N) occur in the initial stage. During the second stage, the cleavage of the weaker bonds (e.g., Cal–Cal, Cal–H, and Car–N) occur at mild temperature. In the end, Car–Cal, Car–O, and Car–S with higher bond energy are difficult to crack. Since the main decomposition of volatiles occur in the temperature range of 300–600 °C, the study of bond-cleavage only take peak 2, 3, and 4 into account. The major source for tar formation may be the cleavage of Cal–Cal and Car–Cal bonds which related to peak 3 and peak 4, respectively. Therefore, optimum temperature for the yield of tar is around the temperature of peak 4.
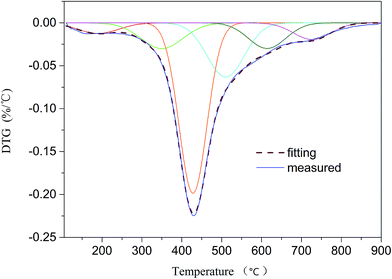 |
| | Fig. 5 DTG curve and fitting results. | |
Table 7 Assignment of peaks from DTG profile
| Peak no. |
Possible origin |
Peak temperature (°C) |
| 1 |
Release of bonded water and decarboxylation |
190 |
| 2 |
Cleavage of Cal–O, Cal–S, and Cal–N |
350 |
| 3 |
Cleavage of Cal–Cal, Cal–H, and Car–N |
428 |
| 4 |
Cleavage of Car–Cal, Car–O, and Car–S |
510 |
| 5 |
Carbonate decomposition |
614 |
| 6 |
Condensation of aromatic rings |
727 |
3.3.2 NBO analysis. The natural of chemical reaction is the breakage and recombination of chemical bonds during the reaction process. The bond strength is often related to bond length and bond order. Longer the bond, the smaller bond order and the easier the bond ruptures. Ru et al.41 predicted reaction sites of Huadian kerogen according to bond length and bond order. NBO analysis is a helpful for gaining information on bond characters.42 The average bond parameters of HLH lignite molecular model are listed in Table 8.
Table 8 The average bond parameters of HLH lignite molecular model
| Bond type |
Bond length (Å) |
Bond order |
| C(heterocycle)–S(heterocycle) |
1.816 |
1.086 |
| C(heterocycle)–N(heterocycle) |
1.375 |
1.400 |
C(carbonyl)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(carbonyl) O(carbonyl) |
1.231 |
1.729 |
C(carboxyl)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(carboxyl) O(carboxyl) |
1.247 |
1.759 |
| C(carboxyl)–O(carboxyl) |
1.389 |
1.027 |
| C(aromatic)–O(phenol) |
1.391 |
1.031 |
| C(aromatic)–O(ether) |
1.432 |
0.942 |
| C(aliphatic)–O(ether,hydroxy) |
1.452 |
0.947 |
| C(aromatic)–C(aromatic) |
1.413 |
1.335 |
| C(aliphatic)–C(aliphatic) |
1.555 |
0.993 |
| C(aliphatic)–C(carbonyl) |
1.510 |
1.010 |
| C(aromatic)–C(carbonyl) |
1.490 |
1.044 |
| C(aliphatic)–C(aromatic) |
1.518 |
1.008 |
It can be seen that the C–S bond existing in thiophene has the longest bond length and the lower bond order, and can easily break at the beginning of the reaction. This is consistent with the study of Miura et al.,43 who proposed that the release of SO2 during pyrolysis is approximately at 300 °C attributed to the breakage of C–S. And the C–C bonds linked to carboxyl carbon, carbonyl carbon, and aliphatic carbon possess the longer bond length in the range of 1.490 to 1.555 Å and the lower bond order (0.993–1.044) are recognized as reaction sites. Meanwhile, the reactivity of C–O bonds (in ether, hydroxy and carboxyl groups) is close to C–C bonds, which may break at mild temperature. The aromatic rings have an effect on the bond strength, which makes C–N exist in heterocycle and C–C belonging to aromatic structures have much higher stability. The behavior of bond-cleavage of molecular model is in accord with DTG analysis of HLH lignite.
4. Conclusions
In this present study, constructing lignite molecular model was to aid the comprehension of energy conversion process, such as pyrolysis, combustion, liquefaction, and gasification. The preliminary 2D molecular structure has been constructed according to the results of experimental methods. Elemental analysis is helpful for determining the formula (C200H195N3S1O32), and thiophene, pyridine, pyrrole, benzene, naphthalene, phenol, and ether were selected as the representative structural units in the model base on 13C NMR, FTIR, and XPS analysis. It is important to highlight the method of adjustment molecular model. Concentrations of main covalent bonds used to adjust molecular model can surmount the problem of selecting representative isomers as well as reflect the essence of chemical reaction. Nine main covalent bond concentrations of HLH lignite were calculated to examine and adjust the molecular model. And then, the optimized 3D conformation was obtained by MM and MD calculation in Materials Studio package (Accelrys). The total energy of optimized structure decreased sharply with excellent spatial structure. Finally, the sequence of bond-cleavage from DTG analysis and molecular simulations were used to examine the correctness of the 3D molecular model. A good agreement in the behavior of bond-cleavage during thermal reaction process between DTG analysis and molecular simulations. Although the constructed model is not the lowest energy conformation of HLH lignite, it is still valuable for considering the problem of isomers and essence of chemical reaction in constructing molecular model.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors gratefully acknowledge the financial support received from the National Natural Science Foundation of China (Grant No. 51676032) and Program for Changjiang Scholars and Innovative Research Team in University (No. IRT13052).
References
- Z. P. Lei, M. X. Liu, H. F. Shui, Z. C. Wang and X. Y. Wei, Fuel Process. Technol., 2010, 91, 783–788 CrossRef CAS.
- Y. Xu, Y. F. Zhang, Y. Wang, G. J. Zhang and L. Chen, J. Anal. Appl. Pyrolysis, 2013, 104, 625–631 CrossRef CAS.
- Q. Q. He, K. Wan, A. Hoadley, H. Yeasmin and Z. Y Miao, Fuel, 2015, 156, 121–128 CrossRef CAS.
- P. Liu, D. X. Zhang, L. L. Wang, Y. Zhou, T. Y. Pan and X. L. Lu, Appl. Energy, 2016, 163, 254–262 CrossRef CAS.
- F. Castro-Marcano, M. F. Russuo Jr, A. C. T. van Duin and J. P. Mathews, J. Anal. Appl. Pyrolysis, 2014, 109, 79–89 CrossRef CAS.
- X. X. Li, M. Zhang, J. Liu and L. Guo, Mol. Simul., 2015, 41, 13–27 CrossRef.
- J. P. Mathews, A. C. Van Duin and A. L. Chaffee, Fuel Process. Technol., 2011, 92, 718–728 CrossRef CAS.
- W. Fuchs and A. G. Sandhoff, Ind. Eng. Chem., 1942, 34, 567 CrossRef CAS.
- J. P. Mathews and A. L. Chaffee, Fuel, 2012, 96, 1–14 CrossRef CAS.
- I. Wender, Catal. Rev., 1976, 14, 97–129 CAS.
- C. V. Philip, R. G. Anthony and Z. D. Cui, ACS Symp. Ser., 1984, 287–302 CrossRef.
- E. A. Wolfrum, ACS Symp. Ser., 1983, 28, 15–17 Search PubMed.
- J. L. Faulon, P. G. Hatcher, G. A. Carlson and K. A. Wenzel, Fuel Process. Technol., 1993, 34, 277–293 CrossRef CAS.
- S. Bhoi, T. Banerjee, K. Mohanty, S. Bhoi, T. Banerjee and K. Mohanty, RSC Adv., 2015, 6, 2559–2570 RSC.
- H. Kumagai, J. Hayashi, T. Chiba and K. Nakamura, Fuel and Energy Abstracts, 1999, 43, 2 Search PubMed.
- T. Takanohashi and H. Kawashima, Energy Fuels, 2002, 16, 379–387 CrossRef CAS.
- Ü. Lille, I. Heinmaa and T. Pehk, Fuel, 2003, 82, 799–804 CrossRef.
- Z. Y. Liu, Sci. Sin.: Chim., 2014, 44, 1431–1438 CrossRef CAS.
- X. J. Guo, Z. Y. Liu, Q. Y. Liu and S. Lei, Fuel Process. Technol., 2015, 135, 133–149 CrossRef CAS.
- S. Lei, Q. Y. Liu, X. J. Guo, W. Z. Wu and Z. Y. Liu, Fuel Process. Technol., 2013, 108, 125–132 CrossRef.
- B. Zhou, S. Lei, Q. Y. Liu and Z. Y. Liu, Fuel, 2016, 184, 799–807 CrossRef CAS.
- A. Marzec, Fuel Process. Technol., 2002, 77, 25–32 CrossRef.
- L. Qian, Y. J. Zhao, S. Z. Sun, H. W. Che, H. Chen and D. Wang, Fuel Process. Technol., 2014, 118, 327–334 CrossRef CAS.
- Q. Wang, Q. Liu, Z. C. Wang, H. P. Liu, J. R. Bai and J. B. Ye, Fuel Process. Technol., 2017, 160, 170–177 CrossRef CAS.
- S. R. Kelemen, M. Afeworki, M. L. Gorbaty, M. Sansone, P. J. Kwiatek, C. C. Walters, H. Freund and M. Siskin, Energy Fuels, 2007, 21, 1548–1561 CrossRef CAS.
- Z. K. Li, X. Y. Wei, H. L. Yan and Z. M. Zong, Fuel, 2015, 153, 176–182 CrossRef CAS.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS.
- H. P. Gümüş, Ö. Tamer, D. Avcı and Y. Atalay, Spectrochim. Acta, Part A, 2014, 129, 219–226 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven Jr J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D. 01, Gaussian, Inc., Wallingford CT, 2010 Search PubMed.
- J. H. Xiang, F. G. Zeng, B. Li, Z. Li, L. M. Fen and L. H. Zhen, J. Fuel Chem. Technol., 2013, 41, 391–400 CrossRef CAS.
- X. H. Guan, Y. Liu, D. Wang, Q. Wang, M. S. Chi, S. Liu and C. G. Liu, Energy Fuels, 2015, 29, 4122–4136 CrossRef CAS.
- A. M. Gyul'maliev, G. S. Golovin and S. G. Gagarin, Solid Fuel Chem., 2007, 41, 257–266 CrossRef.
- J. P. Wang, G. Y. Li, R. Guo, A. Q. Li and Y. H. Liang, Energy Fuels, 2017, 31, 124–132 CrossRef CAS.
- H. L. Lin, K. J. Li, X. W. Zhang and H. X. Wang, Energy Fuels, 2016, 30, 3809–3814 CrossRef CAS.
- F. Yang, Y. C. Hou, W. Z. Wu, M. Niua, S. H. Rena and Q. Wanga, Fuel, 2017, 189, 408–418 CrossRef CAS.
- J. H. Tong, X. M. Jiang, X. X. Han and X. Y. Wang, Fuel, 2016, 181, 330–339 CrossRef CAS.
- M. S. Solum, A. F. Sarofim, R. J. Pugmire, T. H. Fletcher and H. F. Zhang, Energy Fuels, 2001, 15, 961–971 CrossRef CAS.
- S. R. Kelemen, M. Afeworki and M. L. Gorbaty, Energy Fuels, 2002, 16, 1450–1462 CrossRef CAS.
- J. H. Xiang, F. G. Zeng, H. Z. Liang, B. L. Sun, L. Zhang, M. F. Li and J. B. Jia, J. Fuel Chem. Technol., 2011, 39, 481–488 CrossRef CAS.
- K. M. Lu, W. J. Lee, W. H. Chen and T. C. Lin, Appl. Energy, 2013, 105, 57–65 CrossRef CAS.
- X. Ru, Z. Q. Cheng, L. H. Song, H. Y. Wang and J. F. Li, J. Mol. Struct., 2012, 1030, 10–18 CrossRef CAS.
- F. Weinhold, J. Comput. Chem., 2012, 33, 2363–2379 CrossRef CAS PubMed.
- K. Miura, K. Mae, M. Shimada and H. Minami, Energy Fuels, 2001, 15, 629–636 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The detailed structural information of Huolinhe lignite model (PDF). See DOI: 10.1039/c7ra07387a |
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Qing Wang*b and
Ying Liub
*a,
Qing Wang*b and
Ying Liub
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, and O–H. These bond concentrations of model can be determined by eqn (1).21
O, and O–H. These bond concentrations of model can be determined by eqn (1).21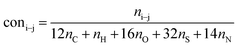
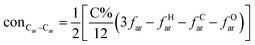
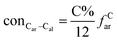
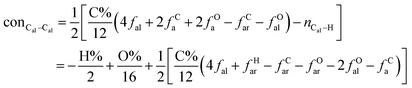
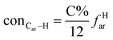
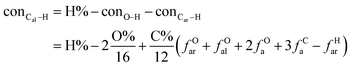
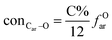
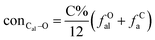
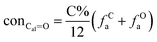
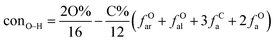
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) and carbon bound to oxygen by three bonds (O
O) and carbon bound to oxygen by three bonds (O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–O) are much smaller, which agrees with the results of FTIR and 13C NMR spectra analysis. The carbon bound to one oxygen by a single bond (e.g., C–O, C–OH, etc.) is the main existence of oxygen. However, little information regarding the distribution of ether (C–O) and hydroxyl (C–OH) can be obtained by XPS and 13C NMR spectra analysis. The final forms of oxygen in molecular structure can be achieved through model adjustment. At last, 2D molecular model was initially constructed according to chemical structural characteristics getting by experimental methods.
C–O) are much smaller, which agrees with the results of FTIR and 13C NMR spectra analysis. The carbon bound to one oxygen by a single bond (e.g., C–O, C–OH, etc.) is the main existence of oxygen. However, little information regarding the distribution of ether (C–O) and hydroxyl (C–OH) can be obtained by XPS and 13C NMR spectra analysis. The final forms of oxygen in molecular structure can be achieved through model adjustment. At last, 2D molecular model was initially constructed according to chemical structural characteristics getting by experimental methods.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O
O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 856.73
856.73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 240.72
240.72![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(carbonyl)
O(carbonyl)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(carboxyl)
O(carboxyl)











