Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Computational insights on the role of film thickness on the physical properties of ultrathin polysulfone membranes†
S. S. M. Lock,
K. K. Lau *,
A. M. Shariff,
Y. F. Yeong and
M. A. Bustam
*,
A. M. Shariff,
Y. F. Yeong and
M. A. Bustam
Research Center for CO2 Capture, Department of Chemical Engineering, Universiti Teknologi PETRONAS, 32610 Perak Darul Ridzuan, Malaysia. E-mail: laukokkeong@utp.edu.my
First published on 15th September 2017
Abstract
Although it has been reported that physical properties of polymeric membranes inherit thickness dependent characteristics, typically when they are subjected to confinement at an ultrathin dimension (<1000 Å), deviations from their bulk counterpart are still not completely understood. An empirical investigation of physical properties for an ultrathin membrane at laboratory scale is difficult, time consuming, and costly which is attributed to challenges to fabricate defect-free films with ultrathin thickness and that requires special instruments at critical conditions. In our current work, a Soft Confining Methodology for Ultrathin Films was conducted to simulate ultrathin polysulfone polymeric membranes of varying thicknesses, l, to resemble their actual size in the thickness dimension. Subsequently, physical properties of the constructed ultrathin films, e.g., density and glass transition temperature, have been elucidated from an atomistic insight. Quantitative empirical models have been proposed to capture thickness-dependent physical properties upon ultrathin confinement. In addition, free volume and cavity distribution was also quantified in order to elucidate the evolution in membrane morphology and to satisfy a previous research gap of deficiency in system dimension dependent cavity sizes. On the whole, it was found that a thinner structure exhibits higher structural density and lower glass transition temperature, as well as lower free volume and cavity sizes. The findings from the present work are anticipated to propose an alternative from a molecular simulation aspect to circumvent complexities associated with experimental preparation and testing of ultrathin polymeric membranes, while providing direct elucidation and quantification of thickness-dependent physical properties in order to enhance understanding at a molecular perspective.
1. Introduction
A smaller dense polymeric membrane thickness can be rationalized as having a smaller resistance through the barrier that controls the relative rate of transport of various species, which contributes to larger permeation that can remove impurities under a smaller membrane area requirement.1–3 To date, virtually all gas separation membranes are fabricated in the order of 1000 Å or less to be commercially viable (e.g., large feed flux and high impurities content).4 Nevertheless, a bottleneck to further expand usage of ultrathin polymeric membranes in industrial applications has emerged. A major challenge has arisen from deviation of thin polymeric films as compared to their bulk state,5 typically when the membrane material is created upon confinement (i.e., less than 1000 Å thick). Some physical properties that have been reported to exhibit thickness-dependent characteristics in previously published literature include glass transition temperature, coefficient of thermal expansion, mechanical modulus and loss, dielectric and acoustical equivalents, and reduction capacity, as well as rate of diffusion through the polymeric film.6 Deviation of thickness-dependent physical properties upon confinement is still not completely understood and remains an intriguing area of debate. The empirical investigation of properties for ultrathin membrane at a laboratory scale is difficult, time consuming, and costly because of challenges to fabricate defect-free films at a smaller thickness that requires special instruments at critical conditions (such as high rotation speed, and elevated temperature and pressure).7–10 In addition, although in a real experimental set-up nanofilms are typically grown on a support, computationally via modelling free-standing sheets, one can enquire into the inherent stability and physical properties of different nanofilm structures independently of a specific support.11In this context, molecular simulation has been proposed as a feasible alternative to provide insights into material behaviour in a confined system from an atomistic point of view, usually achieved via a coupling of molecular dynamics (MD) and a Monte Carlo (MC) technique.12 Several published literature reports have been devoted to simulation of ultrathin polymer films adopting different methodologies in the manner of user-defined pseudo codes to simulate interactions between a polymer and interfaces; i.e., typically work demonstrated by Mansfield and Theodorou, Baschnagel & his co-workers, and Kim & Yamamoto and Torres et al.13–19 Mansfield and Theodorou pioneered molecular simulation of free standing thin polymer films and compared it to cases of strongly and weekly interacting interfaces in order to study the effect of surfaces on the equilibrium structure and dynamic behaviour of polymer melts by means of dynamic Monte Carlo simulation evolving beads in a lattice model.13 In later work by Baschnagel & his co-workers, a series of papers have been published in the work of MD for thin polymer films through adaptation of the bond-fluctuation lattice model, in which non-entangled polymer melts confined between two solid walls were simulated.14–16 In later work, Baschnagel & co-workers also simulated free surfaces through manipulation of a softer wall potential defined manually by end users, which resulted in enhanced dynamics next to the surfaces.17 Kim & Yamamoto conducted MD simulations on a supercooled liquid to evaluate the effect of finite sizes to the relaxation adopting periodic boundary condition (PBC) methodology through incremental numbers of interacting atoms while ignoring the confinement effect.18 Their studies depicted a pronounced size effect observed in the relaxation behaviour at temperatures below the critical temperature, TC, when size of the cooperative particle motions becomes comparable to the unit cell length of the small system. Torres et al. adopted a coarse-grained continuum representation of unentangled polymers to simulate free standing and supported polymeric films in the near vicinity of glass transition.19 Recently, Nie et al. employed dynamic Monte Carlo simulations to study local segmental mobility and local Tgs in ultrathin polymer films, in which their simulation results provide new insights into elucidation of key factors underlying the layer Tg from a molecular level point of view.20 A comprehensive review pertaining to molecular simulation and modelling of material in confined geometries has been provided in work by Alcoutlabi & McKenna.21
From review of previously published literature, it is found that various methodologies have been proposed to simulate polymeric structures upon nano scale confinement. Nonetheless, previous works pertained almost exclusively to implementation of ultrathin molecular structures as end effects, while analysis based upon the constructed structures to study physical properties upon confinement received less scrutiny. This limitation has been attributed to requirements of complicated user-defined pseudo codes and inevitably high performance computers to perform molecular modelling of any reasonably sized system. Complexity associated to molecular simulation work has hindered further applications in other fields, such as engineering and pharmaceuticals, in which physical properties play an important role in governing material selection. Based on the above motivation, molecular design software has emerged over recent years which directly supports the construction of molecular models in a graphical-interface manner while providing additional analytical tools to predict physical properties of a simulated structure. Nonetheless, to date in order to reduce simulation time in such molecular systems, the only possible way for researchers is to consider a smaller simulated structure, which has been compensated by using PBC and assuming uniform characteristics throughout the polymeric matrix, to represent its corresponding real system of any size.22–24 Therefore, it is of paramount importance to simulate ultrathin polymeric films through incorporation of film thickness effects in order to elucidate physical properties. The objective is to acquire a better fundamental elucidation underlying the characteristics of ultrathin polymeric films, typically for membrane gas separation considering the adverse effect of sample sizes to physical properties, which can be consequently employed in design and selection of membrane materials.
In particular, it is of utmost vitality to elucidate the physical characteristic of free volume distribution in amorphous polymers in order to evaluate their spatial arrangement and membrane morphology. Rather than adopting a single free volume value that merely describes the amount of free spaces contained within a polymer structure, cavity distribution provides additional intuitive information regarding allocated cavity sizes as a route for channeling a certain gas molecule.25 Among commonly employed methods in locating and sizing cavities is the Cavity Energetic Sizing Algorithm (CESA), which was originally developed by in't Veld et al. to determine cavity size distribution in liquids, including hard sphere (HS) and Lennard-Jones (LJ) fluids, SPC/E water, as well as for two isomeric polyimides based on energetic considerations. In this approach, a cavity is defined as the space with a well-defined centre, whereby a local minimum in repulsive particle energy field is defined, while overlapping cavities form clusters, which are representative of free volume distribution.26,27 The procedure and equations underlying CESA have been reviewed in Fig. S1 in ESI.†
Wang et al. employed the CESA algorithm to demonstrate that free volume distribution is vital in characterizing the separation performance of two high free volume polymers, poly[1-(trimethylsilyl)-1-propyne] (PTMSP) and a random copolymer of 2,2-bis (trifluoromethyl)-4,5-difluoro-1,3-dioxole (TFE/BDD) with a similar total free volume but highly distinct permeability performance.28 In another work, Wang et al. also adopted CESA to study cavity size distribution and diffusion in para and meta isomers of polymers.29 Jiang et al. adapted CESA to demonstrate that newly proposed thermally reduced (TR) polymers have higher cavity size distribution as compared to their precursors, which further facilitates research work in this particular material.30 Golzar et al. extended the application of CESA to determine the free volume distribution of nano sized silica particles-filled membranes in order to demonstrate improvement of gas permeability with existence of fillers.31 In our recent work, we adapted CESA to elucidate cavity size distributions of several polymeric membranes commonly adapted in gas separation, ranging from low to high free volume polymers, which have been further correlated with gas permeability data to provide an intuitive explanation related to disparity observed among transport properties of the polymeric membranes.25 Similarly, to date, CESA has merely been applied in a glassy polymer structure with a well-defined periodic boundary to permit considerable simplification to the modelling process. The question of system size dependent cavity size distribution remains open and one that has not been addressed yet.
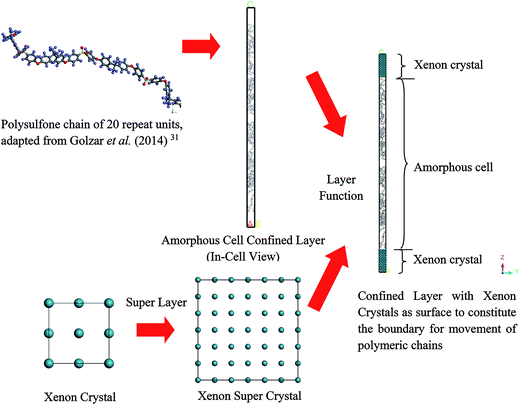
Hence, the objective of this study is to investigate the effect of confinement towards physical properties of polymeric membranes at the nanoscale dimension in order to elucidate the appreciably thickness dependent deviation from bulk structure, which has remained elusive until currently.32 In our present work, a Soft Confining Methodology for Ultrathin Films (SCMUF) was implemented to incorporate the influence of finite size effect upon confinement in molecular dynamics simulations adopting Materials Studio 8.0 molecular software. The “soft” terminology earns its name since the physical system under consideration can be flexibly altered and compacted according to the subjected simulation conditions. The methodology has been evolved and improvised from Liu et al. work that proposed xenon crystals as a confining layer to compact a polymeric structure into a well-defined density distribution for creating molecular models of amorphous polymer surfaces.33 Nonetheless, in this work, rather than refrain the study to elucidation of merely the polymer surfaces that has provided scarce information involving the entire molecular structure, the ideology has been extended to simulate ultrathin PSF membrane films of varying thicknesses (<1000 Å). In short, the novelty of our current work has been highlighted from two standpoints. First, unlike previous work that adopted a well-defined periodic boundary condition to simulate bulk polymer membrane without consideration of sample size effects with Materials Studio molecular software, a soft confining methodology was adopted to simulate membrane films at nanoscale dimensions with varying size, which resembles its actual thicknesses. Second, physical properties of the constructed PSF films, which include that of density, glass transition temperature, free volume and cavity distribution, were analyzed from a molecular perspective and quantified to address interrogation of thickness-dependent properties and morphology in polymeric membranes that have not been resolved in previous works.
2. Methodology
The methodology is subdivided into two major sections: (1) molecular simulation to construct PSF polymeric films, and (2) physical property analysis.2.1 Molecular simulation
In this section, details of the information and procedure adopted for model construction of PSF polymeric films at varying finite dimensions based on SCMUF through employing Materials Studio molecular software are elaborated. Overview and chronological development underlying the simulation methodology is provided in Fig. S2 in ESI.† On the whole, the methodology proposes combination of a molecular modeling sequential procedure and a self-defined script to simulate actual dimensions of polymeric membranes upon confinement with varying thicknesses. In all circumstances the computation of molecular simulation was performed from 3 initial configurations, and the average value was reported to ensure statistical certainty. To the best of our knowledge, SCMUF is a pioneering molecular simulation work that incorporates the effect of film thickness to construct ultrathin membrane systems within Materials Studio, which has surpassed previous works that merely adopted the periodic boundary condition (PBC).The repeat unit of a pure PSF monomer, which was created in Materials Studio 8.0, was adapted to simulate polymeric membranes, such as that depicted in Fig. 1.
 | ||
| Fig. 1 The chemical structure for a polysulfone repeated single chain; purple: hydrogen, grey: carbon, yellow: sulphur, red: oxygen atom. | ||
To simulate a pure PSF membrane, a PSF chain of 20 repeat units with head-to-tail orientation and isotactic tacticity was located in the Forcite module of Materials Studio 8.0, which was subsequently subjected to energy minimization and geometry optimization.31 A polymeric chain of 20 repeat units was employed since it has been demonstrated in previous work by Golzar et al. to be relatively successful in simulating bulk PSF polymeric membranes without consideration of sample size and confinement effects. In addition, the relatively shorter polymeric chain was employed to increase the success rate of compacting within confined dimensions. An explanation was attributed to the rationalization that longer chains get entangled together in comparison to their shorter counterparts,41 which increases intermolecular resistance during molecular treatment within the confined space, further leading to increments in computational cost and chances of termination throughout MD. Other than that, it has been demonstrated in previously published literature that the properties of a physical system are governed and dominated by mobility of the faster moving (shorter) polymer chains.42,43 In our current work, the same number of repeat units to constitute a polymeric chain of the same length as the initial configuration was adopted consistently in all simulation cases regardless of the cell dimensions. A similar approach was employed in previous simulation work by Neyertz & Brown to elucidate the influence of system size without confinement in molecular dynamics simulations of gas permeation in glassy polymers.44 It was reported in their work that this approach is more feasible since structural properties were found to be virtually chain length dependent due to bias towards formation of larger cavities in longer chains, such as that demonstrated in previous works by Cuthbert et al.45,46 The COMPASS force field was adopted alongside the smart algorithm, which is a combination of the steepest descent, adjusted basis set Newton–Raphson (ABNR), and quasi-Newton algorithms in a cascading manner, in order to refine geometry of the initial polymeric chain (convergence tolerance energy of 0.001 kcal mol−1, force of 0.5 kcal mol−1 Å−1, displacement of 0.015 Å with maximum number of iterations of 500 for an independent optimization).31
Initially, polymeric chains with 20 repeat units, as prepared earlier in Section 2.1.2, were folded into an amorphous cell module adopting the Confined Layer task with the number of polymeric chains as summarized in Table 1. The confined layer was selected to build the thin polymeric films in order to satisfy the criterion of mere molecular interactions in the x–y plane, while movement in the z direction, which is regarded as being the orientation perpendicular to surface of the polymeric film, was restricted. An orthorhombic lattice type was selected, whereby the confined layer was constructed normally along the thickness (C) direction. The polymeric chains were embedded in the hypothetical confined layer at an initial density of 0.6 g cm−3 since ramping from this low density has been suggested to increase the success rate of compacting the polymeric chains at the restraint alignment.47
| Thickness (Å) | Number of PSF chains | Average initial layer dimensions of PSF films after cropping the xenon crystal and relocating the polymers (Å3) | Average final layer dimensions of PSF polymeric membrane film after MD (Å3) | Average volume shrinkage (Å3) | Average chain end-to-end distance (Å) |
|---|---|---|---|---|---|
| ∼100 | 2 | 16.90 × 16.90 × 129.50 | 16.03 × 16.03 × 91.87 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 379.50 379.50 |
60.06 (±0.03) |
| ∼200 | 4 | 16.55 × 16.55 × 235.08 | 14.89 × 14.89 × 203.34 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 306.06 306.06 |
61.90 (±0.86) |
| ∼300 | 6 | 15.95 × 15.95 × 358.48 | 15.72 × 15.72 × 287.77 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 084.95 084.95 |
63.69 (±1.02) |
| ∼400 | 8 | 15.43 × 15.43 × 496.41 | 14.99 × 14.99 × 422.54 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 242.94 242.94 |
64.12 (±1.25) |
| ∼500 | 10 | 15.57 × 15.57 × 602.89 | 15.17 × 15.17 × 515.68 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 482.68 482.68 |
67.44 (±1.40) |
| ∼600 | 12 | 15.42 × 15.42 × 729.77 | 15.14 × 15.14 × 620.92 | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 195.05 195.05 |
69.00 (±1.46) |
| ∼700 | 14 | 15.06 × 15.06 × 880.63 | 14.73 × 14.73 × 766.48 | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 424.67 424.67 |
70.22 (±1.74) |
| ∼800 | 16 | 14.92 × 14.92 × 1009.63 | 14.99 × 14.99 × 846.61 | 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 516.75 516.75 |
73.45 (±1.62) |
| ∼900 | 18 | 15.43 × 15.43 × 1048.37 | 15.13 × 15.13 × 933.31 | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 950.63 950.63 |
74.90 (±2.09) |
| ∼1000 | 20 | 15.58 × 15.58 × 1146.52 | 15.32 × 15.32 × 1026.79 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 312.06 312.06 |
77.60 (±2.53) |
In the work of Liu et al. (2012), they mentioned that xenon crystals are sufficient to form the confining layer since it has a flat crystal slice, inert characteristic, and hypothetically is a solid at 298 K and 1 atm,33 which is in good accordance with simulation conditions of the present study (308.15 K and 2 atm). It is important to note that, in reality, although a xenon crystal does not exist at such operating conditions, the hypothetical structure provided a flat surface with inert atoms that are suitable for confining purposes, which has been demonstrated with success in previous literature.33,48 Therefore, xenon atoms arranged in a crystalline structure were adopted in our current work to confine molecular movement along the surface direction. The xenon crystals of a Fm3m space group with a face-centered cubic (FCC) structure were adopted consistently in the current study.49 The single crystal unit for xenon employed in this study is depicted in Fig. 3.
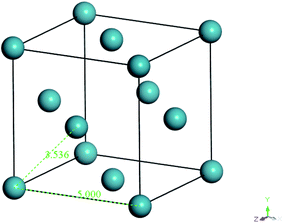 | ||
| Fig. 3 Specification and configuration of one single xenon crystal unit used as a repulsive surface in the present study. | ||
From Fig. 3, it is found that lattice specification within the cell edge is 5 Å, whereas distance to the nearest xenon atom neighbor is 3.5 Å, which is in good accordance with values of previously published works (∼6 Å and ∼4 Å respectively),49–51 while being convenient for replication in all directions to a create super cell to constitute sufficient repulsive surfaces. Specification of the xenon crystals, after expanding in xyz directions applied in this work for different membrane thicknesses, has been kept constant at 15.0 × 15.0 × 50.0 Å3.
Later, the built-in layer function in Materials Studio 8.0 was employed to insert a PSF polymeric unit in between two xenon crystal substrates, with the xenon crystalline structure being the first and third, while the PSF confined layer was the second layer, respectively. The layer was constructed by keeping all the component layers constant at the initial thicknesses and utilizing orientation from the second layer.
Then, the initial constructed atomistic configuration was subsequently minimized and optimized adopting a series of protocols. First, a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 energy minimization step was conducted to remove any undesirable configurations including overlapping and close contact. Subsequently, the Geometry Optimization task in the Forcite module was adapted to optimize the structure by proposing a low energy conformation. In this task, the COMPASS force field was consistently adopted with the smart algorithm. Subsequently, in order to achieve the ideal structure, which is the lowest energy configuration with the most realistic geometry, a molecular dynamics equilibrium run was implemented on the amorphous cell structure in the isothermal–isobaric (NPT) ensemble with a total simulation time of 1000 ps. The pressure of the system was maintained at 2 atm while the temperature was fixed at a constant value of 308.15 K with a Nose thermostat and Berendsen barostat. Throughout this step, the equation of motion was integrated by the velocity Verlet algorithm with a time step of 1 fs for all simulation conditions. Throughout the molecular dynamics (MD) simulation, the xenon crystal surface functions as a repulsive wall that arbitrarily rebounds the PSF atoms back into the MD box if they move close to it. When the PSF atoms are shifted towards the interior of the MD box, the xenon crystals naturally occupy the void space left behind by the PSF atoms. The same ideology holds throughout the MD process, whereby the iterative repulsion between xenon crystals and PSF atoms rebound the chains towards the centre of the hypothetical box, which constrains them inside the confined layer to constitute a dense PSF polymeric membrane structure, such as that depicted in Fig. 4.
000 energy minimization step was conducted to remove any undesirable configurations including overlapping and close contact. Subsequently, the Geometry Optimization task in the Forcite module was adapted to optimize the structure by proposing a low energy conformation. In this task, the COMPASS force field was consistently adopted with the smart algorithm. Subsequently, in order to achieve the ideal structure, which is the lowest energy configuration with the most realistic geometry, a molecular dynamics equilibrium run was implemented on the amorphous cell structure in the isothermal–isobaric (NPT) ensemble with a total simulation time of 1000 ps. The pressure of the system was maintained at 2 atm while the temperature was fixed at a constant value of 308.15 K with a Nose thermostat and Berendsen barostat. Throughout this step, the equation of motion was integrated by the velocity Verlet algorithm with a time step of 1 fs for all simulation conditions. Throughout the molecular dynamics (MD) simulation, the xenon crystal surface functions as a repulsive wall that arbitrarily rebounds the PSF atoms back into the MD box if they move close to it. When the PSF atoms are shifted towards the interior of the MD box, the xenon crystals naturally occupy the void space left behind by the PSF atoms. The same ideology holds throughout the MD process, whereby the iterative repulsion between xenon crystals and PSF atoms rebound the chains towards the centre of the hypothetical box, which constrains them inside the confined layer to constitute a dense PSF polymeric membrane structure, such as that depicted in Fig. 4.
An alternate sequence of energy minimization and geometry optimization was conducted in the Forcite module employing conditions as summarized in Section 2.1.3. After this stage, an annealing procedure consisting of one annealing cycle was performed on the polymeric layer by adopting the temperature cycle protocol inherent in the Anneal task of the Forcite module. Throughout the cycle, the system was heated and cooled back with an interval of 20 °C between 353.15 K and 653.15 K (corresponding to 15 heating ramps per cycle), which is well above the glass transition temperature of bulk polysulfone (Tg,bulk = 459.15 K). At each temperature, 100 ps NPT were conducted, which constitute to a total annealing simulation time of 3 ns. At this step, in order to control simulation temperature at the designated heating temperature and pressure of 2 atm, the Nose thermostat with Q ratio of 0.01 and Berendsen barostat with decay constant of 0.1 ps were employed continuously. Later, molecular dynamics run at 2 atm and 308.15 K were conducted in the NPT ensemble of the Forcite Dynamic module with the Berendsen barostat and Nose thermostat for a total simulation time of 1000 ps and a time step of 1 fs. When approaching the endpoint of the NPT run, an additional 500 ps of Canonical (NVT) ensemble was conducted at a temperature of 308.15 K on the equilibrated polymeric structure. The NPT-NVT molecular treatment was repeated until changes in the successive density values were within predefined tolerance. The final cell specifications for different PSF membrane samples, after completing the molecular dynamics treatment, are provided in Table 1.
2.2 Physical property analysis
In this section, simulation processes to study different physical properties of the simulated polymeric membranes are provided. Theoretically, the procedures are repeated to ensure reproducibility in order to validate a reasonable simulation methodology and to obtain average calculated values.So far, there is no perfect theory for the glass transition phenomenon.55 Nonetheless, it has been proposed that Tg can be determined through varying properties of interest predicted by molecular dynamics methodology such as density, free volume, specific volume, radial distribution function, non-bond energy, torsion energy, mean squared displacement, and modulus. In this study, Tg was obtained from change in the volumetric property which, to the best of our knowledge, is the most common theory put forward by Fox and Flory to date.56 Nonetheless, limitations in adaptation of molecular dynamics methodology for determination of Tg, typically those based on transition in volumetric change, have to be highlighted a priori for readers’ attention. First, a relatively larger deviation in Tg prediction is observed within materials with non-homogeneity in free volume distribution since glass transition is a strong function of density. In other words, local Tg theoretically persists throughout the film that affects its accuracy should it be determined through adaptation of volumetric behaviour.20,57 The second constraint is related to the time scale of MD simulation, whence it is merely restricted to relatively short simulation times (roughly in the regime of several pento to nanoseconds) to resolve atomic vibrations. On the other hand, cooling rate has a strong effect on the resulting properties attributed to the time-dependent response of amorphous polymers, which also needs to be accounted for when comparing MD simulations and experiments.58 Consequently, cooling rates are many orders of magnitude faster than those normally used in experiments, which contributes to deviations between simulation data and actual laboratory observations. However, an approach based on alterations in volumetric properties is still the most common approach for monitoring glass transition temperature in a MD study.31 The reasons have been rationalized through the findings that Tg in a structure of non-homogenous free volume can be sufficiently characterized through the average response of the film throughout its thickness.59 In addition, the relatively shorter time scale has proven to be able to provide satisfactory prediction of Tg within an acceptable limit in several published literatures,31 or minimally to provide some insightful trends in a qualitative manner60 while a semi-empirical model has to be employed to correlate experimental findings to simulation results quantitatively in such circumstances.57–59 Our simulation work is a typical example of the latter. Selection of the Tg determination approach in our MD work coincides with recent findings by Mohammadi et al. that volumetric properties are computationally less expensive while being able to provide agreeable accordance to experimental observations.61
In this study, Tgs of PSF samples were determined by mimicking the heating and cooling protocols in a laboratory scale by adapting a series of thermodynamic treatments in the Forcite Module. First, the optimized and equilibrated configuration for each dimension was subjected to an additional Canonical (NVT) ensemble at 308.15 K with a time step of 1 fs and total simulation time of 10 ps by framing the output every 1000 steps. This procedure aims to obtain the trajectory files of PSF polymeric films with 10 frames for each thickness, such that an average Tg can be deduced to increase accuracy of the computed value when a series of thermodynamic treatments is iterated, while calculating an independent Tg for each frame. Overall, the Tg can be determined by running numerous cycles of NPT dynamics at different temperatures and plotting the density at each independent temperature. An individual frame located within the PSF trajectory was exposed to gentle heating from 300.15 K to 500.15 K through NPT dynamics at different temperatures, which surpasses that of the bulk glass transition temperature of the PSF polymer, with an interval of 1 K. At each designated temperature, a 100 ps NPT dynamic ensemble of 1 fs time step was conducted at 2 atm pressure. Thereafter, the system is cooled down from 500.15 K to 300.15 K with a temperature interval of 1 K employing the same NPT ensemble protocol while computing density of the structure at each temperature. This protocol is looped over all frames contained in the trajectory file and eventually the values are averaged at the end of the simulations.
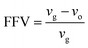 | (1) |
In eqn (1), vg is specific volume of the polymeric glass at a specific temperature and vo is occupied volume of the polymer chain.
In order to separate regions of occupied polymeric chains and free volume, the Connolly Surface function embedded within Materials Studio was consistently employed throughout all polymeric membrane samples by using medium grid resolution, 0.4 Å grid intervals, and 1.3 Å Connolly probe radius.63,64 The probe radius is equivalent to the kinetic radius of gaseous helium in order to capture any possible free channels in the polymeric matrix since it has the finest geometry among all gas penetrants. In addition, the FFV (Bondi) parameter has been generally evaluated based on Bondi's group contribution methodology, such as that depicted in expression (2).65
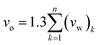 | (2) |
In expression (2), n is total number of functional groups into which the repeat unit structure of a polymer is divided, while (vw)k is van der Waals volume of the group, such as that proposed by Van Krevelen.66 The specific volume of the PSF polymer films of varying thicknesses was computed based on the reciprocal of the simulated density from MD simulation, while vo = 0.6903 cm3 g−1 was consistently employed for all conditions in the current work for FFV (Bondi) computation.
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) t and
t and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i correspond to the vector position of the test particle and interacting atom while φt indicates the Lennard Jones 6–12 interaction force. All these parameters can be conveniently extracted from Materials Studio simulation software for subsequent computational work.
i correspond to the vector position of the test particle and interacting atom while φt indicates the Lennard Jones 6–12 interaction force. All these parameters can be conveniently extracted from Materials Studio simulation software for subsequent computational work.3. Results and discussion
In this section, results pertaining to molecular simulation of PSF polymeric membranes at different thicknesses upon confinement are presented, alongside several analyses of the simulated structure to elucidate morphology and physical properties evolution associated with the dimensional changes.3.1 Molecular structure and density of PSF polymeric film
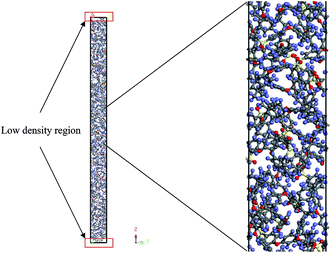
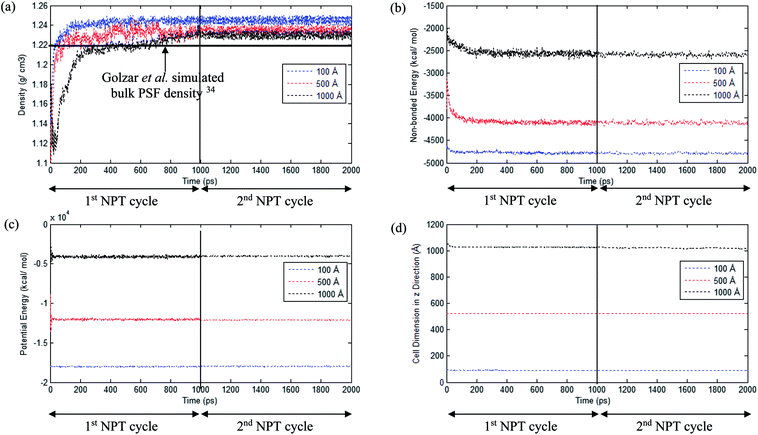
An example of the finalized PSF polymeric film of ∼200 Å after performing the sequence of molecular dynamics treatment is provided in Fig. 5. As illustrated, the PSF polymeric chains are confined within the thickness of the film. The molecules arrange in a manner to form free volumes within the confined layer which promote a transport mechanism of gas penetrants through it. When approaching a region in close proximity to the free surface of the PSF layers, an area of lower density molecular structure has been observed. The simulation result is consistent with previously published literature which report the existence of a decaying density vicinity that is naturally located at the polymer's surface.67,68 As summarized in Table 1, insertion of a different number of PSF chains with constraints along the thickness is capable of producing polymeric films of varying thicknesses. In the current simulation study, it is found that an increment in 2 polymeric chains contributes to enhancement of membrane thickness by approximately 100 Å. The xenon crystals are depicted to have greater impact in a thinner structure by preparing the PSF films at initial dimensions that are closer to the final configurations, whilst that of the thicker polymeric membranes demonstrates a larger volume reduction after molecular dynamics simulation attributed to larger flexibility in the spacial dimension for reestablishment of molecular arrangement.In the current study, to preliminarily evaluate that the simulation time is of considerable length to attain thermodynamic equilibrium and that the simulated membrane structures possess the physical properties that are comparable with experimental conditions, three parameters, such as energy (potential energy and non-bonded energy), density, and thickness of the molecular structure, were monitored consistently throughout the course of the MD procedure. The density, non-bonded and potential energy, as well as cell thickness versus time step for a PSF film with cell dimensions of ∼100 Å, ∼500 Å and ∼1000 Å are provided as examples in Fig. 6.
As seen in Fig. 6, the parameters converge to approximately fixed values typically after 200 ps time steps of MD simulation in the ∼100 Å and ∼500 Å polymeric structures, while the ∼1000 Å molecular structure requires longer simulation time; this can be rationalized through larger structural inhomogeneity in the larger films carried through combinations of smaller structures via layer to layer methodology. It is seen that density increases to the equilibrated value in the 1st NPT cycle. After relaxation in the 1st cycle NVT molecular procedure, minimal fluctuation is depicted in the 2nd NPT cycle, suggesting that the systems have reached thermodynamic equilibrium. The energy parameters are found to experience decrement during the course of simulation since the most plausible molecular structure is the one with the least energy configuration. On the other hand, the cell length is restricted to a smaller dimension when the molecular system is compacted to an arrangement of higher density. In addition, it is also depicted that when the system surpasses that of 1000 ps time steps, the density curves are nearly fixed within a range between 1.23 to 1.25 g cm−3 dependent upon finite size of the PSF films.62,69 The values are in close agreement with previously simulated bulk PSF by Golzar et al. (1.22 g cm−3),31 which supports the claim that these PSF polymeric structures have been constructed via a high accuracy simulation procedure since the system was ramped from a low density configuration without confining any constraints and boundaries throughout the molecular dynamics process.
From Fig. 6, it is also depicted that the potential and non-bonded energy of PSF membranes are in accordance with sample thicknesses, with a larger dimension demonstrating larger values. This observation is attributed to a larger number of neighboring and interacting molecules under consideration within a bigger system. On the contrary, it is illustrated from Fig. 6(a) that density exhibits a negative correlation, whereby a thicker PSF polymeric film results in a lower density. This observation is consistent with experimental reports from previously published literature by Rozenberg et al. and Shishatskii et al.; they elucidate the effect of system size upon confinement towards density in their respective polymeric systems associated to epoxy-polymers and poly(methyl methacrylate) as well as poly(vinyltrimethylsilane) (PVTMS) and poly(trimethylsilylnorbornene) (PTMSNB).70,71 Variation in density among polymeric films of different thicknesses close to confinement has been rationalized through the ease of a volume relaxation mechanism in thinner structures. This contention was explained via enhanced mobility of polymeric chains in the vicinity of a free surface, further promoting the formation of a more equilibrated and hence denser structure.72
To rectify legitimacy of the claim, chain end-to-end distance of PSF films at varying dimensions were evaluated since this property characterizes extent of structural relaxation from initial configuration. In this work, the chain end-to-end distance is defined as the distance between the carbon and oxygen atoms which are attached, respectively, at the end of the PSF chain. A PSF polymeric chain of 20 repeat units with end-to-end distance of 368.62 Å consistently was adopted as the initial configuration for molecular dynamics simulation (Fig. S3 in ESI† to guide reader); this is in good agreement with that from Golzar et al. simulation work with a starting geometry of 337.74 Å31 that demonstrates its applicability in applications of molecular simulation work in subsequent studies.
Through execution of the procedure as outlined in Section 2.1 and alteration of the polymer configuration throughout the course of molecular simulation, the average end-to-end distances of PSF chains in various dimensions of polymeric membranes are summarized in Table 1, while some examples of final configuration of the PSF polymeric films illustrating the evolution in the chain length of different thicknesses are provided in Fig. S4 of ESI.† On the whole, the end-to-end distance of a PSF chain experiences increments with the thickness of the PSF polymeric film. The distinction among chain packing can be rationalized though an explanation of the presence of an interfacial layer, whereby that is defined as the interface region in which dynamics differ from bulk and polymer conformations.73 The decreased film thickness results in an increase of the fraction of interfacial layers, which have more free volume or cavity, such as that proven in Fig. 5 of our simulation study. In other words, the fraction of chains in the interfacial layer that has stronger mobility will be increased.20 These interfacial chains inherit a flexible configuration for an augmented relaxation mechanism and therefore possess more conformations; thus the end-to-end distance of polymer chains decreases. Enhanced relaxation in ultrathin structures has been supported in various published literatures, be it experimental observations74–76 or simulation works.77 A shorter chain length implies that the PSF chains are capable of folding and packing more efficiently to constitute a denser polymeric structure.
The effect of thickness, l, on specific volume of the simulated PSF films, v, is depicted in Fig. 7. It is found to be in a satisfactory agreement to the inverse proportion with horizontal asymptote correlation, such as that provided in (3).
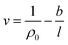 | (3) |
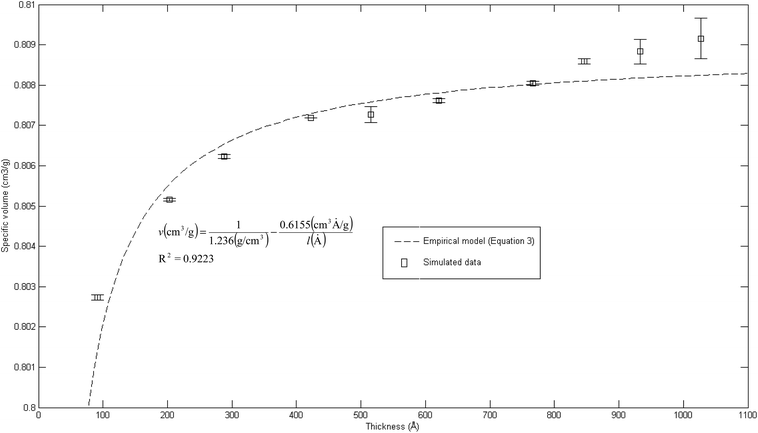 | ||
| Fig. 7 Effect of film thickness on specific volume of the polymeric film, fitted with empirical model (eqn (3)). | ||
In eqn (3), ρ0 = 1.236 g cm−3, is the limiting density of the PSF polymer while b = 0.6155 cm3. Å g−1 corresponds to a material constant that characterizes the sensitivity of thickness to relaxation of the polymer chains.
According to the model, an increment in specific volume with film thickness is especially apparent at smaller dimensions when the surface effect plays a more pivotal role to enhance relaxation of polymeric chains and mobility of free volumes to the free surface.78 Nonetheless, the densification effect at thinner structure levels with an increment in film thickness is attributed to a larger distance between the free surface and polymeric chains. In addition, a larger number of molecules in a bigger structure also contribute to greater interacting forces and spatial restrictions that refrain effective packing of a polymeric chain.
A similar experimental observation was reported by Shishatskii et al. who studied the effect of thickness to measured laboratory density of polymers, e.g., PVTMS and PTMSNB, albeit at a much higher dimension in a micrometer scale.71 The satisfactory quantification describing impact of thickness to specific volume of a polymeric film between a simulated structure and actual experimental observation demonstrates the applicability of current molecular simulation procedures to generate PSF polymeric membranes of varying thicknesses, which can be applied in further analyses to study the effect of membrane thickness on physical properties. Nonetheless, observation of greater simulated densities as compared to predicted values at thicker polymeric films, typically within dimensions of ∼900 Å and ∼1000 Å, suggests that diminishing the surface effect progresses at a lower rate. This reckoning can be reasoned by the layer to layer methodology used to construct polymeric structures, whereby inherent deviations in smaller structures that form the basis for simulation were carried over to constitute larger uncertainties. This reasoning was supported via larger standard deviations observed in the ∼900 Å and ∼1000 Å polymeric membranes, which urged further research in future work to verify the applicability and limitations of the methodology, particularly in larger structures (>1000 Å). To preliminarily verify accuracy of the layer to layer methodology, a ∼300 Å structure was created via combination of the ∼100 Å polymeric structures created in previous sections (e.g. ∼300 Å = ∼100 Å + ∼100 Å + ∼100 Å), while being subjected to a similar molecular treatment protocol like the ∼900 Å and ∼1000 Å films. The evolution throughout MD is provided in Fig. S5 in the ESI.† It is seen that the structure converges to an approximate fixed value albeit at a longer simulation time (∼800 ps) as compared to a structure created via conventional SCMUF methodology; this can be rationalized through greater inhomogeneity inherent through combination of several independent layers. Similarly, the structure exhibits alterations, such as increments in density and reduction in non-bonded and potential energy, as well as convergence to final film thickness, such as that explained in Section 3.1. In the same manner, the amount of fluctuation decreases after the 1st cycle NPT-NVT molecular treatment, which justifies that the molecular structure has attained its equilibration state, typically in the 2nd NPT cycle. The final molecular structure density created through layer to layer methodology is 1.2401 g cm−3 in 288.4 Å polymeric films, which is in good accordance to that created via conventional methodology with density of 1.2403 g cm−3 in a 287.8 Å thick structure.
3.2 Glass transition temperature
In order to further evaluate characteristics of the developed PSF polymeric membranes, glass transition temperature is another important property to be elucidated since it characterizes transitional and relaxation changes in a polymer. As highlighted earlier, this property has been widely reported to be dependent on thickness of a polymer in previously published literature, which serves as an add-on to validate the accuracy of simulated structures. The simulation procedures as outlined in Section 2.2.2 were employed in order to independently compute Tgs of PSF polymeric membranes with varying thicknesses. Variations in specific volume versus temperature for PSF polymeric membranes at ∼100 Å, ∼500 Å and ∼1000 Å were plotted and are provided as examples in Fig. 8.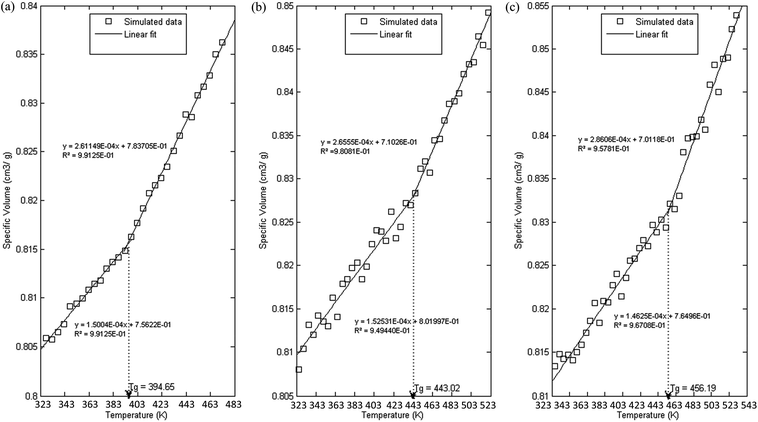 | ||
| Fig. 8 Specific volume versus temperature for PSF polymeric membranes of (a) 100 Å, (b) 500 Å and (c) 1000 Å. | ||
As can be seen from Fig. 8, all the polymeric membranes experience similar behavior with changes in temperature regardless of the thickness. Initially, the specific volume increases linearly with an increment in temperature, and then shows an abrupt alteration in the value before continuing to embark in another linear region. Change in linear relationship is demonstrated through the difference in slope between the two curves, whereby the first at lower temperature is representative of the glassy state region, while the latter describes the rubbery state. The point at which the glassy and rubbery linear correlation meet to form an intercept provides a graphical representation of the glass transition temperature, Tg. The simulated behavior is consistent with the experimental observation reported by Zoller et al., who investigated pressure–temperature–volume relationships in bulk PSF over a wide range of operating conditions.79
It is found that with an increment in thickness of a PSF polymeric membrane, at the same temperature, the specific volume is at a higher value due to lower structural density as explained in the previous section. The intersection between the glassy and rubbery state is also shifted towards larger values, contributing to a larger glass transition temperature, Tg, in thicker PSF polymeric membranes. In other words, the glass transition evolution does not occur at the same specific volume, which is consistent with a recent experimental observation by Huang & Roth that examined the temperature-dependent specific volume of supported polystyrene with film thickness.80 In addition, there is generally also a reduced difference between the liquid- and glassy-state slopes in a thinner film as compared to its bulker counterpart, indicating a reduction in the strength of glass transition upon nanoconfinement, a behavior also seen in previously published literature by Kawana & Jones and Ellison & Torkelson.81,82
The plot of glass transition temperatures versus PSF membrane thickness is provided in Fig. 9.
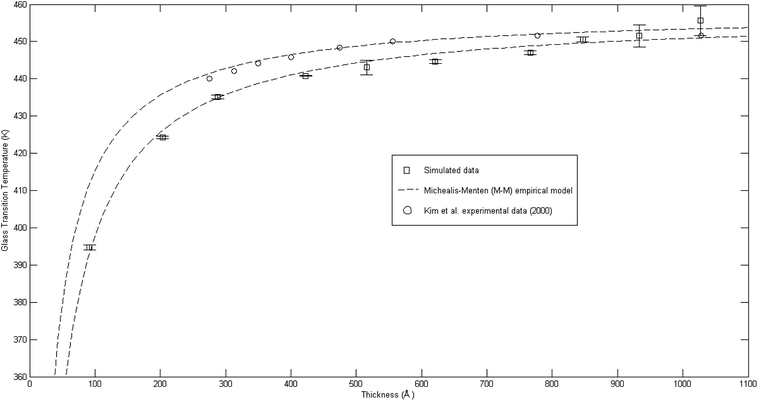 | ||
Fig. 9 Comparison of glass transition temperatures between simulated data (□), Kim et al. (2000) experimental data (○),67 and Michealis–Menten empirical model prediction (![[dash dash, graph caption]](https://www.rsc.org/images/entities/char_e091.gif) ). ). | ||
As seen from Fig. 9, the glass transition temperature, Tg, demonstrates a thickness dependent characteristic, whereby it increases with increments in the film thickness, which is in good agreement with the trend reported by previous works describing glass transition temperatures in polymers.54 The Tg depression is found to be substantially perceptible in the thinner polymeric films, typically those beneath 600 Å, while the glass transition temperature increases asymptotically with increments in the film thickness. Keddie et al. and Forrest et al. also established findings via experimental observation that reduction in Tg was exhibited in free standing polystyrene (PS), poly (methyl methacrylate) (PMMA) on gold-coated silicon, and PS on hydrogen-terminated silicon surfaces for film thicknesses below 600 Å.83–86 It can be depicted that a pattern seems to follow the form of growth with saturation, which can be described via the Michealis–Menten (M–M) function, such as that provided in (4).
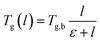 | (4) |
In expression (4), Tg(l) is the thickness-dependent glass transition temperature, Tg,b characterizes the bulk glass transition temperature, l is thickness of the polymeric film, and ε is a material constant that describes the function growth saturation rate.
In order to further validate accuracy of the simulated PSF polymeric structures, the results were compared to published experimental glass transition temperatures at different thicknesses by Kim et al.67 It is found that the simulated data demonstrates a similar trend to that published by Kim et al., which confirms the Michealis–Menten (M–M) correlation to quantify the dependency of glass transition temperature with respect to thickness. The parameters to fit the Michealis–Menten (M–M) empirical model for both the simulated and Kim et al. (2000) experimental data are summarized in Table 2.
| Polysulfone system | Tg,b (K) | ε (Å) |
|---|---|---|
| Kim et al. experiment67 | 458.0 | 10.30 |
| Simulated structure | 457.6 | 15.02 |
| Percentage deviation (%) | −0.09 | 45.83 |
As depicted in Table 2, the bulk glass transition temperature, Tg,b, for both conditions are in good agreement with one another, and also published values for PSF polymer79 with percentage deviation of less than 0.1%, which demonstrated high applicability of this correlation. On the other hand, deviation has been observed between the ε values of simulated and experimental data; these characterize the strength and sensitivity of a specific material to depression of glass transition temperature, whereby simulated structures generally demonstrate an enlarged effect in comparison to experimental results by Kim et al. through larger ε (percentage deviation ∼ 46%). The relatively higher percentage difference in the ε physical parameter between a simulated and experimental observed condition can be rationalized through their small values, whereby a small deviation is expected to amplify the percentage error, and the nature of testing conditions. It has been reported that there existed a Si substrate as support for the fabricated PSF polymeric films in Kim et al. (2000) experimental work, in which the interaction between substrate and polymeric film slightly retards the mobility of polymeric chains, as compared to simulated PSF membranes with free surfaces. This contention was supported by Kim et al., who highlighted presence of the interaction between polymer and substrate but confirmed that it is not large enough to affect the glass transition behavior since the reduction with decreasing thickness still persists. Another reason can be possibly attributed to the limitation in MD time scale, as explained earlier, that contributes to the observed deviation. Nevertheless, the consistent behavior between simulated and experimentally observed phenomena provides satisfactory justification that the developed MD approach is a reasonable procedure to construct PSF membranes of different thicknesses. In addition, a difference between experimental and simulation data in a quantitative manner emphasizes that polymeric chains within ultrathin films with free surfaces exhibit enhanced relaxation (depressed glass transition temperature when the polymer undergoes transition from the rubbery to glassy state) in comparison to its counterpart with support, which was usually employed on a laboratory scale to grow ultrathin films. The deviations thereafter highlighted the importance of molecular simulation work, whereby the elucidation of a polymeric film can be done independently without interference from any specific support, which is a limitation required in experimental conditions and has been demonstrated to retard polymeric relaxation.
3.3 Free volume
Fig. 10 depicts some examples of simulated cells for pure PSF with varying membrane thicknesses (e.g. ∼100 Å, ∼500 Å and ∼1000 Å).As shown in Fig. 10, grey indicates the occupied region while blue characterizes those of the free space. The ratio of blue to grey area increases with increments in film thickness, which reflects the rise in existence of free volume, with the area of free volume in the order of: ∼100 Å < ∼200 Å < ∼300 Å < ∼400 Å < ∼500 Å < ∼600 Å < ∼700 Å < ∼800 Å < ∼900 Å < ∼1000 Å. This phenomenon has been rationalized through enhanced mobility of PSF polymeric chains in the vicinity of a free surface within a thinner structure to constitute denser membranes, as explained in Section 3.1; this further contributes to less free space within the membrane. A similar observation has been reported in work by Wang et al., whereby free volume in polyimide membrane decreases with increments in membrane density.87
By employing the Connolly Surface module in Materials Studio, the occupied, free, and total volume of each PSF slab with different thicknesses are conveniently computed; these were adopted to calculate FFV (MS), such as those summarized in Table 3.
| Thickness (Å) | Occupied volume, v0 (Å3) | Free volume, vf (Å3) | Total volume, vg (Å3) | FFV (MS) | FFV (Bondi's) |
|---|---|---|---|---|---|
| ∼100 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 837.75 837.75 |
3769.25 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 607.00 607.00 |
0.1597 | 0.14005 |
| ∼200 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 528.68 528.68 |
7554.26 | 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 082.94 082.94 |
0.1676 | 0.14263 |
| ∼300 | 59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 121.78 121.78 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 991.49 991.49 |
71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 113.26 113.26 |
0.1686 | 0.14379 |
| ∼400 | 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 676.24 676.24 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 268.54 268.54 |
94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 944.78 944.78 |
0.1713 | 0.14483 |
| ∼500 | 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 279.73 279.73 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 393.14 393.14 |
118672.87 | 0.1718 | 0.14490 |
| ∼600 | 117782.67 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 544.37 544.37 |
142327.03 | 0.1725 | 0.14525 |
| ∼700 | 137366.74 | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 938.65 938.65 |
166305.39 | 0.1740 | 0.14570 |
| ∼800 | 156853.16 | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 380.19 380.19 |
190233.35 | 0.1755 | 0.14611 |
| ∼900 | 175959.61 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 690.83 690.83 |
213650.43 | 0.1764 | 0.14658 |
| ∼1000 | 198267.53 | 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 722.55 722.55 |
240990.08 | 0.1773 | 0.14693 |
In addition to those, FFV (Bondi) was computed and tabulated in Table 3 as well to provide comparisons with FFV (MS). FFV deduced from Bondi's manner demonstrates a remarkably similar trend with thickness as the reported thickness dependence of FFV found through Materials Studio, which confirms applicability of the methodology. In short, the FFVs demonstrate an increment with film thickness, with a rise typically apparent in thinner PSF membranes, while the increment slows at higher dimensions due to deterioration of the free surface effect as explained earlier. The good accordance in trending stimulates further adaptation of the methodology to determine quantitative analysis of polymeric membrane free volume in material mathematical modelling in future work.
3.4 Cavity distribution
As highlighted earlier in Section 1.0, since the transport phenomenon of penetrants within a polymeric membrane is dependent upon the empty space phase of the material, it is essential to elucidate cavity size distributions, which act as routes for channeling of specific gas molecules. The cavity size distribution was calculated according to the CESA algorithm as highlighted in Section 2.2.4 since it provides an alternative means for examining the effect of thickness on cavity characteristics. Fig. 11 shows the computed cavity size in histogram and cumulative distribution for each PSF membrane thickness.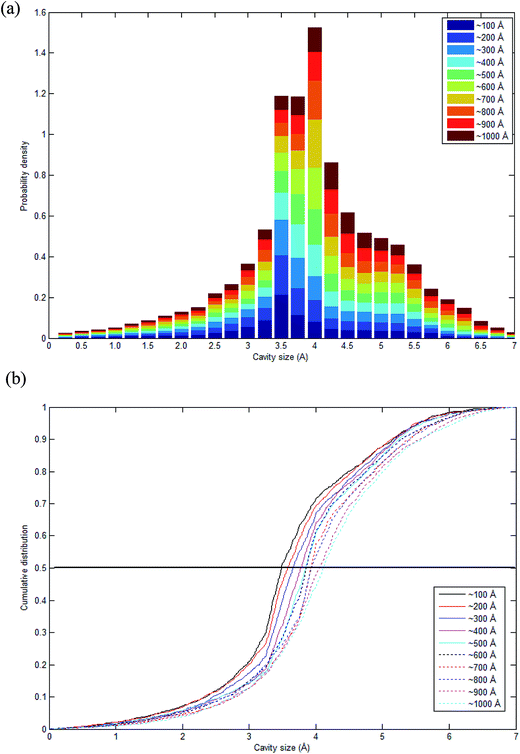 | ||
| Fig. 11 Schematic representation of (a) stacked histogram and (b) cumulative size distribution of cavity size in PSF polymeric membranes of varying thicknesses. | ||
The cavity size ranges between 0 to 7 Å, which is in good accordance with previous molecular simulation results reported by Wang et al.29 and Golzar et al.31 for bulk PSF membrane. It is seen from Fig. 11(a) that the cavity size distribution is shifted towards a larger size with increments in the membrane thickness. For instance, the majority of cavity sizes within a ∼100 Å membrane, which are found within a 3.25–3.5 Å range, were reallocated to a larger range of 4–4.25 Å in ∼1000 Å PSF polymeric film. In summary, a cavity diameter with the highest probability density has been found in a larger size when correlated to the membrane thickness. Another spatial parameter, which presents the characteristics of cavities in a polymer structure, is the average cavity size, x, which was computed based on (5), and further summarized in Table 4.
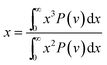 | (5) |
| Thickness (Å) | Average cavity size (Å) |
|---|---|
| ∼100 | 3.62 (±1.10) |
| ∼200 | 3.66 (±1.10) |
| ∼300 | 3.75 (±1.08) |
| ∼400 | 3.84 (±1.06) |
| ∼500 | 3.88 (±1.08) |
| ∼600 | 3.90 (±1.08) |
| ∼700 | 3.98 (±1.06) |
| ∼800 | 4.00 (±1.10) |
| ∼900 | 4.08 (±1.11) |
| ∼1000 | 4.13 (±1.12) |
In eqn (5), x is the cavity size and P(v) is the probability distribution obtained from CESA. As seen in Table 4, through increments in the membrane thickness, the average cavity size also exhibits increments since a majority of the cavities are found at larger dimensions in comparison to their thinner counterparts.
In order to quantitatively compare the cavity size distribution of PSF polymeric films with varying thicknesses, the cumulative distribution was evaluated, such as that provided in Fig. 11(b). As is seen from the figure, cumulative distributions for thicker PSF polymeric membranes are moved to larger cavity sizes. In the ∼100 Å PSF film, 50% of the cavities exceed those of ∼3.5 Å in diameter, and 50% of the cavities in the ∼500 Å PSF slab surpass ∼3.75 Å, whereas in the ∼1000 Å polymeric membrane, half of the cavity diameters go beyond that of ∼4.25 Å. As depicted in Fig. 10, the blue areas in the ∼100 Å are agglomerated into smaller individual cavities, while those in the thicker PSF polymeric membranes in ∼500 Å and ∼1000 Å are found to inherit larger and more continuous characteristics. The observation of larger void elements in bulker PSF polymeric membranes is rationalized through lower density, which indicates that the polymeric chains are packed less efficiently and more sparsely with respect to one another, subsequently contributing to formation of bigger cavity sizes.
4. Conclusion
The objective of this study is to investigate effect of thickness to morphology and physical properties in ultrathin polymeric films, typically those upon confinement. In this work, a Soft Confining Methodology for Ultrathin Film (SCMUF) was conducted in Materials Studio 8.0 simulation software to incorporate the influence of finite size effect upon confinement in molecular dynamics simulations. This is the first instance that a molecular system, which resembles its actual size in the thickness dimension, has been simulated in Materials Studio to construct ultrathin polysulfone membranes at varying finite sizes (<1000 Å). Subsequently, the framework within Materials Studio was utilized to elucidate the effect of thickness upon confinement to physical properties of a polymeric material. The density, glass transition temperature, free volume, and cavity distribution were simulated to elucidate the nature of thickness-dependent confinement towards characteristics and relaxation of polymeric membranes. We showed the effect of thickness to the aforementioned parameters is in satisfactory accordance with those obtained from actual laboratory observations. It was found that via increments in the polymeric molecules within bulker structures, the fraction of interfacial layer that characterizes enhanced structural relaxation and mobility decreases, which subsequently results in a rise in the end-to-end distance. This poses higher resistance to polymer segmental motion throughout the molecular simulation process, contributing to lower structural density, higher glass transition temperature, higher free volume, and higher cavity sizes. The remarkable agreement with actual experimental observations and intuitive phenomenological explanation underlying the effect of thickness to characteristics of ultrathin films at a nanoscale dimension demonstrated that molecular simulation methodology is of sufficient reliability to simulate ultrathin polymeric membranes of varying thicknesses. Overall, the applicability of simulation methodology suggests that it can be applied extensively in future work to design any ultrathin membrane systems to predict their physical properties and separation performance more accurately. In addition, this approach can also be employed to study the distinct behavior of ultrathin membrane films in various thickness-dependent phenomena, such as plasticization and physical aging, to substantiate any further interpretations. This is important because the question of these size-dependent characteristics remains open and has to be resolved due to impact of these non-ideal effects on the separation mechanism of membranes. In previous studies, it has been reported that a smaller dense polymeric membrane thickness can be rationalized as a smaller resistance through a barrier that controls the relative rate of transport of various species; this contributes to larger permeation to remove impurities under a smaller membrane area requirement. Nonetheless, it is found that although a thinner ultrathin polymeric membrane inherits a higher permeance characteristic, making it a highly sought after structure as compared to its bulk counterpart by exhibiting a higher driving force and hence smaller area requirement, a thinner membrane also demonstrates the drawback of accelerated relaxation. This has been demonstrated through depressed glass transition temperature in the present work, further contributing to larger density, lower free volume, and cavity sizes. Therefore, the findings of our present study suggest that membrane thickness in ultrathin films is required to be optimized to improve separation efficiency through lower membrane barrier resistance and higher void spaces that form the channels for transport of a specific gas penetrant.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work is done with the support from Universiti Teknologi PETRONAS.References
- H. J. Jung, S. H. Han, Y. M. Lee and Y.-K. Yeo, Korean J. Chem. Eng., 2011, 28, 1497–1504 CrossRef CAS.
- S. S. M. Lock, K. K. Lau, F. Ahmad and A. M. Shariff, Int. J. Greenhouse Gas Control, 2015, 36, 114–134 CrossRef CAS.
- S. S. M. Lock, K. K. Lau and A. M. Shariff, J. Ind. Eng. Chem., 2015, 21, 542–551 CrossRef CAS.
- D. F. Sanders, Z. P. Smith, R. Guo, L. M. Robeson, J. E. McGrath, D. R. Paul and B. D. Freeman, Polymer, 2013, 54, 4729–4761 CrossRef CAS.
- X.-Y. Zhang and Y.-H. Ding, RSC Adv., 2014, 4, 44214–44222 RSC.
- L. Singh, P. J. Ludovice and C. L. Henderson, Thin Solid Films, 2004, 449, 231–241 CrossRef CAS.
- I. Pinnau and W. J. Koros, J. Appl. Polym. Sci., 1992, 46, 1195–1204 CrossRef CAS.
- R. Datta, S. Dechapanichkul, J. S. Kim, L. Y. Fang and H. Uehara, J. Membr. Sci., 1992, 75, 245–263 CrossRef CAS.
- A. F. Ismail and L. P. Yean, J. Appl. Polym. Sci., 2003, 88, 442–451 CrossRef CAS.
- D. Wang, Z. Wang, L. Wang, L. Hu and J. Jin, Nanoscale, 2015, 7, 17649–17652 RSC.
- S. M. Kozlov, I. Demiroglu, K. M. Neyman and S. T. Bromley, Nanoscale, 2015, 7, 4361–4366 RSC.
- K. E. Gubbins, Y.-C. Liu, J. D. Moore and J. C. Palmer, Phys. Chem. Chem. Phys., 2011, 13, 58–85 RSC.
- K. F. Mansfield and D. N. Theodorou, Macromolecules, 1989, 22, 3143–3152 CrossRef CAS.
- K. Binder, A. Milchev and J. Baschnagel, Annu. Rev. Mater. Sci., 1996, 26, 107–134 CrossRef CAS.
- J. Baschnagel, C. Mischler and K. Binder, J. Phys. IV, 2000, 10, Pr7 Search PubMed.
- C. Mischler, J. Baschnagel, S. Dasgupta and K. Binder, Polymer, 2002, 43, 467–476 CrossRef CAS.
- F. Varnik, J. Baschnagel and K. Binder, Phys. Rev. E, 2002, 65, 021507 CrossRef CAS PubMed.
- K. Kim and R. Yamamoto, Phys. Rev. E, 2000, 61, 1–4 CrossRef.
- J. A. Torres, P. F. Nealey and J. J. de Pablo, Phys. Rev. Lett., 2000, 85, 3221–3224 CrossRef CAS PubMed.
- Y. Nie, Z. Zhou, T. Hao, X. Ye and W. Yang, Macromol. Theory Simul., 2016, 25, 187–195 CrossRef CAS.
- M. Alcoutlabi and G. B. McKenna, J. Phys.: Condens. Matter, 2005, 17, R461–R524 CrossRef CAS.
- G. Adam and J. H. Gibbs, J. Chem. Phys., 1965, 43, 139–146 CrossRef CAS.
- N. Modi, M. Winterhalter and U. Kleinekathofer, Nanoscale, 2012, 4, 6166–6180 RSC.
- R. Lu, Z. Meng, D. Rao, Y. Wang, Q. Shi, Y. Zhang, E. Kan, C. Xiao and K. Deng, Nanoscale, 2014, 6, 9960–9964 RSC.
- S. S. M. Lock, K. K. Lau, I. L. S. Mei, A. M. Shariff and Y. F. Yeong, Procedia Eng., 2016, 148, 855–861 CrossRef CAS.
- P. J. in't Veld, M. T. Stone, T. M. Truskett and I. C. Sanchez, J. Phys. Chem. B, 2000, 104, 12028–12034 CrossRef.
- F. T. Willmore, X. Wang and I. C. Sanchez, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 1385–1393 CrossRef CAS.
- X.-Y. Wang, K. M. Lee, M. T. Stone, I. C. Sanchez and B. D. Freeman, Polymer, 2004, 45, 3907–3912 CrossRef CAS.
- X.-Y. Wang, P. J. in't Veld, Y. Liu, B. D. Freeman and I. C. Sanchez, Polymer, 2005, 46, 9155–9161 CrossRef CAS.
- Y. Jiang, F. T. Willmore, D. Sanders, Z. P. Smith, C. P. Ribeiro, C. M. Doherty, A. Thorton, A. J. Hill, B. D. Freeman and I. C. Sanchez, Polymer, 2011, 52, 2244–2254 CrossRef CAS.
- K. Golzar, S. Amjad-Iranagh, M. Amani and H. Modarress, J. Membr. Sci., 2014, 451, 117–134 CrossRef CAS.
- A. Barnard, C. M. Li, R. Zhou and Y. Zhao, Nanoscale, 2012, 4, 1042–1043 RSC.
- H. Liu, Y. Li, W. E. Krause, O. J. Rojas and M. A. Pasquinelli, J. Phys. Chem. B, 2012, 116, 1570–1578 CrossRef CAS PubMed.
- http://accelrys.com/products/materials-studio/index.html.
- A. Chremos, E. Glynos and P. F. Green, J. Chem. Phys., 2015, 142, 044901 CrossRef PubMed.
- A. Chremos and J. F. Douglas, J. Chem. Phys., 2015, 143, 111104 CrossRef PubMed.
- A. Jabbarzadeh, J. D. Atkinson and R. I. Tanner, Macromolecules, 2003, 36, 5020–5031 CrossRef CAS.
- M. E. Tuttle, Structural Analysis of Polymeric Composite Materials, CRC Press, Boca Raton, 2nd edn, 2012 Search PubMed.
- K. C. Ludema, in The Role of Coatings in the Prevention of Mechanical Failures, ed. T. R. Shives and W. A. Willard, National Bureau of Standards Special Publication, Washington, 2010 Search PubMed.
- S. H. Jain, K. Murata and T. Anazawa, Macromol. Chem. Phys., 2003, 204, 893–902 CrossRef CAS.
- A. Malevanets and J. M. Yeomans, Europhys. Lett., 2000, 52, 231 CrossRef CAS.
- E. A. Jordan, R. C. Ball, A. M. Donald, L. J. Fetters, R. A. L. Jones and J. Klein, Macromolecules, 1988, 21, 235–239 CrossRef CAS.
- J. M. Kim and C. Baig, J. Chem. Phys., 2016, 144, 081101 CrossRef PubMed.
- S. Neyertz and D. Brown, Macromolecules, 2004, 37, 10109–10122 CrossRef CAS.
- T. R. Cuthbert, N. J. Wagner and M. E. Paulaitis, Macromolecules, 1997, 30, 3058–3065 CrossRef CAS.
- T. R. Cuthbert, N. J. Wagner, M. E. Paulaitis, G. Murgia and B. D'Aguanno, Macromolecules, 1999, 32, 5017–5028 CrossRef CAS.
- C. Forrey, D. M. Saylor, J. S. Silverstein, J. F. Douglas, E. M. Davis and Y. A. Elabd, Soft Matter, 2014, 10, 7480–7494 RSC.
- Y. Zhou, Doctor of Philosophy, Texas A&M University, 2014 Search PubMed.
- L. Meyer, in Advances in Chemical Physics, ed. P. Stuart and A. Rice, John Wiley & Sons, Bristol, 1969, vol. 16, p. 346 Search PubMed.
- A. J. Eatwell and B. L. Smith, Philos. Mag., 1961, 6, 461–463 CrossRef CAS.
- D. R. Sears and H. P. Klug, J. Chem. Phys., 1962, 37, 3002–3006 CrossRef CAS.
- J. Azadmanjiri, C. C. Berndt, J. Wang, A. Kapoor and V. K. Srivastava, RSC Adv., 2016, 6, 109361–109385 RSC.
- J. Bicerano, in Prediction of Polymer Properties, CRC Press, 2002 Search PubMed.
- J. H. Kim, J. Jang and W.-C. Zin, Langmuir, 2001, 17, 2703–2710 CrossRef CAS.
- M. Scott Shell, P. G. Debenedetti and A. Z. Panagiotopoulos, Fluid Phase Equilib., 2006, 241, 147–154 CrossRef.
- T. G. Fox Jr. and P. J. Flory, J. Appl. Phys., 1950, 21, 581–591 CrossRef.
- C. S. Stevenson, J. G. Curro and J. D. McCoy, J. Chem. Phys., 2017, 146, 203322 CrossRef PubMed.
- C. Li, G. A. Medvedev, E.-W. Lee, J. Kim, J. M. Caruthers and A. Strachan, Polymer, 2012, 53, 4222–4230 CrossRef CAS.
- R. P. White and J. E. G. Lipson, Phys. Rev. E, 2011, 84, 041801 CrossRef PubMed.
- D. Chen and H. G. Zachmann, Polymer, 1991, 32, 1612–1621 CrossRef CAS.
- M. Mohammadi, H. Fazli, M. Karevan and J. Davoodi, Eur. Polym. J., 2017, 91, 121–133 CrossRef CAS.
- J. Ahn, W.-J. Chung, I. Pinnau and M. D. Guiver, J. Membr. Sci., 2008, 314, 123–133 CrossRef CAS.
- M. A. A. R. Quddus, O. J. Rojas and M. A. Pasquinelli, Biomacromolecules, 2014, 15, 1476–1483 CrossRef CAS PubMed.
- G. Shen, Q. Mei, V. B. Prakapenka, P. Lazor, S. Sinogeikin, Y. Meng and C. Park, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6004–6007 CrossRef CAS PubMed.
- A. Bondi, Physical properties of molecular crystals, liquids and glasses, John Wiley & Sons, New York, 1968 Search PubMed.
- D. W. Van Krevelen, in Properties of Polymers (Third, completely revised edition), Elsevier, Amsterdam, 1997, pp. 71–107 Search PubMed.
- J. H. Kim, J. Jang and W.-C. Zin, Langmuir, 2000, 16, 4064–4067 CrossRef CAS.
- S. Peter, H. Meyer and J. Baschnagel, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 2951–2967 CrossRef CAS.
- S. Kim, L. Chen, J. K. Johnson and E. Marand, J. Membr. Sci., 2007, 294, 147–158 CrossRef CAS.
- B. A. Rozenberg, V. I. Irzhak and L. M. Bogdanova, in Relaxation in Polymers, ed. M. Pietralla and W. Pechhold, Steinkopff, Darmstadt, 1989, pp. 187–197 Search PubMed.
- A. M. Shishatskii, Y. P. Yampol'skii and K. V. Peinemann, J. Membr. Sci., 1996, 112, 275–285 CrossRef CAS.
- P. H. Pfromm, in Materials Science of Membranes for Gas and Vapor Separation, John Wiley & Sons, Ltd, 2006, pp. 293–306 Search PubMed.
- S. Cheng, B. Carroll, V. Bocharova, J.-M. Carrillo, B. G. Sumpter and A. P. Sokolov, J. Chem. Phys., 2017, 146, 203201 CrossRef PubMed.
- R. A. L. Jones, Curr. Opin. Colloid Interface Sci., 1999, 4, 153–158 CrossRef.
- C. B. Roth and J. R. Dutcher, J. Electroanal. Chem., 2005, 584, 13–22 CrossRef CAS.
- H. K. Nguyen, D. Prevosto, M. Labardi, S. Capaccioli, M. Lucchesi and P. Rolla, Macromolecules, 2011, 44, 6588–6593 CrossRef CAS.
- S. S. M. Lock, K. K. Lau, A. M. Shariff and Y. F. Yeong, J. Cleaner Prod., 2017, 162, 914–937 CrossRef CAS.
- T. Alfrey, G. Goldfinger and H. Mark, J. Appl. Phys., 1943, 14, 700–705 CrossRef CAS.
- P. Zoller, J. Polym. Sci., Polym. Phys. Ed., 1978, 16, 1261–1275 CrossRef CAS.
- X. Huang and C. B. Roth, J. Chem. Phys., 2016, 144, 234903 CrossRef PubMed.
- S. Kawana and R. A. L. Jones, Phys. Rev. E, 2001, 63, 021501 CrossRef CAS PubMed.
- C. J. Ellison and J. M. Torkelson, Nat. Mater., 2003, 2, 695–700 CrossRef CAS PubMed.
- J. L. Keddie, R. A. L. Jones and R. A. Cory, Faraday Discuss., 1994, 98, 219–230 RSC.
- J. L. Keddie, R. A. L. Jones and R. A. Cory, Europhys. Lett., 1994, 27, 59 CrossRef CAS.
- J. A. Forrest, K. Dalnoki-Veress, J. R. Stevens and J. R. Dutcher, Phys. Rev. Lett., 1996, 77, 2002–2005 CrossRef CAS PubMed.
- J. A. Forrest, K. Dalnoki-Veress and J. R. Dutcher, Phys. Rev. E, 1997, 56, 5705–5716 CrossRef CAS.
- L. Wang, R. S. Dumont and J. M. Dickson, RSC Adv., 2016, 6, 63586–63596 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra07277e |
| This journal is © The Royal Society of Chemistry 2017 |