Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effect of paramagnetic species on T1, T2 and T1/T2 NMR relaxation times of liquids in porous CuSO4/Al2O3
Carmine D'Agostino *a,
Pierre Bräuera,
Pavida Charoen-Rajaparkb,
Matthew D. Croucha and
Lynn F. Gladdena
*a,
Pierre Bräuera,
Pavida Charoen-Rajaparkb,
Matthew D. Croucha and
Lynn F. Gladdena
aDepartment of Chemical Engineering and Biotechnology, University of Cambridge, Philippa Fawcett Drive, Cambridge, CB3 0AS, UK. E-mail: cd419@cam.ac.uk; Tel: +44 (0)1223 335245
bHarvard School of Engineering and Applied Sciences (SEAS), Harvard University, 29 Oxford St, Cambridge, MA 02138, USA
First published on 20th July 2017
Abstract
The presence of paramagnetic species has a well-known strong effect on the NMR relaxation times of liquids. This is well-known in solution but it is also the case when liquids are confined in porous materials containing paramagnetic impurities deposited over solid surfaces, such as ions of certain metals. In the literature only a few studies have been conducted on this subject. In particular, the effect of paramagnetic impurities on the ratio of relaxation times, T1/T2, has not been fully elucidated and the few published results are somehow still fragmentary and in some cases inconsistent. Yet, a clear understanding of this behaviour is crucial in order to further extend and implement NMR relaxation techniques to study surface interactions in porous materials, in particular porous catalysts, where paramagnetic species can be present as residual impurities from the catalyst manufacturing processes or as a part of the active catalytic components. In this work, the effect of small amounts of paramagnetic species deposited over the surface of porous solids on NMR relaxation times has been investigated for a variety of CuSO4-doped alumina samples, in order to understand the behaviour of T1, T2 and particularly the ratio T1/T2 as a function of paramagnetic species content. The results show that the single values of the fluid relaxation times are strongly affected by the presence of paramagnetic impurities deposited over the solid surface, with the relaxation rates 1/T1 and 1/T2 being proportional to the content of paramagnetic ions, as expected from theory; conversely, the T1/T2 ratio does not change significantly. This is in line with some theoretical considerations and some previous results reported in the literature, suggesting that whilst single values of T1 and T2 are strongly affected by the presence of paramagnetic relaxation sinks, the T1/T2 ratio is to a large extent independent of their concentration at the surface, whilst it depends on changes in molecular mobility due to changes in strength of surface interactions, which affect the surface correlation and residence times.
Introduction
In the past decades NMR relaxation time analysis has been a tool gaining much attention, particularly due to its ability to investigate and explore molecular dynamics of molecules confined inside porous materials. Its applications range from determination of pore size distribution,1,2 investigation of dynamic changes in porous structures,3,4 surface interactions of guest molecules in construction materials,5,6 oil-bearing rocks7,8 and very recently heterogeneous catalysts.9–13 Recently, it has also been shown that the ratio of the longitudinal relaxation time to the transverse relaxation time, T1/T2, can be related to an energy of surface interactions and is a useful indicator to quantify the strength of surface interaction in porous catalysts.11,12NMR T1 and T2 relaxation is caused by fluctuations in local magnetic fields, which are modulated by rotational and translational motions.11 Several sources contribute to NMR relaxation, most notably spin–spin dipolar interactions, spin–electron paramagnetic interactions, chemical shift anisotropy, which may be significant in solids, and spin rotation, the latter significant for gaseous species.14,15 Here, we are primarily concerned with the case of liquid species inside highly mesoporous materials, that is, with a high surface-to-volume ratio, whereby surface relaxation dominates the measured relaxation times.5 In the case of liquids in porous materials used in catalytic applications, such as porous metal oxide supports, the main source of local fields is that caused by spin–spin dipolar interactions, e.g., hydrogen bonding of molecules with the hydroxylated surface, where two nuclear spins, or dipoles, are involved. However, the catalyst manufacturing process may lead to the presence of small amounts of impurities, which are paramagnetic in nature, e.g., ions with unpaired electrons. In some cases, such species can also be part of the active catalytic components, i.e., used as promoters or doping agents. Unpaired electrons generate a magnetic moment that is much greater than that of the proton; hence, these paramagnetic species can be a particularly efficient source of relaxation, affecting significantly the NMR relaxation times of liquids even when present at low concentrations, through electron–spin interactions, which is similar in nature to the dipole–dipole interaction between nuclear spins but with a much greater coupling constant.16
In order to interpret properly NMR relaxation time measurements of liquids in porous catalysts and infer the strength of surface interaction from their values, it becomes therefore important to understand how such paramagnetic species affect the single relaxation times T1 and T2 but most importantly T1/T2, which can be considered an indicator of strength of surface interactions.12,17 Based on theoretical considerations18 and some previous experimental findings,19 the presence and concentration of paramagnetic species have a significant effect on the single values of T1 and T2. In particular, the theory predicts that the observed longitudinal, 1/T1, and transverse, 1/T2, relaxation rates of fluids in a porous medium will be linearly proportional to the concentration of paramagnetic ions at the solid surface, according to:18
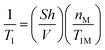 | (1) |
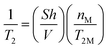 | (2) |
It is clear from eqn (1) and (2) that the ratio T1/T2 is independent on the content of paramagnetic species,7 hence it should not vary, at least in theory, with the content of paramagnetic ions. Changes in T1/T2 will therefore be primarily due to changes in molecular dynamics over the surface, which are taken into account in the T1M and T2M terms,19 affecting T1 and T2 to a different extent,11 which are directly related to the nature of surface interactions. It is noted that changes in T1/T2 can also be caused by molecular diffusion in the presence of strong internal gradients,20–22 which will essentially further affect T2, hence leading to an increase of T1/T2.3 The use of very short echo times and/or recently developed methods20 can correct this effect, hence leading to a T1/T2 ratio that does not depend on the presence of such internal gradients.
The focus of this work is on understanding the behaviour of T1, T2 and particularly the ratio T1/T2 of liquids in the presence of different amounts of the same paramagnetic ions deposited over solid surfaces. According to our knowledge, only a few works on the subject have been reported. Most of the work available in the literature has looked at Fe3+ paramagnetic impurities, for a large part dealing with rocks or construction materials. Bryar et al.23 looked at the effect of Fe3+ paramagnetic species in quartz sand and silica gel samples on the T1 relaxation time of fluids. This study did not, however, report any data on T2; hence, it is not possible to infer the effect of paramagnetic Fe3+ on the T1/T2 ratio. The most notable report on the subject is perhaps that of Foley et al.,19 who studied the effect of paramagnetic species on NMR relaxation of fluids at solid surfaces, using water-saturated calcium silicates powder with known concentrations of iron, Fe3+, or manganese, Mn2+, paramagnetic ions. Their results showed that for manganese doped powder, the single T1 and T2 relaxation times decrease significantly with increasing amount on manganese ions, i.e., 1/T1 and 1/T2 relaxation rates are enhanced by the presence of paramagnetic species. However, both relaxation rates showed a similar slope, indicating that the ratio T1/T2 is independent on the concentration of paramagnetic species, as the theory suggests.5,7,18 However, on the contrary, for the iron-doped samples, in the higher concentration range the T2 value decreases more rapidly than T1, with a slight increase of T1/T2 values, which seems to be attributed to increasing surface interactions with the relaxation sink,24 i.e., changes in molecular dynamics over the surface. It is noted that many data points for the 1/T1 and 1/T2 plots for iron-doped samples have a high degree of scattering, which the authors attributed to uncertainties in the determination of water volume during sample preparation. The change in T1/T2 observed for iron and not for manganese-doped species could also be attributed to the presence of magnetic field gradients rather than amount of paramagnetic species. Indeed, iron-bearing species have been shown to have high internal gradients,3 with an effect on T1 and T2 of fluids in porous materials similar to that reported by Foley and co-workers.19
In summary, most of the work on the effect of paramagnetic species deposited on solid surfaces has been looking at Fe3+ ions, whereby internal gradients may cause an artificial increase in T1/T2; in addition, some results seem to show inconsistencies and studies have mostly focused on rocks and ceramics, whereas materials used in catalyst manufacturing, such as porous metal oxides, have been overlooked.
It is therefore clear that the current knowledge on the subject is still fragmentary and further work would certainly contribute to a better understanding, particularly in terms of improving the analysis and interpretation of NMR relaxation data in porous catalysts. In this work, we have investigated the NMR relaxation time behaviour of liquids inside porous γ-Al2O3 used for catalyst preparation, doped with different amount of paramagnetic CuSO4 salt, as Cu2+, in order to understand how the concentration of paramagnetic species affect the single relaxation times, T1 and T2, and their ratio T1/T2. The aim of this work is to assess the effect of paramagnetic species in porous solid materials used for catalyst preparation and hence to improve the understanding and interpretation of NMR relaxation data in porous catalysts, particularly when the interest is in surface interactions.12
Experimental
Sample preparation
The γ-Al2O3 used for the experiments, referred to as Al2O3 hereafter, was supplied by Johnson Matthey. BET and BJH analysis was carried out in order to obtain the textural properties of the porous oxide, which has an average pore size of 12 nm, a pore volume of 0.52 cm3 g−1 and a surface area 90 m2 g−1. Samples of Al2O3 doped with CuSO4 were prepared with a procedure similar to what has been reported in the literature.25 Al2O3 particles were dried in the oven at 105 °C for 3 h and then added to aqueous solutions of copper(II) sulphate pentahydrate at known composition. The particles were stirred and left within the solutions for at least 24 h. The moist solids were removed from the solution after impregnation and then dried in an oven at 70 °C for 2 h and at 150 °C for further 2 h, stirring several times during the drying process in order to ensure a more homogeneous drying. The actual content of paramagnetic CuSO4 salt inside the Al2O3 particles was estimated by knowing the CuSO4 concentration of the aqueous bulk solution filling the pore space used for the wet impregnation and the pore volume, obtained from BET analysis, of a known amount of solid used for the sample preparation.Magnetic susceptibility measurements
The magnetic susceptibility of each sample was determined using a Sherwood Scientific Mk-1 susceptibility balance. Quoted values are volume susceptibilities in rationalised units, and have been corrected for porosity.NMR experiments
All the NMR experiments were performed on a Bruker Biospin DMX 300 operating at a 1H frequency of 300.13 MHz. NMR relaxation times T1 and T2 were measured using standard inversion recovery and CPMG techniques, respectively.26 In the CPMG pulse sequence, a small echo spacing value of 250 μs was used in order to minimise any possible internal gradient effects.27 The experiments were conducted using 5 mm NMR tubes. Solid samples were prepared by soaking Al2O3 porous particles in 1-octanol, which was used as the probe species, for at least 24 h. The particles were dried on a pre-soaked filter paper in order to remove any excess liquid on the external surface and finally transferred into the NMR tube. To ensure a saturated atmosphere inside the NMR tube, hence minimising errors due to evaporation, a small amount of liquid was placed onto adsorbent filter paper, which was then placed under the cap of the NMR tube. The NMR tube was then sealed with parafilm. It is also noted that the liquid of choice has a relatively high boiling point; hence evaporation during the measurements can be neglected. Indeed, NMR spectra before and after the relaxation experiments were acquired in order to check for any possible signal drop due to evaporation of liquid from the pore space, which was negligible for all samples.Results and discussion
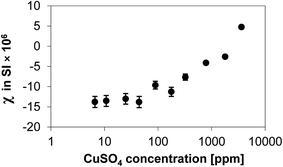
In order to verify the degree of paramagnetism introduced by the deposition of CuSO4 onto the Al2O3 surface, the various CuSO4/Al2O3 samples were characterised by magnetic susceptibility measurements. The results of these measurements are reported in Fig. 1. The plateau at low CuSO4 concentration (<100 ppm) can be assumed to be equal to the susceptibility of the alumina substrate. It can be clearly seen that as the content of CuSO4 increases, the porous solid becomes more paramagnetic in nature, with the values of the volume magnetic susceptibility (measured in SI) becoming positive as the CuSO4 concentration increases. A significant increase can be observed above a concentration of 100 ppm.The values of T1 and T2 for 1-octanol inside the CuSO4/Al2O3 samples are reported in Fig. 2 as a function of CuSO4 dopant concentration. In order to have a clearer comparison between T1 and T2, the results are plotted on both x and y log scale, as also suggested elsewhere in studies on the effect of paramagnetic impurities in highly viscous solutions.28
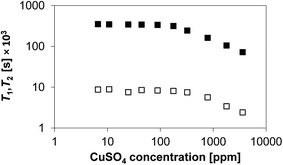 | ||
| Fig. 2 T1 (closed squares) and T2 (open squares) relaxation time values of 1-octanol in CuSO4/Al2O3 samples as a function of CuSO4 concentration. Error bars are too small to be seen. | ||
From Fig. 2 it is clear that both T1 and T2 show a similar trend, with T2 being much shorter than T1. This is expected as 1-octanol is able to interact with the surface via hydrogen bonding, hence a T1/T2 ≫ 1 is expected.13,29 It can be observed that below a concentration of approximately 100 ppm a plateau for T1 and T2 can be observed. Above such concentration, the values of both T1 and T2 start decreasing significantly. This observation ties in with the magnetic susceptibility results shown in Fig. 1, which shows that above the same concentration the samples become significantly more paramagnetic, hence a rapid decrease in relaxation time values is largely expected. Another point to note, by comparing Fig. 1 and 2, is that the relaxation time plateau for both T1 and T2 in Fig. 2 corresponds essentially to the background magnetic susceptibility of the alumina support, as shown in Fig. 1. Therefore, at low CuSO4 concentrations (below 100 ppm) the individual relaxation times are sensitive only to the substrate. This has implications when studying supports and catalysts and suggests that at such low concentrations, the single relaxation times are to a large extent insensitive to metal loading, in this case as CuSO4 salt. It is noted that such low concentrations are likely to be those usually associated to possible impurities that might be present in porous catalytic materials, due to a particular manufacturing process, for example. This is important to consider when using NMR relaxation time analysis to study porous supports, where small amounts of such paramagnetic impurities can be present. This finding also supports and confirms assumptions made in previous work when studying porous solid oxide supports, some of which likely to contain low content of paramagnetic impurities.12
The 1/T1 and 1/T2 relaxation rates are reported in Fig. 3. The data present some degree of scattering at low concentration of CuSO4, which might be due to sample preparation issues, as observed previously when performing similar experiments,19 especially when doping porous solids with tiny amounts of doping agent as in this case. It is however clear that the rates show a direct proportionality with the content of paramagnetic species. This agrees with the Korringa, Seevers and Torrey theory,30 which predicts that single relaxation rates for liquids in porous media, 1/T1 and 1/T2, will be linearly proportional to the concentration of paramagnetic ions at the solid surface.19,30 As expected, an increasing amount of paramagnetic species affects significantly the relaxation rates.
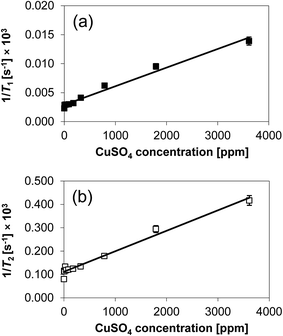 | ||
| Fig. 3 (a) 1/T1 and (b) 1/T2 of 1-octanol in CuSO4/Al2O3 samples as a function of CuSO4 concentration. The solid line is a linear least square fitting to the data. | ||
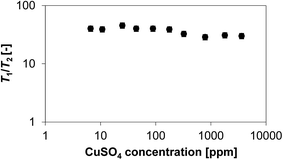
It is now of interest to understand how the amount of paramagnetic species affects the ratio of relaxation times T1/T2. Based on theoretical considerations previously discussed, the main factors affecting this ratio are changes in molecular mobility at surface due to changes in the nature of interaction of the liquid with the surface adsorption sites, i.e., T1/T2 increases with increasing strength of surface interaction,12,17,31 and potentially the presence of internal gradients,3 which also leads to an increase in T1/T2. However, such a ratio should be independent on the amount of paramagnetic centres.7 Fig. 4 shows the plot of T1/T2 for 1-octanol in CuSO4/Al2O3 samples as a function of CuSO4 concentration.
It is clear that whilst the increasing amount of paramagnetic CuSO4 affects significantly the single T1 and T2 relaxation times, the ratio T1/T2 is approximately independent on the concentration of CuSO4. This is in line with theoretical predictions and agrees with the data reported by Foley et al.19 on porous materials doped with paramagnetic manganese ions. It is noted that the T1/T2 ratio shows slightly lower values at higher amounts of paramagnetic species. This effect is nowhere close in magnitude to that observed for single values of T1 and T2. The slightly decreasing trend in T1/T2 with increasing CuSO4 concentration also excludes internal gradient effects, otherwise an opposite trend should be observed, i.e., T1/T2 should increase.3 Such small variations in T1/T2 could be attributed to changes in the surface properties due to the deposition of the salt, which may affect the adsorption strength of the liquid over the surface, hence changing the mobility at the surface.4
In summary, the results shown here show that the content of paramagnetic species deposited over the surface has a significant effect on single T1 and T2 relaxation times, and corresponding relaxation rates, of liquids inside porous materials. However, both relaxation times are affected in a similar fashion; hence their ratio does not vary significantly. This is in line with the theory and with previous experimental findings. The small variations in the T1/T2 ratio are attributed to changes in molecular mobility over the surface induced by interactions of the probe molecules with the surface adsorption sites.
Conclusions
The effect of paramagnetic impurities over porous catalyst support on NMR relaxation times has been investigated using liquid-saturated CuSO4/Al2O3 samples, in order to understand the behaviour of T1, T2 and the ratio T1/T2 as a function of paramagnetic species content. Whilst single values of relaxation times, T1 and T2, are strongly affected by the presence of paramagnetic impurities, with the relaxation rates 1/T1 and 1/T2 being proportional to the content of paramagnetic ions, the ratio does not change significantly with increasing content of paramagnetic species, experiencing only a slight decrease. Such variations are much smaller than those observed for the single values of T1 and T2 and are attributed to changes in molecular mobility due to changes in surface interaction. This agrees with theoretical considerations and with some previous results reported in the literature, suggesting that the T1/T2 ratio is independent of the concentration of paramagnetic sinks at the surface and is affected by changes in molecular mobility due to surface interactions affecting the surface residence time. The results presented here clarify previous inconsistencies reported in the literature and contribute to improve the understanding of NMR relaxation techniques applied to heterogeneous catalysts and hence aid NMR relaxation times analysis and interpretation on porous materials used for catalytic applications.Acknowledgements
Carmine D'Agostino is grateful to Wolfson College, Cambridge. Jonathan Mitchell is acknowledged for useful discussion on the work.References
- X. N. Li, Y. Q. Li, C. Chen, D. W. Zhao, X. J. Wang, L. Zhao, H. Shi, G. H. Ma and Z. G. Su, J. Porous Mater., 2015, 22, 11–20 CrossRef CAS.
- O. Mohnke and B. Hughes, Water Resour. Res., 2014, 50, 5309–5321 CrossRef.
- C. Casieri, F. De Luca, L. Nodari, U. Russo, C. Terenzi and V. Tudisca, J. Appl. Phys., 2012, 112, 084904 CrossRef.
- K. M. Song, J. Mitchell, H. Jaffel and L. F. Gladden, J. Mater. Sci., 2010, 45, 5282–5290 CrossRef CAS.
- P. J. McDonald, J. P. Korb, J. Mitchell and L. Monteilhet, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 9 Search PubMed.
- P. J. McDonald, J. Mitchell, M. Mulheron, P. S. Aptaker, J. P. Korb and L. Monteilhet, Cem. Concr. Res., 2007, 37, 303–309 CrossRef CAS.
- S. Godefroy, M. Fleury, F. Deflandre and J. P. Korb, J. Phys. Chem. B, 2002, 106, 11183–11190 CrossRef CAS.
- S. Godefroy, J. P. Korb, M. Fleury and R. G. Bryant, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 13 CrossRef PubMed.
- C. D'Agostino, G. L. Brett, P. J. Miedziak, D. W. Knight, G. J. Hutchings, L. F. Gladden and M. D. Mantle, Chem.–Eur. J., 2012, 18, 14426–14433 CrossRef PubMed.
- C. D'Agostino, T. Kotionova, J. Mitchell, P. J. Miedziak, D. W. Knight, S. H. Taylor, G. J. Hutchings, L. F. Gladden and M. D. Mantle, Chem.–Eur. J., 2013, 19, 11725–11732 CrossRef PubMed.
- J. Mitchell, L. M. Broche, T. C. Chandrasekera, D. J. Lurie and L. F. Gladden, J. Phys. Chem. C, 2013, 117, 17699–17706 CAS.
- C. D'Agostino, J. Mitchell, M. D. Mantle and L. F. Gladden, Chem.–Eur. J., 2014, 20, 13009–13015 CrossRef PubMed.
- C. D'Agostino, M. R. Feaviour, G. L. Brett, J. Mitchell, A. P. E. York, G. J. Hutchings, M. D. Mantle and L. F. Gladden, Catal. Sci. Technol., 2016, 6, 7896–7901 Search PubMed.
- J. Keeler, Understanding NMR Spectroscopy, Wiley, Chichester, UK, 2005 Search PubMed.
- M. Levitt, Spin Dynamics: Basics of Nuclear Magnetic Resonance, John Wiley & Sons Inc., Somerset, New Jersey, US, 2001 Search PubMed.
- A. Abragam, The Pinciples of Nuclear Magnetism, Oxford University Press, New York, 1961 Search PubMed.
- D. Weber, J. Mitchell, J. McGregor and L. F. Gladden, J. Phys. Chem. C, 2009, 113, 6610–6615 CAS.
- R. L. Kleinberg, W. E. Kenyon and P. P. Mitra, J. Magn. Reson., Ser. A, 1994, 108, 206–214 CrossRef CAS.
- I. Foley, S. A. Farooqui and R. L. Kleinberg, J. Magn. Reson., Ser. A, 1996, 123, 95–104 CrossRef CAS PubMed.
- J. Mitchell, T. C. Chandrasekera and L. F. Gladden, J. Chem. Phys., 2010, 132, 10 CrossRef PubMed.
- J. Mitchell, T. C. Chandrasekera, M. L. Johns, L. F. Gladden and E. J. Fordham, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 026101 CrossRef CAS PubMed.
- J. Mitchell, T. C. Chandrasekera, S. T. Roberts, D. J. Holland, A. Blake, E. J. Fordham and L. F. Gladden, in Magnetic Resonance in Porous Media, Amer Inst Physics, Melville, 2011, vol. 1330, pp. 35–38 Search PubMed.
- T. R. Bryar, C. J. Daughney and R. J. Knight, J. Magn. Reson., 2000, 142, 74–85 CrossRef CAS PubMed.
- R. L. Kleinberg, S. A. Farooqui and M. A. Horsfield, J. Colloid Interface Sci., 1993, 158, 195–198 CrossRef CAS.
- T. Sakamoto, H. Yonehara and C. J. Pac, J. Org. Chem., 1994, 59, 6859–6861 CrossRef CAS.
- E. Fukushima and S. W. Roeder, Experimental pulse NMR, Addison-Weslkey, Reading, US, 1981 Search PubMed.
- O. Mohnke and N. Klitzsch, Vadose Zone J., 2010, 9, 846–857 CrossRef CAS.
- Private communication (2008) with T. H. Kim of the MIT Department of Physics.
- C. D'Agostino, S. Chansai, I. Bush, C. Gao, M. D. Mantle, C. Hardacre, S. L. James and L. F. Gladden, Catal. Sci. Technol., 2016, 6, 1661–1666 Search PubMed.
- J. Korringa, D. O. Seevers and H. C. Torrey, Phys. Rev., 1962, 127, 1143–1150 CrossRef CAS.
- M. S. Katsiotis, M. Fardis, Y. Al Wahedi, S. Stephen, V. Tzitzios, N. Boukos, H. J. Kim, S. M. Alhassan and G. Papavassiliou, J. Phys. Chem. C, 2015, 119, 3428–3438 CAS.
| This journal is © The Royal Society of Chemistry 2017 |