5,6-Di(2-fluoro-2,2-dinitroethoxy)furazano[3,4-b]pyrazine: a high performance melt-cast energetic material and its polycrystalline properties

Abstract

5,6-Di(2-fluoro-2,2-dinitroethoxy)furazano[3,4-b]pyrazine was synthesized in a three-step process starting from 3,4-diaminofurazan (DAF) including a significant nucleophilic substitution reaction under the catalytic effect of trisodium phosphate dodecahydrate. Characterization of this molecule indicates that it possesses a higher crystal density than that of 2,4,6-trinitrotoluene (TNT) at ambient temperature with acceptable melting-point and energetic properties approaching those of 1,3,5-trinitro-1,3,5-triazacyclohexane (RDX) but with a higher thermal stability and lower sensitivity towards impact and friction. To investigate its polycrystalline properties, differential scanning calorimetry (DSC), powder-X-ray-diffraction (PXRD) and ab initio calculation using the Viena Ab initio simulation package (VASP) were employed.

---

Introduction

Melt-cast energetic materials have been used in civil mining, aero-propellants and military ammo for decades since 2,4,6-trinitrotoluene (TNT) was synthesized by J. Willbrand in 1893.¹ However, the underlying issues of TNT restricted its manufacture and applications, such as cracks, exudation, voids, irreversible growth, etc.² After the proposal of the “Green energetic materials” concept, research on new candidates to replace TNT has been ongoing for the past several years. As shown in Fig. 1, polynitroazoles featuring methyl groups were developed at first since the presence of methyl groups similar to that in TNT helped to decrease the melting point, such as 1-methyl-2,4,5-trinitroimidazole (MTNI), 1-methyl-3,4,5-trinitropyrazole (MTNP) and 1-methyl-3,5-dinitro-1,2,4-triazole (DNMT).³ As for the methyl group, nitrofurazan-compounds were also discovered because of their low melting point and high energy, such as 3,4-bis(3-nitrofurazan-4-yl)furoxan (DNTF), 3-(4-aminofurazan-3-yl)-4-(4-nitrofurazan-3-yl)furazan (ANTF) and 4,4′′-dinitro-[3,3′,4′,3′′]-tris-[1,2,5]-oxadiazole (BNTF).⁴ However, the safety of a scalable process for these compounds was still problematic. The search for TNT candidates has never stagnated. Recently, the nitrazapropane moiety was incorporated into the synthetic decoration of energetic materials with low melting-point.⁵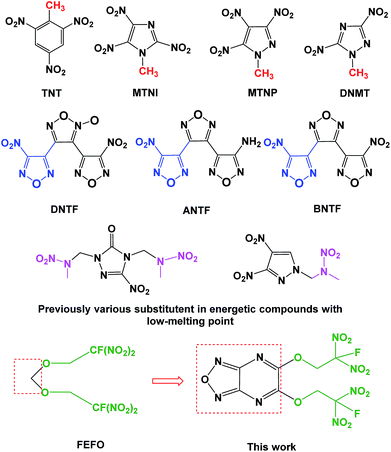

Fig. 1 A variety of molecular design and synthesis strategies for obtaining energetic compounds with low melting-point.

To date, plenty of fluorine containing polynitro-aryl-triazoles and nitrate ester or nitramine derivatives of fluoro derivatives were developed as melt cast explosives.⁶ Fluorodinitro- (FDN-) moiety is an attractive decorating explosophore group, which can improve the thermal stability and decrease the mechanical sensitivity comparing with trinitromethyl moieties. For the past several years, FDN-moiety was introduced into the design and synthesis of energetic materials based on different frameworks such as 1,4-dioxane, 1,3,5-tirazine, carbamate, nitramine, bis-tetrazolyl-dihydroborate, bi(1,2,4-oxadiazoles), 2H-tetrazole and azofurazan.⁷ Among them, bis(2-fluoro-2,2-dinitroethyl)formal (FEFO) is a commercial energetic plasticizer because of its good mechanical, aging and moulding properties, which has been applied in rocket propellants as an important formula but its safety performance still existed.⁸ Other energetic plasticizers bearing FDN-moieties such as bis(1-fluoro-1,1-dinitromethyl)difurazalyl ether (FOF-13), 1,3-bis(2,2,2-fluoro-dinitroethyoxy)-2,2-bis(difluoramino)propane (SYEP) and fluorodinitroethyl boron esters were studied for their analogous performance to FEFO.⁹ To date, the similar structures as FEFO in energetic heterocyclic compounds were less released in literatures. Recently, fluorodinitroethyl ethers was successfully synthesized based on 1,2,4,5-tetrazines, which brought the possibilities for synthesizing other heterocyclic frameworks bearing FDN-ethers.¹⁰

In a continuing effort to seek more FDN-based energetic materials with high performance, we designed a new structure by using fused furazano[3,4-b]pyrazine to replace the methylene bridge in FEFO (Fig. 1). The aims of this strategy were to: (a) improve the heat of formation (HOF) and chemical energy because of their relatively higher HOF of furazan and pyrazine¹¹ in N-heterocycles than that in carbon chains; (b) cause positive effect of ring strain energy¹² in fused heterocyclic frameworks on detonation performance and thermal stability of the target molecule; (c) produce intramolecular conjugated, coplanar and intermolecular π–π stacking effect¹³ on the crystal packing and structural stability, etc. Herein we report on a eco-friendly and easy scale-up method of synthesizing 5,6-di(2-fluoro-2,2-dinitroethoxy) furazano[3,4-b]pyrazine within three steps from the starting material 3,4-diaminofurazan (DAF). Likewise, its special polycrystalline properties and physicochemical performance are further investigated in detail.

Results and discussion

Synthesis

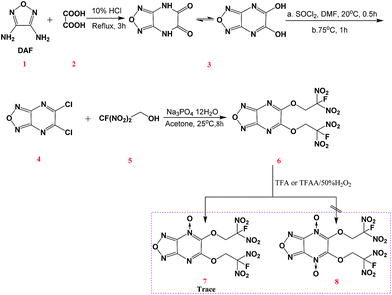
Three pathways for obtained FDN-based energetic compounds were proposed as shown in Scheme 1. The first route (a) is the Mannich reaction with the assistance of Lewis bases and 2-fluoro-2,2-dinitroethanol (FDNE). The second route (b) is so-called esterification through the nucleophilic substitution of chlorine atoms with FDNE. The third route (c) is the fluorination reaction by exchanging potassium or ammonium in gem-dinitro carbon with fluorine atoms in selectfluor™ or XeF₂. Among them, fluorination is relatively easy in most cases but usually synthesizing the precursor is complicated; Mannich reaction has close relationship with the selectivity and reactivity of substrates; esterification needs catalyzed bases to perform nucleophilic substitution.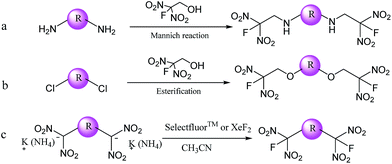

Scheme 1 Three pathways for synthesizing FDN-based compounds (R represents different organic frameworks).

Chavez et al. reported a two-step esterification of 3,6-dichloro-1,2,4,5-tetrazine by first introduction of 2,4,6-collidine in dichloromethane (DCE) with FDNE, followed by 4-(N,N-dimethylamino)pyridine (DMAP) with FDNE to obtain a bis-substituted FDN-based tetrazine compound.¹⁰ Though this method is very effective for synthesizing above-mentioned compounds, it is still complicated and difficult for further purification. As shown in Scheme 2, we firstly synthesized 5,6-dihydroxyfurazano[3,4-b]pyrazine (3) from a cyclization of 3,4-diaminofurazan and oxalic acid.¹⁴ Subsequently, 5,6-dichlorofurazano[3,4-b]pyrazine (4) was synthesized by a mixture of 3 and SOCl₂ in DMF at 75 °C. The nucleophilic substitution of 5,6-di(2-fluoro-2,2-dinitroethoxy)furazano[3,4-b]pyrazine (6) was realized by a mixture of 4 and 2-fluoro-2,2-dinitroethanol (5) in acetone under the catalytic effect of trisodium phosphate dodecahydrate at 25 °C for 8 h. We also tried to synthesize 6 by using sodium carbonate or sodium hydroxide instead of trisodium phosphate dodecahydrate, but the substitution reaction was not complete or there was a decomposition of FDNE occurred in sodium hydroxide solution. The whole reaction process was monitored by TLC (ethyl acetate : petroleum ether = 1 : 3). Compound 6 was very stable upon storage under ambient conditions and was soluble in high-polar solvent such as ethanol, acetone and methanol. We also attempted to synthesize its N-oxide derivatives 7 and 8 by using previously effective N-oxidation condition in tetrazine system (trifluoroacetic acid (TFA) or trifluoroacetic acid anhydride (TFAA) with 50% hydrogen peroxide),¹⁵ and just confirmed a trace of 7 under the analysis of mass spectrum but still could not obtain the target compounds. We supposed that the chemical reactivity of nitrogen atoms in pyrazine ring was not comparable with those in tetrazine ring.

Scheme 2 Synthesis of 6 starting from DAF.

Multinuclear NMR spectroscopy

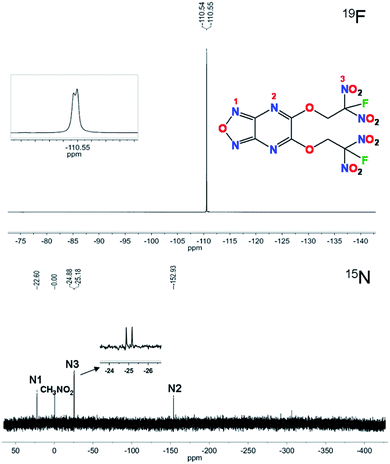
Compound 6 was characterized by ¹H, ¹³C, ¹⁵N and ¹⁹F NMR spectroscopy. In the ¹H NMR spectrum, chemical shifts of CH₂ show coupling constant of 5.95 ppm (J_H–F = 15.0 Hz). The ¹³C signals for CH₂, CF(NO₂)₂, NCN and OCN are observed at 65.1 ppm, 119.6 ppm, 150.3 ppm and 153.9 ppm, respectively (as shown in the ESI†). The signal of CH₂ splits into a doublet due to J_C–F coupling with a coupling constant of 20.1 Hz. For carbon atom in CF(NO₂)₂, the signal also splits into a doublet because of J_C–F coupling with a coupling constant of 299.4 Hz. The carbon atoms in fused rings are normal, which show single signals. As shown in Fig. 2, the ¹⁹F NMR spectrum shows the fluorine shift at −110.5 ppm as a doublet due to J_F–N coupling with a coupling constant of 4.7 Hz. In the ¹⁵N NMR spectra the nitrogen atom in furazan is observed at −22.6 ppm and that in pyrazine is at −152.9 ppm, while for gem-dinitro the signal shows a doublet because of its J_N–F coupling with a coupling constant of 15.2 Hz.

Fig. 2 ¹⁹F and ¹⁵N NMR spectroscopy of 6 in d₆-DMSO.

Crystal structure

The single-crystal of compound 4 was obtained by slow evaporation of methanol, while 6-A and 6-M suitable for single-crystal X-ray diffraction were obtained by slow evaporation of 6 in anhydrous acetone and methanol at ambient temperature, respectively. The crystal and structure data of 6-A and 6-M at 130 K are listed in Table 1, respectively. The crystal and structure data of 4 at 293(2) K and 6-M at 293(2) K, selected bond lengths, angles, torsion angles and hydrogen bonds are listed in the ESI.†

Table 1 Crystal data and structure refinement details for 6 re-crystallized from acetone (6-A) and methanol (6-M)

	6-A	6-M
Formula	C8H4F2N8O11	C8H4F2N8O11
Mw [g mol^−1]	426.19	426.19
T [K]	130	130
Crystal size [mm^3]	0.10 × 0.05 × 0.03	0.18 × 0.10 × 0.02
Crystal system	Orthorhombic	Orthorhombic
Space group	Fdd2	Pca21
a [Å]	10.833(2)	10.9222(18)
b [Å]	14.932(2)	13.057(2)
c [Å]	18.906(4)	10.5202(17)
α [°]	90	90
β [°]	90	90
γ [°]	90	90
V [Å^3]	3058.2(11)	1500.3(3)
Z	8	4
λ [Å]	0.71073	0.71073
ρcalc [g cm^−3]	1.851	1.887
μ [mm^−1]	0.186	0.190
F (000)	1712	856
θ Range [°]	2.561–31.188	1.560–30.584
Reflections collected	7542/2354	14 547/4524
Index ranges	−15 ≤ h ≤ 15	−15 ≤ h ≤ 15
	−17 ≤ k ≤ 21	−15 ≤ k ≤ 18
	−27 ≤ l ≤ 27	−15 ≤ l ≤ 14
Rint	0.0535	0.0288
Data/restraints/parameters	2354/1/132	4524/1/262
Final R index [I > 2σ(I)]	R1 = 0.0396	R1 = 0.0322
	wR2 = 0.0705	wR2 = 0.0795
Final R index [all data]	R1 = 0.0888	R1 = 0.0383
	wR2 = 0.0860	wR2 = 0.0828
GOF on F2	0.955	1.055
CCDC number	1535226	1535228

---

5,6-Dichlorofurazano[3,4-b]pyrazine (4) crystallizes in the orthorhombic space group Pbca with eight formulas per unit cell and a density of 1.961 g cm⁻³ at 293(2) K (molecular structure and crystal packing are displayed in the ESI†). The torsion angles of O1–N1–C1–N3 (179.50(16)°) and N3–C1–C2–N2 (−179.89(17)°) reveal that the furazan ring are coplanar with neighboring fused pyrazine ring.

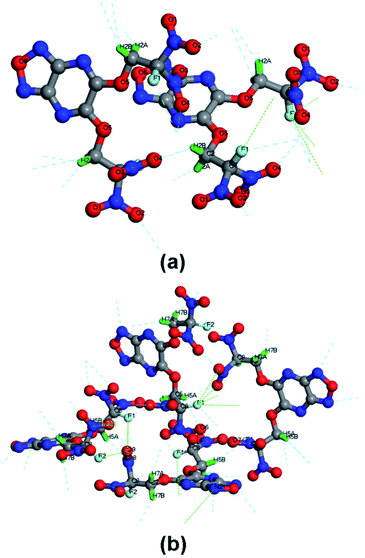
The crystal structure of 6 is depicted in Fig. 3. To our surprise, single crystals of 6 grew from acetone and methanol show different polymorph. We also crystallized 6 in other solvents such as ethyl acetate and dichloromethane, but just obtained the same crystalline forms as that in methanol. 6-A crystallizes in the orthorhombic space group Fdd2 with eight formulas per unit cell and a density of 1.851 g cm⁻³ at 130 K, while 6-M crystallizes in the orthorhombic space group Pca2₁ with four formulas per unit cell and a density of 1.887 g cm⁻³ at 130 K. After substituted by FDN moiety, the fused furazano[3,4-b]pyrazine ring system still shows a planar arrangement, which is reflected in the dihedral angels of almost 180° (O1–N1–C1–N3, −178.4(6)°, N1–C1–C2–N4, 179.7(6)°, O1–N1–C1–C2, 0.1(8)°). Additionally, the torsion angels of C2–N4–C3–O3 (−177.2(5)°) and C7–O3–C3–C4 (−176.3(5)°) indicate that OCH₂ is nearly in the same plane with fused ring system. The C–F bond lengths in 6-A and 6-M are in the range of 1.315–1.332 Å, which is normal in most of energetic compounds featuring fluorodinitro-groups.⁸

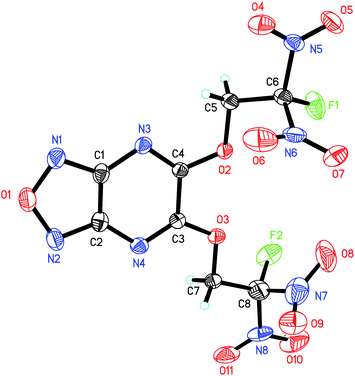Fig. 3 ORTEP representations of single-crystal X-ray structure of 6 shown at the 50% probability level.

Polycrystalline properties

Crystal packing and intermolecular interactions such as hydrogen-bonds and π–π interaction in energetic compounds have drawn much attention by experimental studies. Quantum chemical methods were employed for interpreting those contacts between molecules may contribute to their enhanced thermal, impact and friction stabilities.¹⁶ In the previous work,¹⁷ four types of crystal packing have been discovered in low-sensitivity and high-energy explosives (LSHEs). It can be seen from Fig. 4 wherein the crystal packing of 6-A shows wavelike stacking form while 6-M shows a “bowl” like trapeziform stacking. The later one is unusually seen in those of previously reported LSHEs. This buffer structure with bottom may help reduce the formation of so-called “hot spots” when the mechanical stimuli is introduced, and also have positive effect on decreasing the sensitivities and improving stability.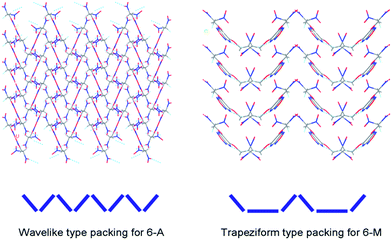

Fig. 4 Crystal packing of single-crystal X-ray structure for 6-A and 6-M with different types of packing form.

Herein, to describe quantitatively interactions in polymorphism of compound 6, we used the Bader's QTAIM method¹⁸ and ab initio calculations to analyze the real-space quantum–mechanical interactions in periodic solids based on the electron densities and related scalar fields. This method was firstly and successfully used to analyze chemical bonding interactions in β-phase of the 1,3,5,7-tetranitro-1,3,5,6-tetraazacyclooctane (HMX) by A. A. Pinkerton et al.¹⁹ With respect to the XB network in the crystal, the forms of XBs surrounding 6-A and 6-M are different due to their different polymorph (Fig. 5). The (3, −1) bond critical points (BCPs) of the intermolecular XBs, together with their related electronic and energy data of 6-A and 6-M at 130 K are listed in Table S20† (the computational details can be found in the ESI†). There are six types of XBs found in 6-A and 6-M, respectively. Although one type of hydrogen bond can be found in 6-A, the distances of hydrogen bonds lie in the range of 2.469–2.643 Å which suggest these are strong. For 6-M, there are two types of hydrogen bonds found, with their distances ranging from 2.503 Å to 2.873 Å. In 6-A, the strongest type of XB is C–H⋯O (E_XB = 5.52158 kJ mol⁻¹), while for 6-M the strongest types are C–H⋯O (E_XB = 6.56344 kJ mol⁻¹) and C–H⋯N (E_XB = 6.44252 kJ mol⁻¹). Comparing with strong hydrogen bond, halogen bond energies basically lie in the weak range of 0.82226–5.02857 kJ mol⁻¹ and distances ranging from 2.975 Å to 3.363 Å in 6-M (3.004–3.472 Å in 6-A) which indicate that halogen bonding interaction is weak and also in accord with the tendency to form strong XBs (I > Br > Cl > F).²⁰ In addition, it is worth noting that the total E_XB of 6-M is higher than those of insensitive energetic compounds such as FOX-7 (60.452 kJ mol⁻¹) and LLM-105 (50.362 kJ mol⁻¹).²¹

Fig. 5 XBs surrounding 6-A (a) and 6-M (b) with labelled atoms. For clarity, the crystalline cell was transferred into primitive cell from conventional cell due to its high symmetry of 6-A crystalline cell.

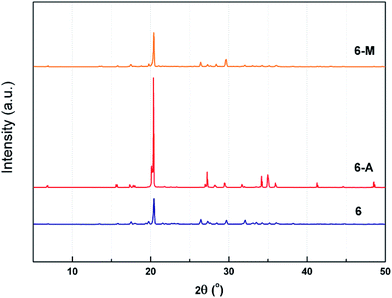
To further study the effect of polymorphism on crystalline properties experimentally, powder X-ray diffraction (PXRD) was employed. It is obvious from Fig. 6 that the powder sample of 6 at 2θ is basically similar with those of 6-M, while 6-A shows different peaks at 2θ ranging from 15° to 20°, 25° to 30°, 33° to 36° and 40° to 50°. The above-mentioned PXRD patterns confirm the presence of different polymorph and even a variety of conformation, just like those of FOX-7 or CL-20.²²

Fig. 6 PXRD spectra of 6, 6-A and 6-M.

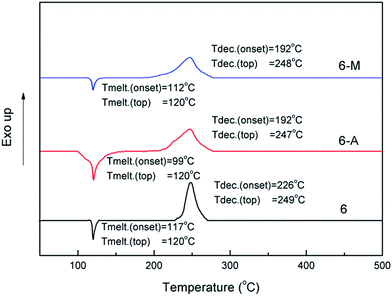
The onset melting point and onset decomposition temperature of powder sample 6 as well as its crystals were obtained by using differential scanning calorimetry (DSC) measurement and shown in the Fig. 7. Powder 6 shows a onset melting point at 117 °C, which is slightly higher than that of TNT but still meets the requirement of melt-cast process in energetic materials.⁵ It shows a onset decomposition temperature at 226 °C, which is better than that of RDX but lower than that of TNT. For 6-A and 6-M, it is worth noting that the onset melting point of 6-A and 6-M all move up, especially 6-A shows 18 °C ahead of 6 while 6-M shows only 5 °C in advance. Though the decomposition peaks of three samples do not change basically, the onset decomposition temperature of 6-A and 6-M clearly move up and show nearly 34 °C ahead of 6.

Fig. 7 DSC plot of 6, 6-A and 6-M at the heating rate of 5 °C min⁻¹.

Energetic and physical properties

The energetic and physical properties are summarized in Table 2. The heats of formation were calculated using the Gaussian 09 (Revision D.01) suite of programs based on the isodesmic reaction.²³ 6 gives a negative heat of formation of −166.1 kJ mol⁻¹ (−0.39 kJ g⁻¹), which has been enhanced compared with similar compound featuring bis-FDN-moiety,^7f but still lower than those with mono-FDN-moiety.^7g Based on the heat of formation and its corresponding density at ambient temperature, the detonation and combustion parameters were performed by using EXPLO5 (version 6.02) code.²⁴ All calculated results are also listed in Table 2. The computed detonation velocity of 6 (8512 m s⁻¹) is comparable with that of RDX (8795 m s⁻¹), which is higher than the famous melt-cast explosive TNT (6881 m s⁻¹). Its detonation pressure (32.4 GPa) is also comparable with that of RDX (34.9 GPa).

Table 2 Energetic and physical properties of 6

	6	TNT^26	RDX^26
a Density measured by single-crystal X-ray diffraction at 25 °C or adopted from the literatures.b Oxygen balance.c Calculated detonation velocity.d Calculated detonation pressure.e Heat of formation.f Onset melting point measured by DSC.g Onset decomposition temperature measured by DSC.h Impact sensitivity measured by BAM drop-hammer test.i Friction sensitivity measured by a BAM friction tester.j Electrostatic discharge device.k Specific impulse.
ρ (g cm^−3)^a	1.83	1.65	1.80
OB (%)^b	−26.3	−74	−21.6
D (m s^−1)^c	8512	6881	8795
P (GPa)^d	32.4	19.5	34.9
ΔHf (kJ mol^−1)/(kJ g^−1)^e	−166.1/(−0.39)	−67.0/(−0.30)	92.6/(0.42)
Tm (°C)^f	117	81	204
Tdec (°C)^g	226	295	210
IS (J)^h	17	15	7.4
FS (N)^i	252	240	120
ESD (J)^j	0.13	0.37 (ref. 27)	0.20 (ref. 27)
Isp (s)^k	258	209	258

---

To evaluate its safety properties, the sensitivities towards impact and friction were determined by using a standard BAM Fallhammer and a BAM friction tester. Compound 6 show impact sensitivity (IS) of 17 J, suggesting it is comparable with that of TNT (15 J) and more insensitive than that of RDX (7.4 J). The measured friction sensitivity (FS) of 6 (252 N) also reveals its insensitivity as that of TNT (240 N) and exceeds that of RDX (120 N). The electrostatic discharge test (ESD) was performed to determine the ignitable possibility of energetic material, which show that 6 is more sensitive (0.13 J) compared with TNT (0.37 J) and RDX (0.20 J) but still in the scope of insensitivity towards electrostatic discharge (for human body, the values are within the range of 0.005–0.02 J).²⁵

Conclusions

In this study we have developed a new and convenient synthetic route for 5,6-di(2-fluoro-2,2-dinitroethoxy)furazano[3,4-b]pyrazine (6) by nucleophilic substitution directly of 5,6-dichlorofurazano[3,4-b]pyrazine (4) with 2-fluoro-2,2-dinitroethanol (5). Experimental results show that 6 has realizable melt-castable properties, high decomposition temperature exceeding 200 °C and exhibits better detonation properties (D: 8512 m s⁻¹, P: 32.4 GPa) than those of TNT. Worth noting that it also indicates slightly better insensitivities (IS: 17 J, FS: 252 N) than those of TNT. For the polycrystalline properties, PXRD and DSC reveal that different polymorph has significant effect on their phase structure and thermal properties, respectively. Moreover, the ab initio simulations of unit cell in crystal indicate that hydrogen and halogen bonding interaction in 6-M is stronger than that of 6-A. The above-mentioned performance not only suggest that the incorporation of FDN moiety into framework with high HOF is helpful for enhancing the energetic properties but also show that 6 has the potential as an ingredient in melt-cast energetic materials.

Experimental section

Safe cautions

Although none of the above-mentioned energetic materials have exploded or detonated in the procedure of this research, small scale and safety training are strongly encouraged. Mechanical actions such as scratching and scraping must be avoided. Manipulations should be performed behind a polymethyl methacrylate (PMMA) guard with at least 12 mm thickness. Face shield, eye protection and leather gloves must be strictly put on.

General methods

All reagents were purchased from Sigma Aldrich or J&K in analytical grade and were used as received. ¹H, ¹³C, ¹⁵N and ¹⁹F NMR spectra were recorded on a 300 MHz (Bruker AVANCE 300) or 500 MHz (Bruker AVANCE 500) nuclear magnetic resonance spectrometer. Chemical shifts in the ¹H and ¹³C spectra are reported relative to Me₄Si, ¹⁵N NMR to MeNO₂ and ¹⁹F NMR to CCl₃F as external standards. The melting point and decomposition temperature were recorded on a differential scanning calorimeter-thermal gravity (TGA/DSC1, METTLER TOLEDO LF/1100) at a heating rate of 5 °C min⁻¹. Infrared (IR) spectra were measured on Thermofisher Nicolet 800 FT-IR spectrometer in the range of 4000–400 cm⁻¹ as KBr pellets at 20 °C. Elemental analyses (C, H, N) were carried out on a elemental analyzer (Vario EL Cube, Germany). The phases of the samples were obtained via powder X-ray diffraction (PXRD, X'Pert Pro, PANanlytical, Netherlands).

Computational methodology

Intermolecular interaction in polycrystalline systems was analyzing by using VASP (Vienna Ab initio Simulation Package)²⁸ with first-principles pseudopotentials constructed by projected augmented waves (PAW), representing an all-electron DFT technique with a frozen-core approximation.^29,30 The PAW potentials indicate the numerical advantages of pseudopotential calculations while retaining the physics of all-electron calculations, involving the correct nodal behavior of the valence electron wave functions and the ability to include upper core states in addition to valence states in the self-consistent iterations. The H1s, C2s2p, N2s2p, O2s2p and F2s5p orbitals were taken as valence states, and the exchange-correlation functional was treated with the generalized gradient approximation (GGA) following the Perdew, Burke and Ernzerhof (PBE) formulation.³¹

The static calculations and structure optimization were performed using the conjugate gradient method with 3 × 3 × 3 Monkhorst–Pack k-point sampling in reciprocal space and a plane-wave basis set with an energy cutoff of 850 eV. The DFT-D2 method of Grimme³² was used to correct long-range dispersion interactions. In DFT-D2 method, dispersion corrections are calculated not only for forces acting on the atoms, but also for the stresses on the unit cell, and thus a simultaneous optimization of all degrees of freedom is permitted. The self-consistent convergence criteria of energy were set to 1 × 10⁻⁷ for electronic relaxation. The intra- and intermolecular hydrogen bonds and halogen bonds (XBs) in the crystal were analyzed by Bader's QTAIM method and ab initio calculations, with the Critic2, a code for determining the real-space quantum–mechanical interactions in periodic solids based on the electron densities and other related scalar fields.^33,34 The core and valence electron densities of a crystal were acquired from ab initio (density functional theory, DFT) calculations implemented in VASP code. The XB energy or the bond dissociation energy of XB (E_XB) was predicted using an empirical equation E_XB = −(1/2)v³⁵ and used to assess XB strength in terms of electron densities (ρ) at the bond critical points, after which the potential energy densities (v) was obtained.

The heat of formation was computed by Gaussian 09 code. First, the geometric optimization, frequency analysis and single-point energies of compound 6 were accomplished by using the M06-2X with the 6-311+G** basis set.³⁶ Then, the atomization energies were obtained by employing the G2 ab initio method or from NIST Chemistry Webbook³⁷ and solid phase heat of formation was computed via isodesmic reactions. The solid-state heat of formation can be estimated by subtracting the heats of formation from gas-phase heats of formation. The heat of sublimation can be estimated following the Trouton's rule,³⁸ which is shown in the eqn (1):

ΔH_sub = 188/J mol⁻¹ K⁻¹ T (1)

Here, T represents either the melting point or the decomposition temperature when no melting occurs prior to decomposition. Detonation parameters were carried out in the EXPLO5 (V6.02) program using X-ray densities which were converted to room temperature values via the following equation:³⁹

ρ_{298 K} = ρ_T/[1 + α_ν(298−T₀) (2)

where the coefficient of volume expansion α_ν is 1.5 × 10⁻⁴ K⁻¹, ρ_T and T₀ are the crystal density and the relative temperature, respectively.

X-ray diffraction

A colorless prismatic crystal of dimension 0.20 × 0.17 × 0.12 mm³ (4), colorless block crystal of dimension 0.10 × 0.05 × 0.03 mm³ (6-A), colorless prismatic crystal of dimension 0.20 × 0.17 × 0.10 mm³ (6-M), and colorless plate crystal of dimension 0.18 × 0.10 × 0.02 mm³ (6-M) were mounted on a MiteGen MicroMesh using a small amount of Cargille Immersion Oil. Data were collected on a Bruker three-circle platform diffractometer equipped with a SMART APEX II CCD detector. A kryo-Flex low-temperature device was used to keep the crystals at 293(2) K and 130 K during data collection. Data collection was performed and the unit cell was initially refined using APEX2. Data reduction was carried out using SAINT and XPREP. Corrections were applied for Lorentz, polarization, and absorption effects using SADABS. The structures were further solved and refined with the aid of the programs using direct methods and least-squares minimization by SHELXS-97 and SHELXL-97 code.⁴⁰ The full-matrix least-squares refinement on F² involved atomic coordinates and anisotropic thermal parameters for all non-H atoms. The H atoms were included using a riding model. The non-H atoms were refined anisotropically. The finalized CIF files were checked with checkCIF, and deposited at the Cambridge Crystallographic Data Centre as supplementary publications 4 (293 K), 6-A (130 K), 6-M (293 K) and 6-M (130 K) (the crystalline parameters were listed in the ESI†). Intra- or intermolecular hydrogen-bonding interactions were analyzed with Diamond software (version 3.2 K) as well as the illustrations of molecular structures.

5,6-Dichlorofurazano[3,4-b]pyrazine (4)

3,4-Diaminofurazan (DAF) (50 g, 0.5 mol) and anhydrous oxalic acid (49.5 g, 0.55 mol) were suspended in 10% HCl (80 mL) at ambient temperature, and the above mixture was refluxed for another 3 h. Under the reaction temperature, the mixture became clear solution and then white precipitate appeared. The precipitate was filtered, washed with cold water and dried in air to give 5,6-dihydoxyfurazano[3,4-b]pyrazine (3) (white solid, 69.5 g, yield 90.3%).¹⁴ 5–10 °C, 3 (8 g, 52 mmol) was suspended in SOCl₂. DMF (8 mL) was added dropwise to the above mixture with a temperature below 15 °C. Then the mixture was stirred for 0.5–1 h at 20 °C and for 1–2 h at 75 °C. Under 75 °C, the mixture became a clear-yellow solution. After cooling to the ambient temperature, the solution was poured slowly into ice water (500 mL), the precipitate was filtered and dried in air to give the product (4) (white solid, 4.7 g, yield 48.0%). ¹³C{¹H} NMR (DMSO-d₆, 125.78 MHz): δ = 155.8, 151.4 ppm.

2-Fluoro-2,2-dinitroethanol (5)

5 was synthesized by an improved method according to the literature (colorless oil, 5.8 g, yield 49.1%).^{9c 1}H NMR (CDCl₃, 300.06 MHz): δ = 2.62 ppm (t, J_H–F = 7.5 Hz, 1H, OH), 4.66 ppm (dd, J_H–F = 15.0 Hz, 2H, OCH₂); ¹³C NMR (CDCl₃, 75.46 MHz): δ = 61.8 ppm (d, J_C–F = 21.2 Hz, OCH₂), 121.1 ppm (d, J_C–F = 289.7 Hz, CF(NO₂)₂); ¹⁹F(CDCl₃, 282.30 MHz): −111.7 ppm. HPLC purity >99.7%.

5,6-Di(2-fluoro-2,2-dinitroethoxy)furazano[3,4-b]pyrazine (6)

To a solution of 4 (0.96 g, 5 mmol) and 5 (1.7 g, 11 mmol) in acetone (20 mL) was added trisodium phosphate dodecahydrate (1.8 g, 5 mmol) in portions. The mixture was stirred at ambient temperature for 8 h. The precipitate was filtered off and then the filtrate was evaporated under vacuum, recrystallized in ethanol and water to yield 6 (white solid, 1.92 g, yield 89.3%), m.p. 115–117 °C. ¹H NMR (DMSO-d₆, 500.20 MHz): δ = 5.95 ppm (d, J_H–F = 15.0 Hz, 4H, OCH₂); ¹³C NMR (DMSO-d₆, 125.78 MHz): δ = 65.1 ppm (d, J_C–F = 20.1 Hz, OCH₂), 119.6 ppm (d, J_C–F = 299.4 Hz, CF(NO₂)₂), 150.3 ppm (N=C–N), 153.9 ppm (N=C–O); ¹⁵N (DMSO-d₆, 50.68 MHz): −22.6 ppm, −25.0 ppm (d, J_N–F = 15.2 Hz), −152.9 ppm; ¹⁹F(DMSO-d₆, 470.66 MHz): −110.5 ppm (d, J_F–N = 4.7 Hz). IR (KBr pellet): 3442 (m), 1614 (s), 1556 (w), 1508 (w), 1436 (w), 1402 (w), 1332 (w), 1301 (w), 1260 (w), 1226 (w), 1020 (w), 997 (w), 867 (w), 850 (w), 794 (w), 592 (w), 491 (w) cm⁻¹. Elemental analysis for C₈H₄F₂N₈O₁₁ (426.19): C 22.55, H 0.95, N 26.29%; found: C23.17, H 1.02, N 25.15%.

Acknowledgements

We are indebted to the Science and Technology Development Foundation of China Academy of Engineering Physics (Grant No. 2015B0302055), the National Natural Science Foundation of China (Grant No. 11402237), and NSAF Foundation of National Natural Science Foundation of China and China Academy of Engineering Physics (Grant No. U1530262) for funding of this work. Mr Yinshuang Sun and Mrs Min Zhong are gratefully acknowledged for the assistance in performing the BAM and ESD sensitivity tests. National Supercomputer Centre in Guangzhou (NSCCGZ) is also thanked for the support with the quantum chemical calculations.

Notes and references

1. J. Akhavan, The chemistry of Explosives, The Royal Society of Chemistry, Thomas Graham House, Cambridge, 2nd edn, 2004.
2. (a) J. P. Agrawal, High Energy Materials: Propellants, Explosives and Pyrotechnics, Wiley-VCH, Weinheim, 1st edn, 2008; (b) T. M. Klapötke, Chemistry of High-Energy Materials, De Gruyter, Berlin, 3rd edn, 2015.
3. (a) A. B. Sheremetev, E. A. Ivanova, N. P. Spiridonova, S. F. Melnikova, I. V. Tselinsky, K. Y. Suponitsky and M. Yu Antipin, J. Heterocycl. Chem., 2005, 42, 1237–1242; (b) G. Herve, C. Roussel and H. Graindorg, Angew. Chem., Int. Ed., 2010, 49, 3177–3181; (c) Y. Zhang, Y. Guo, Y. H. Joo, D. A. Parrish and J. M. Shreeve, Chem.–Eur. J., 2010, 16, 10778–10784; (d) R. Duddu, P. R. Dave, R. Damavarapu, R. Surapaneni and D. Parrish, Synth. Commun., 2009, 39, 4282–4288; (e) P. Ravi and S. P. Tewari, Propellants, Explos., Pyrotech., 2012, 37, 544–548; (f) Q. Ma, T. Jiang, Y. Chi, Y. Chen, J. Wang, J. Huang and F. Nie, New J. Chem., 2017, 41, 4165–4172.
4. (a) R. V. Tsyshevsky and M. M. Kuklja, Molecules, 2013, 18, 8500; (b) A. I. Stepanov, D. V. Dashko and A. A. Astrat'ev, Chem. Heterocycl. Compd., 2013, 49, 776; (c) P. Pagoria, M. X. Zhang, A. Racoveanu, A. D. Hope, R. Tsyshevsky and M. M. Kuklja, Molbank, 2014, 2014, M824; (d) Q. Yi, D. Liang, Q. Ma, M. Huang, B. Tan, Y. Liu and Y. Chi, Propellants, Explos., Pyrotech., 2016, 41, 906–911.
5. T. M. Klapötke, A. Penger, C. Pflüger and J. Stierstorfer, New J. Chem., 2016, 40, 6059–6069.
6. (a) S. Garg and J. M. Shreeve, J. Mater. Chem., 2011, 21, 4787–4795; (b) A. S. Kumar, N. Kommu, V. D. Ghule and A. K. Sahoo, J. Mater. Chem. A, 2014, 2, 7917–7926; (c) D. Srinivas and V. D. Ghule, RSC Adv., 2016, 6, 7712–7716; (d) N. Kommu, A. S. Kumar, J. Raveendra, V. D. Ghule and A. K. Sahoo, Asian J. Org. Chem., 2016, 5, 138–146.
7. (a) B. S. Fedorov, N. I. Golovina, S. P. Smirnov and I. Sh Abdrakhmanov, Chem. Heterocycl. Compd., 2002, 38, 385–389; (b) V. V. Bakharev, A. A. Gidaspov and E. V. Golovin, Russ. J. Gen. Chem., 2007, 77, 1104–1107; (c) T. M. Klapötke, B. Krumm, R. Moll, S. F. Rest, W. Schnick and M. Seibald, J. Fluorine Chem., 2013, 156, 253–261; (d) T. M. Klapötke, B. Krumm, S. F. Rest, M. Reynders and R. Scharf, Eur. J. Inorg. Chem., 2013, 2013, 5871–5878; (e) R. Haiges, C. B. Jones and K. O. Christe, Inorg. Chem., 2013, 52, 5551–5558; (f) M. A. Kettner, K. Karaghiosoff, T. M. Klapötke, M. Sućeska and S. Wunder, Chem.–Eur. J., 2014, 20, 1–11; (g) M. A. Kettner and T. M. Klapötke, Chem.–Eur. J., 2015, 21, 3755–3765; (h) Y. Tang, H. Gao, G. H. Imler, D. A. Parrish and J. M. Shreeve, RSC Adv., 2016, 6, 91477–91482.
8. (a) D. A. Clchra, W. M. Koppes and H. G. Adolph, J. Chem. Eng. Data, 1986, 31, 372–373; (b) S. A. Shackelford, R. R. McGuire and R. E. Cochoy, J. Org. Chem., 1992, 57, 2950–2953; (c) C. M. Tarver, D. M. Hoffman, P. A. Urtiew and W. C. Tao, J. Energ. Mater., 1996, 14, 217–256.
9. (a) A. B. Sheremetev, In the proceedings of the 29^th International Annual Conference of ICT, Karlsruhe, Germany, 1998, vol. 58, pp. 1–6; (b) V. Grakauskas, J. Org. Chem., 1973, 38, 2999–3004; (c) T. M. Klapötke, B. Krumm and R. Moll, Chem.–Eur. J., 2013, 19, 12113–12123.
10. (a) D. E. Chavez, L. Mitchell and D. A. Parrish, In the proceedings of the 19^th Seminar on New Trends in Research of Energetic Materials, Padubice, Czech Republic, 2016, 2016, pp. 147–153; (b) D. E. Chavez, D. A. Parrish and L. Mitchell, Angew. Chem., Int. Ed., 2016, 55, 8666–8669.
11. (a) J. Zhang and J. M. Shreeve, J. Am. Chem. Soc., 2014, 136, 4437–4445; (b) H. Huang, Y. Shi, Y. Liu and J. Yang, Chem.–Asian J., 2016, 11, 1688–1696; (c) P. Pagoria, Propellants, Explos., Pyrotech., 2016, 41, 452–469.
12. (a) K. B. Wiberg, Angew. Chem., Int. Ed., 1986, 25, 312–322; (b) B. M. Gimarc and M. Zhao, Coord. Chem. Rev., 1997, 158, 385–412; (c) S. E. Wheeler, K. N. Houk, P. R. Schleyer and W. D. Allen, J. Am. Chem. Soc., 2009, 131, 2547–2560; (d) R. D. Rach and O. Dmitrenko, J. Org. Chem., 2002, 67, 2588–2599; (e) Q. Wu, L. Tan, Z. Hang, J. Wang, Z. Zhang and W. Zhu, RSC Adv., 2015, 5, 93607–93614.
13. (a) D. E. Chavez, J. C. Bottaro, M. Petrie and D. A. Parrish, Angew. Chem., Int. Ed., 2015, 54, 12973–12975; (b) M. S. Klenov, A. A. Guskov, O. V. Anikin, A. M. Churakov, Y. A. Strelenko, I. V. Fedyanin, K. A. Lyssenko and V. A. Tartakovsky, Angew. Chem., Int. Ed., 2016, 55, 1–5; (c) D. G. Piercey, D. E. Chavez, B. L. Scott, G. H. Imler and D. A. Parrish, Angew. Chem., Int. Ed., 2016, 55, 1–5; (d) M. C. Schulze, B. L. Scott and D. E. Chavez, J. Mater. Chem. A, 2015, 3, 17963–17965; (e) Q. Ma, Y. Chen, L. Liao, H. Lu, G. Fan and J. Huang, Dalton Trans., 2017, 46, 74677–75479; (f) Q. Ma, H. Lu, Y. Qu, L. Liao, J. Li, G. Fan and Y. Chen, Cent. Eur. J. Energ. Mater., 2017, 14, 281–295.
14. (a) A. K. Zelenin and M. L. Trudell, J. Heterocycl. Chem., 1997, 34, 1057–1060; (b) V. Thottempudi, P. Yin, J. Zhang, D. A. Parrish and J. M. Shreeve, Chem.–Eur. J., 2014, 20, 542–548.
15. (a) H. Wei, H. Gao and J. M. Shreeve, Chem.–Eur. J., 2014, 20, 16943–16952; (b) H. Wei, J. Zhang and J. M. Shreeve, Chem.–Asian J., 2015, 10, 1130–1132.
16. (a) J. Zhang, Q. Zhang, T. T. Vo, D. A. Parrish and J. M. Shreeve, J. Am. Chem. Soc., 2015, 137, 1697–1704; (b) J. Zhang and J. M. Shreeve, J. Phys. Chem. C, 2015, 119, 12887–12895; (c) P. Yin, L. A. Mitchell, D. A. Parrish and J. M. Shreeve, Chem.–Asian J., 2017, 12, 378–384; (d) Q. Ma, G. Fan, L. Liao, H. Lu, Y. Chen and J. Huang, ChemPlusChem, 2017, 82, 474–482; (e) Q. Ma, H. Lu, L. Liao, Y. Chen, B. Cheng, G. Fan and J. Huang, J. Therm. Anal. Calorim., 2017, 127, 2517–2529.
17. Y. Ma, A. Zhang, C. Zhang, D. Jiang, Y. Zhu and C. Zhang, Cryst. Growth Des., 2014, 14, 4703–4713.
18. R. F. W. Bader, A Quantum Theory The International Series of Monographs of Chemistry, Atoms in Molecules, ed. J. Halpen and M. L. H. Green, Oxford Clarendon Press, Oxford, 1990.
19. E. A. Zhurova, V. V. Zhurov and A. A. Pinkerton, J. Am. Chem. Soc., 2007, 129, 13887–13893.
20. (a) N. Ramasubbu, R. Parthasarathy and P. Murray-Rust, J. Am. Chem. Soc., 1986, 108, 4308–4314; (b) Raatikainen and K. Rissanen, Cryst. Growth Des., 2000, 10, 3638–3646; (c) N. R. Goud, O. Bolton, E. C. Burgess and A. J. Matzger, Cryst. Growth Des., 2016, 16, 1765–1771.
21. L. Meng, Z. Lu, Y. Ma, X. Xue, F. Nie and C. Zhang, Cryst. Growth Des., 2016, 16, 7231–7239.
22. (a) B. Gao, D. Wang, J. Zhang, Y. Hu, J. Shen, J. Wang, B. Huang, Z. Qiao, H. Huang, F. Nie and G. Yang, J. Mater. Chem. A, 2014, 2, 19969–19974; (b) X. Zhou, Z. Lu, Q. Zhang, D. Chen, H. Li, F. Nie and C. Zhang, J. Phys. Chem. C, 2016, 120, 13434–13442.
23. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 D.01, Gaussian Inc., Wallingford, USA, 2010.
24. M. Sućeska, EXPLO5, version 6.02, Croatia, 2013.
25. T. M. Klapötke and T. G. Witkowski, ChemPlusChem, 2016, 81, 357–360.
26. (a) M. S. Westwell, M. S. Searle, D. J. Wales and D. H. Williams, J. Am. Chem. Soc., 1995, 117, 5013–5015; (b) Y. Zhang, D. A. Parrish and J. M. Shreeve, J. Mater. Chem. A, 2013, 1, 585–593; (c) T. T. Vo, J. Zhang, D. A. Parrish, B. Twamley and J. M. Shreeve, J. Am. Chem. Soc., 2013, 135, 11787–11790.
27. (a) T. M. Klapötke, M. Leroux, P. C. Schmid and J. Stierstorfer, Chem.–Asian J., 2016, 11, 844–851; (b) T. M. Klapötke, M. Q. Kurz, R. Scharf, P. C. Schmid, J. Stierstorfer and M. Sućeska, ChemPlusChem, 2015, 80, 97–106.
28. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
29. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
30. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 59, 1758.
31. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
32. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
33. A. Otero-de-la-Roza, M. A. Blanco, A. Martín Pendás and V. Luaña, Comput. Phys. Commun., 2009, 180, 157–166.
34. A. Otero-de-la-Roza, E. R. Johnson and V. Luaña, Comput. Phys. Commun., 2014, 185, 1007–1018.
35. E. Espinosa and E. Molins, J. Chem. Phys., 2000, 113, 5686.
36. (a) L. A. Curtiss, K. Raghavachari, P. C. Redfern and J. A. Pople, J. Chem. Phys., 1997, 106, 1063–1079; (b) Y. Qu, Q. Zeng, J. Wang, Q. Ma, H. Li, H. Li and G. Yang, Chem.–Eur. J., 2016, 22, 1–7; (c) Q. Zeng, Y. Qu, J. Li and H. Huang, RSC Adv., 2016, 6, 77005–77012; (d) Q. Ma, H. Gu, H. Lu, L. Liao, J. Huang, G. Fan, J. Li and D. Liu, ChemistrySelect, 2017, 2, 4567–4571; (e) Q. Ma, G. Fan, L. Liao and J. Huang, Polycyclic Aromat. Compd., 2017, 37, 327–344.
37. NIST Chemistry WebBook, NIST Standard Reference Database, 69, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, 2005.
38. (a) F. Trouton, Philos. Mag., 1884, 18, 54–57; (b) P. Atkins, Physical Chemistry, Oxford University Press, 1978.
39. (a) C. Xue, J. Sun, B. Kang, Y. Liu, X. Liu, G. Song and Q. Xue, Propellants, Explos., Pyrotech., 2010, 35, 333–339; (b) D. Fischer, T. M. Klapötke, M. Reymann, J. Stierstorfer and M. B. R. Völkl, New J. Chem., 2015, 39, 1619–1627.
40. (a) G. M. Sheldrick, SHELXS-97, Program for solution of crystal structures, University of Gottingen, Germany, 1997; (b) G. M. Sheldrick, SHELXL-97, Program for refinement of crystal structures, University of Gottingen, Germany, 1997.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 1535226–1535228 and 1535921. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7ra07035g

---