Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tunable electromagnetically induced transparency based on terahertz graphene metamaterial
Xunjun He *ab,
Yiming Huanga,
Xingyu Yanga,
Lei Zhuc,
Fengmin Wua and
Jiuxing Jiang*a
*ab,
Yiming Huanga,
Xingyu Yanga,
Lei Zhuc,
Fengmin Wua and
Jiuxing Jiang*a
aSchool of Applied Sciences, Harbin University of Science and Technology, Harbin, 150080, China. E-mail: hexunjun@hrbust.edu.cn; jiangjiuxing@hrbust.edu.cn
bDepartment of Physics, University of California at Berkeley, Berkeley, California 94720, USA
cCommunication and Electronics Engineering Institute, Qiqihar University, Qiqihar, 161006, China
First published on 17th August 2017
Abstract
By patterning graphene on a SiO2/Si substrate, in this paper, we designed and numerically investigated a terahertz electromagnetically induced transparency (EIT) graphene metamaterial, which consists of two coupled split ring resonators (SRRs) placed in an orthogonally twisted fashion, acting as the bright and dark elements, respectively. The calculated surface currents show that the dark mode excited by the near field coupling between two resonators can induce a distinct transparency peak in the transmission spectrum. Moreover, the amplitude and position of the transparency peak as well as the corresponding group delay can be actively tuned by changing the relaxation time or Fermi energy of graphene. Therefore, the graphene metamaterial with the actively tunable EIT peak exhibits potential applications in light storage, modulators, tunable sensors and switchers.
Introduction
The electromagnetically induced transparency (EIT) effect, caused by the quantum destructive interference between two different excitation pathways, was first observed in a three level atomic system.1 Recently, the classical Lorenz oscillator model has also realized analogues of the EIT effect by the interference of normal modes rather than quantum interference.2,3 Specially, metamaterial-based EIT-like effect has attracted considerable attention due to its potential applications in slow light, sensing, filtering, switching, and nonlinear devices.4–8 Currently, different EIT-like metamaterials have been proposed and experimentally demonstrated from microwave9 to terahertz,10 near-infrared,11 visible,12 and even ultraviolet regions.13 Unfortunately, most of these EIT metamaterials can only work at a fixed wavelength range, which significantly hampers the developments and applications of the EIT-like effect.To expand the operating frequency range, the ability to actively tune the EIT response in metamaterials is very important and attractive for their potential applications. Currently, several approaches have been explored to artificially control the EIT behavior of different metamaterials, such as thermal control of the EIT window in superconducting metamaterials,14,15 optical tuning of the EIT-like metamaterial integrating photoconductive material16,17 as well as structure reconfiguration by MEMS technology.18,19 However, those tunable methods depend highly on the nonlinear properties of active materials, which inevitably results in low modulation depth and range. In addition, the possibility and reliability for massive fabrication are still limited by complex structure and process.
Since discovered in 2004, graphene has triggered a new round of research boom due to its unique electric, mechanical, and thermal properties.20,21 Moreover, the conductivity of grapheme can be dynamically controlled by doping, which is unable to obtain in conventional metal structures.22 Currently, different tunable graphene-based metamaterials have been investigated by patterning, stacking or integrating graphene to realize tunable devices and EIT-like effect.23–29 For example, the structure-engineered graphene micro-ribbon arrays can actively control plasmon resonances by electrostatic doping.23 The patterning or stacking graphene structure can realize tunable terahertz metamaterials.24–26 The graphene metamaterial consisting of a graphene dipole antenna and a graphene monopole–antenna-pair can induce tunable PIT window by doping.27 The hybrid graphene/metamaterial structures can actively modulate the THz light.28,29 In this paper, we proposed a graphene-based terahertz EIT metamaterial, unit cell of which consists of two coupled split ring resonators placed in orthogonally twisted fashion, acting as the bright and dark elements, respectively. The destructive interference resulting from strong near field coupling between two resonators can induce an EIT window. Moreover, the amplitude and position of the EIT window as well as the associated group delay can be actively tuned by changing the relaxation time or Fermi energy of graphene. Therefore, the graphene metamaterial with tunable EIT window can show the potential applications in light storage, modulators, tunable sensors and switchers.
Design and simulation of EIT structure
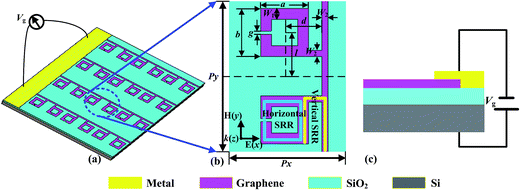
In this paper, a terahertz graphene metamaterial was designed to actively control EIT window, as shown in Fig. 1(a). The unit cell of the graphene metamaterial is composed of two coupled graphene split ring resonators (SRRs) placed in orthogonally twisted fashion, where the vertical and horizontal SRRs structures can serve as the bright and dark elements respectively (as shown in Fig. 1(b)). In the unit cell structure, one of the side arms of the vertical SRRs acts as a base arm of the horizontal SRRs, while another side is connected by a graphene wire to act as the top gate. Moreover, all periodic graphene structures are patterned on the light doped Si substrate covering with the thin SiO2 layer, as shown in Fig. 1(c). In this structure, the corresponding structural parameters shown in Fig. 1(b) are as following: px = py = 100 μm, a = b = 31 μm, w1 = 7 μm, w2 = 4 μm, g = 2 μm, l = 28 μm, and d = 26 μm.In order to explore EIT response of the proposed terahertz graphene metamaterial, numerical calculations were carried out using the commercial finite difference time domain (FDTD) software package (CST Microwave Studio), where periodic boundary conditions were used for a unit cell in x- and y-directions, and perfectly matched layer boundary condition was applied in z plane. The plane wave polarizing along x-direction was normally incident to the structure surface along z-direction, as shown in Fig. 1(b). In the numerical calculations, the relative permittivities of the SiO2 layer and Si substrate were taken as 3.9 and 11.7 respectively, while the graphene was assumed to be an effective medium with thickness of d = 0.34 nm and relative complex permittivity of εr(ω) = 1 + jσ(ω)/(ωε0tg), in which the conductivity σ(ω) can be described as:30
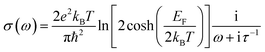 | (1) |
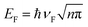 | (2) |
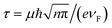 | (3) |
Results and discussions
Mechanism of EIT
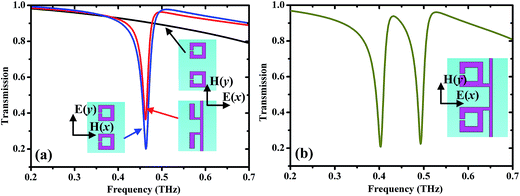
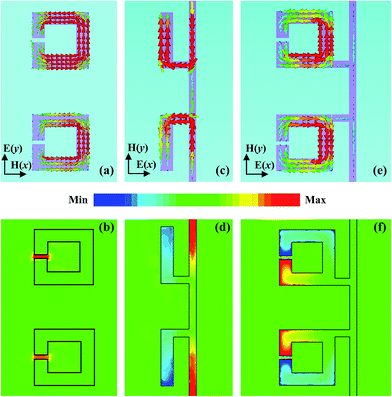
To clarify underlying forming process of the EIT window, the transmission spectra of three different structures with Fermi energy of 0.1 eV, which are the isolated vertical SRRs array, the isolated horizontal SRRs array, and the combined structure array (EIT structure), were calculated respectively, as shown in Fig. 2. It can be observed from Fig. 2(a) that when the incident wave excites along x-direction, the isolated vertical SRRs structure shows an obvious resonance at 0.463 THz (as illustrated by the red solid curve). However, in this case, the isolated horizontal SRRs structure is inactive because of the lack of electric field excitation (as depicted by the black solid curve). With electric field excitation along y-direction, on the other hand, a sharp resonance in the isolated horizontal SRRs structure can be easily excited at the same frequency as that of the isolated vertical SRRs structure (as shown by the blue solid curve). Thus, the vertical and horizontal SRR structures can serve as the bright and dark mode for the electric field excitation along x-direction, respectively. When these two types of resonators are combined together with a unit cell to form the EIT structure, and moreover the EIT structure is excited with the x-direction polarized electric field, the electromagnetic energy received in the bright mode can be transferred into the dark mode through the near field coupling between two resonators. As a result, the destructive interference resulting from the near field coupling between two modes induces a pronounced transparency window at 0.435 THz (as shown in Fig. 2(b)), which is well-known as the metamaterial-based EIT-like phenomenon.33To gain insight into the mechanism of the transparency window, the surface current and electric field distributions are calculated, as shown in Fig. 3. As observed in Fig. 3(a) and (b), the circulating currents in the isolated horizontal SRR structure are excited at 0.463 THz as the electric field excitation along y-direction, and the electric fields are concentrated in split gap of the horizontal SRR structure. For the isolated vertical SRR structure with y-direction polarized electric field excitation, however, the surface currents and electric field, similar to that of the isolated horizontal SRR structure, can be also observed at 0.463 THz, as displayed in Fig. 3(c) and (d). Thus, both the electric field and surface current distribution patterns confirm that the bright and dark modes are the typical LC resonance with different quality factor (Q), as shown in Fig. 2(a). Fig. 3(e) and (f) show the surface current and electric field distribution characteristics of the EIT structure at 0.435 THz. In the EIT structure, we notice that the dark mode is excited, while the bright mode is suppressed due to near field coupling between the vertical and horizontal SRR structures. The reasons are that the electric field redistribution caused by the vertical SRR structure enables the generation of the y-component of the electric field, activating the LC resonance in the horizontal SRR structure. Then, the indirectly excited dark mode couples back to the bright mode, as a result, the destructive interference resulting from the near field coupling between two modes induces a prominent transparency window.
Relaxation time dependence of EIT
According to the eqn (1), we notice that the conductivity of graphene depends on the relaxation time τ. Next, the effect of the relaxation time on the transparency window of the proposed EIT structure is investigated, which is hardly reported so far.34 Fig. 4 shows the transmission spectra for different τ and the other parameters same as those used in Fig. 2. It can be seen that as τ increases, the amplitude of the transparency peak is gradually enhanced, while the location of the transparency peak is almost unchanged (gray region as shown in Fig. 4). For example, for lower values of τ, the absorption becomes dominant, and the transmission efficiency reduces due to higher loss. In contrast, for higher ones, an enhanced EIT peak can be observed, thus, the modulation depth (Tmod, Tmod = ΔT/Tmax) of about 20% is obtained at 0.435 THz as increasing the relaxation time from 2.76 ps to 41.33 ps. The enhanced reasons are that the charge carriers contributed to two coupled graphene SRRs structures increase with the relaxation time increasing, leading to the enhancement of the coupling strength between two resonant elements, as a result, a sharp transparency window is induced at 0.435 THz.35 Therefore, the amplitude of the transparency peak can be actively tuned by changing the relaxation time.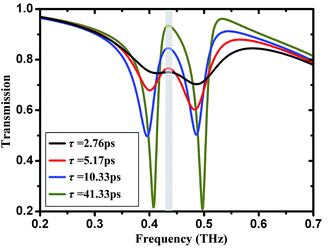 | ||
| Fig. 4 Transmission spectra of the proposed terahertz EIT metamaterial for various relaxation time from 2.76 ps to 41.33 ps. | ||
Fermi energy dependence of EIT
To further explore modulation of the transparency window, the transmission spectra of the designed EIT structure with different Fermi energy are also calculated, as shown in Fig. 5. As observed, the transparency peak shows a clear blue-shift in the interested frequency range as increase in Fermi energy from 0.1 eV to 0.5 eV, while the corresponding amplitude is almost unchanged (gray region in Fig. 5). This blue-shifting behavior can be attributed to change in resonant frequency of two graphene resonators, in which the resonant frequency can be written as f ∝ EF.36,37 Based on the tunable response, moreover, the designed structure can realize the switching and modulation functions in the interested frequency range. For example, the transmission amplitude of the EIT structure can be switched between 0.09 and 0.91 at 0.60 THz as changing Fermi energy from 0.2 eV to 0.3 eV, or between 0.06 and 0.90 at 0.676 THz as changing Fermi energy from 0.3 eV to 0.5 eV. In addition, as varying Fermi energy in the range of 0.1–0.5 eV, the position of the transparency window can be modulated in the range of 0.435–0.676 THz, and the corresponding frequency modulation depth (fmod = Δf/fmax) is 36%. Moreover, the modulation range and depth can be further improved by increasing the value of Fermi energy, as demonstrated in the previous results.38 Therefore, an actively controllable transparency window in our EIT structure can be obtained by changing Fermi energy of the graphene.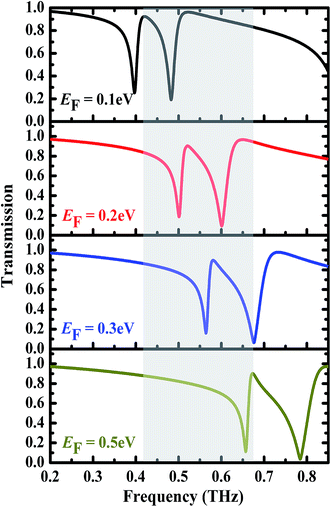 | ||
| Fig. 5 Transmission spectra of the proposed terahertz EIT metamaterial with various values of Fermi energy from 0.1 eV to 0.5 eV. | ||
Group delay of EIT
As well known, a remarkable characteristic of EIT-like response is strong phase dispersion in transparent window region, which can reduce the group velocity. Thus, tunable characteristics of the transparency window in EIT structure is also utilized to actively control slow light behavior. As expected, our designed EIT structure can also exhibit sharp phase dispersion in the transparency window region (no shown here), which indicates that it is very extremely attractive for slow-light controls.15 According to ref. 39 and 40, the group delay can be calculated by the expression: τg = −dφ/dω where φ and ω = 2πf are the phase shift and frequency of transmission spectrum, respectively. Fig. 6 shows the calculated group delays of our EIT structure for different relaxation time. As observed in Fig. 6, the positive and negative group delays can be obtained in the vicinity of the transparency window, which correspond to slow and fast light effects respectively. Moreover, the slow light effect can be actively tuned through changing the relaxation time from 2.76 ps to 41.33 ps. For example, for τ = 2.76 ps, the calculated group delay has a lower value of 0.245 ps at 0.435 THz, whereas as τ = 41.33 ps, a larger group delay value of 7.29 ps is obtained at 0.435 THz. Thus, the proposed EIT structure allows for active modulation of group delay up to 30 times by controlling the relaxation time. To further explore active controlling of slow light effect, the group delays of the designed EIT structure with different Fermi energy are also calculated, as shown in Fig. 7. We observe that the region of the group delay exhibits clear blue-shift, and becomes slightly wide with Fermi energy increasing from 0.1 eV to 0.5 eV (different color regions in Fig. 7). In addition, we also notice that the corresponding peak value of the group delay can be tuned from 7.7 ps to 15.7 ps. Therefore, these results show that active controlling of slow light effect can be obtained through changing the relaxation time or Fermi energy, which would enhance the applications of graphene-based metamaterials devices in the future terahertz telecommunication field.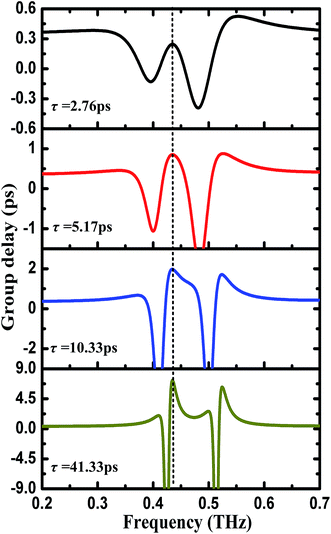 | ||
| Fig. 6 Group delay of the proposed terahertz EIT metamaterial for various relaxation time from 2.76 ps to 41.33 ps. | ||
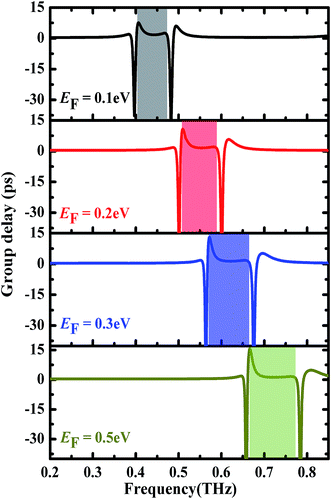 | ||
| Fig. 7 Group delay of the proposed terahertz EIT metamaterial with various values of Fermi energy from 0.1 eV to 0.3 eV. | ||
Conclusions
In conclusion, we have numerically demonstrated an actively controllable EIT window in a terahertz graphene metamaterial consisting of two coupled split ring resonators placed in orthogonally twisted fashion. The surface currents reveal that the destructive interference resulting from the near field coupling between two resonators induces a distinct transparency window. As change in the relaxation time from 2.76 ps to 41.33 ps, more importantly, the EIT structure can realize the modulation depth of 20% in the transparency peak and the active controlling of up to 30 times in the group delay at 0.435 THz. By shifting the Fermi energy, in addition, both the transparency window and the corresponding group delay range show clearly blue-shift. Therefore, the graphene-based metamaterial with actively tunable EIT window can exhibit the potential applications in developing novel devices, such as modulators, switches buffers, and optical delays.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work is supported by the National Natural Science Foundation of China (51672062, 51575149, 61501275 and 51402075), Heilongjiang Province Natural Science Foundation of China (F201309 and QC2015073), the Postdoctoral Science-Research Developmental Foundation of Heilongjiang Province (LBH-Q11082), the Youth Academic Backbone Support Plan of Heilongjiang Province Ordinary College (1253G026), Special Funds of Harbin Innovation Talents in Science and Technology Research (2014RFQXJ031) and Science Funds for the Young Innovative Talents of HUST (201104).References
- K. J. Boller, A. Imamoglu and S. E. Harris, Phys. Rev. Lett., 1991, 66, 2593 CrossRef CAS PubMed.
- A. H. Safavi-Naeini, T. P. Mayer, J. Chan, M. Eichenfield, M. Winger, Q. Lin, J. T. Hill, D. E. Chang and O. Painter, Nature, 2011, 472, 69–73 CrossRef CAS PubMed.
- L. Dai, Y. Liu and C. Jiang, Opt. Express, 2011, 19, 1461–1469 CrossRef PubMed.
- L. V. Hau, S. E. Harris, Z. Dutton and C. H. Behroozi, Nature, 1999, 397, 594 CrossRef CAS.
- M. M. Kash, V. A. Sautenkov, A. S. Zibrov, L. Hollberg, G. R. Welch, M. D. Lukin, Y. Rostovtsev, E. S. Fry and M. O. Scully, Phys. Rev. Lett., 1999, 82, 5229 CrossRef CAS.
- J. Zhang, G. Hernandez and Y. Zhu, Opt. Lett., 2008, 33, 46–48 CrossRef PubMed.
- R. W. Boyd, J. Opt. Soc. Am. B, 2011, 28, A38 CrossRef CAS.
- V. M. Acosta, K. Jensen, C. Santori, D. Budker and R. G. Beausoleil, Phys. Rev. Lett., 2013, 110, 213605 CrossRef CAS PubMed.
- P. Tassin, L. Zhang, R. Zhao, A. Jain, T. Koschny and C. M. Soukoulis, Phys. Rev. Lett., 2012, 109, 187401 CrossRef PubMed.
- L. Qin, K. Zhang, R. W. Peng, X. Xiong, W. Zhang, X. R. Huang and M. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 125136 CrossRef.
- Z. Ye, S. Zhang, Y. Wang, Y. Park, T. Zentgraf, G. Bartal, X. Yin and X. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 155148 CrossRef.
- N. Liu, L. Langguth, T. Weiss, J. Kastel, M. Fleischhauer, T. Pfau and H. Giessen, Nat. Mater., 2009, 8, 758–762 CrossRef CAS PubMed.
- C. Argyropoulos, F. Monticone, G. D'Aguanno and A. Alù, Appl. Phys. Lett., 2013, 103, 143113 CrossRef.
- C. Kurter, P. Tassin, L. Zhang, T. Koschny, A. P. Zhuravel, A. V. Ustinov, S. M. Anlage and C. M. Soukoulis, Phys. Rev. Lett., 2011, 107, 04390 CrossRef PubMed.
- W. Cao, R. Singh, C. H. Zhang, J. G. Han, M. Tonouchi and W. L. Zhang, Appl. Phys. Lett., 2013, 103, 101106 CrossRef.
- J. Q. Gu, R. Singh, X. J. Liu, X. Q. Zhang, Y. F. Ma, S. Zhang, S. A. Maier, Z. Tian, A. K. Azad, H. T. Chen, A. J. Taylor, J. G. Han and W. L. Zhang, Nat. Commun., 2012, 3, 1151 CrossRef PubMed.
- X. Su, C. Ouyang, N. Xu, S. Tan, J. Gu, Z. Tian, R. Singh, S. Zhang, F. Yan, J. Han and W. Zhang, Sci. Rep., 2015, 5, 10823 CrossRef CAS PubMed.
- P. Pitchappa, M. Manjappa, C. P. Ho, R. Singh, N. Singh and C. K. Lee, Adv. Opt. Mater., 2016, 4, 541–547 CrossRef CAS.
- X. J. He, Q. X. Ma, P. Jia, L. Wang, T. Y. Li, F. M. Wu and J. X. Jiang, Integr. Ferroelectr., 2015, 161, 85–91 CrossRef CAS.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- A. N. Grigorenko, M. Polini and K. S. Novoselov, Nat. Photonics, 2012, 6, 749–758 CrossRef CAS.
- K. S. Novoselov, V. I. Fal'ko, L. Colombo, P. R. Gellert, M. G. Schwab and K. Kim, Nature, 2012, 490, 192–200 CrossRef CAS PubMed.
- L. Ju, B. S. Geng, J. Horng, C. r Girit, M. Martin, Z. Hao, H. A. Bechtel, X. G. Liang, A. Zettl, Y. R. Shen and F. Wang, Nat. Nanotechnol., 2011, 6, 630 CrossRef CAS PubMed.
- X. Y. He, P. Q. Gao and W. Z. Shi, Nanoscale, 2016, 8, 10388–10397 RSC.
- X. Y. He, F. T. Lin, F. Liu and W. Z. Shi, Nanotechnology, 2016, 27, 485202 CrossRef PubMed.
- X. Y. He, Carbon, 2015, 82, 229–237 CrossRef CAS.
- X. L. Zhao, C. Yuan, L. Zhu and J. Q. Yao, Nanoscale, 2016, 8, 15273–15280 RSC.
- F. Valmorra, G. Scalari, C. Maissen, W. Y. Fu, C. Schonenberger, J. W. Choi, H. G. Park, M. Beck and J. Faist, Nano Lett., 2013, 13, 3193 CrossRef CAS PubMed.
- P. Q. Liu, I. J. Luxmoore, S. A. Mikhailov, N. A. Savostianova, F. Valmorra, J. Faist and G. R. Nash, Nat. Commun., 2015, 6, 8969 CrossRef CAS PubMed.
- W. W. Tang, L. Wang, X. S. Chen, C. L. Liu, A. Q. Yu and W. Lu, Nanoscale, 2016, 8, 15196 RSC.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197 CrossRef CAS PubMed.
- Y. Zhang, Y.-W. Tan, H. L. Stormer and P. Kim, Nature, 2005, 438, 201 CrossRef CAS PubMed.
- S. Zhang, D. A. Genov, Y. Wang, M. Liu and X. Zhang, Phys. Rev. Lett., 2008, 101, 047401 CrossRef PubMed.
- X. L. Zhao, C. Yuan, L. Zhu and J. Q. Yao, Nanoscale, 2016, 8, 15273–15280 RSC.
- F. R. Ling, G. Yao and J. Q. Yao, Sci. Rep., 2016, 6, 34994 CrossRef CAS PubMed.
- J. Ding, B. Arigong, H. Ren, M. Zhou, J. Shao, M. Lu, Y. Chai, Y. Lin and H. Zhang, Sci. Rep., 2014, 4, 6128 CrossRef CAS PubMed.
- J. X. Jiang, Q. F. Zhang, Q. X. Ma, S. T. Yan, F. M. Wu and X. J. He, Opt. Mater. Express, 2015, 5, 1962 CrossRef CAS.
- D. Rodrigo, O. Limaj, D. Janner, D. Etezadi, F. J. García de Abajo, V. Pruneri and H. Altug, Science, 2015, 349, 165 CrossRef CAS PubMed.
- T. Zentgraf, S. Zhang, R. F. Oulton and X. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 195415 CrossRef.
- L. Zhang, P. Tassin, T. Koschny, C. Kurter, S. M. Anlage and C. M. Soukoulis, Appl. Phys. Lett., 2010, 97, 241904 CrossRef.
| This journal is © The Royal Society of Chemistry 2017 |