Open Access Article
Open Access ArticleSize of the rare-earth ions: a key factor in phase tuning and morphology control of binary and ternary rare-earth fluoride materials†
Pushpal Ghosh *a,
Rahul Kumar Sharmaa,
Yogendra Nath Chouryala and
Anja-Verena Mudring‡
*a,
Rahul Kumar Sharmaa,
Yogendra Nath Chouryala and
Anja-Verena Mudring‡
 *bc
*bc
aSchool of Chemical Science and Technology, Department of Chemistry, Dr H. S. Gour University (A Central University), Sagar-470003, Madhya Pradesh, India. E-mail: pushpalghosh27@gmail.com
bDepartment of Materials Science and Engineering, Iowa State University, Ames, IA 50014, USA. E-mail: mudring@iastate.edu
cThe Critical Materials Institute, Ames Laboratory, Ames, IA 50011, USA
First published on 3rd July 2017
Abstract
In an ionic liquid assisted solvothermal synthesis developed by us for the synthesis of rare-earth (RE) fluorides, it is possible to control the product formation by the choice of the rare earth ion. For rare-earth cations with smaller ionic radii (below 1.075 Å), cubic NaREF4 with a spherical morphology is obtained, whilst for rare-earth cations with radii between 1.08 Å and 1.13 Å, the formation of hexagonal NaREF4 with a nanorod-like morphology is observed. For rare earth ions with a larger radius than that of La3+ (1.216 Å), instead of ternary fluorides, binary fluorides REF3 in the trigonal modification is obtained. The growth mechanism behind this morphology change is explained from atomistic origin using electron microscope studies. The lattice strain changes with the rare-earth fluoride phase. For cubic NaREF4 a tensile strain is observed, whilst for the hexagonal and trigonal binary fluoride a compressive strain is observed. The optical properties of the obtained materials promises use for various optoelectronic applications.
1. Introduction
Over the last decade rare-earth (RE) ion doped materials have drawn tremendous attention in the field of photonic and biophotonic applications.1–10 With respect to their narrow emission bands, large Stokes shifts, weak autofluorescence and decay times typically in the range of milliseconds, RE-doped materials in certain respects are superior to organic dyes and semiconductors.11,12 A judicious choice of the host and dopant ion/ion pairs is a precondition to obtain the desired optical materials.1 The main criteria in the choice of a suitable host matrix are a low phonon energy, a high refractive index and easy incorporation of dopants together with chemical and thermal stability.13 Based on these criteria, binary and ternary fluorides appear to be effective host materials for RE3+ ion doping.14–22 For rare-earth trifluorides, REF3, two polymorphs are known. Their relative stability depends on the rare earth ionic radius and temperature. For the lighter REF3 (RE = La–Nd) with larger ionic radius the trigonal tysonite type of structure (LaF3, P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c1) is the stable form, whilst for the heavier REF3 with smaller RE3+ (Dy–Lu, Y, YF3 type) and the orthorhombic β-YF3 (Pnma) is the preferred structure. REF3 with RE3+ ions that have a size in between are dimorphic with the orthorhombic form being the room temperature stable phase and the tysonite structure being the high temperature phase.23–25 Similarly, sodium ternary rare earth fluorides are known to form two polymorphs: a cubic phase and a hexagonal phase.26 Whilst classical high temperature synthesis methods typically lead to the thermodynamically stable form, on the nanoscale by a judicious choice of the reaction conditions, it is possible to selectively obtain the less stable form. For nanomaterials, it is possible to tune the crystal phase by variation of the reaction conditions, such as temperature, pH of the reaction, Ln3+/F− ratio, addition of a surfactant or capping agent, calcination temperature etc.27–30 Recently a strategy for phase tuning that relies on ion doping has been developed for NaREF4 NCs (nanocrystals).31–33 For optical materials, either the trigonal REF3 form or, even more, the hexagonal modification of NaREF4 is the researcher's choice due to the higher luminescence efficiency. A wide number of NaREF4 materials doped with various RE3+ ions as up and down converting materials have been reported.34–42 By tuning the crystal phase of the host materials, the luminescence dynamics of the RE ion can be tuned.14,18,26,29 Similarly morphology is an important parameter to tune the luminescence dynamics as illustrated by Mai et al. which had prepared sodium europium fluoride nanospheres, nanopolyhedra and nanorods and compared their fluorescence emission spectra on the basis of different morphologies.37 Similar morphology dependent studies have been reported for other rare-earth doped materials.43–46
c1) is the stable form, whilst for the heavier REF3 with smaller RE3+ (Dy–Lu, Y, YF3 type) and the orthorhombic β-YF3 (Pnma) is the preferred structure. REF3 with RE3+ ions that have a size in between are dimorphic with the orthorhombic form being the room temperature stable phase and the tysonite structure being the high temperature phase.23–25 Similarly, sodium ternary rare earth fluorides are known to form two polymorphs: a cubic phase and a hexagonal phase.26 Whilst classical high temperature synthesis methods typically lead to the thermodynamically stable form, on the nanoscale by a judicious choice of the reaction conditions, it is possible to selectively obtain the less stable form. For nanomaterials, it is possible to tune the crystal phase by variation of the reaction conditions, such as temperature, pH of the reaction, Ln3+/F− ratio, addition of a surfactant or capping agent, calcination temperature etc.27–30 Recently a strategy for phase tuning that relies on ion doping has been developed for NaREF4 NCs (nanocrystals).31–33 For optical materials, either the trigonal REF3 form or, even more, the hexagonal modification of NaREF4 is the researcher's choice due to the higher luminescence efficiency. A wide number of NaREF4 materials doped with various RE3+ ions as up and down converting materials have been reported.34–42 By tuning the crystal phase of the host materials, the luminescence dynamics of the RE ion can be tuned.14,18,26,29 Similarly morphology is an important parameter to tune the luminescence dynamics as illustrated by Mai et al. which had prepared sodium europium fluoride nanospheres, nanopolyhedra and nanorods and compared their fluorescence emission spectra on the basis of different morphologies.37 Similar morphology dependent studies have been reported for other rare-earth doped materials.43–46
In this article we report the phase and morphology selective synthesis of rare earth doped binary and ternary rare-earth fluorides employing an ionic liquid (IL) assisted solvothermal method. 1-ethyl-3-methyl imidazolium bromide (C2mimBr) is used as the structure controlling agent. The RE3+/F− ratio is taken as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 in all the cases. Depending on the ionic radius of the chosen host RE3+ ion, a different NaREF4 polymorph for a given RE or even only formation of the binary REF3 is observed. For example, in the ionic radius range of 1.075 Å to 1.042 Å, cubic NaREF4 particles with sphere-like morphology are obtained (Scheme 1).47 However, for RE′′3+ ions with larger ionic radius in the range of 1.13 to 1.095 Å (for Sm3+ to Tb3+), hexagonal sodium ternary fluoride with nanorod-like morphology is obtained. A drastic change occurs when a RE′′3+ ion with quite a large radius is chosen like La3+ (1.216 Å). Instead of a ternary fluoride, the binary fluoride with hexagon like morphology is obtained (Scheme 1). Normally phase transition and morphology control of nanomaterials need at least one of the following changes: heating at high temperature, change of the reaction parameters like reactant ratio, pH etc. and other external influences.48–52 This type of tuning of the crystal phase, lattice strain, morphology and most importantly nature of the product depending on the ionic radius or size of the RE3+ ion is novel and not reported earlier to the best of our knowledge.
8 in all the cases. Depending on the ionic radius of the chosen host RE3+ ion, a different NaREF4 polymorph for a given RE or even only formation of the binary REF3 is observed. For example, in the ionic radius range of 1.075 Å to 1.042 Å, cubic NaREF4 particles with sphere-like morphology are obtained (Scheme 1).47 However, for RE′′3+ ions with larger ionic radius in the range of 1.13 to 1.095 Å (for Sm3+ to Tb3+), hexagonal sodium ternary fluoride with nanorod-like morphology is obtained. A drastic change occurs when a RE′′3+ ion with quite a large radius is chosen like La3+ (1.216 Å). Instead of a ternary fluoride, the binary fluoride with hexagon like morphology is obtained (Scheme 1). Normally phase transition and morphology control of nanomaterials need at least one of the following changes: heating at high temperature, change of the reaction parameters like reactant ratio, pH etc. and other external influences.48–52 This type of tuning of the crystal phase, lattice strain, morphology and most importantly nature of the product depending on the ionic radius or size of the RE3+ ion is novel and not reported earlier to the best of our knowledge.
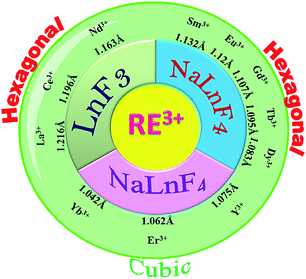 | ||
| Scheme 1 Tuning of crystal phase and nature of product (binary/ternary) depending on the size of the RE3+ ions for RE-doped NaREF4. | ||
2. Experimental
2.1 Synthesis
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8. The mixture was poured into a Teflon™ lined autoclave (Parr Instruments, Moline, Illinois, USA) and subsequently heated at 200 °C for 4 hours. The obtained nanocrystals was washed several times with ethanol, methanol and finally acetone and dried in an oven at 80 °C.
8. The mixture was poured into a Teflon™ lined autoclave (Parr Instruments, Moline, Illinois, USA) and subsequently heated at 200 °C for 4 hours. The obtained nanocrystals was washed several times with ethanol, methanol and finally acetone and dried in an oven at 80 °C.| Name of the sample | Crystal phase | Crystallite size (nm) | Reaction time & temperature | Concentration of NaCl solution/M | Concentration of the rare-earth nitrate solution/M | Concentration of NH4F solution/M |
|---|---|---|---|---|---|---|
| NaYF4:Eu3+ (P1) | Cubic | 17.32 | 4 h & 200 °C | 0.265 | 0.265 | 2.126 |
| LaF3:Dy3+ (P2) | Trigonal | 10.30 | 4 h & 200 °C | 0.21 | 0.21 | 1.680 |
| CeF3 (P3) | Trigonal | 11.8 | 4 h & 200 °C | 0.21 | 0.21 | 1.680 |
| CeF3:Tb3+ (P4) | Trigonal | 12.03 | 4 h & 200 °C | 0.208 | 0.209 | 1.671 |
| NdF3 (P5) | Trigonal | 14.8 | 4 h & 200 °C | 0.205 | 0.205 | 1.644 |
| NaSmF4 (P6) | Hexagonal | 10.41 | 4 h & 200 °C | 0.200 | 0.200 | 1.644 |
| NaGdF4:Eu3+ (P7) | Hexagonal | 9.13 | 4 h & 200 °C | 0.196 | 0.196 | 1.568 |
| NaTbF4:Ce3+ (P8) | Hexagonal | 7.59 | 4 h & 200 °C | 0.193 | 0.193 | 1.55 |
| NaDyF4 (P9) | Hexagonal (major) + cubic (minor) | 25.8 | 4 h & 200 °C | 0.188 | 0.190 | 1.526 |
| NaErF4:Yb3+ (P10) | Cubic | 16.56 | 4 h & 200 °C | 0.187 | 0.187 | 1.502 |
| NaYbF4:Er3+ (P11) | Cubic | 9.5 | 4 h & 200 °C | 0.184 | 0.184 | 1.47 |
2.2 Characterization
PXRD (powder X-ray diffraction) measurements were carried out on a Huber G70 diffractometer (Rimsting, Germany) using Mo-Kα radiation (λ = 0.07107 nm). The crystallite size was calculated using the Scherer equation D = Kλ/β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, where K = 0.9, D represents crystallite size (Å), λ is the wavelength of the Mo-Kα radiation, and β is the corrected half-width of the diffraction peak. TEM (transmission electron microscopy; a FEI Tecnai STWIN-T30 using 300 kV electron beam source) was used to investigate the shape, size and lattice structure of the nanocrystals dispersed on a carbon coated copper grid from acetone solution. Morphological characterization was also carried out by SEM (scanning electron microscopy) using a NOVA NANO SEM-450, FEI. Excitation, emission spectra and decay time of all samples were recorded on a Fluorolog 3 (HORIBA JOBIN YVON, Germany) luminescence spectrometer equipped with steady and pulsed Xe lamps for sample excitation and a photomultiplier for signal detection.
θ, where K = 0.9, D represents crystallite size (Å), λ is the wavelength of the Mo-Kα radiation, and β is the corrected half-width of the diffraction peak. TEM (transmission electron microscopy; a FEI Tecnai STWIN-T30 using 300 kV electron beam source) was used to investigate the shape, size and lattice structure of the nanocrystals dispersed on a carbon coated copper grid from acetone solution. Morphological characterization was also carried out by SEM (scanning electron microscopy) using a NOVA NANO SEM-450, FEI. Excitation, emission spectra and decay time of all samples were recorded on a Fluorolog 3 (HORIBA JOBIN YVON, Germany) luminescence spectrometer equipped with steady and pulsed Xe lamps for sample excitation and a photomultiplier for signal detection.
3. Result and discussion
3.1 Structural characterization by powder X-ray diffraction and phase evolution
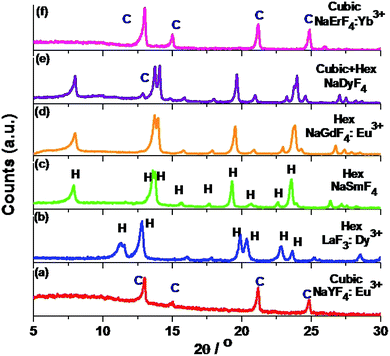
Solvothermal conversion of sodium chloride and an appropriate amount of yttrium and europium nitrate in ethanol/water solution in the presence of [C2mim]Br yielded nanosized NaYF4:Eu3+ (P1). For a reaction time of 4 hours at 200 °C, only cubic NaYF4:Eu3+ (P1) is obtained (Fig. 1a). A detailed study of the effect of the IL, reaction temperature and reactant ratio (Ln3+/F−) has already been reported by us earlier.14 Now this synthesis protocol is explored for other elements of the rare earth series. It turned out that, depending on the rare earth ion size, different products, either a ternary NaREF4 polymorph or binary REF3 in the tysonite type of structure are obtained (Fig. 1 and Scheme 1). In the case of Y3+, with an ionic radius of 1.075 Å (using the Shannon radius47 for a 9-fold co-ordination) cubic NaYF4 (P1) (Fig. 1) nanocrystals are obtained. For RE3+ ions with an ionic radius in the range of 1.13 to 1.095 Å (for Sm3+ to Tb3+), hexagonal sodium ternary fluoride (NaLnF4: Ln = Sm3+, Gd3+, Tb3+ (P6–P8) in Table 1) is obtained (see Fig. 1, S1† and Table 1).Interestingly, for Dy3+ where the ionic radius is in between that of Tb3+ and Er3+, the cubic modification starts to appear with the majority phase being hexagonal (P9) (as shown in Fig. 1). When the ionic radius is lesser due to lanthanide contraction as in case of Er3+ (1.062 Å) and Yb3+ (1.042 Å) only the cubic polymorph (NaErF4 and NaYbF4, P10 and P11) is obtained (Fig. 1, S1† and Table 1). At the start of the lanthanide series (for example, for La3+ with an ionic radius of 1.216 Å), the formation of the binary rare earth fluoride (P2) instead of the ternary fluoride is observed and this trend is maintained until Nd3+ (ionic radius 1.163 Å). It can be anticipated that for smaller size, as for Y3+ and for Er3+, Yb3+, the reaction rate is quite faster which leads to the formation of the kinetic product, the cubic phase. When the size of the RE3+ ion is larger, as for La3+, the reaction rate is slower causing the formation of the binary fluoride instead of the ternary fluoride. For RE3+ ions within the range of 1.132 to 1.093 Å, reaction rate is optimum for the generation of thermodynamically stable hexagonal ternary fluoride. This kind of phase tuning depending on the size of the RE3+ ion is novel and not previously reported to the best of our knowledge.
3.2 Lattice strain
Generally, the broadening of the diffraction peaks in a PXRD pattern depends upon strain and crystallite size. It is previously noticed that change in the interatomic distance induces the perturbation in the lattice parameter of crystalline nanomaterials leading to stress generation at nanoscale particles. And it is well known that higher the size-volume ratio more will be the strain at the nanoscale level.53 Herein, the lattice strain in the as-prepared nanoparticles can be attributed to the change in ionic radius of the RE3+ of the host materials. Lattice strain is changing with changing the ionic radius of RE3+ ion in lanthanide series. It means, lattice parameter of host lattice is perturbing in period. It is possible to calculate the lattice strain according to the function derived by Williamson and Hall:51
β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ = 1/D + η θ/λ = 1/D + η![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ θ/λ
| (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ against sin
θ/λ against sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ, the strain is the slope and the crystallite size (D) can be derived from the intercept (Fig. 2 and Table 2).52 The lattice strain clearly depends on the size of the rare earth precursor ion. For example, for the binary fluorides where the ionic radius of the precursor RE ion is in the range of 1.216 Å to 1.163 Å (La3+ to Nd3+), compressive strain is obtained (Table 2). The lattice strain for CeF3:Tb3+ (P4) is compressive (−3.11%) and the crystallite size obtained from the intercept with the x-axis is 17.31 nm which matches with the size obtained from Scherrer equation (Fig. 2a). Likewise, for the RE3+ ions with medium ionic radius (1.132 Å to 1.083 Å for Sm3+ to Dy3+ ions) where the crystal phase is again hexagonal, the obtained lattice strain is compressive (Table 2). For example for NaGdF4 (P7), a compressive strain of −2.17% is obtained and crystallite size is ∼21 nm (Fig. 2b). However when the size of the rare earth ion is less, for example, for Y3+ and for Er3+ and Yb3+ due to lanthanide contraction, the cubic phase is observed and a drastic change is noticed in lattice strain i.e., tensile strain is obtained. Fig. 3c shows the plot for NaErF4:Yb3+ (P10) showing a tensile strain of +0.19%. Earlier we have reported that cubic sodium yttrium fluoride shows tensile strain however its hexagonal analogue shows compressive strain. Compressive strain is typically observed for smaller crystallite sizes.50
θ/λ, the strain is the slope and the crystallite size (D) can be derived from the intercept (Fig. 2 and Table 2).52 The lattice strain clearly depends on the size of the rare earth precursor ion. For example, for the binary fluorides where the ionic radius of the precursor RE ion is in the range of 1.216 Å to 1.163 Å (La3+ to Nd3+), compressive strain is obtained (Table 2). The lattice strain for CeF3:Tb3+ (P4) is compressive (−3.11%) and the crystallite size obtained from the intercept with the x-axis is 17.31 nm which matches with the size obtained from Scherrer equation (Fig. 2a). Likewise, for the RE3+ ions with medium ionic radius (1.132 Å to 1.083 Å for Sm3+ to Dy3+ ions) where the crystal phase is again hexagonal, the obtained lattice strain is compressive (Table 2). For example for NaGdF4 (P7), a compressive strain of −2.17% is obtained and crystallite size is ∼21 nm (Fig. 2b). However when the size of the rare earth ion is less, for example, for Y3+ and for Er3+ and Yb3+ due to lanthanide contraction, the cubic phase is observed and a drastic change is noticed in lattice strain i.e., tensile strain is obtained. Fig. 3c shows the plot for NaErF4:Yb3+ (P10) showing a tensile strain of +0.19%. Earlier we have reported that cubic sodium yttrium fluoride shows tensile strain however its hexagonal analogue shows compressive strain. Compressive strain is typically observed for smaller crystallite sizes.50
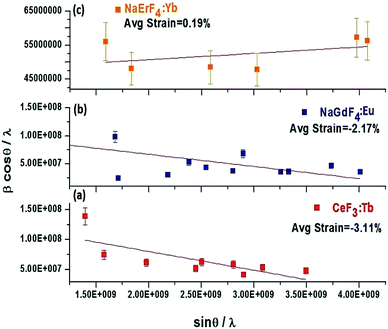 | ||
Fig. 2 Plot of β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ against sin θ/λ against sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ for CeF3:Tb3+ (a) NaGdF4:Eu3+ (b) and NaErF4:Yb3+ (c) prepared solvothermally using [C2mim]Br at 200 °C. θ/λ for CeF3:Tb3+ (a) NaGdF4:Eu3+ (b) and NaErF4:Yb3+ (c) prepared solvothermally using [C2mim]Br at 200 °C. | ||
| S. no. | Sample | Ionic radius (Å) | Crystal phase | Average strain (±5.0%) | Crystallite size (nm)a | Lattice strain |
|---|---|---|---|---|---|---|
| a Estimated deviation. | ||||||
| 1. | LaF3:Dy3+ (P2) | 1.216 | Trigonal | −8.1 | 11.83(±0.2) | Compressive |
| 2. | CeF3:Tb3+ (P4) | 1.196 | Trigonal | −3.11 | 17.31(±0.2) | Compressive |
| 3. | NdF3 (P5) | 1.163 | Trigonal | −2.01 | 12.3(±0.3) | Compressive |
| 4. | NaSmF4 (P6) | 1.132 | Hexagonal | −1.245 | 19.68(±0.2) | Compressive |
| 5. | NaGdF4:Eu3+ (P7) | 1.107 | Hexagonal | −2.17 | 20.99(±0.2) | Compressive |
| 6. | NaTbF4 (P8) | 1.095 | Hexagonal | −1.87 | 23.09(±0.2) | Compressive |
| 7. | NaDyF4 (P9) (hexagonal) | 1.083 | Hexagonal | −0.73 | 21.8(±0.2) | Compressive |
| 8. | NaYF4:Eu3+ (P1) | 1.075 | Cubic | +0.89 | 21.2(±0.2) | Tensile |
| 9. | NaErF4:Yb3+ (P10) | 1.062 | Cubic | +0.19 | 15.99(±0.3) | Tensile |
| 10. | NaYbF4:Er3+ (P11) | 1.042 | Cubic | +0.7 | 22.5(±0.2) | Tensile |
3.3 Structural characterizations by scanning electron microscope
To investigate the morphology of the nanoparticles, SEM images are analyzed in detail. Fig. 3a shows the SEM images of CeF3:Tb3+ doped nanocrystals showing nanoparticles with hexagon-like disc shape, whilst for LaF3:Dy3+ (P2) shows cube like morphology (Fig. S2a† inset). A clear change in morphology is observed for NaGdF4:Eu3+ (P7) doped nanocrystals (Fig. 3b). Though the majority of the nanocrystals look spherical, some bunches of cylindrical shape nanostructures are noticed (Fig. 3b). A similar observation is made for NaDyF4 (P9) nanocrystals (Fig. 3c). PXRD analyses show that for both NaGdF4:Eu3+ and NaDyF4 the hexagonal modification is the majority phase and the cubic the minority. For NaYF4 nanocrystals doped with Eu3+ ions, spherical nanoparticles are obtained (Fig. 3d). Though the crystal phase is same as that of NaYF4 and ionic radius of Eu3+ is comparable with Y3+, NaErF4:Yb3+ (P10) shows almost monodisperse, oval shaped particles with a higher crystallinity and higher particle size (16.56 nm) which nicely matches with the crystallite size obtained from the Scherrer equation (Fig. 3e). Interestingly, some cubes can be noticed among the oval shaped nanoparticles (Fig. 3e). A similar observation can be made for the NaYbF4:Er3+ (P11) nanoparticles (Fig. 3f) though particle size is little bigger.3.4 Structural characterizations by transmission electron microscope
To understand the morphology evolution from its atomistic origin, TEM images are analyzed in detail. 10 representative examples, LaF3:Dy3+ (P2); CeF3:Tb3+ (P4); NdF3 (P5); NaSmF4 (P6); NaGdF4:Eu3+ (P7); NaTbF4:Ce3+ (P8); NaDyF4 (P9); NaYF4:Eu3+ (P1); NaErF4:Yb3+ (P10) and NaYbF4:Er3+ (P11) are taken from the three classes of fluoride materials made based on the ionic radius/size of the RE3+ ion.From Fig. 4a and b, it is noticed that hexagonal benzene like particles were found which have narrow range of aspect ratio (ca. 1.15 to 2.4). Most of the particles are isotropic (length of diagonal is same) in size. Small size particles are usually spherical whereas well matured particles have attended the highly regular hexagonal like shape. From HRTEM images, it can be seen that the growth of these particles are predominantly occurring along the (111) plane (as shown in Fig. 5a and b). And the spacing between the planes is 0.325 nm for the CeF3. So it can be inferred that the [C2mim]+ ion can serve as a capping agent based on the strong interaction with the (111) facets which favour the directional growth of the hexagonal phase. As the most exposed facets of the CeF3:Tb3+ nanorods are (111) planes, the energy difference between them is minimal, facilitating the oriented attachment via twin boundaries which is noticed in the encircled area of Fig. 5b.54,55
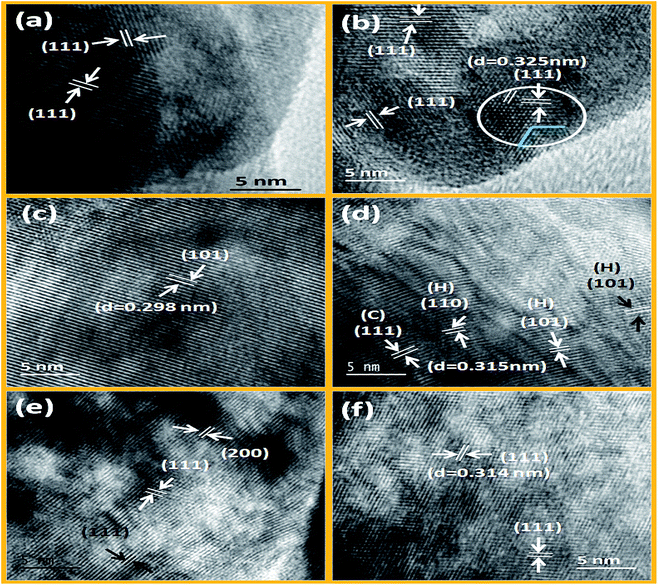 | ||
| Fig. 5 HRTEM images of LaF3:Dy3+, CeF3:Tb3+ (a and b) NaGdF4:Eu3+, NaDyF4 (c and d) and NaErF4:Yb3+, NaYbF4:Er3+ (e and f) nanocrystals prepared solvothermally at 200 °C. | ||
The shape of the particles was also confirmed through the SAED images of LaF3 and CeF3, where single crystalline hexagonal diffraction patterns were observed (Fig. S5a and b†). Bright diffracting planes are belonging to (111), (112), (113), (300), (311) and (111), (112), (113), (222) planes of the LaF3 and CeF3 respectively. Thus, it is evidently confirmed that (111) plane is the dominating plane for both LaF3 and CeF3 nanoparticles (shown in Fig. S5a and b†). Furthermore, a′ b′ and b′ c′ planes are equally spaced (3.16 nm−1) and edge length of the drawn benzene like shape is 5.51 nm−1 in CeF3:Tb3+ single crystal (see Fig. S5b†). However, in the case of NdF3 significant changes in the shape were noticed (Fig. 4c). Here mixed (hexagonal, spherical and few tubular) morphology is found with wide range of particle size. Aspect ratio (1.020–8.55) of these particles is abruptly increased than the LaF3 and CeF3 nanoparticles. Analysis reveals that regularity of hexagonal structure is gradually decreased from La to Nd. This is attributed to the contraction of crystal lattice volume of binary rare earth fluorides with decreasing the ionic radius of RE3+ ions. Consequently, anisotropic growth of the nanoparticle would be occurred in distorted hexagonal/trigonal unit cell. Therefore regularity of hexagonal disc is gradually being transformed to distorted hexagonal form.
However, in ternary hexagonal NaREF4 (Sm to Tb), shape of the particles is drastically changed into irregular, branched-tubular shape with higher aspect ratio (ca. 1.14–9.8) that is much higher than the previous binary fluorides i.e. NdF3 (as shown in Fig. 4c and d). As can be seen from the TEM images, dispersibility of these particles is gradually decreasing from NaSmF4 to NaTbF4:Ce3+. In the case of NaSmF4 obtained nanoparticles are highly dispersed whereas in the case of NaTbF4 particles are agglomerated. Here, (101) plane is highly exposed plane with spacing of 0.298 nm for the hexagonal NaGdF4:Eu3+ nanoparticles (see Fig. 5c). From low magnification TEM images, it can be prominently seen that the however, in HRTEM image of the NaDyF4, both (111) [cubic] and (101) [hexagonal] planes are appearing (Fig. 5d). The calculated spacing (0.315 nm) between the lattice fringes is belonging to the (111) plane of the cubic NaDyF4 nanoparticles. SAED image of the same sample indicates that it is polycrystalline in nature and diffracting planes correspond to the (112), (300) and (311) planes (see in Fig. S5c and d†). In present cases, distribution of sodium and RE3+ is completely different than that of binary rare earth fluorides. Hexagonal unit cell of ternary rare-earth fluorides are contracting gradually due to contraction of inter-atomic bond length and causes anisotropic growth leading to the formation of tubular structure. Furthermore, on moving from Sm to Tb, dispersibility of tubular nanoparticles is also decreasing (as shown in Fig. 4d–f), which is attributed to the increased surface energy. In period, charge density (e/r) gradually increases with decreasing the ionic radius of RE3+. Consequently, surface energy increases and agglomeration of particles is taken place. On the other hand, mixed phase is obtained in NaDyF4. Since cubic phase is appearing along with hexagonal phase so irregular spherical as well as tubular both types morphology are obtained (Fig. S3†). In other words, it can be said that Dy3+ is the conduit ion between hexagonal and cubic phase of ternary rare earth fluorides.
In the case of small size RE3+ ions (1.075–1.042 Å), nicely dispersed, relatively more spherical-shaped nanoparticles are obtained (Fig. 4g–i). This group of RE3+ ions forms cubic ternary rare-earth fluoride nanoparticles under the similar experimental conditions. Significant changes are noticed in the shape of the cubic phase NaYF4 to NaYbF4 nanoparticles. Aspect ratio of these particles is gradually decreasing to the unity and the shape is getting increasingly spherical. It was further confirmed from the HRTEM images, that in NaErF4:Yb3+ major planes are (111) and (200), while (111) is the only dominating plane in case of NaYbF4:Er3+ (see Fig. 5e and f). Besides this, dispersity of the nanoparticles is also increasing along with shape from NaYF4 to NaYbF4. From the diffraction patterns, it is evident that as-prepared nanoparticles are polycrystalline and planes can be assigned to (222), (422), (400) and (311), (222), (331) for NaErF4:Yb3+ and NaYbF4:Er3+ nanoparticles respectively (Fig. S5e and f†).
In cubic phase all lattice parameters (a = b = c) of the unit cell are same. So the growth of the as-prepared nanoparticles would be isotropic. Promptness of spherical shape is dependent on the isotropic nature of cubic phase. For example, relatively large ion is forming irregular spherical nanoparticles (for example NaYF4) while more spherical nanoparticles are found in NaErF4:Yb and NaYbF4:Er. And the average size of nanoparticles are ca. 55.3 nm, 104.95 nm and 151.63 nm for NaYF4:Eu, NaErF4:Yb and NaYbF4:Er respectively. From Fig. S4,† in histogram it can be nicely seen that size distribution of the particles are very much comparable to the calculated average size of the nanoparticles. Moreover, narrow range of size distribution is observed for the NaYF4:Eu nanoparticles whereas wide range of size distribution is occurred in case of NaYbF4:Er (Fig. S4†). Thus from TEM images it can be said that isotropic nature of cubic phase is increasing with decreasing the ionic radius of RE3+ ions in period. Thus from all observations it can be inferred that RE3+ ions in period not only governs the phase and type of products but also controlled morphology of the as-obtained products under similar reaction conditions (Fig. 6).
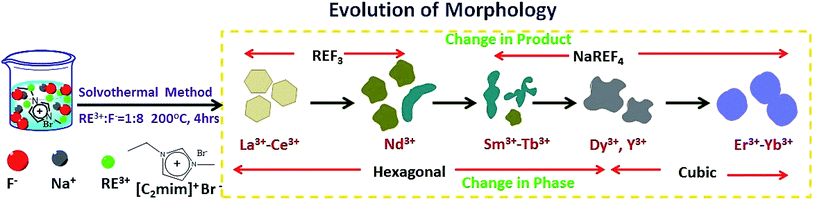 | ||
| Fig. 6 Schematic presentation of trend of morphology evolution of binary/ternary rare-earth fluorides along the period of lanthanide series. | ||
3.5 Optical characterizations
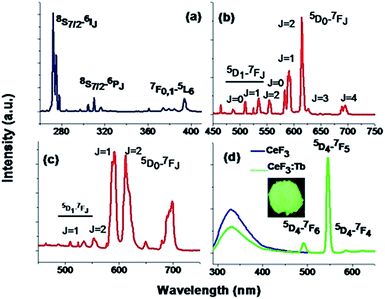
Fig. 7 and S7† depicts the photoluminescence (PL) spectra of eight representative compounds, cubic NaYF4:Eu3+ (P1), hexagonal NaGdF4:Eu3+ (P7), hexagonal CeF3 (P3), CeF3:Tb3+ (P4), LaF3:Dy3+ (P2), NaSmF4 (P6), NaTbF4:Ce (P8) and NaDyF4 (P9) respectively. Fig. 7a shows the excitation spectra of 1 mol% Eu3+ doped NaGdF4 nanocrystals measured at room temperature, monitoring the 5D0–7F2 electric dipole transition of the Eu3+ ion at 615 nm. Narrow transition lines of Gd3+ at 272 nm (8S7/2–6IJ) and 310 nm (8S7/2–6PJ) along the characteristic ones of Eu3+ especially at 393 nm appear. Fig. 7b shows the PL spectrum of hexagonal NaGdF4:Eu3+ nanocrystals obtained upon 393 nm excitation. It shows the electric dipole transition arises due to 5D0–7F2 at 615 nm which is stronger than the magnetic dipole transitions arise at 591 nm. The asymmetry parameter (Ω2) using Judd–Ofelt theory was calculated for better understanding [for details see ESI†].56,57 Calculated Ω2 value for the above mentioned sample is 11.6 × 10−20 cm2. When Eu3+ ions doped in cubic NaYF4 under excitation at 393 nm, the magnetic dipole transition shows stronger emission than the electric dipole transition. This indicates that Eu3+ ion is staying in more symmetric environment compared to the hexagonal NaGdF4:Eu3+ sample. This is further confirmed by the lower asymmetry parameter Ω2 value of 3.75 × 10−20 cm2 for cubic Eu3+ ion doped NaYF4 nanoparticles. Thus the Eu3+ ion can be used as a spectroscopic probe to monitor phase transition. Another important point which is observed is the presence of the transitions from higher energy levels like 5D1, 5D2, 5D3 etc. in both the cubic NaYF4 and hexagonal NaGdF4 doped with Eu3+. This hints that these materials can be useful for quantum cutting down conversion purposes which has potential use in energy saving lighting devoid of mercury.14,50 Fig. S7a† shows the emission spectrum of LaF3:Dy3+ (1%) under 348 nm excitation. The emission peaks appear at 475 nm and 571 nm and are assigned to 4F9/2–6H15/2 and 4F9/2–6H13/2 transitions respectively. When NaDyF4 nanoparticles are excited under 348 nm excitation, emission peak at 469 nm appears which is due to 4F9/2–6H15/2 transition (Fig. S7d†). In the case of NaSmF4, very weak emission at 600 nm is found on exciting the nanoparticles under 365 nm. This transition corresponds to 4G5/2–6H7/2 of NaSmF4 (as shown in Fig. S7b†).Fig. 7d shows the emission spectra of CeF3 and CeF3:Tb3+ nanocrystals dispersed in dimethyl sulphoxide (DMSO) solution and excited into the 4f–5d absorption band of Ce3+. A broad emission band ranging from 300 nm to 400 nm with a maximum of 330 nm is observed for CeF3. Parity allowed transition of the lowest component of the 2D state to the spin–orbit components of the ground state 2F5/2,7/2 of Ce3+ ion is the cause of the origin of this particular emission band. A strong excitation peak near 270 nm monitored with the emission wavelength of 330 nm corresponds to the transitions from the ground state 2F5/2 of Ce3+ to the different components of the excited Ce3+ 5d states (Fig. S6†).58 During the excitation of CeF3:Tb3+ sample (Fig. 7d) a significant decrease in PL intensities of Ce3+ ion occurs and the appearance of new peaks at 490, 545 and 586 happens. Appearance of these new peaks is due to the transitions of 5D4–7F6,5,4 for Tb3+ ion. Here, Ce3+ ions are excited first and then energy transfer took place from Ce3+ to Tb3+ ions which non-radiatively decay to the 5D4 excited level of Tb3+ ions. Finally radiative decay happens from this level to the various underlying levels of 5FJ=0–6 of Tb3+ ions. Incidentally the energy levels of Tb3+ ions are suitable for an energy transfer taking place from the Ce3+ ion upon excitation with an UV source. When CeF3:Tb3+ powder samples are irradiated with UV light, an intense green colour emission which is due to the magnetic dipole transition (5D4–7F5) with ΔJ = ±1 of at 545 nm which can be observed with the bare eye (inset of Fig. 7d). The energy transfer efficiency (ηET) from donor (Ce3+) to acceptor (Tb3+) is calculated using the equation ηET = 1 − Id/Id0, where Id0 and Id are the luminescence emission intensities of donor in the absence and presence of acceptor (Tb3+) respectively. 40.80% energy transfer efficiency (ηET) is obtained in DMSO solution. However similar kind of energy transfer from Ce3+ to Tb3+ occurs in case of NaTbF4:Ce3+ (P8) nanocrystal and presented in Fig. S7c.†
4. Conclusions
In summary, we have succeeded in preparing phase and morphology controlled RE3+ doped binary (LnF3) and ternary rare-earth fluoride (NaREF4) using an IL-based solvothermal method. Crystal phase, lattice strain, morphology and most importantly nature of fluorides (binary/ternary) are tuned by judiciously selecting the size of the RE3+ ion, keeping the other reaction parameters same. To the best of our knowledge, the phase and morphology tuning on the basis of ionic radius/size of the chosen RE3+ ion are not reported yet. When size of the RE3+ ions are small like for Y3+ ions or for Er3+ and Yb3+, the reaction rate is quite faster and kinetically controlled cubic polymorph of NaREF4 (RE = Y3+, Er3+ and Yb3+) with spherical morphology is obtained. A drastic change in morphology as well as crystal phase is noticed for NaREF4 with RE = Sm3+, Eu3+, Tb3+, Gd3+. Here the sizes of the RE3+ ions are in intermediate size and the formation of the thermodynamically stable hexagonal phase occurs. When the same reaction technique is attempted for La3+, Ce3+ and Nd3+, instead of the ternary fluoride, hexagon-shaped particles of the binary fluoride are obtained. This is due to the quite larger size of the RE3+ ion which plays a pivotal role in kinetics. HRTEM analysis shows that the [C2mim]+ cation attaches to the (111) plane and favor the directional growth of the hexagonal phase LnF3. Analysis reveals that lattice strain can be crystal phase dependent. Both the trigonal binary and hexagonal ternary fluoride shows compressive strain whereas cubic ternary fluoride shows tensile strain. Strong emission peaks, higher energy transition of Eu3+ ion for NaYF4:Eu3+ and NaGdF4:Eu3+ ion and efficient energy transfer from Ce3+ to Tb3+ shows promises in different optoelectronic applications of prepared lanthanide doped materials. Last but not the least, this methodology based on the ionic radius or size of the ions can be applied for any other series of fluorides in the periodic table.Acknowledgements
RKS, YNC and PG would like to acknowledge support from the Science and Engineering Research Board (Start-Up Research Grant for Young Scientist) and UGC Start Up Grant for financial support. RKS acknowledge Dr H. S. Gour University for financial support through a graduate fellowship. AVM acknowledges support from DOE as this work was in part be supported by the Critical Materials Institute. Authors acknowledge the support from Sophisticated Instrumentation Centre (SIC) of Dr H. S. Gour University for SEM and TEM measurements.Notes and references
- F. Wang and X. Liu, Chem. Soc. Rev., 2009, 38, 976 RSC.
- J.-C. Bünzli, Chem. Rev., 2010, 110, 2729 CrossRef PubMed.
- C. Bouzigues, T. Gacoin and A. Alexandrou, ACS Nano, 2011, 11, 8488 CrossRef PubMed.
- G. Chen, T. Y. Ohulchanskyy, S. Liu, W.-C. Law, F. Wu, M. Swihart, H. Ågren and P. N. Prasad, ACS Nano, 2012, 6, 2969 CrossRef CAS PubMed.
- D. A. Chengelis, A. M. Yingling, P. D. Badger, C. M. Shade and S. Petoud, J. Am. Chem. Soc., 2005, 127, 16752 CrossRef CAS PubMed.
- E. C. Ximendes, W. Q. Santos, U. Rocha, U.K. Kagola, F. S-Rodríguez, N. Fernández, A. da S. G-Neto, D. Bravo, A. M. Domingo, B. del Rosal, C. D. S. Brites, L. D. Carlos, D. Jaque and C. Jacinto, Nano Lett., 2016, 16, 1695 CrossRef CAS PubMed.
- J. M. Meruga, A. Baride, W. Cross, J. J. Kellar and P. Stanley May, J. Mater. Chem. C, 2014, 2, 2221 RSC.
- M. Pedroni, F. Piccinelli, T. Passuello, M. Giarola, G. Mariotto, S. Polizzi, M. Bettinelli and A. Speghini, Nanoscale, 2011, 3, 1456 RSC.
- Z. Zhang, X. Ma, Z. Geng, K. Wang and Z. Wang, RSC Adv., 2015, 5, 33999 RSC.
- S. Kasturi, V. Sivakumar and D. Y. Jeon, Luminescence, 2016, 31, 1138 CrossRef CAS.
- N. Mauser, D. Piatkowski, T. Mancabelli, M. Nyk, S. Mackowski and A. Hartschuh, ACS Nano, 2015, 9, 3617 CrossRef CAS PubMed.
- C. Wang, L. Cheng, Y. Liu, X. Wang, X. Ma, Z. Deng, Y. Li and Z. Liu, Adv. Funct. Mater., 2013, 23, 3077 CrossRef CAS.
- K. Krämer, D. Biner, G. Frei, H. U. Güdel, M. P. Hehlen and S. R. Lüthi, Chem. Mater., 2004, 16, 1244 CrossRef.
- P. Ghosh, S. Tang and A.-V. Mudring, J. Mater. Chem., 2011, 21, 8640 RSC.
- P. Rahman and M. Green, Nanoscale, 2009, 1, 214 RSC.
- S. Zeng, G. Ren, C. Xu and Q. Yang, CrystEngComm, 2011, 13, 4276 RSC.
- D. Yang, Y. Dai, P. Ma, X. Kang, M. Shang, Z. Cheng, C. Li and J. Lin, J. Mater. Chem., 2012, 22, 20618 RSC.
- K. A. Abel, J.-C. Boyer and F. C. J. M. van Veggel, J. Am. Chem. Soc., 2009, 131, 14644 CrossRef CAS PubMed.
- H. Wang and T. Nann, ACS Nano, 2009, 3, 3804 CrossRef CAS PubMed.
- J.-C. Boyer, F. Vetrone, L. A. Cuccia and J. A. Capobianco, J. Am. Chem. Soc., 2006, 128, 7444 CrossRef CAS PubMed.
- F. Wang, Y. Han, C. S. Lim, Y. Lu, J. Wang, J. Xu, H. Chen, C. Zhang, M. Hong and X. Liu, Nature, 2010, 463, 1061 CrossRef CAS PubMed.
- R. K. Sharma, A.-V. Mudring and P. Ghosh, J. Lumin., 2017, 189, 44 CrossRef CAS.
- X. Sun, Y.-W. Zhang, Y.-P. Du, Z.-G. Yan, R. Si, L.-P. You and C.-H. Yan, Chem.–Eur. J., 2007, 13, 2320 CrossRef CAS PubMed.
- S. N. Achary and A. K. Tyagi, Mater. Res. Bull., 2001, 36, 1441 CrossRef CAS.
- I. M. Ranieri, S. L. Baldochi and D. Klimm, J. Solid State Chem., 2008, 181, 1070 CrossRef CAS.
- P. Ptacek, H. Schäfer, K. Kömpe and M. Haase, Adv. Funct. Mater., 2007, 17, 3843 CrossRef CAS.
- D. Chen, P. Huang, Y. Yu, F. Huang, A. Yang and Y. Wang, Chem. Commun., 2011, 47, 5801 RSC.
- Q. Zhang and Y. Bing, Chem. Commun., 2011, 47, 5867 RSC.
- P. Ghosh and A. Patra, J. Phys. Chem. C, 2008, 112, 19823 Search PubMed.
- X. Zhai, S. Liu, Y. Zhang, G. Qin and W. Qin, J. Mater. Chem. C, 2014, 2, 2037 RSC.
- A. Aebischer, M. Hostettler, J. Hauser, K. Krämer, T. Weber, H. U. Güdel and H.-B. Bürgi, Angew. Chem., Int. Ed., 2006, 45, 2802 CrossRef CAS PubMed.
- M. Wang, Q.-L. Huang, H.-X. Zhong, X.-T. Chen, Z.-L. Xue and X.-Z. You, Cryst. Growth Des., 2007, 7, 2106 CAS.
- G. Xiang, J. Zhang, Z. Hao, X. Zhang, Y. Luo, S. Lü and H. Zhao, CrystEngComm, 2014, 16, 2499 RSC.
- M. Pang, X. Zhai, J. Feng, S. Song, R. Deng, Z. Wang, S. Yao, X. Ge and H. Zhang, Dalton Trans., 2014, 43, 10202 RSC.
- W. Zhang, F. Ding and Y. S. Chou, Adv. Mater., 2012, 24, OP236 CAS.
- N. Niu, F. He, S. Huang, S. Gai, X. Zhang and P. Yang, RSC Adv., 2012, 2, 10337 RSC.
- H.-X. Mai, Y.-W. Zhang, R. Si, Z.-G. Yan, L.-D. Sun, L.-P. You and C.-H. Yan, J. Am. Chem. Soc., 2006, 128, 6426 CrossRef CAS PubMed.
- Y. Liu, D. Tu, H. Zhu, R. Li, W. Luo and X. Chen, Adv. Mater., 2010, 22, 3266 CrossRef CAS PubMed.
- L. Wang, R. Yan, Z. Huo, L. Wang, J. Zeng, J. Bao, X. Wang, Q. Peng and Y. Li, Angew. Chem., Int. Ed., 2005, 44, 6054 CrossRef CAS PubMed.
- X. Chen, D. Peng, Q. Jua and F. Wang, Chem. Soc. Rev., 2015, 44, 1318 RSC.
- G. Chen, H. Ågren, T. Y. Ohulchanskyy and P. N. Prasad, Chem. Soc. Rev., 2015, 44, 1680 RSC.
- G.-S. Yi and G.-M. Chow, Chem. Mater., 2007, 19, 341 CrossRef CAS.
- A. Grzechnik, P. Bouvier, W. A. Crichton, L. Farina and J. Köhler, Solid State Sci., 2002, 4, 895 CrossRef CAS.
- D. Yang, Y. Dai, P. Ma, X. Kang, M. Shang, Z. Cheng, C. Li and J. Lin, J. Mater. Chem., 2012, 22, 20618 RSC.
- Y. Zhang, X. Li, Z. Hou and J. Lin, Nanoscale, 2014, 6, 6763 RSC.
- Y. Zhang, X. Li, X. Kang, Z. Hou and J. Lin, Phys. Chem. Chem. Phys., 2014, 16, 10779 RSC.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751 CrossRef.
- R. K. Sharma, Y. N. Chouryal, S. Chaudhari, J. Saravanakumar, S. R. Dey and P. Ghosh, ACS Appl. Mater. Interfaces, 2017, 9, 11651 CAS.
- E. R. Parnham, A. M. Z. Slawin and R. E. Morris, J. Solid State Chem., 2007, 180, 49 CrossRef CAS.
- P. Ghosh and A.-V. Mudring, Nanoscale, 2016, 8, 8160 RSC.
- G. K. Williamson and W. H. Hall, Acta Metall., 1953, 1, 22 CrossRef CAS.
- P. Ghosh and A. Patra, J. Phys. Chem. C, 2007, 111, 7004 CAS.
- A. M. Smith, A. M. Mohs and S. Nie, Nat. Nanotechnol., 2009, 4, 56–63 CrossRef CAS PubMed.
- R. L. Penn and J. F. Banfield, Science, 1998, 281, 969 CrossRef CAS PubMed.
- R. L. Penn and J. F. Banfield, Am. Mineral., 1999, 84, 871 CrossRef CAS.
- B. R. Judd, Phys. Rev., 1962, 127, 750 CrossRef CAS.
- G. S. Ofelt, J. Chem. Phys., 1962, 37, 511 CrossRef CAS.
- P. Ghosh, A. Kar and A. Patra, Nanoscale, 2010, 2, 1196 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra06741k |
| ‡ Fellow of Royal Society of Chemistry (FRSC). |
| This journal is © The Royal Society of Chemistry 2017 |