Calcium hydroxide doped by KNO₃ as a promising candidate for thermochemical storage of solar heat

Abstract

New materials for thermochemical storage of concentrated solar heat are highly desirable for making this emerging technology competitive with the traditional sensible and latent heat storage. Keeping this in mind, we have prepared calcium hydroxide modified with potassium nitrate and studied its de-/rehydration dynamics by differential scanning calorimetry and thermogravimetry techniques. The following notable observations are described for the modified Ca(OH)₂: (1) an acceleration of the dehydration and reduction of its temperature as compared with the pure hydroxide; (2) the temperature reduction depends on the KNO₃ content Y and reaches 35 °C at Y = 5 wt%; (3) the addition of KNO₃ only slightly reduces the dehydration heat which remains promising for heat storage applications. Fast rehydration of the doped CaO is observed at T = 290–360 °C and P(H₂O) = 23–128 mbar, and its rate strongly depends on both temperature and pressure. De- and rehydrated products were studied by the BET analysis and IR-spectroscopy to elucidate possible ways for the salt to influence the Ca(OH)₂ dehydration. The mechanism involving a chemical interaction between the salt and the hydroxide is discussed. The new material exhibits a large heat storage density, fast de-/rehydration and adjustable decomposition temperature, and may be considered as a promising candidate for thermochemical storage of concentrated solar energy.

---

1. Introduction

The present increase in the world's energy demand along with restrictions on the use of fossil fuels has spurred research activity in the area of renewable energy including concentrated solar radiation. Development of concentrated solar power (CSP) technologies has made heat with middle-temperature potential (200–500 °C) available and useful for production of overheated steam followed by the generation of electricity.¹ For instance, parabolic troughs are able to maintain the focal line temperature in an interval of 350–400 °C ² and parabolic dishes allow temperatures of 250–700 °C to be obtained.³

Heat storage mitigates a mismatch between energy supply and demand inevitably present if one uses the solar radiation as a source of heat. Therefore, storage of middle-temperature heat is one of the crucial technologies for systems using solar concentrators for heat production which makes heat available on cloudy days or at night.

There are three ways to store middle-temperature heat. The first one is sensible heat storage by rocks, sand, oil, etc.⁴ The second way involves fusion of salts,⁵ mainly nitrates,^6,7 or metals.⁸ The third way represents heat storage by means of chemical reactions⁹ or adsorption,¹⁰ i.e. heat is stored in a form of chemical species. Sensible and latent heat storages are well-developed and used commercially. Thermochemical heat storage is an attractive alternative to the first two methods since it ensures a higher energy storage density and negligible thermal losses.

Middle-temperature thermochemical heat storage (MT-THS) is an emerging technology with a limited range of promising chemical reactions and materials. The MT-THS may be carried out by decomposition of NH₃,¹¹ NH₄HSO₄,¹² dehydrogenation of MgH₂ ¹³ or cyclohexane,¹⁴ etc. For the last decades, metal hydroxides were widely studied as materials for MT-THS.⁹ One of the most promising hydroxides is Ca(OH)₂ which stores heat in the course of its dehydration:

Ca(OH)_2(s) = CaO_(s) + H₂O_(g), Δ_rH^o₂₉₈ = 104.4 kJ mol⁻¹. (1)

This endothermic process corresponds to heat storage while during the exothermic rehydration the stored heat is released.¹⁵ Calcium hydroxide ensures a high heat storage density up to 1400 kJ kg⁻¹ or 3.1 GJ m⁻³ (the real volumetric density, however, may be ca. two times lower due to lower apparent density of Ca(OH)₂). This hydroxide is non-corrosive, non-hazardous, inexpensive and stable over cycling.¹⁶ Due to these virtues, reaction (1) was proposed for CSP applications¹⁷ and chemical heat pumps.^18,19

A simple chemical heat pump, that operates under a closed cycle mode, consists of two vessels, namely, a reactor where reaction (1) takes place and a condenser/evaporator (Fig. 1a). During the heat storage stage (1 → 2 on Fig. 1b), middle-temperature heat is supplied to the reactor to initiate the hydroxide decomposition. The resultant water vapour condenses in the condenser at constant pressure. During this stage, the valve between the vessels is open and water vapour moves freely from the reactor to the condenser as no other gas is present in the unit.

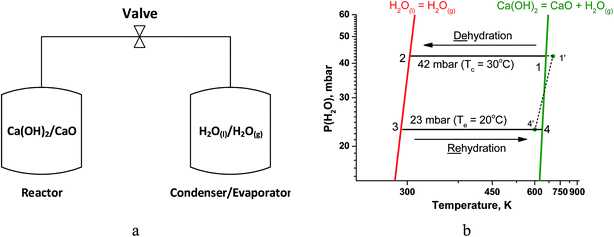Fig. 1 (a) Schematic representation of a closed THS system. (b) Schematics of thermodynamic cycle of H₂O/CaO heat storage studied in the paper.

At the heat release stage, a low-grade ambient heat (at 20–30 °C) is supplied to the evaporator (the same vessel as the condenser) to generate vapour (at point 3, Fig. 1b) and carry out the isobaric rehydration of CaO (3 → 4). During this stage, water vapour moves freely from the evaporator to the reactor, and the useful heat is released to a consumer at point 4.

According to the Gibbs phase rule, the equilibrium of reaction (1) is monovariant for bulk phases since both CaO and Ca(OH)₂ exist only in one form. Hence, there is an one-to-one correspondence between temperature T and water vapour pressure P(H₂O) over the solids.²⁰ This correspondence is expressed by a linear form of the van't Hoff equation (Fig. 1b, green line):

where Δ_rH^o(T) and Δ_rS^o(T) stand for the variations of enthalpy and entropy in the course of reaction (1), P₀ is a standard pressure (1 bar). According to this equation, at P(H₂O) = 24 mbar the equilibrium temperature is 362 °C.²¹ However, the dehydration of Ca(OH)₂ proceeds with the rate acceptable for practical use only at T ≥ 400 °C since a driving force is required for the process to start. Therefore, under real conditions, point 1 on Fig. 1b shifts to higher temperature (point 1′). Similarly, the rehydration needs some supercooling, therefore point 4 is shifted towards lower temperatures (point 4′).

Increasing the dehydration rate at the lower temperature is beneficial as it could (a) facilitate the heat storage, (b) broaden the range of heat sources available for MT-THS, and (c) increase the second-law efficiency of MT-THS by adjusting the dehydration temperature to the temperature of the heat source.²²

A thermophysical approach to increasing the hydroxide dehydration rate does not change thermodynamic parameters of reaction (1) and consists in amelioration of transport properties of the hydroxide grain or bed which affect the overall efficiency of heat storage in real devices. For instance, use of copper fins intensifies the heat transfer in the bed and decomposition rate of Ca(OH)₂ bed.²³ The addition of graphite to Ca(OH)₂ also enhances heat transfer and accelerates the dehydration.²⁴ Coating of Ca(OH)₂ with SiO₂ nanoparticles prevents agglomeration of oxide particles during dehydration,²⁵ however, gradual degradation of the material due to a side chemical reaction was found afterwards. Impregnation of Ca(OH)₂ into vermiculite matrix to accelerate the dehydration was reported in ref. 26. Recently, composites of Ca(OH)₂ and sodium silicate with enhanced mechanical properties have been proposed for MT-THS.²⁷

The complementary approach suggests a chemical modification of calcium hydroxide by various additives to reduce the dehydration temperature. Homogeneous doping of Ca(OH)₂ with Al³⁺, Zn²⁺, Cu²⁺, and Ni²⁺ (1–5 at% of a doping cation) was shown to lower the dehydration temperature and increase the process rate at 450 °C.²⁸ Based on the kinetic analysis, the authors discussed possible reasons for the rate enhancement, namely, the introduction of additional nucleation sites (e.g. point substitution defects) and lowering the activation energy. It was theoretically shown that the doping Ca(OH)₂ with Li⁺ and Mg²⁺ can reduce the energy barrier for the dehydration.²⁹ This conclusion was experimentally corroborated for the lithium additive in ref. 30.

First attempt to chemically modify Ca(OH)₂/CaO system for MT-THS was made by using LiCl as a heterogeneous doping additive to improve rehydration reactivity of the resulting CaO.³¹ The range of modifying salts was significantly expanded in ref. 21 where several classes of alkali metal salts (nitrates, acetates, chlorides and sulphates) were systematically screened to elucidate their effect on the Ca(OH)₂ dehydration. The maximal reduction of the dehydration temperature was revealed for KNO₃ as a doping salt.

So far, a detailed study of the novel composite KNO₃/Ca(OH)₂ has not been carried out. The comprehensive investigation of its de-/rehydration kinetics is necessary to consider its applicability for CSP storage in closed THS cycles. This work is aimed at such study. The emphasis is put on the properties of the modified material KNO₃/Ca(OH)₂ important for CSP storage as well as on the understanding the effect of modification. The dehydration temperature, heat storage capacity, de- and rehydration kinetics as a function of temperature and vapour pressure are reported and analyzed. A mechanism of the KNO₃ effect on the Ca(OH)₂ dehydration is also discussed in the light of data obtained by various physicochemical methods.

2. Experimental

2.1. Materials preparation

A reference calcium hydroxide (hereinafter referred to as CH) was prepared by hydration of CaO (>99.9%) which was preliminarily calcined at 900 °C for 4 hours for the elimination of possible carbonate impurities. The hydration was carried out by degassed distilled water. A mixture of CaO and water was sealed in an autoclave and kept at T = 110 °C for 18 hours. The resultant Ca(OH)₂ was filtered and washed by distilled degassed water.

Composites KNO₃/Ca(OH)₂ with a varied salt content of 0.5–20 wt% were prepared by mixing CH with KNO₃ (>99.9%, Reakhim Ltd). A mechanical mixture of Ca(OH)₂ and KNO₃ in necessary proportion was placed in a flask and the distilled degassed water was added. The subsequent drying at 60 °C in vacuum under vigorous stirring ensured a uniform salt distribution over Ca(OH)₂ surface. Finally, the material was dried at 120 °C. We will refer to a sample with KNO₃ weight content Y% as PN/CH-Y (Potassium Nitrate/Calcium Hydroxide-Y) (Table 1).

Table 1 Salt content in the samples KNO₃/Ca(OH)₂

Sample	Content, wt%	Content, mol%
PN/CH-0.5	0.5	0.4
PN/CH-1	1.0	0.7
PN/CH-2	2.0	1.5
PN/CH-5	5.0	3.7
PN/CH-10	10.0	7.5
PN/CH-15	15.0	11.4
PN/CH-20	20.0	15.5

---

The material PN/CH-5 was calcined in air at 400 °C for 2 hours (PN/CaO). The resulting PN/CaO was rehydrated by water vapour (0.2 bar) at 60 °C for 1 hour to get the rehydrated material PN/CH-5-r.

2.2. Materials characterization

Differential scanning calorimetry (DSC). The DSC measurements were carried out with a NETZSCH DSC 404C Pegasus in dry argon flow (200 ml min⁻¹) at a constant heating rate of 15 K min⁻¹. Both temperature and sensitivity calibrations of S type thermocouple were conducted with a standard calibration set (In, Sn, Bi, Zn, CsCl). Prior to a measurement, a dry sample (7–10 mg) was sealed in a 25 μl aluminium crucible with an orifice in its lid. The DSC signal was corrected with a baseline from two empty crucibles subjected to the same temperature program. We have chosen the onset temperature (T_onset) as a characteristic of the dehydration start. The error of the temperature measurements was ±1 °C. The random error of dehydration heat measurement was ±30 J g⁻¹.

Thermogravimetry (TG). Dehydration and rehydration kinetics were studied by using a Rubotherm magnetic suspension balance equipped with a heater and a vacuum gauge. The system of valves connected the measuring cell either to a vacuum pump or to an evaporator/condenser. The evaporator/condenser ensured a fixed water vapour pressure over the sample during the TG experiments. The conditions of kinetic measurements were chosen so as to imitate those in a closed-cycle THS unit briefly discussed in the Introduction (Fig. 1).

Dehydration kinetics was studied at T = 370, 380, 390, and 400 °C and P(H₂O) = 23 mbar that corresponds to T_c = 20 °C in the condenser. It was chosen as a typical ambient temperature at which water vapour released during dehydration was condensed. A sample of 35–40 mg (fine powder) was placed in a measuring cell which was hermetically sealed afterwards. The small mass of the sample ensured that the heat and mass transfer limitations within the material had negligible effect on the overall reaction kinetics. After sealing, the cell was vacuumed by a pump. After this, the sample was dried at 120 °C. Then, water vapour was introduced into the measuring cell by connecting it to the evaporator. After gaining a constant weight, the cell temperature was quickly increased from 120 °C to a specified one, and the dehydration occurred at constant pressure (23 mbar).

Rehydration kinetics was systematically studied either at fixed water vapour pressure P(H₂O) = 23 mbar and various T = 290, 300 and 310 °C or at fixed temperature T = 330 °C and various P(H₂O) = 23, 32 and 43 mbar. These correspond to the pressures of saturated water vapour at ambient temperatures, respectively, 20 °C, 25 °C, and 30 °C, because the ambient heat is expected to be used to generate for free water vapour during the heat release (rehydration) stage. Moreover, additional experiments were done at T = 360 °C and P(H₂O) = 128 mbar (T_e = 51 °C) in order to have a brief idea how the materials perform at a higher vapour pressure. Before the experiments, a sample was fully dehydrated under vacuum at T = 400 °C. After that, the reaction chamber, still under vacuum, was cooled down to the desired rehydration temperature. Then, the rehydration was initiated by connection of the measuring cell with the evaporator maintained at T_e = 20 °C, 25 °C, and 30 °C to fix the appropriate vapour pressure over the sample. Every rehydration kinetic experiment was repeated thrice in order to ensure reproducibility.

The conversion degree for both de- and rehydration was determined as

α = [m(0) − m(t)]/m_H2O, (3)

where m(t) is the sample mass at time t, and m_H2O is the theoretical mass loss.

Infrared spectroscopy. FTIR spectra were recorded in transmittance mode (4000–200 cm⁻¹, 30 scans, resolution 4 cm⁻¹) using a BOMEM MB102 spectrometer. The samples were prepared by a standard method of pelletizing the studied material (∼2 mg) with CsI (500 mg).

Powder X-ray diffraction analysis. Powder XRD was carried out by using a Siemens D-500 diffractometer equipped with a heater. The XRD-patterns were recorded with Cu K_α radiation filtered by graphite monochromator. The experiments were conducted at 25, 290 and 400 °C in air. The scanning was carried out in 2θ intervals of 15–40° at room temperature and of 16–36° at elevated temperatures with a step of 0.05° and accumulation time of 1 s.

N₂ adsorption isotherms. The porous structure of the samples was examined by N₂ adsorption at 77 K and P/P₀ = 0.005–0.995 with a Quantachrome NOVA 1200e Pore Analyzer. Before the measurements, a sample was degassed in vacuum at 150 °C for 3 hours. The surface area was calculated by the Brunauer–Emmett–Teller (BET) method with the reference area of N₂ molecule taken as 0.162 nm².

3. Results

3.1. DSC analysis

The DSC curves of the doped Ca(OH)₂ (PN/CH-Y) exhibit a broad endothermic peak of the Ca(OH)₂ dehydration (Fig. 2a). The position of the peak depends on the KNO₃ content: the dehydration start temperature or the onset temperature T_onset decreases from 494 °C to 459 °C when the KNO₃ content increases from 0 to 5 wt% (Fig. 2b). Even small quantities of KNO₃ considerably affect the dehydration, e.g. a 0.5% KNO₃ additive reduces T_onset by 19 °C. At Y = 5 wt%, the minimal T_onset is reached. Thus, varying the KNO₃ content is an efficient and convenient tool for managing the Ca(OH)₂ dehydration temperature within the 35 °C range below that of the pure Ca(OH)₂ (CH).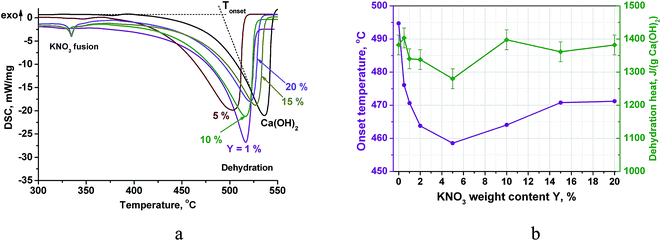

Fig. 2 DSC-thermograms of PN/CH-Y materials (a), the dehydration temperature and heat at various salt contents (b).

At larger salt contents (Y ≥ 10%), a small endothermic peak appears at 334 °C (Fig. 3a). This effect can be ascribed to a fusion of crystalline KNO₃.³² The apparent specific heat of KNO₃ melting calculated by the peak integration at Y = 20% is about 12 J g⁻¹. This value is lower than calculated from the melting heat of bulk KNO₃ and the salt content in PN/CH-20 (21 J g⁻¹). The discrepancy indicates that the state of potassium nitrate in the mixtures PN/CH-Y differs from its bulk crystalline state.

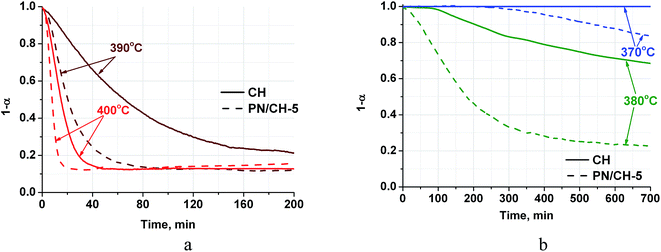Fig. 3 Dehydration kinetic curves for CH and PN/CH-5 at T = 390–400 °C (a) and 370–380 °C (b), P(H₂O) = 23 mbar.

Integration of the DSC dehydration peaks demonstrates that the estimated heat of dehydration also reaches a minimum at Y = 5% along with the onset temperature. For PN/CH-5, a dehydration heat of 1280 J g⁻¹ is only 7% less than the dehydration heat of CH, therefore, it is still promising for MT-THS. For the further detailed study of the dehydration/rehydration kinetics, we have chosen the material with the minimal dehydration temperature, namely, PN/CH-5.

3.2. Dehydration kinetics

Complete dehydration of CH in vacuum shows the total weight loss m_H2O/m₀ = 0.240–0.244. This value is in good agreement with the theoretical loss (0.243) calculated from the stoichiometry of reaction (1). For PN/CH-5, the weight loss equals 0.230 that also fits the reaction stoichiometry if one makes a correction for the salt content.

The dehydration kinetic curves for CH and PN/CH-5 at 390 °C and 400 °C are of a decelerating type and do not have induction period (Fig. 3a). The doped material PN/CH-5 exhibits a half-conversion time shorter by a factor of 2–3 (Table 2). At 380 °C, CH exhibits a sigmoid kinetic curve with the induction period of about 100 min, whereas the induction period for PN/CH-5 is absent (Fig. 3b) and the ratio of half-conversion times (τ_0.5(CH)/τ_0.5(PN/CH-5)) exceeds 5. An induction period in gas–solid reactions is commonly ascribed to a low rate of the nuclei formation.³³ Therefore, one may suggest that the doping of Ca(OH)₂ with KNO₃ facilitates the nucleation.

Table 2 Half-conversion time (min) for dehydration of CH and PN/CH-5 at various temperatures

Temperature, °C	CH	PN/CH-5
380	—	180
390	65	20
400	15	7

---

At 370 °C no dehydration of CH is detected for at least 2600 min (only the first 700 min are displayed in Fig. 3b). This may be due to a low driving force for nucleation as the reaction is close to its equilibrium. Indeed, the equilibrium temperature, calculated from the thermodynamic data of ref. 34, at P = 23 mbar equals 361 °C that is just 9 °C lower than the temperature of the discussed dehydration run. It is important that the doped hydroxide PN/CH-5 yet starts to decompose at this temperature, albeit after an induction period of 250–300 min (Fig. 3b). Thus, the doped material shows higher dehydration rates at T = 370–400 °C as compared with the pure Ca(OH)₂ under the conditions typical for a closed THS cycle, therefore, it may be regarded as a promising candidate for MH-THS.

3.3. Rehydration kinetics

The rehydration kinetic curves (Fig. 4) may be divided into two parts. Jump of the water vapour pressure at t = 0 results in a sharp rise of the sample weight. It takes 5–10 s and corresponds to approximately 20% of the total weight change m_H2O. Further weight evolution lasts 100–200 min. In ref. 35, the authors observed alike behaviour for MgO and conjectured that the fast process may be related to water adsorption on the oxide surface and the following chemical hydration. In our case, the similar effect is observed. The adsorption is followed by rapid rehydration of an oxide layer adjacent to the external surface of CaO particles. The thickness of this layer L can be roughly estimated from the following equation under stipulation of spherical particle shapewhere Δα is the jump of the conversion right after the vapour introduction, is the relation of molar volumes, r₀ is the radius of initial particles determined from the BET analysis (see 3.4.). Numerical solution of eqn (4) gives L = 0.8 nm. This product layer creates a diffusion barrier for water molecules, thus slowing down the rehydration at t > 10 s.

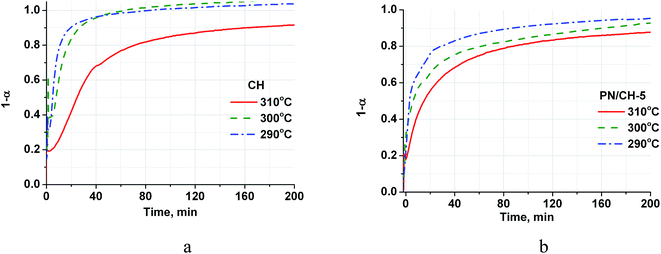Fig. 4 Isothermal kinetic curves of the CH (a) and PN/CH-5 (b) rehydration at different temperatures and P = 23 mbar.

The rehydration rate is strongly affected by the reaction temperature and this dependence is quite unusual because the rate decreases with the temperature increase (Fig. 4). Indeed, at a constant P(H₂O) of 23 mbar, the temperature rise from 290 °C to 310 °C leads to the reduction of the half-conversion time by a factor of 5 (Table 3). At a constant P(H₂O) of 23 mbar, the equilibrium dehydration temperature is equal to 368 °C, therefore the temperature rise from 290 °C to 310 °C reduces the difference between the real and equilibrium temperatures and, hence, the driving force for dehydration.³⁶

Table 3 Half-conversion times (min) for rehydration of CH and PN/CH-5 at various temperatures and vapour pressures

P(H2O), mbar	Temperature, °C	CH	PN/CH-5
23	290	5	3
23	300	8	5
23	310	25	15
32	330	125	104
43	330	7	10
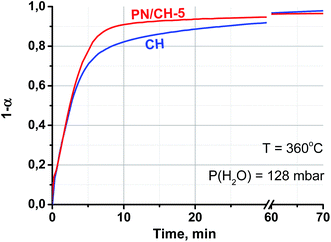
128	360	3	3

---

The vapour pressure strongly affects the rehydration rate as well (Fig. 5). The half-conversion time decreases by a factor of 10–17 when the pressure increases only from 32 to 43 mbar which formally gives the dependence τ ∼ P⁻⁸. Thus, the rehydration rate increases at higher vapour pressure which can be easily controlled by a proper choice of the evaporator temperature T_e. For instance, the vapour pressures mentioned above correspond to T_e equal 25 and 30 °C, respectively. Hence, the ambient heat can be used to directly generate water vapour for fast rehydration reaction. This results in a maximal temperature lift of (265–285)°C which could be used for upgrading the ambient heat up to the middle temperature level.

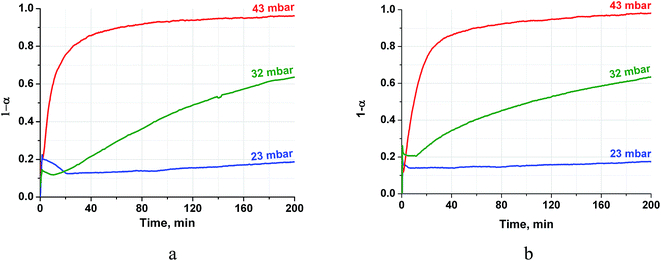Fig. 5 Isobaric kinetic curves of the CH (a) and PN/CH-5 (b) rehydration at T = 330 °C and different pressures.

Thus, the heat stored from an external source at T > 380 °C (i.e. solar concentrator) can be returned at around 300 °C by supplying heat at the temperature of the environment. The returned heat, even if at the lower temperature, still has commercial value and may be further used for various purposes such as steam generation, organic Rankine cycles, etc.

It is worth mentioning that the rehydration rate is less sensitive to the salt presence than the dehydration one. For the doped hydroxide, the rate is somewhat larger at low conversions and smaller at high conversions (see Fig. 4–6 and Table 3). At high P(H₂O) = 128 mbar, the kinetic curves coincide at α < 0.55 (Fig. 5). At α > 0.55, the doped hydroxide is rehydrated slightly faster. The enlargement of CaO particles can be responsible for lower rehydration rate at high conversions, since the thickness of the product layer becomes larger (see 3.4). In any case, the rehydration rate is high enough and can be further enhanced by even small increasing the vapour pressure.

Fig. 6 Rehydration kinetic curves at T = 360 °C and P(H₂O) = 128 mbar.

3.4. BET analysis of N₂ adsorption isotherms

The initial CH has a specific surface area S of (15.1 ± 0.2) m² g⁻¹ (Table 4). Evaluation of the particle radiuswhere ρ is the particle density (2.2 g cm⁻³ for Ca(OH)₂ and 3.4 g cm⁻³ for CaO), gives 22 nm for the CH particles. The CH dehydration yields a disperse CaO (r ≈ 8 nm, Table 4) with a larger specific surface area which is close to that (30–60 m² g⁻¹) reported in ref. 37. This high surface area results in increasing the free energy of CaO formation, which makes the dehydration process less favourable from the thermodynamic point of view and, therefore, increases the driving force of dehydration as well as the dehydration temperature as discussed in 4.2.

Table 4 The BET surface area and estimated particle radius for the pure (CH) and KNO₃-doped Ca(OH)₂ (PN/CH-5) and products of their dehydration

Sample	BET surface area, m^2 g^−1	Particle radius, nm
CH	15.1 ± 0.2	22
PN/CH-5	12.8 ± 0.1	26
CaO	29.5 ± 0.5	8
PN/CaO	7.3 ± 0.1	31

---

The modification of calcium hydroxide with KNO₃ slightly reduces its specific surface area (Table 4) probably due to the coating of Ca(OH)₂ particles by the salt and partial blocking of its surface. The specific surface area of PN/CaO is 4 folds lower as compared with CaO obtained from CH, hence, the KNO₃ addition to CH results in coarser CaO particles.

3.5. Infrared spectroscopy

Infrared spectra of CH and PN/CH-5 exhibit a narrow band at 3642 cm⁻¹ corresponding to O-H vibrations as well as bands at 543, 393 and 307 cm⁻¹ attributed to lattice vibrations of Ca(OH)₂. In addition, the material PN/CH-5 exhibits bands related to vibrations of nitrate in KNO₃, namely, 1360 (ν₃), 1049 (ν₁) and 831 (ν₄) cm⁻¹. Bands at 1472, 1423, 1116, 1080 and 873 cm⁻¹ of low intensity in PN/CH-5 suggest the presence of carbonate-ions in minor quantities (Fig. 7).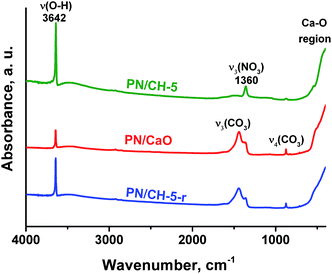

Fig. 7 IR-spectra of PN/CH-5 and products of its de- and rehydration recorded in the range 4000–200 cm⁻¹.

Vibrations of nitrate-ion in PN/CH-5 undergo appreciable changes during the material de- and rehydration. The band ν₃ (E′) at 1360 cm⁻¹ corresponding to the twice degenerated vibration of nitrate-ion splits into two bands at 1380 and 1362 cm⁻¹ after calcination (Fig. 8a). The band ν₄ at 830 cm⁻¹ also splits, and the band ν₁ at 1049 cm⁻¹ disappears (Fig. 8b). These observations show that potassium nitrate does not preserve its crystalline structure after dehydration and the symmetry of nitrate-ion lowers. The rehydration leads to partial restore of the initial bands, however, band ν₁ at 1049 cm⁻¹ does not restore at all. This band is active in KNO₃ with the aragonite structure, thus, the rehydration does not lead to a complete restoration of the initial KNO₃. We suppose that the band splitting during dehydration may be a manifestation of a chemical interaction between the nitrate and the hydroxide as discussed in 4.3.

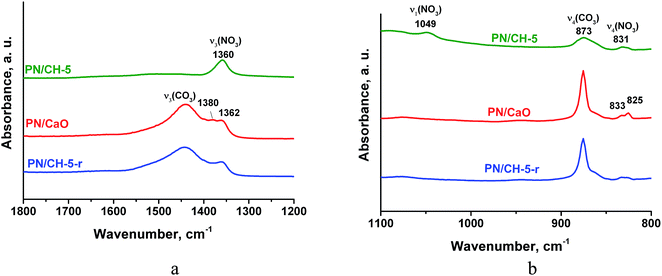Fig. 8 IR-spectra of PN/CH-5 and products of its de- and rehydration in a narrow range of 1800–800 cm⁻¹ for illustration of the nitrate state changes.

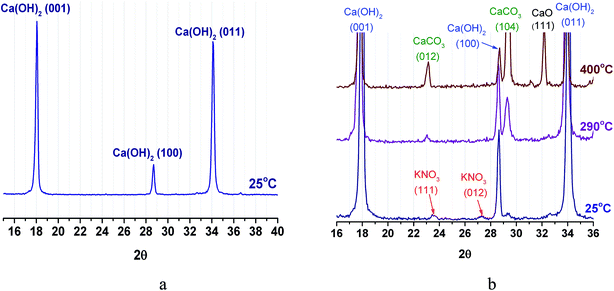
3.6. Powder X-ray diffraction analysis

Powder XRD pattern of CH at room temperature exhibits reflexes of merely portlandite (Ca(OH)₂) phase (Fig. 9a). For PN/CH-5 at 25 °C, reflexes of low intensity from α-KNO₃ phase are detected (Fig. 9b).

Fig. 9 XRD patterns of CH (a) and PN/CH-5 (b).

At 290 °C, the peaks of KNO₃ vanish. This may indicate a loss of the KNO₃ crystalline structure already at T = 290 °C, i.e. at temperature which is much lower than the melting point of pure KNO₃ (334 °C (ref. 32)). This effect resembles the disappearance of NaNO₃ reflexes observed on heating of NaNO₃/Mg(OH)₂.²² Therefore, we assume that for the KNO₃/Ca(OH)₂ case this effect may be likewise caused by the nitrate–hydroxide interaction which may lead to the PN/CH-5 dehydration at the lower temperature (see 4.3). At 400 °C, the dehydration proceeds and reflexes of lime (CaO) appear. Reflexes of calcite (CaCO₃), initially absent, appear at 290 °C, probably, due to the interaction of Ca(OH)₂ with CO₂ from air directly inside the XRD measurement chamber.

The strong interaction of Ca(OH)₂ and CaO with CO₂ resulting in the formation of CaCO₃ is well-known and widely used for removal of CO₂ from air and other gases in industry.³⁸ This carbonate is more stable than Ca(OH)₂ as its decarbonation temperature is above 800 °C. Therefore, reaction (1) can be used for MT-THS only in CO₂-free conditions, i.e. in closed systems containing only water vapour in the gas phase.¹⁹ We have maintained such conditions in the majority of experiments performed in this study. As a result, the data obtained on the effect of KNO₃ additive on the Ca(OH)₂ dehydration and rehydration are reproducible.

4. Discussion

4.1. Estimation of the specific power of heat storage and release

The specific power W [kW kg⁻¹] of heat storing/releasing process is an important parameter that defines a size of THS unit. It can be evaluated aswhere ΔH^o is the enthalpy of reaction (1), M is the molar mass of Ca(OH)₂ (74.1 g mol⁻¹) for dehydration and pure CaO (56.1 g mol⁻¹) for rehydration. The maximal specific power W_max during the pure hydroxide dehydration is 1.0 kW kg⁻¹ (or 2.2 kW dm⁻³) at 400 °C and P(H₂O) = 23 mbar (Fig. 10a), that is quite promising. However, at a lower temperature, the power sharply falls down (e.g. to 20 W kg⁻¹ at 380 °C) which makes application of pure Ca(OH)₂ unfeasible under these conditions. For the heat release (rehydration) stage, a high W_max-value of 1–3 kW kg⁻¹ (or 3.4–10 kW dm⁻³) can be obtained under the conditions fixed in this work. The doped hydroxides show the W_max-value higher by a factor of 2–2.5 and 1.1–1.5 for both de- and rehydration, respectively. The rehydration stage, when the heat is generated for a consumer, can be further accelerated by lowering the process temperature (Fig. 10a) and increasing the vapour pressure (Fig. 10b).

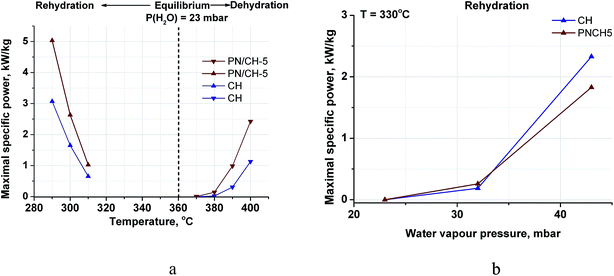Fig. 10 Maximal specific power of de-/rehydration of CH and PN/CH-5 at various temperatures (a) and pressures (b).

Hence, the doped Ca(OH)₂ can transform (store or release) more heat (in a unit time) in less unit volume, which makes an excellent base for creating compact MT-THS units. Indeed, a reactor containing 1 dm³ Ca(OH)₂ can ensure more than 4 kW power during the heat generation stage.

4.2. Contribution of the surface energy

The maximal specific power for both de- and rehydration dramatically lowers to almost zero as the system approaches the equilibrium (Fig. 10a). Therefore, an appreciable difference between the actual process temperature and the equilibrium one is necessary to drive the process. The equilibrium temperature of reaction (1) is estimated above considering the thermodynamic data for the bulk hydroxide and oxide tabulated in ref. 39. The equilibrium reaction temperature is defined as an intersection of lines Δ_fG^o_pro(T) and Δ_fG^o_rea(T) that are the temperature dependencies of the free formation energy of the products and reagents, respectively. For bulk Ca(OH)₂ and CaO, this equilibrium is schematically represented by bold lines on Fig. 11 with the intersection at point A (the bulk equilibrium). For disperse calcium hydroxide and oxide, appropriate contributions of their surface energies, Δ_sG^o_pro and Δ_sG^o_rea, may affect the equilibrium. If Δ_sG^o_pro > Δ_sG^o_rea (the case shown on Fig. 11 by dashed lines), the intersection should shift to a higher temperature (point B) that agrees with our experimental data on the dehydration of the pure Ca(OH)₂.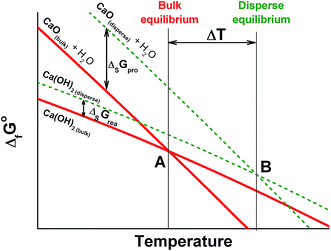

Fig. 11 Schematic illustration of the surface energy contribution and its effect on to the equilibrium temperature of reaction (1) for the bulk (A) and disperse (B) phases.

The surface area of the dehydration product PN/CaO is 4 times lower as compared to pure CaO (see 3.4.). This effect diminishes the contribution of the oxide surface energy to the total free energy of products, thus, making the dehydration more favourable from the thermodynamic point of view and shifting point B on Fig. 11 to a lower temperature for the KNO₃-doped materials. This gives a thermodynamic explanation of the observed reduction of the Ca(OH)₂ dehydration temperature.

4.3. KNO₃–Ca(OH)₂ interaction

Thus, the doping of Ca(OH)₂ with KNO₃ leads to lowering of the dehydration temperature and accelerates its dehydration. The following observations are made upon examination of the effect:

(a) DSC signals of the doped KNO₃ melting are absent at low salt contents;

(b) surface area of the salt-doped dehydration product is lower as compared with the non-doped CaO;

(c) X-ray diffraction peaks of KNO₃ vanish at 290 °C that is 44 °C lower than the KNO₃ melting point;

(d) IR bands of nitrate vibrations split after calcination which may indicate the NO₃ symmetry lowering.

These effects can be considered as an indication of an interaction between the nitrate and the hydroxide. Alike effects were found for NaNO₃/Mg(OH)₂ in ref. 22 and were ascribed to the salt-hydroxide chemical interaction.

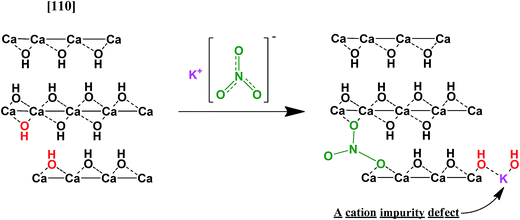
A hypothetical mechanism of the interaction is an embedding of nitrate-ions into the brucite-like lattice of Ca(OH)₂ occurring in a surface-adjacent layer (Fig. 12). Indeed, such process would lead to a collapse of the KNO₃ structure and lowering of the nitrate symmetry. Moreover, it can create additional structural imperfections which could facilitate nucleation during dehydration at lower temperatures.³⁰ These defects can also lead to lowering the surface area of the resulting CaO due to alleviating mechanical strains which relax during the dehydration due to cracking CaO particles off the reaction front thus increasing the specific surface area of the product. This alleviation can result in less fracturing and larger CaO particles as compared with dehydration of the pure Ca(OH)₂.

Fig. 12 A scheme of nitrate–hydroxide interaction.

5. Conclusions

This paper is aimed at the synthesis and study of KNO₃-doped Ca(OH)₂ keeping in mind opportunity to use this material for storage of concentrated solar heat. The doping of Ca(OH)₂ by KNO₃ results in a significant acceleration of the dehydration as well as in the reduction of the dehydration temperature as compared with the pure hydroxide. This reduction is a function of the salt content and, thus, can be intentionally managed. The dehydration temperature reaches a minimum for the material KNO₃/Ca(OH)₂ with 5 wt% of the salt (ΔT = 35 °C). The dehydration heat is reduced only by 7% when KNO₃ is added (1280 J g⁻¹) and remains promising for heat storage.

The material KNO₃(5 wt%)/Ca(OH)₂ shows higher dehydration rate at T = 370–400 °C as compared with the pure calcium hydroxide under the conditions typical for a closed THS cycle for storing CSP. The rehydration rate is less sensitive to the salt presence than the dehydration one. For the doped hydroxide, the rate is somewhat larger at low conversions and smaller at high conversions. The cycle dynamic analysis shows that the doped Ca(OH)₂ can store or release more heat (in a unit time) in the same volume, than the pure Ca(OH)₂. This creates a robust basis for designing compact and efficient units for storage of concentrated solar heat.

The KNO₃ addition dramatically lowers the surface area of the dehydration product (CaO). This reduces the contribution of the oxide surface energy to the total free energy of products and makes the dehydration more thermodynamically profitable. This effect may contribute to the observed depression of the dehydration temperature.

Complementary physical methods provide an indication of an interaction between the nitrate and the hydroxide, which is responsible for the observed effects. A possible mechanism of this interaction can be an embedding of nitrate-ions into the brucite-like lattice that may facilitate a nucleation stage and accelerate the dehydration reaction.

Thus, the modification of Ca(OH)₂ with potassium nitrate appears to provide a valuable opportunity to enhance the dehydration rate at T < 400 °C as well as to vary the product texture. The reported material KNO₃/Ca(OH)₂ exhibits a large heat storage density and adjustable reaction temperature and may be considered as a promising new candidate for storage of concentrated solar heat. In a broader sense, the approach of modification by salts can be applied for improving the kinetics and thermodynamics of decomposition of other materials interesting for storage of concentrated solar heat, such as carbonates.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge the contribution from Dr T. A. Krieger on measuring X-ray diffraction patterns and Dr Yu. A. Chesalov on recording IR-spectra. This work was conducted within the framework of budget project No. 0303-2016-0013 of the Boreskov Institute of Catalysis. One of the authors (A. Shkatulov) thanks the Russian Foundation for Basic Researches (project 16-38-00503) for partial financial support.

Notes and references

1. L. F. Cabeza, A. Solé, X. Fontanet, C. Barreneche, A. Jové, M. Gallas, C. Prieto and A. I. Fernández, Appl. Energy, 2017, 185, 836–845.
2. Y. Tian and C. Y. Zhao, Appl. Energy, 2013, 104, 538–553.
3. D. Goswami, Principles of Solar Engineering, CRC Press, New York, 2015.
4. M. Medrano, A. Gil, I. Martorell, X. Potau and L. F. Cabeza, Renewable Sustainable Energy Rev., 2012, 14, 56–72.
5. F. J. Ruiz-Cabañas, A. Jové, C. Prieto, V. Madina, A. I. Fernández and L. F. Cabeza, Sol. Energy Mater. Sol. Cells, 2017, 159, 526–535.
6. D. Zhou and P. Eames, Sol. Energy Mater. Sol. Cells, 2016, 157, 1019–1025.
7. G. García-Martín, M. I. Lasanta, V. Encinas-Sánchez, M. T. de Miguel and F. J. Pérez, Sol. Energy Mater. Sol. Cells, 2017, 161, 226–231.
8. M. Liu, W. Saman and F. Bruno, Renewable Sustainable Energy Rev., 2012, 16, 2118–2132.
9. L. André, S. Abanades and G. Flamant, Renewable Sustainable Energy Rev., 2016, 64, 703–715.
10. A. Jabbari-Hichri, S. Bennici and A. Auroux, Sol. Energy Mater. Sol. Cells, 2015, 140, 351–360.
11. K. M. Lovegrove, A. Luzzi, I. Soldiani and H. Kreetz, Sol. Energy, 2004, 76, 331–337.
12. S. M. Ranade, M.-C. Lee and W. Prengle, Sol. Energy, 1986, 37, 375–388.
13. M. Felderhoff and B. Bogdanović, Int. J. Mol. Sci., 2009, 10, 325–344.
14. Y. I. Aristov, V. N. Parmon, G. Cacciola and N. Giordano, Int. J. Energy Res., 1993, 17, 293–303.
15. Y. A. Criado, M. Alonso, J. C. Abanades and Z. Anxionnaz-Minvielle, Appl. Therm. Eng., 2014, 73, 1085–1092.
16. F. Schaube, L. Koch, A. Wörner and H. Müller-Steinhagen, Thermochim. Acta, 2012, 538, 9–20.
17. F. Schaube, A. Wörner and R. Tamme, Trans. ASME: J. Sol. Energy Eng., 2011, 133, 031006.
18. H. Ogura, T. Yamamoto and H. Kage, Energy, 2003, 28, 1479–1493.
19. M. N. Azpiazu, J. M. Morquillas and A. Vasquez, Appl. Therm. Eng., 2003, 23, 733–741.
20. E. Halstead and A. Moore, J. Chem. Soc., 1957, 3873–3875.
21. A. I. Shkatulov and Y. I. Aristov, Energy, 2015, 85, 667–676.
22. A. I. Shkatulov, T. A. Krieger, V. I. Zaikovskii, Y. A. Chesalov and Y. I. Aristov, ACS Appl. Mater. Interfaces, 2014, 6, 19966–19977.
23. A. Kanzawa and Y. Arai, Sol. Energy, 1981, 27, 289–294.
24. J. Kariya, J. Ryu and Y. Kato, ISIJ Int., 2015, 55, 457–463.
25. C. Roßkopf, S. Afflerbach, M. Schmidt, B. Görtz, T. Kowald, M. Linder and R. Trettin, Energy Convers. Manage., 2015, 97, 94–102.
26. J. Kariya, J. Ryu and Y. Kato, Appl. Therm. Eng., 2016, 94, 186–192.
27. Y. A. Criado, M. Alonso and J. C. Abanades, Sol. Energy, 2016, 135, 800–809.
28. M. S. Murthy, P. Raghavendrachar and S. V. Sriram, Sol. Energy, 1986, 36, 53–62.
29. J. Yan and C. Y. Zhao, Chem. Eng. Sci., 2014, 117, 293–300.
30. J. Yan and C. Y. Zhao, Chem. Eng. Sci., 2015, 138, 86–92.
31. T. Kito and N. Kobayashi, Kagaku Kogaku Ronbunshu, 2012, 38, 172–175.
32. CRC Handbook of chemistry and physics, ed. D. R. Lide, 90^th edn, 2010, pp. 4–83.
33. A. K. Galwey and M. E. Brown, Thermal decomposition of ionic solids, Elsevier, 1999, p. 106.
34. NIST-JANAF Thermochemical tables, ed. M. W. Chase, Woodbury, New York, 4^th edn, part I, Al-Co, 1998.
35. Y. Kato, Y. Sasaki and Y. Yoshizawa, Energy, 2005, 30, 2144–2155.
36. G. Lebon, D. Jou and J. Casas-Vázquez, Understanding Non-equilibrium Thermodynamics: Foundations, Applications, Frontiers, Springer-Verlag, Berlin, 2008, p. 92.
37. M. Hartman, O. Trnka, K. Svoboda and J. Kocurek, Chem. Eng. Sci., 1994, 49, 1209–1216.
38. J. M. Valverde, J. Mater. Chem. A, 2013, 1, 447–468.
39. I. Barin, Thermochemical Data of Pure Substances, Weinheim, New York, 1989.

---