Theoretical investigation on the mechanism of the OH-initiated degradation process of reactive red 2 azo dye

Abstract

The degradation treatments of azo dyes using various advanced oxidation processes (AOPs) have attracted considerable attention. Recently, our research group reported the degradation of reactive red 2 (RR2) azo dye in the newly designed ozone aerated internal micro-electrolysis filter (OIEF) system, the treatment performance of which is excellent. However, the reaction channels along which the RR2 dianion degrades remain to be deciphered at the molecular reaction level. Here, we report the degradation mechanism of the RR2 dianion by means of the density functional theory. The OH-initiated model in aquatic conditions has been adopted in the quantum chemical calculations due to the key role of the hydroxyl radical in the AOPs. According to our calculation results, there are three possible C-attack electrophilic substitution channels for the RR2 dianion and two C-attack channels for its hydrazone tautomer. It has been found that in each possible channel, the primal step is the initial association between the hydroxyl radical and one of the sulfonic groups, leading to the formation of a pre-reaction complex which is provided with a distinct hydrogen bond feature where the hydroxyl radical serves as a proton donor. The tautomerization between the azo and hydrazone forms was also found to have an influence on the distribution of degradation intermediates and products. The theoretical results we present are consistent with previous theoretical studies and our experimental findings and may shed some light on the improvements of the degradation treatments for RR2 and other structurally similar azo dye pollutants.

---

Introduction

Azo dyes are the most widely utilized reagents in the organic dye market with a market share of up to 60–70%.^1,2 They are also extensively used in various industrial fields such as plastics, inks, varnish paper, paints, leather, color solvents, drugs, food, and cosmetics.^3,4 Due to the stability of the azo group, it is commonly difficult to decompose when exposed to light or under acidic, basic, or oxidizing conditions.⁵ As a consequence, these azo dyes, particularly those containing aromatic rings, are resistant to conventional biological and even chemical wastewater treatments,^6–9 and have become hazardous materials in the water environment because of their toxicity, carcinogenicity, and bioaccumulation.^10,11

Great efforts have been devoted to tackling the effluent polluted by aromatic azo dyes, and the advanced oxidation process (AOP) is still one of the most common techniques researched and designed for the degradation, decolorization, and mineralization of pollutants under aqueous condition in recent years.^12–25 The AOPs include a variety of effective and sustainable strategies such as homogeneous and heterogeneous photo-catalysis upon near-UV or visible irradiation, ozonation, Fenton, nonthermal plasmas, electrolysis, ultrasound, and wet air oxidation.

Particularly, in our recent experimental studies, the ozone aerated internal micro-electrolysis filter (OIEF) system was designed and applied to the treatment of the azo dye reactive red 2 (RR2). The degradation efficiency was evaluated and the degradation by-products were identified in comparison with the ozonation and IE treatments. The result showed that the complete decolorization and 82% TOC removal rate can be achieved in the OIEF system, which provided a luciferous prospect for the practical application in the treatments of azo dye waste water at neutral or alkaline pH.^26,27 However, the microscopic mechanism remains to become unraveled at the molecular reaction level.

It is generally accepted that, the key purpose to all of these AOP techniques is to create highly reactive oxygen species in the aqueous phase, especially the hydroxyl radical, which are capable to destroy the target pollutants.^28,29 Moreover, to this date, the ability to generate hydroxyl radicals is used to characterize and evaluate the AOPs.³⁰ In fact, the OH-initiated model has been extensively used in theoretical investigations on the reaction mechanisms of AOPs in aquatic environment.^31–33

On the other hand, the organic sulfonic acids are usually very strong in the organic acid family. For example, the pK_as of benzenesulfonic and methanesulfonic acids are ca. −2.5 and −2.0, respectively,³⁴ and the pK_a of reactive red 1 dye is −3.3.³⁵ Thus, it can be inferred that for the main pH value range in the experimental study, the computational investigation adopting the dianion structure of RR2 is appropriate and reliable.

Accordingly, as a subsequent research following our previous experimental work and in order to decipher the intricate degradation mechanism of RR2 dye in the presence of hydroxyl radicals, here we report a computational study on the potential energy surfaces of reaction between RR2 dianion and hydroxyl radical based on the dual descriptor data.

Computational methods

The stationary points in the potential energy surfaces (PESs) were fully optimized at the density functional theory (DFT) level of theory employing the B3LYP functional.^36–38 To make a balance between the computational precision and cost, the 6-31+G(d) basis set was used for all the atoms. Once a geometrical optimization process was completed, the harmonic frequency calculation was carried out at the same level to determine the converged structure to be a minimum or a transition state. To confirm the right connections between transition states and minima along the reaction coordinates, the intrinsic reaction coordinate (IRC) analyses starting from all the transition state structures were carried out towards both forward and reverse directions. The local quadratic approximation method^39,40 was used in the IRC calculations when needed. To take the deviation between the computational model of harmonic vibration and the actual anharmonic molecular vibration into consideration, the zero point vibrational energy (ZPE) was corrected by a scaling factor of 0.977.⁴¹ In order to cope with the influence on the reaction PES induced by the bulk surrounding water molecules, the solvent effect was implicitly represented using the SMD model.⁴² To check the accuracy of the 6-31+G(d) basis set, the single point energies were further refined at the B3LYP/6-311++G(d,p) level.

All the electronic structure calculations were carried out by means of the GAUSSIAN09 program suite.⁴³ The molecular structures were displayed by using the Avogadro (version 1.2.0n) software.⁴⁴

For such a large and structurally intricate reactant as RR2, it is almost impractical to take all the reaction channels into account. The favorable reactive sites of RR2 by electrophilic attacks can be concisely predicted by the dual descriptor (Δf) data.⁴⁵ The dual descriptor is defined as follows:

Δf = ρ_N+1(r) − 2ρ_N(r) + ρ_N−1(r) ≈ ρ^S_N+1(r) − ρ^S_N−1(r) (1)

where ρ_N(r) denotes the electron density at the coordinate (r) of the molecule (or ion) with N electrons, and ρ^S_N+1(r) represents the electron spin density at the coordinate (r) of the molecule (or ion) with N + 1 electrons. The dual descriptor data of RR2 dianion were calculated and visualized by the Multiwfn program (version 3.3.8)⁴⁶ on the basis of the electronic structure results obtained by the GAUSSIAN09 program suite.

Results and discussion

The dual descriptor (Δf) data of RR2 dianion and its hydrazone tautomer

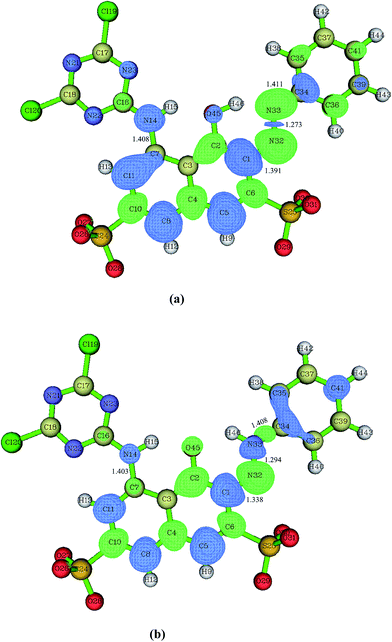
As shown in Fig. 1, at the B3LYP/6-31+G(d) level, the RR2 dianion has a quasi C_s symmetry with all the atoms almost in one plane with the exception of the four oxygen atoms in the two sulfonic groups. Since there are two sulfonic groups, the sulfonic group made up of S24, O26, O27, and O28 atoms will be referred to as sulfonic group 1, and the other one will be called sulfonic group 2 for convenience. Additionally, the oxygen and hydrogen atoms in the attacking hydroxyl radical will be labeled as O47 and H48, respectively. The C7–N14, C1–N32, and N33–C34 distances in the equilibrium structure of RR2 dianion are 1.408, 1.391, and 1.411 Å, respectively. These three bond lengths are all shorter than the typical C–N single bond length of 1.47 Å, but longer than the C=N double bond length of 1.29 Å, indicating strong conjunction effects over these moieties. The H46, O45, C2, C1, N32, and N33 atoms form a quasi planar six-member ring structure, with the H46–O45–C2–C1 dihedral angle being −0.3°, which facilitates the tautomerization between the azo and hydrazone forms of RR2. All the Cartesian coordinates of the computed stationary points have been presented in the ESI, please see the ESI† materials for details.

Fig. 1 The dual descriptor (Δf) data of azo form (a, RR2) and hydrazone form (b, HRR2) of RR2 dianion obtained at the B3LYP/6-31+G(d) level. If Δf > 0 (green), then the site is favorable for a nucleophilic attack, whereas if Δf < 0 (blue), then the site is favorable for an electrophilic attack. Key bond lengths are also given in angstrom.

When azo dye molecule contains hydroxyl group at the neighboring position of azo group, especially at the ortho position in aromatic ring, the hydrazone tautomer may usually exist. As shown in Fig. 1(b), the C7–N14 and N33–C34 distances in the equilibrium structure of hydrazone tautomer of RR2 dianion (referred to as HRR2 hereafter) are 1.403 and 1.408 Å, respectively, close to those in the azo tautomer, while the C1–N32 distance is 1.338 Å, shorter than that in the azo tautomer by 0.053 Å, longer than the typical C=N double bond length of 1.29 Å by about 0.048 Å. In water solution, the absorption range from 400 to 440 nm typically corresponds to the azo forms of azo dyes, while the absorption band of hydrazone forms typically lies between 475 and 510 nm.⁴⁷ The UV-vis spectrum of RR2 dye we obtained experimentally (Fig. 1(b) in ref. 27)²⁷ shows that neither absorption regions can be neglected, indicating that the degradation processes starting from the azo and hydrazone forms are both likely to occur.

For relatively small size or structurally simple molecules, the potential energy profiles would be generally constructed along all the possible reaction channels.^48,49 When the RR2 dianion is attacked by the ˙OH radical, however, due to the fairly large size and structural complexity of RR2 dianion, it is an extremely heavy computational workload to take all the possible reaction channels into account, which is unaffordable at present. Since the hydroxyl radical is a strong electrophilic species,⁵⁰ to give a rational explanation on degradation mechanism of the RR2 dianion on the condition where plenty of hydroxyl radicals are provided, the potential energy profiles will be constructed based on the prediction of the favorable reactive sites by electrophilic attacks.

Fig. 1(a) presents the dual descriptor data of RR2 dianion in aquatic environment. The favorable reactive sites by the electrophilic attacks are the C1, C5, C7, C8, C11, C34, and N14 atoms. In addition, our experimental results have shown that the decolorization of RR2 is very fast.^26,27 This can be attributed to the fact that the large delocalization π conjunction structure of RR2 decomposes rapidly into smaller π conjunction fragments, leading to the increased energy differences between the frontier occupied and unoccupied molecular orbitals, and as a result the corresponding absorption electronic transition energies shift to the UV region from visible region of absorption spectrum. The electrophilic substitution attacks on the C5, C8, and C11 sites by hydroxyl radicals clearly play marginal roles in the rapid destruction of the large delocalization π conjunction structure of RR2. Therefore, it can be deduced that the most probable primary steps of the degradation reactions are the cleavages of C7–N14 and C1–N32=N33–C34 bonds.^26,27 Accordingly, the electrophilic substitution attacks on the C34, C1, C7, and N14 sites by hydroxyl radicals will be taken into account in this study. While for HRR2, as illustrated in Fig. 1(b), the favorable reactive sites by the electrophilic attacks are the C1, C5, C8, C11, C34, C35, C36, C41, N14, and N33 sites. And by the same token, the electrophilic attacks on the N33, C1, C34, and N14 sites which may probably lead to the rapid decolorization of RR2 dye will be considered here.

The reaction channel for ˙OH attacking the C34, C1, C7, and N14 sites of RR2

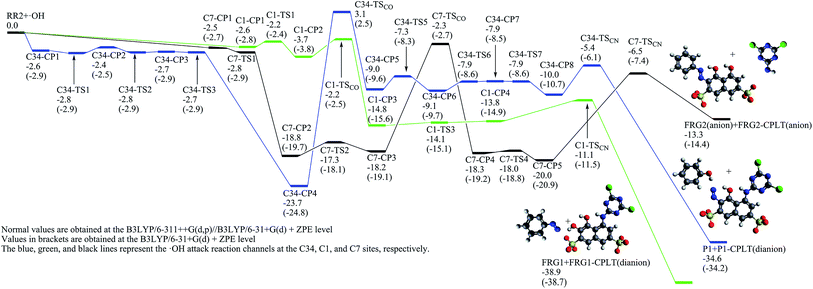
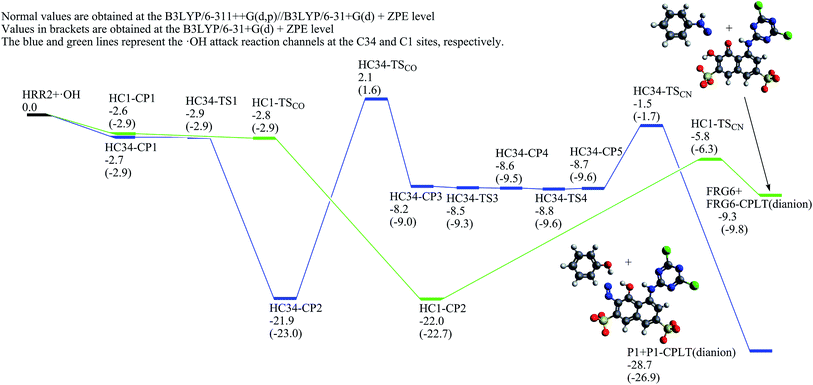
The ˙OH induced degradation process of RR2 mainly includes two important steps, the formation of ˙OH radical adduct and the cleavage of the target chemical bond (C–N or N–N bond).

When the C34 site is electrophilically attacked by hydroxyl radical, the C34–N33 bond may be cleaved, leading to the formation of phenol (P1) and P1-CPLT products. As shown in Fig. 2, this electrophilic substitution process starts from the formation of a pre-reaction complex labeled as C34-CP1, where the hydroxyl radical is captured by one of the sulfonic groups (sulfonic group 2) and the H48–O30 distance is 1.748 Å as illustrated in Fig. 4. With respect to the reactant RR2 + ˙OH, (and for convenience, the relative energies will be all given at the B3LYP/6-311++G(d,p)//B3LYP/6-31+G(d) + ZPE level with respect to RR2 + ˙OH or HRR2 + ˙OH, unless otherwise noted), the relative energy of C34-CP1 is −2.6 kcal mol⁻¹. Via transition state C34-TS1, intermediate C34-CP2, transition state C34-TS2, intermediate C34-CP3, and transition state C34-TS3, the hydroxyl radical can attach to the C36 atom by forming the C–O bond, leading to the formation of C34-CP4. A transition state C34-TS_CO is associated with the formation of the ˙OH radical adduct at the target C34 site (C34-CP5). The relative energy of C34-TS_CO is 3.1 kcal mol⁻¹. From C34-CP5 to C34-CP8, the torsions of the H48–O47–C34–N33 and O47–C34–N33–N32 dihedral angles take place. C34-CP8 can dissociate into phenol (P1, the D12 product in ref. 26) and P1-CPLT products by overcoming an energy barrier C34-TS_CN, the relative energy of which is −5.4 kcal mol⁻¹. The cleavage of the C34–N33 bond is a heterolytic process, leading to the formation of neutral phenol and P1-CPLT dianion.

Fig. 2 The calculated potential energy profiles of the reaction channels for azo form of RR2 dianion (RR2) (energies in kcal mol⁻¹).

Fig. 3 The calculated potential energy profiles of the reaction channels for hydrazone form of RR2 dianion (HRR2) (energies in kcal mol⁻¹).

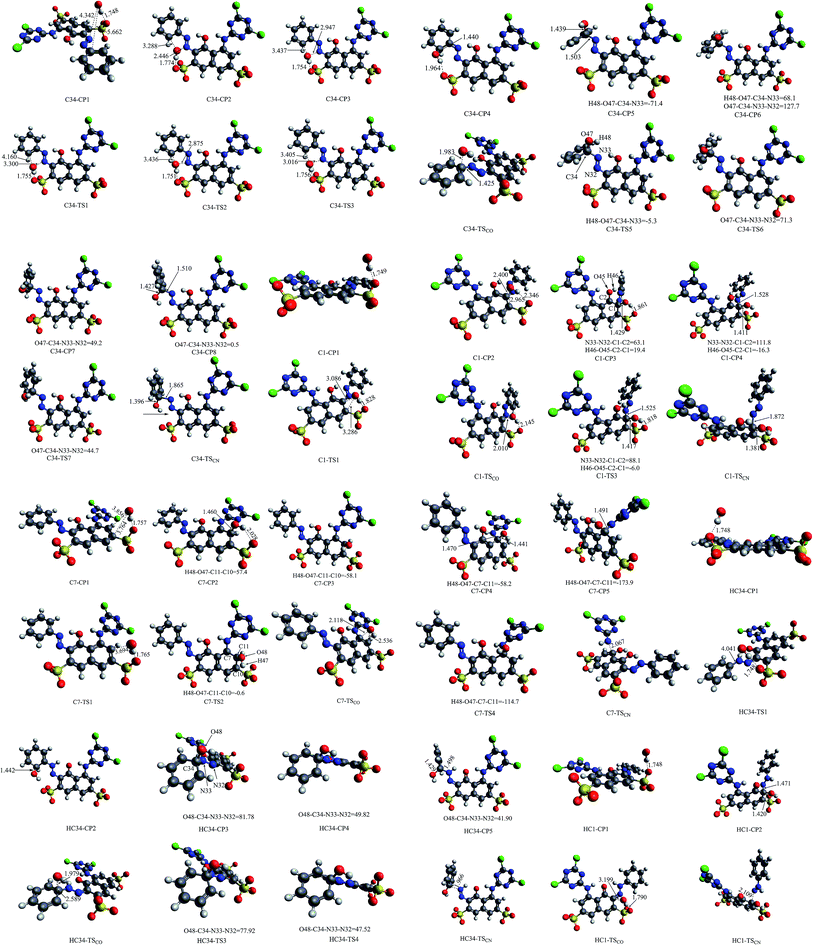Fig. 4 The structures of stationary points on the calculated potential energy profiles (bond lengths in angstrom and dihedral angles in degree).

It should be pointed out that, in some cases, for example, C34-CP7 lies only 0.02 kcal mol⁻¹ below C34-TS7 at the B3LYP/6-31+G(d) level, while with the ZPE correction, the relative energy of C34-CP7 is higher than C34-TS7 by about 0.08 kcal mol⁻¹. These cases may indicate negative transition states, which are not uncommon and have been reported in certain literatures.^51–54

On the C1-attack pathway, the pre-reaction complex C1-CP1 is formed at first, the energy of which is −2.6 kcal mol⁻¹, very close to that of C34-CP1. The transition state C1-TS_CO corresponds to the formation of the radical adduct at the C1 site (C1-CP3). The C1-TS3 is responsible for the torsions of the N33–N32–C1–C2 and H46–O45–C2–C1 dihedral angles. By finally overcoming the energy barrier of C1-TS_CN, the C1–N32 cleavage can take place. The relative energy of C1-TS_CN is −11.1 kcal mol⁻¹. Different from the case of C34–N33 cleavage, the C1–N32 bond fission is a homolytic process, which generates the neutral FRG1 radical and FRG1-CPLT dianion.

Jiao et al.⁵⁵ studied the OH-initiated C–N and N–N bond cleavages of alizarin yellow R (AYR, see Scheme 1) and its anion form (AYRA) computationally at the MPW1K/6-311+G(d,p)//B3LYP/6-31G(d) with the integral equation formalism polarized continuum model (IEF-PCM) used in the single point energy calculation. They found that for AYRA, the C–N bond cleavage is kinetically competitive with, but thermodynamically more favorable than the N–N bond cleavage.⁵⁵ Their conclusion is in line with the corresponding experimental finding, that is, the phenol was observed as major product in the oxidation degradation of AYRA.⁵⁶ In the present paper, the dual descriptor result suggests that the attacks by ˙OH at both the N32 and N33 sites of the azo group, which are associated with the N–N bond cleavage,⁵⁵ are not favorite. This is consistent with the computational conclusion reported by Jiao et al.⁵⁵ In detail, for C-attack on AYRA, according to the constructed energy profiles, the C4 site (see Scheme 1) is slightly more favorable kinetically, and much more favorable thermodynamically than the C1 site.⁵⁵ On the reaction pathway for RR2 dianion attacked by ˙OH at the C34 site in this study, the transition state for the formation of radical adduct (C34-TS_CO), the transition state for the C34–N33 cleavage (C34-TS_CN), and the dissociation fragments generated by the C34–N33 cleavage (P1 + P1-CPLT) all lie above the corresponding points on the C1-attack pathway (C1-TS_CO, C1-TS_CN, and FRG1 + FRG1-CPLT) by 5.3, 5.6, and 4.3 kcal mol⁻¹, respectively. This suggests that although the degradation caused by the ˙OH attack at the C34 site is not hard to occur because the highest energy barrier of this channel is only slightly higher (∼3.1 kcal mol⁻¹) than RR2 + ˙OH, it may not be a major channel in comparison with the C1-attack channel from both kinetic and thermodynamic viewpoints.

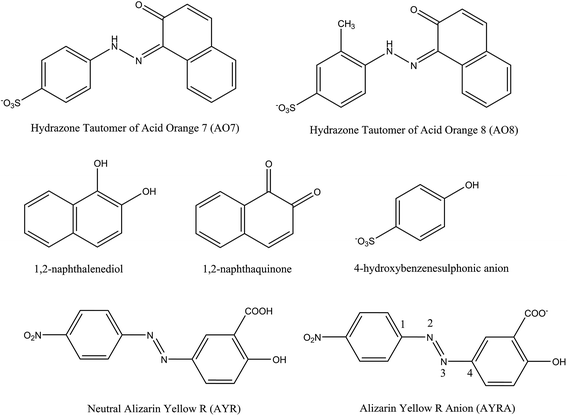Scheme 1 Schematic structures of the azo compounds and the degradation intermediates identified in literature.

FRG1 is the most probable precursor intermediate for the formations of nitrosobenzene (P2) and nitrobenzene (P3). As presented in Fig. 5, FRG1 can react with one hydroxyl radical at the N13 site to generate trans FRG1-OH-CP, which is a barrierless process and exothermic by 39.5 kcal mol⁻¹ at the B3LYP/6-311++G(d,p)//B3LYP/6-31+G(d) + ZPE level. The molecular trans FRG1-OH-CP can further react with another hydroxyl radical at N12, leading to the formation of FRG1-2OH-CP1, which is also an exothermic reaction process without energy barrier. This molecule–radical association process is exothermic by only 1.6 kcal mol⁻¹. FRG1-2OH-TS1 is responsible for the rotation movement of the attacking hydroxyl radical and FRG1-2OH-TS2 corresponds to the formation of N12–O16 bond in FRG1-2OH-CP3. It is noteworthy that the relative energy of FRG1-2OH-CP3 is higher than that of FRG1-OH-CP + ˙OH by 5.9 kcal mol⁻¹, indicating this is an endothermic process. From FRG1-2OH-CP3, through a hydrogen abstraction process by the third hydroxyl radical via the intermediate FRG1-3OH-CP1, FRG1-3OH-CP2 can be yielded which is a process with large amount of heat release by 78.2 kcal mol⁻¹. Via FRG1-3OH-TS, FRG1-3OH-CP2 can isomerize to FRG1-3OH-CP3 with respect to the torsion of the H15–O14–N13–N12 dihedral angle. When the fourth hydroxyl radical approaches to the N13 atom of FRG1-3OH-CP3, a pre-reaction complex FRG1-4OH-CP1 is formed at first, the relative energy of which is −0.1 kcal mol⁻¹ with respect to FRG1-3OH-CP3 + ˙OH. By overcoming the C–O bond formation transition state FRG1-4OH-TS1 and the N–N bond cleavage transition state FRG1-4OH-TS2, FRG1-4OH-CP1 can degrade into the nitrosobenzene molecule (P2) and H₂NO₂ radical.

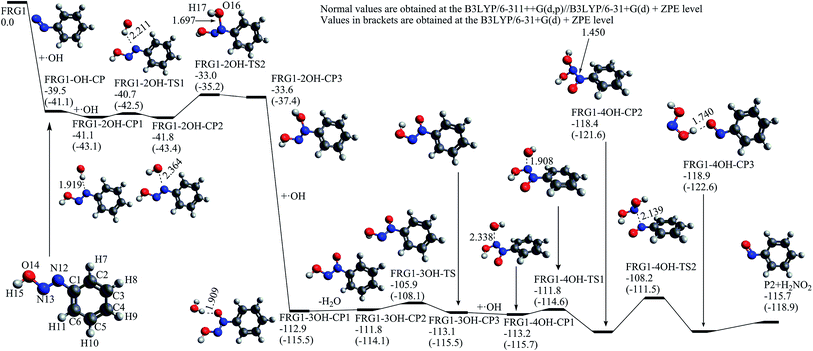Fig. 5 The calculated potential energy profile and the stationary point structures of the reaction channel from FRG1 to nitrosobenzene (P2) (energies in kcal mol⁻¹, bond lengths in angstrom).

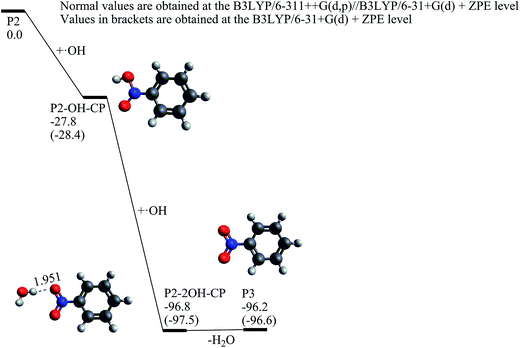
Once the nitrosobenzene product is formed, it can be further oxidized by two hydroxyl radicals resulting in the nitrobenzene (P3) molecule. As shown in Fig. 6, at first, the N atom in P2 is associated with a hydroxyl radical to form P2-OH-CP, which is exothermic by 28.4 kcal mol⁻¹ without any substantial barrier. When the second hydroxyl radical is attached to P2-OH-CP, P2-2OH-CP can be yielded with a great deal of heat release by 69.1 kcal mol⁻¹. By losing one water molecule, P2-2OH-CP can convert to the nitrobenzene product, which is an endothermic process by only 0.6 kcal mol⁻¹. The potential energy profile from P2 to P3 shows that if there exist plenty of hydroxyl radicals in the aquatic environment, it is very likely for the P2 product to be oxidized to the P3 product.

Fig. 6 The calculated potential energy profile and the stationary point structures of the reaction channel from nitrosobenzene (P2) to nitrobenzene (P3) (energies in kcal mol⁻¹, bond lengths in angstrom).

The C7–N14 cleavage can take place when the C7 or N14 atom is attacked by the ˙OH radical. According to the obtained dual descriptor data of RR2, the two atoms are both favorable reactive sites for electrophilic attacks. For the attack by ˙OH at the C7 site, a pre-reaction complex, labeled as C7-CP1, was located on the reaction pathway. The relative energy of C7-CP1 is −2.8 kcal mol⁻¹, which is close to those of the pre-reaction complexes C34-CP1 on the C34-attack and C1-CP1 on the C1-attack pathways. C7-CP2 and C7-CP3 are both the radical adducts at the C11 site, between which the main structural difference is the H48–O47–C11–C10 dihedral angle. The transition state C7-TS_CO corresponds to the formation of radical adduct at the C7 site from C7-CP3. The relative energy of C7-TS_CO is −2.3 kcal mol⁻¹, slightly lower than the corresponding transition state C1-TS_CO on the C1-attack pathway by 0.1 kcal mol⁻¹. C7-TS4 corresponds to the torsion of H48–O47–C7–C11 dihedral angle which connects C7-CP4 on the reactant side and C7-CP5 on the degradation side. C7-CP5 can finally degrade into FRG2 and FRG2-CPLT fragments by conquering the C1-TS_CN energy barrier. The relative energy of C1-TS_CN is −6.5 kcal mol⁻¹. The C7–N14 bond fission is a heterolytic process, that is, the two electrons in C7–N14 bonding orbital are both distributed into the FRG2 fragment, leading to the formations of FRG2 and FRG2-CPLT fragments which are both provided with one negative charge. The relative energy of FRG2 and FRG2-CPLT fragments is 13.3 kcal mol⁻¹, which is 25.6 kcal mol⁻¹ higher than that of the C1-attack products. Thus it can be concluded that from viewpoint of energy, in comparison with C1-attack, the C7-attack is competitive in kinetics but unfavorable in thermodynamics.

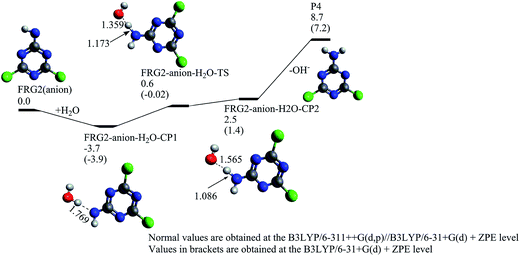
In acidic pH solution, the yielded fragment FRG2 (anion) can directly react with a proton to generate P4. At the B3LYP/6-311++G(d,p)//B3LYP/6-31+G(d) + ZPE level, this process will be exothermic by about 158.3 kcal mol⁻¹, indicating it may take place very efficiently. While under the near-neutral or alkaline pH conditions, the intermediate FRG2 (anion) may react with a water molecule, as illustrated in Fig. 7. At first, a pre-reaction complex labeled as FRG2-anion-H₂O-CP1 is formed, and then the FRG2 abstracts one hydrogen atom from the water molecule via FRG2-anion-H₂O-TS and results in the formation of reaction complex FRG2-anion-H₂O-CP2. Relative to FRG2 (anion) + H₂O, the energy of FRG2-anion-H₂O-TS is 0.6 kcal mol⁻¹. FRG2-anion-H₂O-CP2 can dissociate into the neutral P4 and hydroxide ion without energy barrier above the endothermicity. The relative energy of P4 + OH⁻ is 8.7 kcal mol⁻¹ above FRG2 (anion) + H₂O. Provided with the fact that the FRG2 (anion) and FRG2-CPLT (anion) can be generated from RR2 + ˙OH which is an exothermic process of 13.3 kcal mol⁻¹, it can be anticipated that the formation of P4 is not hard to occur. Experimentally, the P4 product, i.e. 2-amine 4,6-dichloro-1,3,5-triazine has been detected extensively in O₃, IE, and OIEF degradation systems with the initial pH = 7.²⁶ It should also be pointed out that in our previous experiment, the optimal pH for the TOC removal is around 9, and the degradation efficiency drops when the pH value increases to 10.²⁶ It is generally considered that the generation of hydroxyl radical from ozone decomposition could be accelerated with the increasing pH value,⁵⁷ and the decrease of degradation rate at pH = 10 is mainly ascribed to the appearance of the free radical scavengers, such as carbonate and sulfate at a high pH (>7).^26,27,58 According to our calculation, the hydroxide ion is the co-product in the degradation channel leading to 2-amine 4,6-dichloro-1,3,5-triazine under the neutral and alkaline pH conditions. From the viewpoint of reaction equilibrium, the increase in the amount of hydroxide ion may inhibit the formations of degradation products in this channel, which may also be one of the reasons why the degradation rate drops at high pH.

Fig. 7 The calculated potential energy profile and the stationary point structures of the reaction channel from FRG2 to 2-amine 4,6-dichloro-1,3,5-triazine in neutral or alkaline condition (energies in kcal mol⁻¹, bond lengths in angstrom).

When the N14 atom of RR2 is attacked by hydroxyl radical, the C7–N14 bond fission would result in the formation of the FRG3 and FRG3-CPLT1 fragments. The most probable fission products which have the lowest energy are the neutral FRG3 and FRG3-CPLT1 (dianion). Nevertheless, the relative energy of these degradation products is 39.9 kcal mol⁻¹, which is too high for degradation on this pathway to take place as compared with the channel along which the C7 atom is attacked. This indicates that the attack on the N14 atom by hydroxyl radical may not play an important role in the fission of C7–N14 bond in the degradation process.

The reaction channel for ˙OH attacking the N33, C1, C34, and N14 sites of HRR2

Different from the situation of the azo form of RR2 dianion, the dual descriptor result shows that the N33 site of HRR2 is one of the favorable sites by electrophilic attack. The N32–N33 distance in HRR2 is 1.294 Å, longer than that in azo form by 0.021 Å, which indicates that in the tautomerization from azo form to hydrazone form the N–N bond strength is somewhat weakened. As a result, the C–N and N–N cleavages induced by the electrophilic attack on the N33 site were both considered. As shown in Fig. S1,† the N–N cleavage by the N33-attack would finally yield the neutral FRG4 and FRG4-CPLT dianion fragments, the relative energy of which is 15.9 kcal mol⁻¹ with respect to HRR2 + ˙OH at the B3LYP/6-311++G(d,p)//B3LYP/6-31+G(d) + ZPE level. The C–N cleavage pathway by N33-attack would lead to the degradation fragments of the neutral FRG5 and FRG5-CPLT dianion. The relative energy of the FRG5 and FRG5-CPLT dianion is 41.8 kcal mol⁻¹. From viewpoint of energy, these two endothermic processes imply the N33-attack pathway is thermodynamically prohibited. Aviyente et al.⁵⁹ investigated the ultrasonic degradation processes of hydrazone forms of two monoazo dyes C.I. Acid Orange 7 (AO7) and C.I Acid Orange 8 (AO8) by means of both experimental and computational approaches. As shown in Scheme 1, the molecular structures of AO7 and AO8 are similar with that of RR2, that is, the azo group is connected with a phenyl group on one side and a naphthyl group on the other side, and a hydroxyl radical substituent is attached to the naphthyl group at the ortho-position of the azo group. They found that the energy barrier along the N-attack pathway on the C=N double bond is 11.6 kcal mol⁻¹ higher than that along the C-attack pathway on the C=N double bond at the MPW1K/6-31+G(d,p)//MPW1K/6-31G(d) level. And according to the intermediate structures identified by the HPLC, GC-MS, CE-MS, and CE-UV/DAD analyses in previous studies on the advanced oxidation of AO7,^60–62 they concluded that the ˙OH radical addition by the N-attack cannot compete with the C-attack pathway. Here in this study on the degradation process of HRR2, the possibility of N-attack on the C1=N32 double bond is ruled out in terms of the dual descriptor data, that is, the N32 atom is not a favorite site by hydroxyl radical attack. It can be seen that the dual descriptor result of the electrophilic attack on the C1=N32 double bond for hydrazone form of RR2 dye provides a prediction which is consistent with the previous theoretical PES and experimental results on the hydrazone tautomer of azo dye which has similar structure.

As shown in Fig. 3, similar to the situation of the azo tautomer, a pre-reaction complex HC1-CP1 was found to locate on the C1-attack pathway of HRR2. The transition state HC1-TS_CO is corresponding to the formation of the ˙OH radical adduct HC1-CP2 at the C1 site from HC1-CP1, and the relative energy of HC1-TS_CO is −2.8 kcal mol⁻¹ with respect to HRR2 + ˙OH. The C1–N32 cleavage can take place via the transition state HC1-TS_CN, the relative energy of which is −5.8 kcal mol⁻¹. The IRC calculation confirms that via HC1-TS_CO the FRG6 and FRG6-CPLT dissociation fragments can be yielded. The transition states HC1-TS_CO and HC1-TS_CN both lie below HRR2 + ˙OH, indicating the degradation along this channel is possible in terms of potential energy. Aviyente et al.⁵⁹ investigated the potential energy surfaces of the ˙OH radical addition reactions on the C sites of the C=N double bonds for hydrazone tautomers of AO7 and AO8. Their calculated results have shown that for both molecules, the energy barriers for the additions of ˙OH at the C sites of the C=N double bonds are below the reactants (AO7 + ˙OH or AO8 + ˙OH). The section of potential energy profile we calculated for the ˙OH addition reaction at the C1 site of HRR2 is qualitatively consistent with Aviyente et al.'s computational results. In addition, the radical adduct HC1-CP2 lies 22.0 kcal mol⁻¹ below HRR2 + ˙OH, which is close to the relative energies (−24.6 and −20.8 kcal mol⁻¹) of the radical adducts for hydrazone tautomers of AO7 and AO8 dyes calculated by Aviyente et al.⁵⁹ at the MPW1K/6-31G(d) level, indicating a hydroxyl radical adduct with fairly low relative energy may probably locate on the C-attack degradation pathway of hydrazone tautomer of similar azo dye. The PES section of the C–N cleavage was not considered by Aviyente et al.,⁵⁹ while the experimental findings^60–62 as mentioned above have shown that the 1,2-naphthalenediol (or 1,2-naphthaquinone, see Scheme 1) is the important intermediate structure detected in the AOP degradation of AO7, which provides a clue to the feasibility of this reaction channel.

The attack by ˙OH radical at the C34 site is another important possible pathway for the AOP degradation of HRR2. The pre-reaction complex on this pathway is HC34-CP1, the energy of which is −2.7 kcal mol⁻¹ with respect to HRR2 + ˙OH. Via transition state HC34-TS1, HC34-CP2 can be formed, which is the radical adduct at the C35 site of HRR2. The hydroxyl radical at the C35 site in HC34-CP2 can migrate to the C34 site in HC34-CP3 via transition state HC34-TS_CO. From HC34-CP3 to HC34-CP5, the major structural variation is the torsion of the O47–C34–N33–N32 dihedral angle and the energy barriers for this process can be virtually ignored. The C–N cleavage could take place by overcoming the transition state HC34-TS_CN, the relative energy of which is −5.8 kcal mol⁻¹. Interestingly, the IRC calculation shows that starting from HC34-TS_CN, the C–N cleavage products are P1 and P1-CPLT, the same as the case of the C34-attack channel of RR2. Overall, HC34-TS_CO is the highest energy barrier on this reaction pathway, nevertheless it lies only 2.1 kcal mol⁻¹ above HRR2 + ˙OH. In comparison with the C1 site, the attack at the C34 site is slightly unfavorable in kinetics, but much more feasible in thermodynamics due to the fairly low energy of the yielded cleavage products P1 + P1-CPLT (−28.7 kcal mol⁻¹), which is different from the case of RR2 where the C1-attack is preferable to the C34-attack both kinetically and thermodynamically as mentioned above. Theoretically, this degradation channel was not taken into account by Aviyente et al.,⁵⁹ while in the experiments,^60–62 the 4-hydroxybenzenesulphonic anion (see Scheme 1) intermediate has been detected in AOP degradation process of AO7, which gives the evidence that the attack by ˙OH at the C site of the phenyl group is possible. In addition, as mentioned above, the P1 product has also been identified to be the degradation product of RR2 dye in our O₃, IE, and OIEF system, proving the feasibility of this channel, although a small amount of this product may be generated from the degradation of the azo form of RR2 dye.

The attack by hydroxyl radical on the N14 site of HRR2 results in the formations of FRG3 and FRG3-CPLT2 (dianion) fragments. The relative energy of FRG3 + FRG3-CPLT2 (dianion) fragments is 42.3 kcal mol⁻¹ with respect to HRR2 + ˙OH, indicating the electrophilic attack by ˙OH on this site is thermodynamically unfavorable, which is the same as the case of the N14-attack channel of RR2.

Mechanism of OH-initiated degradation processes of RR2 and HRR2, and implication for the AOP degradation of RR2 dye

On each of the three probable degradation pathways of RR2, the first step is the initial association between the H atom in the attacking hydroxyl radical and the O atom in one of the sulfonic groups of RR2. The H48–O30, H48–O31, and H48–O28 distances are 1.748, 1.749, and 1.757 Å in the pre-reaction complexes C34-CP1, C1-CP1, and C7-CP1, respectively, which are slightly shorter than the typical hydrogen bond in water determined to be 1.84 Å by Zeidler et al. using the TTM3-F model.⁶³ Another significant structural feature of a hydrogen bond in which the hydroxyl radical serves as proton donor is that the OH⋯X structure is almost linear. When X = OH₂, the O–H⋯OH₂ angle was predicted to be 178.7° according to Lai and Chou's computational results obtained at the UCCSD/6-31++G** level of theory.⁶⁴ Here, the O47–H48–O30, O47–H48–O31, O47–H48–O28 angles in C34-CP1, C1-CP1, and C7-CP1 are 174.7, 174.6, and 175.2°, respectively. Energetically, the complexes C34-CP1, C1-CP1, and C7-CP1 lie −2.6, −2.6, and −2.5 kcal mol⁻¹ below the reactant RR2 + ˙OH, all in the energy range of the typical O–H⋯O hydrogen bond (8–34 kJ mol⁻¹).⁶⁵ All these features indicate that the pre-reaction complexes C34-CP1, C1-CP1, and C7-CP1 are formed with distinct hydrogen bond characteristic where the hydroxyl radical serves as the proton donor. For HRR2, these features of structure and energy also exist in the pre-reaction complexes HC34-CP1 and HC1-CP1. It should be also noted that although the B3LYP functional may not be the best choice for the computational investigation on the hydrogen bonds, it has been proven to be able to describe the geometries and strengths of the hydrogen bonds^66–69 and has been employed in our study due to its relatively small computational cost. The influence of the polarization function basis set of the hydrogen atom in the hydrogen bond was also taken into consideration, that is, the 6-31+G(d,p) basis set was used for the H48 atom (referred to as 6-31+G(d,p)-H48) in the structural optimizations and frequency analyses of the complexes C34-CP1, C1-CP1, and C7-CP1 for comparison. The calculation results show that the structures of C34-CP1, C1-CP1, and C7-CP1 obtained by using the 6-31+G(d,p)-H48 basis set are close to those obtained at the 6-31+G(d) level, with slight shortenings of the H48–O30, H48–O31, and H48–O28 distances by less than 0.03 Å. The relative energies of C34-CP1, C1-CP1, and C7-CP1 obtained at the 6-31+G(d,p)-H48 level are −1.8, −1.7, and −1.5 kcal mol⁻¹, respectively, which are also very close to those obtained at the 6-31+G(d) level, with the largest deviation less than 1.5 kcal mol⁻¹. Accordingly, it can be concluded that, at least qualitatively, the formation of hydrogen bond between the hydroxyl radical and one of the sulfonic groups plays an important role in the initial association process between RR2 (or HRR2) and hydroxyl radical.

For all the three probable primary C-attack reaction pathways of RR2 and two probable C-attack reaction pathways of HRR2 as mentioned above, the OH-initiated degradations are multistep processes. And on each reaction pathway, the highest energy barrier to be conquered is the transition state which corresponds to the C–O bond formation for the radical adduct at the target reaction site (C34, C1, or C7 for RR2, and C34 or C1 for HRR2), rather than the transition state associated with the C–N bond cleavage. The same tendency between the energy barriers of the formation of hydroxyl radical adduct and C–N cleavage has also been reported by Jiao et al.⁵⁵ for ˙OH electrophilic attacks at the C1 and C4 sites of AYR.

According to our calculations for RR2, all the energy barriers in the three degradation channels are lower than the reactant RR2 + ˙OH, with only one exception of the transitions state C34-TS_CO in C34-attack channel of RR2 which lies only 3.1 kcal mol⁻¹ above. The situation for HRR2 is similar to that for RR2, that is, the relative energy of HC34-TS_CO is 2.1 kcal mol⁻¹ which is the only barrier lying above HRR2 + ˙OH. This indicates that the degradations of RR2 along the C34, C1, and C7 attack pathways and its hydrazone tautomer along the C34 and C1 pathways are all feasible to take place.

In fact, our experimental studies have shown that the phenol (P1) and 2-amine 4,6-dichloro-1,3,5-triazine (P4) products, which are respectively the important tagged products of C34-attack and C7-attack channels, are all detected and identified in the ozone, IE, and OIEF systems.²⁶ While for the C1-attack channel, as mentioned above, the primarily yielded degradation intermediate FRG1 can be oxidized by four hydroxyl radicals to form nitrosobenzene (P2), which can further react with another two hydroxyl radicals generating nitrobenzene (P3). Elovitz and von Gunten⁷⁰ proposed that the concentration variation trend of p-chlorobenzoic acid (pCBA) could be used to evaluate the concentration of ˙OH under some conditions. As suggested by Ruan et al.²⁵ and according to our previous experimental results²⁶ using pCBA as indicator of the amount of the produced hydroxyl radicals, it could be considered that, qualitatively, the abundance of hydroxyl radicals produced in the ozone system is higher than that in the IE system, and both are much lower than that in the OIEF process. According to the potential energy profile as illustrated in Fig. 5, for transformation from FRG1 to P2, there are three main steps in which substantial energy barriers need to be conquered, that is, from FRG1-2OH-CP1 to FRG1-2OH-CP3 via FRG1-2OH-TS2 (8.1 kcal mol⁻¹), from FRG1-3OH-CP2 to FRG1-3OH-CP3 via FRG1-3OH-TS (5.9 kcal mol⁻¹), and from FRG1-4OH-CP1 to P2 via FRG1-4OH-TS2 (5.0 kcal mol⁻¹). Under the condition where the concentration of produced hydroxyl radicals is low, the oxidation reaction process from FRG1 to P2 may be interrupted by two reasons. One is that there are not enough hydroxyl radicals to participate into the total oxidation process, and the other is that the three energy barriers mentioned above could not be overcome since the exothermic steps in this oxidation process, mainly including the steps from FRG1 to FRG1-OH-CP and from FRG1-2OH-CP3 to FRG1-3OH-CP1, could not provide sufficient energy due to lack of hydroxyl radicals. This may probably be the case for the IE system. While in the ozone system, moderate amount of hydroxyl radicals can be generated, and it is possible for FRG1 to convert to P2 and further to P3 partially through oxidation processes. In the OIEF system, a large amount of hydroxyl radicals are produced which can be used for the oxidation reactions of intermediate FRG1 and the yielded P2 product. Because P2 can be easily oxidized to P3 by hydroxyl radicals as mentioned above, it can be anticipated that in the OIEF system the amount of P2 may be very small. Experimentally, neither P2 nor P3 was detected in the IE system, and both P2 and P3 were observed in ozone system, while only P3 was identified in the OIEF system.²⁶ Our calculated potential energy profiles provide a rational explanation on the experimental findings.

In addition, the comparison between the OH-initiated degradation mechanisms of RR2 and HRR2 demonstrates that for RR2, the C1-attack pathway is more favorable than the C34-attack channel both kinetically and thermodynamically, and the C7-attack channel is kinetically competitive with, but thermodynamically much less favorable than the C1-attack pathway, while for HRR2, the C34-attack channel is slightly less favorable kinetically, but much more favorable thermodynamically than the C1-attack route as mentioned above. It can be seen that the favorable routes in the OH-initiated degradation processes of the two tautomers are not the same and the degradation intermediates and products can be controlled, in some sense, by the tautomerization between RR2 and HRR2. Experimentally, Huang et al.⁷¹ observed the azo-hydrazone tautomerization of two disperse yellow dyes and verified the molecular structures by means of UV-vis spectrum, ¹H NMR, and single-crystal XRD techniques. They found that the pH control and metal–ion complexation are two possible approaches which could affect the equilibrium of reaction between the two tautomers, that is, for example, the amount of azo form will increase and that of hydrazone form will accordingly decrease when the pH value of the solution increases. Therefore, it can be anticipated that the experimental strategies which have the abilities to change the ratio between the azo and hydrazone tautomers of azo dyes may play a significant role in the field of intermediate and product control for treatment of wastewater which is polluted by relevant azo dyes.

In order to evaluate the reaction rate constant, the Gibbs free energy profiles were also constructed at the B3LYP/6-311++G(d,p)//B3LYP/6-31+G(d) level with the thermal corrections at the temperature of 298.15 K and pressure of 1 atm. As shown in Fig. S2 and S3,† the relative Gibbs free energies of the reactant RR2 (or HRR2) + ˙OH and the degradation fragments become lower than their relative energies obtained at the B3LYP/6-311++G(d,p)//B3LYP/6-31+G(d) + ZPE level. This is mainly caused by the fact that their entropy values are greater than those of the reaction complexes and transition states. In spite of this, the competitive relationship between different reaction channels in Gibbs free energy profiles is almost identical to that in the potential energy profiles obtained at the B3LYP/6-311++G(d,p)//B3LYP/6-31+G(d) + ZPE level. For multistep reaction, Murdoch⁷² suggested a general solution for finding the rate-determining step. The reaction coordinate can be divided into several stages, and each stage begins with the reactant or an intermediate and terminates with the first intermediate or product which is more stable than the starting point of this stage. For each stage, the energy difference between the transition state with the highest energy and the beginning point of this stage, referred to as ΔG_th-s, is computed. The ΔG_th-s for all the stages will be compared, and the stage with the largest ΔG_th-s will be taken as the rate-determining step. According to the Gibbs free energy profiles, for C34-attack of RR2, the rate-limiting step is the stage from C34-CP4, via C34-TS_CO, C34-CP5, C34-TS5, C34-CP6, C34-TS6, C34-CP7, C34-TS7, C34-CP8, and C34-TS_CN, to P1 + P2-CPLT, where the highest energy barrier is C34-TS_CO. For C1-attack of RR2, the rate-limiting step in the reaction coordinate is the stage which starts from the reactant RR2 + ˙OH, via C1-CP1, C1-TS1, C1-CP2, and C1-TS_CO, to C1-CP3, in which the highest energy barrier is C1-TS_CO. For C7-attack of RR2, the rate-determining step is the stage from C7-CP2, via C7-TS2, C7-CP3, C7-TS_CO, C7-CP4, and C7-TS4, to C7-CP5, and the highest barrier in this stage is C7-TS_CO. While for C34-attack of HRR2, the rate-determining step is the stage from HC34-CP2, via HC34-TS_CO, HC34-CP3, HC34-TS3, HC34-CP4, HC34-TS4, HC34-CP5, HC34-TS_CN, to the dissociation product P1 + P1-CPLT, and the highest barrier in this stage is HC34-TS_CO, and for C1-attack of HRR2, the rate-determining step is the stage from HC1-CP2, via HC1-TS_CN, to the dissociation product FRG6 + FRG6-CPLT, and the only one energy barrier in this stage is HC1-TS_CN. The reactions in rate-determining steps in the C34-attack and C7-attack routes of RR2 as well as the C34-attack and C1-attack channels of HRR2 are considered to be unimolecular reactions because they start from the reaction complexes. The reaction rate constants (k) for the four steps are predicted to be, in terms of the conventional transition state theory, 3.3 × 10⁻⁷, 3.8 × 10⁰, 4.8 × 10⁻⁵, and 1.2 × 10 s⁻¹, respectively. The rate-determining step in C1-attack channel of RR2 starts from the reactant RR2 + ˙OH, and the reaction can be consequently seen as a bimolecular one. The ΔG_th-s value between C1-TS_CO and RR2 + ˙OH is 7.7 kcal mol⁻¹, the lowest one among all the five rate-determining steps mentioned above, and the k is calculated to be 3.5 × 10⁸ (mol L⁻¹)⁻¹ s⁻¹, lying in the range of 10⁸–10¹⁰ (mol L⁻¹)⁻¹ s⁻¹ which is the typical rate constant range of reactions between hydroxyl radical and organic compounds in aqueous solution.⁷³ While on the other hand, the experimental efforts (including using pCBA and phenol as indicators of the ˙OH concentration) to quantitatively measure the ˙OH concentration in our OIEF system were fruitless, thus it is unfortunate that the obtained rate constant cannot be converted to the degradation rate of RR2, although the latter has been determined in our previous experiment.^26,27

Conclusion

The OH-initiated degradation mechanisms of RR2 azo dye and its tautomer HRR2 have been investigated by means of the dual descriptor data and the constructed potential energy profiles. It can be concluded that the most favorable route for RR2 is the attack by ˙OH at the C1 site, and the C7-attack may play a competitive role in kinetics, and for HRR2, the C1-attack is slightly preferable in kinetics and C34-attack channel is much more favorable in thermodynamics. The tautomerization between azo and hydrazone forms has influence on the distribution of degradation intermediates and products. In aquatic environment, in each of the three electrophilic substitution channels of RR2 and the two for HRR2, the initial capture of the hydroxyl radical by one of the sulfonic groups is the primal step. The pre-reaction complexes are provided with distinct hydrogen bond characteristic, in which the hydroxyl radicals serve as proton donors and the O atoms in the sulfonic groups are the proton acceptors. The distributions of the nitrosobenzene and nitrobenzene products are associated closely with the concentrations of the hydroxyl radicals generated by various AOP techniques.

Our theoretical results agree well with our previous experimental findings and the theoretical investigations on similar molecules in literature. The confirmed initial capture mechanism of hydroxyl radical by the sulfonic groups of RR2 with the hydrogen bond feature and influence of tautomerization between azo and hydrazone forms on the degradation intermediates and products may shed some light on the improvements of the degradation treatments for RR2 and other structurally similar azo dye pollutants.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was supported by the Major Science and Technology Program for Water Pollution Control and Treatment of China (Grant No. 2015ZX07206-006-04 and Grant No. 2015ZX07306001-04) and the National Key Research and Development Plan of China – the Inter-governmental International Cooperation in Scientific and Technological Innovation Major Special Project (Grant No. 2016YFE0123400).

References

1. K. Pachhade, S. Sandhya and K. Swaminathan, J. Hazard. Mater., 2009, 167, 313–318.
2. J. Mathieu-Denoncourt, C. J. Martyniuk, S. R. de Solla, V. K. Balakrishnan and V. S. Langlois, Environ. Sci. Technol., 2014, 48, 2952–2961.
3. A. Shimizu, Y. Takuma, S. Kato, A. Yamasaki, T. Kojima, K. Urasaki and S. Satokawa, J. Fac. Sci. Technol., Seikei Univ., 2013, 50, 1–4.
4. Z. Y. Lv, X. J. Liu, B. Jia, H. Wang, Y. Wu and Z. P. Lu, Sci. Rep., 2016, 6, 11.
5. A. Latif, S. Noor, Q. M. Sharif and M. Najeebullah, J. Chem. Soc. Pak., 2010, 32, 115–124.
6. T. Robinson, G. McMullan, R. Marchant and P. Nigam, Bioresour. Technol., 2001, 77, 247–255.
7. A. Stolz, Appl. Microbiol. Biotechnol., 2001, 56, 69–80.
8. X. D. Qin, Z. W. Zhu, G. Liu, H. M. Fu, H. W. Zhang, A. M. Wang, H. Li and H. F. Zhang, Sci. Rep., 2015, 5, 8.
9. C. M. So, M. Y. Cheng, J. C. Yu and P. K. Wong, Chemosphere, 2002, 46, 905–912.
10. S. H. Xie, P. Huang, J. J. Kruzic, X. R. Zeng and H. X. Qian, Sci. Rep., 2016, 6, 10.
11. M. Z. Khan, S. Singh, S. Sultana, T. R. Sreekrishnan and S. Z. Ahammad, New J. Chem., 2015, 39, 5597–5604.
12. P. Navarro, J. A. Gabaldon and V. M. Gomez-Lopez, Dyes Pigm., 2017, 136, 887–892.
13. T. X. H. Le, T. V. Nguyen, Z. A. Yacouba, L. Zoungrana, F. Avril, E. Petit, J. Mendret, V. Bonniol, M. Bechelany, S. Lacour, G. Lesage and M. Cretin, Chemosphere, 2016, 161, 308–318.
14. J. J. Wang and R. B. Bai, Water Res., 2016, 101, 103–113.
15. J. Gao, S. G. Yang, N. Li, L. J. Meng, F. Wang, H. He and C. Sun, Appl. Surf. Sci., 2016, 379, 140–149.
16. A. S. Fajardo, R. C. Martins, C. A. Martinez-Huitle and R. M. Quinta-Ferreira, Electrochim. Acta, 2016, 210, 96–104.
17. A. Azizi, M. R. A. Moghaddam, R. Maknoon and E. Kowsari, Desalin. Water Treat., 2016, 57, 14083–14092.
18. S. Garcia-Segura, A. S. Lima, E. B. Cavalcanti and E. Brillas, Electrochim. Acta, 2016, 198, 268–279.
19. B. Ramirez, V. Rondan, L. Ortiz-Hernandez, S. Silva-Martinez and A. Alvarez-Gallegos, J. Environ. Manage., 2016, 171, 29–34.
20. D. N. Yang, Y. T. Liu, J. Mo, X. Jiang and Z. S. Yang, Desalin. Water Treat., 2016, 57, 6393–6400.
21. Q. Y. Wu, Y. Li, W. L. Wang, T. Wang and H. Y. Hu, J. Environ. Sci., 2016, 41, 227–234.
22. S. Venkatesh, A. R. Quaff, N. D. Pandey and K. Venkatesh, Desalin. Water Treat., 2016, 57, 4135–4145.
23. S. A. S. Chatha, S. Kiran, T. Gulzar, S. Kamal, A. Ghaffar and M. N. Chatha, Oxid. Commun., 2016, 39, 1604–1614.
24. A. Thiam, E. Brillas, J. A. Garrido, R. M. Rodriguez and I. Sires, Appl. Catal., B, 2016, 180, 227–236.
25. X.-C. Ruan, M.-Y. Liu, Q.-F. Zeng and Y.-H. Ding, Sep. Purif. Technol., 2010, 74, 195–201.
26. X. B. Zhang, W. Y. Dong, F. Y. Sun, W. Yang and J. Dong, J. Hazard. Mater., 2014, 276, 77–87.
27. X. B. Zhang, W. Y. Dong and W. Yang, Chem. Eng. J., 2013, 233, 14–23.
28. C. Comninellis, A. Kapalka, S. Malato, S. A. Parsons, L. Poulios and D. Mantzavinos, J. Chem. Technol. Biotechnol., 2008, 83, 769–776.
29. K. E. O'Shea and D. D. Dionysiou, J. Phys. Chem. Lett., 2012, 3, 2112–2113.
30. S. Gligorovski, R. Strekowski, S. Barbati and D. Vione, Chem. Rev., 2015, 115, 13051–13092.
31. X. He, Q. Zeng, Y. Zhou, Q. X. Zeng, X. F. Wei and C. Y. Zhang, J. Phys. Chem. A, 2016, 120, 3747–3753.
32. R. Sreekanth, K. P. Prasanthkumar, M. M. S. Paul, U. K. Aravind and C. T. Aravindakumar, J. Phys. Chem. A, 2013, 117, 11261–11270.
33. Y. Gao, Y. Ji, G. Li and T. An, Water Res., 2014, 49, 360–370.
34. https://www2.chemistry.msu.edu/faculty/reusch/VirtTxtJml/acidity2.htm.
35. https://www.drugbank.ca/drugs/DB03474#identification.
36. A. D. Becke, Phys. Rev. A, 1988, 38, 3098.
37. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
38. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
39. M. Page and J. W. McIver, J. Chem. Phys., 1988, 88, 922–935.
40. M. Page, C. Doubleday and J. W. McIver, J. Chem. Phys., 1990, 93, 5634–5642.
41. I. M. Alecu, J. J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2872–2887.
42. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
43. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford, CT, USA, 2009.
44. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17.
45. C. Morell, A. Grand and A. Toro-Labbe, J. Phys. Chem. A, 2005, 109, 205–212.
46. T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580–592.
47. J. Oakes and P. Gratton, J. Chem. Soc., Perkin Trans. 2, 1998, 1857–1864.
48. Q. Z. Zhang, R. Gao, F. Xu, Q. Zhou, G. B. Jiang, T. Wang, J. M. Chen, J. T. Hu, W. Jiang and W. X. Wang, Environ. Sci. Technol., 2014, 48, 5051–5057.
49. Y. H. Sun, Q. Z. Zhang and W. X. Wang, RSC Adv., 2016, 6, 61794–61802.
50. F. De Vleeschouwer, V. Van Speybroeck, M. Waroquier, P. Geerlings and F. De Proft, Org. Lett., 2007, 9, 2721–2724.
51. X.-N. Wu, Y.-X. Zhao, W. Xue, Z.-C. Wang, S.-G. He and X.-L. Ding, Phys. Chem. Chem. Phys., 2010, 12, 3984–3997.
52. Y.-X. Zhao, X.-N. Wu, J.-B. Ma, S.-G. He and X.-L. Ding, J. Phys. Chem. C, 2010, 114, 12271–12279.
53. J.-B. Ma, X.-N. Wu, Y.-X. Zhao, X.-L. Ding and S.-G. He, Phys. Chem. Chem. Phys., 2010, 12, 12223–12228.
54. S. Feyel, J. Döbler, R. Hoeckendorf, M. K. Beyer, J. Sauer and H. Schwarz, Angew. Chem., Int. Ed., 2008, 47, 1946–1950.
55. X. W. Jiao, H. Yu, Q. W. Kong, Y. Luo, Q. Chen and J. P. Qu, J. Phys. Org. Chem., 2014, 27, 519–526.
56. Q. Chen, F. Wang, J. M. Song and J. Y. Yuan, Acta Sci. Circumstantiae, 2009, 29, 175–180.
57. M. Muthukumar, D. Sargunamani and N. Selvakumar, Dyes Pigm., 2005, 65, 151–158.
58. C. H. Wu, C. Y. Kuo and C. L. Chang, J. Hazard. Mater., 2008, 153, 1052–1058.
59. A. S. Ozen, V. Aviyente, G. Tezcanli-Guyer and N. H. Ince, J. Phys. Chem. A, 2005, 109, 3506–3516.
60. K. Vinodgopal and P. V. Kamat, in Environmental Applications of Ionizing Radiation, John Wiley & Sons, 1998.
61. S. Takeda, Y. Tanaka, Y. Nishimura, M. Yamane, Z. Siroma and S. Wakida, J. Chromatogr. A, 1999, 853, 503–509.
62. K. Hustert and R. G. Zepp, Chemosphere, 1992, 24, 335–342.
63. A. Zeidler, P. S. Salmon, H. E. Fischer, J. C. Neuefeind, J. M. Simonson, H. Lemmel, H. Rauch and T. E. Markland, Phys. Rev. Lett., 2011, 107, 5.
64. C. H. Lai and P. T. Chou, J. Comput. Chem., 2007, 28, 1357–1363.
65. B.-F. LIang, Fundamentals of Inorganic Chemistry, Tsang Hai Book Publishing Co., 2007.
66. J. A. Platts, H. Maarof, K. D. M. Harris, G. K. Lim and D. J. Willock, Phys. Chem. Chem. Phys., 2012, 14, 11944–11952.
67. M. Lozynski, D. Rusinska-Roszak and H. G. Mack, J. Phys. Chem. A, 1998, 102, 2899–2903.
68. I. V. Alabugin, M. Manoharan, S. Peabody and F. Weinhold, J. Am. Chem. Soc., 2003, 125, 5973–5987.
69. A. D. Rabuck and G. E. Scuseria, Theor. Chem. Acc., 2000, 104, 439–444.
70. M. S. Elovitz and U. von Gunten, Ozone: Sci. Eng., 1999, 21, 239–260.
71. X. C. Chen, T. Tao, Y. G. Wang, Y. X. Peng, W. Huang and H. F. Qian, Dalton Trans., 2012, 41, 11107–11115.
72. J. R. Murdoch, J. Chem. Educ., 1981, 58, 32–36.
73. G. V. Buxton, C. L. Greenstock, W. P. Helman and A. B. Ross, J. Phys. Chem. Ref. Data, 1988, 17, 513–886.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra05727j

---