Half-metallicity of the bulk and (001) surface of NbFeCrAl and NbFeVGe Heusler compounds: a first-principles prediction

Abstract

Using first-principles calculations based on density-functional theory, the structural, electronic and magnetic properties in the bulk and (001) surfaces of quaternary Heusler compounds NbFeCrAl and NbFeVGe are investigated. For the bulk, the two compounds exhibit half-metallicity with band gaps of 0.4 eV and 0.2 eV in the majority-spin direction at their equilibrium lattice constants. The total magnetic moments are 2 μ_B following the Slater–Pauling formula: M_t = 24 − Z_t rule. The half-metallicity can be maintained in the range of 5.76–6.07 Å and 5.96–6.10 Å (lattice constant), and 0.971–1.035 and 0.962–1.033 (c/a) for NbFeCrAl and NbFeVGe compounds, respectively. The half-metallicity is destroyed on the Fe–Cr, Nb–Al, Fe–V, and Nb–Ge terminated (001) surfaces, and the spin-polarization ratio sharply decreases below 50% for NbFeCrAl and NbFeVGe compounds.

---

1. Introduction

R. A. de Groot et al.¹ first reported a half-metallic ferromagnet (HMF) in the half-Heusler compound NiMnSb in 1983. Afterwards, HMFs^2–5 have received more and more attention as promising candidates for electronic devices, such as tunnel junctions, spin valves, etc.^6,7 Many theoretical efforts using first-principles calculations were carried out to predict new HMFs in Heusler compounds and other material systems. For HM materials, the electronic structure shows a metallic feature in one spin direction while it shows semiconductivity with a band gap at the Fermi level (E_F) in the other spin direction. Thus, the HM materials are supposed to have a conduction electron spin polarization ratio of 100%. Another essential feature of HM materials is that the total spin moment of one formula unit is an integer. The half-metallicity can easily be destroyed by defects, temperature and stress for the HM materials with a small HM band gap. So it is necessary to search for new materials with a large HM band gap for their application in the spintronic devices.

Heusler compound is a huge material system and contains rich functional properties, such as superconducting materials, thermoelectric materials, phase transformation materials, topological materials and also HM materials. Many Heusler compounds with 3d transition elements, such as Sc-based, Ti-based, V-based, Cr-based, Mn-based, Fe-based, Co-based and Ni-based compounds,^2,5,8–32 have been investigated widely and synthesized successfully. Many of them, e.g. Co₂CrGa,³³ Mn₂CoZ (Z = Al, Ga, Si, Sb),³⁴ CoFeMnSi,³⁵ Fe₂CoSi,³⁶ Co₂Mn_1−xFe_xSi⁶ and FeCoCrSi,³⁷ have been found to exhibit HM character by both theoretical and experimental studies. The thin films of Co₂Cr_0.6Fe_0.4Al, which has large tunneling magnetoresistances of 16% at room temperature and 26.5% at 5 K, have been reported as a spin valve type tunneling junction by Inomata et al.³⁸ Y. K. Takahashi et al. have successfully demonstrated the large spin signal (ΔR_S) of 12.8 mΩ with a highly spin-polarized Co₂Fe(Ge_0.5Ga_0.5).⁷ Feng et al. have grown the film of the novel Ti₂MnAl on Si (001) by using magnetron sputtering.³⁹ Moreover, the magnetization of these Heusler compounds is found to obey the Slater–Pauling rule: M_t = Z_t − 18 or M_t = Z_t − 24, where the M_t and Z_t represent for the total magnetic moment and the number of total valence electrons in per unit cell, respectively.^29,40,41

Very recently, some HM materials containing 4d transition metal elements, for example, Zr-based,^2,40,42–53 Ru-based⁵⁴ and Rh-based⁵⁵ Heusler compounds, have been predicted widely by first-principles calculations. To the best of our knowledge, experiments of a few quaternary Heusler compounds containing 4d elements, such as CoRhMnZ (Z = Ga, Sn, Sb) and the alloy Co_0.5Rh_1.5MnSb,⁵⁶ have been investigated, but other researches currently are focused on prediction theoretically for HM materials. A very important characteristic for Heusler compounds with 4d transition elements is that the width of HM band gap is usually bigger than that only with 3d transition metal elements, which is beneficial to the stability of the half-metallicity in practical applications. It is also worth to note that the Rh-based compounds Rh₃Z (Z = Si, Ge, Sn, Pb)⁵⁵ obey Slater–Pauling rule: M_t = Z_t − 28 rather than M_t = Z_t − 24 or M_t = Z_t − 18, which enlarge the scope to explore new HM materials in Heusler compounds. The joint efforts of more new elements and the extended Slater–Pauling rule will further promote the development of new HM materials.

From these aspects, Nb element is one of the 4d transition metal elements and one of the nearest neighbors of Zr in the period table. The Nb-based Heusler compounds can be good choice for developing HM materials because they are not only promising to hold large HM band gap but also quite ease to synthesize. Compared with many Zr-based quaternary compounds,^{40,43,44,51–53} there are few investigations on Nb-based quaternary Heusler compounds no matter in theory or in experiment. In this work, we predict two Nb-based quaternary HM Heusler compounds, named NbFeCrAl and NbFeVGe. The results indicate they are both perfect HM materials with 100% spin polarization under the ground state. The total magnetic moments are 2 μ_B following the Slater–Pauling formula: M_t = 24 − Z_t rule. Moreover, the half-metallic character is found be retained in a large range of lattice distortion for both NbFeCrAl and NbFeVGe, serving as another advantage for their practical applications. The surface effect on their the half-metallicity is also discussed in detail.

2. Computational details

For quaternary Heusler compounds (here, NbFeCrAl and NbFeVGe) with space group F4̄3m (space group no. 216), there are three possible atomic arrangement fashions (type I, type II, and type III) as shown in Fig. 1 according to the different occupation of Cr (V), Nb, Fe atoms to (0, 0, 0), (0.25, 0.25, 0.25), (0.5, 0.5, 0.5) crystal sites while the Al (Ge) atom occupies (0.75, 0.75, 0.75) crystal site. The three possible atomic arrangement fashions and the detailed atomic occupations are listed in Table 1. The electronic structures and magnetic properties of NbFeCrAl and NbFeVGe compounds were performed by CASTEP code. The CASTEP code is based on the pseudopotential method⁵⁷ with a plane-wave basis set. We used the ultrasoft pseudopotential to describe the interaction between the atom core and valence electrons and performed the generalized gradient approximation (GGA) in the scheme of Perdew–Burke–Ernzerh (PBE) for the exchange-correction functional methods.^44,55 In order to ensure good convergence, the parameters were set as a cutoff energy of 400 eV and a mesh of 12 × 12 × 12 k-points for bulk. Meanwhile, the calculations maintain to ensure good convergence until the energy deviation is less than 1 × 10⁻⁶ eV per atom. The surface slabs were constructed by cleaving the optimized bulk structure along Miller index (001) crystal direction.⁵⁸ Four kinds of (001) surfaces were studied by adopting a slab model which included nine monolayers of atom for NbFeCrAl and NbFeVGe compounds. The parameters were set as a cutoff energy of 400 eV and a mesh of 6 × 6 × 1 k-points for surface.

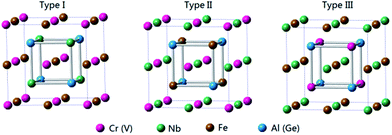Fig. 1 Three possible atomic arrangement fashions of quaternary Heusler compounds NbFeCrAl and NbFeVGe.

Table 1 The atomic occupations of NbFeCrAl and NbFeVGe with different atomic arrangement fashions

Type	4a (0, 0, 0)	4b (0.25, 0.25, 0.25)	4c (0.5, 0.5, 0.5)	4d (0.75, 0.75, 0.75)
Type I	Cr (V)	Nb	Fe	Al (Ge)
Type II	Cr (V)	Fe	Nb	Al (Ge)
Type III	Nb	Cr (V)	Fe	Al (Ge)

---

3. Results and discussion

In order to gain the equilibrium lattice constants of the NbFeCrAl and NbFeVGe compounds, the total energies as a function of lattice constant are shown in Fig. 2. We consider the situations of nonmagnetic (NM) and ferromagnetic (FM) states. It is clearly seen that the lowest energy appears in the type I atomic arrangement fashion with FM state. The equilibrium lattice constants are 6.02 Å and 6.05 Å for NbFeCrAl and NbFeVGe compounds, respectively. Subsequently, all the further investigations only focus on type I atomic arrangement fashions with FM state.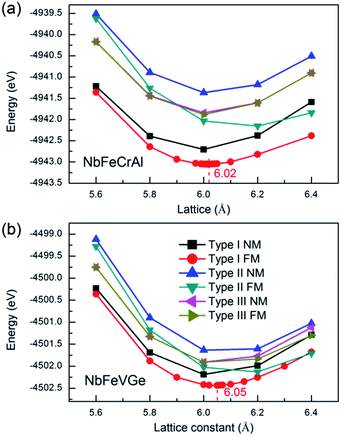

Fig. 2 Total energy values as a function of lattice constant in the nonmagnetic (NM) and ferromagnetic (FM) states for NbFeCrAl (a) and NbFeVGe (b) compounds with three atomic arrangement fashions.

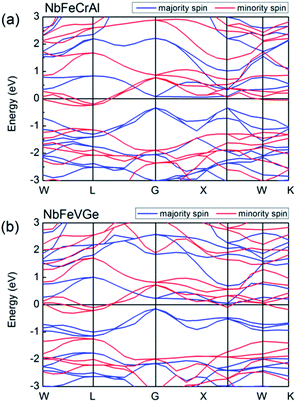
Fig. 3 shows the band structures of NbFeCrAl and NbFeVGe compounds at their equilibrium lattice constants with type I atomic arrangement fashion at FM state. The Fermi level crosses some of valence bands in minority-spin direction, which indicates a metallic interaction. In majority-spin direction, the band structure shows a semiconducting nature due to a band gap of 0.4 eV (for NbFeCrAl) and 0.2 eV (for NbFeVGe) occurring at the Fermi level. So band structures indicate that NbFeCrAl and NbFeVGe compounds have a half-metallicity.

Fig. 3 Band structures of NbFeCrAl (a) and NbFeVGe (b) compounds.

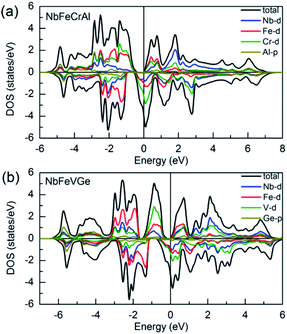
Fig. 4 shows the total density of states (TDOS) patterns and partial density of states (PDOS) patterns of 4d orbits of Nb atom, 3d orbits of Fe, Cr, V atoms and p orbits of main group Al, Ge atoms for NbFeCrAl and NbFeVGe compounds. It can be seen that both NbFeCrAl and NbFeVGe compounds have a band gap at the Fermi level in the majority-spin direction, while the Fermi level locates at a side of a high DOS peak in the minority-spin direction, which is corresponding to the band structures as shown in Fig. 3 and indicates the half-metallicity of NbFeCrAl and NbFeVGe compounds. The hybridization between the p orbits of the Al, Ge atoms and the d orbits of transition atoms makes mainly contributions to the distribution of the TDOS around −5 eV. The strong hybridization between d states of Nb, Co (Rh) and Cr atoms spread in the wide energy range from −3 eV to +3 eV for NbFeCrAl and NbFeVGe compounds. With the help of band structures, it is clear that the HM band gap in the majority-spin direction occurs between e_u and t_1u states originating from the hybridization between 3d states of Fe and Cr (V) atoms. The calculated total spin moments of NbFeCrAl and NbFeVGe compounds are both 2 μ_B. The integral value of total spin moment is one of the essential features of half-metallic compounds.⁵⁹ The number of total valence electrons in per unit cell are 22 for NbFeCrAl and NbFeVGe compounds, so, these two compounds obey the Slater–Pauling formula: M_t = 24 − Z_t rule.

Fig. 4 The total density of states (TDOS) and partial density of states (PDOS) projected on the 4d orbits of Nb atom, 3d orbits of Fe, Cr, V atoms and p orbits of Al, Ge atoms for NbFeCrAl (a) and NbFeVGe (b) compounds.

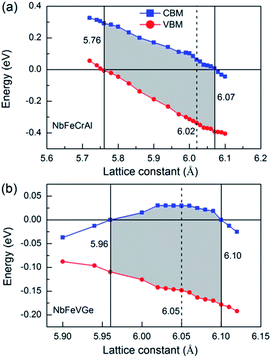
In practical application, the external stress and lattice thermal expansion are two important factors to destroy half-metallicity. To simulate and analyze the effect of the external stress and lattice thermal expansion on the half-metallicity, the effect of lattice distortion, including axial and uniaxial strain, on half-metallicity were investigated. The energy values of conduction band minimums (CBM, blue square) and valence band maximums (VBM, red circle) are used to characterize the half-metallicity under different lattice distortion for NbFeCrAl and NbFeVGe compounds, as shown in Fig. 5. When the Fermi level goes across conduction bands or valence bands, namely, CBM shows a negative value or VBM shows a positive value, the half-metallicity is destroyed. From Fig. 5, the half-metallicity can be kept in the range of 5.76–6.07 Å for NbFeCrAl and in the range of 5.96–6.10 Å for NbFeVGe. The maximum width of band gap occurs near the equilibrium lattice constant and can reach 0.42 eV and 0.2 eV for NbFeCrAl and NbFeVGe compounds, respectively.

Fig. 5 The energy values of conduction band minimums (CBM, blue square) and valence band maximums (VBM, red circle) in the majority-spin direction as a function of lattice constant for NbFeCrAl (a) and NbFeVGe (b) compounds.

The total and atomic magnetic moments as a function of lattice constant are shown in Fig. 6 for NbFeCrAl and NbFeVGe compounds. It is clear that the total magnetic moments are both 2 μ_B when the compounds show a half-metallicity. For NbFeCrAl, the calculated magnetic moments of Cr and Nb atoms increase while the magnetic moments of Fe and Al atoms remain unchanged with increasing lattice constant (see Fig. 6(a)). The magnetic moment of Cr atom is antiparallel to that of Nb atom. So, the total magnetic moment is unchanged with increasing lattice constant due to the mutual compensation between Cr atom and Nb atom. For NbFeVGe (see Fig. 6(b)), the situation is similar to NbFeCrAl, but all atomic magnetic moments have only a small change with increasing lattice constant.

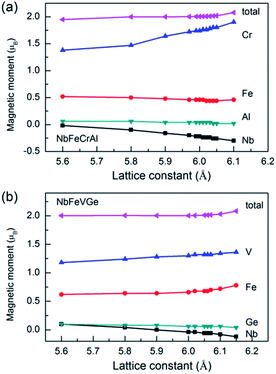Fig. 6 The total and atomic magnetic moments as a function of lattice constant for NbFeCrAl (a) and NbFeVGe (b) compounds.

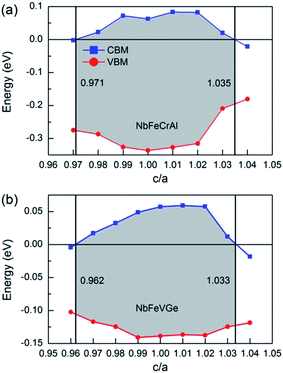
The effect of the uniaxial strain on half-metallicity was also investigated for NbFeCrAl and NbFeVGe compounds. The energy values of CBM and VBM under different c/a ratio are shown in Fig. 7 for NbFeCrAl and NbFeVGe compounds. The a and c represent the lattice constants in different directions and the c/a indicates the degree of the tetragonal distortion. From Fig. 7, the half-metallicity of NbFeCrAl and NbFeVGe compounds can be kept in the c/a range of 0.971–1.035 and 0.962–1.033, respectively. The largest gaps are 0.41 eV and 0.196 eV at c/a = 1.01 for NbFeCrAl and NbFeVGe compounds. The width of gaps decreases when c/a deviates from 1.01 to the smaller or bigger values.

Fig. 7 The energy values of conduction band minimums (CBM, blue square) and valence band maximums (VBM, red circle) in the majority-spin direction as a function of c/a for NbFeCrAl (a) and NbFeVGe (b) compounds, respectively.

We calculated the magnetic moments with c/a from 0.9 to 1.1. The total and atomic magnetic moments as a function of c/a are shown in Fig. 8. For NbFeCrAl, the total moment is 2 μ_B. All atomic magnetic moments and the half-metallicity are maintained when the c/a changes in the range of 0.971–1.035. The total magnetic moment and the magnetic moments of Fe and Cr atoms increase when the c/a is out of the range of 0.971–1.035. For NbFeVGe, the situation is similar to NbFeCrAl. The total moment is also 2 μ_B. All atomic magnetic moments and the half-metallicity are maintained in the c/a range of 0.962–1.033. When the c/a is out of the range, the magnetic moment of Fe atom increases with the increasing or decreasing c/a, which leads to the increase of total magnetic moment.

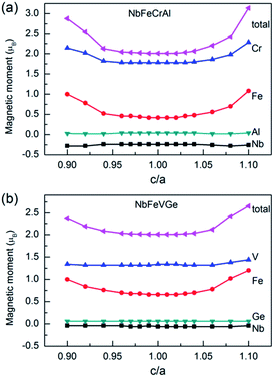Fig. 8 The total and atomic magnetic moments as a function of c/a for NbFeCrAl and NbFeVGe compounds.

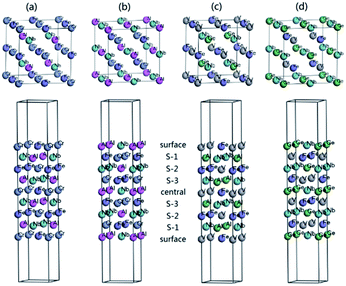
For the practical application in spintronic devices, the HM materials are usually fabricated to a thin film. However, the electronic properties of surface usually differ from that of the bulk. The surface is possible to destroy the half-metallicity and decrease the spin-polarization ratio. So, the investigation of the surface effect on half-metallicity is very important.^32,60–66 Here, we investigate the half-metallicity and spin-polarization depending on the terminated (001) surface for NbFeCrAl and NbFeVGe compounds. Owing to the atomic equivalent occupation in the lattice, there are two kinds of terminated (001) surface in type I structure. The corresponding slab models with nine monolayers of atom are given in Fig. 9 and used in our surface calculations for NbFeCrAl (Fig. 9(a) and (b)) and NbFeVGe (Fig. 9(c) and (d)) compounds. To form an epitaxial thin film, internal five atomic layers are fixed as the slabs and two atomic layers in two sides of the slabs are allowed to relax by the total energy and atomic force calculations.

Fig. 9 (a) The nine layer Fe–Cr terminated (001) surface and (b) Nb–Al terminated (001) surface for NbFeCrAl compound. (c) The nine layer Fe–V terminated (001) surface and (d) Nb–Ge terminated (001) surface for NbFeVGe compound.

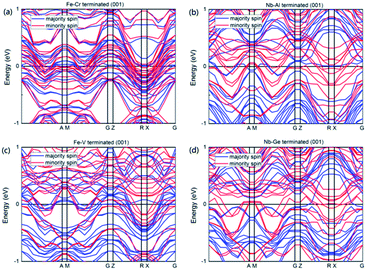
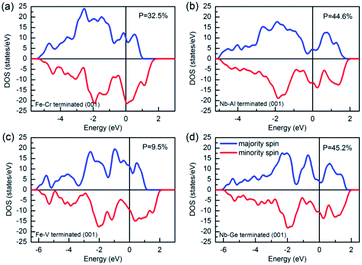
Fig. 10 shows the calculated band structures of the terminated (001) surfaces for NbFeCrAl and NbFeVGe compounds. It can be seen that for all the terminated (001) surfaces, the Fermi level has a metallic intersection both in majority-spin and minority-spin directions, which indicates that the half-metallicity is destroyed on the terminated (001) surfaces for NbFeCrAl and NbFeVGe compounds. Furthermore, the TDOSs of the terminated (001) surfaces as shown in Fig. 11 are obviously different from the bulk as shown in the Fig. 3. Based on the spin polarization ratio formula: P = (N_up − N_down)/(N_up + N_down), the P in Fe–Cr, Nb–Al, Fe–V and Nb–Ge terminated (001) surfaces decreases to 32.5% and 44.6%, 9.5% and 45.2% from the 100% in bulk, respectively.

Fig. 10 Majority-spin and minority-spin band structures of the Fe–Cr terminated (001) surface (a), Nb–Al terminated (001) surface (b) of NbFeCrAl compound and Fe–V terminated (001) surface (c), Nb–Ge terminated (001) surface (d) of NbFeVGe compound.

Fig. 11 Total density of states (TDOS) of the Fe–Cr terminated (001) surface (a), Nb–Al terminated (001) surface (b) of NbFeCrAl compound and Fe–V terminated (001) surface (c), Nb–Ge terminated (001) surface (d) of NbFeVGe compound. Fermi level E_F is set at zero energy.

4. Conclusions

In summary, the first-principles calculations based on density-functional theory were performed to investigate structural, electronic and magnetic properties of quaternary Heusler compounds NbFeCrAl and NbFeVGe. Their equilibrium lattice constants are 6.02 Å and 6.05 Å, respectively. These two compounds are predicted to be half-metallic materials with band gaps of 0.4 eV and 0.2 eV at equilibrium lattice constants in the bulk. The half-metallicity can be kept in the range of 5.76–6.07 Å and 5.96–6.10 Å (lattice constant), and 0.971–1.035 and 0.962–1.033 (c/a) for NbFeCrAl and NbFeVGe compounds, respectively. The total magnetic moment of 2 μ_B is satisfied with the Slater–Pauling formula: M_t = 24 − Z_t rule. For (001) surfaces, the half-metallicity is destroyed and the spin-polarization ratio sharply decreases on all the terminated (001) surfaces for NbFeCrAl and NbFeVGe compounds.

Acknowledgements

This work was supported by Natural Science Foundation of Hebei Province (No. E2016202383), the Scientific Research Project for High Level Talent in Colleges and Universities of Hebei Province (No. GCC 2014042), Chongqing City Funds for Distinguished Young Scientists (No. cstc2014jcyjjq50003) and the Program for Leading Talents in Science and Technology Innovation of Chongqing City (No. CSTCKJCXLJRC19).

References

1. R. A. de Groot, F. M. Mueller, P. G. van Engen and K. H. J. Buschow, Phys. Rev. Lett., 1983, 50, 2024–2027.
2. A. Birsan, Curr. Appl. Phys., 2014, 14, 1434–1436.
3. G. D. Liu, X. F. Dai, S. Y. Yu, Z. Y. Zhu, J. L. Chen, G. H. Wu, H. Zhu and J. Q. Xiao, Phys. Rev. B, 2006, 74, 054435.
4. G. Y. Gao, L. Hu, K. L. Yao, B. Luo and N. Liu, J. Alloys Compd., 2013, 551, 539–543.
5. N. Kervan and S. Kervan, J. Magn. Magn. Mater., 2012, 324, 645–648.
6. S. Wurmehl, G. H. Fecher, H. C. Kandpal, V. Ksenofontov, C. Felser and H. J. Lin, Appl. Phys. Lett., 2006, 88, 032503.
7. Y. K. Takahashi, S. Kasai, S. Hirayama, S. Mitani and K. Hono, Appl. Phys. Lett., 2012, 100, 052405.
8. S. Picozzi, A. Continenza and A. J. Freeman, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 094421.
9. S. Ishida, S. Kawakami and S. Asano, Mater. Trans., 2004, 45, 1065–1069.
10. S. Ishida, S. Mizutani, S. Fujii and S. Asano, Mater. Trans., 2006, 47, 464–470.
11. J. Waliszewski, L. Dobrzyński, A. Malinowski, D. Satuła, K. Szymański, W. Prandl, T. Brückel and O. Schärpf, J. Magn. Magn. Mater., 1994, 132, 349–358.
12. L. Chioncel, E. Arrigoni, M. I. Katsnelson and A. I. Lichtenstein, Phys. Rev. B, 2009, 79, 125123.
13. F. Ahmadian and A. Salary, Intermetallics, 2014, 46, 243–249.
14. X. P. Wei, Y. D. Chu and J. B. Deng, J. Magn. Magn. Mater., 2014, 354, 345–348.
15. L. Zhang, X. T. Wang, H. Rozale, J. W. Lu and L. Y. Wang, J. Supercond. Novel Magn., 2016, 29, 349–356.
16. F. Taşkın, M. Atiş, O. Canko, S. Kervan and N. Kervan, J. Magn. Magn. Mater., 2017, 426, 473–478.
17. L. Feng, C. C. Tang, S. J. Wang and W. C. He, J. Alloys Compd., 2011, 509, 5187–5189.
18. F. Ahmadian, J. Supercond. Novel Magn., 2013, 26, 381–388.
19. Q. L. Fang, J. M. Zhang and K. W. Xu, J. Magn. Magn. Mater., 2014, 349, 104–108.
20. S. Galehgirian and F. Ahmadian, Solid State Commun., 2015, 202, 52–57.
21. S. T. Qi, J. Shen and C. H. Zhang, Mater. Chem. Phys., 2015, 164, 177–182.
22. X. M. Zhang, X. F. Dai, H. Y. Jia, G. F. Chen, H. Y. Liu, H. Z. Luo, Y. Li, X. Yu, G. D. Liu, W. H. Wang and G. H. Wu, Comput. Mater. Sci., 2012, 65, 456–460.
23. X. M. Zhang, X. F. Dai, G. F. Chen, H. Y. Liu, H. Z. Luo, Y. Li, W. H. Wang, G. H. Wu and G. D. Liu, Comput. Mater. Sci., 2012, 59, 1–5.
24. I. Galanakis, K. Özdoğan, E. Şaşıoğlu and B. Aktaş, Phys. Rev. B, 2007, 75, 172405.
25. J. Li, Y. X. Li, G. X. Zhou, Y. B. Sun and C. Q. Sun, Appl. Phys. Lett., 2009, 94, 242502.
26. X. F. Dai, G. D. Liu, L. J. Chen, J. L. Chen and G. H. Wu, Solid State Commun., 2006, 140, 533–537.
27. H. Z. Luo, F. B. Meng, G. D. Liu, H. Y. Liu, P. Z. Jia, E. K. Liu, W. H. Wang and G. H. Wu, Intermetallics, 2013, 38, 139–143.
28. H. Z. Luo, H. W. Zhang, Z. Y. Zhu, L. Ma, S. F. Xu, G. H. Wu, X. X. Zhu, C. B. Jiang and H. B. Xu, J. Appl. Phys., 2008, 103, 083908.
29. S. Skaftouros, K. Özdoğan, E. Şaşıoğlu and I. Galanakis, Phys. Rev. B, 2013, 87, 024420.
30. M. Jourdan, J. Minár, J. Braun, A. Kronenberg, S. Chadov, B. Balke, A. Gloskovskii, M. Kolbe, H. J. Elmers, G. Schönhense, H. Ebert, C. Felser and M. Kläui, Nat. Commun., 2014, 5, 3974.
31. J. M. K. Al-zyadi, M. H. Jolan and K. L. Yao, J. Magn. Magn. Mater., 2016, 403, 8–13.
32. J. M. K. Al-zyadi, G. Y. Gao and K. L. Yao, J. Alloys Compd., 2013, 565, 17–21.
33. R. Y. Umetsu, K. Kobayashi, R. Kainuma, A. Fujita, K. Fukamichi, K. Ishida and A. Sakuma, Appl. Phys. Lett., 2004, 85, 2011.
34. G. D. Liu, X. F. Dai, H. Y. Liu, J. L. Chen, Y. X. Li, G. Xiao and G. H. Wu, Phys. Rev. B, 2008, 77, 014424.
35. X. F. Dai, G. D. Liu, G. H. Fecher, C. Felser, Y. X. Li and H. Y. Liu, J. Appl. Phys., 2009, 105, 07E901.
36. Y. Du, G. Z. Xu, X. M. Zhang, Z. Y. Liu, S. Y. Yu, E. K. Liu, W. H. Wang and G. H. Wu, EPL, 2013, 103, 37011.
37. Y. Du, G. Z. Xu, E. K. Liu, G. J. Li, H. G. Zhang, S. Y. Yu, W. H. Wang and G. H. Wu, J. Magn. Magn. Mater., 2013, 335, 101–104.
38. K. Inomata, S. Okamura, R. Goto and N. Tezuka, Jpn. J. Appl. Phys., 2003, 42, L419–L422.
39. W. W. Feng, X. Fu, C. H. Wan, Z. H. Yuan, X. F. Han, N. V. Quang and S. Cho, Phys. Status Solidi RRL, 2015, 9, 641–645.
40. S. Berri, M. Ibrir, D. Maouche and M. Attallah, J. Magn. Magn. Mater., 2014, 371, 106–111.
41. I. Galanakis, P. H. Dederichs and N. Papanikolaou, Phys. Rev. B, 2002, 66, 174429.
42. X. T. Wang, T. T. Lin, H. Rozale, X. F. Dai and G. D. Liu, J. Magn. Magn. Mater., 2016, 402, 190–195.
43. R. K. Guo, G. D. Liu, X. T. Wang, H. Rozale, L. Y. Wang, R. Khenata, Z. M. Wu and X. F. Dai, RSC Adv., 2016, 6, 109394.
44. X. T. Wang, Z. X. Cheng, J. L. Wang, L. Y. Wang, Z. Y. Yu, C. S. Fang, J. T. Yang and G. D. Liu, RSC Adv., 2016, 6, 57041.
45. X. T. Wang, Y. T. Cui, X. F. Liu and G. D. Liu, J. Magn. Magn. Mater., 2015, 394, 50–59.
46. X. T. Wang, Z. X. Cheng, J. L. Wang, H. Rozale, L. Y. Wang, Z. Y. Yu, J. T. Yang and G. D. Liu, J. Alloys Compd., 2016, 686, 549–555.
47. Z. Y. Deng and J. M. Zhang, J. Magn. Magn. Mater., 2016, 409, 28–33.
48. Z. Y. Deng and J. M. Zhang, J. Magn. Magn. Mater., 2016, 397, 120–124.
49. S. Yousuf and D. C. Gupta, Mater. Chem. Phys., 2017, 192, 33–40.
50. X. P. Wei, Y. L. Zhang, T. Wang, X. W. Sun, T. Song, P. Guo and J. B. Deng, Mater. Res. Bull., 2017, 86, 139–145.
51. S. Berri, M. Ibrir, D. Maouche and M. Attallah, Comput. Mater. Sci., 2014, 1, 26–31.
52. H. H. Xie, Q. Gao, L. Li, G. Lei, G. Y. Mao, X. R. Hu and J. B. Deng, Comput. Mater. Sci., 2015, 103, 52–55.
53. Q. Gao, H. H. Xie, L. Li, G. Lei, J. B. Deng and X. R. Hu, Superlattices Microstruct., 2015, 85, 536–542.
54. T. Djaafri, A. Djaafri, A. Elias, G. Murtaza, R. Khenata, R. Ahmed, S. B. Omran and D. Rached, Chin. Phys. B, 2014, 23, 087103.
55. X. T. Wang, X. F. Dai, L. Y. Wang, X. F. Liu, W. H. Wang, G. H. Wu, C. C. Tang and G. D. Liu, J. Magn. Magn. Mater., 2015, 378, 16–23.
56. V. Alijani, J. Winterlik, G. H. Fecher, S. S. Naghavi, S. Chadov, T. Gruhn and C. Felser, J. Phys.: Condens. Matter, 2012, 24, 046001.
57. D. Vanderbilt, Phys. Rev. B, 1990, 41, 7892–7895.
58. R. A. Evarestov, A. V. Bandura, M. V. Losev, E. A. Kotomin, Y. F. Zhukovskii and D. Bocharov, J. Comput. Chem., 2008, 29, 2079–2087.
59. X. F. Ge and Y. M. Zhang, J. Magn. Magn. Mater., 2009, 321, 198–202.
60. I. Galanakis, J. Phys.: Condens. Matter, 2002, 14, 6329–6340.
61. G. Y. Gao and K. L. Yao, J. Appl. Phys., 2012, 112, 023712.
62. C. Loschen, J. Carrasco, K. M. Neyman and F. Illas, Phys. Rev. B, 2007, 75, 035115.
63. G. Y. Gao and K. L. Yao, J. Appl. Phys., 2009, 106, 053703.
64. J. M. K. Al-zyadi, G. Y. Gao and K. L. Yao, J. Magn. Magn. Mater., 2013, 330, 1–5.
65. J. M. K. Al-zyadi, G. Y. Gao and K. L. Yao, Solid State Commun., 2012, 152, 1244–1248.
66. V. Alijani, J. Winterlik, G. H. Fecher and C. Felser, Appl. Phys. Lett., 2011, 99, 222510.

---