View PDF VersionPrevious ArticleNext Article

Open Access Article
This Open Access Article is licensed under a Creative Commons Attribution-Non Commercial 3.0 Unported Licence
DOI: 10.1039/C7RA05322C (Paper) RSC Adv., 2017, 7, 31027-31032

First-principles study of decomposition mechanisms of Mg(BH4)2·2NH3 and LiMg(BH4)3·2NH3

Xiaowei Chenab, Renquan Lia, Guanglin Xiac, Hongsheng Hea, Xiuqing Zhanga, Weidong Zou*a and Xubin Yu*b
aDepartment of Physics, School of Science, Jimei University, Xiamen, 361021, China. E-mail: phyzwd@jmu.edu.cn
bDepartment of Materials Science, Fudan University, Shanghai 200433, China. E-mail: yuxuebin@fudan.edu.cn
cInstitute for Superconducting and Electronic Materials, University of Wollongong, North Wollongong, NSW, Australia

Received 11th May 2017 , Accepted 6th June 2017

First published on 15th June 2017

Abstract

The decomposition mechanisms of Mg(BH4)2·2NH3 and LiMg(BH4)3·2NH3 were studied by using density functional theory calculations. Compared to that of Mg(BH4)2·2NH3, the incorporation of LiBH4 with the formation of LiMg(BH4)3·2NH3 slightly increased Bader charges of B atoms, meanwhile it decreased Bader charges of N atoms. Mg(BH4)2·2NH3 shows a low ammonia vacancy diffusion barrier, but relatively high ammonia vacancy formation energy, which lead to a low concentration of NH3 vacancies and limit NH3 transportation. In contrast to that of Mg(BH4)2·2NH3, LiMg(BH4)3·2NH3 has a relatively high ammonia vacancy formation energy and diffusion barrier, which suppresses ammonia release. The incorporation of LiBH4 and Mg(BH4)2·2NH3 does not decrease but increases the hydrogen formation barrier of LiMg(BH4)3·2NH3, resulting in a slight increase in the dehydrogenation peak temperature, consistent with experimental results.

Introduction

Recently, many efforts have been devoted to B–N based chemical hydrides as potential hydrogen storage materials because of their high theoretical hydrogen capacity.1–3 For instance, ammonia borane (AB), with a high H-capacity of 19.6 wt%, is a typical B–N based hydride for chemical hydrogen storage.1 However, upon decomposition of AB, accompanied volatile compounds of ammonia, diborane, and borazine are evolved, which lead to a reduction of dehydrogenation capacity and are fatal for fuel cell applications.1,4 Many different approaches have been adopted to facilitate hydrogen release from AB during the last decade.5–10 Recent studies show that the substitution of H atoms in the NH3 unit of AB by alkali metals with the formation of single or double metal amidoborane (MAB) is an effective way to improve the dehydrogenation properties of AB in terms of the reduced H2 release temperatures, accelerated H2 release kinetics, and minimized borazine evolved.5,6,11–17

Ammine metal borohydrides (AMBs), which show favourable hydrogen storage properties competitive with ammonia borane, have been developed recently as promising materials for hydrogen storage.18–31 However, many of these composites suffer from the release of undesirable gas of ammonia during dehydrogenation. Further experimental results show that the purity of gas released and dehydrogenation temperature of AMBs can be improved by using double-cation substitutions approach and tuning BH4/NH3 ration.15,24,32,33 The experimental and theoretic studies indicate that ammonia is weakly bound to the metal cations with low electronegativity (<1.2) in AMBs, therefore tend to release ammonia at low temperature.32,34 Although these studies have provided valuable insight for understanding the decomposition processes of single metal cation AMBs, the results may not be applicable to double cations AMBs. For instance, Mg(BH4)2·2NH3 (with electronegativity of 1.31 for Mg cation) mainly release hydrogen along with a small amount of ammonia.23 The incorporation of LiBH4 (with low electronegativity of 0.98 for Li cation) and Mg(BH4)2·2NH3 with the formation of double cations ammine borohydride, LiMg(BH4)3·2NH3 results in improving the purity of gas released compared to Mg(BH4)2·2NH3.35 Further improved dehydrogenation of ammine magnesium borohydride by tuning the NH3/BH4 ratios and combining Mg(BH4)2·2NH3 with MgH2 and NaAlH4 were reported.36–39

The mixed-cation strategy offers a promising route toward tuneable dehydrogenation of ammine metal borohydrides, however, a detail study of the dehydrogenation mechanism is still needed for further improving their dehydrogenation performance. Herein, we presented a comparison study of the electronic structure and dehydrogenation mechanisms of Mg(BH4)2·2NH3 and LiMg(BH4)3·2NH3 by density functional theory (DFT) calculation.

Computational method

Mg(BH4)2·2NH3 crystallizes in the orthorhombic structure with space group of Pcab and lattice parameters of a = 17.4872(4) Å, b = 9.4132(2) Å, c = 8.7304(2) Å.23 LiMg(BH4)3·2NH3 has a hexagonal structure with space group P63 and lattice constants of a = b = 8.0002(1) Å and c = 8.3944 Å.35 The geometric structures were optimized by DFT calculation as implemented in MedeA@VASP code.40 To describe the weak van der Waals H+⋯−H dihydrogen bonds, the optB86b-vdW functional41–43 was adopted for geometric optimization. Plane waves with kinetic energy cutoff of 500 eV were used. The generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE) was adapted to treat the exchange and correlation of electronics.44,45 The projector-augmented wave (PAW) approach was used to describe the electron-ion interactions46 with 1s2s2p of Li, s2p1 of B, s2p3 of N, s2p0 of Mg as the explicit valence electrons. The Brillouin zones were sampled by Monkhorst–Pack k-point meshes47 with meshes points spacing less than 0.05 per Å for both Mg(BH4)2·2NH3 and LiMg(BH4)3·2NH3. Structural relaxations of atomic positions were carried out until the total energies and residual forces were less than 1.0 × 10−5 eV and 0.02 eV Å−1, respectively. For the calculation of NH3 vacancy formation energies and H2 formation energies, 1 × 2 × 2 supercells of Mg(BH4)2·2NH3 and 2 × 2 × 2 supercells of LiMg(BH4)3·2NH3 were used. Our tests showed that the used of 1 × 2 × 2 supercells of Mg(BH4)2·2NH3 and 2 × 2 × 2 supercells of LiMg(BH4)3·2NH3 with k-point mesh spacing less than 0.05 per Å yield energies that converged within 0.01 eV (f.u.)−1. The NH3 diffusion barriers and H2 formation barriers were estimated by using climbing image nudged elastic band (CI-NEB) method.48,49

The NH3 vacancy formation energy was estimated using the following equation:

Ec = Etotal − E(AMBs-NH3) − E(NH3)
where Etotal is the total energy of the AMBs supercells; E(NH3) represents the energy of isolate NH3 molecule; E(AMBs-NH3) is the total energy of the AMBs supercells after NH3 molecules are removed. The positive energy of Ec indicates that the creation of NH3 vacancy is an endothermic process; while the negative energy of Ec indicates that the creation of NH3 vacancy is an exothermic process.

The concentration of ammonia vacancy in Mg(BH4)2·2NH3 and LiMg(BH4)3·2NH3 could be estimated by the following equation50

c = NsitesNconfig[thin space (1/6-em)]exp(Ec/kT)
where Ec is the formation energy of NH3 vacancy; Nsites represents the number of sites that the defect can be incorporated; Nconfig is the number of configurations per site in which the vacancy can be formed; k and T represent Boltzmann constant and temperature, respectively.

Results and discussion

Electronic structure

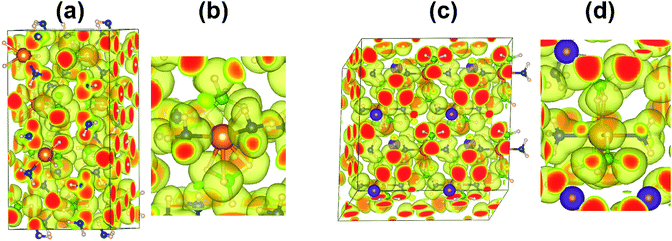
The electron localization function (ELF) and charge transfer between the H, N, B atoms and metal cations (Li and Mg) were analysed to understand the bonding characters of Mg(BH4)2·2NH3 and LiMg(BH4)3·2NH3. The H atoms bond to N atom and B atom are represent as (N)H and (B)H, respectively. As shown in Fig. 1, the calculated ELF shows the covalent bonding of N–H and B–H. Although the Mg–H bonds are mainly ionic, the distorted ELF isosurfaces around (B)H, (N)H and Mg indicate partial covalent bond feature of Mg–H. The low ELF value around Li indicates the essentially ionic bonding character of Li–H. Table 1 shows the Bader charges of (B)H, N(H), N, B and Mg for Mg(BH4)2·2NH3 are −0.58/−0.64, 0.44, −1.30, 1.59 and 1.65, respectively. The Bader charge of Li is 0.90 for LiMg(BH4)3·2NH3, indicates a strong ionization of the Li cation. Hence, Li cation transfers most of its 2s electron to neighbouring BH4 unit, similar to that of LiBH4. Compared to Mg(BH4)2·2NH3, the incorporation of LiBH4 with the formation of LiMg(BH4)3·2NH3 barely affects the charge distribution of H and Mg. The Bader charge of B is slightly increased and Bader charge of N is slightly decreased in LiMg(BH4)3·2NH3.
image file: c7ra05322c-f1.tif
Fig. 1 The calculated electron localization function (ELF) for (a) Mg(BH4)2·2NH3 and (c) LiMg(BH4)3·2NH3 plotted as yellow-colored transparent isosurfaces at a level of 0.6; (b) and (d) present zoomed-in view showing more details for Mg(BH4)2·2NH3 and LiMg(BH4)3·2NH3, respectively. The green, pink, orange, purple and blue colors represent B, H, Mg, Li and N atoms, respectively.
Table 1 Bader charge of Mg(BH4)2·2NH3 and LiMg(BH4)3·2NH3
Atom Bader charge
Mg(BH4)2·2NH3 LiMg(BH4)3·2NH3
Li — 0.90
Mg 1.65 1.64
B 1.59 1.67
N −1.30 −1.32/−1.34
(B)H −0.58/−0.64 −0.63
(N)H 0.44 0.45

Ammonia vacancy formation energies and diffusion barriers

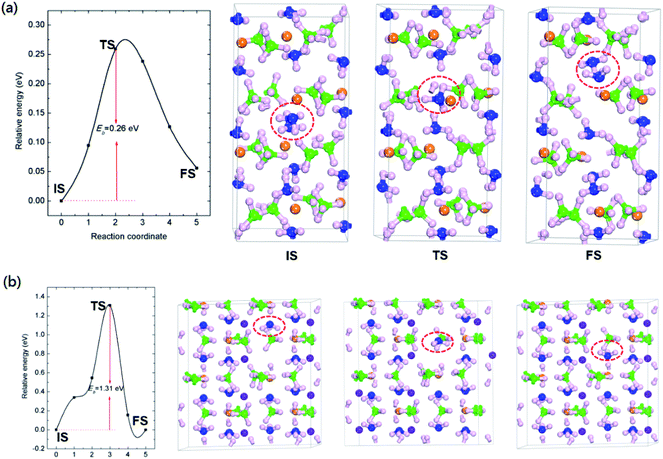
As demonstrated by previous report, Mg(BH4)2·2NH3 started to release hydrogen at temperature around 120 °C, with a maximum hydrogen release rate at 205 °C.23 A small amount of NH3 was released along with hydrogen evolution from Mg(BH4)2·2NH3. The LiMg(BH4)3·2NH3 shows dehydrogenation performance comparable to that of Mg(BH4)2·2NH3, with dehydrogenation peak located at 221 °C.35 In addition, incorporation of LiBH4 with Mg(BH4)2·2NH3 suppresses ammonia release.

The formation and transport properties of NH3 vacancy are crucial to the thermodynamics and kinetics of ammonia release from AMBs. To understand the microscopic mechanisms behind the release of ammonia, the formation and diffusivity of NH3 were studied. The NH3 vacancy was created by directly removed a NH3 unit from Mg(BH4)2·2NH3 and LiMg(BH4)3·2NH3.

As shown in Table 2, the calculated NH3 removal energies are 1.81 and 1.97 eV for Mg(BH4)2·2NH3 and LiMg(BH4)3·2NH3, respectively. The relatively high NH3 removal energies indicates that the formation of NH3 vacancies are thermodynamics unfavourable at low temperature, resulting in low concentration of ammonia vacancy for those two composites. The high formation energy of NH3 vacancies can attribute to the coordination bond of Mg–N and H+⋯−H dihydrogen network.

Table 2 Calculated NH3 vacancy formation energies (Ec), diffusion barriers (Eb) and activation energies (Q = Eb + Ec) for Mg(BH4)2·2NH3 and LiMg(BH4)3·2NH3
  Ec (eV) Eb (eV) Q (eV)
Mg(BH4)2·2NH3 1.81 0.26 2.07
LiMg(BH4)3·2NH3 1.97 1.31 3.28

In addition to the formation energies of NH3 vacancies, the diffusive of NH3 vacancies is also importance for ammonia release. The diffusion paths were calculated by moving a NH3 unit from a nearby lattice site into the vacancy. The diffusion barrier is defined as the energy difference between the saddle point and the ground state. The activation energy (Q) for self-diffusion of ammonia can be obtained by combining the calculated vacancy formation energy with the diffusion barrier. As summarized in Fig. 2 and Table 2, for Mg(BH4)2·2NH3, the calculated energy barrier and activation energy of ammonia diffusion are 0.26 and 2.07 eV, respectively. It should be noted that the NH3 diffusion barrier is relatively low, the formation energy of NH3 vacancy is the dominate term in the activation energy for ammonia diffusion. The relatively high formation energy would result in low concentration of NH3 vacancy, which limit its transport in Mg(BH4)2·2NH3. This is in agreement with previous report that only a small amount of NH3 was released during decomposition of Mg(BH4)2·2NH3.23


image file: c7ra05322c-f2.tif
Fig. 2 The calculated energetic profiles, initial (IS), transition (TS) and final (FS) geometric structure of NH3 diffusion for (a) Mg(BH4)2·2NH3 and (b) LiMg(BH4)3·2NH3. Eb represents the calculated energy barrier. The green, pink, orange, purple and blue colors represent B, H, Mg, Li and N atoms, respectively.

The calculated ammonia vacancy diffusion barrier and activation energy of LiMg(BH4)3·2NH3 are 1.31 and 3.28 eV, respectively. Compared to that of Mg(BH4)2·2NH3, the relatively high ammonia diffusion barrier and activation energy indicate that low concentration and mobility of ammonia vacancy in LiMg(BH4)3·2NH3, in inconsistent with experimental results that the dehydrogenation purity of Mg(BH4)2·2NH3 can be improved by introducing LiBH4 with the formation of LiMg(BH4)3·2NH3.35

Hydrogen formation energies and barriers

Our previous studies suggest that the initial dehydrogenation of AMBs is achieved by combination of H atoms from NH3 and H atoms from BH4 groups.51,52 Therefore, H2 formation energies were calculated by moving one (N)H and one (B)H atom away from host N or B atom to form a hydrogen molecule with H–H distance of 0.74 Å in the supercell of AMBs. The geometry optimization was first performed by fixed the H2 positions and relaxed the rest of the atoms, following by full relaxed all of the atoms in the supercell. In agreement with our previous studies, the formation of H2 molecules lead to significant rearrangement of the surrounding lattice, which may result in overestimated the hydrogen formation energies. In addition, both Mg(BH4)2·2NH3 and LiMg(BH4)3·2NH3 started to release hydrogen at temperature higher than their melting point. In other word, the crystal structure of Mg(BH4)2·2NH3 and LiMg(BH4)3·2NH3 disappeared before hydrogen evolved. Therefore, we further calculated the hydrogen formation energies by using the molecule model in which two formula units of Mg(BH4)2·2NH3 and LiMg(BH4)3·2NH3 were placed in a cubic cell with lattice parameter of 20 Å.

As shown in Table 3, the calculated hydrogen formation energies by using supercell of AMBs are 0.84 and 1.22 eV for Mg(BH4)2·2NH3 and LiMg(BH4)3·2NH3, respectively. In consistent with our previous theoretical study, the dissociation of H2 results in dramatic movement of around atoms.51 The hydrogen formation energies calculated by molecule model are −0.11 and 0.08 eV for Mg(BH4)2·2NH3 and LiMg(BH4)3·2NH3, respectively. The combination of the (N)H and (B)H results in rearrangement of the surrounding atoms, similar with our previous report.51 The NH2 and BH3 units reoriented and BH3 units moved toward NH2 to form NH2–BH3 complexes. The N–B distances reduce to 1.58 Å, indicating the formation of N–B bond during dehydrogenation, in agreement with experimental observation.14,35 However, the lengths of Li–N, Mg–N, B–H and N–H bonds keep almost the same after structural rearrangements.

Table 3 Formation energies of H2 release via (N)H and (B)H combination by using crystal model (EH2-C) and molecule model (EH2-M)
  EH2-C (eV) EH2-M (eV)
Mg(BH4)2·2NH3 0.84 −0.11
LiMg(BH4)3·2NH3 1.22 0.08

The low H2 formation energies of Mg(BH4)2·2NH3 and LiMg(BH4)3·2NH3 suggest that the formation of hydrogen is thermodynamic favourable at low temperature. Therefore, the energy barrier of H2 formation is the key of those two composites release hydrogen at temperature above 100 °C.

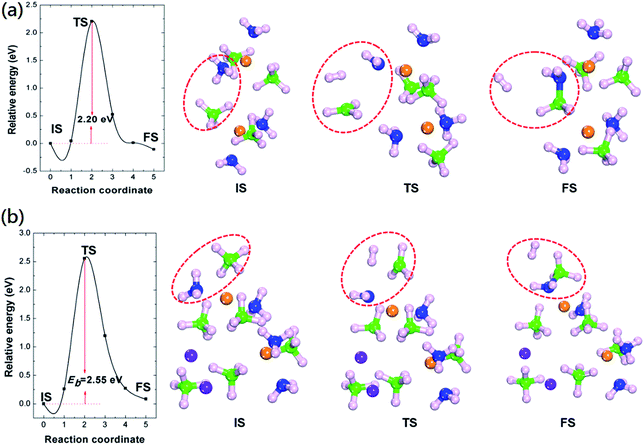
We further calculated the energy barriers of H2 formation and the results were summarized in Fig. 3. The calculated energy barrier of H2 formation from Mg(BH4)2·2NH3 is 2.20 eV. The transition geometric structure of hydrogen release from Mg(BH4)2·2NH3 (Fig. 3(a)) shows the broken of B–H and N–H bonds with the formation of H2 molecule. The H2 molecule is located between NH2 and BH3 units with H2–NH2 and H2–BH3 distances of 2.47 and 2.31 Å, respectively. Meanwhile, the NH2 unit move toward Mg cation and lead to slightly reduce the Mg–N distance from 2.16 to 1.95 Å. The calculated hydrogen formation energy barrier of LiMg(BH4)3·2NH3 is 2.55 eV, which is 0.35 eV higher than that of Mg(BH4)2·2NH3. Previous experimental results show dehydrogenation peak of 205 °C and 221 °C for Mg(BH4)2·2NH3 and LiMg(BH4)3·2NH3, respectively.23,35 The relatively high dehydrogenation peak of LiMg(BH4)3·2NH3 can be attributed to the high hydrogen formation barrier. The transition geometric structure of hydrogen release from LiMg(BH4)3·2NH3 is similar to that of Mg(BH4)2·2NH3. The H2 molecule is located between NH2 and BH3 unit. The H2–NH2 distance in transition structure of LiMg(BH4)3·2NH3 is 2.24 Å, which is 0.23 Å shorter than that in Mg(BH4)2·2NH3. And the H2–BH3 distance in transition structure of LiMg(BH4)3·2NH3 is 2.11 Å, which is 0.20 Å shorter than that in Mg(BH4)2·2NH3. In addition, the NH2 unit shortening its distance to the Mg cation from 2.19 to 1.95 Å, similar to that of Mg(BH4)2·2NH3.


image file: c7ra05322c-f3.tif
Fig. 3 The calculated energetic profiles, initial (IS), transition (TS) and final (FS) geometric structure of H2 formation for (a) Mg(BH4)2·2NH3 and (b) LiMg(BH4)3·2NH3. Eb represents the calculated energy barrier. The green, pink, orange, purple and blue colours represent B, H, Mg, Li and N atoms, respectively.

Although the above calculations show a low NH3 diffusion barrier for Mg(BH4)2·2NH3, the formation energy of NH3 vacancy is relatively high, which results in low concentration of NH3 vacancy in Mg(BH4)2·2NH3. Therefore, the Mg(BH4)2·2NH3 mainly releases hydrogen accompany with a small amount of ammonia during decomposition. In contrast to that of Mg(BH4)2·2NH3, LiMg(BH4)3·2NH3 shows relatively high formation energy and diffusion barrier of NH3 vacancy, which limit both the concentration and transport of ammonia, therefore improve the dehydrogenation purity. The calculated hydrogen formation barrier of LiMg(BH4)3·2NH3 is slightly higher than that of Mg(BH4)2·2NH3, therefore incorporation of LiBH4 with Mg(BH4)2·2NH3 may not decrease the dehydrogenation temperature.

Conclusions

First-principles calculations based on density functional theory were carried out to investigate the decomposition mechanisms of Mg(BH4)2·2NH3 and LiMg(BH4)3·2NH3. The electronic structure analysis indicates that Mg–H interaction in those two composites are mainly ionic with partial covalent bond feature. The incorporation of LiBH4 and Mg(BH4)2·2NH3 with the formation of LiMg(BH4)3·2NH3 barely affects the charge distribution of H and Mg. The Bader charge of B is slightly increased and Bader charge of N decreased due to the incorporation of LiBH4. Although the NH3 diffusion barrier for Mg(BH4)2·2NH3 is low, the relatively high formation energy of NH3 vacancy lead to low concentration of NH3 vacancy and limit its transportation, in agreement with experimental results that Mg(BH4)2·2NH3 mainly releases hydrogen along with a small amount of ammonia. The LiMg(BH4)3·2NH3 shows relatively high ammonia vacancy formation energy and diffusion barrier, which suppress ammonia release compared to Mg(BH4)2·2NH3. The incorporation of LiBH4 and Mg(BH4)2·2NH3 does not decrease the hydrogen formation barriers, instead slightly increase the hydrogen formation barriers of LiMg(BH4)3·2NH3, in agreement with experimental results that LiMg(BH4)3·2NH3 shows a dehydrogenation peak slightly higher than that of Mg(BH4)2·2NH3.

Acknowledgements

This work is supported by the National Science Fund for Distinguished Young Scholars (51625102), National Natural Science Foundation of China (51601068, 11605073) and Natural Science Foundation of Fujian Province (2016J05129, 2017J05009).

Notes and references

  1. A. Staubitz, A. P. M. Robertson and I. Manners, Chem. Rev., 2010, 110, 4079–4124 CrossRef CAS PubMed.
  2. C. W. Hamilton, R. T. Baker, A. Staubitz and I. Manners, Chem. Soc. Rev., 2009, 38, 279–293 RSC.
  3. Z. Xiong, C. K. Yong, G. Wu, P. Chen, W. Shaw, A. Karkamkar, T. Autrey, M. O. Jones, S. R. Johnson and P. P. Edwards, Nat. Mater., 2008, 7, 138–141 CrossRef CAS PubMed.
  4. T. B. Marder, Angew. Chem., Int. Ed., 2007, 46, 8116–8118 CrossRef CAS PubMed.
  5. L. Li, X. Yao, C. Sun, A. Du, L. Cheng, Z. Zhu, C. Yu, J. Zou, S. C. Smith and P. Wang, Adv. Funct. Mater., 2009, 19, 265–271 CrossRef CAS.
  6. X. Kang, Z. Fang, L. Kong, H. Cheng, X. Yao, G. Lu and P. Wang, Adv. Mater., 2008, 20, 2756–2759 CrossRef CAS PubMed.
  7. A. Paul and C. B. Musgrave, Angew. Chem., Int. Ed., 2007, 119, 8301–8304 CrossRef.
  8. W. R. H. Wright, E. R. Berkeley, L. Alden, R. T. Baker and L. G. Sneddon, Chem. Commun., 2011, 47, 3177–3179 RSC.
  9. X. Kang, J. Luo, Q. Zhang and P. Wang, Dalton Trans., 2011, 40, 3799–3801 RSC.
  10. B. Meredig and C. Wolverton, Nat. Mater., 2012, 12, 123–127 CrossRef PubMed.
  11. A. Karkamkar, C. Aardahl and T. Autrey, Mater. Matters, 2007, 2, 6–9 CAS.
  12. H. Wu, W. Zhou, F. E. Pinkerton, M. S. Meyer, Q. Yao, S. Gadipelli, T. J. Udovic, T. Yildirim and J. J. Rush, Chem. Commun., 2011, 47, 4102–4104 RSC.
  13. J. Luo, X. Kang and P. Wang, Energy Environ. Sci., 2013, 6, 1018–1025 CAS.
  14. Y. S. Chua, H. Wu, W. Zhou, T. J. Udovic, G. Wu, Z. Xiong, M. W. Wong and P. Chen, Inorg. Chem., 2012, 51, 1599–1603 CrossRef CAS PubMed.
  15. G. Xia, Y. Tan, X. Chen, Z. Guo, H. Liu and X. Yu, J. Mater. Chem. A, 2013, 1, 1810–1820 CAS.
  16. J. Spielmann, G. Jansen, H. Bandmann and S. Harder, Angew. Chem., Int. Ed., 2008, 120, 6386–6391 CrossRef.
  17. X. Chen, Y.-J. Zhao and X. Yu, Phys. Chem. Chem. Phys., 2013, 15, 893–900 RSC.
  18. Y. H. Guo, X. B. Yu, W. W. Sun, D. L. Sun and W. N. Yang, Angew. Chem., Int. Ed., 2011, 123, 1119–1123 CrossRef.
  19. Y. H. Guo, G. L. Xia, Y. Zhu, L. Gao and X. B. Yu, Chem. Commun., 2010, 46, 2599–2601 RSC.
  20. P. A. Chater, W. I. David, S. R. Johnson, P. P. Edwards and P. A. Anderson, Chem. Commun., 2006, 2439–2441 RSC.
  21. H. Chu, G. Wu, Z. Xiong, J. Guo, T. He and P. Chen, Chem. Mater., 2010, 22, 6021–6028 CrossRef CAS.
  22. F. Yuan, Q. F. Gu, X. W. Chen, Y. B. Tan, Y. H. Guo and X. B. Yu, Chem. Mater., 2012, 24, 3370–3379 CrossRef CAS.
  23. G. Soloveichik, J. H. Her, P. W. Stephens, Y. Gao, J. Rijssenbeek, M. Andrus and J. C. Zhao, Inorg. Chem., 2008, 47, 4290–4298 CrossRef CAS PubMed.
  24. Y. H. Guo, H. Wu, W. Zhou and X. B. Yu, J. Am. Chem. Soc., 2011, 133, 4690–4693 CrossRef CAS PubMed.
  25. L. H. Jepsen, M. B. Ley, R. Cerný, Y. Lee, Y. W. Cho, D. B. Ravnsbaek, F. Besenbacher, J. Skibsted and T. R. Jensen, Inorg. Chem., 2015, 54, 7402–7414 CrossRef CAS PubMed.
  26. K. Wang, J. Zhang and X. Lang, Phys. Chem. Chem. Phys., 2016, 18, 7015–7018 RSC.
  27. J. M. Huang, L. Z. Ouyang, Q. F. Gu, X. B. Yu and M. Zhu, Chem.–Eur. J., 2015, 21, 14931–14936 CrossRef CAS PubMed.
  28. J. Huang, Y. Tan, J. Su, Q. Gu, R. Cerný, L. Ouyang, D. Sun, X. Yu and M. Zhu, Chem. Commun., 2015, 51, 2794–2797 RSC.
  29. Y. J. Yang, Y. F. Liu, Y. Li, M. X. Gao and H. G. Pan, J. Mater. Chem. A, 2015, 3, 570–578 CAS.
  30. Y. Li, Y. F. Liu, X. Zhang, D. Zhou, Y. H. Lu, M. X. Gao and H. G. Pan, J. Mater. Chem. A, 2016, 4, 8366–8373 CAS.
  31. Y. J. Yang, Y. F. Liu, Y. Li, X. Zhang, M. X. Gao and H. G. Pan, J. Mater. Chem. A, 2015, 3, 11057–11065 CAS.
  32. Z. Tang, Y. Tan, H. Wu, Q. Gu, W. Zhou, C. M. Jensen and X. Yu, Acta Mater., 2013, 61, 4787–4796 CrossRef CAS.
  33. A. Emdadi, S. Demir, Y. Kışlak and A. Tekin, J. Phys. Chem. C, 2016, 120, 13340–13350 CAS.
  34. E. Welchman and T. Thonhauser, J. Mater. Chem. A, 2017, 5, 4084–4092 CAS.
  35. W. W. Sun, X. W. Chen, Q. F. Gu, K. S. Wallwork, Y. B. Tan, Z. W. Tang and X. B. Yu, Chem.–Eur. J., 2012, 18, 6825–6834 CrossRef CAS PubMed.
  36. Y. Yang, Y. Liu, Y. Li, M. Gao and H. Pan, Chem.–Asian J., 2013, 8, 476–481 CrossRef CAS PubMed.
  37. Y. Yang, Y. Liu, H. Wu, W. Zhou, M. Gao and H. Pan, Phys. Chem. Chem. Phys., 2013, 16, 135–143 RSC.
  38. Y. Yang, Y. Liu, Y. Zhang, Y. Li, M. Gao and H. Pan, J. Alloys Compd., 2014, 585, 674–680 CrossRef CAS.
  39. Y. Li, Y. Liu, X. Zhang, Y. Yang, M. Gao and H. Pan, Int. J. Hydrogen Energy, 2016, 41, 2788–2796 CrossRef CAS.
  40. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
  41. J. Klimes, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131 CrossRef.
  42. J. Klimes, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2009, 22, 022201 CrossRef PubMed.
  43. M. Dion, H. Rydberg, E. Schroder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS PubMed.
  44. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
  45. J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533–16539 CrossRef CAS.
  46. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
  47. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
  48. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
  49. G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
  50. C. G. van de Walle and J. Neugebauer, J. Appl. Phys., 2004, 95, 3851 CrossRef CAS.
  51. X. W. Chen and X. B. Yu, J. Phys. Chem. C, 2012, 116, 11900–11906 CAS.
  52. X. W. Chen, F. Yuan, Y. B. Tan, Z. W. Tang and X. B. Yu, J. Phys. Chem. C, 2012, 116, 21162–21168 CAS.
This journal is © The Royal Society of Chemistry 2017