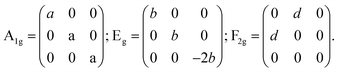Temperature-dependent optical phonon behaviour of a spinel Zn₂TiO₄ single crystal grown by the optical floating zone method in argon atmosphere

Abstract

The spinel Zn₂TiO₄ single crystals were grown via optical floating zone technology in an argon atmosphere for the first time, the as-grown crystals were dark blue and transparent. And the as-grown crystals, free of bubbles and with low angle grain boundary, grow along the a-axis direction. The annealed crystals were colorless and transparent, and the chemical valence of as-grown and annealed single crystals was characterized by X-ray photoelectron spectra. The room-temperature polarized Raman spectra of spinel Zn₂TiO₄ crystal were presented and the in situ temperature-dependent Raman spectra of the crystals were also described. DSC results of Zn₂TiO₄ were also discussed.

---

1. Introduction

Spinel structured materials, including normal (AB₂O₄) and inverse (A₂BO₄) spinels, have attracted increased research attention because of their utility in high-temperature ceramics,^1,2 magnetism,^3,4 superhard materials,⁵ and pressure sensors.^6,7 Zinc titanate (Zn₂TiO₄) with an inverse spinel structure has outstanding dielectric properties.^8,9 Thus, the materials are widely applied in microwave devices.¹⁰ Zinc titanate is a regenerable high-effect catalyst sorbent for contaminants obtained from hot coal gases, such as H₂S, As, and Se.^11–13 Many studies on the optical, photoelectrochemical, and electrical properties of Zn₂TiO₄ under various conditions have been reported.^14–17

The potential uses of Zn₂TiO₄ in optical, microwave dielectric, and catalyst applications strongly depend on the optical phonon behaviour of the crystals, which can be determined by intrinsic contributions of their phonon modes together with possible extrinsic contributions of polarizable domains, grain boundaries, polar defects, and/or space charges.¹⁰ However, studies on the properties of Zn₂TiO₄ focus mainly on polycrystalline samples. Several extrinsic factors, including the different preparation methods, differences in grain size, and degree of phase purity, can seriously affect the properties of Zn₂TiO₄. Single-crystal samples with well-crystallized orientations can help eliminate extrinsic defects and provide a better understanding of the intrinsic characteristics of these materials.

The Raman is an available and non-destructive spectral measurement method providing many invaluable information on the lattice dynamics and order-disorder of materials.¹⁸ The spectra of vibration modes in various wavenumbers are excellent in materials investigations.^19,20 At the same time, pressure-induced phase transformation in spinel Zn₂TiO₄ has previously been reported.²¹

The quality of grown crystal, grown by optical floating zone method, is effected by growth speed, rotating rate and growth atmosphere. The effects of growth speed and rotating rate have been investigated and high quality crystals have been obtained by optimize the growth speed and rotating rate in an oxygen atmosphere.²² On the other hands, the growth atmosphere is a very important parameter, which can influence the crystal quality and chemical valence of some elements in materials. In current work, we try to grow Zn₂TiO₄ crystals under argon atmosphere by the optical floating zone method for the first time. Beside, aiming to determine opportunities for applying Zn₂TiO₄ materials at various temperatures, the temperature-dependent Raman spectra of Zn₂TiO₄ crystals are described in this work for the first time. The temperature-dependent Raman shifts and full width at half maximum (FWHM) of Zn₂TiO₄ were studied, and shows an anomalous temperature-dependent behaviour below 273 K.

2. Experimental section

The Zn₂TiO₄ powders were synthesised by calcining stoichiometric amounts of ZnO (Alfa Aesar, 4N) and TiO₂ (Alfa Aesar, 4N) at 1500 K for 20 h with an intermediate grinding. The Zn₂TiO₄ powders were packed into a cylindrical shape rubber tube and then pressed hydrostatically upto 70 MPa in a cold isostatic press to form a cylindrical rod of 4–6 mm in diameter and 50–100 mm in length. The rods were sintered in air at 1600 K for 10 h for use as the feed and support rods.

The Zn₂TiO₄ single crystals were grown in the optical floating zone furnace (CSI FZ-T-10000-H-VI-VP, Crystal systems, Inc., Japan) under an argon atmosphere. A crystal seed, grown in previous work,²² a-axis direction was used in this work. The growth speed was 10 mm h⁻¹; the argon flow of 100 sccm; the feeding and seeding rods were rotated in opposite directions at the rate of 5 rpm.

The crystal structure was characterized with a Rigaku D/max-r A 12 kW X-ray diffractometer (XRD) with Cu Kα radiation. The X-ray photoelectron spectra (XPS) were taken on an ESCALAB 250 electron energy spectrometer with Mg Ka (12 530.6 eV) as the X-ray excitation source. Macroscopic defects such as low-angle grain boundaries and inclusions were studied with an Olympus Model BX-51 polarizing microscope in transmission configuration. To determine the directions of the as-prepared crystals, a Bruker D8 Discover AXS equipped with a GADDS two-dimensional X-ray diffractometer (XRD²) was used.

The Raman scattering spectra were recorded by using a Jobin-Yvon LABRAM-HR 800 spectrometer equipped with an air-cooled CCD detector and a confocal Olympus microscope (50× objective). The measurements were carried out in backscattering geometry, using the 514.5 nm line of an Ar ion laser with power of 40 mW (Spectra Physics Stabilite 2017) as excitation source. Edge filter for stray light rejection, polarizer, and half-wave plate were also used. In-site temperature Raman spectra measurements were achieved via a THMSE 600 heating/cooling stage (Linkam Scientific Instruments) attached to the Raman spectrometer in the temperature range from 107 K to 817 K.

The Differential scanning calorimetry (DSC) measurements were performed using a DSC 204F1 Netzsch calorimeter, with a heating rate of 10 K min⁻¹. The sample was placed in an aluminum capsule which was sealed filled with argon and pierced once inside the DSC apparatus.

3. Results and discussion

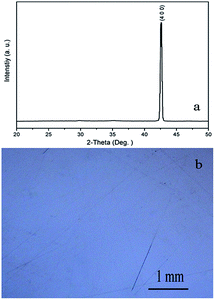
The Zn₂TiO₄ crystals grown previously in air conduction is brown and transparent by our group.²² In this work, the crystals grown in the argon atmosphere are dark blue and transparent, as shown in Fig. 2a. After annealed in an oxygen atmosphere at 1200 K for 10 h, the blue color fades to colorless and transparent, also shown in Fig. 2b. The powder XRD pattern of the as-grown crystal is shown in Fig. 1a. All the peaks can be indexed to the diffraction peaks of the Zn₂TiO₄ spinel (Ref: ICSD code: 080851), indicating that the as-grown crystal is spinel Zn₂TiO₄ without any other phase. The powder XRD pattern of the annealed crystal was also measured; its peak positions and relative intensity are unchanged, indicating that the annealing has no effect on the crystal structure.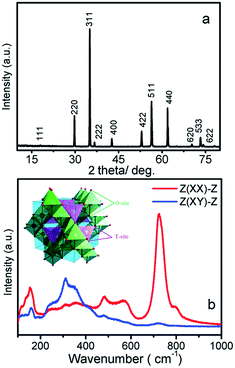

Fig. 1 (a) The powder XRD pattern of as-grown Zn₂TiO₄ crystal; (b) the room-temperature polarized Raman spectrum of the Zn₂TiO₄ and inset shown cell of spinel Zn₂TiO₄.

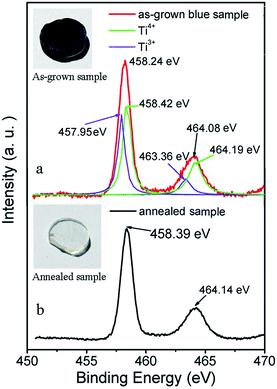Fig. 2 XPS spectra of Ti 2p for as-grown and annealed sample, the inserts show photographs of as-grown and annealed Zn₂TiO₄ samples.

To clarify the color changing machine between the as-grown and annealed crystals, XPS measurements (Fig. 2) were performed to investigate the chemical states of Ti atoms in the as-grown and annealed samples. Compared with the peaks of annealed sample (Ti 2p_3/2 at 458.39 and Ti 2p_1/2 at 464.14 eV), the bonds for as-grown crystal (Ti 2p_3/2 at 458.24 and Ti 2p_1/2 at 464.08 eV) show a shift towarded lower binding energy. After deconvolution, the Ti 2p bonds of as-grown crystal can be divided into four bonds at 457.95, 458.42, 463.36 and 464.19 eV, which represent Ti³⁺ 2p_3/2, Ti⁴⁺ 2p_3/2, Ti³⁺ 2p_1/2 and Ti⁴⁺ 2p_1/2, respectively. It indicates the existence of Ti³⁺ ions in the as-grown crystal. The Zn₂TiO₄ crystals were grown in an argon atmosphere. When the feeding rod has been heated up to its melting point the oxygen atoms in the lattice are driven away easily forming oxygen vacancies and the Ti⁴⁺ ions are reduced to Ti³⁺ ions. After annealed in the oxygen, the oxygen vacancies were eliminated, Ti³⁺ ions were oxidized to Ti⁴⁺ again and the color fades to colorless and transparent.

The orientation of as-grown Zn₂TiO₄ crystal was measured by XRD², as shown in Fig. 3a. From which, we can know that the crystal grows along a-axis direction, which is same as the crystal seed direction. The micro-defects, including the low-angle crystal boundaries and bubbles of the as-fabricated Zn₂TiO₄ single crystal, were also observed via the micropolariscopy in the cross transmission arrangement, as shown in the Fig. 3b. In the wafer, we cannot find bubbles or low-angle grain boundaries.

Fig. 3 (a) XRD² patterns of Zn₂TiO₄ crystal wafer (b) the wafer under polarizing microscope in the transmission configuration.

At room temperature, Zn₂TiO₄ is an inverse spinel, structure formula can be written as (Zn(TiZn)O₄), with a space group of Fd3̄m and typically described by a 56 atom unit cell. In this unit cell, 32 oxygen atoms comprise a face-centered cubic lattice with associated interstitial octahedral (O) and tetrahedral (T) sites. These T-sites are occupied by half of the divalent Zn cations, while O-sites are randomly filled with a stoichiometric mixture of divalent Zn and tetravalent Ti cations, as shown in the insert of Fig. 2. However, the smallest Bravais cell contains only 14 atoms. Thus, according to factor group analysis, the irreducible representations of these modes are:²¹

A_1g(R) + E_g(R) + F_1g+ 3F_2g(R) + 2A_2u + 2E_u + 4F_1u(IR) + 2F_2u. (1)

where the five first order Raman modes, including A_1g(R), E_g(R), and 3F_2g(R), are Raman active with the following Raman tensors:

The Raman tensors are signification in the polarized Raman investigation of Zn₂TiO₄, especially in spectrum-scattering intensity, which is directionally dependent under an intrinsic coordinate system. According to Raman tensor and polarization selection rules, in the XX, YY, and ZZ polarized configurations, the incident scattering lights are parallel with the direction of a specific crystalline axis, E_g and A_1g modes can be detected and the F_2g can be obtained in the XY and YX. Fig. 1b illustrates the room temperature polarized Raman spectrum of a Zn₂TiO₄ crystal. In the Z(XX)-Z configuration, A_1g and E_g mode are expected. The bond at 721 cm⁻¹ dominate in the spectrum. The second strong bond is located at 478 cm⁻¹. The intensity of others become very low. And the 721 cm⁻¹ indexed as A_1g and peak at 478 cm⁻¹, which is indexed as F_2g in previous work⁷ that is disagree with our polarized results. So that the peak at 478 cm⁻¹ should be indexed as E_g according to polarization selection rules. While in the Z(XY)-Z configuration, three peaks at 257, 308 and 348 cm⁻¹ become stronger and dominate the spectrum. Also, according to the Raman polarization selection rules, these three mode should be indexed as F_2g. The A_1g mode located at 721 cm⁻¹ corresponds to the ZnO₄ mode, which reflects the local lattice effect in the tetrahedral sublattice, which can be supported by R. Cuscó et. al.²³ In their article they find second-order Raman active Zn–O chine band located just at 721 cm⁻¹. And the lowest wavenumber mode at 257 cm⁻¹ should be attributed T′(Zn) or coupled T′(Zn) and BO₆ bending mode, supporting by M. Maczka et. al.²⁴ Thus, the three modes at 308, 348, and 478 cm⁻¹ involve TiO₆ or ZnO₆ modes, which reflect local lattice effects in the octahedral sublattice. The three leakage Raman peaks observed at 154, 567, and 794 cm⁻¹ do not belong to the first-order Raman modes of Zn₂TiO₄. The peak at 154 cm⁻¹ is considered as a plasma effect from the laser, the peak at 567 cm⁻¹ is considered a result of order-disorder in the Zn₂TiO₄,²¹ and the peak at 794 cm⁻¹ has yet to be identified.

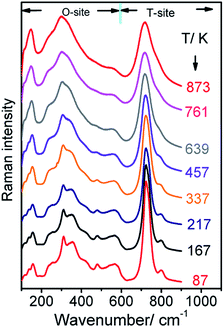
To investigate temperature effects on the spinel structure of Zn₂TiO₄, Raman spectra were collected in the temperature range of 107–817 K, as shown in Fig. 4. The vibration mode of A_1g exhibits obvious softening and broadening and other Raman modes below 600 cm⁻¹ become fuzzier because the widths were too wide to be recognized when the temperature increases from 107 K to 817 K. Given thermal effects, the five modes shift toward lower wavenumbers as the temperature increases. Moreover, the E_g mode disappears when the temperature beyond 639 K.

Fig. 4 Raman spectra of the Zn₂TiO₄ single crystal with the temperatures from 107 K to 817 K.

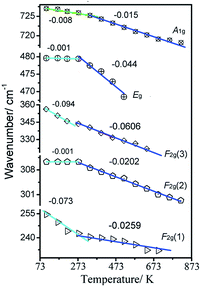
The Raman peaks of F_2g(1), F_2g(2), F_2g(3), E_g, and A_1g were fitted to a Lorentzian line shape, and the Raman wavenumber of these modes and FWHM of the A_1g mode were obtained, as shown in Fig. 5 and 6, respectively. From Fig. 5, the Raman peak positions of F_2g(1), F_2g(2), and A_1g shift toward lower wavenumbers direction as the temperature increases from 107 K to 273 K. However, the Raman peak positions of the E_g and F_2g(2) modes are stable in this region. When the temperature reaches 273 K, the speed of five modes shift toward lower wavenumbers changed.

Fig. 5 The wavenumber variations of modes as a function of temperature for the Zn₂TiO₄ crystal.

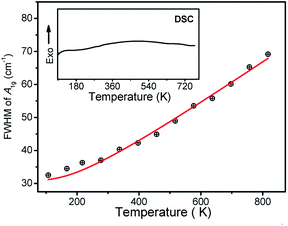Fig. 6 Linewidth of A_1g modes at cm⁻¹ as a function of temperature. The inset shows DSC result of Zn₂TiO₄ sample.

On the other hands, considering the thermal effects observed, the red-shift of the five phonon modes in the spinel Zn₂TiO₄ system indicates the sensitivity of cation distribution in the system as the temperature increases. The wavenumbers of the modes E_g and F_2g(2) decrease more rapidly as the temperature increases to beyond 273 K. By contrast, when the sample is heated up to 273 K, the decrease rates of the F_2g(1) and F_2g(3) modes slow down. While the A_1g attributed to T-site lattice vibration is more stable and the decrease rate change at 337 K, which is later than other bands.

Base on the theory from ‘Thermodynamics of crystals’,²⁵ the damping of phonon can be attributed to phonon–phonon, spin–phonon or crystal field–phonon interactions. In second-order perturbation, the temperature-dependent FWHM only arises through cubic anharmonic interactions corresponding to decay and combination process. The best fit to the data of A_1g modes is obtained by only assuming the combination of the observed phonon with another phonon of wavenumber ω′ to create a third excitation wavenumber ω′′, where ω′′ = ω + ω′. The temperature-dependent FWHM of modes can be fitted by the function as follows:^25–27

F(λ) = F₁(λ) + F₂(λ)[n(ω) − n(ω + ω′)] (2)

where F₁(λ) is the FWHM at 0 K and F₂(λ) is a temperature-independent factor that reflects the strength of the cubic anhamornic interaction and the factor n(ω′) is the Bose–Einstein occupation number expressed as:^25–27

n(ω′) = {exp[ℏΔ_o(ω′)/kT] − 1}⁻¹ (3)

where Δ_o(ω′) refers to the harmonic frequency, ℏ is Planck's constant, k is Boltzmann's constant, and T is absolute temperature. The temperature-dependent FWHM of A_1g mode cannot be fitted using eqn (2), as shown in the Fig. 6. It can be observed anomalous changes below 273 K.

As shown in Fig. 4, the relative Raman intensities of T and O-sites, which are characterized by modes beyond and below 600 cm⁻¹, change as the temperature increases. At 107 K, the spinel Zn₂TiO₄ is highly ordered, and the Raman intensity at 721 cm⁻¹, as the strongest bond, is significantly higher than that of bonds below 600 cm⁻¹. As the temperature increases, the relative intensity at 721 cm⁻¹ decreases gradually. The relative intensity reflects the relative content of the corresponding mode compared with other modes. Decreases in the relative intensity of the mode at 721 cm⁻¹ imply a reduction in the relative content for the vibration of the T-site. This finding can be attributed to the dislocation of Zn²⁺ cations from T-sites to O-site, while Ti⁴⁺ cations may move from O-sites to T-sites and the Ti⁴⁺ cations at T-sites are no Raman activity. Thus, the interchange results in disorder in the entire inverse spinel structure of Zn₂TiO₄ when the temperatures increases because of the imbalance between these two valences, which are common phenomena, called order-disorder effect, in spinel materials.^28,29

To confirm our assumption, DSC measured on Zn₂TiO₄ sample was performed in the range of 95 to 750 K, which is same as temperature dependent Raman result, as shown in the inset of Fig. 6. The DSC curves for Zn₂TiO₄ cooled down to 95 K firstly, using liquid nitrogen. And then heated up to 750 K at a scanning rate of 10 K min⁻¹. The DSC curve shows no inflection point in the whole range. It is indicated that Zn₂TiO₄ has no phase transition in the temperature range. The phenomenon in the temperature dependent Raman result can be attributed to the order-disorder effect.

4. Conclusions

Spinel Zn₂TiO₄ single crystals were grown by optical floating zone technology. The as-grown crystals are free of bubble and low angle grain boundary, and grow along the a-axis direction. The room-temperature polarized Raman spectra of the as-grown crystal was identified. The in-site temperature-dependent Raman spectra of spinel Zn₂TiO₄ were also described and the structure disorder in the Zn₂TiO₄ appeared with increasing the temperature, which may indicate the cations migration between tetrahedral and octahedral sites, which is confirmed by DSC result.

Acknowledgements

The financial support from the National Foundation for Fostering Talents of basic Science (Grant No. J1103202), the National Natural Science Foundation of China (Grant No. 11274137, 11074090, 11304113), Education and research project of Jilin Province education department (No. 2016401) and the Open Project of State Key Laboratory of Inorganic Synthesis and Preparative Chemistry (Jilin University) (No. 2017-6) are greatly appreciated.

Notes and references

1. W.-L. Lee, S. Watauchi, V. L. Miller, R. J. Cava and N. P. Ong, Science, 2004, 303(5664), 1647–1649.
2. F. Wu, N. Li, Y. Su, L. Zhang, L. Bao, J. Wang, L. Chen, Y. Zheng, L. Dai, J. Peng and S. Chen, Nano Lett., 2014, 14(6), 3550–3555.
3. K. M. Kojima, R. Kadono, M. Miyazaki, M. Hiraishi, I. Yamauchi, A. Koda, Y. Tsuchiya, H. S. Suzuki and H. Kitazawa, Phys. Rev. Lett., 2014, 112(8), 087203.
4. A. S. Burange, S. R. Kale, R. Zboril, M. B. Gawande and R. V. Jayaram, RSC Adv., 2014, 4(13), 6597–6601.
5. A. Zerr, G. Miehe, G. Serghiou, M. Schwarz, E. Kroke, R. Riedel, H. Fuesz, P. Kroll and R. Boehler, Nature, 1999, 400(6742), 340.
6. S.-H. Shim, T. S. Duffy and G. Shen, Nature, 2001, 411(6837), 571–574.
7. Z. W. Wang, R. T. Downs, V. Pischedda, R. Shetty, S. K. Saxena, C. S. Zha, Y. S. Zhao, D. Schiferl and A. Waskowska, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68(9), 094101.
8. P. R. Guagliardo, E. R. Vance, G. R. Lumpkin, M. G. Blackford, K. Sudarshan, J. Davis, S. Samarin and J. F. Williams, J. Am. Ceram. Soc., 2013, 96(10), 3286–3289.
9. R. L. Miliard, R. C. Peterson and B. K. Hunter, Am. Mineral., 1995, 80, 885.
10. Y. Yang, R. Scholz, H. J. Fan, D. Hesse, U. Gosele and M. Zacharias, ACS Nano, 2009, 3(3), 555.
11. K. Jothimurugesan and S. K. Gangwal, Ind. Eng. Chem. Res., 1998, 37(5), 1929.
12. S. Lew, A. F. Sarofim and M. Flytzani-Stephanopoulos, Chem. Eng. Sci., 1992, 47(6), 1421.
13. J. J. Huang, J. T. Zhao, X. F. Wei, Y. Wang and X. P. Bu, Powder Technol., 2008, 180(1–2), 196.
14. M. V. Nikolić, N. Obradović, K. M. Paraskevopoulos, T. T. Zorba, S. M. Savić and M. M. Ristić, J. Mater. Sci., 2008, 43(16), 5564.
15. K. H. Yoon, J. Cho and D. H. Kang, Mater. Res. Bull., 1999, 34(9), 1451.
16. C. F. Li, Y. Bando, M. Nakamura, N. Kimizuka and H. Kito, Mater. Res. Bull., 2000, 35(3), 351.
17. A. C. Chaves, S. J. G. Lima, R. C. M. U. Araújo, M. A. M. A. Maurera, E. Longo, P. S. Pizani, L. G. P. Simões, L. E. B. Soledade, A. G. Souza and I. M. G. d. Santos, J. Solid State Chem., 2006, 179(4), 985.
18. J. I. Colless, X. G. Croot, T. M. Stace, A. C. Doherty, S. D. Barrett, H. Lu, A. C. Gossard and D. J. Reilly, Nat. Commun., 2014, 5, 3716.
19. S. Merkel, A. F. Goncharov, H. k. Mao, P. Gillet and R. J. Hemley, Science, 2000, 288(5471), 1626–1629.
20. R. Cuscó, E. Alarcón-Lladó, J. Ibáñez, L. Artús, J. Jiménez, B. Wang and M. J. Callahan, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75(16), 165202.
21. Z. W. Wang, S. K. Saxena and C. S. Zha, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66(2), 0241031.
22. L. Li, H. Yang, D. Wang, G. Feng, B. Li, Z. Gao, D. Xu, Z. Ding and X. Liu, J. Cryst. Growth, 2010, 312(24), 3561.
23. R. Cuscó, E. Alarcón-Lladó, J. Ibáñez, L. Artús, J. Jiménez, B. Wang and M. J. Callahan, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75(16), 165202.
24. M. Mączka, M. Ptak, M. Kurnatowska and J. Hanuza, Mater. Chem. Phys., 2013, 138(2–3), 682–688.
25. D. C. Wallace, Thermodynamics of crystals, 1972, wiley, New York, pp. 582–583.
26. F. D. Medina and W. B. Daniels, J. Chem. Phys., 1976, 64(1), 150–161.
27. H. Wang, F. D. Medina, Y. D. Zhou and Q. N. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45(18), 10356–10362.
28. H.-P. Liu, R. N. Schock and D. L. Anderson, Geophys. J. R. Astron. Soc., 1975, 42(1), 217–250.
29. Y. Y. Liao, Y. W. Li, Z. G. Hu and J. H. Chu, Appl. Phys. Lett., 2012, 100(7), 071905.

---