Ab initio mechanical and thermal properties of FeMnP_1−xGa_x compounds as refrigerant for room-temperature magnetic refrigeration

Abstract

Density functional theory was used to identify possible Fe₂P-type giant magnetocaloric FeMnP_1−xGa_x compounds. The calculated formation energies, elastic constants and phonon spectra confirm the energetic, mechanical and dynamical stability of hexagonal FeMnP_1−xGa_x compounds in both the ferromagnetic and paramagnetic states. The predicted magnetic moment, elastic properties, and Curie temperature of FeMnP_0.67Ga_0.33 are close to those obtained for FeMnP_0.67Ge_0.33 compounds using the same calculation scheme. The entropy changes and latent heat of FeMnP_0.67Ga_0.33 are similar with those of FeMnP_0.67Ge_0.33. The electronic density of states and charge density analysis indicate that the FeMnP_1−xGa_x compounds have similar electronic structures to those of FeMnP_1−xGe_x. These results predict that FeMnP_1−xGa_x is a possible candidate refrigerant for room-temperature magnetic refrigeration.

---

Introduction

Hexagonal Fe₂P-type transition metal FeMn-based magnetocaloric materials (FeMnP_1−xT_x, T = As, Si, Ge) are driving tremendous research interest because of their promising application in solid-state refrigeration as energy efficient, environment friendly alternative to the traditional gas-compressor based cooling scheme.^1–9 This family of materials exhibit a first-order magnetoelastic transition close to room temperature.^10–12 Significant exchange striction, in which the hexagonal lattice parameter c decreases and a increases with a very small volume change, is observed during the paramagnetic (PM) to ferromagnetic (FM) transition.^10,13 This leads to large local strain in the polycrystalline samples, and therefore good mechanical stability across the phase transition becomes very important for FeMn-based giant magnetocaloric (GMC) materials because they work under repeated magnetic and thermal cycles.^5,6,10,14

To obtain materials with good performance in magnetic refrigeration, extensive experimental investigation of FeMnP_1−xSi_x compounds has been performed.^8,9,11–17 The thermal hysteresis decreases to less than 1 K and the isothermal entropy change |S_iso| increases to ∼9.0 J kg⁻¹ K⁻¹ around the Curie temperature,¹² which can be continuously tailored.^4,5,16,18 However, the weak mechanical stability across the phase transition restricts the applicability of FeMnP_1−xSi_x compounds in practical devices. One way to optimize the mechanical stability of FeMnP_1−xSi_x compounds is to dope them with interstitial B atoms.^{10,12,14,18–20} Another viable way to improve the mechanical properties of these compounds is to replace Si atoms with other elements to adjust the bonding between atoms.^21,22 Si and Al have been suggested to be the most ideal substitutes for the toxic As element in MnFeP_1−xAs_x compounds,^23,24 although experimentalists have failed to alloy Al into hexagonal Fe₂P-type magnetocaloric materials. From the viewpoint of alloying, Ga is a possible candidate because it has a similar outermost electronic structure and atomic size to Ge. However, no theoretical investigations have been performed to determine the structural, magnetic, and electronic properties of FeMnP_1−xGa_x and FeMnP_1−xGe_x compounds.

Here, we report the possibility of developing GMC compounds by alloying Ga into hexagonal Fe₂P-type compounds by quantum mechanical calculations. The static and dynamic stabilities of FeMnP_1−xGa_x compounds in different states are verified by total energy and elastic constant calculations. In addition, the mechanical properties of FeMnP_1−xT_x (T = Ga, Ge) in different magnetic states are evaluated. The thermodynamic properties of FeMnP_1−xGa_x compounds were calculated and they are compared with those of FeMnP_1−xGe_x compounds to determine the possibility of using them in magnetic refrigeration.

Computational details

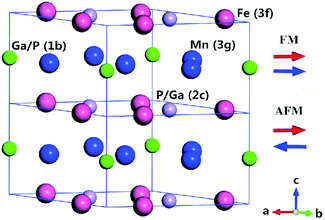
The Fe₂P-type hexagonal structure has the symmetry of space group P6(̄)2m, in which three atoms occupy four different crystal sites. Usually, the Fe atom prefers the 3f (x₁, 0, 0) site and the Mn atom occupies the 3g (x₂, 0, 0.5) site.²⁵ There are two different atomic sites for the metalloid atoms, namely, 2c (0.333, 0.667, 0) and 1b (0, 0, 0.5). Local occupation disorder of P and Si atoms at 2c and 1b sites in FeMnP_1−xSi_x compounds was observed in the experiment.²⁶ However, site occupation order between 2c and 1b sites is expected for FeMnP_1−xGe_x and FeMnP_1−xGa_x compounds because of the larger atomic radii of these dopant atoms than P and Si atoms. Therefore, we chose the occupation of Ga (or Ge) atom at the 1b site for x = 0.33 and at the 2c for x = 0.67. The FM state was calculated self consistently with the primitive cell (half of the cell shown in Fig. 1), while the PM state was modeled by an antiferromagnetically ordered 1 × 1 × 2 supercell structure (Fig. 1). Antiferromagnetic model is usually used to simulate the paramagnetic state of transition metals and their alloys, and it can practically capture the physics observed in experiment.^27–29 The magnetic moments of the transition metal atoms were set to be parallel in the primitive cells and an antiparallel alignment of magnetic moments between primitive cells was established to form the antiferromagnetic (AFM) order. In this case, the long-range FM order along the c axis is broken, but short-range magnetic order still exits,³⁰ so this supercell structure models the magnetic state just above the Curie temperature.

Fig. 1 Cell structure of hexagonal phase FeMnP_1−xGa_x compounds. For the case of x = 0.33, Ga occupies the 1b site, and for x = 0.67, Ga occupies the 2c site. For the FM state, the magnetic moments of the unit cells are aligned parallel, and for the AFM state the magnetic moments in the upper and lower unit cells are aligned antiparallel.

The total electronic energy was calculated by the projector augmented wave method³¹ in the framework of density functional theory,^32,33 as implemented in the Vienna ab initio simulation package (VASP).^34,35 The exchange correlation effect was evaluated by the generalized gradient approximation parameterized by Perdew, Burke, and Ernzerhof.³⁶ The accuracy of PBE functional for FeMn based Fe₂P type alloys has previously been confirmed.^17,51 The scalar relativistic scheme was used and the spin–orbit coupling effect was omitted. Mn (3d⁶4s¹), Fe (3d⁷4s¹), P (3s²3p³), Ga (3d¹⁰4s²4p¹), and Ge (3d¹⁰4s²4p²) electrons were treated as valance states.³⁷ The cutoff energy of the plane wave basis was set to 530 eV, and the convergence criterion of self-consistent electronic relaxation was set to 10⁻⁵ eV per atom. For ionic relaxation, the force convergence criterion of 0.01 eV Å⁻¹ was used. The Monkhorst–Pack scheme³⁸ was used for Brillouin zone sampling, with an 11 × 11 × 17 k-point mesh for the FM state and an 11 × 11 × 9 k-point mesh for the AFM state. With these computational settings, the total energies of compounds with different magnetic states were calculated for different volume V and c/a values. The equation of state was fitted with the Murnaghan equation,³⁹ and then the bulk modulus and the equilibrium volume were obtained. The five independent elastic constants were calculated by the energy-strain method used in ref. 40, with isochoric strain δ of 0.00 to ±0.05. The phonon spectra were calculated by phonopy code.⁴¹ For FM and AFM states, 72 atom and 144 atom 2 × 2 × 2 supercells were used, respectively. An accurate prediction of the thermodynamic properties should be based on the quasiharmonic approximation (QHA)⁴² with a direct ab initio phonon spectrum calculation.⁴¹ However, this is a very difficult task for multicomponent compounds with large unit cells. An alternative method is based on Debye theory.⁴³ This method has been used to calculate the thermodynamic properties of the FeMnP_1−xSi_x system⁴⁴ and gives good agreement with the properties obtained from the QHA.²⁶

Therefore, the thermodynamic properties of the FeMnP_1−xGa_x compounds were calculated by the quasiharmonic Debye–Slater model implemented in the Gibbs2 code.⁴⁵

Results and discussion

Structure and stability

FeMnP_1−xT_x (T = Si, Ge, As) compounds crystallize in a hexagonal structure with space group P6(̄)2m. They exhibit a first-order FM to PM transition at the Curie temperature. Lattice constant a decreases and c increases with almost zero change in the volume during the phase transition. For FeMnP_0.8Ge_0.2 compounds, the experimentally observed lattice constants a and c are 6.18 and 3.31 Å for the FM state and 6.06 and 3.46 Å for the PM state, respectively. The calculated a and c values for 33 atom% Ge compounds are very close to the experimental results, as listed in Table 1. A small increase in the cell volume is observed in FeMnP_0.8Ge_0.2 compounds⁴⁶ across the FM–PM transition, although the compounds with the AFM configuration have smaller cell volumes than those with FM order. This deviation can be understood by the anharmonic effect. Taking into account thermal expansion, the cell volume of FeMnP_0.67Ge_0.33 calculated with AFM order (i.e., the PM state) will increase to 36.93 ų, which is larger than the value of 36.51 ų obtained for FM order at 0 K. The total and local magnetic moments of FM FeMnP_0.67Ge_0.33 obtained from the calculation are very close to those from experiments (Table 1). Unfortunately, no experimental local magnetic moments of PM FeMnP_1−xGe_x have been reported, and thus quenching of the local moment at 3f (Fe) cannot be verified. DFT level calculations of PM state in Fe₂P²¹ and FeMnP_1−xSi_x (ref. 8) indicate that the magnetic moment at 3f sites will disappear in the PM state. Hence, our results are in agreement with those calculations. A recent experimental study of FeMnP_0.5Si_0.5 compounds suggested that DFT calculations underestimate the magnetic moment of PM compounds at the 3f site.¹⁹ However, we attribute this discrepancy between theory and experiment to local disorder of P and Si atoms in FeMnP_0.5Si_0.5 compounds. Because Fe moment quenching at 3f site is not observed in the AFM state for FeMnP_0.33Ge_0.67 compounds (Table 1), there is a strong local environment dependence of the magnetic moment at the 3f site in this class of compounds. The significantly lower, but not zero, Fe moment at 3f site in PM FeMnP_0.5Si_0.5 compounds¹⁹ can be easily understood. The predicted relative positions of 3f and 3g sites (x₁ and x₂) for FeMnP_0.67Ge_0.33 are significantly different from the experimental values shown in Table 1, which can be ascribed to Fe/Mn disorder and the lower concentration of Ge in Mn_1.1Fe_0.9P_0.8Ge_0.2 compounds.

Table 1 Lattice parameters (a, c, V), magnetic moments, energy E₀, and factional atomic positions x₁ (Fe) and x₂ (Mn) of the FeMnP_1−xGa_x compounds. For reference, both the theoretical and experimental values of FeMnP_1−xGe_x compounds are shown

		Mag. Ord.	a (Å)	c (Å)	V (Å^3 per f.u.)	E0 (eV per f.u.)	μtot (μB per f.u.)	μFe (μB)	μMn (μB)	x1	x2
a Experimental results for Mn1.1Fe0.9P0.8Ge0.2 compounds. FM are the values at 10 K and PM are those 295 K from ref. 46 and 47.
FeMnP1−xTx
x = 0.33	Ga	FM	6.14	3.36	36.61	−22.74	4.38	1.49	2.96	0.274	0.588
		AFM	5.83	3.67	35.90	−22.68	0.00	0.00	2.83	0.262	0.570
	Ge	FM	6.16	3.33	36.51	−23.46	4.39	1.46	2.99	0.271	0.591
		AFM	5.86	3.61	35.71	−23.38	0.00	0.00	2.80	0.262	0.575
FeMnP0.8Ge0.2^a
		FM (10 K)	6.18	3.31	36.43	—	—	1.71	3.01	0.2558	0.5956
		PM (295 K)	6.06	3.46	36.70	—	—	—	—	0.2527	0.5916
x = 0.67	Ga	FM	6.56	3.05	37.83	−21.69	4.63	1.68	3.03	0.252	0.623
		AFM	6.66	2.91	37.27	−21.52	0.00	1.29	2.99	0.256	0.622
	Ge	FM	6.42	3.15	37.39	−22.99	4.44	1.55	2.98	0.250	0.612
		AFM	6.47	3.10	37.51	−22.70	0.00	1.49	2.95	0.251	0.614

---

For the FeMnP_1−xGa_x compounds considered in this study, the structural and magnetic parameters are very close to those obtained for FeMnP_1−xGe_x compounds. This is in accordance with our expectation because of the similar atomic sizes and electronic configurations of Ga and Ge, with the only difference between these atoms being that Ga has one less p electron. Interestingly, a decrease in the c parameter and expansion is observed across the FM–PM transition in both FeMnP_0.33Ge_0.67 and FeMnP_0.33Ga_0.67 compounds. This has not been reported in experiment and should be further discussed in detail.

The atomic distances between the four components of the compounds were measured from the fully relaxed cell structures with different magnetic order, and they are listed in Table 2. Experimental observation shows that the interplane metal-to-metal and metal-to-metalloid distances D(Fe–Mn), D(Fe–Ge), and D(Mn–P) increase while the intraplane atomic distances D(Fe–P) and D(Mn–Ge) decrease across the FM–PM phase transition. Ab initio calculation and AFM modeling of the FeMnP_0.67Ge_0.33 compounds show the same trend for variation of the atomic distances with the phase transition. These conclusions are still valid even though the volume expansion effect was taken into account. For instance, the predicted Curie temperature T_c is 590 K and the corresponding coefficient of thermal expansion (CTE) is approximately 3.6 × 10⁻⁵ K⁻¹ (see Fig. 5). Considering thermal expansion, D(Fe–P) at 590 K is 2.240 Å, which is still smaller than D(Fe–P) = 2.271 Å of the FM state at 0 K. Similarly, the relaxed D(Fe–Mn) of the AFM FeMnP_0.67Ge_0.33 compounds at 590 K will be larger than that obtained for the FM state at 0 K, even though the calculated D(Fe–Mn) for AFM is smaller at 0 K. The predicted evolution of the atomic distances of the FeMnP_1−xGa_x compounds shows almost the same features as those of FeMnP_1−xGe_x. Interestingly, FeMnP_0.33Ga_0.67 and FeMnP_0.33Ge_0.67 compounds show the opposite atomic distance evolution trend during the phase transition. This result can be attributed to c decreasing with the phase transition.

Table 2 Atomic distances (D in Å) of FeMnP_1−xGa_x and FeMnP_1−xGe_x compounds

		Mag. Ord.	D(Fe–Mn)	D(Fe–P)	D(Fe–Ga/Ge)	D(Mn–P)	D(Mn–Ga/Ge)	D(P–Ga/Ge)
a Experimental results for Mn1.1Fe0.9P0.8Ge0.2 compounds. FM are the values at 10 K and PM are those 295 K from ref. 46 and 47.
FeMnP1−xTx
x = 0.33	Ga	FM	2.561	2.254	2.376	2.502	2.530	3.925
		AFM	2.565	2.180	2.384	2.520	2.505	3.830
	Ge	FM	2.581	2.271	2.358	2.500	2.522	3.927
		AFM	2.575	2.192	2.367	2.511	2.486	3.832
FeMnP0.8Ge0.2^a
		FM (10 K)	2.672	2.358	2.2874	2.5026	2.499	—
		PM (295 K)	2.686	2.311	2.3039	2.5225	2.476	—
x = 0.67	Ga	FM	2.662	2.247	2.496	2.473	2.560	4.081
		AFM	2.617	2.236	2.519	2.518	2.531	4.094
	Ge	FM	2.694	2.246	2.451	2.491	2.534	4.024
		AFM	2.622	2.244	2.476	2.501	2.523	4.011

---

To evaluate the stability of the predicted FeMnP_1−xGa_x compounds, the formation energies were calculated by

ΔE_{FeMnP1−xGax} = E_{FeMnP1−xGax} − E_Fe − E_Mn − (1 − x)E_P − xE_Ga

here, E_Fe, E_Mn, E_P, and E_Ga are the energy per atom for α-Fe, α-Mn, white phosphorus, and α-Ga, respectively. Fig. 2 shows the c/a dependence of the formation energy of FeMnP_1−xGa_x compounds with different magnetic configurations. The FM state is energetically more stable than its AFM counterpart. The energy difference between the two magnetic states E = E_AFM − E_FM is 0.02 eV per atom for FeMnP_0.67Ga_0.33 and 0.06 eV per atom for FeMnP_0.33Ga_0.67, suggesting that FeMnP_0.33Ga_0.67 could have a much larger T_c than FeMnP_0.67Ga_0.33.

Fig. 2 c/a dependence of the formation energies of FeMnP_1−xGa_x compounds in different magnetic states. The formation energies of the FeMnP_1−xGe_x compounds at equilibrium are also shown for comparison. (a) x = 0.33. (b) x = 0.67.

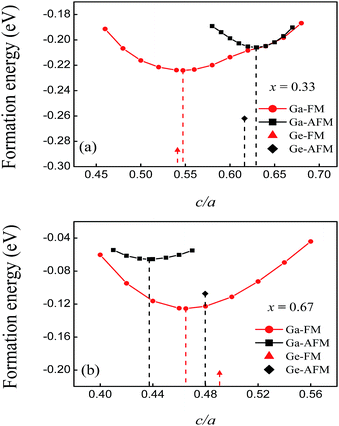
The negative formation energies of all of the compounds in the different magnetic states indicate that alloying of these elements is an exothermic reaction. The formation energies of the FM and AFM states of FeMnP_0.67Ga_0.33 are −0.224 and −0.206 eV per atom, respectively. These values are close to those obtained for the FeMnP_0.67Ge_0.33 compounds, as shown in Fig. 2(a). The absolute values of the formation energies of FeMnP_0.33Ga_0.67 are smaller than those of FeMnP_0.67Ga_0.33. The formation energy curves of the FM and AFM states of FeMnP_0.67Ga_0.33 overlap around c/a of the equilibrium AFM state, which suggests that the FM to AFM transition could occur by simple axial elongation. The curves of the FeMnP_0.33Ga_0.67 compounds show different characteristics. According to the analysis presented above, the predicted FeMnP_1−xGa_x compounds are energetically stable.

Mechanical properties

Magnetocaloric materials work in a repeated thermal and magnetization cycle, so good mechanical stability around their phase transition temperature is required. In addition, for crystals with hexagonal symmetry, a dynamical stability condition of C₄₄ > 0, C₁₁ > C₁₂, C₁₁C₃₃ > (C₁₃)², and C₃₃ (C₁₁ + C₁₂) > 2(C₁₃)² must be satisfied.⁴¹ The calculated elastic constants of the FeMnP_1−xGa_x and FeMnP_1−xGe_x compounds are listed in Table 3. According to the elastic constants, the predicted FeMnP_1−xGa_x compounds are mechanically stable. In combination with the formation energy analysis, we can conclude that the hexagonal phases of the FeMnP_1−xGa_x compounds are stable in both the FM and AFM states. Namely, this class of compounds could exhibit a FM to PM transition similar to those of FeMnP_1−xGe_x and FeMnP_1−xSi_x compounds.

Table 3 Elastic constants (in GPa) of FeMnP_1−xGa_x and FeMnP_1−xGe_x compounds

FeMnP1−xTx		Mag. Ord.	C11	C12	C13	C33	C44	B	R	Cs	C66
x = 0.33	Ga	FM	219.3	68.96	114.5	150.2	107.7	130.7	−0.18	130.6	75.2
		AFM	240.6	94.74	88.86	227.1	95.1	139.1	−0.04	434.2	72.9
	Ge	FM	282.4	108.1	129.0	197.0	112.4	162.5	−0.24	268.6	87.2
		AFM	273.5	103.2	102.8	260.1	104.5	158.2	−0.03	484.7	85.3
x = 0.67	Ga	FM	216.0	79.61	76.97	169.6	90.3	117.1	−0.15	327.0	68.2
		AFM	214.0	97.57	87.06	152.3	97.92	120.5	−0.27	267.9	58.2
	Ge	FM	265.4	95.28	105.5	198.2	108.6	146.9	−0.17	335.3	85.1
		AFM	229.2	91.53	117.7	168.9	104.1	141.0	−0.18	187.9	68.8

---

For both the FeMnP_0.67Ga_0.33 and FeMnP_0.67Ge_0.33 compounds, there are marginal decreases in the bulk modulus B and shear moduli C₄₄ and C₆₆ with the FM to AFM transition. However, there are large differences in the C_s and c axial compressibility values of the hexagonal crystals of both the FeMnP_0.67Ga_0.33 and FeMnP_0.67Ge_0.33 compounds in the FM and AFM states, suggesting that the magnetic order has a strong effect on the crystal structure (c/a) of this class of compounds. For FeMnP_0.33Ga_0.67 and FeMnP_0.33Ge_0.67, the elastic constants show the opposite trend for the FM and AFM states compared with those for the compounds with lower Ga and Ge concentration. This can be ascribed to the opposite trends of the lattice parameters during the phase transition.

Exchange strain (lattice parameter changes) is always accompanied by the FM–PM phase transition. Therefore, magnetocaloric materials should be sufficiently mechanically stable to bear a large internal strain. The polycrystalline bulk and shear moduli obtained by different averaging schemes,^40,41 Young's modulus E, Poisson's ratio v, the Debye temperature θ_D, and the Grüneisen constant γ are listed in Table 4. According to the Pugh criteria,⁴⁸ the FeMnP_1−xGa_x and FeMnP_1−xGe_x compounds with x = 0.33 are ductile (B/G > 1.75 and v > 0.26) in the FM state and brittle (B/G < 1.75 and v < 0.26) in the AFM state. The situation is reversed for x = 0.67, where the FM state is brittle and AFM state is ductile.

Table 4 Polycrystalline bulk modulus (B) and shear modulus (G) in GPa under the Voigt, Reuss, and Hill averaging schemes, Young's modulus (E) in GPa, Poisson's ratio v, Debye temperature θ_D in K, and Grüneisen constant γ for the FeMnP_1−xT_x compounds

FeMnP1−xTx		Mag. Ord.	BV	BR	GV	GR	AVR	GH	BH	BH/GH	E	v	θD	γ
x = 0.33	Ga	FM	131.6	130.7	77.48	54.68	0.17	66.08	131.2	1.985	169.7	0.284	441.7	1.82
		AFM	139.3	139.1	81.69	80.27	0.01	80.98	139.2	1.718	203.5	0.256	486.5	1.83
	Ge	FM	166.0	162.5	88.77	78.68	0.06	83.72	164.3	1.962	214.7	0.282	493.6	1.85
		AFM	158.3	158.2	92.08	90.96	0.01	91.52	158.3	1.729	230.2	0.258	515.3	1.85
x = 0.67	Ga	FM	118.7	117.1	74.31	71.36	0.02	72.83	117.9	1.692	182.0	0.244	445.0	1.85
		AFM	124.9	120.5	71.83	64.11	0.05	67.74	122.7	1.811	171.6	0.267	427.0	1.83
	Ge	FM	149.0	146.9	88.63	83.21	0.03	85.92	148.0	1.722	216.0	0.257	480.3	2.22
		AFM	142.3	141.0	75.43	62.10	0.10	68.77	141.7	2.060	177.6	0.291	432.2	1.98

---

The cases investigated in this study are the two extreme cases where Ga (or Ge) only occupies the 1b or 2c site. According to the current result, we speculate that site occupation disorder of P and Ga/Ge elements may increase the ductility of compounds with x = 0.33 in the AFM state.

Phonon spectra

The phonon band structures and densities of states of FeMnP_0.67Ga_0.33 compounds in different magnetic states are shown in Fig. 3. No imaginary frequency was observed in phonon modes for both FM (Fig. 3(a)) and AFM (Fig. 3(b)) states, confirming the dynamical stability of the compounds in different magnetic state. Comparing the phonon DOS of compounds in different magnetic state, the acoustic modes in the low frequency (0–2 THz) part are similar. The optical modes are reasonably different for FM and AFM states, especially the optical mode between frequency range 9.5–14 THz. In the moderate temperature, the difference between low frequency part of optical phonon modes for FM and AFM states determines the evolution of thermal properties of the compounds across FM–PM (AFM) phase transition. From Fig. 3(c) one can find that the phonon of AFM state is a bit softer than that of FM state for frequency larger than 2 THz. A small difference in optical modes of FM and AFM states for frequency above 2 THz, thus a small difference in the vibrational entropy and the heat capacity C_v is expected in the isothermal process. The quantitative analysis on thermal properties of the compounds is given in next section.

Fig. 3 Phonon spectra of FeMnP_0.67Ga_0.33 compounds. (a) Ferromagnetic state, (b) antiferromagnetic state. (c) Phonon densities of states.

Electronic structure

To understand the structural and magnetic properties calculated above, the electronic density of states (DOS) and charge density difference (CDD) were analyzed. In the total DOS (TDOS) of FeMnP_1−xGa_x and FeMnP_1−xGe_x compounds with different magnetic states shown in Fig. 4, the overall shapes of the TDOS are similar for FeMnP_1−xGa_x and FeMnP_1−xGe_x compounds, although the Fermi level of FeMnP_1−xGa_x moves towards a lower energy state because Ga has one less electron than Ge. This leads to a larger DOS value at the Fermi level for FeMnP_1−xGa_x compounds, and thus results in smaller shear moduli compared with those of FeMnP_1−xGe_x (Table 3).⁴⁹ According to the force theorem,⁵⁰ alloy system having larger density of state at Fermi level is more sensitive to lattice strain and endows the system with smaller elastic modulus. Comparing TDOS of FeMnP_0.67Ga_0.33 in different magnetic states, one can find that AFM state always has larger DOS value at Fermi level than that of FM state, namely AFM state should have smaller shear moduli. This qualitative analysis is in line with the self consistent results of shear moduli C₄₄ and C₆₆ for FM and AFM states.

Fig. 4 Calculated TDOS of the FeMnP_1−xGa_x and FeMnP_1−xGe_x compounds. (a) FeMnP_0.67Ga_0.33, (b) FeMnP_0.33Ga_0.67. (c) FeMnP_0.67Ge_0.33. (d) FeMnP_0.33Ge_0.67.

The two spin channels are symmetric for the AFM state of all of the compounds, indicating disappearance of the overall magnetic moment of the AFM cell. Because of the breaking symmetry, several bands split and new states appear close to the Fermi level as the compounds undergo the FM to PM transition. Comparing the electronic DOS of the AFM and FM states, significant electronic redistribution occurs during the phase transition.

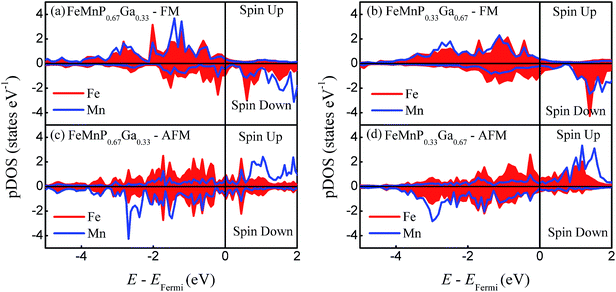
To estimate the evolution of the bonding characteristics and local magnetic moment with the phase transition, the site-projected density of states (pDOS) of FeMnP_1−xGa_x are plotted in Fig. 5. In the FM phase, Mn and Fe share almost all of the pDOS peak for both x = 0.33 and 0.67, that means there is strong covalent-like bonding between Fe and Mn. As the FM order breaks, the pDOS behaves differently. For FeMnP_0.67Ga_0.33, the spin-up and spin-down channels of Fe become symmetric, indicating disappearance of the local magnetic moment at the 3f Fe site. For FeMnP_0.33Ga_0.67, the pDOS of Fe is still asymmetric and has a certain local moment. While the bonding characteristics between Mn and Fe significantly change during the phase transition, only the spin-down channels of Fe and Mn have obvious overlap in the pDOS peaks.

Fig. 5 Calculated pDOS of the FeMnP_1−xGa_x compounds. (a) Ferromagnetic state of FeMnP_0.67Ga_0.33, (b) ferromagnetic state of FeMnP_0.33Ga_0.67. (c) Antiferromagnetic state of FeMnP_0.67Ga_0.33. (d) Antiferromagnetic state of FeMnP_0.33Ga_0.67.

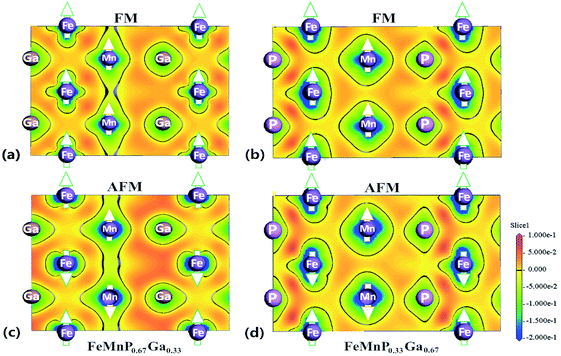
Fig. 6 shows the charge redistribution characteristics with the FM–PM transition. Comparing the CDD in the ac plane of FeMnP_0.67Ga_0.33 in the FM (Fig. 6(a)) and AFM (Fig. 6(c)) states, there is significant redistribution of electrons around Fe. However, no significant electronic redistribution close to Fe is detected for FeMnP_0.33Ga_0.67. These results indicate that occupation of P atoms on different sites is crucially important for the magnetic properties of this family of compounds. Surprisingly, the electronic distribution between Fe(↓) and Mn atoms with different magnetic polarization is symmetric for AFM FeMnP_0.67Ga_0.33 (Fig. 6(c)). However, asymmetric electronic distribution between Fe(↓) atoms and Mn(↑) and Mn(↓) atoms is observed for FeMnP_0.33Ga_0.67, where the magnetic moment of 3f Fe survives during the phase transition. There is more electron density between Fe(↓) and Mn(↓) atoms than between Fe(↓) and Mn(↑) atoms. This picture indicates that the 3f-Fe site of FeMnP_0.67Ga_0.33 cannot show spin polarization in the AFM states.

Fig. 6 CDD of FeMnP_1−xGa_x compounds in the FM and AFM states. (a) Ferromagnetic state of FeMnP_0.67Ga_0.33, (b) ferromagnetic state of FeMnP_0.33Ga_0.67. (c) Antiferromagnetic state of FeMnP_0.67Ga_0.33. (d) Antiferromagnetic state of FeMnP_0.33Ga_0.67.

From the viewpoint of the energetics,^17,51 FeMnP_0.67Ga_0.33 in the AFM state shows shrinkage in the basal plane, and thus a large overlap in the electron cloud between Fe and P occurs. Hence, the kinetic energy, which is lower for the spin-degenerate states and leads to a decrease of the magnetic moment, becomes the dominant term in the total energy. Asymmetric electronic distribution in the rectangle formed by two Mn atoms and two P atoms is also detected, indicating the strong influence of the magnetic order in the electronic distribution.

Comparing CDD in Fig. 6(a) and (c), denser charge is observed around Ga for AFM state, indicating that Ga–Fe and Ga–Mn bonding is strengthened. In other words, the redistribution of charge around Ga is responsible for the splitting and right shift of optical mode (∼10 THz) of Ga in AFM state. Due to the shrinkage of Fe–P distance in AFM state, the covalent like interaction between Fe and P become stronger (CDD between Fe and P become much denser for AFM state) and thus the vibration frequency of optical mode of P and Fe increased reasonably from ∼11.5 THz for FM state to ∼13 THz for AFM state.

Thermodynamic properties

Materials for magnetic refrigeration usually work under constant pressure and elevated temperature. Therefore, the Gibbs free energy of compounds with different magnetic order are calculated and compared for elevating temperature to determine T_c.²⁶ The Gibbs free energy is expressed as
where m represents the FM or AFM magnetic state. The vibrational free energy was estimated by the Debye model,⁴⁵ and the free energy of thermal electronic excitation was calculated within the single electron excitation picture.⁴¹

Another term that should be taken into account for the PM state is the magnetic entropy. The static energy of the PM state was simulated with an ordered AFM cell and did not include the entropy contribution from magnetic disorder. The magnetic entropy of the PM state can be estimated using the mean-field approximation:⁵² , where μ_i is the magnetic moment at the ith site. The total Gibbs free energy of the PM state then becomes G_tot(P,T) = G(P,T,AFM) − S_mT.

The Gibbs free energy difference ΔG(P,T) = G(P,T,AFM) − G(P,T,FM) − S_mT was calculated for FeMnP_1−xGa_x as a function of temperature. ΔG(P,T) for FeMnP_0.67Ge_0.33 is also shown in Fig. 7(a) for comparison. ΔG(P,T) gradually decreases and intersects with the abscissa axis at a certain temperature, which defines T_c, as shown in Fig. 7(a). The decrease of ΔG(P,T) at elevated temperature is mainly from magnetic entropy, but the non-constant slope of ΔG(P,T) suggests that the anharmonic effect is still playing a considerable role.

Fig. 7 Calculated Gibbs free energy G (a), entropy S (b), specific heat at constant pressure C_P (c), and linear CTE (d) as a function of temperature.

The predicted T_c for FeMnP_0.67Ge_0.33 is 590 K, which is close to the measured T_c = 405 K for FeMnP_0.67Ge_0.33 compounds and T_c = 580 K for FeMnP_0.5Ge_0.5 compounds,^44,53 verifying that the present scheme can give a reliable prediction of T_c. The difference between experiment and theory could be ascribed to the missing entropy contributions from spin wave excitation and phonon–phonon interactions. The T_c values of FeMnP_1−xGa_x are 500 and 770 K for x = 0.33 and 0.67, respectively, indicating T_c increases as a function of the Ga concentration. Similar characteristics have also been found for Fe₂P_1−xSi_x,⁵⁴ FeMnP_1−xSi_x,¹⁶ and FeMnP_1−xGe_x (ref. 46 and 47) compounds.

The temperature dependence of the total entropy of the compounds is plotted in Fig. 7(b). The entropy change of FeMnP_0.67Ge_0.33 around the phase transition is ΔS = 66.69 J K⁻¹ kg⁻¹, which is comparable with the experimental value of 49.74 J K⁻¹ kg⁻¹ for Fe_1.1Mn_0.9P_0.8Ge_0.2 at T_c = 278 K.⁴⁶ FeMnP_0.67Ga_0.33 exhibits an entropy change of ΔS = 69.34 J K⁻¹ kg⁻¹ around T_c, which is similar in magnitude to ΔS of FeMnP_0.67Ge_0.33 and close to the experimental value for FeMnP_0.67Si_0.33 of ΔS = 58.6 J K⁻¹ kg⁻¹.⁵⁵ FeMnP_0.33Ga_0.67 shows a much larger entropy change than FeMnP_0.67Ga_0.33 of ΔS = 89.26 J K⁻¹ kg⁻¹.

The entropy change can be divided into the vibrational and magnetic entropy changes: ΔS = ΔS_vib + ΔS_m. Here, the contribution of thermal electronic excitation is omitted because it is too small to have a measurable effect. For FeMnP_0.67Ga_0.33 and FeMnP_0.67Ge_0.33, the ΔS_vib values are −2.78 and −4.56 J K⁻¹ kg⁻¹ for the FM–PM transition, respectively. And ΔS_vib = −20.4 J K⁻¹ kg⁻¹ for FeMnP_0.33Ga_0.67, and thus adding the magnetic entropy term ΔS_m the total entropy change becomes 89.26 J K⁻¹ kg⁻¹. Therefore, the magnetic entropy is playing major role on the entropy change of the compounds. And further, the decrease in the vibrational entropy is partially account for the relatively higher T_c for FeMnP_1−xGa_x and FeMnP_1−xGe_x compounds than that of FeMnP_1−xSi_x.^26,27

Fig. 7(c) and (d) shows the temperature dependence of the heat capacity under constant pressure and the linear CTE, respectively. They are discontinuous at T_c, which is a feature of first-order phase transitions. For first-order phase transition, the latent heat is defined as L = ΔS × T_c. The estimated latent heats for FeMnP_1−xGa_x are 34.67 (x = 0.33) and 68.73 kJ kg⁻¹ (x = 0.67), and the value for FeMnP_0.67Ge_0.33 is 39.35 kJ kg⁻¹.

The jump in the CTE does not contradict with experimental observations of a very small volume change of ∼1% at T_c for FeMnP_1−xSi_x and FeMnP_1−xGe_x compounds.²⁴ Assuming that FeMnP_0.67Ge_0.33 is in full FM order just before the phase transition and in the PM state just above T_c, the volume per unit formula at T_c = 590 K for FM order is 38.83 ų and that for AFM order is 38.57 ų. The change in volume is at most ∼1%, which is still in line with experimental findings. Similar results were obtained for the FeMnP_1−xGa_x compounds.

Conclusions

Density functional theory was used to investigate the mechanical and thermophysical properties of Fe₂P-type FeMnP_1−xT_x (T = Ga, Ge; x = 0.33, 0.67) compounds, and thus identify the possibility of substituting phosphorus with gallium rather than silicon or germanium and obtaining GMC compounds with better mechanical stability with FM to PM phase transitions. The predicted formation energies, elastic constants and phonon spectra show that the different magnetic states of the hexagonal phase of FeMnP_1−xGa_x are energetically and mechanically stable. The predicted magnetic moment, Curie temperature, and entropy change of FeMnP_0.67Ga_0.33 are very close to those of FeMnP_0.67Ge_0.33, a well-known GMC compounds. Therefore, it is expected that FeMnP_1−xGa_x could be a candidate for room temperature magnetic refrigeration.

The relatively large single crystalline elastic constants show the mechanical stability of this family of compounds in both the FM and AFM states. This ensures the long-term applicability of FeMnP_1−xGa_x in magnetic refrigeration facilities under repeated thermal and magnetic cycles. Both FeMnP_0.67Ga_0.33 and FeMnP_0.67Ge_0.33 show good ductility in the FM state. However, their AFM states are brittle. Conversely, the FM states of FeMnP_0.33Ga_0.67 and FeMnP_0.33Ge_0.67 are brittle and their AFM states exhibit good ductility. However, it is expected that the occupation disorder of P and Ga/Ge could increase the ductility of the compounds in the AFM states. Our DFT calculations indicate that elements like Ga with three valence electrons could also be alloyed into the hexagonal phase of FeMn-based Fe₂P type GMC compounds. Experimental synthesis of FeMnP_1−xGa_x compounds, and thus verification of their magnetocaloric properties, is expected.

Acknowledgements

The authors acknowledge financial support from the National Natural Science Foundation of China (grant numbers 11464037 and 50901039) and the Inner Mongolia Natural Science Foundation (grant number 2016MS0113), and the support from NJYT-12-B07.

Notes and references

1. K. A. Gschneidner Jr, V. K. Pecharsky and A. O. Tsokol, Rep. Prog. Phys., 2005, 68, 1479–1539.
2. A. Smith, C. Bahl, R. Bjork, K. Engelbrecht, K. K. Nielsen and N. Pryds, Adv. Energy Mater., 2012, 2, 1288–1318.
3. O. Tegus, E. Brück, K. H. J. Buschow and F. R. de Boer, Nature, 2002, 415, 150–152.
4. E. Brück, O. Tegus, D. T. C. Thanh and K. H. J. Buschow, J. Magn. Magn. Mater., 2007, 310, 2793–2799.
5. E. Brück, O. Tegus, L. Zhang, X. W. Li, F. R. de Boer and K. H. J. Buschow, J. Alloys Compd., 2004, 383, 32–36.
6. L. Song, G. F. Wang, Z. Q. Ou, O. Haschaolu, O. Tegus, E. Brück and K. H. J. Buschow, J. Alloys Compd., 2009, 474, 388–390.
7. N. T. Trung, Z. Q. Ou, T. J. Gortenmulder, O. Tegus, K. H. J. Buschow and E. Brück, Appl. Phys. Lett., 2009, 94, 102513.
8. N. H. Dung, Z. Q. Ou, L. Caron, L. Zhang, D. T. C. Thanh, G. A. de Wijs, R. A. de Groot, K. H. J. Buschow and E. Brück, Adv. Energy Mater., 2011, 1, 1215–1219.
9. V. Hoglin, M. S. Andersson, T. Sarkar, P. Nordblad and M. Sahlberg, J. Magn. Magn. Mater., 2015, 374, 455–458.
10. Z. Gercsi, E. K. Delczeg-Czirjak, L. Vitos, A. S. Wills, A. Daoud-Aladine and K. G. Sandeman, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 024417.
11. N. H. Dung, L. Zhang, Z. Q. Ou and E. Brück, Appl. Phys. Lett., 2011, 99, 092511.
12. F. Guillou, G. Porcari, H. Yibole, N. van Dijk and E. Brück, Adv. Mater., 2014, 26, 2671–2675.
13. S. Berri, J. Supercond. Novel Magn., 2016, 29, 1309–1315.
14. P. Roy, E. Torun and R. A. de Groot, Phys. Rev. B, 2016, 93, 094110.
15. L. Caron, M. Hudl, N. H. Hoglin, C. P. Gomez, M. Sahlberg, E. Brück, Y. Andersson and P. Nordblad, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 094440.
16. V. Hoglin, J. Cedervall, M. S. Andersson, T. Sarkar, M. Hudl, P. Nordblad, Y. Andersson and M. Sahlberg, RSC Adv., 2015, 5, 8278–8284.
17. M. Hudl, P. Nordblad, T. Bjorkman, O. Eriksson, L. Haggstrom, M. Sahlberg, Y. Andersson, E. K. Delczeg-Czirjak and L. Vitos, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 134420.
18. X. F. Miao, L. Caron, P. Roy, N. H. Dung, L. Zhang, W. A. Kockelmann, R. A. de Groot, N. H. van Dijk and E. Brück, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 174429.
19. H. Yibole, F. Guillou, L. Caron, E. Jimenez, F. M. F. de Groot, P. Roy, R. de Groot and E. Brück, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 014429.
20. F. Guillou, K. Ollefs, F. Wilhelm and A. Rogalev, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 224427.
21. H. Wang, Z. D. Zhang, R. Q. Wu and L. Z. Sun, Acta Mater., 2013, 61, 2919–2925.
22. S. Berri, J. Magn. Magn. Mater., 2016, 401, 667–672.
23. E. Brück, Handb. Magn. Mater., 2007, 17, 235–291.
24. E. Brück, J. Phys. D: Appl. Phys., 2005, 38, 381–391.
25. M. J. Neish, M. P. Oxley, J. Guo, B. C. Sales, L. J. Allen and M. F. Chisholm, Phys. Rev. Lett., 2015, 114, 106101.
26. D. T. Cam Thanh, E. Brück, O. Tegus, J. Klaasse and K. Buschow, J. Magn. Magn. Mater., 2007, 310, e1012–e1014.
27. X. Moya, S. Kar-Narayan and N. D. Mathur, Nat. Mater., 2014, 13, 439–450.
28. P. Roy, E. Torun and R. A. de Groot, Phys. Rev. B, 2016, 93, 165101.
29. M. E. Gruner, W. Keune, B. Roldan Cuenya, C. Weis, J. Landers, S. I. Makarov, D. Klar, M. Y. Hu, E. E. Alp, J. Zhao, M. Krautz, O. Gutfleisch and H. Wende, Phys. Rev. Lett., 2015, 114, 057202.
30. X. F. Miao, L. Caron, J. Cedervall, P. C. M. Gubbens, P. D. de Réotier, A. Yaouanc, F. Qian, A. R. Wildes, H. Luetkens, A. Amato, N. K. van Dijk and E. Brück, Phys. Rev. B, 2016, 94, 014426.
31. P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953–17979.
32. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871.
33. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
34. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
35. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
36. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
37. S. Berri, Chin. Phys. B, 2017, 55, 195–202.
38. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
39. F. D. Murnaghan, Proc. Natl. Acad. Sci. U. S. A., 1994, 244–247.
40. L. Vitos, Computational Quantum Mechanics for Materials Engineers: the EMTO Method and Applications, Springer-Verlag, 2007, pp. 107–113.
41. G. Grimvall, Thermophysical Properties of Materials, Elsevier Science B V, 1999, pp. 27–40.
42. A. Togo, L. Chaput, I. Tanaka and G. Hug, Phys. Rev. B, 2010, 81, 174301.
43. J. Slater, Introduction to Chemical Physics, McGraw-Hill, 1939, vol. 152, pp. 488–489.
44. B. Wurentuya, S. Ma and O. Tegus, et al., J. Phys.: Condens. Matter , submitted.
45. A. Otero-de-la-Roza, D. Abbasi-Perez and V. Luana, Comput. Phys. Commun., 2011, 182, 2232–2248.
46. M. Yue, H. G. Zhang, D. M. Liu and J. X. Zhang, Chin. Phys. B, 2015, 24, 017505.
47. D. Liu, M. Yue, J. X. Zhang, T. M. McQueen, J. W. Lynn, X. L. Wang, Y. Chen, J. Y. Li, R. J. Cava, X. B. Liu, Z. Altounian and Q. Huang, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 014435.
48. S. F. Pugh, Philosophical Magazine, 1954, 45, 823–843.
49. H. L. Zhang, M. P. J. Punkkinen, B. Johansson, S. Hertzman and L. Vitos, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 184105.
50. A. R. Mackintosh and O. K. Anderson, Electrons at the Fermi Surface, Cambridge University Press, 1980, pp. 149–224.
51. G. J. Li, W. Li, S. Schönecker, X. Q. Li, E. K. Delczeg-Czirjak, Y. O. Kvashnin, O. Eriksson, B. Johansson and L. Vitos, Appl. Phys. Lett., 2014, 105, 262405.
52. G. Grimvall, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 12300–12301.
53. X. W. Li, O. Tegus, L. Zhang, W. Dagula, E. Brück, K. H. J. Buschow and F. R. de Boer, IEEE Trans. Magn., 2003, 39, 3148–3150.
54. P. Jernberg, A. A. Yousif, L. Häggström and Y. Andersson, J. Solid State Chem., 1984, 53, 313–322.
55. Z. Ou, Magnetic structure and phase formation of magnetocaloric Mn-Fe-P-X compounds, Delft University of Technology, 2013.

---