In vitro–in vivo and pharmacokinetic evaluation of solid lipid nanoparticles of furosemide using Gastroplus™

Abstract

In this work, we conducted pharmacokinetic studies and established the in vitro and in vivo correlation (IVIVC) of furosemide (FRS) loaded solid lipid nanoparticles (FSLN). A bioanalytical method using RP-HPLC was developed and validated to evaluate the pharmacokinetic properties of FSLN and FRS suspension (FSP). The pharmacokinetic parameters were analyzed using various pharmacokinetic compartment models (one, two and three) and non-compartmental analysis. The IVIVC was accomplished using numerical deconvolution (single Weibull and double Weibull), the Wagner-Nelson (one compartment model) and the Loo-Riegelman method (two and three compartment model) via GastroPlus™ software. The method was developed and successfully validated for the quantification of FRS in plasma. An enhancement in C_max from 2261.7 ng mL⁻¹ (FSP) to 3604.7 ng mL⁻¹ FSLN, and AUC_0→24 from 10 130 ng h mL⁻¹ (FSP) to 17 077 ng h mL⁻¹ (FSLN) indicated an enhancement in the oral bioavailability of FRS when given in the form of SLN. In the statistical analysis, the Loo-Riegelman method was found to be the best-fit deconvolution method for establishing the IVIVC of FSLN. As an innovative approach, having more restrictive and conclusive IVIVC, the entire plasma profile of the convoluted and observed was divided into three time phases, (i) 0 → 0.5 h, (ii) 0.5 → 3 h and (iii) 3 → 24 h, and statistically analyzed to demonstrate IVIVC. The study showed that FSLN could be a potential drug carrier for the delivery of FRS with improved bioavailability.

---

Introduction

Oral formulations are the most widely used and desirable dosage forms because of their ease of administration, accompanied by greater convenience to patients. However, they are subject to low systemic absorption of drug candidates belonging to class II of the biopharmaceutical classification system (BCS) and have solubility issues. Furthermore, the issue of formulation development is even more challenging for the BCS class IV drug candidates that are both less soluble and have poor permeability issues, causing low bioavailability and high intra- and inter-subject variability.^1,2

With the advent of nanomedicine, continuous research efforts are underway to minimize undesirable side effects and improve the therapeutic efficacy.³ A plethora of research approaches (e.g. polymeric nanoparticles, liposomes, nanocrystals, nanoemulsions, micelles and mixed micelles) have been employed to overcome problems associated with BCS II and IV drugs.^3,4 However, deficiencies of harmless polymers with regulatory compliance and high price have restricted the extensive applications of polymeric nanoparticles in clinical medicine.^5–7 To overcome these restrictions, lipids have been used as a material of choice for the development of solid lipid nanoparticles (SLN).^8,9 Analogous to nanoemulsions, SLN make up a colloidal drug delivery system that employs solidified lipids, such as high melting fatty acids, glycerides or waxes.^3,10 Furthermore, SLNs are stabilized by using surfactant(s) (natural/synthetic) that are biocompatible and biodegradable and belong to the generally recognized as safe (GRAS) category.^3,11,12 Additionally, SLNs have some other advantages such as (i) enhanced bio-absorption of encapsulated drug, (ii) ability to modify the drug release behavior, (iii) improvement of tissue distribution and (iv) drug targeting via surface engineering.^13,14

Furosemide (FRS) is a high ceiling diuretic given in the management of edema linked with cardiac, renal, and hepatic failure and the treatment of hypertension. It is a BCS class IV drug because of its low solubility and low permeability, which result in reduced bioavailability.^15,16 FRS acts by inhibiting the reabsorption of sodium and chloride in the ascending loop of Henle and distal tubules. Peak plasma drug concentrations (C_max) occur between 1 to 1.5 h, with variable bioavailability and low permeability, which result in reduced bioavailability.^15–17 The dosage form, underlying disease conditions and food substantially influence the rate and extent of bioavailability following oral administration. The permeability and drug delivery related concerns of FRS have been addressed using various formulation maneuvers. The recent studies employing nanosuspensions,¹⁸ chitosan coated liposomes,¹⁹ colloidal carriers (niosome encapsulated self-microemulsifying drug delivery system),²⁰ polyamidoamine dendrimer complexes,²¹ proniosomes,²² supramolecular complexes, solid dispersion, co-crystals, and micro-emulsions are well documented in literature.^23–26

The first objective of this investigation was to develop and validate a bioanalytical method to estimate the pharmacokinetics of FRS loaded SLN (FSLN) and FRS suspensions (FSP) using the RP-HPLC method. The second objective was to compare the pharmacokinetics of FSLN and FSP and select the appropriate pharmacokinetic model, followed by in vitro and in vivo correlation (IVIVC). We used the GastroPlus™ software to evaluate the pharmacokinetic parameters of FSLN and FSP. Furthermore, the IVIVCPlus™ module of the GastroPlus™ software was used to estimate the correlation function to select the best-fit IVIVC model employing various deconvolution methods. The plasma drug concentration–time profile was reconstructed from in vitro drug release data and then predicted in order to establish the correlation between in vitro drug release and systemic availability (convolution).

Materials and methods

Materials

Furosemide and Venlafaxine hydrochloride (as an internal standard, IS) were obtained from Unicure India Limited, India, as a gift sample. Compritol 888 ATO (CMP), a mixture of mono-, di- and triglycerides of behenic acid (glyceryl behenate), was a kind gift from Gattefossé, France. Cremophor RH 40 (CRH40), a mixture of hydrogenated vegetable fatty acids with a chain length of 10–18 carbon atoms, was a generous gift from BASF, UK. HPLC grade acetonitrile, methanol and analytical grade hydrochloric acid, sodium hydroxide pellets and sodium dihydrogen phosphate were obtained from Merck India Limited, Mumbai, India. An electronic balance (AG-135, Mettler-Toledo, Germany), pH meter (pH Testr, Eutech Instruments, Singapore) and a sonicator (Takashi, Japan, Tokyo) were also used.

Methods

Preparation of SLN. The SLN was fabricated using the phase-inversion temperature (PIT) technique as reported earlier.¹⁰ Accurately weighed CMP and CRH40 were heated in a glass beaker and mixed together until a clear mixture was obtained (10 °C above the melting point of the solid lipid). Hot aqueous phase (Millipore water), was slowly added with continuous stirring on a magnetic stirrer (IKA, Germany) at 350 rpm, then it was allowed to cool to room temperature to obtain a transparent colloidal dispersion of SLN.

Chromatographic system and conditions. The chromatographic system used to perform the method development and validation consisted of an LC-20AD quaternary pump, an SPD-M20A photodiode array detector (PDA), and SIL 20 AC autosampler, connected to a communication & bus module CBM 20A (Shimadzu, Kyoto, Japan). Chromatographic analysis was performed on an Agilent column (150 × 4.6 mm internal diameter, 5.0 μm particle size) Agilent Technologies, California, USA. Separation was performed using a mobile phase of sodium dihydrogen phosphate (20 mM, pH 4): acetonitrile (35 : 65, v/v) at a flow rate of 1.0 mL min⁻¹. The eluent was monitored using a PDA detector at wavelength 229 nm for FRS. The column was maintained at ambient temperature and an injection volume of 50.0 μL was used.

Preparation of stock and standards. The primary stock solution was prepared by dissolving 10 mg of FRS in a 10 mL volumetric flask containing methanol, and the volume was made up to 10 mL to obtain the stock of 1 mg mL⁻¹ of FRS in methanol. Plasma standards of FRS in the range of 100–5000 ng mL⁻¹ were prepared. Afterwards, four quality control (QC) samples were prepared at the lower limit of quantification (LLOQ = 105.6 ng mL⁻¹), low (LQC = 302 ng mL⁻¹), medium (MQC = 2520 ng mL⁻¹) and high (HQC = 4200 ng mL⁻¹) quality control levels. The prepared bio-samples were then processed as described in the sample preparation section and analyzed by the proposed method with an IS of 1 ppm.

Analyte extraction from plasma. The solid phase extraction (SPE) method was used to extract the analyte from the plasma sample. Oasis HLB (Hydrophilic Lipophilic Balance) cartridges, supplied by Waters Corporation, USA, were used. The cartridges were conditioned with methanol (1 mL) and equilibrated with deionized water (1 mL). Mobile phase (200 μL) and 5% v/v formic acid (100 μL) were added to the prepared sample (500 μL). After vortexing for 5 min the sample was loaded onto the cartridges. The cartridges were then washed with 5% methanolic aqueous solution (1 mL) and finally eluted with methanol (1 mL). The eluates were evaporated to dryness. The obtained residues were then reconstituted in 500 μL of the mobile phase.

Drug administration and sample collection. To study the pharmacokinetic parameters of the FSLN and FSP, male Sprague-Dawley rats (200–250 gm) were used. The rats were randomly separated into two groups: the control group to be treated by FSP, and the test group treated by FSLN; each consisting of six animals. The animals were housed under standard conditions (24 ± 2 °C, 60% RH), and water was given ad libitum. No food was supplied 18 hours prior to dosing. This study was performed in accordance with CPCSEA (Committee for the Purpose of Control and Supervision of Experiments on Animals) guidelines and was approved by the Institutional Animal Ethics Committee (BIT/PH/IAEC/10/2015) of BIT, Mesra. The control group received FSP (prepared in 0.5% sodium carboxymethyl cellulose), while the test group was treated by FSLN at a dosing rate of 15 mg kg⁻¹.²⁷ The blood samples were collected in centrifuge tubes containing K₂EDTA (1.8 mg mL⁻¹, NOVAC POLYMED, supplied by Poly Medicure Ltd., Faridabad, India), from the retro-orbital plexus using heparinized glass capillary tubes at different time points (0, 0.25, 0.5, 1.5, 2, 3, 6, 9, 12 and 24 h) after dosing. The blood samples were centrifuged at 3000 rpm for 15 min to separate the plasma. Isolated plasma samples were stored at −20 °C until further analysis.

Method validation

Selectivity. The test for selectivity was carried out using six different lots of blank rat plasma batches processed by the SPE method and analyzed to determine the extent to which endogenous substances may contribute to interferences for the analyte. The blank plasma sample was compared with that containing FRS, at the LLOQ. The aim of performing the selectivity study with blank plasma samples was to ensure the quality of the results of sample analysis. The area of the interfering peak at the retention time of the analyte should be <20% of the peak area response of the analyte in the LLOQ sample.^28,29

Linearity and range. The various concentrations of standard solutions were prepared in the range of 105.6–5000 ng mL⁻¹, containing 1 ppm of IS to assess the linearity. A standard curve was prepared after plotting the peak area ratio of FRS and IS versus plasma concentration of the analyte. Linearity was evaluated by analyzing the standard curve.³⁰

Accuracy and precision. The accuracy of the analytical method was assessed by comparing a known concentration of FRS to the experimental value. The accuracy and precision of the analytical method in the individual samples were assessed by analyzing QC samples (LLOQC, LQC, MQC and HQC). After processing, each QC sample was estimated in six replicates. The accuracy was expressed as % bias, and precision was determined as the percent coefficient of variation (% CV). The acceptance criterion of precision at each QC level is less than ±15.0% deviation from nominal concentration (except LLOQ, where it must not be more than ±20.0%).²⁸

Recovery. The extraction recovery study for FRS was carried out at three QC levels, low (LQC = 302 ng mL⁻¹), medium (MQC = 2520 ng mL⁻¹) and high (HQC = 4200 ng mL⁻¹), in rat plasma, with six replicates. Recovery was calculated by comparing the area responses of the extracted samples with the responses of the analyte from post-extracted blank plasma samples spiked with analytes at equivalent concentrations.^28,31

Sensitivity. The developed bioanalytical method must be sensitive enough to measure the analyte to enable proper estimation of the pharmacokinetic parameters. Sensitivity was analyzed in six lots of screened plasma and spiked LLOQ samples. The lowest standard on the calibration curve was to be accepted as the LLOQ, if the analyte response was at least five times greater than that of the extracted blank plasma. The mean value of accuracy at LLOQ should not deviate by more than 25%, and precision determined should not exceed 25% of the % CV.²⁸

Pharmacokinetic analysis. Pharmacokinetic (PK) parameters were assessed using the PKPlus™ module of Gastroplus™ (version 9.0, Simulations Plus Inc., Lancaster, CA, USA). Various pharmacokinetic parameters were evaluated, including peak plasma drug concentration (C_max), the time to achieve peak plasma drug concentration (t_max), area under the plasma drug concentration–time curve from time zero to time t (AUC_0→t), AUC from time zero to infinity (AUC_0→∞), area under the moment curve (AUMC), clearance (CL), half-life (t_1/2), mean residence time (MRT), absorption rate constant (K_a), elimination rate constant (K_el), volume of distribution (V_d) and micro-constants. Additionally, various pharmacokinetic compartment models (one, two and three compartments) were statistically analyzed and the best-fit model was selected on the basis of the correlation coefficient (R²) and other statistical tests like Schwartz Criterion (SC) and Akaike Information Criterion (AIC).^30,31

Assessment of in vitro–in vivo correlation. The process of establishing IVIVC was done by importing the in vitro release data for the optimized formulation in silico, according to our previous publication,¹⁰ followed by in vivo plasma concentration data, into the IVIVC module of GastroPlus™ software. Deconvolution methods (DM) implemented for establishing correlation were Wager-Nelson-1-compartment (WN1C), Loo-Riegelman-2-compartment (LR2C), Loo-Riegelman-3-compartment (LR3C), Numerical deconvolution single Weibull (NDSW) and numerical deconvolution double Weibull (NDDW). Prior to executing the deconvolution methods, the plasma concentration–time data were analysed by one compartment, two compartment and three compartment methods, using the PKPlus™ module of GastroPlus™, and the relevant PK parameters were exported in the pharmacokinetic tab of the software. After exporting, deconvolution was carried out followed by correlation establishment (linear, power function, second and third order polynomial). The best correlation function was then automatically selected on the basis of R², standard error of prediction (SEP) and mean absolute error (MAE). Finally, convolution was carried out and statistically evaluated using the mean absolute percent prediction error (MAPPE) for two main PK parameters i.e., C_max and AUC. Additionally, the true plasma drug concentration–time profile and reconstructed plasma drug concentration were statistically studied.

Results and discussion

Fabrication of SLN

In this study, an experimental assembly was developed to fabricate the FSLN with small particle size and low polydispersity index, using the phase inversion temperature technique. Phase inversion is related to a change in the nature of the surfactant from water-soluble to oil-soluble. At the inversion point, surfactants have an approximately equal affinity towards both oil and aqueous phases; consequently, the interfacial tension is very much reduced and results in the formation of an emulsion with low globule size, i.e., a nanoemulsion.^32,33 The size of the FSLN was determined by transmission electron microscopy (Fig. 1A) and dynamic light scattering (25.54 nm) (Fig. 1B), and both methods were in good agreement, as discussed in our previous report.¹⁰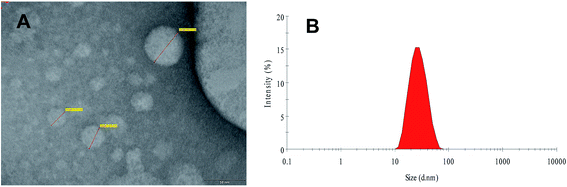

Fig. 1 Transmission electron microscopic image (A) and size distribution curve of FRSM loaded SLN (B) [reproduced with permission¹⁰].

Furthermore, it was observed that at elevated temperature, the turbid pre-emulsion (w/o) inverts to the stable emulsion (o/w). In this study, initially, a turbid pre-emulsion was obtained by heating and then slowly cooling to room temperature, by using a non-ionic ethoxylated surfactant (CRH40), whose surface interfacial characteristics at the globule interface are considerably temperature dependent.¹⁰ Generally, with increasing temperature, ethoxylated surfactant molecules have the tendency for dehydration of the polyethylene oxide chain.^32,33 The SLN produced from the PIT method showed good physical properties and stability over time.¹⁰

Method development

Successful analysis of an analyte in biological fluids relies on the optimization of sample preparation, chromatographic separation, and interference free detection. In the process of the bioanalytical method development for FRS, mobile phase composition and flow rate were optimized by trying different aqueous and non-aqueous phase combinations at different flow rates. Phosphate buffer solution (PBS) (pH 3–7 and 20 mM) and ammonium acetate buffers (pH 3–7 and 10 mM) were studied in combination with acetonitrile (50, 60, and 70%). Mobile phase composition and flow rate were finally selected based on the criteria of peak properties and sensitivity. Among the explored buffers, phosphate buffer gave a peak with good symmetry and resolution, hence it was selected for the method development.

Increasing the concentration of buffer (>20 mM) led to the peak tailing, eventually resulting in poor resolution. In contrast to this, using reduced concentrations (<20 mM) of buffer decreased the sensitivity in this setting. The optimum concentration of phosphate buffer was found to be 20 mM, which gave better resolution with enhanced sensitivity. A variable effect of pH was also observed. On increasing the pH of the mobile phase, a negative charge was increased on the stationary phase, which decreased the retention of FRS, causing faster elution. On the other hand, decreasing the pH caused a reduction of negative charge on the stationary phase, which resulted in a decrease in the elution of the analyte. A suitable pH of 4 was set after many trials and errors; finally, the optimized mobile phase was found to be 35 : 65 (PBS : ACN). In this experiment, venlafaxine HCl (IS) was eluted first, followed by FRS, with the retention times of 3.5 min and 5.5 min, respectively, and a runtime of 6 minutes. The flow rate was maintained at 1 mL min⁻¹ and absorbance was observed at 229 nm. Recovery of the analyte was carried out by solid phase extraction; therefore, the optimized extraction procedure should exhibit consistent recovery at all QC levels without any interference from endogenous components. Columns used in HPLC are produced in a variety of length and internal diameter combinations, with various particle sizes. HPLC column dimensions (length and internal diameter) generally affect the sensitivity, speed of analysis, and consequently the efficiency. The selection of column by taking dimensions into consideration wholly depends on the application, analysis, preparative methods, and the number of analytes present in the single analysate; hence, the column with the required dimensions to achieve an efficient, sensitive and fast analysis should be selected.^34,35 The length of the column has an important effect on the efficiency of chromatographic separation, i.e., the efficiency increases with column length; a two fold increase in the column length enhances the resolution by a factor of 1.4. Short column length will give short run times with diminished backpressure, which has limited applications. Longer columns generally exhibit better resolution, but with increased analysis time and the excess use of mobile phase (solvents), resulting in the higher cost of analysis.^34,35 In this study, a 15 cm column was used, which showed good resolution and less retention time (Fig. 2). Particle size is of prime importance when selecting the stationary phase. On reducing the particle size, the efficiency of the column increases. Smaller particle size contributes to improved separation, but at the cost of increased column backpressure. Larger particles reduce the efficiency of the column, which results in poor separation. Herein, a column with 5 μm particle size was employed in order to achieve better efficiency by avoiding the issues related to backpressure.^34,35 Columns with small internal diameters show high sensitivity, but with an increase in back pressure. On the other hand, larger diameter columns require higher flow rates, resulting in the use of the larger volume of the mobile phase. To troubleshoot the problem of back pressure and wastage of solvents, a column with internal diameter of 4.6 mm was selected for better sensitivity. In an effort to increase the sensitivity of the method, different wavelengths were used, 235, 254 and 280 nm, for detection purposes.³⁶ In our study, the better sensitivity with lower interference for FRS was achieved at wavelength 229 nm. The performance of the HPLC assay was assessed by selectivity, linearity, precision, accuracy, sensitivity, extraction recovery, and freeze–thaw stability of extracts.

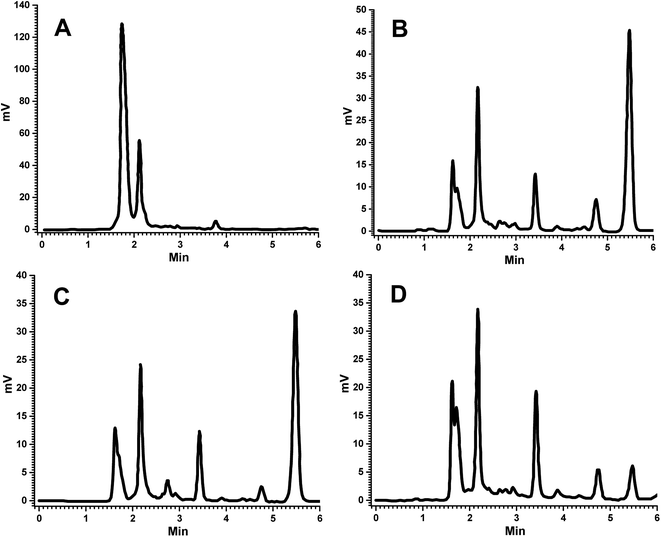Fig. 2 Representative chromatograms of (A) blank plasma, (B) FSLN in plasma, (C) FRS suspension in plasma at 1.5 h and (D) FRSM peak in plasma at LLOQ.

Method validation

The bioanalytical method was developed and then validated for quantification of FRS in the plasma samples. The determination of the selectivity of a bioanalytical method is of paramount importance to distinguish and calculate the analyte in the presence of other possible interfering components in the biological samples, such as endogenous materials, metabolites, medication and other xenobiotics related substances; therefore, some corroboration is needed to confirm that the compound quantified is the intended molecule.^28,29 For this purpose, the analysis of blank samples of the plasma were performed. Samples were tested for selectivity, which was estimated at the LLOQ. No significant interference was observed at the retention of FRS and IS in various plasma lots. No endogenous component showed any interfering peak at the retention time of FRS and IS (Fig. 2A and B). Hence, the absence of any peak response in the blank plasma sample at IS and analyte retention time revealed the selectivity of the method, which is in good conformity with that of USFDA and EMEA guidelines (generally, the absence of interfering components is accepted where the response is less than 20% of the lower limit of quantification for the analyte and 5% for the internal standard). Comparison of the chromatograms of the blank (Fig. 2A) and spiked sample (Fig. 2D) indicated the selectivity of the method. Furthermore, the representative chromatograms of plasma collected at 1.5 h of FSLN and FSP after oral administration are depicted in Fig. 2B and C, respectively, indicating no interference of plasma components at retention time. In this study, the method proposed is selective in the quantification of FRS in the rat plasma.

To prepare a standard curve in the range of 105.6 ng mL⁻¹ to 5000 ng mL⁻¹, FRS concentration was plotted against peak area ratio of FRS to IS (area of analyte/area of IS). The standard curve was depicted by the linear equation, y = 0.0006x + 0.0353, with the correlation coefficient R² = 0.997. The lower limit of quantification (LLOQ) of the developed method was 105.6 ng mL⁻¹. The intra-day accuracy of FRS ranged from 90.74% to 105.35%, at four QC levels (LLOQC, LQC, MQC and HQC) with the precision varying from 0.54% to 6.22% (Table 1). Furthermore, the inter-day accuracy of FRS varied from 97.03% to 104.58%, of the same QC levels with the precision in the range of 0.65–5.66% (Table 1). The outcomes of the tested plasma samples were in good agreement and within the acceptable limits of accuracy and precision as per the USFDA and EMEA guidelines for bioanalytical method validation. The average concentration must be less than 15% of the nominal values for the QC samples, except for the LLOQ, which must be less than 20% of the nominal value as per the USFDA and EMEA guidelines for bioanalytical method validation.^28,29 In this method, the achieved LLOQ of 105.6 ng mL⁻¹ was validated to match the sensitivity requirements. The precision value obtained was less than 10%, and the accuracy value was less than ±5%, which is in good agreement with that of USFDA guidelines.²⁸

Table 1 Intra and inter-day accuracy and precision of furosemide in rat plasma (n = 6)

Levels	Spiked concentration (ng mL^−1)	Mean concentration found (ng mL^−1) ± SD	Accuracy (%)	% bias	Precision (% CV)
Intra-day
LLOQC	105.6	108.80 ± 6.77	103.03	3.03	6.22
LQC	302	310.83 ± 12.78	102.92	2.92	4.11
MQC	2520	2286.83 ± 25.08	90.74	−9.25	1.10
HQC	4200	4424.56 ± 24.01	105.35	5.35	0.54
Inter-day
LLOQC	105.6	108.63 ± 5.37	102.87	2.86	4.94
LQC	302	297.11 ± 16.83	98.38	−1.62	5.66
MQC	2520	2445.35 ± 27.54	97.03	−2.96	1.12
HQC	4200	4392.16 ± 28.61	104.58	4.58	0.65

---

Various plasma extraction methods were assessed to obtain clean plasma samples in order to avoid probable interferences. The protein precipitation procedure offers a simple and rapid method of extraction with clean plasma, but exhibits a considerable degree of unacceptability, due to high levels of noise.³⁰ The liquid–liquid extraction (LLE) method, however, resulted in a clean sample with comparatively less noise, but the extraction method was tedious, involving multiple steps of extraction. Moreover, in the present work, rat plasma was used as a biological sample, where the volume of plasma for the study was low; therefore, the LLE technique was not adopted. The solid phase extraction (SPE) method was employed, having the advantages of extracts with considerably lower lipid levels (which is an important cause of noise and interference in chromatograms), and higher and consistent extraction recovery of the analyte and IS. The solid phase extraction (SPE) method, when used for the extraction of plasma samples using Oasis HLB cartridges, unquestionably gives comparatively clean extracts with very low noise, and shows high sensitivity with low plasma volume. The cartridge used consisted of hydrophilic–lipophilic balanced water-wettable reversed phase sorbent for a wide spectrum of requirements. It was made from a definite ratio of two monomers, the lipophilic divinyl benzene and hydrophilic N-vinyl pyrrolidone, which offer better reversed phase capacity with neutral polar hook for enhanced retention of polar analytes. Additional advantages of the HLB cartridge are that it can be employed at extremes of pH and in a wide range of solvents. Furthermore, the water wettable sorbent in the cartridge showed better retention capacity for a broad range of analytes, despite the sorbent bed running dry during conditioning and/or sample loading, leading to the conclusion that this SPE method is more robust and rugged, avoiding the need for repeat preparation. The advantages of the HLB cartridge also include higher retention capacity; i.e., more analytes are retained with fewer breakthroughs, further improving the reproducibility of the extraction procedure. As per the USFDA guidelines, the recovery need not be 100%, but the level of recovery of the analyte must be reproducible and consistent at all QC levels (LQC, MQC, and HQC).²⁸ The method of extraction explained in the present work provides a rapid technique for separating the analytes from the plasma sample. Here, the proposed method demonstrates consistent recovery of FRS from the rat plasma sample. The mean absolute recovery ranged from 43.9–58.6% for FRS at three QC levels (LQC, MQC, and HQC), with the precision varying from 3.5% to 5.1% (Table 2).

Table 2 Extraction recovery and freeze thaw stability of furosemide in rat plasma (n = 6)

Extraction recovery
Levels	% mean recovery (±SD)	% CV
LQC	47.30 (±1.66)	3.5
MQC	43.90 (±2.15)	4.9
HQC	58.60 (±3.00)	5.1

---

Freeze thaw stability
Levels	Spiked concentration (ng mL^−1)	Initial mean concentration found (ng mL^−1) ± SD	% CV	% accuracy	Final mean concentration found (ng mL^−1) ± SD	% CV	% accuracy	% absolute stability
LQC	302	306.23 (8.94)	2.92	101.40	301.17 (10.23)	3.40	99.72	98.35
MQC	2520	2496.12 (25.51)	1.02	99.05	2415.54 (39.84)	1.65	95.85	96.77
HQC	4200	4261.46 (23.83)	0.60	101.46	4194.83 (28.34)	0.68	99.87	98.44

---

The analyte stability is an important parameter in plasma samples, which should be assessed by the developed bioanalytical method and must mimic the analysis conditions that could be faced during handling and sample preparation.³⁰ The absolute stability of the FRS at LQC, MQC, and HQC, covering the freeze/thaw conditions, is shown in Table 2. The FRS spiked in rat plasma was stable after three freeze–thaw cycles over time. The freshly prepared QC samples showed acceptable accuracy in the range of 99.05–101.46%, and precision from 2.92% to 0.60% (Table 2). Freshly prepared QC samples were then compared with the sample after freeze–thawing; the accuracy ranged from of 95.85–99.87%, with the precision from 3.4% to 0.68% (Table 2). The percent absolute stability after freeze–thawing was in the range of 96.77–98.44%.

This method was demonstrated to be reproducible and accurate for the estimation of FRS in rat plasma.

Pharmacokinetics study

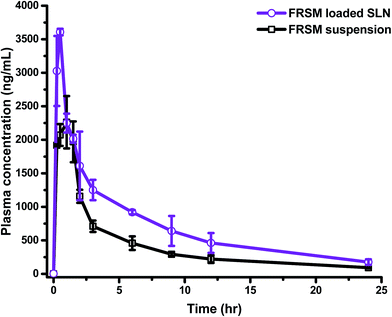
Generally, drug carriers go into the organs away from the target site, and are then carried to the desired organ through blood circulation. Absorption of the drug from its site of administration is a necessary process before going into the systemic circulation. The rate and extent of drug absorption differ, depending on the route of administration/application, the physiological environment of the site of drug uptake, and absorption mechanism. These preconditions are applicable for all routes of drug administration, except for i.v. administration, where the drug is already in circulation, and topical application in which the drug is applied to the desired site directly. In the gastrointestinal tract (GIT), the drug passes through a layer of epithelial cells, having tight junctions, before entering into the systemic circulation; hence, drugs face a greater difficulty in drug absorption after oral administration.³⁷ To overcome the problems of poor absorption and low bioavailability of drugs, due to low solubility and/or low permeability, such molecules need to be circulated by employing various nanocarriers.

The developed and validated bioanalytical method was fruitfully implemented to evaluate the pharmacokinetic parameters after oral administration of FSLN and FSP. The comparative plasma drug concentration–time profile of FSLN and FSP is depicted in Fig. 3. Furthermore, the pharmacokinetic parameters evaluated by non-compartmental and compartmental analysis (one, two and three) are tabulated in Table 3.

Fig. 3 The comparative plasma concentration time profile of furosemide loaded SLN and suspension.

Table 3 Pharmacokinetic parameters of FRSM loaded SLN and FRSM suspension obtained after non-compartmental and compartmental analysis by the PKPlus™ module of GastroPlus™ software (n = 3)

PK parameters	FSLN				FSP
	NCA	One Comp	Two Comp	Three Comp	NCA	One Comp	Two Comp	Three Comp
Cmax (ng mL^−1)	3604.7	—	—	—	2261.7	—	—	—
tmax (h)	0.5	—	—	—	1	—	—	—
AUC0–t (ng h mL^−1)	17 077	—	—	—	10 130	—	—	—
AUC0–∞ (ng h mL^−1)	19 200	—	—	—	11 400	—	—	—
AUMC (ng h^2 mL^−1)	190 100	—	—	—	106 400	—	—	—
t1/2 (h)	—	6.222	7.61	38.79	—	5.103	8.233	27.77
MRT (h)	9.903	—	—	—	9.333	—	—	—
Kel (h^−1)	0.081	—	—	—	0.073	—	—	—
CL (L h^−1)	0.234	0.174	0.24	0.193	1.754	1.388	1.801	1.548
Vd (L)	—	1.564	—	—	—	10.22	—	—
Vc (L)	—	—	0.96	0.808	—	—	2.859	3.205
Vss (L)	2.322	—	—	—	16.37	—	—	—
Ka (h^−1)	—	7.34 × 10^4	5.733	4.491	—	334.2	1.504	1.728
K10 (h^−1)	—	0.111	0.25	0.239	—	0.136	0.630	0.483
K12 (h^−1)	—	—	0.625	0.992	—	—	1.004	0.821
K21 (h^−1)	—	—	0.449	0.711	—	—	0.239	0.348
K13 (h^−1)	—	—	—	0.107	—	—	—	0.211
K31 (h^−1)	—	—	—	0.028	—	—	—	0.038
R^2	—	0.7401	0.9834	0.9867	—	0.756	0.971	0.9699
AIC	—	−21.84	−53.15	−53.92	—	−19.03	−43.98	−42.48
SC	—	−20.65	−51.16	−51.13	—	−17.84	−41.99	−39.69

---

The non-compartmental method is more versatile, in that it does not assume any specific compartmental model and produces accurate outcomes. This method is widely used in bioequivalence studies that have the advantage of minimal assumptions about the data-generating process, which has been collected in a very structured way.³⁸ The pharmacokinetic compartment modeling consists of a description of the fate of a drug with respect to time. The benefit of compartmental over some non-compartmental analyses is the ability to predict the concentration at any given time point. In the one compartment model, the time course of plasma drug concentration, estimated after the administration can be adequately explained by considering the body as a single kinetically homogenous unit, which has no barriers to the movement of the drug, with a first order disposition process (Fig. 4A). In the two and three compartment models, the drug concentration is estimated as function of time, after assuming the body as comprised of highly vascular organs/tissue (central compartment) or less vascular organs (peripheral compartment) after the extravascular/intravascular administration (Fig. 4B and C). Fig. 4 demonstrates the relative comparison and fitness of superposition between true and simulated plasma drug concentrations (using one, two and three compartment models) and the respective compartment models are displayed in the inset of Fig. 4. The drug molecules generally leave the site of administration (after absorption) to come into the central compartment; from there they are transported to the peripheral compartment and exchanged (distribution) and then eliminated irreversibly (excreted and metabolized). This movement of drug from one compartment to another compartment is characterized by transfer rate constants (micro-constants).³⁰ An increase in C_max from 2261.7 ng mL⁻¹ (FSP) to 3604.7 ng mL⁻¹ (FSLN) (1.59 fold), and AUC_0→24 from 10 130 ng h mL⁻¹ (FSP) to 17 077 ng h mL⁻¹ (FSLN) (1.69 fold) confirmed an enhancement in the oral bioavailability of FRS when ferried via SLNs. The obvious explanation for the bioavailability enhancement of FRS is the developed carrier system (SLN), containing lipid as the main constituent. Lipids are usually known for the enhancement of oral absorption of the drug, and can be formulated in the carriers with low particle size.³⁹ However, factors like enzymes, pH of GIT, ionic strength, ingested food materials, residence time, absorption window, solubility and rate of dissolution also influence the delivery of the drug.⁴⁰ Other than these factors, SLN play an active role in the augmentation of oral uptake after bringing the drug in the solubilized form into the GIT subsequent to the formation of micelles, because of the breakdown of the triglycerides into the surface active mono- and diacylglycerols with the action of lipases, which further stimulate the bile salt secretion endogenously.^41,42 Other factors contributing to enhanced oral bioavailability can be linked to the reduction of particle size, which facilitates the absorption rate of the drug. Various researchers have demonstrated that an increase in the surface area associated with a decrease in particle size leads to adequate and consistent absorption in the GIT.^43–45 In a previous study, AUC_0→24 and C_max values of FRS nanosuspension were approximately 1.38- and 1.68-fold greater than that of the pure drug, respectively.¹⁸ In addition to the micellar pathway, the oral uptake of drug molecules might be synergized by the absorption mechanism of fatty acids, di- and monoacylglycerols, which are incorporated into the SLN inherently, or formed after the degradation of triglycerides by GI lipases. In addition to the solubilization, the presence of surfactants in the formulation may also provide an adequate environment for the enhancement of bioavailability. Cremophor RH40 (ethoxylated hydrogenated castor oil), the surfactant employed in the synthesis of SLN, is known to enhance the absorption by inhibiting the P-glycoprotein efflux pump.⁴⁶

Fig. 4 Overlay plot of true (red circle) and simulated (black curve) plasma concentration time profile of FSLN using (A) one compartment, (B) two compartment and (C) three compartment models. The inset shows the corresponding pharmacokinetics models.

Furthermore, an increase in the absorption rate constant (K_a) from 1.504 h⁻¹ (FSP) to 5.733 h⁻¹ (FSLN) (3.81 fold), confirmed the enhanced rate of absorption of FRS when ferried through SLN. It is the rate of absorption that determines the time required for the administered drug to attain an effective plasma concentration and may therefore influence the onset time of the drug effect. Hence, the rate of absorption affects both the peak plasma concentration (C_max) and the time it takes to reach this peak (t_max). Another important pharmacokinetic parameter, the mean residence time (MRT), is the arithmetic mean of the amount of time that a drug molecule exists in the body before being eliminated. The reason behind the estimation of the mean residence time is that each molecule spends a different amount of time in the body, with some molecules lasting for a very short period and others lasting longer.⁴⁷ In this study, the MRT of FSLN was 9.903 h, while FSP exhibited 9.333 h (Table 3), probably due to the protein binding of SLN, which creates a more hydrophilic particle surface and thus prolongs the circulation time.⁴⁸ On the basis of statistical analysis, (R² closer to 1.0, and smaller AIC and SC), the one compartment model was found to be poorly fitted to describe the pharmacokinetics of FSLN as well as FRS. The R², AIC and SC of one the compartment model for FSLN and FSP were found to be 0.7401, −21.84, −20.65 and 0.756, −19.03, −17.84, respectively (Table 3), implying non dependence on one compartment and suggesting the movement of the drug across less vascular organs (peripheral compartments) from plasma. This was also confirmed by the non-superimposable observed and simulated plasma concentration profile of FSLN (Fig. 4A). The fitted compartment model corresponded to two and three, as can be observed by the superposition of observed and simulated plasma concentration profiles (Fig. 4B and C) as well as from statistical analysis (Table 3). The R², AIC and SC of the two compartment model for FSLN and FSP were found to be 0.9834, −53.15, −51.16 and 0.971, −43.98, −41.99, respectively (Table 3). Similarly, the R², AIC and SC of the three compartment model for FSLN and FSP were found to be 0.9867, −53.92, −51.13 and 0.9699, −42.48, −39.69, respectively (Table 3).

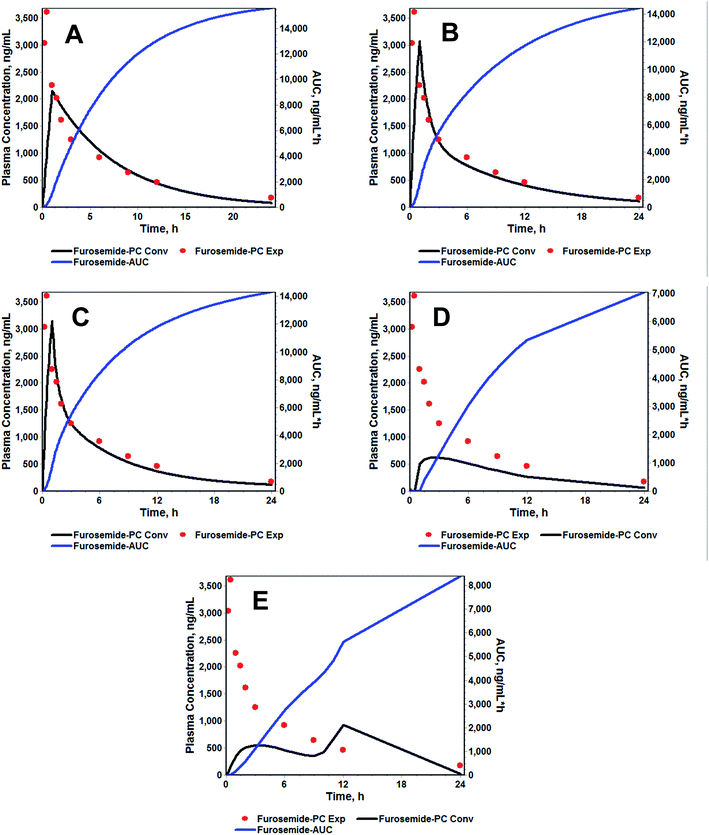
In vitro–in vivo correlation (IVIVC)

For the modified-release dosage form, IVIVC is an important design component. It is defined as a predictive mathematical model describing the relationship between an in vitro property of a dosage form and a relevant in vivo response.⁴⁹ The drug release data generally provide the information on in vitro characteristics, whereas the in vivo properties are depicted by a plasma drug concentration–time profile. The data obtained from in vitro and in vivo studies are mathematically treated in order to set up a correlation; generally, a correlation is predicted when the in vitro drug release from the pharmaceutical formulation is the step that determines the absorption kinetics.³⁰ Correlation between the in vitro and in vivo properties is mathematically represented by nonlinear or linear methods.³¹ However, the plasma drug concentration data is not correlated as such to the in vitro drug release data; first, the data have to be transformed to the underlying fraction absorbed in vivo, either by compartmental analysis, or the linear method. The linear method is generally established mathematically by employing the deconvolution/convolution method. The numerical deconvolution/convolution method is generally selected, since it does not make any pharmacokinetic model assumptions. By employing a compartmental approach, the rate of in vivo absorption can be calculated when the pharmacokinetic parameters of the drug are known.⁵⁰

For the estimation of the plasma drug concentrations (output function), if dissolution data (input function) is available, the procedure is known as convolution; on the other hand, i.e., obtaining a fraction absorbed in vivo, if plasma drug concentrations are provided, the procedure will be called deconvolution.^30,31 On the basis of in vitro drug release profiles and pharmacokinetic data of the FSLN, the IVIVC was evaluated using GastroPlus™ (IVIVCPlus™ module). The deconvolution approaches used were WN1C, LR2C, LR3C, NDSW and NDDW to calculate the fraction of drug absorbed. Fig. 5 demonstrates the extent of superposition between observed and convoluted plasma drug concentration–time profile, along with the relation between AUC and time using WN1C (Fig. 5A), LR2C (Fig. 5B), LR3C (Fig. 5C), NDSW (Fig. 5D) and NDDW (Fig. 5E). The correlation function associated with each deconvolution approach with percent prediction error (PPE) between observed and predicted values of C_max and AUC_0→t is tabulated in Table 4. The statistics of reconstructed plasma drug concentration–time profiles from convolution are demonstrated by R², SEP, and MAE (Table 4). The Wagner-Nelson method (one-compartment pharmacokinetic model) is depicted by the equation, 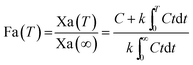, where, ‘Fa(T)’ is the fraction of drug bioavailable at time (T), ‘Xa(T)’ and ‘Xa(∞)’ are cumulative amounts of drug absorbed up to time ‘T’ and infinity, ‘C’ is the concentration of drug in the central compartment at time ‘T’, and ‘k’ is the first order elimination rate constant. Here, the power correlation function was best fitted as demonstrated by the equation y = 0.805(x)^5.74×10−6 where, x = fraction released in vitro and y = fraction absorbed in vivo. The observed and predicted C_max using WN1C was found to be 3604.7 ng mL⁻¹ and 2157.0 ng mL⁻¹, respectively, with the PPE of 40.17 (Table 4). PPE was calculated according to the following equation: .

Fig. 5 IVIVC indicating the correlation of observed and convoluted plasma drug concentration time profile using the following methods: (A) Wagner-Nelson method; (B) Loo-Riegelman method, two compartment; (C) Loo-Riegelman method, three compartment; (D) numerical deconvolution single Weibull; (E) numerical deconvolution double Weibull.

Table 4 Correlation function and statistical analysis of the in vitro–in vivo correlation of furosemide loaded solid lipid nanoparticles using various methods and models

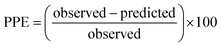IVIVC methods	Correlation function	Pharmacokinetic parameter						Statistical analysis
		Cmax (ng mL^−1)			AUC0–t (ng h mL^−1)			R^2	SEP	MAE
		Obs.	Pred.	PPE	Obs.	Pred.	PPE
Wagner-Nelson method (one compartment)	Power	3604.7	2157	40.17	17 077	15 600	8.65	0.38	1064.2	541.5
Numerical deconvolution single Weibull	3^rd order polynomial		624	82.69		7039	58.78	0.336	1618.5	1123.9
Numerical deconvolution double Weibull	Power		932	74.15		8393	50.85	0.327	1619.2	1182.3
Loo-Riegelman method (two compartment)	Power		3069	14.87		14 400	15.67	0.555	851.5	484.7
Loo-Riegelman method (three compartment)	Power		3150	12.62		14 300	16.26	0.587	804.5	454.5

---

Similarly, the observed and predicted AUC_0→24 of FSLN using the same method were 17 077 ng h mL⁻¹ and 15 600 ng h mL⁻¹, respectively, with the PPE of 8.65% (Table 4). Furthermore, statistics of reconstructed plasma drug concentration–time profile showed poor fitting, indicated by small R² (0.38), and large SEP (1064.2) and MAE (541.5) (Table 4). The poor IVIVC exhibited by the WN1C deconvolution approach is readily understood, since the pharmacokinetic profile of optimized formulation of FRS showed the two/three compartment model fit rather than the one compartment model. However, considering the small PPE of 8.65% for AUC using WN1C, it becomes difficult to conclude that IVIVC is acceptable in terms of AUC alone. Hence, in order to be more restrictive and conclusive, we divided the entire profile into three time phases, (i) 0 → 0.5 h, (ii) 0.5 → 3 h and (iii) 3 → 24 h, for both convoluted and observed plasma concentration profiles with respective time intervals, and AUC was calculated for each phase. In order to avoid any confusion, we did not describe these phases as absorption phase, distributive phase, and elimination phase, because the Wagner-Nelson method is applicable to one compartment kinetics without any distributive phase assumption (no peripheral compartment). In addition, care was taken to include the same number of time points (according to the experimentally collected plasma time points) to avoid any bias. This was essential because when there are many time points within the given range, the AUC calculated using trapezoidal rule gives a much better approximation. This is because when there are many time points, the consecutive distance between two points becomes more linear, rather than a curve, which fits the geometry of a trapezoid, where all sides are linear. It is worth noting that we have digitized the convoluted profile and we had the liberty to select ‘n’ plasma time points. However, we selected time points that corresponded only to the actual collected time intervals for the obvious reason stated above. PPE for each phase was calculated and analyzed (Table 5). The PPE of AUC_0→0.5, AUC_0.5→3 and AUC_3→24 using WN1C were found to be 49.23, 3.71 and 16.63, respectively, suggesting only AUC_0.5→3 was best approximated to the observed AUC (PPE = 3.71) within time limits from 0.5 to 3 hours. The analysis precludes the PPE of 8.65 of overall AUC_0→24 on the basis of higher PPE for both AUC_0→0.5 (PPE = 49.23) and AUC_3→24 (PPE = 16.63).

Table 5 Area under curve analysis of true and convoluted plasma concentration time profiles at different time intervals

Deconvolution method	AUC(0→0.5)		AUC(0.5→3)		AUC(3→24)
	Observed	Convoluted	Observed	Convoluted	Observed	Convoluted
Wagner-Nelson method (one compartment)	1206.50	612.50	4860.91	5041.13	11 009.97	9179.04
PPE	49.23		3.71		16.63
Loo-Reigelman (two compartment)	1206.50	553.23	4860.91	4911.29	11 009.97	9483.86
PPE	54.15		1.04		13.86
Loo-Reigelman (three compartment)	1206.50	584.28	4860.91	4990.33	11 009.97	9280.65
PPE	51.57		2.66		15.71

---

The correlation functions of LR2C and LR3C were exhibited by power functions and were mathematically represented as y = 1.195 × x^0.163 and y = 1.186 × x^0.163, respectively. As can be observed in the equation, the power term associated with ‘x’ is same in both the equations, while the coefficient terms vary only in second and third decimals, suggesting no significant difference. The predicted C_max using LR2C and LR3C were found to be 3069 ng mL⁻¹ and 3150 ng mL⁻¹, respectively, with PPE less than 15.0 as compared to the observed C_max (Table 4) (PPE using LR2C and LR3C for C_max were 14.87 and 12.62, respectively). Similarly, the predicted AUC using LR2C and LR3C were found to be 14 400 ng h mL⁻¹ and 14 300 ng h mL⁻¹, respectively, with PPE of 15.67 and 16.26, respectively. The PPE of AUC_0→0.5, AUC_0.5→3 and AUC_3→24 using LR2C and LR3C was found to be 54.15, 1.04, 13.86 and 51.57, 2.66, 15.71, respectively. If we correspond AUC_0→0.5, AUC_0.5→3 and AUC_3→24 to absorption, distribution and elimination phase (which is more suited in Loo-Reigelman method as compared to Wagner-Nelson, which includes the provision of peripheral compartments), than it can be interpreted that for both LR2C and LR3C, observed and predicted AUC within the absorption phase was not correlated (on the basis of high PPE of > 50). This may be because of the smaller number of plasma drug concentration–time points (at 0.5 and 1.0 h) taken during the absorption phase. The convoluted AUC during the distribution and elimination phase for LR2C were 4911.29 ng h mL⁻¹ and 9483.86 ng h mL⁻¹, respectively, with PPE less than 15.0 (PPE of AUC during the distribution and elimination phases were 1.04 and 13.86, respectively) (Table 5). Similarly, the convoluted AUC of the distribution and elimination phases for (LR3C were 4990.33 ng h mL⁻¹ and 9280.65 ng h mL⁻¹, with PPE of 2.66 and 15.71, respectively) (Table 5). The statistics for the reconstructed plasma drug concentration–time profile represented by R², SEP, and MAE for LR2C and LR3C ranging between 0.555 and 0.587, 804.5–851.5, 454.5–484.7 (Table 4) suggesting marginally small difference between LR2C and LR3C. This can also be observed by better superposition of the convoluted and observed plasma concentration–time profile (except for absorption phase). However, if we strictly compare only the AUC of the distribution and elimination phase, LR2C seems to have an edge over LR3C, on the basis of the least PPE of 1.04 and 13.86 (for LR2C) vis-à-vis PPE of 2.66 and 15.71 (for LR3C).

In the present study, we also explored NDSW and NDDW for possible IVIVC methodology, however, both these models were not appropriate, as observed by the non-superposition of observed and convoluted plasma drug concentration profiles (Fig. 5D and E). NDSW and NDDW were expressed by a 3^rd order polynomial function; (y = −0.042 + 1.2 × 10⁻³ × x + 2.086 × x² − 1.096 × x³) and power function; y = 1.042 × x^1.646, respectively (Table 4). The numerical deconvolution method uses the inverse operation of the convolution integral and the principle of superposition, which states that the response is dose proportional and time invariant, to calculate an input rate function.^51,52 The PPE of C_max and AUC for NDSW and NDDW ranged between 74.15–82.69 and 50.85–58.78, respectively, suggesting the model's inconclusive reliability. The observation is further bolstered by the poor statistical analysis of reconstructed plasma drug concentration–time profile (R²: 0.327–0.336; SEP: 1618.5–1619.2; MAE: 1123.9–1182.3) for LR2C and LR3C.

LR2C and LR3C were the preferred deconvolution approaches to establish the IVIVC of optimized FSLN on the basis of the overall PPE, SEP, MAE and R².

Conclusion

A simple, sensitive bioanalytical method was developed using RP-HPLC. The unknown plasma concentrations of FRS were successfully determined in the plasma samples of rats by using the solid phase extraction technique. Here, venlafaxine HCl was used as an internal standard and linearity was obtained in the range of 105.6–5000 ng mL⁻¹, with the R² = 0.997. The method was found to be selective and sensitive. The GastroPlus™ software was employed to evaluate various pharmacokinetic parameters using compartmental and non-compartmental approaches. FSLN, as compared to FSP, showed an increase in C_max, AUC, and K_a, with the decrease in t_max depicting the enhanced bioavailability and fast onset of action. IVIVC was established with the help of IVIVCPlus™, an IVIVC toolkit of GastroPlus™. On the statistical analysis of various IVIVC approaches, Loo-Riegelman was found to be the best fit. The study showed that SLN could be a potential drug carrier to ferry the FRS with enhanced bioavailability, after oral administration.

Conflicts of interest

The authors report no conflicts of interest.

Ethical statement

Animals used in the study were maintained in accordance to CPCSEA (Committee for the Purpose of Control and Supervision of Experiments on Animals) guidelines and was approved by Institutional Animal Ethics Committee (BIT/PH/IAEC/10/2015) of BIT, Mesra. No Human subjects were involved in the study.

Acknowledgements

Authors thank University Grants Commission (UGC), Government of India, New Delhi, for providing financial assistance for this research under UGC-BSR scheme (F-7-32/2007-BSR). Sandeep Kumar Singh acknowledges Pukyong National University, Busan, South Korea (National Research Foundation of Korea, Ministry of Education, grant no. 2012R1A6A1028677) for providing postdoctoral fellowship and Birla Institute of Technology for granting the study leave.

References

1. P. Fasinu, V. Pillay, V. M. Ndesendo, L. C. du Toit and Y. E. Choonara, Biopharm. Drug Dispos., 2011, 32, 185–209.
2. S. K. Singh, P. R. P. Verma and B. Razdan, Drug Dev. Ind. Pharm., 2010, 36, 933–945.
3. W. Mehnert and K. Mäder, Adv. Drug Delivery Rev., 2001, 47, 165–196.
4. S. K. Singh, P. R. P. Verma and B. Razdan, Pharm. Dev. Technol., 2010, 15, 469–483.
5. D. F. Emerich and C. G. Thanos, J. Drug Targeting, 2007, 15, 163–183.
6. V. Wagner, A. Dullaart, A.-K. Bock and A. Zweck, Nat. Biotechnol., 2006, 24, 1211.
7. L. Zhang, F. Gu, J. Chan, A. Wang, R. Langer and O. Farokhzad, Clin. Pharmacol. Ther., 2008, 83, 761–769.
8. E. Souto, S. Wissing, C. Barbosa and R. Müller, Int. J. Pharm., 2004, 278, 71–77.
9. R. H. Muller, M. Radtke and S. A. Wissing, Adv. Drug Delivery Rev., 2002, 54(suppl. 1), S131–S155.
10. H. Ali and S. K. Singh, Part. Sci. Technol., 2017 DOI:10.1080/02726351.2017.1295293.
11. M. Ghadiri, S. Fatemi, A. Vatanara, D. Doroud, A. R. Najafabadi, M. Darabi and A. A. Rahimi, Int. J. Pharm., 2012, 424, 128–137.
12. H. Vaghasiya, A. Kumar and K. Sawant, Eur. J. Pharm. Sci., 2013, 49, 311–322.
13. T. Yuan, L. Qin, Z. Wang, J. Nie, Z. Guo, G. Li and C. Wu, Asian J. Pharm. Sci., 2013, 8, 39–47.
14. T. Göppert and R. Müller, Int. J. Pharm., 2005, 302, 172–186.
15. G. E. Granero, M. R. Longhi, M. J. Mora, H. E. Junginger, K. K. Midha, V. P. Shah, S. Stavchansky, J. B. Dressman and D. M. Barends, J. Pharm. Sci., 2010, 99, 2544–2556.
16. C.-Y. Wu and L. Z. Benet, Pharm. Res., 2005, 22, 11–23.
17. H. Ali, S. K. Singh and P. R. P. Verma, J. Pharm. Invest., 2015, 45, 385–398.
18. B. P. Sahu and M. K. Das, J. Nanopart. Res., 2014, 16, 2360.
19. I. Vural, C. Sarisozen and S. S. Olmez, J. Biomed. Nanotechnol., 2011, 7, 426–430.
20. A. A. Sultan, S. A. El-Gizawy, M. A. Osman and G. M. El Maghraby, J. Pharm. Pharmacol., 2016, 68, 324–332.
21. B. Devarakonda, D. P. Otto, A. Judefeind, R. A. Hill and M. M. de Villiers, Int. J. Pharm., 2007, 345, 142–153.
22. A. Azeem, N. Jain, Z. Iqbal, F. J. Ahmad, M. Aqil and S. Talegaonkar, Pharm. Dev. Technol., 2008, 13, 155–163.
23. S.-C. Shin and J. Kim, Int. J. Pharm., 2003, 251, 79–84.
24. N. R. Goud, S. Gangavaram, K. Suresh, S. Pal, S. G. Manjunatha, S. Nambiar and A. Nangia, J. Pharm. Sci., 2012, 101, 664–680.
25. C. Garnero, A. K. Chattah and M. Longhi, J. Pharm. Biomed. Anal., 2014, 95, 139–145.
26. A. Zvonar, K. Berginc, A. Kristl and M. Gašperlin, Int. J. Pharm., 2010, 388, 151–158.
27. L. H. Nielsen, T. Rades and A. Mullertz, Int. J. Pharm., 2015, 490, 334–340.
28. USFDA, Guidance for Industry: Bioanalytical Method Validation, US Department of Health and Human Services, Food and Drug Administration, Center for Drug Evaluation and Research, Center for Veterinary Medicine, New Hampshire Ave., Silver Spring, MD, 2013.
29. E. M. A., Guideline on Bioanalytical Method Validation, Committee for Medicinal Products for Human Use, Churchill Place, Canary Wharf, London, United Kingdom, 2011.
30. S. Verma and S. K. Singh, J. Pharm. Biomed. Anal., 2016, 124, 10–21.
31. J. K. George, S. K. Singh and P. R. P. Verma, Ther. Delivery, 2016, 7, 305–318.
32. D. Morales, J. M. Gutiérrez, M. Garcia-Celma and Y. Solans, Langmuir, 2003, 19, 7196–7200.
33. P. Fernandez, V. André, J. Rieger and A. Kühnle, Colloids Surf., A, 2004, 251, 53–58.
34. D. T. T. Nguyen, D. Guillarme, S. Rudaz and J. L. Veuthey, J. Sep. Sci., 2006, 29, 1836–1848.
35. M. J. Tessalone, CHROMacademy: Paving the Way for Continued Education in Analytical Science, Advanstar Communications Inc., Duluth, MN, USA, 2014.
36. Y. S. El-Saharty, J. Pharm. Biomed. Anal., 2003, 33, 699–709.
37. H. Ali and S. K. Singh, Ther. Delivery, 2016, 7, 691–709.
38. T. Jaki and M. J. Wolfsegger, Stat. Med., 2012, 31, 1059–1073.
39. S. Chakraborty, D. Shukla, B. Mishra and S. Singh, Eur. J. Pharm. Biopharm., 2009, 73, 1–15.
40. Z. Cai, Y. Wang, L. J. Zhu and Z. Q. Liu, Curr. Drug Metab., 2010, 11, 197–207.
41. B. K. Nanjwade, D. J. Patel, R. A. Udhani and F. V. Manvi, Sci. Pharm., 2011, 79, 705–727.
42. C. J. Porter, N. L. Trevaskis and W. N. Charman, Nat. Rev. Drug Discovery, 2007, 6, 231–248.
43. H. Li, X. Zhao, Y. Ma, G. Zhai, L. Li and H. Lou, J. Controlled Release, 2009, 133, 238–244.
44. C. Y. Zhuang, N. Li, M. Wang, X. N. Zhang, W. S. Pan, J. J. Peng, Y. S. Pan and X. Tang, Int. J. Pharm., 2010, 394, 179–185.
45. A. Hanafy, H. Spahn-Langguth, G. Vergnault, P. Grenier, M. Tubic Grozdanis, T. Lenhardt and P. Langguth, Adv. Drug Delivery Rev., 2007, 59, 419–426.
46. Y. Tayrouz, Clin. Pharmacol. Ther., 2003, 73, 397–405.
47. J. Fan and I. A. de Lannoy, Biochem. Pharmacol., 2014, 87, 93–120.
48. M. Rahman, S. Laurent, N. Tawil, L. H. Yahia and M. Mahmoudi, in Protein-Nanoparticle Interactions, Springer, 2013, pp. 21–44.
49. J. Shen and D. J. Burgess, J. Controlled Release, 2015, 219, 644–651.
50. H. Rettig and J. Mysicka, Dissolution Technol., 2008, 15, 6.
51. F. Langenbucher, Eur. J. Pharm. Biopharm., 2003, 56, 429–437.
52. P. Veng-Pedersen, Adv. Drug Delivery Rev., 2001, 48, 265–300.

---