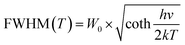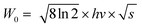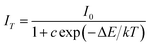DOI:
10.1039/C7RA03813E
(Paper)
RSC Adv., 2017,
7, 27422-27430
Luminescence properties and its red shift of blue-emitting phosphor Na3YSi3O9:Ce3+ for UV LED†
Received
3rd April 2017
, Accepted 4th May 2017
First published on 23rd May 2017
Abstract
A series of Na3YSi3O9:Ce3+ phosphors have been synthesized via a conventional high temperature solid-state reaction. Each crystal structure was characterized by X-ray diffraction (XRD) and refined by the Rietveld method. Luminescence properties of Na3YSi3O9:Ce3+ phosphors such as emission red shifts, fluorescence decay curves, thermal stability, and CIE values were systematically investigated. Upon 300 nm excitation, the emission peaks of Na3YSi3O9:Ce3+ phosphors red shift from 385 nm to 415 nm with Ce3+ concentration increasing from 0.002 to 0.11. Moreover, this red-shift phenomenon also occurs with an excitation wavelength from 270 nm to 340 nm as the Ce3+ concentration determined, which has been explained using the centroid shift and crystal field splitting. The quenching concentration of Ce3+ in the host Na3YSi3O9 is determined to be about 3 mol% and the critical distance is calculated to be about 16.623 Å. The energy dispersion mechanism between Ce3+ ions was verified to be a dipole–dipole interaction. Temperature-dependent luminescence of Na3YSi3O9:0.03Ce3+ from 25 °C to 250 °C was evaluated, and the corresponding activation energy ΔE is 0.277 eV. Not only crystal field splitting but also centroid shift plays an important role in the red-shift of the Na3YSi3O9:Ce3+ phosphors, which may contribute to future research in designing novel solid phosphors by modifying composition of the host lattice to affect crystal field splitting and centroid shift, and then adjusting emission wavelengths to match the purposed application.
1. Introduction
As a new generation of light sources, phosphors converting white-light-emitting diodes (WLEDs) have attracted increasing attention in academic and industrial fields due to advantages such as long lifetime, saving energy, high efficiency, and environmentally friendly character.1,2 Commercially, the most convenient way of creating WLEDs is to combine the yellow-emitting phosphor Y3Al5O12:Ce3+ (YAG:Ce3+) with blue LED chips.3 However, owing to the lack of a red spectral component, WLEDs often have highly correlated color temperature (CCT > 4500 K) and a low color rendering index (CRI, Ra < 75).4–7 An alternative strategy is the combination of near-UV LED chips with red-, green-, and blue-emitting phosphors as a trichromatic approach, which will produce excellent CRI values.8 Therefore, it is very important to develop new phosphors to realize better optical requirements.
Due to its excellent thermal and chemical stability, low cost and excellent water-resistance, silicate materials have been widely studied.9 Na3YSi3O9 crystallized in an orthorhombic system with space group of P212121(19). These compounds possesses a mixed octahedral–tetrahedral framework, where the YO6 octahedrals are isolated from each other by SiO4 tetrahedrals.10 Several research reports on Na3YSi3O9 phosphors have been published, such as Na3YSi3O9:Bi3+,Eu3+ phosphor,11 Na3(Y1−aLna)Si3O9 (Ln = Eu, Tb, Tm) phosphors,10 and Na3YSi3O9:Tm3+,Dy3+ phosphors.12 On the other hand, there is little research information on the Ce3+ doped Na3YSi3O9 phosphor. A Ce3+-activated phosphor often shows high efficiency in many hosts because of a 4f–5d parity allowed electric dipole transition. Moreover, due to the outer shell 5d orbits of Ce3+ ions, the emission band peak is sensitive to the host lattice,13,14 which can be shifted from UV to the visible range; for example, the yellow-orange-emitting CaAlSiN3:Ce3+,13 blue-emitting Ca8La2(PO4)6O2:Ce3+,15 green-emitting CaY2Si2S8:Ce3+,16 and yellow-emitting LaSr2AlO5:Ce3+.17,18 Herein, a series of Ce3+-doped Na3YSi3O9 phosphors were synthesized via a conventional high temperature solid-state reaction. Crystal structures, luminescence properties, decay curves, and thermal stability were systematically investigated. The Na3YSi3O9:Ce3+ phosphor shows blue emission and the emission band peak shifts red with increasing excitation wavelengths and Ce3+ content. Because electronegative vacancies affect charge distribution around the Ce3+ ions, the 5d energy levels shift down; thus, spectra with determined Ce3+ shift red and broaden under different excitation. As Ce3+ concentration increases, the emission shifts red and is ascribed to enhancement of the crystal field strength surrounding Ce3+ ions and the centroid shift of Ce3+ ions. Considering these factors in emission spectra, an interesting experiment may be to design solid solution phosphors via controlling crystal field splitting together with a centroid shift when seeking future novel phosphors.
2. Experimental section
2.1 Materials and synthesis
The Na3YSi3O9:Ce3+ phosphors were prepared via a conventional high temperature solid-state reaction. All starting materials, i.e., Na2CO3 (A.R.), SiO2 (A.R.), Y2O3 (A.R.) and CeO2 (4 N), were weighed according to stoichiometric ratios (Sinopharm Chemical). All raw materials were mixed and ground thoroughly in an agate mortar for 1 h, and then the homogenous mixture was put in an aluminum crucible with a cover. Next, the crucible was put in a muffle furnace with continuous sintering at 1100 °C in a reducing atmosphere for 6 h. The product was cooled down to room temperature naturally, and subsequently pulverized for further measurements.
2.2 Measurement and characterization
The crystal structure of the as-prepared phosphor was determined by X-ray diffraction (XRD) analysis using a Bruker-D8 powder diffractometer (XRD) with Cu Kα (λ = 1.54078 Å). All data were collected over a 2θ range from 10° to 80°. Room temperature excitation and emission spectra were detected using a Hitachi F-4600 spectrophotometer with a 150 W Xe lamp. Temperature-dependent luminescence properties were measure using the same spectrophotometer with a self-made heating attachment and a computer-controlled electric furnace. Decay curves were recorded on a FLS980 fluorescence spectrophotometer with a nanosecond flash nF920 as the excitation resource.
3. Results and discussion
3.1 Phase formation and crystal structure
Fig. 1 shows the XRD pattern of the as-synthesized Na3YSi3O9:0.03Ce3+ phosphor and the standard pattern (ICSD #20774) of Na3YSi3O9. By comparing the diffraction peaks of XRD patterns, the XRD pattern of Na3YSi3O9:0.03Ce3+ agrees well with the standard pattern and no other phase is observed, demonstrating that a single phase of Na3YSi3O9:0.03Ce3+ phosphor has been obtained without any notable impurities. In Na3YSi3O9, the effective ionic radii of Na+ (CN = 6), six-coordinated Y3+ and four-coordinated Si4+ are 1.02 Å, 0.88 Å, and 0.26 Å, while the ionic radii of Ce3+ is 1.01 Å. Considering the ionic radii differences between the doped ions and cations, there may a be potential for Ce3+ ions to occupy both Na+ sites and Y3+ sites in Na3YSi3O9. In fact, according to Bragg's equation 2d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = nλ, the shrinkage of cell volume will lead to an increase of the 2-theta value. When a larger cation is replaced by smaller doping ions, the 2-theta value shifts right.19 The main diffraction peaks shift to a higher angle in the enlarged view from 20° to 35° (Fig. 1), which indicates that Ce3+ ions substituted the position of Na+ sites in the Na3YSi3O9 host lattice.
θ = nλ, the shrinkage of cell volume will lead to an increase of the 2-theta value. When a larger cation is replaced by smaller doping ions, the 2-theta value shifts right.19 The main diffraction peaks shift to a higher angle in the enlarged view from 20° to 35° (Fig. 1), which indicates that Ce3+ ions substituted the position of Na+ sites in the Na3YSi3O9 host lattice.
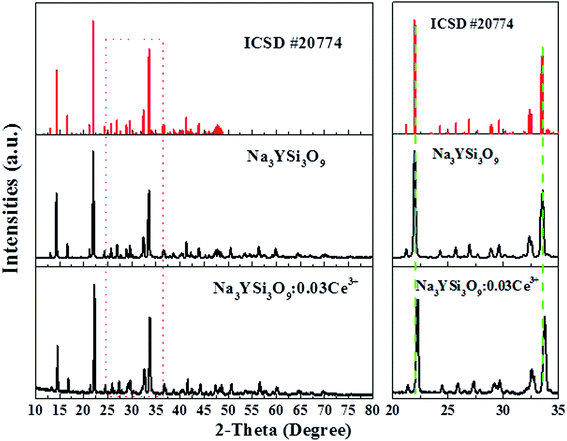 |
| | Fig. 1 Powder XRD pattern of the Na3YSi3O9:0.03Ce3+ phosphor with the standard pattern (ICSD #20774). | |
To further understand phase purity and occupancy of Ce3+ ions, a Rietveld structure refinement of the as-prepared sample was performed using the general structure analysis system (GSAS) program as shown in Fig. 2a.20 The standard Na3YSi3O9 was used as an initial structure model, and the refined parameters, residual factors of un-doped Na3YSi3O9 and Na3YSi3O9:0.03Ce3+ are summarized in Table 1. Results of the Rietveld refinement further demonstrate that the doping of Ce3+ ions did not generate any impurity in Na3YSi3O9. Un-doped Na3YSi3O9 and Na3YSi3O9:0.03Ce3+ crystallized in an orthorhombic system with a space group of P212121(19), and the lattice parameters for Na3YSi3O9:0.03Ce3+ were fitted to be a = 15.0363(4) Å, b = 15.1427(5) Å, c = 15.2095(3) Å, α = β = γ = 90°, V = 3463.08(5) Å3, and Z = 16, and the reliability factors are χ2 = 7.048, Rwp = 17.37% and Rp = 12.81%, while the parameters for un-doped Na3YSi3O9 are a = 15.0384(1) Å, b = 15.1478(0) Å, c = 15.2135(9) Å, α = β = γ = 90°, V = 3465.64(0) Å3, Z = 16, χ2 = 6.560, Rwp = 17.01%, Rp = 12.95%. Comparing the refined parameters of Na3YSi3O9:0.03Ce3+ with the parameters of un-doped Na3YSi3O9, we observed that values of the refined parameters were smaller after doping Ce3+ ions, which is caused by the fact that the larger host cations were replaced by smaller doping ions. The atomic occupancy of Ce and Na is provided in Table S1 in the ESI† which further confirmed that Ce3+ ions occupied the six-coordinated Na+ sites. Fig. 2b presents the coordination spheres of six-coordinated Na+ ions, forming distorted octahedrons with Si4+ ions coordinated by four oxygen atoms in a regular tetrahedron and the Y3+ ions in regular [YO6]9− octahedrons along the a-direction. The distorted [NaO6]11− octahedron connected with the [SiO4]4− tetrahedron and [YO6]9− octahedron by sharing edges or corners to form a three-dimensional framework. Moreover, the distorted [NaO6]11− octahedron connected with another six-coordinated Na+ ion by the O2− point.
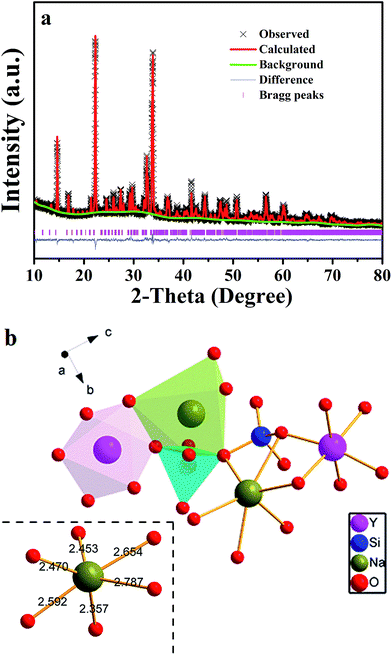 |
| | Fig. 2 (a) Powder XRD pattern of Na3YSi3O9:0.03Ce3+ with its corresponding Rietveld refinement (red solid line) and residuals (blue line in the bottom); (b) the coordination sphere of six-coordinated Na+ in the Na3YSi3O9 host matrix. | |
Table 1 Rietveld refinement and crystal date for Na3YSi3O9 and Na3YSi3O9:0.03Ce3+
| Compound |
Standard Na3YSi3O9 |
Un-doped Na3YSi3O9 |
Na3YSi3O9:0.03Ce3+ |
| Symmetry |
Orthorhombic |
Orthorhombic |
Orthorhombic |
| Space group |
P212121 |
P212121 |
P212121 |
| a (Å) |
15.0330 |
15.0384(1) |
15.0363(4) |
| b (Å) |
15.1420 |
15.1478(0) |
15.1427(5) |
| c (Å) |
15.2130 |
15.2135(9) |
15.2095(3) |
| α (deg) |
90 |
90 |
90 |
| β (deg) |
90 |
90 |
90 |
| γ (deg) |
90 |
90 |
90 |
| V (Å3) |
3462.93 |
3465.64(0) |
3463.08(5) |
| Z |
16 |
16 |
16 |
| Rwp% |
— |
17.01 |
17.37 |
| Rp% |
— |
12.95 |
12.81 |
| χ2 |
— |
6.560 |
7.048 |
3.2 Photoluminescence properties and the red-shift emissions of Na3YSi3O9:Ce3+ phosphors
Photoluminescence emission (PL, λex = 300 nm) and excitation (PLE, λem = 402 nm) spectra of Na3YSi3O9:0.03Ce3+ are depicted in Fig. 3a. The PLE spectrum represents a broad hump from 240 nm to 375 nm, assigned to electron transition from the 4f energy level to different 5d sub-levels of Ce3+ ions. Upon 300 nm excitation, the Na3YSi3O9:0.03Ce3+ phosphor shows a broad emission band from 340 nm to 570 nm peaking at 402 nm, which is attributed to the spin-allowed 5d–4f transitions of Ce3+ ions. For the sake of clarity, the PL asymmetric band de-convoluted by Gaussian functions fit with good approximation with two Gaussian curves peaking at 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 490 cm−1 (∼425 nm) and 25
490 cm−1 (∼425 nm) and 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 544 cm−1 (∼391 nm), as shown in Fig. 3b. The energy difference was calculated to be 2054 cm−1, which is close to that between 2F5/2 and 2F7/2 (generally ≈2000 cm−1).21 Herein, the two Gaussian peaks are ascribed for the transitions from the lowest 5d excited state to the 2F5/2 and 2F7/2 ground states of Ce3+ ions due to spin–orbit coupling. That is to say, there exists only one type of emission center in the Na3YSi3O9 host lattice, which is consistent with Ce3+ ion substituting the six-coordinated Na+ site in Na3YSi3O9.
544 cm−1 (∼391 nm), as shown in Fig. 3b. The energy difference was calculated to be 2054 cm−1, which is close to that between 2F5/2 and 2F7/2 (generally ≈2000 cm−1).21 Herein, the two Gaussian peaks are ascribed for the transitions from the lowest 5d excited state to the 2F5/2 and 2F7/2 ground states of Ce3+ ions due to spin–orbit coupling. That is to say, there exists only one type of emission center in the Na3YSi3O9 host lattice, which is consistent with Ce3+ ion substituting the six-coordinated Na+ site in Na3YSi3O9.
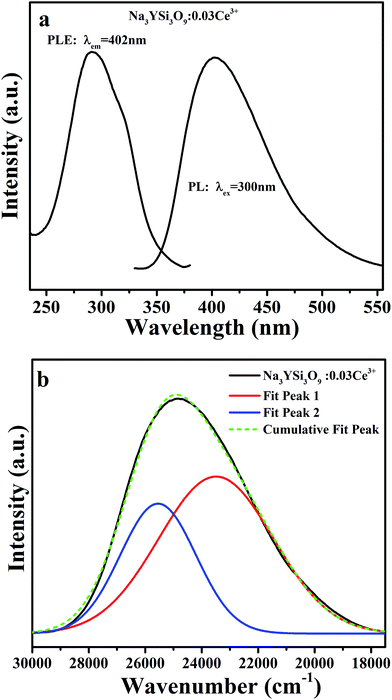 |
| | Fig. 3 (a) The PL (λex = 300 nm) and PLE (λem = 402 nm) spectra of Na3YSi3O9:0.03Ce3+; (b) the PL spectrum of Na3YSi3O9:0.03Ce3+ and its Gaussian components. | |
Fig. 4a and b present the PL spectra of Na3YSi3O9:0.03Ce3+ and Na3YSi3O9:0.09Ce3+ excited with various excitation wavelengths, respectively. The emission of Na3YSi3O9:xCe3+ samples excited under different wavelengths (270–340 nm) are shown in Fig. S1 and a summary is listed in Table S2.† When the excitation wavelength gradually increased from 270 nm to 340 nm, the emission of Na3YSi3O9:0.03Ce3+ shifted to longer wavelengths from 398 nm to 418 nm, and the emissions of Na3YSi3O9:0.09Ce3+ shifted from 411 nm to 431 nm. Here, due to the fixed Ce3+ concentration, the explanation of the red shift by crystal field splitting is excluded. The ∼20 nm red shift is supposed to be ascribed to a 5d centroid shift of Ce3+. Because of different valence states and the charge mismatch originating from doping ions Ce3+ on the Na+ site in Na3YSi3O9, two vacancies with one Ce3+ ion would exist according to the formal equation: 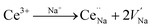 .22 Vacancies with a charge would appear because of the different valence states and the possible charge compensation behavior originating from Ce3+ ions substituting for the Na+ sites. Meanwhile, the electronegative vacancies will affect charge distribution with its chemical environment around the Ce3+ ion, and is reflected by the centroid shift with 5d levels of Ce3+.23 Since the bond length and bond angle of six-coordinated Na+ are different, as shown in Fig. 2b, the effect of vacancies on Ce3+ could not be always identical to all doping Ce3+ ions in Na3YSi3O9. Therefore, the effect of these vacancies not only shifts down the centroid of 5d levels leading to the emission red shift, but also broadens the spectra (Fig. 4).
.22 Vacancies with a charge would appear because of the different valence states and the possible charge compensation behavior originating from Ce3+ ions substituting for the Na+ sites. Meanwhile, the electronegative vacancies will affect charge distribution with its chemical environment around the Ce3+ ion, and is reflected by the centroid shift with 5d levels of Ce3+.23 Since the bond length and bond angle of six-coordinated Na+ are different, as shown in Fig. 2b, the effect of vacancies on Ce3+ could not be always identical to all doping Ce3+ ions in Na3YSi3O9. Therefore, the effect of these vacancies not only shifts down the centroid of 5d levels leading to the emission red shift, but also broadens the spectra (Fig. 4).
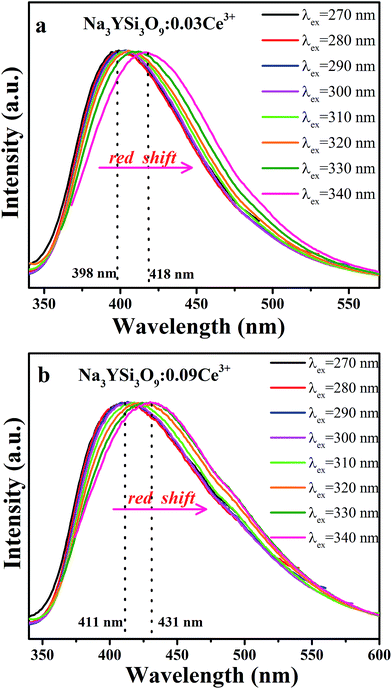 |
| | Fig. 4 (a) The normalized PL spectra of Na3YSi3O9:0.03Ce3+ excited with different excitation wavelengths; (b) the normalized PL spectra of Na3YSi3O9:0.09Ce3+ excited with different excitation wavelengths. | |
Fig. 5 illustrates the PL spectra of Na3YSi3O9 with different Ce3+ ion concentrations under 300 nm excitation. Except for intensity, the PL spectra of Na3YSi3O9:xCe3+ (x = 0.002, 0.01, 0.03, 0.05, 0.07, 0.09, and 0.11) have similar spectral profiles with a continuous 30 nm red-shift of Ce3+ emission from 385 nm to 415 nm as the concentration of Ce3+ increases gradually, exhibiting a larger shift than that of Fig. 4a and b.
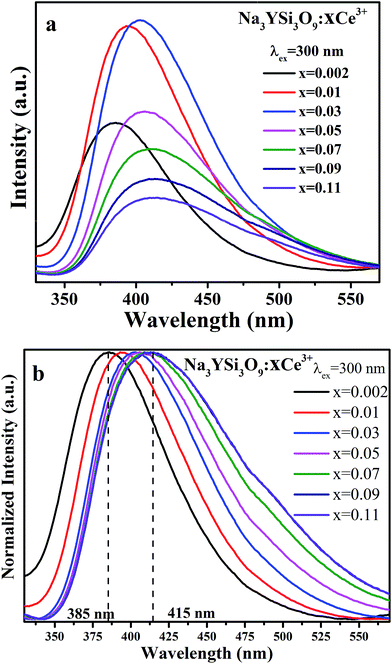 |
| | Fig. 5 (a) The PL spectra of Na3YSi3O9:xCe3+ (x = 0.002, 0.01, 0.03, 0.05, 0.07, 0.09, 0.11) phosphors under 300 nm excitation; (b) the normalized PL spectra of Na3YSi3O9:xCe3+ excited under 300 nm. | |
Comparing the 20 nm red shift of the 5d centroid shift in Fig. 4 with the 30 nm red-shift of the Ce3+ emission as the concentration of Ce3+ increased in Fig. 5, the difference of that red shift should be noted. Mostly, the emission shift phenomenon results from a crystal field splitting effect as referenced in other works.24–26 Therefore in this paper, not only crystal field splitting should be considered, but the centroid shift should be also taken into account with the red shift.
It is established that the Dieke diagram of 4f energy levels is almost invariant while the energies of 5d states are influenced 50 times stronger by the host compound than those of 4f states.27 When lanthanide ions are present in a compound, the lowest level of the 5d configuration would shift down as the emission shifted red. The down shift D(3+,A) of the first 4f–5d transition of Ce3+ is caused from two contributions, namely, centroid shift (εc) and crystal field splitting (εcfs),15,28 as illustrated in Fig. 6. The centroid shift is the shift of 5d centroid energy relative to free Ce3+ ions, which is 6.35 eV (51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 230 cm−1), while crystal field splitting is the energy difference between the lowest and highest 5d-level.15,28 The 4f–5d transition energy of Ce3+ ions doped in Na3YSi3O9 can be written as:27
230 cm−1), while crystal field splitting is the energy difference between the lowest and highest 5d-level.15,28 The 4f–5d transition energy of Ce3+ ions doped in Na3YSi3O9 can be written as:27
| | |
Efd(3+,A) = Efd(3+,free) − D(3+,A)
| (1) |
where
Efd(3+,free) is the energy for the first 4f–5d transition of free Ce
3+ ions. The relationship between
D(3+,A) and
εc(3+,A) and
εcfs(3+,A) can be related as:
29| |
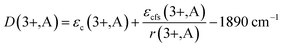 | (2) |
where 1/
r(3+,A) is the fraction of
εcfs that adds to the red shift, and which depends on the type of polyhedron.
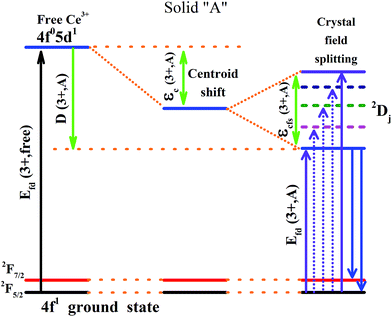 |
| | Fig. 6 Schematic diagram of the centroid shift εc(3+,A), crystal field splitting εcfs(3+,A), red shift D(3+,A) and emission of Ce3+ in a certain compound. | |
Origin of the centroid shift is very complicated and determined by chemical (covalence) and physical (polarizability) properties of the anions coordinating Ce3+.27,28 Based on the model that describes the correlated motion between 5d electron and ligand electrons, the 5d centroid shift for Ce3+ can be given as:15,30
| |
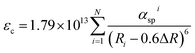 | (3) |
where
Ri is the distance between Ce
3+ and anion
i in the undistorted lattice. The summation is over all
N anions that coordinate Ce
3+ and 0.6Δ
R is a correction for lattice relaxation around Ce
3+. Note
αspi (10
−30 m
−3) is the spectroscopic polarizability of anion
i, and it is an important parameter that includes the effects of correlated motion and covalence between Ce
3+ and also the anions and other possible contributions to the centroid shift. For the oxides:
15,30,31| | |
αosp = 0.33 + 4.8/χav2
| (4) |
where
χav is the weighted average of the electronegativity of the cations in the oxide compounds. Due to the electronegative defect around Ce
3+ ions, the value of
χav for Ce
3+ in the Na
3YSi
3O
9 would be smaller and the 5d centroid shift
εc of Ce
3+ is more obvious according to
eqn (3) and
(4). Naturally, the 4f–5d transition energy of Ce
3+ ions with the vacancies would be lower.
Crystal field splitting is related to the shape and size of the first anion coordination polyhedron around Ce3+.27,28 There is an empirical relationship between εcfs and the average distance (R) from the central ion to its ligand anions:15,28
The βploy values are in the ratio of 1, 0.89, 0.79, 0.42, and 0.42 for octahedral, cubic, dodecahedral, tricapped trigonal prism, and cuboctahedral, respectively;28 anyhow, it is a constant for Na3YSi3O9. The εcfs would decrease with the average distance (R) increasing, as obtained from eqn (5). The smaller Ce3+ ions substituted in the position of six-coordinated Na+ sites in Na3YSi3O9 leads to the shrinkage of cell volume, which then would decrease the average distance (R) and increase the strength of the crystal field. With the doping of Ce3+ ions, more electronegative vacancies will affect charge distribution of its chemical environment around the luminescence center Ce3+. Therefore, the centroid shift of Ce3+ is larger and the energy of the 5d-levels of Ce3+ is lower. Moreover, the shrinkage effect will be more effective and the strength of the crystal field increases with Ce3+ ions' concentration, leading to larger energy difference between the lowest and highest 5d-level. Finally, the lowest 5d-level of Ce3+ ions shift down, resulting in the emissions of the Na3YSi3O9:xCe3+ red shift, too. Thus, both centroid shift and crystal field splitting play important roles in the red shift of Na3YSi3O9:xCe3+ phosphors.27
Emission intensities increase with Ce3+ contents until a maximum intensity is achieved, and then the intensity begins to decrease with x beyond the critical concentration due to energy dispersion between Ce3+ ions, namely, a concentration quenching effect.32 The concentration-dependent luminescence spectra are shown in Fig. 7a, and the critical concentration of Ce3+ in Na3YSi3O9 is 0.03 mol. The critical distance (Rc) for energy transfer among Ce3+ ions is necessary to further understand the interaction mechanisms, which was often calculated by using a concentration quenching method and the relationship given by Blasse:33
| |
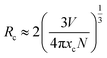 | (6) |
where
V is the volume of the unit cell,
xc is the critical concentration, and
N is the number of cations in the unit cell. Herein, the values are
V = 3463.08 Å
3,
xc = 0.03, and
N = 48. Thus, the
Rc of Ce
3+ was calculated to be 16.623 Å. There are three mechanisms for the nonradiative energy transfer: exchange interaction, radiation reabsorption, and electric multipolar interaction.
34 Owing to the typical critical distance of the exchange interaction being about 5 Å, the exchange interaction only fits the energy transfer of forbidden transitions.
35,36 Therefore, the electric multipolar interactions are dominant in the energy transfer process. According to Dexter
's theory, the mechanism of the interaction between Ce
3+ ions can be expressed by the following equation:
35,37| |
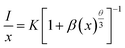 | (7) |
in which
x is the activator concentration, not less than the critical concentration,
I/
x is the emission intensity (
I) per activator concentration (
x), and
k and
β are constants for the same excitation condition for a given host lattice.
θ is a function of electric multipolar character and
θ = 6, 8, 10 corresponds to dipole–dipole (d–d), dipole–quadrupole (d–q), and quadrupole–quadrupole (q–q) interactions, respectively. As represented in
Fig. 7b, the correlation between lg(
I/
x) and lg(
x) can be fitted linearly with a slope of −1.639 equaling to
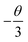
. The
θ value is determined to be 4.917, which is close to 6. Therefore, the concentration quenching mechanism of Na
3YSi
3O
9:
xCe
3+ is mainly accounted for by a dipole–dipole interaction.
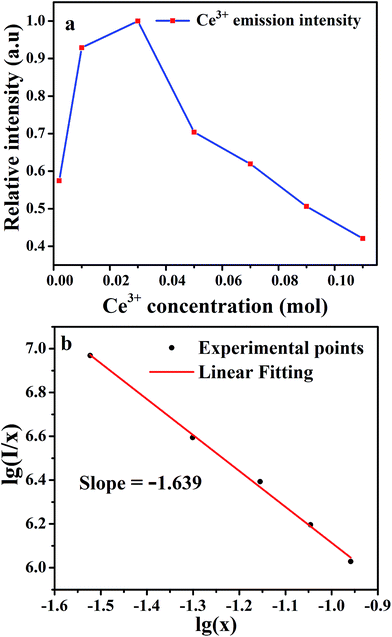 |
| | Fig. 7 (a) The dependence of Ce3+ emission intensity as a function of the Ce3+ content; (b) linear fitting of the relationship of lg(I/x) vs. lg(x) in Na3YSi3O9:xCe3+ (x = 0.002–0.11) phosphors beyond the quenching concentration. | |
To further explore the energy transfer process, the decay curves of Ce3+ ions in Na3YSi3O9:xCe3+ phosphors by monitoring 402 nm excited by 320 nm were also measured (Fig. 8). As discussed above, the electronegative vacancies will affect the interaction of the charge distribution with its chemical environment around Ce3+ ions, which would modify fluorescence dynamics of the Ce3+ ions. Results revealed that the fluorescence decays deviated from the single-exponential rule, and this deviation is more obvious with doping Ce3+ content. The decay curves were fitted with a second-order exponential decay model as:24
| |
I = A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ1) + A2 exp(−t/τ1) + A2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ2) exp(−t/τ2)
| (8) |
where
I is the luminescence intensity,
A1 and
A2 are constants, and
τ1 and
τ2 are the short and long lifetimes for exponential components. The average decay time
τ can be calculated as:
| | |
τ = (A1τ12 + A1τ22)/(A1τ1 + A1τ2)
| (9) |
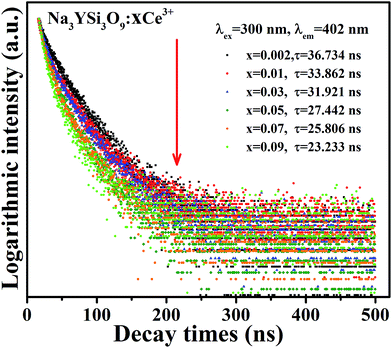 |
| | Fig. 8 Decay curves and lifetimes of Ce3+ emission in Na3YSi3O9:xCe3+ (x = 0.002–0.09) phosphors (excited at 320 nm, monitored at 402 nm). | |
The average decay times τ are calculated to be 36.734, 33.862, 31.921, 27.442, 25.806, and 23.233 ns for Na3YSi3O9:xCe3+ (x = 0.002, 0.01, 0.03, 0.05, 0.07, and 0.09) phosphors. All the results show that the lifetime τ of the 5d1–4f1 transitions of Ce3+ ions in Na3YSi3O9 decreases with Ce3+ concentration, indicating energy dispersion between Ce3+ ions. The measured lifetime is also related to the total relaxation rate expressed as:11
| | |
1/τ = 1/τ0 + Anr + Pt
| (10) |
where
τ0 is the radiative lifetime,
Anr is the nonradiative rate due to multi-phonon relaxation, and
Pt is the energy transfer rate between Ce
3+ ions. With increasing Ce
3+ concentration, the distance between Ce
3+ ions decreases. Then, both the Ce
3+–Ce
3+ energy transfer rate (corresponding to
Pt) and the probability of energy transfer to quenching sites (corresponding to
Anr) increase. As a result, the lifetimes are shortened with increasing concentrations of Ce
3+.
3.3 Thermal stability of Na3YSi3O9:Ce3+ phosphor
Thermal stability is important for practical applications due to its significant influence on light output and CRI. Temperature-dependent PL spectra of the Na3YSi3O9:0.03Ce3+ phosphor excited by 300 nm are depicted in Fig. 9. When the temperature increased from 25 °C to 250 °C, the luminescence intensity decreased gradually to 56.97% at 100 °C. Thermal stability of Na3YSi3O9:0.03Ce3+ and commercial BAM:Eu2+ is shown in the inset of Fig. 9. Thermal quenching can be explained by a configuration coordinate diagram. At high temperature, the electron–phonon interaction is intensive, and the electrons in the 5d excited state could be thermally activated to the 4f ground state through the crossing point between the excited state and the ground state. The nonradiative thermal relaxation process results in decreased luminescence intensity.38 The full width at the half maximum (FWHM) of PL spectrum increases with the temperature, which can be described by using the Boltzmann distribution:39| |
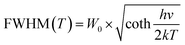 | (11) |
| |
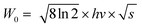 | (12) |
where W0 is the FWHM at 0 K, hv represents the vibrational phonon energy which interacts with the electronic transitions, S means the Huang–Rhys parameter, and k is the Boltzmann constant. It is assumed that hv is the same for both 4f ground state and 5d excited state of Ce3+ ions. When the temperature increases, the electron–phonon interaction becomes dominate and the excited electrons spread to higher vibration levels, and then, the increasing transition from different levels result in the increase of FWHM.36
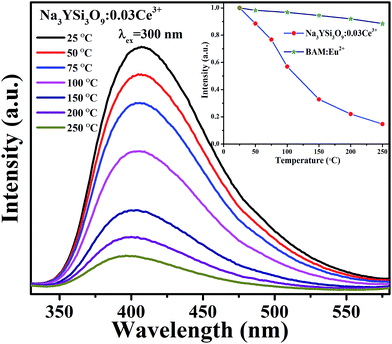 |
| | Fig. 9 Temperature-dependent PL spectra of Na3YSi3O9:0.03Ce3+ phosphor; the inset shows the emission of Na3YSi3O9:0.03Ce3+ and the commercial BAM as a function of temperature when excited at 300 nm. | |
To further investigate the relationship of emission intensity with temperature, the activation energy (ΔE) for thermal quenching can be estimated using the Arrhenius equation:40
| |
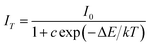 | (13) |
where
I0 is the initial intensity,
IT is the intensity at different temperatures,
c is a constant, Δ
E is the activation energy for thermal quenching, and
k is the Boltzmann constant (8.62 × 10
−5 eV). According to the equation, the activation energy Δ
E is calculated to be 0.277 eV by the relationship of ln[(
I0/
IT) − 1] against 1/
kT, as shown in
Fig. 10.
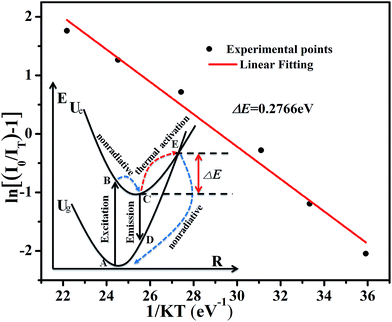 |
| | Fig. 10 The linear fitting of ln[(I0/It) − 1] vs. 1/kT for thermal quenching of Na3YSi3O9:0.03Ce3+; the inset shows the configuration coordinate diagram for an explanation of thermal quenching. | |
3.4 CIE color coordinates
The variations of Commission International de L' Eclairage (CIE) chromaticity coordinates of the Na3YSi3O9:xCe3+ (x = 0.002, 0.01, 0.03, 0.05, 0.07, 0.09, and 0.11) phosphors are determined based on the PL spectra excited at 300 nm (Fig. 11). The CIE chromaticity diagram is tuned from (0.149, 0.057) to (0.164, 0.172) with increasing concentrations of Ce3+ ions from 0.002 to 0.11. The result indicates that the chromaticity coordinates of Na3YSi3O9:xCe3+ phosphors can be modulated over a wide range by appropriately changing the concentrations.
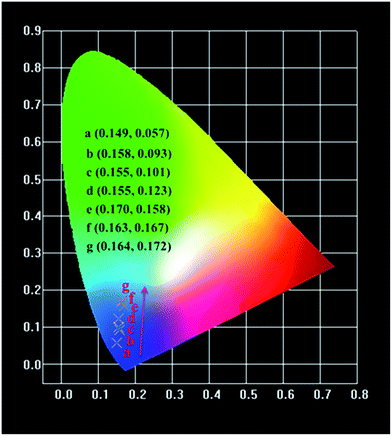 |
| | Fig. 11 CIE chromaticity diagram of Na3YSi3O9:xCe3+ (x = 0.002–0.11) phosphors excited at 300 nm. | |
4. Conclusion
In summary, a serious of blue-emitting Na3YSi3O9:Ce3+ phosphors were synthesized via a traditional solid-state reaction. Results of X-ray diffraction (XRD) and Rietveld refinement analysis indicate that the doping of Ce3+ ions did not cause any impurities in Na3YSi3O9. Concentration quenching of Na3YSi3O9:Ce3+ occurs and the critical quenching concentration was determined to be about 3 mol%. The energy transfer critical distance was calculated to be about 16.626 Å. The corresponding quenching mechanism was verified to be a dipole–dipole interaction. The activation energy ΔE of Ce3+ ion was calculated to be 0.277 eV. The CIE chromaticity coordinates of Na3YSi3O9:xCe3+ phosphors can be tuned in a wide range from (0.149, 0.057) to (0.164, 0.172) with Ce3+ ions increasing from 0.002 to 0.11. Upon 300 nm excitation, the emission peaks of Na3YSi3O9:0.03Ce3+ phosphors shifted to a longer wavelength of 20 nm as the Ce3+ concentration was determined and to 30 nm when Ce3+ concentration increased from 0.002 to 0.11. The spectral red-shift phenomenon is explained by a centroid shift and crystal field splitting. Therefore, some novel phosphors, especially in solid solution, may be prepared by combining centroid shift and crystal field splitting to adjust an emission for application.
Acknowledgements
This work is financially supported by the National Nature Science Foundation of China (11104366), the Natural Science Foundation Project of Chong Qing (cstc2014jcyjA50018), Scientific and Technological Research Program of Chongqing Municipal Education Commission (KJ1500913, KJ1500937) and the Science and Technology Innovation Project of CQUT.
References
- M. R. Krames, O. B. Shchekin, R. Mueller-Mach, G. O. Mueller, L. Zhou, G. Harbersand and M. G. Craford, J. Disp. Technol., 2007, 3(2), 160–175 CrossRef CAS.
- T. G. Kim, H. S. Lee, C. C. Lin, T. Kim, R. S. Liu, T. S. Chan and S. J. Im, Appl. Phys. Lett., 2010, 96(6), 061904 CrossRef.
- K. S. Sohn, D. H. Park, S. H. Cho, J. S. Kwak and J. S. Kim, Chem. Mater., 2006, 18(7), 1768–1772 CrossRef CAS.
- S. Lee and S. Y. Seo, J. Electrochem. Soc., 2002, 149(11), J85–J88 CrossRef CAS.
- A. Setlur, Electrochem. Soc. Interface, 2009, 16(4), 32–36 Search PubMed.
- Z. Hao, J. Zhang, X. Zhang, X. Sun, Y. Luo, S. Lu and X. Wang, Appl. Phys. Lett., 2007, 90, 261113 CrossRef.
- Y. Shi, Y. Wang, Y. Wen, Z. Zhao, B. Liu and Z. Yang, Opt. Express, 2012, 20(19), 21656–21664 CrossRef CAS PubMed.
- S. J. Gwak, P. Arunkumar and W. B. Im, J. Phys. Chem. C, 2014, 118(5), 2686–2692 CAS.
- V. R. Bandi, B. K. Grandhe, K. Jang, S. S. Kim, D. S. Shin, Y. I. Lee, J. M. Lim and T. Song, J. Lumin., 2011, 131(11), 2414–2418 CrossRef CAS.
- D. Ananias, L. D. Carlos and J. Rocha, Opt. Mater., 2006, 28(6), 582–586 CrossRef CAS.
- C. H. Kim, H. L. Park and S. Mho, Solid State Commun., 1997, 101(2), 109–113 CrossRef CAS.
- W. Zhao, S. An, B. Fan and S. Li, J. Lumin., 2013, 143, 71–74 CrossRef CAS.
- Y. Q. Li, N. Hirosaki, R. J. Xie, T. Takeda and M. Mitomo, Chem. Mater., 2008, 20(21), 6704–6714 CrossRef CAS.
- Y. He, J. Zhang, W. Zhou, J. Han, Z. Qiu, L. Yu, C. Rong and S. Lian, J. Am. Ceram. Soc., 2014, 97(5), 1517–1522 CrossRef CAS.
- M. Shang, G. Li, D. Geng, D. Yang, X. Kang, Y. Zhang, H. Lian and J. Lin, J. Phys. Chem. C, 2012, 116(18), 10222–10231 CAS.
- S. P. Lee, C. H. Huang and T. M. Chen, J. Mater. Chem. C, 2014, 2(42), 8925–8931 RSC.
- W. B. Im, N. N. Fellows, S. P. DenBaars, R. Seshadri and Y. I. Kim, Chem. Mater., 2009, 21(13), 2957–2966 CrossRef CAS.
- W. B. Im, K. Page, S. P. DenBaars and R. Seshadri, J. Mater. Chem., 2009, 19(46), 8761–8766 RSC.
- X. Zhang and M. Gong, J. Alloys Compd., 2011, 509(6), 2850–2855 CrossRef CAS.
- A. C. Larson and R. B. Von Dreele, Los Alamos National Laboratory Report LAUR, 1994, pp. 86–748 Search PubMed.
- G. Blasse and B. C. Grabmaier, Luminescent Materials, Springer-Verlag, Berlin, 1994 Search PubMed.
- W. B. Dai, RSC Adv., 2014, 4(22), 11206–11215 RSC.
- P. Dorenbos, J. Lumin., 2013, 135, 93–104 CrossRef CAS.
- C. H. Huang, P. J. Wu, J. F. Lee and T. M. Chen, J. Mater. Chem., 2011, 21(28), 10489–10495 RSC.
- P. D. Rack and P. H. Holloway, Mater. Sci. Eng., R, 1998, 21(4), 171–219 CrossRef.
- N. Guo, Y. Zheng, Y. Jia, H. Qiao and H. You, J. Phys. Chem. C, 2011, 116(1), 1329–1334 Search PubMed.
- S. Shionoya, W. M. Yen and H. Yamamoto, Phosphor Handbook, CRC press, 2006 Search PubMed.
- P. Dorenbos, J. Lumin., 2002, 99(3), 283–299 CrossRef CAS.
- P. Dorenbos, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62(23), 15640–15649 CrossRef CAS.
- P. Dorenbos, J. Lumin., 2003, 105(2), 117–119 CrossRef CAS.
- T. Wang, Z. Xia, Q. Xiang, S. Qin and Q. Liu, J. Lumin., 2015, 166, 106–110 CrossRef CAS.
- W. B. Im, S. Brinkley, J. Hu, A. Mikhailovsky, S. P. Denbaars and R. Seshadri, Chem. Mater., 2010, 22(9), 2842–2849 CrossRef CAS.
- G. Blasse, Philips Res. Rep., 1969, 24(2), 131–144 CAS.
- J. Zhong, W. Zhuang, X. Xing, R. Liu, Y. Li, Y. Liu and Y. Hu, J. Phys. Chem. C, 2015, 119(10), 5562–5569 CAS.
- D. L. Dexter, J. Chem. Phys., 1953, 21(5), 836–850 CrossRef CAS.
- J. Chen, Y. Liu, L. Mei, H. Liu, M. Fang and Z. Huang, Sci. Rep., 2015, 5, 9673 CrossRef CAS PubMed.
- G. Blasse, Phys. Lett. A, 1968, 28(6), 444–445 CrossRef CAS.
- M. Jiao, Y. Jia, W. Lü, W. Lv, Q. Zhao, B. Shao and H. You, J. Mater. Chem. C, 2014, 2(21), 4304–4311 RSC.
- P. Dorenbos, J. Lumin., 2003, 104(4), 239–260 CrossRef CAS.
- C. H. Huang and T. M. Chen, Inorg. Chem., 2011, 50(12), 5725–5730 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra03813e |
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a and
Jiahua Zhangc
*a and
Jiahua Zhangc
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = nλ, the shrinkage of cell volume will lead to an increase of the 2-theta value. When a larger cation is replaced by smaller doping ions, the 2-theta value shifts right.19 The main diffraction peaks shift to a higher angle in the enlarged view from 20° to 35° (Fig. 1), which indicates that Ce3+ ions substituted the position of Na+ sites in the Na3YSi3O9 host lattice.
θ = nλ, the shrinkage of cell volume will lead to an increase of the 2-theta value. When a larger cation is replaced by smaller doping ions, the 2-theta value shifts right.19 The main diffraction peaks shift to a higher angle in the enlarged view from 20° to 35° (Fig. 1), which indicates that Ce3+ ions substituted the position of Na+ sites in the Na3YSi3O9 host lattice.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 490 cm−1 (∼425 nm) and 25
490 cm−1 (∼425 nm) and 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 544 cm−1 (∼391 nm), as shown in Fig. 3b. The energy difference was calculated to be 2054 cm−1, which is close to that between 2F5/2 and 2F7/2 (generally ≈2000 cm−1).21 Herein, the two Gaussian peaks are ascribed for the transitions from the lowest 5d excited state to the 2F5/2 and 2F7/2 ground states of Ce3+ ions due to spin–orbit coupling. That is to say, there exists only one type of emission center in the Na3YSi3O9 host lattice, which is consistent with Ce3+ ion substituting the six-coordinated Na+ site in Na3YSi3O9.
544 cm−1 (∼391 nm), as shown in Fig. 3b. The energy difference was calculated to be 2054 cm−1, which is close to that between 2F5/2 and 2F7/2 (generally ≈2000 cm−1).21 Herein, the two Gaussian peaks are ascribed for the transitions from the lowest 5d excited state to the 2F5/2 and 2F7/2 ground states of Ce3+ ions due to spin–orbit coupling. That is to say, there exists only one type of emission center in the Na3YSi3O9 host lattice, which is consistent with Ce3+ ion substituting the six-coordinated Na+ site in Na3YSi3O9.

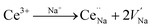 .22 Vacancies with a charge would appear because of the different valence states and the possible charge compensation behavior originating from Ce3+ ions substituting for the Na+ sites. Meanwhile, the electronegative vacancies will affect charge distribution with its chemical environment around the Ce3+ ion, and is reflected by the centroid shift with 5d levels of Ce3+.23 Since the bond length and bond angle of six-coordinated Na+ are different, as shown in Fig. 2b, the effect of vacancies on Ce3+ could not be always identical to all doping Ce3+ ions in Na3YSi3O9. Therefore, the effect of these vacancies not only shifts down the centroid of 5d levels leading to the emission red shift, but also broadens the spectra (Fig. 4).
.22 Vacancies with a charge would appear because of the different valence states and the possible charge compensation behavior originating from Ce3+ ions substituting for the Na+ sites. Meanwhile, the electronegative vacancies will affect charge distribution with its chemical environment around the Ce3+ ion, and is reflected by the centroid shift with 5d levels of Ce3+.23 Since the bond length and bond angle of six-coordinated Na+ are different, as shown in Fig. 2b, the effect of vacancies on Ce3+ could not be always identical to all doping Ce3+ ions in Na3YSi3O9. Therefore, the effect of these vacancies not only shifts down the centroid of 5d levels leading to the emission red shift, but also broadens the spectra (Fig. 4).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 230 cm−1), while crystal field splitting is the energy difference between the lowest and highest 5d-level.15,28 The 4f–5d transition energy of Ce3+ ions doped in Na3YSi3O9 can be written as:27
230 cm−1), while crystal field splitting is the energy difference between the lowest and highest 5d-level.15,28 The 4f–5d transition energy of Ce3+ ions doped in Na3YSi3O9 can be written as:27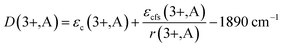

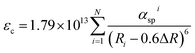
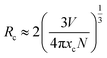
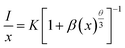
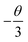 . The θ value is determined to be 4.917, which is close to 6. Therefore, the concentration quenching mechanism of Na3YSi3O9:xCe3+ is mainly accounted for by a dipole–dipole interaction.
. The θ value is determined to be 4.917, which is close to 6. Therefore, the concentration quenching mechanism of Na3YSi3O9:xCe3+ is mainly accounted for by a dipole–dipole interaction.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ1) + A2
exp(−t/τ1) + A2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ2)
exp(−t/τ2)