Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Interaction of human serum albumin with uremic toxins: a thermodynamic study†
Shun Yu abc,
Mirjam Schuchardtd,
Markus Tölled,
Markus van der Gietd,
Walter Zidekd,
Joachim Dzubiellaabc and
Matthias Ballauff*abc
abc,
Mirjam Schuchardtd,
Markus Tölled,
Markus van der Gietd,
Walter Zidekd,
Joachim Dzubiellaabc and
Matthias Ballauff*abc
aSoft Matter and Functional Materials, Helmholtz-Zentrum Berlin, Hahn-Meitner Platz 1, 14109 Berlin, Germany. E-mail: matthias.ballauff@helmholtz-berlin.de
bHelmholtz Virtual Institute “Multifunctional Biomaterials for Medicine”, Kantstr. 55, 14513 Teltow, Germany. Tel: +49 30 8062 43071
cInstitut für Physik, Humboldt-Universität zu Berlin, Newtonstr. 15, 12489 Berlin, Germany
dMedizinische Klinik für Nephrologie, Universitätsmedizin Berlin, Campus Benjamin Franklin, Hindenburgdamm 30, 12203 Berlin, Germany
First published on 25th May 2017
Abstract
We present a comprehensive study of the interaction of human serum albumin (HSA) with two uremic toxins, namely phenylacetic acid (PhAA) and indoxyl sulfate (IDS) in aqueous solution. The interaction of HSA with PhAA is studied for a series of salt concentrations (20–150 mM) and temperature (25, 30 and 37 °C). The effect of in vitro urea modification of HSA upon its binding affinity towards the uremic toxins, is studied under the highest and lowest salt concentrations and the different temperatures. Isothermal titration calorimetry (ITC) is used to study the interaction by analyzing binding affinities and related thermodynamic data. It is found that two PhAA molecules bind to HSA in a sequential binding process with a binding constant kb in the order of ≈104 and ≈103 for the first and second binding respectively. In contrast, IDS binds much stronger to HSA with a total of ≈3 molecules to a high and low affinity binding site in the order of ≈105 and ≈103. Binding of uremic toxins to HSA in all cases show a decreasing binding affinity trend with increasing temperature and higher ionic strength. Thus binding of a second uremic toxin is strongly weakened at 37 °C and 150 mM. Urea induced HSA modification have only minor effect on the binding interaction of the uremic toxins.
1 Introduction
Uremic toxins accumulate in patients with declining renal function which is typically observed in chronic kidney disease (CKD). Uremic toxins are associated with a cardiovascular morbidity and mortality in CKD-patients. The risk is excessive in patients with end-stage renal disease (ESRD), where highest concentrations of uremic toxins occur. Patients with ESRD need renal replacement therapy to eliminate toxic substances.1 High concentrations of toxins are reported in patients with end-stage CKD.2–4 In general, toxins are subdivided into three classes, namely (1) small molecular weight (MW) water-soluble compounds, (2) protein-bound compounds, and (3) larger MW compounds or “middle molecules”.1It has been recognized that several toxins mainly bind to the transport protein human serum albumin (HSA).3,5,6 These small molecules are composed of an aromatic hydrophobic moiety bearing an ionic group. Well studied toxins and their interaction to HSA are p-cresyl sulfate (PCS), hippuric acid (HA) and indoxyl sulfate (IDS).7,8 Bound to HSA, these toxins will inhibit the transport ability of the protein and may lead to structural modifications.4,5,9 Most toxins are found to interact with either one or both of the hydrophobic binding sites Sudlow I and II of HSA located in the subdomains IIA and IIIA.10–13 Due to their tight binding, these small protein-bound and hydrophobic molecules are poorly cleared during conventional dialysis.14,15 The insufficiency of conventional dialysis in the removal of protein-bound toxins presents therefore a major challenge and improving renal dialysis by solving this problem is thus a central task of clinical nephrology.15–17 For this purpose an improved thermodynamic understanding of the interaction of toxins with HSA is absolutely necessary.
The obvious clinical importance of toxins has led to a number of studies of their interaction with proteins. Isothermal titration calorimetry (ITC) is the method of choice to measure enthalpy, entropy and binding affinity directly.18–21 Thus, calorimetric and spectroscopic methods have proven to be very suitable to characterized binding thermodynamics of ligands to proteins, namely ITC10,12,13,22–25 and fluorescence spectroscopy.10,12,13,23–25 Other groups characterized binding isotherms by equilibrium dialysis (ED),3,4,13,26,27 capillary electrophoresis (CE)28–30 and chromatographic techniques.6,27,31 Up to now, however, only a few studies have explored the dependence on temperature.11,13,22,24 Much less is known about the dependence of the binding strength on ionic strength24,32 in detail. However, Böhringer et al. have recently demonstrated in an in vitro study that the fraction of uremic toxins was significantly decreased through hypertonic predilution hemodiafiltration.16 This finding underscores clearly the importance of ionic strength for the binding of toxins to HSA.
In a previous investigation we have explored both the effect of temperature and ionic strength on the binding of a polymeric toxin to HSA.33 There we studied the interaction between an oligmeric poly(acrylic acid) (PAA) and HSA using ITC. PAA provides a model molecule for a charged middle molecular weight toxin bearing carboxylic groups. We found a strong dependence of the binding strength (near the Sudlow II site) on ionic strength which clearly revealed the importance of ionic contributions to polyelectrolyte binding to protein.
In the present study we present a comprehensive study of the binding of small hydrophobic uremic toxins to HSA, again using ITC. Phenylacetic acid (PhAA) is a toxin that has not yet attracted much attention so far. The importance of this toxin derives from the fact that quantitative experiments using equilibrium dialysis (ED) and chromatographic methods have revealed a considerable amount of PhAA present in dialysis patients prior and after dialysis.6,14,16 Furthermore, in a high performance liquid chromatography experiment (HPLC), it has been shown that PhAA accumulation in CKD patients inhibits the expression of inducible nitric oxide synthase and therefore might contribute to the higher cardiovascular risk of these patients.2 The importance of ionic contributions to the binding of this toxin is demonstrated in an in vitro study by Böhringer et al. and forms the basis for establishing a more effective clearance of PhAA by raising the ionic strength.16 Certainly, the binding behavior in an in vivo environment of blood plasma is more a complex process where the specific binding mechanisms cannot be identified anymore.
Indoxyl sulfate is studied as a second toxin because it bears a strong acidic (SO4−) group and studies have found that that 94% of IDS is protein bound and the removal after dialysis is only around 50%.8,34 Hence, a comparison of the thermodynamic data of PhAA bearing a weak acidic group (COO−) with the ones obtained from IDS can reveal details of the ionic interaction and its relation to toxin binding.
It is furthermore known from literature that HSA is modified in pathophysiological conditions caused by chronic renal failure.35 Thus, urea-induced carbamylation of proteins, including HSA, on multiple lysine- and arginine-containing chains occurs. The concentration of urea is chronically elevated in patients with renal failure and the subsequent protein modification was identified as risk factor for mortality.35 The modification of serum albumin might affect binding affinities of uremic toxins and therefore impair its dialysis condition and its subsequent chronically elevated plasma concentrations. We therefore explored the effect of urea-modification on binding affinities of PhAA and IDS to HSA and their structure upon complex formation. The entire thermodynamic analysis based on a comprehensive investigation by ITC will provide a firm basis for further clinical studies related to an improved dialysis technique.
2 Experimental
2.1 Materials
Phenylacetic acid (PhAA) and indoxyl sulfate potassium salt (IDS) were purchased from Sigma-Aldrich (Schnelldorf, Germany) and used as received. Human serum albumin (HSA) was also purchased from Sigma-Aldrich (lyophilized powder, fatty acid free, globulin free, 99%) with molecular weight calculated MW = 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 g mol−1 and its purity verified by SDS-gelelectrophoresis. The buffer morpholin-N-oxide (MOPS) was purchased from Sigma-Aldrich and used as received.
400 g mol−1 and its purity verified by SDS-gelelectrophoresis. The buffer morpholin-N-oxide (MOPS) was purchased from Sigma-Aldrich and used as received.
2.2 In vitro urea modification of albumin
Albumin as purchased by Sigma-Aldrich was dissolved and dialysed against buffer prior to use. In vitro modification of HSA was done in a 10 mM MOPS buffer solution with 15 g L−1 HSA and 10 mM urea at 37 °C and pH 7.4 for 18 h. After incubation, the mixture was dialyzed against buffer using centrifugation dialysis several times.As a first step of the ITC data analysis, the integration of the measured heat Q over time is carried out to obtain the incremental heat ΔQ as a function of the molar ratio x between toxin and protein. For each experiment, the heat of dilution of PhAA and IDS were measured separately by titrating the equivalent uremic toxin into blank buffer solution and subtracted from adsorption heats. After correction, the resulting binding isotherm are fitted using a supplied module for Origin® 7.0 (Microcal). A brief overview of the fitting models used will be given below, however, the interested reader is referred to the manual by Origin for the details of the fitting procedure.36
Errors in concentrations when preparing the samples are seen as a very common source of error directly affecting the analysis of the isotherm and thus all thermodynamic values.37–39 However, in the present study both protein and toxin concentration are well defined.
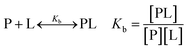 | (1) |
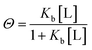 | (2) |
Since only the total concentrations of ligand [L]t and protein [P]t in the solution is known, [L] is expressed as:
| [L]t = [L] + NΘ[P]t | (3) |
For a more complicated binding process, where the protein has two non-identical binding sites, we choose to use a step-wise binding model, which is referred to as Sequential Binding Sites (SBS) model. Here macroscopic binding constants Kb1 and Kb2 refer to a first equilibrium state where one ligand binds to any of the two sites with Kb1 followed by a second stage where the second ligand binds to the remaining free site with Kb2:
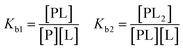 | (4) |
The interpretation of this model must be carried out with care, as misinterpretations of Kb1 and Kb2 being “high” and “low affinity” respectively, are found in literature.43
Binding processes that involve more than exactly one ligand to a corresponding site can be described by the Two Sets of Independent Sites (TSIS) model. Two independent binding constants with corresponding saturation parameters are defined as follows:
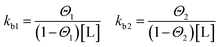 | (5) |
The total ligand concentration in eqn (3) then becomes:
| [L]t = [P] + [P]t (n1Θ1 + n2Θ2) | (6) |
In contrast to the SBS model above, in this case kb1 and kb2 are microscopic binding constants describing the binding affinity of a ligand to the corresponding site. In this model, six free parameters are involved. Namely for each site two enthalpies ΔHITCi, the binding numbers ni to each site i and binding constants kbi respectively.
In an ITC experiment, the total heat of adsorption q is measured typically as an differential heat dq divided by the moles of ligand in the j-th titrant injected dlj with dlj ≈ Vtd[L]t. The incremental heat Q can be expressed as a differential equation:44
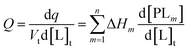 | (7) |
The fitting of the experimental data is performed by calculating the incremental heat Q′ released with each titration and a correction for the displaced volume dVi after each inject ion i:36
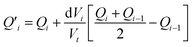 | (8) |
Manually set initial values are used to compare with the measured isotherm. The initial values are then improved by using the standard Marquardt method. These steps are repeated iteratively until a satisfactory fit is achieved.36
The free energy of binding can be calculated for the corresponding binding process using the binding constant:
ΔGb = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kb Kb
| (9) |
Furthermore, the van't Hoff enthalpy can be derived from a series of experiments conducted at different temperature:
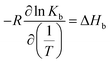 | (10) |
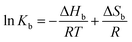 | (11) |
3 Results and discussion
3.1 Binding of phenylacetic acid to native HSA
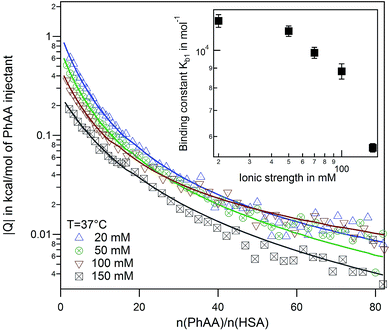
We performed systematic series of ITC experiments with high (I = 150 mM) and low (I = 20 mM) ionic strengths and three different temperatures comprising room temperature 25 °C, a intermediate temperature 30 °C, and the physiological temperature 37 °C. The experiments were performed at pH 7.4 in buffer solution. Typical raw data with ITC titration peaks for adsorption (black curves and points) and dilution (blue curves and points) is shown exemplarily for the adsorption of PhAA to native HSA in Fig. 2a. The integrated isotherms were fitted after subtraction of the heat of dilution with either a Single Set of Independent Sites (SSIS) model, Sequential Binding Sites (SBS) model or Two Set of Independent Sites (TSIS) model‡ in Fig. 2b.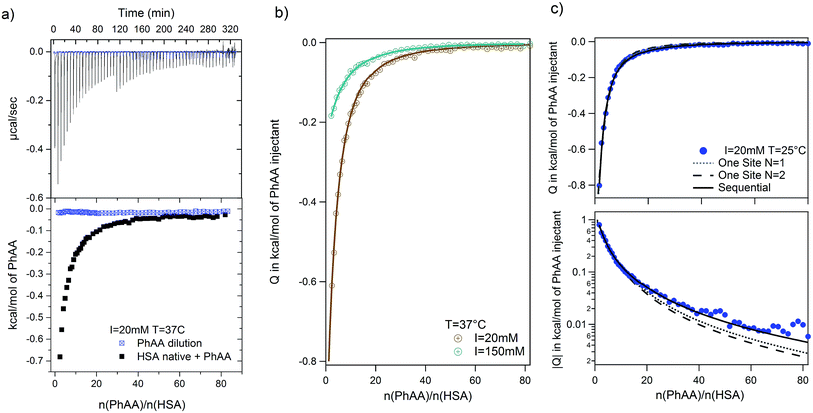 | ||
| Fig. 2 PhAA adsorption to native HSA. (a) Calorimetric titration curves with differential heats per mole Q are shown as a function of molar ratio n(PhAA)/n(HSA) for adsorption (black line and symbols) and the corresponding heats of dilution (blue line and symbols) at I = 20 mM and T = 37 °C. (b) Dilution corrected isotherms with corresponding fits are shown and the data for 150 mM is compared to 20 mM at 37 °C. (c) The quality of different fit models are demonstrated on the example of 20 mM and 37 °C data in a typical ITC plot (top) and a semi-logarithmic plot of |Q|(bottom). Corresponding χ2 values for each fit is given in Table S1 of the ESI.† | ||
All measured signals were weakly exothermic and exhibit similar monotonic curve progression as shown in Fig. 2b. This result is typically observed in the adsorption of small hydrophobic molecules to HSA in other studies as well.13,45,46 Because the overall heat is rather small, dilution must be subtracted as a additional heat signal may affect the results of the fits.
A few more examples are shown in Fig. S1 of the ESI.† Comparing the different binding isotherms and their fitting, it becomes evident that binding behavior is different for different temperature and ionic strength. At high temperature, both models converge towards each other (see Fig. S1b and c†). The affinity Kb2 to bind a second PhAA molecule to HSA becomes very weak for 20 mM salt and 37 °C and vanishes for higher ionic strength at the same temperature (Fig. S1c and Tables S1, 2) in the ESI.† In this case, the data can be well described with the SSIS model with N = 1. For other cases, where two binding sites are present, the SSIS model permanently underestimates binding affinity and enthalpy and produce a rather large error as seen in χ2. A comparison of the results of the fits is given in Table S1 of the ESI.†
| HSA state | I, mM | T = 25 °C | T = 30 °C | T = 37 °C | |||
|---|---|---|---|---|---|---|---|
| ΔGb1, kJ mol−1 | ΔGb2, kJ mol−1 | ΔGb1, kJ mol−1 | ΔGb2, kJ mol−1 | ΔGb1, kJ mol−1 | ΔGb2, kJ mol−1 | ||
| Native | 20 | −24.7 ± 0.1 | −16.9 ± 0.8 | −24.6 ± 0.1 | −17.4 ± 0.7 | −24.2 ± 0.1 | −17.2 ± 0.4 |
| 50 | — | — | — | — | −24.0 ± 0.1 | −17.1 ± 0.4 | |
| 70 | — | — | — | — | −23.7 ± 0.1 | −14 ± 8 | |
| 100 | — | — | — | — | −23.4 ± 0.1 | −14.6 ± 0.9 | |
| 150 | −23.2 ± 0.5 | −20.9 ± 0.1 | −22.8 ± 0.3 | −18.7 ± 0.6 | −22.3 ± 0.1 | — | |
| Modified | 20 | −24.8 ± 0.1 | −18.8 ± 0.4 | −25.1 ± 0.1 | −17.5 ± 0.4 | −25.2 ± 0.2 | −18.8 ± 0.5 |
| 150 | −22.6 ± 0.1 | −15.4 ± 0.9 | −22.5 ± 0.1 | −16.0 ± 0.4 | −21.8 ± 0.1 | −15.6 ± 1.3 | |
| HSA state | I, mM | T = 25 °C | T = 30 °C | T = 37 °C | |||
|---|---|---|---|---|---|---|---|
| ΔGb1, kJ mol−1 | ΔGb2, kJ mol−1 | ΔGb1, kJ mol−1 | ΔGb2, kJ mol−1 | ΔGb1, kJ mol−1 | ΔGb2, kJ mol−1 | ||
| Native | 20 | −31.59 ± 0.06 | −20.68 ± 0.05 | −31.60 ± 0.05 | −20.98 ± 0.09 | −30.49 ± 0.09 | −21.0 ± 0.1 |
| 150 | −29.04 ± 0.05 | −16.0 ± 0.3 | −28.6 ± 0.1 | −15.6 ± 0.6 | −28.1 ± 0.1 | −15.4 ± 1 | |
| Modified | 20 | −30.64 ± 0.06 | −19.96 ± 0.08 | −31.20 ± 0.08 | −20.2 ± 0.1 | −30.44 ± 0.07 | −20.3 ± 0.1 |
| 150 | −29.19 ± 0.08 | −16.9 ± 0.3 | −29.1 ± 0.1 | −17.4 ± 0.3 | −28.3 ± 0.1 | −16 ± 1 | |
 | ||
| Fig. 3 PhAA adsorption to native HSA. Absolute heats |Q| are shown for ionic strength I = 20 mM at different temperatures and respective fits are displayed. | ||
In general, the binding affinity decreases with increasing temperature as has been observed in several cases of adsorption of small molecules to HSA.3,13,24,27 For example, Zaidi et al. have studied interaction between hippuric acid (HA) and HSA and their dependence on temperature using steady state fluorescence quenching measurements and ITC. The ITC data was analyzed using the SBS model likewise and reveal common trends for the temperature dependence of binding constant.
In a direct comparison of the literature data with the present results, binding affinity of the first binding site very much coincides in trend and magnitude as shown in Fig. 4 (brown triangle and spheres).13 For the second binding site, a minor dependence on temperature was observed in the case of PhAA adsorption to HSA. The dependence on temperature can be analyzed according to van't Hoff's law using eqn (10). This equation applies to a system where the change of heat capacity of the system Δcp is small (see Table S2 of the ESI†).
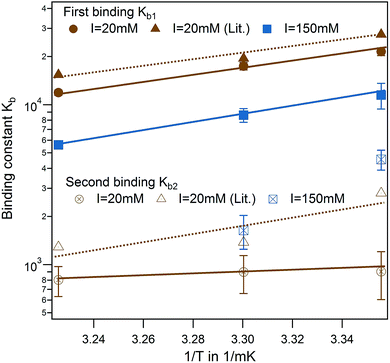 | ||
| Fig. 4 Effect of temperature for PhAA binding to native HSA. Binding affinities for first (full symbols) and second binding process (open symbols) are shown in a van't Hoff plot for I = 20 mM (brown) and I = 150 mM (blue) with corresponding fits according to eqn (10). Literature data for HA-HSA binding with 20 mM sodium phosphate buffer (pH 7.4) are included as triangles with dotted lines as guideline for the eye.13 | ||
van't Hoff plots of the first and second ligand binding process are displayed in Fig. 4 and the results summarized in Table S2 of the ESI.† The analysis of the van't Hoff enthalpy done here is only semi-quantitative since a fully quantitative determination would require measurements at far more temperatures than done here. For the toxin IDS, the enthalpy as measured directly by ITC and van't Hoff enthalpy coincide quite well and ΔHITC is in the present study a good measure for the enthalpy of the binding. In the following, we focus on analysis of the binding free energy ΔGb calculated using eqn (9).
Another interesting feature is observed for I = 150 mM, where a decrease of a second ligand binding with temperature is measured. At high ionic strength and temperature both binding enthalpy and binding constant almost vanishes pointing towards an increased Coulombic screening and thus a weakening of the interaction. This is a plausible explanation for the results obtained recently by Jankowski et al. who measured almost a doubling of released PhAA during hypertonic predilution hemodiafiltration.16 Furthermore, we have shown in previous studies, that ionic strength does contribute significantly towards charge–charge interaction between protein and a short polyelectrolyte.33
A simple Debye–Hückel (DH) perspective for screened electrostatic interactions sketched in the following supports this conclusion. For this, consider the DH interaction between two spherical molecules i and j of valence zi and zj and radii Ri and Rj, respectively, at a binding distance rbind = Rt + Rj, which reads47–50
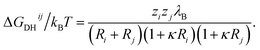 | (12) |
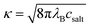 is the inverse Debye screening length and λB ≈ 0.7 nm is the relevant Bjerrum length. We now assume two competing, leading order electrostatic contributions: first, the local attraction of the negatively charged ligand to the binding site at which a few positively charged amino acids are clustered together. Our previous work on the binding of a negative PE chain, for instance, suggested about 2–3 positive charges involved near the Sudlow II site.33 Second, the overall repulsion of the ligand to the sum of all the other charges on HSA which we assume to be located in the HSA center for simplicity. For the attractive term we take that the size of the charged groups at the binding site is on atomistic scales and the same as the ligand, i.e., RPhAA = Rsite ≈ 0.2 nm, such that the binding distance is Rsite + RPhAA ≈ 0.4 nm. The ligand valency is zPhAA = −1, and we assume zsite = +2. According to eqn (12) then the attractive term contributes approximately −7 kJ mol−1 to the binding energy, decreasing in absolute magnitude with increasing ionic strength to about −5.5 kJ mol−1. For the repulsive contribution, we model the protein as a charged sphere of radius RHSA ≈ 3.25 nm (ref. 51 and 52) and a net charge of −14e.§ Thus, to compensate for the positive site, we obtain a remaining net valency of zHSA = −16 which we define to be located in the center of HSA. Due to the relatively large size of HSA, the electrostatic coupling53 is weak and within the validity of the DH treatment. The distance between the bound ligand and the protein center-of-charge is RHSA = RPhAA ≈ 3.45 nm. According to eqn (12) this leads to a repulsive contribution of ≈+3 kJ mol−1 at the lowest, and decreasing rapidly to only ≈+1.5 kJ mol−1 at the highest salt concentration. Hence, the net electrostatic interaction ΔGel = ΔGHSA–PhAADH + ΔGsite–PhAADH ≃ −4 ± 1 kJ mol−1 is attractive and small compared to the total experimental binding energies that are in the range between −25 and −23 kJ mol−1 (cf. Table 1, rounded), decreasing with increasing salt concentration.
is the inverse Debye screening length and λB ≈ 0.7 nm is the relevant Bjerrum length. We now assume two competing, leading order electrostatic contributions: first, the local attraction of the negatively charged ligand to the binding site at which a few positively charged amino acids are clustered together. Our previous work on the binding of a negative PE chain, for instance, suggested about 2–3 positive charges involved near the Sudlow II site.33 Second, the overall repulsion of the ligand to the sum of all the other charges on HSA which we assume to be located in the HSA center for simplicity. For the attractive term we take that the size of the charged groups at the binding site is on atomistic scales and the same as the ligand, i.e., RPhAA = Rsite ≈ 0.2 nm, such that the binding distance is Rsite + RPhAA ≈ 0.4 nm. The ligand valency is zPhAA = −1, and we assume zsite = +2. According to eqn (12) then the attractive term contributes approximately −7 kJ mol−1 to the binding energy, decreasing in absolute magnitude with increasing ionic strength to about −5.5 kJ mol−1. For the repulsive contribution, we model the protein as a charged sphere of radius RHSA ≈ 3.25 nm (ref. 51 and 52) and a net charge of −14e.§ Thus, to compensate for the positive site, we obtain a remaining net valency of zHSA = −16 which we define to be located in the center of HSA. Due to the relatively large size of HSA, the electrostatic coupling53 is weak and within the validity of the DH treatment. The distance between the bound ligand and the protein center-of-charge is RHSA = RPhAA ≈ 3.45 nm. According to eqn (12) this leads to a repulsive contribution of ≈+3 kJ mol−1 at the lowest, and decreasing rapidly to only ≈+1.5 kJ mol−1 at the highest salt concentration. Hence, the net electrostatic interaction ΔGel = ΔGHSA–PhAADH + ΔGsite–PhAADH ≃ −4 ± 1 kJ mol−1 is attractive and small compared to the total experimental binding energies that are in the range between −25 and −23 kJ mol−1 (cf. Table 1, rounded), decreasing with increasing salt concentration.
Clearly, these numbers are highly approximative as, for instance, HSA is non-spherical and detailed charge asymmetry and excluded-volume effects on screening54 have been neglected. However, our estimates exemplify at least some order of magnitude and trends. The estimated attractive electrostatic contribution (between PhAA-site) to the binding is actually similar to monovalent ion pairing affinities found in explicit-water computer simulations.55 While the salt concentration dependence should be qualitatively correct, quantitative details are expected to be more complex than in our simple DH perspective due to very local hydration and polarization effects.55–57
We conclude that the electrostatic interaction is small and thus the major contribution must be of hydrophobic nature, stemming from interactions of the aromatic compound of PhAA (cf. Fig. 1) with the binding site. The total binding free can then be formally expressed as:
| ΔGb = ΔGphob + ΔGel | (13) |
3.2 Binding of phenylacetic acid to modified HSA
In the following we study the effect of carbamylation of HSA through urea35 on the binding affinity to PhAA under the same conditions as in the previous section. This in vitro modification of HSA is known to be found in patients suffering from chronic renal failure conditions, where the urea plasma concentration is chronically elevated.35 To study the urea-modification on the binding behavior of PhAA to HSA, we perform experiments again at I = 20 mM and I = 150 mM at the same three temperatures as before. Binding isotherms and corresponding fits are displayed in the ESI Fig. S2.† Results from the fits are summarized in Table S2 in the ESI† and corresponding binding energies ΔGb using eqn (9) in Table 1.For low ionic strength, binding to urea modified HSA apparently loses its temperature dependence while the strength of binding is principally unchanged. At high ionic strength and physiological condition, binding is even more weakened compared to I = 20 mM for the modified system.
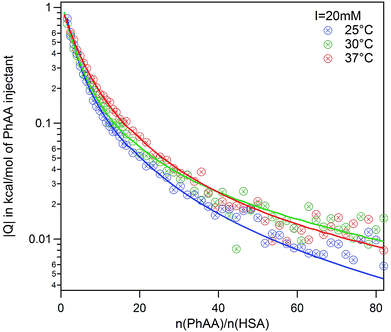
Binding isotherms are equally exothermic and exhibit similar curve shape as in Fig. 3 (data are shown in the ESI Fig. S2†). The binding affinity of the urea modified system to the native HSA system is compared for the first binding process and represented in a van't Hoff plot in Fig. 6.
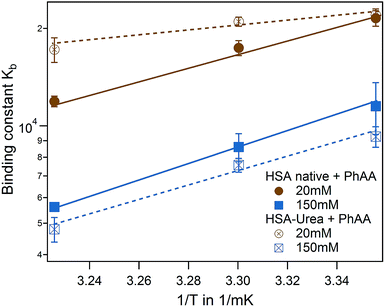 | ||
| Fig. 6 Effect of HSA urea modification on PhAA adsorption. van't Hoff plot of the first binding process for native (filled symbols) and urea modified HSA (empty symbols) with corresponding fits. | ||
For the binding of the second ligand at 20 mM salt, no pronounced temperature dependence is observed in both of the systems (see Table 1). In both cases, binding of the second ligand is associated with a rather small affinity compared to the error of fitting. As a result, it is difficult to resolve a difference in binding affinities in the modified or native system or a corresponding temperature dependence.
3.3 Binding of indoxyl sulfate to native and modified HSA
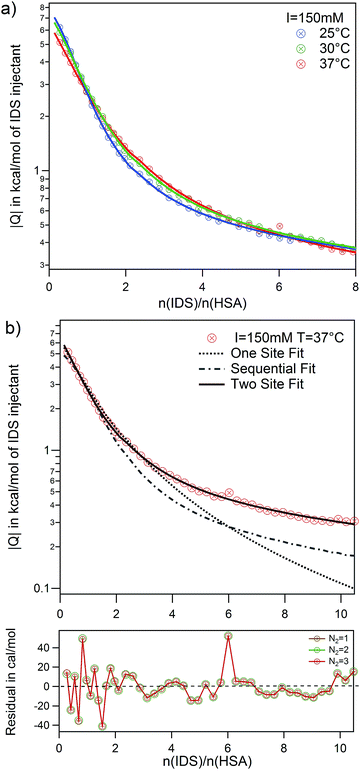
The adsorption of IDS to native and modified HSA was systematically studied at two ionic strengths I = 20 mM and 150 mM and at three temperatures using ITC. Raw data and integrated heats for the adsorption of IDS to native HSA is depicted in Fig. S4 of the ESI.†Again all adsorption processes show similar exothermic isotherms as observed for PhAA adsorption in the section above. An increase in ionic strength from 20 mM to 150 mM show the same effect but overall weaker as observed before (Fig. S3b) in the ESI†. However, in the standard ITC plot, temperature differences between different isotherms are not clearly visible (Fig. S4c) in the ESI†. Therefore logarithmic plots of isotherms and corresponding fits are shown exemplarily for I = 150 mM and three temperatures in Fig. 7a.
Here the necessity to use a two site adsorption model is clear. As demonstrated in the case of IDS adsorption to native HSA at 37 °C and I = 150 mM in Fig. 7b,¶ the data can neither be described by the SSIS (dotted line) nor the SBS (dashed line) model. There are clearly two binding sites present for IDS with different binding stoichiometry. Using the two set of independent sites TSIS model (solid line), ITC isotherms can be very well described at all measuring conditions. However, the number of IDS molecules adsorbed at the second site N2 cannot be well determined by a fit of the ITC data. Residual errors for fits with different fixed parameter N2 (ranging from one to three) show no significant change. It is however not surprising that fitting a monotonic curve with six parameters implies the risk of fitting of too many free parameters.65
Several studies on the adsorption of IDS to HSA confirm the existence of two binding sites with different binding affinity.3,27 Crystallographic analysis of IDS complexed with HSA suggests that one IDS molecule bind to subdomain IIIA while two molecules bind to subdomain IIA of HSA.66 Sakai et al. measured IDS adsorption on HSA at 25 °C and 67 mM phosphate buffer at pH 7.4 using equilibrium dialysis. They found two binding sites with N1 = 1 and N2 = 3 for high and low affinity binding site, respectively.3 A more recent study from Watanabe et al. using ultrafiltration found at same pH and temperature but different buffer, a slightly lower N2 = 1.6.27 Based on these findings, it appears reasonable to fix N2 between one and three and average the results. As the residuals between each fits are small (see Fig. 7b), we use the standard deviation as error for each averaged parameter. Thus, even with an uncertainty of N2 = 2 ± 1, the binding affinity kb2 obtained are robust and reliable. However, the binding enthalpy ΔH2 is strongly correlated with the fitting parameter N2 and errors for ΔHITC2 and consequently ΔS2 are accordingly large. All results obtained from the fits are summarized in Table S3 of the ESI.†
Binding of IDS to HSA is generally an order of magnitude stronger than PhAA to HSA in all measured cases. However, caution is required when comparing a macroscopic binding affinity Kb to a microscopic binding affinity kb. The microscopic affinity k1 for example describes explicitly the binding process of Ni ligands to site 1 while the macroscopic affinity Kb1 assumes binding of either one of the two potential ligands to any of the two sites.
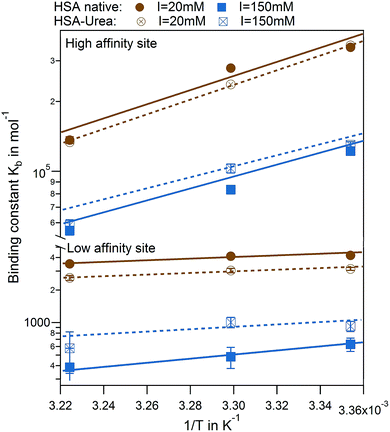
The effect of urea modification is rather small. van't Hoff analysis comparing native to urea modified HSA reveal temperature dependence of binding for both binding sites, while the dependency is more pronounced for the high affinity site rather than the low affinity site (Fig. 8). The binding enthalpies for the high affinity site measured directly by ITC ΔHITC1 agree well with the binding enthalpies derived from the van't Hoff plot (see Table S3 of the ESI†).
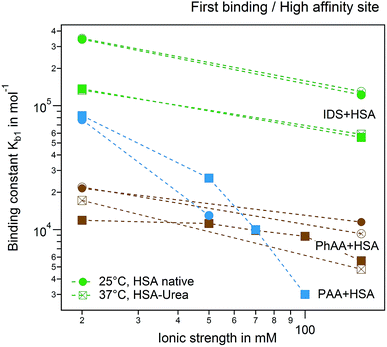
A plot of all results comparing the effect of urea modification on the adsorption of PhAA and IDS is shown in Fig. 9. Additionally, the presented results are put into context to earlier investigations on the interaction between a multiply charged “middle molecule”, namely a polyvalent polyacrylic acid (PAA) chain with HSA, to gain a deeper insight into different contributions to binding.33 In Fig. 9 the binding affinity of the small toxins IDS and PhAA to HSA exhibit in all cases moderate decreasing binding affinities to both native and modified HSA while binding of PAA is strongly weakened due to a decreasing counterion-release entropy with rising salt concentration.33 For the present ligands, the hydrophobic interaction plays an dominant role in the binding process as expected.
4 Conclusions
We presented a study of the binding of two representative protein-bound uremic toxins indoxyl sulfate (IDS) and phenylacetic acid (PhAA) to native and urea modified HSA using ITC. Binding of these ligands to HSA were in all cases exothermic and thus enthalpy driven. Analyzing the isotherms with appropriate binding models reveal that there are two binding sites for both of the two uremic toxins with different binding affinities and stoichiometry. Binding of PhAA to native HSA feature a subtle ionic strength dependency which can be estimated approximately by a Debye–Hückel approach.47 The main contribution towards binding is attributed to favorable hydrophobic interaction that can be well compared to computer simulations for a ligand-protein model system.58 The influence of urea modification of HSA towards binding appears to be rather weak and does not in principal alter interaction between ligand and protein.Acknowledgements
The Helmholtz Virtual Institute for Multifunctional Biomaterials for Medicine are gratefully acknowledged for financial support. The authors thank the Helmholtz Association for funding of this work through Helmholtz-Portfolio Topic “Technology and Medicine”. The authors thank B. Egbers for excellent technical assistance. J. D. thanks the Deutsche Forschungsgemeinschaft (DFG) for financial support. The authors acknowledge useful discussions with R. Gregor Weiβ.References
- R. Vanholder, R. de Smet, G. Glorieux and W. Zidek, Kidney Int., 2003, 63, 1934–1943 CrossRef CAS PubMed
.
- J. Jankowski, M. van der Giet, V. Jankowski, S. Schmidt, M. Hemeier, B. Mahn, G. Giebing, M. Tölle, H. Luftmann, H. Schlüter, W. Zidek and M. Tepel, J. Clin. Invest., 2003, 112, 256–264 CrossRef CAS PubMed
.
- T. Sakai, K. Yamasaki, T. Sako, U. Kragh-Hansen, a. Suenaga and M. Otagiri, Pharm. Res., 2001, 18, 520–524 CrossRef CAS
.
- L. Viaene, P. Annaert, H. de Loor, R. Poesen, P. Evenepoel and B. Meijers, Biopharm. Drug Dispos., 2013, 34, 165–175 CrossRef CAS PubMed
.
- T. Sakai, A. Takadate and M. Otagiri, Biol. Pharm. Bull., 1998, 18, 1755–1761 Search PubMed
.
- Y. Itoh, A. Ezawa, K. Kikuchi, Y. Tsuruta and T. Niwa, Anal. Bioanal. Chem., 2012, 403, 1841–1850 CrossRef CAS PubMed
.
- R. Vanholder, N. Meert, E. Schepers, G. Glorieux, A. Argiles, P. Brunet, G. Cohen, T. Drüeke, H. Mischak, G. Spasovski, Z. Massy and J. Jankowski, Nephrol., Dial., Transplant., 2007, 22, 3115–3121 CrossRef CAS PubMed
.
- O. Deltombe, W. Van Biesen, G. Glorieux, Z. Massy, A. Dhondt and S. Eloot, Toxins, 2015, 7, 3933–3946 CrossRef CAS PubMed
.
- P. Gulyassy and T. Depner, Am. J. Kidney Dis., 1983, 2, 578–601 CrossRef CAS PubMed
.
- X. Li and Y. Yan, J. Mol. Struct., 2015, 1082, 170–173 CrossRef CAS
.
- M. Ishtikhar, G. Rabbani and R. H. Khan, Colloids Surf., B, 2014, 123, 469–477 CrossRef CAS PubMed
.
- M. T. Rehman, H. Shamsi and A. U. Khan, Mol. Pharm., 2014, 11, 1785–1797 CrossRef CAS PubMed
.
- N. Zaidi, M. R. Ajmal, G. Rabbani, E. Ahmad and R. H. Khan, PLoS One, 2013, 8, e71422 CAS
.
- F. Brettschneider, M. Tölle, M. von der Giet, J. Passlick-Deetjen, S. Steppan, M. Peter, V. Jankowski, A. Krause, S. Kühne, W. Zidek and J. Jankowski, Artif. Organs, 2013, 37, 409–416 CrossRef CAS PubMed
.
- R. C. Vanholder, S. Eloot and G. L. Glorieux, Am. J. Kidney Dis., 2016, 67, 664–676 CrossRef CAS PubMed
.
- F. Böhringer, V. Jankowski, P. R. Gajjala, W. Zidek and J. Jankowski, ASAIO J., 2015, 61, 55–60 CrossRef PubMed
.
- J. Jankowski, W. Zidek, V. Brettschneider and S. Jankowski, Method of dialysis for removing protein-bound toxins from the blood of patients using high-frequency electromagnetic fields, 2014 Search PubMed
.
- S. Leavitt and E. Freire, Curr. Opin. Struct. Biol., 2001, 11, 560–566 CrossRef CAS PubMed
.
- V. Ball and C. Maechling, Int. J. Mol. Sci., 2009, 10, 3283–3315 CrossRef CAS PubMed
.
- J. E. Ladbury, Biochem. Soc. Trans., 2010, 38, 888–893 CrossRef CAS PubMed
.
- L. S. Roselin, M.-S. Lin, P.-H. Lin, Y. Chang and W.-Y. Chen, Biotechnol. J., 2010, 5, 85–98 CrossRef CAS PubMed
.
- X. Li and Z. Yang, Chem.-Biol. Interact., 2015, 232, 77–84 CrossRef CAS PubMed
.
- S. Tayyab, M. S. Zaroog, S. R. Feroz, S. B. Mohamad and S. N. A. Malek, Int. J. Pharm., 2015, 491, 352–358 CrossRef CAS PubMed
.
- B. K. Paul, N. Ghosh and S. Mukherjee, J. Phys. Chem. B, 2015, 119, 13093–13102 CrossRef CAS PubMed
.
- P. Sen, S. Fatima, B. Ahmad and R. H. Khan, Spectrochim. Acta, Part A, 2009, 74, 94–99 CrossRef PubMed
.
- L.-L. Wu, H.-W. Gao, N.-Y. Gao, F.-F. Chen and L. Chen, BMC Struct. Biol., 2009, 9, 31 CrossRef PubMed
.
- H. Watanabe, T. Noguchi, Y. Miyamoto, D. Kadowaki, S. Kotani, M. Nakajima, S. Miyamura, Y. Ishima, M. Otagiri and T. Maruyama, Drug Metab. Dispos., 2012, 40, 1423–1428 CrossRef CAS PubMed
.
- C. Ràfols, S. Zarza and E. Bosch, Talanta, 2014, 130, 241–250 CrossRef PubMed
.
- H. Xu, X.-D. Yu, X.-D. Li and H.-Y. Chen, Chromatographia, 2005, 61, 419–422 CAS
.
- R. Tian, S. Xu, X. Lei, W. Jin, M. Ye and H. Zou, TRAC, 2005, 24, 810–825 CAS
.
- N. Bijari, Y. Shokoohinia, M. R. Ashrafi-Kooshk, S. Ranjbar, S. Parvaneh, M. Moieni-Arya and R. Khodarahmi, J. Lumin., 2013, 143, 328–336 CrossRef CAS
.
- N. Keswani, S. Choudhary and N. Kishore, J. Biochem., 2010, 148, 71–84 CrossRef CAS PubMed
.
- S. Yu, X. Xu, C. Yigit, M. van der Giet, W. Zidek, J. Jankowski, J. Dzubiella and M. Ballauff, Soft Matter, 2015, 11, 4630–4639 RSC
.
- M. Rossi, K. L. Campbell, D. W. Johnson, T. Stanton, D. A. Vesey, J. S. Coombes, K. S. Weston, C. M. Hawley, B. C. McWhinney, J. P. J. Ungerer and N. Isbel, Arch. Med. Res., 2014, 45, 309–317 CrossRef CAS PubMed
.
- A. H. Berg, C. Drechsler, J. Wenger, R. Buccafusca, T. Hod, S. Kalim, W. Ramma, S. M. Parikh, H. Steen, D. J. Friedman, J. Danziger, C. Wanner, R. Thadhani and S. A. Karumanchi, Sci. Transl. Med., 2013, 5, 175ra29 Search PubMed
.
- L. MicroCal, ITC Data Analysis in Origin, 7th edn, 2004 Search PubMed
.
- J. Tellinghuisen and J. D. Chodera, Anal. Biochem., 2011, 414, 297–299 CrossRef CAS PubMed
.
- S. G. Krimmer and G. Klebe, J. Comput.-Aided Mol. Des., 2015, 29, 867–883 CrossRef CAS PubMed
.
- S. Geschwindner, J. Ulander and P. Johansson, J. Med. Chem., 2015, 58, 6321–6335 CrossRef CAS PubMed
.
- L. Indyk and H. F. Fisher, Methods Enzymol., 1998, 295, 350–364 CAS
.
- D. T. Haynie, Biological Thermodynamics, Cambridge University Press, 2001 Search PubMed
.
- G. G. Hammes, Thermodynamics and kinetics for the biological sciences, Wiley-Interscience, John Wiley & Sons. Inc., 2000 Search PubMed
.
- S. Vega, O. Abian and A. Velazquez-Campoy, Methods, 2015, 76, 99–115 CrossRef CAS PubMed
.
- I. Herrera and M. a. Winnik, J. Phys. Chem. B, 2013, 117, 8659–8672 CrossRef CAS PubMed
.
- E. Ahmad, G. Rabbani, N. Zaidi, S. Singh, M. Rehan, M. M. Khan, S. K. Rahman, Z. Quadri, M. Shadab, M. T. Ashraf, N. Subbarao, R. Bhat and R. H. Khan, PLoS One, 2011, 6 CAS
.
- T. Chatterjee, A. Pal, S. Dey, B. K. Chatterjee and P. Chakrabarti, PLoS One, 2012, 7, e37468 CAS
.
- P. Debye and E. Hückel, Phys. Z., 1923, 24, 185–206 CAS
.
- M. B. Jackson, Molecular and Cellular Biophysics, Cambridge University Press, 2006 Search PubMed
.
- G. G. Hammes, Thermodynamics and kinetics for the biological sciences, Wiley-Interscience, John Wiley & Sons. Inc., 2000 Search PubMed
.
- C. Yigit, J. Heyda, M. Ballauff and J. Dzubiella, J. Chem. Phys., 2015, 143, 064905 CrossRef PubMed
.
- A. Luik, Y. Naboka, S. Mogilevich, T. Hushcha and N. Mischenko, Spectrochim. Acta, Part A, 1998, 54, 1503–1507 CrossRef
.
- M. A. Kiselev, I. A. Gryzunov, G. E. Dobretsov and M. N. Komarova, Biofizika, 2001, 46, 423–427 CAS
.
- H. Boroudjerdi, Y.-W. Kim, A. Naji, R. Netz, X. Schlagberger and A. Serr, Phys. Rep., 2015, 416, 129 CrossRef
.
- N. Hoffmann, C. N. Likos and J.-P. Hansen, Mol. Phys., 2004, 102, 857–867 CrossRef CAS
.
- I. Kalcher and J. Dzubiella, J. Chem. Phys., 2009, 130, 134507 CrossRef PubMed
.
- J. Dzubiella, J. Am. Chem. Soc., 2008, 130, 14000 CrossRef CAS PubMed
.
- J. M. Scholtz, H. Qian, V. H. Robbins and R. L. Baldwin, Biochemistry, 1993, 32, 9668–9676 CrossRef CAS PubMed
.
- P. Setny, R. Baron and J. A. Mccammon, J. Chem. Theory Comput., 2010, 6, 2866–2871 CrossRef CAS PubMed
.
- R. S. Spolar, J.-H. Ha and T. Record Jr, Proc. Natl. Acad. Sci. U. S. A., 1989, 86, 8382 CrossRef CAS
.
- C. Tanford, The hydrophobic effect: formation of micelles and biological membranes, New York, Wiley, 1973 Search PubMed
.
- G. Hummer, Nat. Chem., 2010, 2, 906 CrossRef CAS PubMed
.
- J. Dzubiella, J. Stat. Phys., 2011, 145, 227 CrossRef CAS
.
- F. Biedermann, W. M. Nau and H.-J. Schneider, Angew. Chem., Int. Ed., 2014, 53, 11158–11171 CrossRef CAS PubMed
.
- B. Breiten, M. R. Lockett, W. Sherman, S. Fujita, M. Al-Sayah, H. Lange, C. M. Bowers, A. Heroux, G. Krilov and G. M. Whitesides, J. Am. Chem. Soc., 2013, 135, 15579–15584 CrossRef CAS PubMed
.
- C. A. Brautigam, Methods, 2015, 76, 124–136 CrossRef CAS PubMed
.
- J. Ghuman, P. A. Zunszain, I. Petitpas, A. A. Bhattacharya, M. Otagiri and S. Curry, J. Mol. Biol., 2005, 353, 38–52 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra02838e |
| ‡ All models were fitted using the implemented ITC data analysis software for Origin by MicroCal. |
| § The number of charges of the protein can be calculated from the crystal structure. |
| ¶ A further example of fitting quality is shown in the ESI (Fig. S5d†) for modified HSA interaction to IDS. |
| This journal is © The Royal Society of Chemistry 2017 |