Europium complexes: choice of efficient synthetic routes from RM1 thermodynamic quantities as figures of merit

Abstract

We advance the novel general idea that thermodynamic quantities of chemical reactions from RM1 quantum chemical calculations, regarded as figures of merit, are useful to the chemist studying europium complexes. Faced with several different plausible synthetic pathways for the preparation of a given europium complex, the synthetic chemist can now easily compute the RM1 thermodynamic quantities for all of them. As we show, regarding the results as figures of merit, the chemist has a high likelihood of arriving, in an a priori manner, at the most effective synthetic strategy. We further introduce the concept of series of ligands, ordered in terms of their relative displacement abilities in ligand exchange reactions. First, we calculate this series for a few β-diketonate ionic ligands: DBM > BTFA ≈ TTA. Then, we show how this series can help the experimentalist decide, of all possibilities, which would be the most efficient sequence of addition of ionic ligands to obtain the best total reaction yield for the syntheses of mixed ionic ligand europium complexes; and exemplify with two alternate syntheses of [Eu(DBM)(BTFA)(TTA)(TPPO)₂]. The synthetic route that added the ionic ligands according to the calculated series exhibited a yield of 76%; whereas the one that inverted that series displayed less than half that yield: 37%. Then, we introduce the series of relative displacement abilities for the non-ionic ligands considered: both monodentates (both as single ligands and as pairs of ligands) and bidentates: (TPPO,TPPO) > BIPY > PHEN ≈ (PTSO,PTSO) > (DBSO,DBSO) > TPPO > PTSO > DBSO > H₂O. In conclusion, there is seemingly a wealth of useful information to the lanthanide chemistry experimentalist that can be obtained from RM1 quantum chemical calculations of thermodynamic quantities.

---

1. Introduction

Synthesis of europium complexes, especially mixed ligand ones, present a challenge to the chemist. Faced with several different plausible synthetic pathways, it is not always obvious which route will be the most effective. In this article, we present a novel scheme for the a priori choice of the best synthetic pathway from easy and fast RM1 ¹ calculated thermodynamic quantities, which we regard as figures of merit of chemical reactions involving europium trivalent ion complexes. We then carry out experiments to show that by using this scheme, the chemist has indeed a high likelihood of arriving in an a priori manner at the most effective synthetic strategy. We then introduce several new concepts, which we experimentally prove, such as the a priori calculation of displacement abilities of different classes of ligands in ligand exchange reactions; and the ensuing ligand displacement series.

The methodology we advance here is therefore applicable only to complexes of trivalent lanthanide ions, whose ligands contain atoms parameterized in RM1, so far: H, C, N, O, P, S, F, Cl, Br, and I. The trivalent oxidation state of lanthanide ions is usually stable in complexes. Lanthanide complexes display a wide range of applications, such as: contrast agents for enhanced MR imaging of cancer cells in vitro, as well as for a subcutaneous tumor model in vivo;² theranostic agents for photodynamic therapy;³ in the determination of sertraline in pharmaceutical and biological samples;⁴ in the real-time imaging of HClO in live cells and animals;⁵ in the detection of dipicolinic acid as a biomarker of bacterial spores;⁶ in immunoassay tests;⁷ and in sensors due to their magnetic properties.^8,9

The RM1 model for the quantum chemical calculation of lanthanide complexes¹ was recently introduced by our group. Unlike our earlier sparkle models, such as Sparkle/RM1,¹⁰ RM1 attaches orbitals to the europium ion.¹ Accordingly, the RM1 model¹ for lanthanides assumes that the neutral europium atom is represented as {[Xe]4f⁶}6s²5d¹6p⁰. The semiempirical core {[Xe]4f⁶} corresponds to the core of the trication, and the basis set comprised of 5d, 6s and 6p orbitals, was introduced to allow a degree of covalency to occur between the ligands and the europium ion, something that was not possible with the previous sparkle models.

RM1 was originally parameterized to also reproduce enthalpies of formation of organic compounds, and is capable of predicting these properties within 5.8 kcal mol⁻¹ of the experimental value.¹¹ On the other hand, the parameterization of europium within the RM1 model was carried out, not for enthalpies of formation of complexes,¹ but for interatomic distances only. However, for a given complex, any inaccuracies in the computation of the enthalpy of formation will have to do with the europium atom only, because the atoms present in the ligands are already properly taken care of by RM1. But when the problem of interest is a chemical reaction in which the europium ion appears on both sides, the europium related systematic errors might perhaps tend to mostly cancel out, rendering comparisons of enthalpies of reaction, Δ_rH, meaningful.

Ligand displacement reactions of metal complexes are said to be isodesmic when the types of chemical bonds broken in the reactants are equal to the types of bonds formed in the products. In this type of reaction, errors usually cancel out in quantum chemical computations. Another class of reactions is isogyric reactions, when the number of electron pairs in the reactants and products is conserved. In general, in this type of reaction, electron correlation is less significant than usual, and their computational calculations tend to be easier. For the purpose of this article, we also introduce the concept of isocoordinate reactions, i.e., reactions when the number of coordinate bonds is identical in both reactants and products. Finally, when the reactions are not isocoordinate ones, they may be classified into either association reactions or dissociation reactions. Clearly, from the point of view of computational chemistry, the most difficult situation to tackle would be non-isodesmic, non-isogyric, and non-isocoordinate reactions.

Recently, we showed that Sparkle/RM1 ¹⁰ calculations can predict the displacement series of the non-ionic ligands, DBSO, PTSO, and TPPO in the synthesis of [Eu(DBM)₃(L,L′)] complexes.¹² The results indicated that the displacement series should be TPPO > PTSO > DBSO. This displacement series was actually the one observed in the synthesis of complexes [Eu(TTA)₃(L,L′)] and [Eu(BTFA)₃(L,L′)].¹³

Indeed, these Sparkle/RM1 thermodynamic calculations¹² were successful, probably because they involved only isodesmic, isogyric and isocoordinate displacement reactions of non-ionic ligands in europium complexes. For the more general case, in particular, for non-isodesmic, non-isogyric and non-isocoordinate reactions, some degree of covalency between the lanthanide and the ligands must be allowed for the semiempirical quantum chemical thermodynamic calculations to be able to reproduce the experimental trends in the actual thermodynamic properties. That is why the recent RM1 model¹ attaches a semiempirical basis set comprised of 5d, 6s and 6p orbitals to the lanthanide trication, as mentioned in the introduction.

Mixed ligand europium complexes acquired importance after a recent recognition of the fact that their luminescence properties, such as quantum yield, quantum efficiency, or radiative decay rate should be larger than the average of these properties for the respective same-ligand complexes.^12–14 Moreover, mixed ligand complexes may also exhibit triboluminescence, a property which seems to be somewhat correlated with a non-centrosymmetric crystal structure.¹⁵

Syntheses of lanthanide complexes are frequently carried out by means of ligand displacement reactions. In particular, ternary β-diketonate europium complexes [Eu(β)₃(L)₂], where L stands for a non-ionic ligand, can be prepared by the usual synthetic route:^{12,13,16–31}

Thus, this usual synthesis starts by adding ionic ligands – the non-ionic ligands are introduced into the complex structure only in the second step.

Alternatively, this sequence of reactions can be inverted, with the addition of non-ionic ligands occurring in the first step. This is the essence of the faster synthetic route introduced by us¹⁷ for the preparation of [Eu(β)₃(L)₂],

It is overall better because the intermediate complex, of the type [EuCl₂(L)₄]Cl·nH₂O, can be easily prepared and purified, whereas the intermediate in the usual synthesis, [Eu(β)₃(H₂O)₂] may take a much longer time to crystallize.¹⁷ The synthesis of [Eu(β)₃(L)₂] performed in this manner leads to faster overall reaction times and larger overall reaction yields.¹⁷ Comparing the two synthetic routes to prepare ternary complexes of type [Eu(β)₃(L)₂], we verify that the usual route can be described as a sequence of two reactions, in which the ion complex always has the same coordination number, in this case, coordination number 8. However, the ligand displacement reactions of the faster synthesis, advanced by our research group, are more difficult to treat theoretically because, in the first step, the complex reactant [EuCl₂(H₂O)₆]Cl, has coordination number 8, the intermediate complex, [EuCl₂(L)₄]Cl·nH₂O has coordination number 6, and the end product [Eu(β)₃(L)₂], has coordination number 8.

Complexes of the type [Eu(β)₃(L)₂] can be used as precursors of mixed non-ionic ligand complexes of the type [Eu(β)₃(L,L′)]:^12,13

Reactions of this type do occur, provided the non-ionic ligand L′ is able to displace the non-ionic ligand L. We verified experimentally that for the mixed non-ionic ligand complexes, [Eu(β)₃(L,L′)], where the non-ionic ligands may be TPPO, PTSO and DBSO, and where the β-diketonate ligands are TTA or BTFA, that the series of displacement is TPPO > PTSO > DBSO.¹³

However, it would be certainly very useful to know, in an a priori manner, the displacement capacity of a ligand by another in an arbitrary complex. For example, in the synthesis of mixed non-ionic ligand complexes, two possibilities may occur:

[Eu(β)₃(L)₂] + L′ → [Eu(β)₃(L,L′)] + L (6)

or

[Eu(β)₃(L′)₂] + L → [Eu(β)₃(L,L′)] + L′ (7)

Only one of them, however, may actually occur experimentally: either L displaces L′, or L′ displaces L.

As we mentioned above, in this article, we present, for the first time, enthalpies, entropies, and Gibbs free energies for the various ligand displacement reactions involved in the syntheses of mixed ligand lanthanide complexes via RM1 quantum chemical calculations. Since these calculated quantities are not the exact condensed phase thermodynamic quantities, we interpret them as figures of merit for the assessment of synthetic pathways. Since the RM1 model is capable of introducing some covalency in the coordinated bonds, the rational is that it should then be possible to assume that the figures of merit follow the trends in the thermodynamic quantities of different types of ligand displacement reactions, including reactions that are non-isodesmic, non-isogyric, and non-isocoordinate, such as the ones that occur in the two steps of the faster synthesis of complexes of the type [Eu(β)₃(L)₂].¹⁷

We start by addressing the overall reactions to prepare complexes of the type [Eu(β)₃(L,L′)] in order to expose the coordination bond strengths of both ionic and non-ionic ligands involved.¹³ Equipped with the insights thus obtained, we finally carry out a complete a priori RM1 theoretical assessment of six possibilities of synthetic routes for the preparation of the completely mixed ionic ligand complex, [Eu(DBM)(BTFA)(TTA)(TPPO)₂]. Out of these six, we identified the ones that should be the best and the unfavorable routes; carried both of them out in our laboratory, and proved – experimentally – that they led to contrastive synthetic yields, all in line with the theoretical calculations. Finally, we sought to harden the geometries of these complexes in order to enhance their luminescent properties,¹⁴ and prepared complexes [Eu(DBM)(BTFA)(TTA)(PHEN)] and [Eu(DBM)(BTFA)(TTA)(BIPY)], via carefully conceived synthetic routes¹⁴ to allow us to arrive at two ligand displacement series in terms of coordination bond strength: one for ionic ligands and another for non-ionic ligands – both theoretically predicted and experimentally proven.

2. Results and discussion

All reactions here described have been performed in ethanolic solution. Therefore, in order to compute the figures of merit from the model that we are advancing in this article, we assume that all atomic and molecular ions, including ionic complexes, will be fully dissociated, with the exception of potassium chloride which precipitates. We will further assume that these species in solution can be well represented in the calculations by isolated molecules to arrive at thermodynamic quantities that can function as figures of merit. Accordingly, both ionic and neutral species will be calculated as isolated molecules; and the precipitated KCl will be represented simply by the neutral isolated KCl molecule. We will show that the figures of merit obtained from this model are able to correctly identify trends in the thermodynamic properties of the chemical reactions that are useful to the experimentalist.

RM1 enthalpies of formation, ΔH_f, are calculated for isolated molecules and can be compared to the experimental gas-phase enthalpy of formation at 298 K of one mole of a compound from its elements in their standard states. This follows from the manner in which semiempirical methods are parameterized. Therefore, any RM1 calculated enthalpies of reaction, Δ_rH, are for gas-phase reactions. Entropies are also calculated for the isolated molecules at 298 K using the vibrational frequencies (energies) and moments of inertia of the molecule according to standard theoretical techniques,³² and correspond to the absolute entropies of the gas phase molecule at 298 K.³² Note that semiempirical models are capable of calculating gas phase absolute entropies accurately, close to the experimental values. Indeed, according to Barrett and Meier,³³ for AM1, “absolute deviations from experimental values are generally less than 5%, and the temperature dependence of the entropy for one species is evaluated with even better precision”. They also confirm that semiempirical entropies are seemingly more accurate than the enthalpies of formation computed with the same semiempirical model.³³

In this work, all thermodynamic quantities will be calculated for the various species, both reactants and products, as isolated molecules. These properties are thus comparable to experimental gas phase quantities. Such calculated properties are therefore expected to be good figures of merit that follow the trends in their corresponding experimental quantities on the assumption that collective effects, condensed phase effects, solvation effects, etc., which are not taken into account, produce systematic deviations. Consequently, we assume in this article that we are able to mutually compare RM1 calculated gas phase values of thermodynamic quantities for different reactions.

In all reactions, we use potassium β-diketonates, which, upon reacting, form precipitated KCl. However, RM1 is not yet parameterized for potassium. Therefore, in order to proceed with our analysis, we need to know the variations of enthalpy, entropy and free energy of the following reaction in the gas phase: Cl⁻ + K⁺ → KCl. The gas phase bond dissociation energy of molecular KCl is 427 kJ mol⁻¹,³⁴ the ionization potential of atomic potassium is 418.81 kJ mol^−1 35 and the electron affinity of chlorine atom³⁶ is 348.575 kJ mol⁻¹. Therefore, we obtain ΔE = −498 kJ mol⁻¹ for the gas phase reaction Cl⁻ + K⁺ → KCl. The Δ(PV) correction for this reaction at 298 K is −2 kJ mol⁻¹, leading to a Δ_rH = −500 kJ mol⁻¹. The entropy of KCl in gas phase is S° (KCl, g, 298.15 K) = 238.98 ± 0.02 J mol⁻¹ K⁻¹.³⁷ The gas phase entropies of the atomic ions Cl⁻ and K⁺ were calculated from the standard partition functions for monoatomic gases and are taken as 153.3 J mol⁻¹ K⁻¹ and 154.6 J mol⁻¹ K⁻¹, respectively. Therefore, the Δ_rS (298 K,g) for the reaction Cl⁻ + K⁺ → KCl is −68.9 J K⁻¹, and the entropy contribution to Δ_rG (298 K,g), −TΔ_rS (298 K,g), is equal to +21 kJ. Finally, Δ_rG (298 K,g) = −479 kJ for the gas phase reaction Cl⁻ + K⁺ → KCl.

2.1. Thermodynamics of synthesis of mixed non-ionic ligand complexes of the type [Eu(β)₃(L,L′)]

The reactant complex used in all starting reactions was the salt [EuCl₂(H₂O)₆]Cl. It is represented in this way because, from crystallographic data,³⁸ one chloride is simply a counter ion in the unit cell, and, therefore, not coordinated to the europium ion. So, in RM1 calculations, we considered both species, [EuCl₂(H₂O)₆]⁺ and Cl⁻ to be fully ionized in the ethanolic solution. Hence, each is calculated with RM1 as an isolated species. Likewise, the potassium β-diketonates are considered as fully ionized, with the β-diketonates calculated with RM1 and the potassium ion being taken care of as previously described. In this sense, we start by calculating, with RM1, reactions like the following:

[EuCl₂(H₂O)₆]⁺ + 3β⁻ + L + L′ → [Eu(β)₃(L,L′)] + 2Cl⁻ + 6H₂O (8)

Since the β-diketonates were added as potassium salts, the following reaction also takes place:

3K⁺ + 3Cl⁻ → 3KCl (9)

So, the overall model reaction to what actually takes place is:

[EuCl₂(H₂O)₆]⁺ + Cl⁻ + 3β⁻ + 3K⁺ + L + L′ → [Eu(β)₃(L,L′)] + 3KCl + 6H₂O (10)

Of course, the free energy of the overall reaction is the sum of the free energies of the previous two.

Table 1 shows the RM1 model thermodynamic quantities: Gibbs free energies of reaction, Δ_rG; enthalpies of reaction, Δ_rH; and entropic contributions, −TΔ_rS; all calculated for the isolated atomic and molecular species at the temperature of 298 K for each of the overall isocoordinate reactions needed to prepare complexes of the type [Eu(β)₃(L,L′)], where β-diketonate can be DBM, BTFA or TTA, and L,L′ can be TPPO, PTSO or DBSO.

Table 1 RM1 thermodynamic data at 298 K for the overall reactions for the syntheses of mixed non-ionic ligand complexes of the type [Eu(β)₃(L,L′)], where the non-ionic ligands L and L′ are TPPO, PTSO or DBSO; and the β-diketonate ligands are DBM, TTA or BTFA

Overall reactions to prepare complexes [Eu(β)3(L,L′)]	ΔrG (kJ mol^−1)	ΔrH (kJ mol^−1)	−TΔrS (kJ mol^−1)
[EuCl2(H2O)6]^+ + Cl^− + 3K^+ + 3DBM^− + DBSO + TPPO → [Eu(DBM)3(DBSO,TPPO)] + 3KCl + 6H2O	−2063	−2053	−10
[EuCl2(H2O)6]^+ + Cl^− + 3K^+ + 3TTA^− + DBSO + TPPO → [Eu(TTA)3(DBSO,TPPO)] + 3KCl + 6H2O	−1858	−1815	−43
[EuCl2(H2O)6]^+ + Cl^− + 3K^+ + 3BTFA^− + DBSO + TPPO → [Eu(BTFA)3(DBSO,TPPO)] + 3KCl + 6H2O	−1842	−1815	−27
[EuCl2(H2O)6]^+ + Cl^− + 3K^+ + 3DBM^− + PTSO + TPPO → [Eu(DBM)3(PTSO,TPPO)] + 3KCl + 6H2O	−2093	−2054	−39
[EuCl2(H2O)6]^+ + Cl^− + 3K^+ + 3TTA^− + PTSO + TPPO → [Eu(TTA)3(PTSO,TPPO)] + 3KCl + 6H2O	−1889	−1820	−69
[EuCl2(H2O)6]^+ + Cl^− + 3K^+ + 3BTFA^− + PTSO + TPPO → [Eu(BTFA)3(PTSO,TPPO)] + 3KCl + 6H2O	−1862	−1814	−48
[EuCl2(H2O)6]^+ + Cl^− + 3K^+ + 3DBM^− + DBSO + PTSO → [Eu(DBM)3(DBSO,PTSO)] + 3KCl + 6H2O	−2031	−2010	−21
[EuCl2(H2O)6]^+ + Cl^− + 3K^+ + 3TTA^− + DBSO + PTSO → [Eu(TTA)3(DBSO,PTSO)] + 3KCl + 6H2O	−1825	−1768	−57
[EuCl2(H2O)6]^+ + Cl^− + 3K^+ + 3BTFA^− + DBSO + PTSO → [Eu(BTFA)3(DBSO,PTSO)] + 3KCl + 6H2O	−1827	−1767	−60

---

All syntheses of mixed non-ionic ligand complexes are predicted to be spontaneous, Δ_rG < 0. Actually, all reactions were carried out and the target products were isolated and characterized. Δ_rG values for reactions involving DBM ionic ligands are always much more negative than for the corresponding reactions involving either the ionic ligands TTA or BTFA. For example, calculated Δ_rG values for the complexes [Eu(β)₃(DBSO,TPPO)] are −2063 kJ mol⁻¹, −1858 kJ mol⁻¹, and −1842 kJ mol⁻¹, respectively, for the β-diketonates DBM, TTA and BTFA.

Δ_rG values seem to be governed more by the Δ_rH values than by the entropy contribution −TΔ_rS. For example, Δ_rH and −TΔ_rS values of the complex [Eu(DBM)₃(DBSO,TPPO)] are −2053 kJ mol⁻¹, and −10 kJ mol⁻¹, respectively, i.e. Δ_rH corresponds to 99% of Δ_rG (−2063 kJ mol⁻¹). All −TΔ_rS terms in Table 1 are essentially comparable, varying from −10 kJ mol⁻¹ to −69 kJ mol⁻¹, because the reactions are of the isocoordinate type and all the species involved are of the same kind. So, the effect of the ionic ligand DBM can be essentially interpreted in terms of enthalpies of reaction. This suggests that the DBM ionic ligand is more tightly bound to the europium ion when compared to either TTA or BTFA. The –CF₃ group present in the structures of both TTA and BTFA ionic ligands seems to weaken the Eu–O coordinate bond. That is because the –CF₃ group is an electron withdrawing substituent capable of reducing the electronic charge density at the carbonyl group, C=O. On the other hand, this effect does not occur when the ligand coordinated to the europium ion is DBM, whose two phenyl groups do not adversely affect the strength of the coordination bond. Fig. 1 presents this concept in pictorial form. As such, from the RM1 model, it is possible to predict the ionic ligand displacement series for these reactions. In this case, the series is: DBM > BTFA ≈ TTA ≫ Cl⁻, a knowledge which is very useful for the conceptualization of syntheses of mixed ionic ligand complexes.

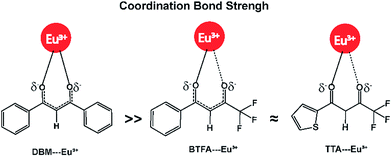Fig. 1 Coordination bond strength order of β-diketonate ligands DBM > BTFA ≈ TTA as affected by the CF₃ substituent group.

2.2. Synthesis of completely mixed ionic ligand complexes [Eu(β)(β′)(β′′)(L)₂] and RM1 thermodynamic aspects

Let us now employ the RM1 model to predict the best route of synthesis of the completely mixed ionic ligand complex, [Eu(DBM)(BTFA)(TTA)(TPPO)₂]. For this task, we chose two TPPO ligands because TPPO is the most tightly bound non-ionic ligand of the three considered in this work.^12,13

We also chose to use the faster synthesis strategy,¹⁷ in which the first step involves a displacement reaction of non-ionic ligands, followed by the three next reactions that lead to precipitate KCl. As such, the complex [Eu(DBM)(BTFA)(TTA)(TPPO)₂] can be synthesized according to:

[EuCl₂(H₂O)₆]Cl + 4TPPO → [EuCl₂(TPPO)₄]Cl + 6H₂O (11)

[EuCl₂(TPPO)₄]Cl + βK → [EuCl₂(β)(TPPO)₃] + KCl + TPPO (12)

[EuCl₂(β)(TPPO)₃] + β′K → [EuCl(β)(β′)(TPPO)₂] + KCl + TPPO (13)

[EuCl(β)(β′)(TPPO)₂] + β′′K → [Eu(β)(β′)(β′′)(TPPO)₂] + KCl (14)

where β, β′ and β′′ are three different β-diketonate ligands. However, the question is: what would be the best order of addition of these three different ionic ligands? Considering the β-diketonate ligands TTA, BTFA and DBM, six possibilities of ionic ligand addition exist:

(1) TTA, then BTFA, and then DBM.

(2) TTA, then DBM, and then BTFA.

(3) BTFA, then TTA, and then DBM.

(4) BTFA, then DBM, and then TTA.

(5) DBM, then TTA, and then BTFA.

(6) DBM, then BTFA, and then TTA.

In the first step of the synthesis of complex Eu(DBM)(BTFA)(TTA)(TPPO)₂, four equivalents of the non-ionic ligand TPPO are added to the salt [EuCl₂(H₂O)₆]Cl to form the intermediate complex [EuCl₂(TPPO)₄]Cl. For this first step, RM1 calculations revealed that the Δ_rG, Δ_rH and −TΔ_rS values are −495 kJ mol⁻¹, −494 kJ mol⁻¹, and −1 kJ mol⁻¹, respectively; while, experimentally, we verified a high reaction yield of 99%. Thus, the next steps of the synthesis will control the overall reaction yield. In terms of reagent waste, it is important that the next steps be carried out in descending order of their yields. We now show that it is possible to use the RM1 model to predict the relative Δ_rG values of the six possibilities of the addition of ionic β-diketonate ligands (TTA, BTFA or DBM). The first addition of the ionic ligand β to the intermediate complex [EuCl₂(TPPO)₄]Cl, leads to the intermediate complex [EuCl₂(β)(TPPO)₃]. Subsequently, the other ionic ligands, β′ and β′′, are added in succession, leading initially to the intermediate complex [EuCl(β)(β′)(TPPO)₂], and then to the target complex [Eu(DBM)(BTFA)(TTA)(TPPO)₂]. Table 2 shows the RM1 thermodynamic quantities of all possibilities for the three reaction steps needed to prepare the target complex using the faster synthesis strategy.¹⁷

Table 2 RM1 thermodynamic properties at 298 K for each possible path of successive reactions, all leading to the synthesis of the mixed ionic ligand complex [Eu(DBM)(TTA)(BTFA)(TPPO)₂] from the precursor complex [EuCl₂(TPPO)₄]⁺. The β-diketonate ligands are DBM, TTA or BTFA

	ΔrG (kJ mol^−1)	ΔrH (kJ mol^−1)	−TΔrS (kJ mol^−1)
Possibility 1
[EuCl2TPPO4]^+ + Cl^− + K^+ + TTA^− → [EuCl2(TTA)(TPPO)3] + KCl + TPPO	−761	−750	−11
[EuCl2(TTA)(TPPO)3] + K^+ + BTFA^− → [EuCl(TTA)(BTFA)(TPPO)2] + KCl + TPPO	−288	−248	−40
[EuCl(TTA)(BTFA)(TPPO)2] + K^+ + DBM^− → [Eu(DBM)(TTA)(BTFA)(TPPO)2] + KCl	−435	−445	10
Possibility 2
[EuCl2TPPO4]^+ + Cl^− + K^+ + TTA^− → [EuCl2(TTA)(TPPO)3] + KCl + TPPO	−761	−750	−11
[EuCl2(TTA)(TPPO)3] + K^+ + DBM^− → [EuCl(TTA)(DBM)(TPPO)2] + KCl + TPPO	−386	−329	−57
[EuCl(TTA)(DBM)(TPPO)2] + K^+ + BTFA^− → [Eu(DBM)(TTA)(BTFA)(TPPO)2] + KCl	−337	−364	27
Possibility 3
[EuCl2TPPO4]^+ + Cl^− + K^+ + BTFA^− → [EuCl2(BTFA)(TPPO)3] + KCl + TPPO	−782	−754	−28
[EuCl2(BTFA)(TPPO)3] + K^+ + TTA^− → [EuCl(BTFA)(TTA)(TPPO)2] + KCl + TPPO	−267	−244	−23
[EuCl(BTFA)(TTA)(TPPO)2] + K^+ + DBM^− → [Eu(DBM)(TTA)(BTFA)(TPPO)2] + KCl	−435	−445	10
Possibility 4
[EuCl2TPPO4]^+ + Cl^− + K^+ + BTFA^− → [EuCl2(BTFA)(TPPO)3] + KCl + TPPO	−782	−754	−28
[EuCl2(BTFA)(TPPO)3] + K^+ + DBM^− → [EuCl(BTFA)(DBM)(TPPO)2] + KCl + TPPO	−363	−330	−33
[EuCl(BTFA)(DBM)(TPPO)2] + K^+ + TTA^− → [Eu(DBM)(TTA)(BTFA)(TPPO)2] + KCl	−339	−359	20
Possibility 5
[EuCl2TPPO4]^+ + Cl^− + K^+ + DBM^− → [EuCl2(DBM)(TPPO)3] + KCl + TPPO	−871	−841	−30
[EuCl2(DBM)(TPPO)3] + K^+ + TTA^− → [EuCl(DBM)(TTA)(TPPO)2] + KCl + TPPO	−276	−238	−38
[EuCl(DBM)(TTA)(TPPO)2] + K^+ + BTFA^− → [Eu(DBM)(TTA)(BTFA)(TPPO)2] + KCl	−337	−364	27
Possibility 6
[EuCl2TPPO4]^+ + Cl^− + K^+ + DBM^− → [EuCl2(DBM)(TPPO)3] + KCl + TPPO	−871	−841	−30
[EuCl2(DBM)(TPPO)3] + K^+ + BTFA^− → [EuCl(DBM)(BTFA)(TPPO)2] + KCl + TPPO	−274	−243	−31
[EuCl(DBM)(BTFA)(TPPO)2] + K^+ + TTA^− → [Eu(DBM)(TTA)(BTFA)(TPPO)2] + KCl	−339	−359	20

---

Assuming that the more negative Δ_rG is, the higher will be the yield of the corresponding reaction, we can, in an a priori manner, verify, from Table 2, that the six possibilities for the first step can be grouped into three sets. Results indicate that DBM should be added first, since its corresponding Δ_rG is the most negative, −871 kJ mol⁻¹, when compared with Δ_rG for the addition of either BTFA, −782 kJ mol⁻¹, or TTA, −761 kJ mol⁻¹. Once more, this can be explained by the coordination bond strength DBM > BTFA ≈ TTA. So, we can infer that the best synthetic strategy would be to prepare complex [Eu(DBM)(BTFA)(TTA)(TPPO)₂] using the following ionic ligand addition order: first DBM, then BTFA, and then TTA, corresponding to possibility 6. Of course, possibility 5 is essentially equivalent to possibility 6, and could as well have been used.

In order to prove that the RM1 model is indeed capable of predicting the best order of addition of ionic ligands for the synthesis of the completely mixed ionic ligand complex [Eu(DBM)(BTFA)(TTA)(TPPO)₂], we synthesized this complex by the two extreme routes: (i) using the RM1 ionic ligand order: first DBM, then BTFA, and then TTA (possibility 6) predicted to be the best order, and (ii) using the opposite order: first TTA, then BTFA, and then DBM (possibility 1), predicted to be the most unfavorable order. Fig. 2 presents the steps carried out for both routes tested, together with the reaction yields obtained for each step, as well as, the overall reaction yield.

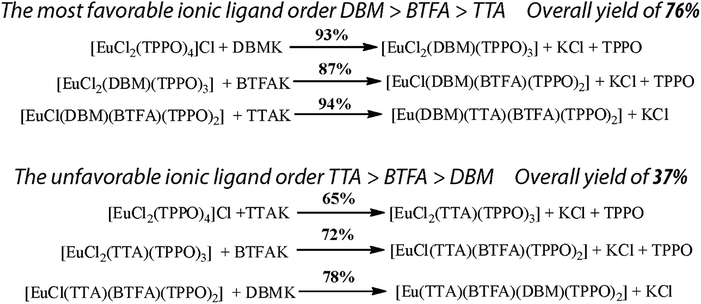Fig. 2 Reaction yields of each step, and overall reaction yields for both possibilities of syntheses of the mixed ionic ligand complex [Eu(DBM)(BTFA)(TTA)(TPPO)₂].

Clearly, from Fig. 2, it is possible to verify that the order of ligand addition deeply affects the overall reaction yields of the syntheses of the all mixed ionic ligand complex [Eu(DBM)(BTFA)(TTA)(TPPO)₂]. The order predicted by RM1 which first added DBM, yielded 76% overall; whereas the opposite order, which first added TTA, yielded 37% overall. For this opposite order route, the yields increased monotonically for the three reactions: 65%, 72%, and 78% in agreement with their respective coordination strengths. The last step, involving the DBM ligand displayed the higher yield in tune with the fact that DBM is the most strongly coordinated of the ionic ligands.

Although it can be argued that synthetic yields may vary depending on the technique of the chemist, the difference in overall yields between 76% and 37% is too large. Besides, all reactions occur in a few minutes. Nevertheless, to be certain that thermodynamic equilibrium had been attained, we left them in reflux for 24 hours. Moreover, it is relatively easy to separate the other products (essentially KCl and, sometimes, TPPO) from the synthesized complex.

2.3. Chloride is the easiest ionic ligand to be displaced by other ionic ligands due to the formation of precipitated KCl salt

The fact that the chloride ion is the most easily displaceable ionic ligand by other ionic ligands deserves special attention. At first, one could conclude that that is because, of all ionic ligands, chloride is the weakest bound to the europium ion. However, that is not accurate. For example, consider the following reactions in Table 3, whose positive Δ_rG values clearly indicate that chloride ions on their own would not be able to be exchanged by any of the other ionic ligands considered: either DBM, BTFA, or TTA. What happens is that the potassium β-diketonates considered in this article are all soluble in ethanol; whereas potassium chloride is not. Indeed, the solubility of potassium chloride in ethanol at 298.15 K is only 0.0064 mol kg⁻¹.³⁹ Therefore, according to our model, when we sum all six chemical equations of Table 3 with K⁺ + Cl⁻ → KCl whose Δ_rG (298 K,g) = −479 kJ, we obtain the third last reactions of all six possibilities of synthesis of [Eu(DBM)(BTFA)(TTA)(TPPO)₂] which are shown in Table 2, all with negative Δ_rG. Consequently, the real reason why chlorides are easily displaced by the other ionic ligands seems to be because of the very significant free energy incentive of −479 kJ due to the formation of the precipitated salt KCl. So, we can predict that, for all ligands considered in this article, a non-ionic ligand would find it very difficult, if not impossible, to displace coordinated chloride ions. That is because non-ionic ligands, of course, do not have alkali cations as counter ions that could ionically bind to the chloride ion and precipitate.

Table 3 RM1 thermodynamic properties at 298 K for the simple displacement reactions of a chloride ion by a β-diketonate ligand in complexes of the type [EuCl(β′)(β′′)(TPPO)₂] to form [Eu(β)(β′)(β′′)(TPPO)₂] without the precipitation of a salt. The β-diketonate ligands are DBM, TTA or BTFA

Reaction of [EuCl(β)(β′)(TPPO)2] + K^+ + β′′^− → [Eu(β)(β′)(β′′)(TPPO)2] + KCl	ΔrG (kJ mol^−1)	ΔrH (kJ mol^−1)	−TΔrS (kJ mol^−1)
[EuCl(TTA)(BTFA)(TPPO)2] + DBM^− → [Eu(DBM)(TTA)(BTFA)(TPPO)2] + Cl^−	+44	+55	−11
[EuCl(TTA)(DBM)(TPPO)2] + BTFA^− → [Eu(DBM)(TTA)(BTFA)(TPPO)2] + Cl^−	+142	+136	+6
[EuCl(BTFA)(TTA)(TPPO)2] + DBM^− → [Eu(DBM)(TTA)(BTFA)(TPPO)2] + Cl^−	+45	+55	−11
[EuCl(BTFA)(DBM)(TPPO)2] + TTA^− → [Eu(DBM)(TTA)(BTFA)(TPPO)2] + Cl^−	+140	+141	−1
[EuCl(DBM)(TTA)(TPPO)2] + BTFA^− → [Eu(DBM)(TTA)(BTFA)(TPPO)2] + Cl^−	+142	+136	+6
[EuCl(DBM)(BTFA)(TPPO)2] + TTA^− → [Eu(DBM)(TTA)(BTFA)(TPPO)2] + Cl^−	+140	+141	−1

---

2.4. RM1 model predicted non-ionic ligand displacement series

So far, we studied the synthesis of the completely mixed ionic ligand complex [Eu(DBM)(BTFA)(TTA)(TPPO)₂]. We will now extend our strategy to understand the thermodynamic aspects of syntheses of other completely mixed ionic ligand complex types: [Eu(DBM)(BTFA)(TTA)(L)₂], [Eu(DBM)(BTFA)(TTA)(L)] and [Eu(DBM)(BTFA)(TTA)(L′)], in which L can be TPPO, PTSO or DBSO and L′ can be PHEN or BIPY. Table 4, shows RM1 thermodynamic aspects of the overall reactions needed to obtain these mixed ionic ligand complexes.

Table 4 RM1 thermodynamic data at 298 K for the overall reactions for the syntheses of mixed ionic ligand complexes of the type [Eu(β)(β′)(β′′)(L)₂], and [Eu(β)(β′)(β′′)(L′)] where the non-ionic ligands L was TPPO, PTSO or DBSO; and L′ was PHEN or BIPY and the β-diketonate ligands were DBM, TTA or BTFA

Overall reactions to prepare mixed ionic ligand complexes	ΔrG (kJ mol^−1)	ΔrH (kJ mol^−1)	−TΔrS (kJ mol^−1)
[EuCl2(H2O)6]^+ + Cl^− + 3K^+ + DBM^− + BTFA^− + TTA^− + 2TPPO → [Eu(DBM)(BTFA)(TTA)(TPPO)2] + 3KCl + 6H2O	−1979	−1937	−42
[EuCl2(H2O)6]^+ + Cl^− + 3K^+ + DBM^− + BTFA^− + TTA^− + 2PTSO → [Eu(DBM)(BTFA)(TTA)(PTSO)2] + 3KCl + 6H2O	−1938	−1854	−84
[EuCl2(H2O)6]^+ + Cl^− + 3K^+ + DBM^− + BTFA^− + TTA^− + 2DBSO → [Eu(DBM)(BTFA)(TTA)(DBSO)2] + 3KCl + 6H2O	−1923	−1847	−76
[EuCl2(H2O)6]^+ + Cl^− + 3K^+ + DBM^− + BTFA^− + TTA^− + PHEN → [Eu(DBM)(BTFA)(TTA)(PHEN)] + 3KCl + 6H2O	−1934	−1846	−88
[EuCl2(H2O)6]^+ + Cl^− + 3K^+ + DBM^− + BTFA^− + TTA^− + BIPY → [Eu(DBM)(BTFA)(TTA)(BIPY)] + 3KCl + 6H2O	−1970	−1883	−88
[EuCl2(H2O)6]^+ + Cl^− + 3K^+ + DBM^− + BTFA^− + TTA^− + TPPO → [Eu(DBM)(BTFA)(TTA)(TPPO)] + 3KCl + 6H2O	−1911	−1862	−49
[EuCl2(H2O)6]^+ + Cl^− + 3K^+ + DBM^− + BTFA^− + TTA^− + PTSO → [Eu(DBM)(BTFA)(TTA)(PTSO)] + 3KCl + 6H2O	−1897	−1819	−78
[EuCl2(H2O)6]^+ + Cl^− + 3K^+ + DBM^− + BTFA^− + TTA^− + DBSO → [Eu(DBM)(BTFA)(TTA)(DBSO)] + 3KCl + 6H2O	−1893	−1834	−59

---

In general, bidentate ligands are more strongly coordinated to metal ions than monodentate ligands. We now address whether or not the bidentate ligands 1,10-phenanthroline (PHEN), and 2,2′-bipiridyl (BIPY) are able to displace two equal monodentate ligands such as TPPO, PTSO, DBSO, or H₂O. From Table 4, it is possible to verify that the overall synthesis of [Eu(DBM)(BTFA)(TTA)(TPPO)₂] is the most favorable, since its Δ_rG term is the most negative, −1979 kJ mol⁻¹. This result indicates that two TPPO non-ionic ligands are coordinated to europium ion more strongly than two PTSO ligands and two DBSO's, for which the Δ_rG values of the respective overall reactions are −1938 kJ mol⁻¹ and −1923 kJ mol⁻¹.

On the other hand, Δ_rG values for the overall reactions involving bidentate ligands PHEN or BIPY are, respectively, −1934 kJ mol⁻¹ and −1970 kJ mol⁻¹. These results suggest BIPY would be able to displace a pair of either PTSO or DBSO ligands, but not a pair of TPPO ligands.

To compare the coordination bond strengths of each non-ionic monodentate ligand with the bidentate ones, we will now consider the calculated thermodynamic quantities of the overall putative reactions involving only one non-ionic monodentate ligand. As such, Δ_rG values for such reactions to obtain complexes of the type [Eu(DBM)(BTFA)(TTA)(L)] are −1911 kJ mol⁻¹, −1897 kJ mol⁻¹ and −1893 kJ mol⁻¹ for complexes [Eu(DBM)(BTFA)(TTA)(TPPO)], [Eu(DBM)(BTFA)(TTA)(PTSO)] and [Eu(DBM)(BTFA)(TTA)(DBSO)], respectively.

These results indicate that monodentate non-ionic ligands L are more weakly coordinated to the europium ion than the bidentate non-ionic ligands PHEN and BIPY. Accordingly, from the results present in Table 4, it is now possible to order the bond strengths of all single non-ionic ligands and double non-ionic ligands considered in this article as: (TPPO,TPPO) > BIPY > PHEN ≈ (PTSO,PTSO) > (DBSO,DBSO) > TPPO > PTSO > DBSO > H₂O.

2.5. Thermodynamic aspects of the syntheses of completely mixed ionic ligand complexes [Eu(β)(β′)(β′′)(L′)] with the faster synthesis strategy

The completely mixed ionic ligand complex [Eu(DBM)(BTFA)(TTA)(TPPO)]₂ was prepared using the concept of the faster synthesis,¹⁷ as described in the previous section. Since, according to the RM1 calculations, two TPPO's cannot be displaced by either PHEN or BIPY, the following two displacement reactions should not occur:

[Eu(β)(β′)(β′′)(TPPO)₂] + PHEN → [Eu(β)(β′)(β′′)(PHEN)] + 2TPPO (15)

[Eu(β)(β′)(β′′)(TPPO)₂] + BIPY → [Eu(β)(β′)(β′′)(BIPY)] + 2TPPO (16)

Indeed, for the reaction in eqn (15), Δ_rG value is +45 kJ mol⁻¹, and for the reaction in eqn (16), Δ_rG value is +8 kJ mol⁻¹.

The usual synthesis of europium complexes has, as its last step, the displacement of non-ionic ligands. However, from the RM1 results, neither BIPY nor PHEN should easily displace a pair of non-ionic ligands. A more efficient alternative is to use the concept of our faster synthesis,¹⁷ when the displacement of non-ionic ligands occurs in its first step. Thus, in order to prepare the fully heteroleptic complexes [Eu(DBM)(BTFA)(TTA)(PHEN)] and [Eu(DBM)(BTFA)(TTA)(BIPY)], we start from complex [EuCl₂(TPPO)₄]Cl. We chose to use this precursor complex in order to verify whether or not the PHEN and BIPY ligands are indeed capable of displacing only one TPPO ligand, but not two TPPO ligands, as the RM1 thermodynamic calculations predict. Accordingly, we first added PHEN or BIPY to complex [EuCl₂(TPPO)₄]Cl and, subsequently, we added the ionic ligands. The order of ionic ligand addition, we employed, was the same predicted to be the best order as already pointed out in the previous section: DBM, then BTFA; and then TTA. In short, the following one-pot syntheses had been already carried out by our research group:⁴⁰

We now turn to RM1 thermodynamic calculations to elucidate and suggest the most probable sequence of reactions that took place in these one-pot syntheses.

The first ligand added was a non-ionic bidentate ligand L′, where L′ can be either PHEN or BIPY. In this step, let us consider the possibilities of displacement of one or two TPPO ligands of the precursor, leading to complexes [EuCl₂(TPPO)₃(L′)]Cl and [EuCl₂(TPPO)(L′)]Cl, respectively. From Table 5, the Δ_rG values for obtaining [EuCl₂(TPPO)₃(PHEN)]Cl and [EuCl₂(TPPO)₃(BIPY)]Cl complexes are, respectively, −92 kJ mol⁻¹ and −118 kJ mol⁻¹, whereas for [EuCl₂(TPPO)₂(PHEN)]Cl and [EuCl₂(TPPO)₂(BIPY)]Cl, the respective values are 48 kJ mol⁻¹ and −4 kJ mol⁻¹. These results indicate that only one TPPO is displaced by either PHEN or BIPY, leading to intermediate complexes of the type [EuCl₂(TPPO)₃(L′)]Cl.

Table 5 RM1 thermodynamic data at 298 K for step 1 of the syntheses of mixed ionic ligand complexes [Eu(DBM)(BTFA)(TTA)(PHEN)] and [Eu(DBM)(BTFA)(TTA)(BIPY)]

Synthesis of [Eu(DBM)(BTFA)(TTA)(PHEN or BIPY)] – step 1	ΔrG (kJ mol^−1)	ΔrH (kJ mol^−1)	−TΔrS (kJ mol^−1)
[EuCl2(TPPO)4]^+ + Cl^− + PHEN → [EuCl2(TPPO)3(PHEN)]^+ + Cl^− + TPPO	−92	−69	−23
[EuCl2(TPPO)4]^+ + Cl^− + PHEN → [EuCl2(TPPO)2(PHEN)]^+ + Cl^− + 2TPPO	48	113	−65
[EuCl2(TPPO)4]^+ + Cl^− + PHEN → [EuCl2(TPPO)4(PHEN)]^+ + Cl^−	25	−56	81
[EuCl2(TPPO)4]^+ + Cl^− + BIPY → [EuCl2(TPPO)3(BIPY)]^+ + Cl^− + TPPO	−118	−106	−12
[EuCl2(TPPO)4]^+ + Cl^− + BIPY → [EuCl2(TPPO)2(BIPY)]^+ + Cl^− + 2TPPO	−4	74	−78
EuCl2(TPPO)4]^+ + Cl^− + BIPY → [EuCl2(TPPO)4(BIPY)]^+ + Cl^−	−38	−94	56

---

Subsequently, the ionic ligand DBM was added to complex [EuCl₂(TPPO)₃(L′)]Cl, a reaction which could, in principle, occur in either of three possibilities, eqn (18)–(20).

[EuCl₂(TPPO)₃(L′)]⁺ + Cl⁻ + K⁺ + DBM⁻ → [EuCl₂(DBM)(TPPO)₃(L′)] + KCl (18)

[EuCl₂(TPPO)₃(L′)]⁺ + Cl⁻ + K⁺ + DBM⁻ → [EuCl₂(DBM)(TPPO)₂(L′)] + KCl + TPPO (19)

[EuCl₂(TPPO)₃(L′)]⁺ + Cl⁻ + K⁺ + DBM⁻ → [EuCl₂(DBM)(TPPO)₃] + KCl + L′ (20)

These reactions can be followed by dissociation of a non-ionic ligand, either TPPO or L′ (PHEN or BIPY). Table 6 shows RM1 thermodynamic data for the possibilities present in eqn (18) to (20).

Table 6 RM1 thermodynamic data at 298 K for step 2 of the syntheses of the mixed ionic ligand complexes [Eu(DBM)(BTFA)(TTA)(PHEN)] and [Eu(DBM)(BTFA)(TTA)(BIPY)]

Synthesis of [Eu(DBM)(BTFA)(TTA)(PHEN or BIPY)] – step 2	ΔrG (kJ mol^−1)	ΔrH (kJ mol^−1)	−TΔrS (kJ mol^−1)
[EuCl2(TPPO)3(PHEN)]^+ + Cl^− + K^+ + DBM^− → [EuCl2(DBM)(TPPO)3(PHEN)] + KCl	−753	−745	−8
[EuCl2(TPPO)3(PHEN)]^+ + Cl^− + K^+ + DBM^− → [EuCl2(DBM)(TPPO)2(PHEN)] + KCl + TPPO	−788	−807	19
[EuCl2(TPPO)3(PHEN)]^+ + Cl^− + K^+ + DBM^− → [EuCl2(DBM)(TPPO)3] + KCl + PHEN	−756	−773	17
[EuCl2(TPPO)3(PHEN)]^+ + Cl^− + K^+ + DBM^− → [EuCl2(DBM)(TPPO)3(PHEN)] + Cl^− + KCl	−332	−400	68
[EuCl2(TPPO)3(PHEN)]^+ + Cl^− + K^+ + DBM^− → [EuCl2(DBM)(TPPO)2(PHEN)] + Cl^− + KCl + TPPO	−294	−289	−5
[EuCl2(TPPO)3(PHEN)]^+ + Cl^− + K^+ + DBM^− → [EuCl2(DBM)(TPPO)3] + Cl^− + KCl + PHEN	−298	−280	−18
[EuCl2(TPPO)3(BIPY)]^+ + Cl^− + K^+ + DBM^− → [EuCl2(DBM)(TPPO)3(BIPY)] + KCl	−648	−732	84
[EuCl2(TPPO)3(BIPY)]^+ + Cl^− + K^+ + DBM^− → [EuCl2(DBM)(TPPO)2(BIPY)] + KCl + TPPO	−790	−792	2
[EuCl2(TPPO)3(BIPY)]^+ + Cl^− + K^+ + DBM^− → [EuCl2(DBM)(TPPO)3] + KCl + BIPY	−722	−736	14
[EuCl2(TPPO)3(BIPY)]^+ + Cl^− + K^+ + DBM^− → [EuCl2(DBM)(TPPO)3(BIPY)] + Cl^− + KCl	−369	−416	47
[EuCl2(TPPO)3(BIPY)]^+ + Cl^− + K^+ + DBM^− → [EuCl2(DBM)(TPPO)2(BIPY)] + Cl^− + KCl + TPPO	−308	−293	−15
[EuCl2(TPPO)3(BIPY)]^+ + Cl^− + K^+ + DBM^− → [EuCl2(DBM)(TPPO)3] + Cl^− + KCl + BIPY	−272	−243	−29

---

From Table 6, eqn (18) is predicted to be the most favorable in terms of Δ_rG. The addition of the DBM ionic ligand to the intermediate complex seems to occur with dissociation of a TPPO non-ionic ligand, leading to the new intermediate complex [EuCl₂(DBM)(TPPO)₂(L′)]. Δ_rG values for the corresponding reactions are −789 kJ mol⁻¹ in average. Moreover, Δ_rG is governed by the enthalpy of reaction, Δ_rH, which for complex EuCl₂(DBM)(TPPO)₂(PHEN)] is −807 kJ mol⁻¹, and for complex [EuCl₂(DBM)(TPPO)₂(BIPY)] is −792 kJ mol⁻¹.

The second ionic ligand added in the one-pot syntheses was BTFA. This addition leads to the possibilities of reactions present in eqn (21)–(25). Table 7 shows RM1 calculated thermodynamic quantities for each possibility of the addition of the BTFA ionic ligand to the intermediate complexes [EuCl₂(DBM)(TPPO)₂(PHEN)] and [EuCl₂(DBM)(TPPO)₂(BIPY)].

[EuCl₂(DBM)(TPPO)₂(L′)] + K⁺ + BTFA⁻ → [EuCl₂(BTFA)(TPPO)₂(L′)] + DBM⁻ + K⁺ (21)

[EuCl₂(DBM)(TPPO)₂(L′)] + K⁺ + BTFA⁻ → [EuCl(DBM)(BTFA)(TPPO)₂(L′)] + KCl (22)

[EuCl₂(DBM)(TPPO)₂(L′)] + K⁺ + BTFA⁻ → [EuCl(DBM)(BTFA)(TPPO)(L′)] + KCl + TPPO (23)

[EuCl₂(DBM)(TPPO)₂(L′)] + K⁺ + BTFA⁻ → [EuCl(DBM)(BTFA)(L′)] + KCl + 2TPPO (24)

[EuCl₂(DBM)(TPPO)₂(L′)] + K⁺ + BTFA⁻ → [EuCl(DBM)(BTFA)(TPPO)₂] + KCl + L′ (25)

Table 7 RM1 thermodynamic data for step 3 of the syntheses of mixed ionic ligand complexes [Eu(DBM)(BTFA)(TTA)(PHEN)] and [Eu(DBM)(BTFA)(TTA)(BIPY)]. The thermodynamic calculations were performed at 298 K

Synthesis of [Eu(DBM)(BTFA)(TTA)(PHEN or BIPY)] – step 3	ΔrG (kJ mol^−1)	ΔrH (kJ mol^−1)	−TΔrS (kJ mol^−1)
[EuCl2(DBM)(TPPO)2(PHEN)] + K^+ + BTFA^− → [EuCl2(BTFA)(TPPO)2(PHEN)] + K^+ + DBM^−	92	101	−9
[EuCl2(DBM)(TPPO)2(PHEN)] + K^+ + BTFA^− → [EuCl(DBM)(BTFA)(TPPO)2(PHEN)] + KCl	−253	−278	25
[EuCl2(DBM)(TPPO)2(PHEN)] + K^+ + BTFA^− → [EuCl(DBM)(BTFA)(TPPO)(PHEN)] + KCl + TPPO	−260	−228	−32
[EuCl2(DBM)(TPPO)2(PHEN)] + K^+ + BTFA^− → [EuCl(DBM)(BTFA)(PHEN)] + KCl + 2TPPO	−166	−74	−92
[EuCl2(DBM)(TPPO)2(PHEN)] + K^+ + BTFA^− → [EuCl(DBM)(BTFA)(TPPO)2] + KCl + PHEN	−256	−216	−40
[EuCl2(DBM)(TPPO)2(BIPY)] + K^+ + BTFA^− → [EuCl2(BTFA)(TPPO)2(BIPY)]^− + K^+ + DBM^−	81	89	−8
[EuCl2(DBM)(TPPO)2(BIPY)] + K^+ + BTFA^− → [EuCl(DBM)(BTFA)(TPPO)2(BIPY)] + KCl	−258	−282	24
[EuCl2(DBM)(TPPO)2(BIPY)] + K^+ + BTFA^− → [EuCl(DBM)(BTFA)(TPPO)(BIPY)] + KCl + TPPO	−284	−244	−42
[EuCl2(DBM)(TPPO)2(BIPY)] + K^+ + BTFA^− → [EuCl(DBM)(BTFA)(BIPY)] + KCl + 2TPPO	−180	−91	−89
[EuCl2(DBM)(TPPO)2(BIPY)] + K^+ + BTFA^− → [EuCl(DBM)(BTFA)(TPPO)2] + KCl + BIPY	−229	−194	−35

---

Results shown in Table 7 suggest that the addition of BTFA occurs by a displacement of one Cl⁻ ligand, which precipitates as KCl salt, together with a dissociation of a TPPO ligand. The corresponding Δ_rG values are −260 kJ mol⁻¹ and −284 kJ mol⁻¹ for [EuCl(DBM)(BTFA)(TPPO)(PHEN)] and [EuCl(DBM)(BTFA)(TPPO)(BIPY)], respectively. In order to obtain the target products [Eu(DBM)(BTFA)(TTA)(PHEN)] and [Eu(DBM)(BTFA)(TTA)(BIPY)], the third ionic ligand added in the one-pot syntheses was TTA. Since TTA ionic ligand is not capable of displacing either DBM or BTFA ionic ligands, this addition leads to displacement of a chloride ligand followed by dissociation of a TPPO ligand. If the TPPO ligand coordination bond was stronger than the coordination bonds of either PHEN or BIPY, the target product would not have been obtained.

Table 8 shows two alternative reactions for the addition of a TTA ligand to the intermediate complexes [EuCl(DBM)(BTFA)(TPPO)(PHEN)] and [EuCl(DBM)(BTFA)(TPPO)(BIPY)], eqn (26) and (27).

[EuCl(DBM)(BTFA)(TPPO)(L′)] + K⁺ + TTA⁻ → [Eu(DBM)(BTFA)(TTA)(L′)] + KCl + TPPO (26)

[EuCl(DBM)(BTFA)(TPPO)(L′)] + K⁺ + TTA⁻ → [Eu(DBM)(BTFA)(TTA)(TPPO)] + KCl + L′ (27)

Table 8 RM1 thermodynamic data for step 4 of the syntheses of mixed ionic ligand complexes [Eu(DBM)(BTFA)(TTA)(PHEN)] and [Eu(DBM)(BTFA)(TTA)(BIPY)]. The thermodynamic calculations were performed at 298 K

Synthesis of [Eu(DBM)(BTFA)(TTA)(PHEN or BIPY)] – step 4	ΔrG (kJ mol^−1)	ΔrH (kJ mol^−1)	−TΔrS (kJ mol^−1)
[EuCl(DBM)(BTFA)(TPPO)(PHEN)] + K^+ + TTA^− → [Eu(DBM)(BTFA)(TTA)(PHEN)] + KCl + TPPO	−300	−249	−51
[EuCl(DBM)(BTFA)(TPPO)(PHEN)] + K^+ + TTA^− → [Eu(DBM)(BTFA)(TTA)(TPPO)] + KCl + PHEN	−290	−208	−82
[EuCl(DBM)(BTFA)(TPPO)(BIPY)] + K^+ + TTA^− → [Eu(DBM)(BTFA)(TTA)(BIPY)] + KCl + TPPO	−281	−246	−35
[EuCl(DBM)(BTFA)(TPPO)(BIPY)] + K^+ + TTA^− → [Eu(DBM)(BTFA)(TTA)(TPPO)] + KCl + BIPY	−233	−171	−62

---

The possibility presented in eqn (26) leads to the target products: [Eu(DBM)(BTFA)(TTA)(PHEN) and Eu(DBM)(BTFA)(TTA)(BIPY). However, in the possibility presented in eqn (27), the target product has not been obtained since the bidentate non-ionic ligand PHEN or BIPY is dissociated from the structure of the complex. Table 8 shows RM1 thermodynamic quantities for both possibilities in eqn (26) and (27).

Results in Table 8, indicate that RM1 clearly predicts that the target fully heteroleptic complexes [Eu(DBM)(BTFA)(TTA)(PHEN)], and [Eu(DBM)(BTFA)(TTA)(BIPY)] are indeed formed, instead of [Eu(DBM)(BTFA)(TTA)(TPPO), and [Eu(DBM)(BTFA)(TTA)(TPPO)]. This result was confirmed to be true, experimentally, for both cases studied.⁴⁰

3. Computational and experimental

3.1. Computational procedure

All calculations were carried out in isolated molecules, not on condensed phases at experimental conditions. That is why we regard the calculated quantities as figures of merit, we expect to be reliable in predicting trends in the thermodynamic properties for all actual reactions considered in this article. The first step of every computational calculation was always full RMl ¹ geometry optimizations of the species involved with the quantum chemical software MOPAC 2012. The keywords used were RM1 GNORM = 0.25 BFGS XYZ. Subsequently, we performed calculations of the vibrational modes and thermodynamic quantities, using the same model and software. The keywords used in this next step were RM1 AUX FORCE THERMO XYZ. For the complexes with counter ions in their structures, such as, the precursor complexes of the type [EuCl₂(L)₄]Cl,³⁸ we considered for the computational calculations only the species present in the coordination polyhedron, [EuCl₂(L)₄]⁺, and the chloride ion, each as an isolated species. For these species, either one of the keywords CHARGE = +1 or CHARGE = −1, as appropriate, was used in the calculations.

To carry out the calculations, we had to assume a coordination configuration for the complexes. Based on similar crystallographic structures deposited in the Cambridge Structural Database,⁴¹ we assumed that for the complexes of the type [Ln(β)₃(L,L′)] the ligands L are placed in the top and bottom axial directions. The structure of the precursor complex [EuCl₂(TPPO)₄]Cl was assumed to be homologous to its crystallographic one,⁴² in which the coordinated chloride ligands are placed in equatorial trans positions, one with respect to the other.

3.2. Materials

Reagents and solvents used were 1,3-diphenylpropane-1,3-dione (DBM, Alfa Aesar, 99%); 4,4,4-trifluoro-1-phenyl-1,3-butanedione (BTFA, Alfa Aesar, 99%); 1-(2-thenoyl)-3,3,3-trifluoroacetone (TTA, Alfa Aesar, 99%); triphenylphosphine oxide (TPPO, Sigma Aldrich, 99%); ethanol (J. T. Baker); hexane (Sigma Aldrich) and chloroform (J. T. Baker).

3.3. Characterization

All europium complexes synthesized in this article were characterized by MALDI-TOF mass spectrometry (Autoflex 3 Smart Beam Vertical spectrometer); elemental analysis (Perkin-Elmer CHN2400); infrared spectroscopy (samples were prepared as KBr disks, and the spectra were measured in a Bruker model IFS 66 spectrophotometer, 4000–400 cm⁻¹); ¹H NMR, ³¹P NMR and ¹⁹F NMR spectroscopy (NMR spectra of all complexes were obtained in CDCl₃ solutions by a Varian Unity Plus 400 MHz). The ESI† contains details of the experimental characterizations, data, spectra and all relevant spectral attributions for all complexes synthesized.

3.4. Syntheses

3.4.1. Synthesis of complex [EuCl₂(TPPO)₄]Cl·3H₂O. A solution of complex [EuCl₂(H₂O)₆]Cl (1 mmol) was prepared in 250 mL of pure ethanol under stirring conditions. Subsequently, TPPO ligand (4 mmol), which was previously dissolved in 50 mL of pure ethanol, was slowly added to the europium solution. The mixture was then left overnight with stirring and under reflux at 75 °C. Subsequently, the solvent was evaporated under reduced pressure until dryness. A white solid, [EuCl₃(TPPO)₄]·3H₂O, was obtained, and purified by recrystallization with a solution of water/ethanol (10 : 1). The supernatant solution was removed with a Pasteur pipette and the resulting solid was dried under vacuum for 24 h. Yield: 99%. Characterization: calculated MALDI-TOF/MS [M + H]⁺ (m/z) 1425.20 found (m/z) 1425.23, elemental analysis calculated C 60.66%, H 4.67%, found C 60.60%, H 4.61%, IR (KBr): νO–H 3461 cm⁻¹, ν=C–H 3090–3015 cm⁻¹, and νP=O 1087 cm⁻¹; ¹H NMR (400 MHz, CDCl₃): δ 7.60–7.31 ppm (m, Ar), and 2.61 ppm (s, OH); ³¹P NMR (162 MHz, CDCl₃): δ 27 ppm.

3.4.2. Synthesis of complex [EuCl₂(TTA)(TPPO)₃]. To a solution of 4 mmol of complex [EuCl₂(TPPO)₄]Cl·3H₂O in 100 mL of pure ethanol, we slowly added, under stirring conditions, 4 mmol of the previously deprotonated ligand TTA (by an equivalent proportion of KOH in a 30 mL solution). The pH of the solution was then adjusted to 6.5, when necessary, by using an KOH/ethanolic (0.1 mol L⁻¹) solution. This mixture was left under reflux (75 °C) and stirring for 24 h. Finally, the solvent was slowly evaporated at room temperature until dryness for a few days. A yellow solid was obtained and washed with water to remove the KCl salt formed. Then, hot hexane was added to remove the displaced TPPO ligand. The solid was recrystallized using ethanol. Yield: 65%. Characterization: calculated MALDI-TOF/MS [M + H]⁺ (m/z) 1280.11, found (m/z) 1279.98; elemental analysis calculated C 58.18%, H 3.94%, found C 58.32%, H 4.13%, IR (KBr): ν=C–H 3056 cm⁻¹, νC=O 1688 cm⁻¹, νP=O 1179–1115 cm⁻¹, νC–F 1287 cm⁻¹, and νS=C 1065 cm⁻¹; ¹H NMR (400 MHz, CDCl₃): δ 8.16 ppm (s, CH), δ 7.65–6.14 ppm (m, Ar), and δ 7.21–6.14 ppm (m, Th); ³¹P NMR (162 MHz, CDCl₃): δ 23 ppm, and δ −75 ppm; ¹⁹F NMR (376 MHz, CDCl₃): δ −82 ppm, and δ −83 ppm.

3.4.3. Synthesis of complex [EuCl₂(DBM)(TPPO)₃]. To a solution of 4 mmol of complex [EuCl₂(TPPO)₄]Cl·3H₂O in 100 mL of pure ethanol, we slowly added, under stirring conditions, 4 mmol of the previously deprotonated ligand DBM (by an equivalent proportion of KOH in a 30 mL solution). The pH of the solution was then adjusted to 6.5, when necessary, by using an KOH/ethanolic (0.1 mol L⁻¹) solution. This mixture was left under reflux (75 °C) and stirring for 24 h. Finally, the solvent was slowly evaporated at room temperature until dryness for a few days. A yellow solid was obtained and washed with water to remove the KCl salt formed. Then, hot hexane was added to remove the displaced TPPO ligand. The solid was recrystallized using ethanol. Yield: 93%. Characterization: calculated MALDI-TOF/MS [M + H]⁺(m/z) 1282.20 found (m/z) 1282.13; elemental analysis calculated C 64.65%, H 4.48%, found C 64.44%, H 4.57%; IR (KBr): ν=C–H 3062 cm⁻¹, νC=O 1594 cm⁻¹, νP=O 1148–1128 cm⁻¹; ¹H NMR (400 MHz, CDCl₃): δ 7.81 ppm (s, CH), and δ 7.56–7.36 ppm (m, Ar); ³¹P NMR (162 MHz, CDCl₃): δ 23 ppm, and δ −76 ppm.

3.4.4. Synthesis of complex [EuCl(TTA)(BTFA)(TPPO)₂]. To a solution of 4 mmol of complex [EuCl₂(TTA)(TPPO)₂] in 100 mL of pure ethanol, we slowly added, under stirring conditions, 4 mmol of the previously deprotonated ligand BTFA (by an equivalent proportion of KOH in a 30 mL solution). The pH of the solution was then adjusted to 6.5, when necessary, by using an KOH/ethanolic (0.1 mol L⁻¹) solution. This mixture was left under reflux (75 °C) and stirring for 24 h. Finally, the solvent was slowly evaporated at room temperature until dryness for a few days. A yellow solid was obtained and washed with water to remove the KCl salt formed. Then, hot hexane was added to remove the displaced TPPO ligand. The solid was recrystallized using ethanol. Yield: 72%. Characterization: calculated MALDI-TOF/MS [M + H]⁺ (m/z) 1183.10 found (m/z) 1183.16; elemental analysis calculated C 54.86%, H 3.58%, found C 54.94%, H 3.49%; IR (KBr): ν=C–H 3062 cm⁻¹, νC=O 1599 cm⁻¹, νP=O 1154–1116 cm⁻¹, νC–F 1185 cm⁻¹, and νS=C 1084 cm⁻¹; ¹H NMR (400 MHz, CDCl₃): δ 8.35 ppm (s, CH), δ 7.62–6.39 ppm (m, Ar), and δ 6.87–6.38 ppm (m, Ar); ³¹P NMR (162 MHz, CDCl₃): δ 29 ppm, and δ −72 ppm; ¹⁹F NMR (376 MHz, CDCl₃): δ −80 ppm.

3.4.5. Synthesis of complex [EuCl(DBM)(BTFA)(TPPO)₂]. To a solution of 4 mmol of complex [EuCl₂(DBM)(TPPO)₂] in 100 mL of pure ethanol, we slowly added, under stirring conditions, 4 mmol of the previously deprotonated ligand BTFA (by an equivalent proportion of KOH in a 30 mL solution). The pH of the solution was then adjusted to 6.5, when necessary, by using an KOH/ethanolic (0.1 mol L⁻¹) solution. This mixture was left under reflux (75 °C) and stirring for 24 h. Finally, the solvent was slowly evaporated at room temperature until dryness for a few days. A yellow solid was obtained and washed with water to remove the KCl salt formed. Then, hot hexane was added to remove the displaced TPPO ligand. The solid was recrystallized using ethanol. Yield: 87%. Characterization: calculated MALDI-TOF/MS [M + H]⁺ (m/z) 1185.19 found (m/z) 1185.26, elemental analysis calculated C 61.86%, H 4.17%, found C 61.97%, H 3.79%; IR (KBr): ν=C–H 3056 cm⁻¹, νC=O 1681 cm⁻¹, νP=O 1179–1116 cm⁻¹, and νC–F 1287 cm⁻¹; ¹H NMR (400 MHz, CDCl₃): δ 7.94 ppm (s, CH), δ 7.57–7.44 ppm (m, Ar), and; ³¹P NMR (162 MHz, CDCl₃): δ 20 ppm, and δ −80 ppm; ¹⁹F NMR (376 MHz, CDCl₃): δ −81 ppm, and −82 ppm.

3.4.6. Synthesis of complex [Eu(DBM)(BTFA)(TTA)(TPPO)₂] obtained via synthetic route 1. To a solution of 4 mmol of complex [EuCl(TTA)(BTFA)(TPPO)₂] in 100 mL of pure ethanol, we slowly added, under stirring conditions, 4 mmol of the previously deprotonated ligand DBM (by an equivalent proportion of KOH in a 30 mL solution). The pH of the solution was then adjusted to 6.5, when necessary, by using an KOH/ethanolic (0.1 mol L⁻¹) solution. This mixture was left under reflux (75 °C) and stirring for 24 h. Finally, the solvent was slowly evaporated at room temperature until dryness for a few days. A yellow solid was obtained and washed with water to remove the KCl salt formed. Then, hot hexane was added to remove the displaced TPPO ligand. The solid was recrystallized using ethanol. Yield: 78%. Characterization: calculated MALDI-TOF/MS [M + H]⁺ (m/z) 1372.21 found (m/z) 1372.24, elemental analysis calculated C 60.44%, H 3.97%, found C 60.27%, H 3.80%; IR (KBr): ν=C–H 3056 cm⁻¹, νC=O 1681 cm⁻¹, νP=O 1179–1116 cm⁻¹, νC–F 1294 cm⁻¹, and νS=C 1065 cm⁻¹; ¹H NMR (400 MHz, CDCl₃): δ 8.21 ppm (s, CH), and δ 7.63–7.29 ppm (m, Ar); ³¹P NMR (162 MHz, CDCl₃): δ 25 ppm, and δ −78 ppm; ¹⁹F NMR (376 MHz, CDCl₃): δ −79 ppm, and δ −80 ppm.

3.4.7. Synthesis of complex [Eu(DBM)(BTFA)(TTA)(TPPO)₂] obtained via synthetic route 6. To a solution of 4 mmol of complex [EuCl(DBM)(BTFA)(TPPO)₂] in 100 mL of pure ethanol, we slowly added, under stirring conditions, 4 mmol of the previously deprotonated ligand TTA (by an equivalent proportion of KOH in a 30 mL solution). The pH of the solution was then adjusted to 6.5, when necessary, by using an KOH/ethanolic (0.1 mol L⁻¹) solution. This mixture was left under reflux (75 °C) and stirring for 24 h. Finally, the solvent was slowly evaporated at room temperature until dryness for a few days. A yellow solid was obtained and washed with water to remove the KCl salt formed. Then, hot hexane was added to remove the displaced TPPO ligand. The solid was recrystallized using ethanol. Yield: 94%. Characterization: calculated MALDI-TOF/MS [M + H]⁺ (m/z) 1372.21 found (m/z) 1372.31, elemental analysis calculated C 60.44%, H 3.97%, found C 60.31%, H 3.56%, IR (KBr): ν=C–H 3056 cm⁻¹; νC=O 1612–1593 cm⁻¹; νP=O 1166–1122 cm⁻¹; νC–F 1281 cm⁻¹; νS=C 1071 cm⁻¹; ¹H NMR (400 MHz, CDCl₃): δ 7.77 ppm (s, CH), and δ 7.57–7.45 ppm (m, Ar); ³¹P NMR (162 MHz, CDCl₃): δ 27 ppm, and δ −73 ppm; ¹⁹F NMR (376 MHz, CDCl₃): δ −78 ppm, and δ −80 ppm.

4. Conclusions

We present for the first-time evidence that RM1 quantum chemical calculations of thermodynamic quantities of chemical reactions involving europium trivalent ions output results which are useful as figures of merit for the experimental chemist, and exemplify with strategies for devising actual syntheses of mixed ligand europium complexes.

Calculations of such figures of merit assume that condensed phase effects alter the calculated thermodynamic quantities in systematic manners, allowing the relative comparison and ordering of the chemical reactions in terms of calculated free energies of the corresponding gas phase reactions, Δ_rG.

We subsequently introduce the concept of strength of coordination bonding of ligands based on the calculation of RM1 thermodynamic quantities using the isolated molecule model, showing, for example, that the CF₃ groups of BTFA and TTA weaken their coordination bonds to the europium ion when compared to DBM.

We then advance the concept of a series of ligands ordered in terms of their relative displacement abilities in ligand exchange reactions. First, we bring out the series of relative displacement abilities for the β-diketonate ligands considered: DBM > BTFA ≈ TTA. Then, we show how this series can help the experimentalist decide with high likelihood, of all possibilities, which would be the most efficient sequence of addition of ionic ligands to obtain the best total reaction yield; and exemplify with two alternate syntheses of [Eu(DBM)(BTFA)(TTA)(TPPO)₂]. Surely, the synthetic route that added the ionic ligands per the series of their relative displacement abilities exhibited a yield of 76%; whereas the one that inverted that series displayed less than half that yield: 37%.

We also showed that the real reason why chloride ions can be easily displaced by other ionic ligands is the formation of the precipitated salt, KCl. This also explains why non-ionic ligands are not capable of displacing chloride ions: because non-ionic ligands lack the alkali metal cation because they need no counter ions. Thus, in such situations, no precipitates would be formed and Δ_rG would not be lowered by −479 kJ mol⁻¹ for the precipitated KCl (or by similar values depending on the cation involved).

Then, we introduce the series of relative displacement abilities for the non-ionic ligands considered: monodentates, both as single and as pairs, and bidentates: (TPPO,TPPO) > BIPY > PHEN ≈ (PTSO,PTSO) > (DBSO,DBSO) > TPPO > PTSO > DBSO > H₂O. We then show how this series can be used to hypothesize which reactions are likely happening in the one-pot syntheses we carried out of [Eu(DBM)(BTFA)(TTA)(PHEN)] and Eu(DBM)(BTFA)(TTA)(BIPY), starting from [EuCl₂(TPPO)₄]Cl.

Finally, according to the displacement series of non-ionic ligands, a PHEN or a BIPY would be unable to displace two TPPOs. Thus the preparation of either of the totally heteroleptic complexes [Eu(DBM)(BTFA)(TTA)(PHEN)], or [Eu(DBM)(BTFA)(TTA)(BIPY)], would not be possible using the intermediate [Eu(DBM)(BTFA)(TTA)(TPPO)₂]. However, knowing that a PHEN or a BIPY can displace a single TPPO, we prepared those compounds in a one-pot synthesis starting from [Eu(Cl)₂(TPPO)₄]Cl. We also put forward, per our RM1 calculations, the most likely sequence of chemical reactions to explicate these one-pot syntheses.

Nowadays, although many articles are published on lanthanide complexes, less than 5% of them use computational chemistry tools.⁴³ Our novel results indicate that there is a wealth of useful information to the lanthanide chemistry experimentalist that can be obtained from easy and fast RM1 quantum chemistry calculations.

Acknowledgements

The authors appreciate the financial support of the following Brazilian Agencies, Institutes and Networks: FACEPE (Pronex), CAPES, and CNPq. The authors also thank Centro de Tecnologias Estratégicas do Nordeste, CETENE, and Dr Júlia F. Campos for the MALDI-TOF mass spectrometry measurements.

References

1. M. A. M. Filho, J. D. L. Dutra, H. L. B. Cavalcanti, G. B. Rocha, A. M. Simas and R. O. Freire, J. Chem. Theory Comput., 2014, 10, 3031–3037.
2. W. Sun, S. Thies, J. Zhang, C. Peng, G. Tang, M. Shen, A. Pich and X. Shi, ACS Appl. Mater. Interfaces, 2017, 9, 3411–3418.
3. J. Schmitt, V. Heitz, A. Sour, F. Bolze, P. Kessler, L. Flamigni, B. Ventura, C. S. Bonnet and É. Tóth, Chemistry, 2016, 22, 2775–2786.
4. A. Lotfi, J. L. Manzoori and A. Mohagheghi, J. Lumin., 2017, 185, 132–140.
5. H. Ma, B. Song, Y. Wang, C. Liu, X. Wang and J. Yuan, Dyes Pigm., 2017, 140, 407–416.
6. M. Donmez, M. D. Yilmaz and B. Kilbas, J. Hazard. Mater., 2017, 324, 593–598.
7. O. A. Goryacheva, N. V. Beloglazova, A. M. Vostrikova, M. V. Pozharov, A. M. Sobolev and I. Y. Goryacheva, Talanta, 2017, 164, 377–385.
8. M. R. Ganjali, M. B. Gholivand, M. Rahimi-Nasrabadi, B. Maddah, M. Salavati-Niasari and F. Ahmadi, Sens. Lett., 2006, 4, 356–363.
9. M. Rahimi-Nasrabadi, M. Behpour, A. Sobhani-Nasab and S. Mostafa Hosseinpour-Mashkani, J. Mater. Sci.: Mater. Electron., 2015, 26, 9776–9781.
10. M. A. M. Filho, J. D. L. Dutra, G. B. Rocha, R. O. Freire and A. M. Simas, RSC Adv., 2013, 3, 16747.
11. G. B. Rocha, R. O. Freire, A. M. Simas and J. J. P. Stewart, J. Comput. Chem., 2006, 27, 1101–1111.
12. N. B. D. Lima, A. I. S. Silva, S. M. C. Gonçalves and A. M. Simas, J. Lumin., 2016, 170, 505–512.
13. N. B. D. Lima, S. M. C. Gonçalves, S. a. Júnior and A. M. Simas, Sci. Rep., 2013, 3, 2395.
14. A. I. S. Silva, V. F. C. Santos, N. B. de Lima, A. Simas and S. M. d C. Gonçalves, RSC Adv., 2016 10.1039/c6ra20609c.
15. Z. Zheng, J. Wang, H. Liu, M. D. Carducci, N. Peyghambarian and G. E. Jabbourb, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2002, 58, m50–m52.
16. F. Xie and Z. Zheng, Phys. B, 2004, 349, 415–419.
17. N. B. D. Lima, A. I. S. Silva, P. C. Gerson, S. M. C. Gonçalves and A. M. Simas, PLoS One, 2015, 10, e0143998.
18. F. R. G. e. Silva, J. F. S. Menezes, G. B. Rocha, S. Alves, H. F. Brito, R. L. Longo and O. L. Malta, J. Alloys Compd., 2000, 303–304, 364–370.
19. G. B. Hadjichristov, I. L. Stefanov, S. S. Stanimirov and I. K. Petkov, Spectrochim. Acta, Part A, 2010, 75, 448–452.
20. O. L. Malta, H. F. Brito, J. F. S. Menezes, F. R. G. Silva, C. D. M. Donegá and S. Alves Jr, Chem. Phys. Lett., 1998, 282, 233–238.
21. E. E. S. Teotonio, H. F. Brito, G. F. de Sá, M. C. F. C. Felinto, R. H. A. Santos, R. M. Fuquen, I. F. Costa, A. R. Kennedy, D. Gilmore and W. M. Faustino, Polyhedron, 2012, 38, 58–67.
22. D. B. A. Raj, B. Francis, M. L. P. Reddy, R. R. Butorac, V. M. Lynch and A. H. Cowley, Inorg. Chem., 2010, 49, 9055–9063.
23. O. Moudam, B. C. Rowan, M. Alamiry, P. Richardson, B. S. Richards, A. C. Jones and N. Robertson, Chem. Commun., 2009, 6649–6651.
24. E. Niyama, H. F. Brito, M. Cremona, E. E. S. Teotonio, R. Reyes, G. E. S. Brito and M. C. F. C. Felinto, Spectrochim. Acta, Part A, 2005, 61, 2643–2649.
25. E. R. Dos Santos, R. O. Freire, N. B. Da Costa, F. A. A. Paz, C. A. De Simone, S. A. Juúnior, A. A. S. Arauújo, L. A. O. Nunes, M. E. De Mesquita and M. O. Rodrigues, J. Phys. Chem. A, 2010, 114, 7928–7936.
26. B. Francis, C. Heering, R. O. Freire, M. L. P. Reddy and C. Janiak, RSC Adv., 2015, 5, 90720–90730.
27. D. F. Parra, A. Mucciolo, D. G. Duarte, H. F. Brito and A. B. Lugão, J. Appl. Polym. Sci., 2006, 100, 406–412.
28. S. S. Stanimirov, G. B. Hadjichristov and I. K. Petkov, Spectrochim. Acta, Part A, 2007, 67, 1326–1332.
29. H. Liang, B. Chen and Z. Zheng, Phys. Status Solidi B, 2004, 241, 3056–3061.
30. B. Chen, J. Xu, N. Dong, H. Liang, Q. Zhang and M. Yin, Spectrochim. Acta, Part A, 2004, 60, 3113–3118.
31. B. Chen, N. Dong, J. Xu, H. Liang, Q. Zhang, M. Yin and Z. Zheng, Spectrochim. Acta, Part A, 2006, 63, 289–294.
32. V. van Speybroeck, R. Gani and R. J. Meier, Chem. Soc. Rev., 2010, 39, 1764.
33. R. A. Barrett and R. J. Meier, J. Mol. Struct.: THEOCHEM, 1996, 363, 203–209.
34. B. deB Darwent, Bond Dissociation Energies in Simple Molecules, U.S. National Bureau of Standards, Washington, 1st edn, 1970.
35. A. Kramida, Y. Ralchenko, J. Reader and NIST ASD Team, NIST Atomic Spectra Database Version 5, National Institute of Standards and Technology, Gaithersburg, MD, 2014, accessed Jul 17, 2016, http://physics.nist.gov/asd.
36. U. Berzinsh, M. Gustafsson, D. Hanstorp, A. Klinkmüller, U. Ljungblad and A.-M. Mårtensson-Pendrill, Phys. Rev. A, 1995, 51, 231–238.
37. E. B. Rudnyi, D. W. Bonnell and J. W. Hastie, Vaporization thermodynamics of KCl, accessed Jul 17, 2016, http://evgenii.rudnyi.ru/doc/papers1/98kcleng.pdf.
38. F. Tambornino, P. Bielec and C. Hoch, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2014, 70, i27.
39. M. Li, D. Constantinescu, L. Wang, A. Mohs and J. Gmehling, Ind. Eng. Chem. Res., 2010, 49, 4981–4988.
40. A. I. S. Silva, V. F. C. Santos, N. B. D. Lima, A. M. Simas and S. M. C. Gonçalves, RSC Adv., 2016, 6, 90934–90943.
41. L. Zuogen, Chin. J. Struct. Chem., 1988, 165.
42. M. J. Glazier, W. Levason, M. L. Matthews, P. L. Thornton and M. Webster, Inorg. Chim. Acta, 2004, 357, 1083–1091.
43. J. D. L. Dutra, T. D. Bispo and R. O. Freire, J. Comput. Chem., 2014, 35, 772–775.

---

Footnote

† Electronic supplementary information (ESI) available: Characterization data: infrared, and ¹H, ¹⁹F, and ³¹P NMR spectra. See DOI: 10.1039/c7ra02019h

---