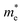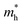Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Single- and few-layer BiOI as promising photocatalysts for solar water splitting
Jiajun Wang*a,
Ming Zhanga,
Jie Mengb,
Qunxiang Li *b and
Jinlong Yang
*b and
Jinlong Yang b
b
aTianjin Key Laboratory of Structure and Performance for Functional Molecules, Key Laboratory of Inorganic–Organic Hybrid Functional Materials Chemistry, Ministry of Education, College of Chemistry, Tianjin Normal University, Tianjin 300387, China. E-mail: hxxywjj@mail.tjnu.edu.cn
bHefei National Laboratory for Physical Sciences at the Microscale, Synergetic Innovation Center of Quantum Information and Quantum Physics, University of Science and Technology of China, Hefei, Anhui 230026, China. E-mail: liqun@ustc.edu.cn
First published on 5th May 2017
Abstract
Recently novel two-dimensional materials for solar water splitting have drawn enormous research attention because of their tunable electronic properties for enhancing photocatalytic performance. Here, based on extensive density functional theory calculations, we clearly reveal that single- and few-layer BiOI have favorable band gaps, light electron effective masses, excellent optical absorptions, and nice band edge alignments with the water redox potentials. Moreover, due to the weak interlayer interactions, these remarkable electronic properties are robust, and almost independent of the layer thickness of the BiOI nanosheets. Our theoretical results suggest that the BiOI nanosheets can be efficient photocatalysts for solar water splitting.
1 Introduction
The increasingly serious energy crisis and the environmental contamination caused by burning fossil fuels have led to the urgent need for renewable and environmentally benign alternative energy resources. Hydrogen, a sustainable and clean energy source with the combustion product of only water, has been considered as a promising energy carrier for the future. Given the natural abundance of water and sunlight, the use of semiconductors with solar energy to split water could provide a practical and reliable route to clean hydrogen fuel generation.1,2 Hence, the development of highly efficient and active semiconductor photocatalysts for hydrogen production is in great demand.Since the pioneering work by Fujishima and Honda on photoelectrochemical water splitting on a TiO2 electrode,3 hundreds of semiconductor materials and their derivatives have been proposed as photocatalysts for water splitting, such as metal oxides, sulfides, nitrides, and oxynitrides.4–8 Unfortunately, photocatalysts for practical applications with relatively high productivity are limited so far.9–11
Usually, for a desirable semiconductor to facilitate photocatalytic water splitting, two important conditions need to be satisfied: (1) the ideal band gap of the semiconductor should be around 2.0 eV to allow for the electrons and holes to overcome kinetic barriers while still harvesting a significant fraction of solar light;12,13 (2) a suitable semiconductor photocatalyst requires a conduction band minimum (CBM) energy that is more negative than the reduction potential of H+/H2 (0 V vs. NHE) and its valence band maximum (VBM) energy must be more positive than the oxidation potential of O2/H2O (1.23 V vs. NHE).14,15 Under these conditions, the excited electrons can participate in the reduction reaction to generate hydrogen and the holes take part in the oxidation reduction reaction generating oxygen when sunlight shines on a semiconductor photocatalyst.
Since the experimental realization of graphene,16 two-dimensional (2D) layered materials, such as metal oxides, MXenes, graphitic C3N4, and transition metal chalcogenides, have attracted intense research interest in the field of photocatalytic water splitting.17–24 These 2D layered semiconductors possess diverse and tunable electronic and optical properties, exhibiting the more efficient use of visible-light in the photocatalytic process.25,26 Moreover, 2D materials not only have ultra-high specific surface areas available for photocatalytic reactions, but they also have the minimum distance for the photogenerated electrons and holes to migrate, reducing the possibility of electron–hole recombination, and then giving high quantum yields.27
In general, the electronic structures of 2D layered semiconductors are strongly dependent on their thicknesses.28,29 From a single-layer to a few layers, the band gap and the conduction and valence band positions will change a lot, such as for MoS2 and phosphorene.30,31 Since accurate control of the layer number is quite difficult in experiments, the potential applications of 2D layered semiconductors as photocatalysts are seriously limited by the thickness-dependent electronic properties. Thus, searching for 2D photocatalysts with suitable, thicknesses-independent band gaps and band edge positions is urgently needed.
Recently, bismuth oxyhalides (BiOX, X = Cl, Br, I), which are a new family of promising photocatalysts, have drawn enormous research attention because of their unique 2D layered structures.32–35 However, the fast recombination of charges and poor conductivity significantly limit the practical application of photocatalytic water splitting for hydrogen production. In order to improve the photocatalytic activity of BiOX, various strategies have been developed, such as doping, the deposition of noble metals, the control of crystal facets, and heterojunctions.36 In particular, great efforts have been devoted to synthesising BiOX nanosheets exposed with {001} facets, which exhibit excellent photocatalytic activities under visible-light illumination.37–42 For instance, Guan et al.38 found that ultrathin BiOCl nanosheets show excellent solar photocatalytic activity, even with an extremely low photocatalyst loading. A similar phenomenon has also been found in BiOBr and BiOI, where these nanosheets with large exposed surface areas of the {001} facets exhibited higher photocatalytic activities.39–42 Among these 2D nanosheets of BiOX, bismuth oxyiodide (BiOI) is considered to be a potentially interesting visible-light active photocatalyst due to the suitable band gap.41 However, only a few computational studies have been carried out on BiOX,43–46 and more attention should be paid to BiOI nanosheets to explore whether these single- and few-layer BiOI have outstanding electronic and optical properties for solar water splitting.
In this work, the stability, electronic and optical properties of single- and few-layer BiOI are systematically investigated based on first principles calculations. We first concentrate on exploring the electronic structure properties, the optical properties and the band edge positions of single-layer BiOI. We then discuss the effect of the layer numbers on the band gaps and the VBM/CBM positions of few-layer BiOI. The obtained results clearly reveal that the BiOI nanosheets possess suitable band gaps, excellent band edge alignment, a superior optical absorption property, and thickness-independent electronic properties. That is to say, BiOI nanosheets should be efficient photocatalysts for solar water splitting.
2 Computational model and methods
First-principles calculations are performed based on density functional theory (DFT) using the Vienna Ab initio Simulation Package (VASP).47 The generalized gradient approximation in the Perdew, Burke, and Ernzerhof form (GGA-PBE) is adopted as the exchange correlation functional48 for the geometry relaxations. In our electronic structure calculations, in order to avoid the disadvantages of GGA-PBE calculations for predicting the band gap and optical absorption spectra, we adopt the Heyd–Scuseria–Ernzerhof (HSE06) hydride functional,49,50 which can successfully describe the electronic structures and defect levels of transition metal oxides.51 Meanwhile, a van der Waals correction proposed by Grimme is also incorporated to better describe nonbonding interactions.52 The interaction between the core and valence electrons is described using the frozen-core projector augmented wave approach.53 A vacuum region greater than 18.0 Å perpendicular to the sheets (along the c-axis) is applied to avoid interactions between the layers caused by the periodic boundary conditions. The cutoff energy is set to 520 eV, and the Monkhorst–Pack mesh of k-points54 with 15 × 15 × 1 points is used to sample the Brillouin zone. All atomic positions are fully relaxed by using the conjugate gradient algorithm until the total energy and atomic forces are converged to 10−5 eV and 0.01 eV Å−1.Here, the VBM and CBM positions of single- and few-layer BiOI are determined by the calculated band gap center energy (EBGC) and the band gaps Eg, as
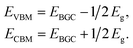 | (1) |
In contrast to the band gaps, the band gap center energies are insensitive to the choice of exchange–correlation functional.55 Thus, the less computationally expensive PBE functional is used with confidence for calculating the EBGC and the more accurate HSE06 functional is employed to calculate the band gaps. To align the energy levels for the different materials, their vacuum levels are set to zero. For the water splitting reaction, the commonly used values of the standard reduction potential for H+/H2 and the oxidation potential for O2/H2O are −4.44 and −5.67 eV, respectively.27
To evaluate the optical properties of single- and few-layer BiOI, the optical absorption spectra are simulated by converting the complex dielectric function to the absorption coefficient αabs according to the following relation,56
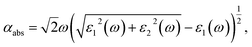 | (2) |
3 Results and discussion
The initial structure for the geometric relaxation of single-layer BiOI is constructed from the (001) plane of the bulk structure. A typical atomic structure is illustrated in Fig. 1(a), and the unit cell is composed of one [Bi2O2]2+ slab and two iodine atoms. Upon relaxation at the PBE level, the lateral lattice constants (a and b, they are equal) for single-layer BiOI are optimized to be 4.02 Å, which is very close to the experimental value of 3.99 Å for bulk BiOI.57 The relative deviation of the lattice parameter is below 1%, indicating that exfoliated free-standing single-layer BiOI can keep its geometric integrity and experiences negligible relaxation or construction.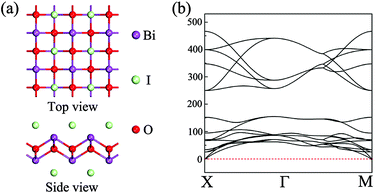 | ||
| Fig. 1 (a) Top and side views of the geometric structure of single-layer BiOI. (b) Phonon spectra for single-layer BiOI along the high-symmetric points in the Brillouin zone. | ||
Subsequently, we compare the stability of single-layer BiOI to its bulk form via calculating the formation energy (Ef), which is defined as
| Ef = E2D/N2D − E3D/N3D, | (3) |
In order to check the dynamical stability of single-layer BiOI, we calculate its phonon spectra by post-processing the force constants calculated with density functional perturbation theory as implemented in VASP and the Phonopy package.59 It can be clearly seen from Fig. 1(b) that no imaginary vibration frequency is found at any wave vector, which indicates that this freestanding single-layer BiOI has a high dynamic stability.
After exploring the possibility of exfoliating single-layer BiOI from its bulk form, we now turn to calculate its electronic properties. The band structures of the single-layer BiOI are calculated by the HSE06 functional, and they are plotted in Fig. 2(a). Clearly, the CBM is located at the Γ point, while the VBM is located between the X and Γ points in the irreducible Brillouin zone. Single-layer BiOI exhibits an indirect semiconductor characteristic. This indirect band gap is predicted to be 2.28 eV, indicating that single-layer BiOI possesses excellent capability for harvesting solar light. Usually, an indirect band gap will make the material a poor absorber of light since phonons are required to mediate electronic excitations from the VBM to the CBM. Fortunately, the direct band gap (2.55 eV) at the Γ point is close to the predicted indirect band gap with an energy difference of 0.3 eV, and thus can partly abate the disadvantage.
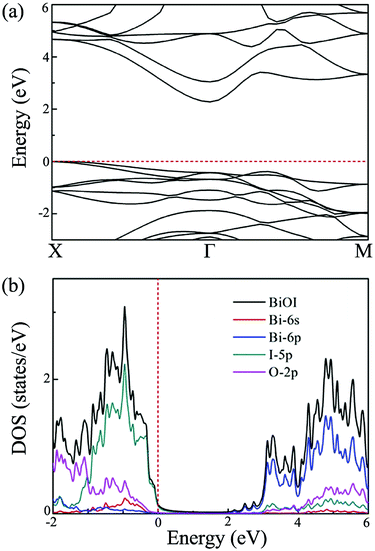 | ||
| Fig. 2 (a) Band structure, and (b) density of states of single-layer BiOI at the HSE level. Here, the Fermi energy is set to zero. | ||
To explore the electronic properties more clearly, we further calculate the total density of states (DOS) and projected DOS for single-layer BiOI. The obtained results are plotted in Fig. 2(b). It is clear that the states near the VBM are mainly contributed to by the 5p orbitals of the I atom, while the states near the CBM mainly originate from the 6p orbitals of the Bi atom. It is thus reasonable to expect that the conduction and valence band edges with different characteristics would cause a big difference between the 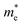 and the
and the 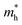 .
.
In general, precise control of the layer number is quite challenging in experiments, thus, the BiOI nanosheet synthesized in experiments is usually of the nanometer-scale thickness.41,42 One would wonder whether the band structure of BiOI could show a thickness-independent behavior. To examine the thickness dependence of their electronic properties, we calculate the band structures of few-layer BiOI (2 to 5 layers) at the HSE level, as shown in Fig. 3. Interestingly, compared with the single-layer, there is little change in the band structures on increasing their thickness. All few-layer BiOI are indirect gap semiconductors. As shown in Table 1, the band gaps decrease very slightly as the thickness increases. For example, the band gap is slightly reduced to 2.22 eV for 5-layer BiOI, which is only a 0.06 eV decrease compared to the band gap value of the single-layer BiOI. That is to say, the band gaps of few-layer BiOI are almost insensitive to the layer thickness, which is in sharp contrast to most other 2D materials, such as MoS2.30,60 The remarkable properties of the BiOI nanosheets are almost insensitive to the layer thickness due to the weak interlayer interactions since the vertical separation between two neighboring layers is predicted to be about 3.97 Å. As an example, we further plot the charge density of the CBM and VBM of 2-layer BiOI in Fig. 3(e). It is clear that the charge density highly localizes within each layer while its distribution at the interfacial region is neglectable, indicating that the interlayer interaction is weak.
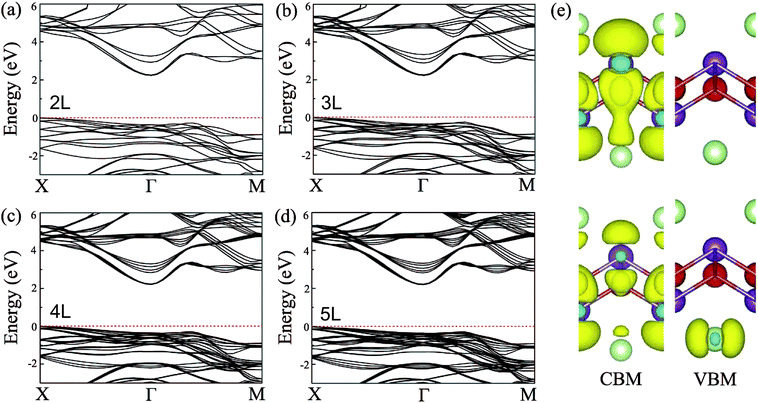 | ||
| Fig. 3 Band structures of the (a) 2-layer, (b) 3-layer, (c) 4-layer, and (d) 5-layer BiOI nanosheets at the HSE06 level. (e) Spatial distribution of charge density of the CBM and VBM of 2-layer BiOI. | ||
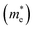 and hole
and hole 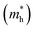 effective mass of single- and few-layer BiOI at the Γ point (for electrons) and at the X point (for holes) in the Brillouin zone in the units of free-electron mass are also listed
effective mass of single- and few-layer BiOI at the Γ point (for electrons) and at the X point (for holes) in the Brillouin zone in the units of free-electron mass are also listed
As we know, the separation and diffusion rate of the photoinduced electrons and holes are important indexes for an excellent photocatalyst.61,62 In general, if the effective mass of the photogenerated carrier is lighter, the carriers will have more probability of reaching the surface reaction sites within their life-time, thus improving the photocatalytic activity.63 In principle, the curvatures of the top of the valence band and bottom of the conduction band determine the hole and electron effective masses, respectively. Here, the effective masses of the electron 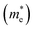 and hole
and hole 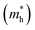 are estimated by fitting parabolic functions to the VBMs and CBMs of single-layer BiOI. The photo-generated electrons have a relatively lighter effective mass with values of 0.36me, which are smaller than those of some common photocatalysts.64,65 The relatively small
are estimated by fitting parabolic functions to the VBMs and CBMs of single-layer BiOI. The photo-generated electrons have a relatively lighter effective mass with values of 0.36me, which are smaller than those of some common photocatalysts.64,65 The relatively small 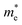 indicates that the migration of photogenerated electrons to the reactive sites would be easier in the photocatalytic process. This is consistent with the high carrier mobility reported by Fan et al.41 On the other hand, the
indicates that the migration of photogenerated electrons to the reactive sites would be easier in the photocatalytic process. This is consistent with the high carrier mobility reported by Fan et al.41 On the other hand, the 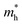 at the VBM is calculated to be 2.46me along X–Γ, thus, the photo-generated holes diffuse relatively slowly. The significant difference between the
at the VBM is calculated to be 2.46me along X–Γ, thus, the photo-generated holes diffuse relatively slowly. The significant difference between the 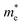 and the
and the 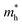 leads to the effective separation of the electron–hole pairs, which may reduce the recombination probability of the photogenerated carriers. As listed in Table 1, similar results are observed for these few-layer BiOI nanosheets.
leads to the effective separation of the electron–hole pairs, which may reduce the recombination probability of the photogenerated carriers. As listed in Table 1, similar results are observed for these few-layer BiOI nanosheets.
As mentioned in the Introduction, to effectively utilize visible light for water splitting, the typical band gap of the semiconductor should lie within the range of 2.0 to 3.0 eV. As shown in Table 1, all of the BiOI nanosheets possess a band gap of about 2.3 eV within the visible spectrum. That is to say, these BiOI nanosheets have great potential to harvest a significant fraction of solar light. Besides a suitable band gap being needed to enhance visible-light absorption, a semiconductor photocatalyst also requires favorable band edge positions to fit the water oxidation and reduction potentials. To confirm whether these BiOI materials are photocatalytically active for water splitting, we calculate the band edge positions for single- and few-layer BiOI relative to the vacuum energy level based on eqn (1). It is well known that the oxidation and reduction abilities are measured by the VBM energy and the CBM energy, respectively. The higher the CBM energy to the hydrogen production level, the stronger the reducing power is, while the lower the VBM energy, the stronger the oxidizing power is.66,67
As shown in Fig. 4(a), for single-layer BiOI, the CBM and VBM are predicted to be located at −4.18 and −6.46 eV, respectively. Comparing with the water redox potentials, the CBM is located at −0.26 eV, just above the reduction potential of H+/H2, whereas the VBM is found to be 0.79 eV below the oxidation potential of O2/H2O. This indicates that both the water oxidation and reduction reactions are thermodynamically feasible for single-layer BiOI without an additional bias voltage. In addition, it should be noted that the standard redox potentials for water splitting shown in Fig. 4(a) are at the condition of pH = 0, and they will increase with pH by pH × 0.059 eV, shifting the oxidation and reduction potentials of water upward.22,23 Clearly, this shift is beneficial to the oxygen evolution reaction while being disadvantageous to the hydrogen reduction reaction. Once the pH values of the solutions exceed about 4.4, the CBM energy of single-layer BiOI will be lower than the reduction potential of H+/H2, and then the reduction reactions will be energetically unfavorable.
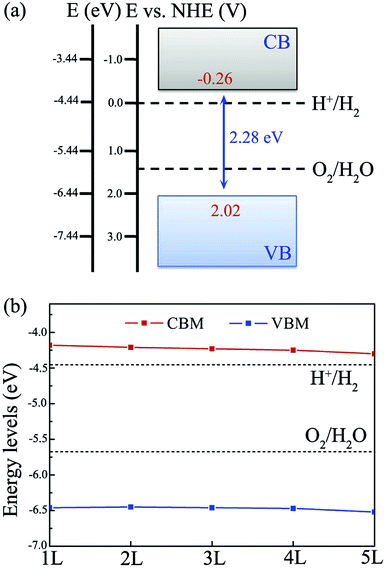 | ||
| Fig. 4 Band edge positions of (a) single-layer BiOI and (b) few-layer BiOI with reference to the water redox potentials of H+/H2 and O2/H2O at pH = 0. | ||
In the case of few-layer BiOI, as shown in Fig. 4(b), the VBM and CBM energy levels for 2- to 5-layer BiOI show minor changes compared to those of the single-layer BiOI. Moreover, all of the BiOI nanosheets have band edges located in energetically favorable positions for both water oxidation and reduction reactions. For 5-layer BiOI, the CBM is about 0.14 eV above the water reduction level, whereas the VBM is about 0.85 eV below the water oxidation potential. This observation suggests that the BiOX nanosheets are still able to produce hydrogen and oxygen with up to 5 layers. Thus, accurate control of the layer number is dispensable during the sample preparation if BiOI is used as a photocatalyst for solar water splitting.
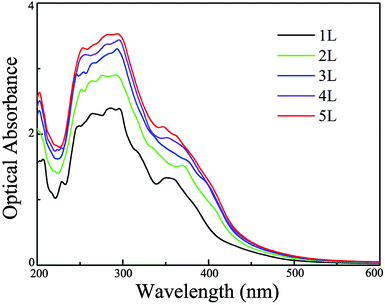
In addition to the above mentioned requirements for an appropriate and thickness-independent band gap and band edge positions, another very important condition for efficient photocatalytic water splitting is that the materials should capture a significant fraction of visible light because it counts for more than 40% of the solar spectrum.68 Consequently, we further simulate optical absorption spectra of single- and few-layer BiOI using the HSE06 functional to examine whether they meet the criteria for efficient visible-light absorption. As shown in Fig. 5, single-layer BiOI has a perfect optical absorption in the solar spectrum since it can harvest the major portion of solar light (400–500 nm), demonstrating its potential as an excellent light-absorber, although single-layer BiOI is an indirect semiconductor. Interestingly, when the layer number increases, the absorption edges do not obviously change while the absorption intensity increases in comparison to that of the single-layer BiOI. From the optical absorption spectra, for up to five layers, the BiOI nanosheets still show substantial adsorption in the visible-light region at about 500 nm. Such a high optical absorption efficiency suggests that the BiOI nanosheets are promising photocatalysts with potential applications in the use of solar energy for water splitting.
As mentioned in the Introduction, to effectively utilize solar energy for water splitting, the optimal band gap of the photocatalyst should lie within the range of 2.0 to 3.0 eV and the band edges should straddle the water redox potentials. Single- and few-layer BiOI have suitable band gaps (2.3 eV) for water splitting, but their CBM positions are located just slightly above the reduction potential of water, which might not have enough thermodynamic driving force for the hydrogen reduction reaction. A feasible method to resolve this problem is with band gap engineering through introducing strain. To assess the effect of strain on the band edge positions, we apply compressive strain on single- and few-layer BiOI. As an example, the positions of the CBM and VBM of bilayer BiOI are plotted in Fig. 6, which provides an important guidance to effectively tune their band edge positions, and then to enhance the efficiency of photocatalytic water splitting. The CBM and VBM positions under a compressive strain of −4.0% shift upwards to higher energy positions with respect to the redox potential levels of water. These CBMs are located above the water reduction potential of about 0.9–1.0 eV. The reduction capability of photogenerated electrons could then be sufficient to generate hydrogen from water.
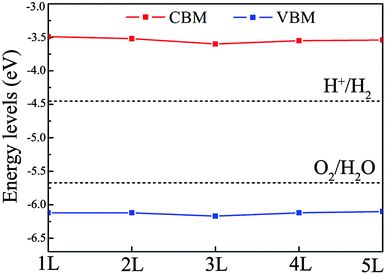 | ||
| Fig. 6 The band edge positions of the single- and few-layer BiOI nanosheets under a compressive strain of −4.0%. | ||
4 Conclusions
In conclusion, we comprehensively investigate the stability, and electronic and optical properties of single- and few-layer BiOI, and explore their potential photocatalytic properties through performing extensive DFT calculations. By analyzing the band gaps, the carrier effective masses, the VBM/CBM positions and the optical absorptions, single- and few-layer BiOI are found to be excellent photocatalysts for solar water splitting. Moreover, these remarkable properties of the BiOI nanosheets are almost insensitive to the layer thickness due to the weak interactions. These theoretical findings suggest that the BiOI nanosheets should be promising candidates for photocatalytic water splitting using solar energy.Acknowledgements
This work was partially supported by the National Key Basic Research Program (No. 2014CB921101), by the State Key R&D Fund of China (No. 2016YFA0200604), by the National Natural Science Foundation of China (No. 21503149, 21473168, and 11634011), by the Doctoral Program Foundation of Tianjin Normal University (No. 52XB1408), and by the Innovative Program of Development Foundation of Hefei Center for Physical Science and Technology. Computational resources have been provided by the CAS, Shanghai and USTC Supercomputer Centers.References
- M. G. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. Mi, E. A. Santori and N. S. Lewis, Chem. Rev., 2010, 110, 6446–6473 CrossRef CAS PubMed.
- X. Chen, S. Shen, L. Guo and S. S. Mao, Chem. Rev., 2010, 110, 6503–6570 CrossRef CAS PubMed.
- A. Fujishima and K. Honda, Nature, 1972, 238, 37–38 CrossRef CAS PubMed.
- R. Asahi, T. Morikawa, T. Ohwaki, K. Aoki and Y. Taga, Science, 2001, 293, 269–271 CrossRef CAS PubMed.
- J. Wang, J. Huang, J. Meng, Q. Li and J. Yang, Phys. Chem. Chem. Phys., 2016, 18, 17517–17524 RSC.
- A. Kudo and Y. Miseki, Chem. Soc. Rev., 2009, 38, 253–278 RSC.
- T. Hisatomi, J. Kubota and K. Domen, Chem. Soc. Rev., 2014, 43, 7520–7535 RSC.
- P. Zhang, J. Zhang and J. Gong, Chem. Soc. Rev., 2014, 43, 4395–4422 RSC.
- R. Asahi, T. Morikawa, H. Irie and T. Ohwaki, Chem. Rev., 2014, 114, 9824–9852 CrossRef CAS PubMed.
- L. Yang, H. Zhou, T. Fan and D. Zhang, Phys. Chem. Chem. Phys., 2014, 16, 6810–6826 RSC.
- N. Serpone, A. V. Emeline, V. K. Ryabchuk, V. N. Kuznetsov, Y. M. Artemev and S. Horikoshi, ACS Energy Lett., 2016, 1, 931–948 CrossRef CAS.
- V. Stevanovic, S. Lany, D. Ginley, W. Tumas and A. Zunger, Phys. Chem. Chem. Phys., 2014, 16, 3706–3714 RSC.
- J. Wang, Q. Meng, J. Huang, Q. Li and J. Yang, J. Chem. Phys., 2014, 140, 174705 CrossRef PubMed.
- X. Jiang, P. Wang and J. Zhao, J. Mater. Chem. A, 2015, 3, 7750–7758 CAS.
- X. Jiang, J. Nisar, B. Pathak, J. Zhao and R. Ahuja, J. Catal., 2013, 299, 204–209 CrossRef CAS.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- L. Wang and T. Sasaki, Chem. Rev., 2014, 114, 9455–9486 CrossRef CAS PubMed.
- S. Ida and T. Ishihara, J. Phys. Chem. Lett., 2014, 5, 2533–2542 CrossRef CAS PubMed.
- Z. Guo, J. Zhou, L. Zhu and Z. Sun, J. Mater. Chem. A, 2016, 4, 11446–11452 CAS.
- H. Zhang, G. Yang, X. Zuo, H. Tang, Q. Yang and G. Li, J. Mater. Chem. A, 2016, 4, 12913–12920 CAS.
- X. Wang, K. Maeda, A. Thomas, K. Takanabe, G. Xin, J. Carlsson, K. Domen and M. Antonietti, Nat. Mater., 2009, 8, 76–80 CrossRef CAS PubMed.
- J. Wang, J. Meng, Q. Li and J. Yang, Phys. Chem. Chem. Phys., 2016, 18, 17029–17036 RSC.
- H. L. Zhuang and R. G. Hennig, Chem. Mater., 2013, 25, 3232–3238 CrossRef CAS.
- H. L. Zhuang and R. G. Hennig, J. Phys. Chem. C, 2013, 117, 20440–20445 CAS.
- J. Liu, X. B. Li, D. Wang, H. Liu, P. Peng and L. M. Liu, J. Mater. Chem. A, 2014, 2, 6755–6761 CAS.
- X. Li, Y. Dai, M. Li, W. Wei and B. Huang, J. Mater. Chem. A, 2015, 3, 24055–24063 CAS.
- A. K. Singh, K. Mathew, H. L. Zhuang and R. G. Hennig, J. Phys. Chem. Lett., 2015, 6, 1087–1098 CrossRef CAS PubMed.
- J. Kang and L.-W. Wang, Phys. Chem. Chem. Phys., 2016, 18, 14805–14809 RSC.
- H. Liu, B. Xu, J.-M. Liu, J. Yin, X. G. W. F. Miao and C.-G. Duan, Phys. Chem. Chem. Phys., 2016, 18, 14222–14227 RSC.
- L. Zhang and A. Zunger, Nano Lett., 2015, 15, 949–957 CrossRef CAS PubMed.
- J. Qiao, X. Kong, Z.-X. Hu, F. Yang and W. Ji, Nat. Commun., 2014, 5, 4475 CAS.
- J. Li, H. Li, G. Zhan and L. Zhang, Acc. Chem. Res., 2017, 50, 112–121 CrossRef CAS PubMed.
- J. Jiang, K. Zhao, X. Xiao and L. Zhang, J. Am. Chem. Soc., 2012, 134, 4473–4476 CrossRef CAS PubMed.
- K. Zhao, L. Zhang, J. Wan, Q. Li, W. He and J. J. Yin, J. Am. Chem. Soc., 2013, 135, 15750–15753 CrossRef CAS PubMed.
- H. Cheng, B. Huang and Y. Dai, Nanoscale, 2014, 6, 2009–2026 RSC.
- D. S. Bhachu, S. J. A. Moniz, S. Sathasivam, D. O. Scanlon, A. Walsh, S. M. Bawaked, M. Mokhtar, A. Y. Obaid, I. P. Parkin, J. Tang and C. J. Carmalt, Chem. Sci., 2016, 7, 4832–4841 RSC.
- L. Zhang, Z. Han, W. Wang, X. Li, Y. Su, D. Jiang, X. Lei and S. Sun, Chem.–Eur. J., 2015, 21, 18089–18094 CrossRef CAS PubMed.
- M. Guan, C. Xiao, J. Zhang, S. Fan, R. An, Q. Cheng, J. Xie, M. Zhou, B. Ye and Y. Xie, J. Am. Chem. Soc., 2013, 135, 10411–10417 CrossRef CAS PubMed.
- H. Feng, Z. Xu, L. Wang, Y. Yu, D. Mitchell, D. Cui, X. Xu, J. Shi, T. Sannomiya, Y. Du, W. Hao and S. X. Dou, ACS Appl. Mater. Interfaces, 2015, 7, 27592–27596 CAS.
- F. Duan, X. Wang, T. Tan and M. Chen, Phys. Chem. Chem. Phys., 2016, 18, 6113–6121 RSC.
- W. Fan, H. Li, F. Zhao, X. Xiao, Y. Huang, H. Ji and Y. Tong, Chem. Commun., 2016, 52, 5316–5319 RSC.
- N. T. Hahn, S. Hoang, J. L. Self and C. B. Mullins, ACS Nano, 2012, 6, 7712–7722 CrossRef CAS PubMed.
- W. Yang, Y. Wen, R. Chen, D. Zeng and B. Shan, Phys. Chem. Chem. Phys., 2014, 16, 21349–21355 RSC.
- H. Zhang, L. Liu and Z. Zhou, Phys. Chem. Chem. Phys., 2012, 14, 1286–1292 RSC.
- X. Zhang, B. Li, J. Wang, Y. Yuan, Q. Zhang, Z. Gao, L.-M. Liu and L. Chen, Phys. Chem. Chem. Phys., 2014, 16, 25854–25861 RSC.
- T. Jing, Y. Dai, X. Ma, W. Wei and B. Huang, Phys. Chem. Chem. Phys., 2016, 18, 7261–7268 RSC.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef.
- J. Wang, S. Chen, Q. Li and J. Yang, Int. J. Hydrogen Energy, 2016, 41, 13050–13057 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- J. Liu, X.-B. Li, D. Wang, W.-M. Lau, P. Peng and L.-M. Liu, J. Chem. Phys., 2014, 140, 054707 CrossRef PubMed.
- M. Gajdos, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045112 CrossRef.
- A. M. Ganose, M. Cuff, K. T. Butler, A. Walsh and D. O. Scanlon, Chem. Mater., 2016, 28, 1980–1984 CrossRef CAS PubMed.
- M. Ashton, S. B. Sinnott and R. G. Hennig, Appl. Phys. Lett., 2016, 109, 192103 CrossRef.
- S. Baroni, S. de Gironcoli, A. D. Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515–562 CrossRef CAS.
- X. Duan, C. Wang, A. Pan, R. Yu and X. Duan, Chem. Soc. Rev., 2015, 44, 8859–8876 RSC.
- J. Wang, Z. Guan, J. Huang, Q. Li and J. Yang, J. Mater. Chem. A, 2014, 2, 7960–7966 CAS.
- T. Jing, Y. Dai, X. Ma, W. Wei and B. Huang, J. Phys. Chem. C, 2015, 119, 27900–27908 CAS.
- K. Ding, B. Chen, Z. Fang, Y. Zhang and Z. Chen, Phys. Chem. Chem. Phys., 2014, 16, 13465–13476 RSC.
- N. Umezawa, O. Shuxin and J. Ye, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 035202 CrossRef.
- J. M. Morbec and G. Galli, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 035201 CrossRef.
- Y. Gai, J. Li, S.-S. Li, J.-B. Xia and S.-H. Wei, Phys. Rev. Lett., 2009, 102, 036402 CrossRef PubMed.
- J. Wang, H. Sun, J. Huang, Q. Li and J. Yang, J. Phys. Chem. C, 2014, 118, 7451–7457 CAS.
- X. Zhang, X. Zhao, D. Wu, Y. Jing and Z. Zhou, Adv. Sci., 2016, 3, 1600062 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2017 |