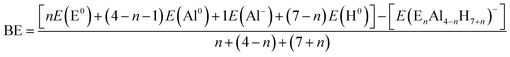Theoretical design of stable hydride clusters: isoelectronic transformation in the E_nAl_4−nH_7+n⁻ series

Abstract

New stable hydrogen-rich metallic hydrides are designed by systematic transformations of the stable known Al₄H₇⁻ species, carried out by successive isoelectronic substitutions of one aluminum atom by one E–H unit at a time (where E = Be, Mg, Ca, Sr and Ba atoms). Searches on the potential energy surfaces (PESs) of EAl₃H₈⁻, E₂Al₂H₉⁻, E₃AlH₁₀⁻ and E₄H₁₁⁻ systems indicate that structural analogues of Al₄H₇⁻ become higher energy isomers as the number of E–H units increases. The electronic descriptors: Vertical Electron Affinity (VEA), Vertical Ionization Potential (VIP) and the HOMO–LUMO gap, suggest that the systems composed of EAl₃H₈⁻, E₂Al₂H₉⁻, E₃AlH₁₀⁻, with E = Be and Mg, would be the most stable clusters. Additionally, for a practical application, we found that the Be–H and Mg–H substitutions increase the hydrogen weight percentage (wt%) in the clusters, compared with the isoelectronic analogue Al₄H₇⁻. The good capacity of beryllium and magnesium to stabilize the extra hydrogen atoms is supported by the increment of the bridge-like E–H–Al, 3center–2electron chemical bonds. Finally, explorations on the PESs of the neutral species (using Na⁺ as counterion) indicate that the NaBe₂Al₂H₉, NaBe₃AlH₁₀ and NaMg₃AlH₁₀ minimum-energy structures retain the original geometric shapes of the anionic systems. This analysis supports the potential use of these species as building blocks for cluster-assembled hydrides in the gas phase.

---

1. Introduction

The assembly of nanostructured materials using atomic clusters as building blocks is one of the most challenging procedures for the design of new substances with desired specific properties. This happens because when going from cluster to the assembled material, the physical and chemical properties may vary greatly.^1–5 For this reason, finding stable enough atomic clusters with particular properties is a key step.^1,4 Among the possible building blocks, aluminum hydrides have received considerable attention due to their high hydrogen content, making them suitable building blocks for potential hydrogen storage materials.^6,7 Experimental and theoretical studies on the closo-alanes series established that the most stable configurations are composed of a polyhedral arrangement, in which the high stability is explained by Wade's rule.^8,9 Likewise, experimental and theoretical studies about the Al_nH_m⁻ series revealed that the Al₄H₇⁻ composition has an exceptional stability and low reactivity.¹⁰ This is rationalized in terms of the Jellium model; the Al₄H₇⁻ species is a closed shell system that contains 20 valence electrons reaching the magic number required by this model. Additionally, the authors proposed that if an alkali atom is added, to donate the charge, this complex could be used as a potential building block to form cluster-assembled hydrides. They found that the tetrahedral-like most stable Al₄H₇⁻ structure is effectively conserved in the presence of a counterion (Fig. 1).¹⁰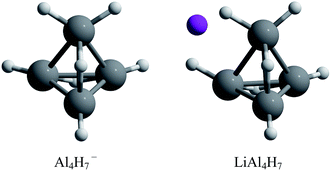

Fig. 1 Lowest energy structures for Al₄H₇⁻ and LiAl₄H₇ systems.¹⁰

A simple yet effective strategy for the theoretical design of new atomic clusters, with enhancing chemical and physical properties, is by replacing one fragment on a well-known stable species by another isoelectronic one (i.e. by an atomic or molecular unity containing the same number valence electrons).^11–13 One example of this design strategy is presented in the AlB₄H₁₁, AlB₅H₁₂ and AlB₆H₁₃ aluminoboranes compounds, where one B of stable boranes is replaced by one Al, which have triggered considerable attention of the worldwide hydrogen storage research community.¹⁴ Recently, we have established an isolobal analogy between the B–H or the Al–H unit and the silicon atom in a series of theoretically designed stable deltahedral compounds.^15,16 The transformation from Si₅²⁻ to B₅H₅²⁻ or Al₅H₅²⁻ has been made possible by successive isoelectronic substitutions of silicon atoms by B–H or Al–H units, respectively, conserving the overall deltahedral structure and chemical bonding pattern. However, evidence shows that isoelectronic substitutions do not necessarily retain the system original structures, especially in the field of cluster chemistry, where the rules and models are constantly being challenged.^17,18 For instance, the silicon analogues of benzene and cyclopentadienyl anion are unstable species. However, the replacement of H by Li gives as result the aromatic and stable Si₆Li₆ and Si₅Li₅⁻ clusters.¹¹

The exceptional stability of Al₄H₇⁻ system leads us to the following question: What would be the impact of replacing aluminum atoms by E–H units (E = Be, Mg, Ca, Sr and Ba) on both the stability and the structure of the resulting system? Theoretically, the new systems should contain more hydrogen per unit cluster. The well-known fact that of group 2 elements in the periodic table, especially beryllium and magnesium, are good hydrogen retainers,^19,20 justifies the possibility of improving the hydrogen storage capability on the systems to be designed. This hypothesis is verified by our theoretical results. Additionally, the resulting most stable structures are also stable in the presence of one counterion, thus enabling their use as building blocks for assembling nanostructured materials for hydrogen storage purposes.

2. Computational details

An unbiased exploration of PESs for the EAl₃H₈⁻, E₂Al₂H₉⁻, E₃AlH₁₀⁻ and E₄H₁₁⁻ (E = Be, Mg, Ca, Sr and Ba) systems, in both, singlet and triplet electronic states, was conducted using the gradient embedded genetic algorithm (GEGA).^21,22 All GEGA calculations were done using the PBE0 (ref. 23 and 24) hybrid density functional in conjunction with the Stuttgart–Dresden pseudopotentials and their respective basis set (SDD).²⁵ The latter contains pseudo-potentials to account for the relativistic effects on the heavy metals. The geometries of all the found structural isomers were further reoptimized at the PBE0/def2-TZVP^26,27 level of theory. Harmonic frequency calculations were performed at the same level of theory to ensure that all the identified isomers are true minima. Subsequent single point calculations at the CCSD(T)²⁸/def2-TZVP//PBE0/def2-TZVP level of theory were done to obtain more accurate stability ordering of the isomers. On the other hand, Wong et al.,²⁹ reported in an experimental and theoretical work that the stability of alanates complexes could be described correctly using high-level electronic structure calculations as G4 (ref. 30) composite method, which combines high-level correlation/moderate basis sets calculations with lower-level correlation/larger basis set calculations, to approximate the results of a more expensive calculations as CCSD(T). We added in the ESI† the comparison between G4 and CCSD(T) relative energies, showing that the effectively the G4 method could be a powerful tool for future works. Different reactivity and electronic stability indexes were calculated on the ground state arrangements to evaluate their stability tendencies. Vertical Electron Affinities (VEAs), which evaluate the possibility of electronic extra charge stabilization, were calculated as the difference between the electronic energies of the corresponding dianion, at the geometry of the monoanion, and the monoanionic cluster. Similarly, the Vertical Ionization Potential (VIP), which is a measure of the resistance of a system to lose an electronic charge, was evaluated as the difference between the electronic energies of the neutral (at the geometry of the anion) and the anionic cluster. The gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), i.e. the HOMO–LUMO gap, was also calculated. According to the maximum hardness principle,³¹ this quantity is directly related to the reactivity tendency of the chemical species.^31,32 We calculated atomic Binding Energies (BEs) as a measure of the resistance of a system to be fragmented into individual atoms. We used the following formulae:
where E(E⁰), E(Al⁰), E(Al⁻) and E(H⁰) correspond to the energies of (E = Be, Mg, Ca, Sr and Ba), Al, Al⁻ and H atoms, respectively, and E(E_nAl_4−nH_7+n)⁻ is the energy of each cluster. The chemical bonding analysis of the lowest energy isomers were performed using the Adaptive Natural Density Partitioning (AdNDP) method, which was developed and wrote by Zubarev and Boldyrev.³³ This approach leads to the partitioning of the charge density into elements with the lowest possible number of atomic centers per electron pair: n center-two electrons (nc–2e), including core electrons, lone pairs, 2c–2e bonds, and so on. All calculations were carried out utilizing the Gaussian 09 program.³⁴ The structures and the AdNDP surfaces were drawn with Chemcraft 1.6 (ref. 35) and Molekel 5.4,³⁶ respectively. Finally, we performed GEGA searches using sodium as counterion to obtain the alkali–clusters complexes.

3. Results and discussions

3.1 Global minima structures

The lowest energy structures obtained after GEGA and refining procedures for E_nAl_4−nH_7+n⁻ systems, with E = Be, Mg, Ca, Sr and Ba, and n = 1–3, are presented in Fig. 2.

Fig. 2 Lowest energy structures for E_nAl_4−nH_7+n⁻ (E = Be, Mg, Ca, Sr and Ba) with n = 1–3. The values in square brackets correspond to relative energies in kcal mol⁻¹, among clusters with same composition, obtained at the CCSD(T)/def2-TZVP//PBE0/def2-TZVP level of theory. In all cases, the systems in multiplicity singlet were more stable than the triplet.

Considering that the high-energy isomers could be stabilized under certain conditions (higher temperatures, chemical environment, or others), we also reported all the isomers (within the range of 10 kcal mol⁻¹ above the lowest energy one) found in the respective singlet PESs (Fig. SI-1 to SI-20†). The searches on the potential energy surfaces (PES) for the first substitution, one aluminum by one E–H unit, located the 1E-1 tetrahedral-like (analogue to the Al₄H₇⁻ system) arrangements as global minima for E = Mg, Ca and Sr. The situation was different for beryllium and barium-doped systems; the tetrahedral analogues were less stable than the corresponding global minima, the boat-shape 1Be-1 and 1Ba-1 structures, by 6.2 and 4.9 kcal mol⁻¹ respectively. We attribute these differences to the atomic size of beryllium and barium, which are more dissimilar with respect to aluminum than magnesium, calcium and strontium. For the substitution of two aluminum atoms by two E–H units, the searches revealed the presence of the 2E-1 tetrahedral analogues as the most stable configurations for E = Mg, Ca, Sr and Ba. This was not the case for beryllium, in which the 2Be-1 global minimum, a planar-like structure stabilized by the presence of a Be–Be dimer, was more stable by 6.4 kcal mol⁻¹. The PESs exploration, for the systems obtained after three substitutions, showed that the tetrahedral analogue configurations, 3E-2, were unstable for E = Be, Ca, Sr and Ba. The only exception, the tetrahedral-like magnesium doped system, was found at 1.2 kcal mol⁻¹ above the 3E-1 global minima. The similarity in the atomic size between aluminum and magnesium atoms could explain the stability of this 3Mg-2 tetrahedral analogue. Instead, the AlH₄ portion and the presence of an E₃ triangle, a fragment capable of incorporating six hydrogen atoms, characterize the 3E-1 global minima structures. Finally, the global minima structures for the total substitutions of the aluminum atoms by E–H units are shown in Fig. 3.

Fig. 3 Lowest energy structures for the E₄H₁₁⁻ (E = Be, Mg, Ca, Sr and Ba) systems.

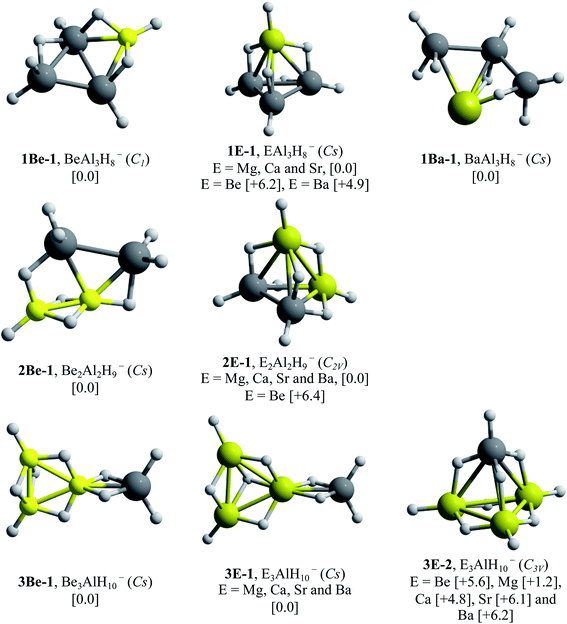
Dissociated forms (consisting of a hydrogen molecule and E₄H₉⁻ clusters) constitute the most stable configurations. This means that the storage of the maximum number of hydrogen atoms in a compact and stable structure by total aluminum replacement is not possible. At this point, we can conclude that systems substituted with one, two and three E–H units were able to generate compact hydrogenated configurations. Remarkably, analogues to Al₄H₇⁻ (EAl₃H₈⁻ (1E-1, E = Mg, Ca and Sr), E₂Al₂H₉⁻ (2E-1, E = Mg, Ca, Sr and Ba) and E₃AlH₁₀⁻ (3E-1, E = Mg) series) adopt tetrahedral-like structures.

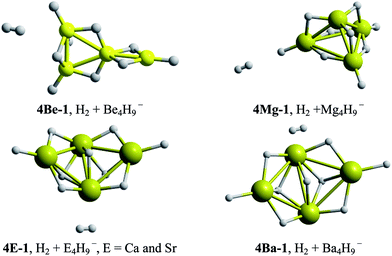
In order to postulate possible candidates as building blocks to assemble structures, our next objective is to explore relative kinetic and thermodynamic stability tendencies among the found global minima. Some energy descriptors, such as Vertical Electronic Affinity (VEA), Vertical Ionization Potential (VIP) and HOMO–LUMO gap, can help to evaluate these relative reactivity tendencies. Likewise, relative Binding Energies (BEs) provide us with a picture about relative thermodynamic stabilities.

3.2 Relative stabilities

Global reactivity descriptors and BEs tendencies for the global energy minima structures of EAl₃H₈⁻, E₂Al₂H₉⁻ and E₃AlH₁₀⁻ series are presented in the Fig. 4.

Fig. 4 Plots for the energy-based stability descriptor values, versus the identity of the minima energy structures for the E_nAl_4−nH_7+n⁻ (E = Be, Mg, Ca, Sr and Ba), n = 1–3, systems. The dashed lines represent values of Al₄H₇⁻ cluster, as a reference.

According to VEA values, systems substituted with one, two and three Be–H and Mg–H units, display the highest capacity to stabilize an extra negative charge in the geometry of the mono-anion, even higher than the Al₄H₇⁻ cluster (dashed lines in Fig. 4). On the other hand, the VIP descriptor shows that systems substituted with three E–H units, with E = Be and Mg, present the highest resistance to be ionized. Similarly, according to the maximum hardness principle,³¹ the same systems showed the lowest reactivity, i.e., the highest HOMO–LUMO gap (see Fig. 4), and therefore, the highest hardness. In fact, the systems doped with two and three E–H units, with E from Be to Sr, are less reactive than the Al₄H₇⁻ cluster. Finally, the binding energy per atom, a thermodynamic stability descriptor, shows that the systems doped with Be–H units exhibit the highest stability.

The values reported in the Table 1 show similarities in binding energies per atom between the Al₄H₇⁻ cluster and the ones containing Be; this behavior can be explained by the proximity between Pauling electronegativities of Al (1.61) and Be (1.57).^37,38

Table 1 Binding energy, per atom, for the systems doped with E–H units

	EAl3H8^− (eV)	E2Al2H9^− (eV)	E3AlH10^− (eV)
Al	2.51	2.51	2.51
Be	2.53	2.56	2.57
Mg	2.41	2.33	2.22
Ca	2.46	2.39	2.28
Sr	2.44	2.36	2.23
Ba	2.47	2.36	2.22

---

In addition, we evaluated two thermochemistry properties (the change in the enthalpies (ΔH) and the Gibbs free energy (ΔG)) as descriptors of the stability of these hydrides to be destroyed in individual atoms. The figures reported in the ESI† (Fig. SI-27) show the same result as the BE analysis: the systems doped with Be–H units exhibit the highest stability. Thinking in a future practical application, we found that the highest gravimetric hydrogen capacity (wt%) is obtained for systems substituted with Be–H units: 8.16, 11.1 and 15.6% for one, two and three Be–H replacements, respectively; while the substitutions with Mg–H units show a smaller increase: 7.75, 8.07, and 9.09%, for one, two and three Mg–H units, respectively. All values compared with the isoelectronic analogue Al₄H₇⁻ (6.09%). Since the Mg and Be hydrogen-rich doped systems are the ones closest to our system of interest (Al₄H₇⁻), we will continue our discussion analyzing the chemical bonding in them.

3.3 Multicenter chemical bonding analysis

The AdNDP results for Be–H and Mg–H replacements are presented in Fig. 5 and 6, respectively. A general observation is that in all the shown structures the hydrogen is incorporated forming metal–hydrogen 2c–2e bonds, where the hydrogen atoms are at the vertices of the structures, and forming metal–hydrogen–metal 3c–2e bonds, where the hydrogen atoms act as bridges, located at the edges. Another general observation is that Al₄H₇⁻ → EAl₃H₈⁻ → E₂Al₂H₉⁻ → E₃AlH₁₀⁻ transformations for E = Be and Mg, are characterized according to the changes in the nature and number of the multicenter σ-chemical bonds. An increase in the number of 3c–2e bonds of metal–hydrogen–metal type, Al–H–Al, Al–H–Be and Be–H–Be, as the substitutions by the Be–H units increase, is observed in Fig. 5: three, four and six bonds for the first, second and third Be–H replacement, respectively. Correlatively, a decrease in the number of intermetallic bonds (Al–Al and Al–Be–Al): two, one and cero bonds, for the first, second and third substitutions, respectively, is observed. A similar situation is presented with the substitutions by the Mg–H units (see Fig. 6): an increase in the number of metal–hydrogen–metal bonds (3c–2e): four, five and six bonds for the first, second and third Mg–H substitutions, respectively. Parallel to this, a decrease in the number of bonds associated to intermetallic interactions is observed: two, one and cero bonds, for the first, second and third Mg–H substitutions, respectively. For comparison, the AdNDP results for the Al₄H₇⁻ cluster are added in Fig. 6. Only two 3c–2e bonds of the Al–H–Al type, while three intermetallic bonds, two of Al–Al (2c–2e) type and one of the Al–Al–Al (3c–2e) type, are observed for this system.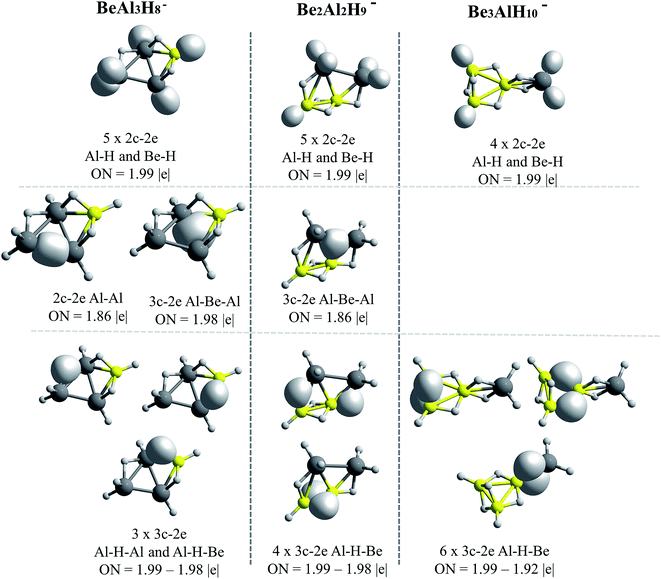

Fig. 5 Bonds recovery by the AdNDP analysis for BeAl₃H₈⁻, Be₂Al₂H₉⁻ and Be₃AlH₁₀⁻ systems. All occupations numbers (ON) are close to ideal value of 2.00 |e|.

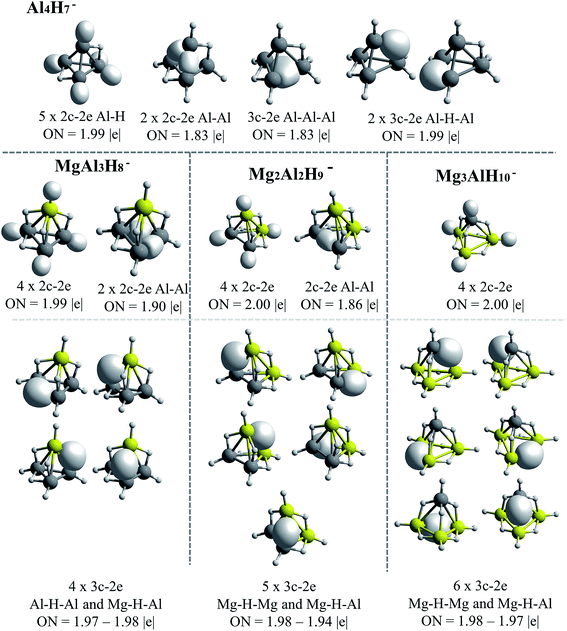Fig. 6 Bonds recovery by the AdNDP analysis for Al₄H₇⁻, MgAl₃H₈⁻, Mg₂Al₂H₉⁻ and Mg₃AlH₁₀⁻ systems. All occupations numbers (ON) are close to ideal value of 2.00 |e|.

The results above indicate that the excess of hydrogen, as the replacements increase, is incorporated in the metal–hydrogen–metal 3c–2e triangular units (being the metals of the same or of a different nature). These hydrogen atoms are in the form of hydrides, each of them stabilized simultaneously by two metals. Indeed, the increase of the metal–hydrogen–metal bonds, with the concomitant decrease of intermetallic bonds, as the replacements increase, occurs in a similar way for both, Be and Mg cases, though their relative energies between their structures are different. This indicates that the metal–hydrogen–metal units are fairly stable, and their three-center binding nature facilitates the weakening of intermetallic bindings. Therefore, as the aluminum atoms replacements increase, the bonding scheme tends to change from intermetallic bonds to bridge-like metal–hydrogen–metal bonds. This situation is evident in the case of the structures containing magnesium (Fig. 6).

Lastly, note that only beryllium atoms can form intermetallic bonds with aluminum atoms. As in the case of BEs, discussed in the previous section, this may be due to the closeness between Be and Al electronegativities. By contrast, Mg atom is less electronegative and cannot form covalent-like bonds.

3.4 Alkali complex

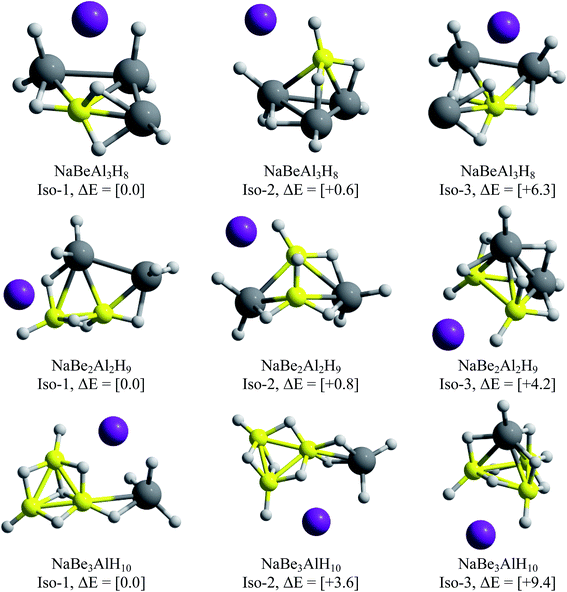
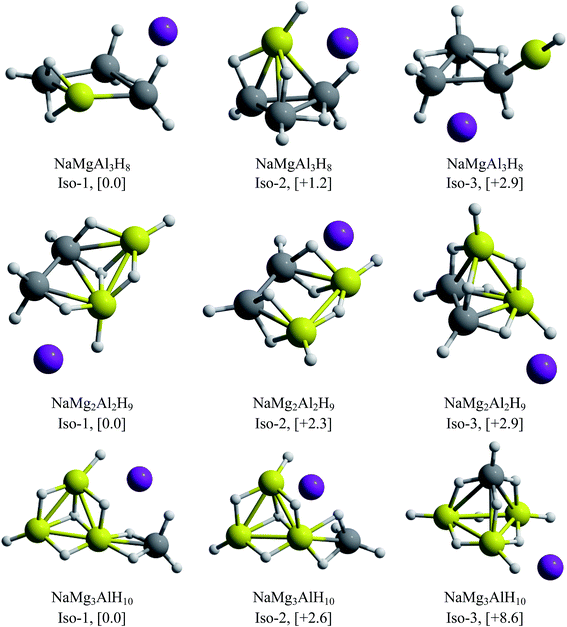
One of the main objectives of this work is to propose an alkali–clusters complex as a potential building block of cluster-assembled hydrides. For this purpose, we performed GEGA searches of the global minimum structures for the clusters containing Be and Mg. The resulting minimum energy structures are illustrated in Fig. 7 and 8.

Fig. 7 Lowest energy isomers for NaBeAl₃H₈, NaBe₂Al₂H₉ and NaBe₃AlH₁₀. The relative energies, in kcal mol⁻¹ (within squared brackets) were calculated at CCSD(T)/def2-TZVP//PBE0/def2-TZVP level of theory.

Fig. 8 Lowest energy isomers for NaMgAl₃H₈, NaMg₂Al₂H₉ and NaMg₃AlH₁₀. The relative energies, in kcal mol⁻¹ (within squared brackets), were calculated at CCSD(T)/def2-TZVP//PBE0/def2-TZVP level of theory.

For the beryllium clusters, the cage analogue of Al₄H₇⁻ is stable only for one Be–H substitution, isomer located only to 0.6 kcal mol⁻¹ with respect to the global minimum (Iso-2). In the cases of two and three Be–H replacements, the tetrahedral analogues are located 4.2 and 9.2 kcal mol⁻¹, with respect to the global minimum, respectively.

The GEGA searches for the Mg-contained cases located the corresponding analogues of Al₄H₇⁻ tetrahedral structure, with one and two Mg–H substitutions, at only +1.2 and +2.9 kcal mol⁻¹ from the global minima. However, this is not the case for three Mg–H substitutions, in which the tetrahedral-like cage is located at 8.6 kcal mol⁻¹ from the global minimum. Finally, two important results are reported in Fig. 7 and 8: (i) the global minima structures of NaBe₂Al₂H₉ and NaBe₃AlH₁₀ contains Be₂Al₂H₉⁻ and Be₃AlH₁₀⁻ hardly modified, and (ii) the global minimum obtained for NaMg₃AlH₁₀ has almost the same geometric shape of Mg₃AlH₁₀⁻ (3E-1, at 0.0 in Fig. 1). Therefore, we can postulate these three alkali–cluster complexes as the potential building block to form cluster-assembled hydrides.

4. Conclusions

A strategy for the theoretical design of new atomic clusters with enhanced chemical and physical properties is presented in this work. The methodology consisted in systematically transforming, the stable Al₄H₇⁻ atomic cluster by successive isoelectronic substitutions of one aluminum atom by one E–H unity, where E = Be, Mg, Ca, Sr and Ba atoms. In a first stage, the searches on the potential energy surfaces (PES) for EAl₃H₈⁻, E₂Al₂H₉⁻, E₃AlH₁₀⁻ and E₄H₁₁⁻ systems, indicated that the tetrahedral-shape tends to be unfavored as the E–H units increase. Secondly, some electronic descriptors of stability as a Vertical Electron Affinity (VEA), Vertical Ionization Potential (VIP) and the HOMO–LUMO gap, suggest that systems composed by EAl₃H₈⁻, E₂Al₂H₉⁻, E₃AlH₁₀⁻, with E = Be and Mg atoms, should be the most stable atomic clusters. The capability of beryllium and magnesium atoms to form bridge 3c–2e (E–H–Al) plays a key role on the stabilization of these systems. Finally, the GEGA searches of alkali-complexes showed that NaBe₂Al₂H₉, NaBe₃AlH₁₀ and NaMg₃AlH₁₀ conformations have the same geometric shapes as the respective anionic systems, thus showing that these configurations are stable and can be postulated as potential building blocks to form cluster-assembled hydrides.

Acknowledgements

E. O and F. F are grateful for the financial support of “El Patrimonio Autónomo Fondo Nacional de Financiamiento para la Ciencia, la Tecnología y la Innovación Francisco José de Caldas” (No. 211665842965). C. Z. H. is grateful to Universidad de Antioquia for financial support through CODI Project No. 10170 and Estrategia de Sostenibilidad 2015–2016. W. T. is grateful to Fondecyt (Grant No. 1140358).

References

1. N. K. Chaki, S. Mandal, A. C. Reber, M. Qian, H. M. Saavedra, P. S. Weiss, S. N. Khanna and A. Sen, ACS Nano, 2010, 4, 5813–5818.
2. S. A. Claridge, A. W. Castleman, S. N. Khanna, C. B. Murray, A. Sen and P. S. Weiss, ACS Nano, 2009, 3, 244–255.
3. S. Mandal, M. Qian, A. C. Reber, H. M. Saavedra, P. S. Weiss, S. N. Khanna and A. Sen, J. Phys. Chem. C, 2011, 115, 23704–23710.
4. M. Qian, A. C. Reber, A. Ugrinov, N. K. Chaki, S. Mandal, H. M. Saavedra, S. N. Khanna, A. Sen and P. S. Weiss, ACS Nano, 2010, 4, 235–240.
5. A. C. Reber, S. N. Khanna and A. W. Castleman, J. Am. Chem. Soc., 2007, 129, 10189–10194.
6. J. Graetz, J. J. Reilly, V. A. Yartys, J. P. Maehlen, B. M. Bulychev, V. E. Antonov, B. P. Tarasov and I. E. Gabis, J. Alloys Compd., 2011, 509, S517–S528.
7. R. Zidan, B. L. Garcia-Diaz, C. S. Fewox, A. C. Stowe, J. R. Gray and A. G. Harter, Chem. Commun., 2009, 3717–3719.
8. A. Grubisic, X. Li, S. T. Stokes, J. Cordes, G. F. Ganteför, K. H. Bowen, B. Kiran, P. Jena, R. Burgert and H. Schnöckel, J. Am. Chem. Soc., 2007, 129, 5969–5975.
9. L. Fu, H. Xie and Y. Ding, Inorg. Chem., 2009, 48, 5370–5375.
10. P. J. Roach, A. C. Reber, W. H. Woodward, S. N. Khanna and A. W. Castleman, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 14565–14569.
11. W. Tiznado, N. Perez-Peralta, R. Islas, A. Toro-Labbe, J. M. Ugalde and G. Merino, J. Am. Chem. Soc., 2009, 131, 9426–9431.
12. E. Osorio, A. Vasquez, E. Florez, F. Mondragon, K. J. Donald and W. Tiznado, PCCP Phys. Chem. Chem. Phys., 2013, 15, 2222–2229.
13. M. Contreras, E. Osorio, F. Ferraro, G. Puga, K. J. Donald, J. G. Harrison, G. Merino and W. Tiznado, Chemistry, 2013, 19, 2305–2310.
14. J.-C. Zhao, D. A. Knight, G. M. Brown, C. Kim, S.-J. Hwang, J. W. Reiter, R. C. Bowman, J. A. Zan and J. G. Kulleck, J. Phys. Chem. C, 2009, 113, 2–11.
15. E. Osorio, A. P. Sergeeva, J. Santos and W. Tiznado, Phys. Chem. Chem. Phys., 2012, 16326–16330.
16. I. Fuenzalida-Valdivia, M. J. Beltran, F. Ferraro, A. Vasquez-Espinal, W. Tiznado and E. Osorio, Chem. Phys. Lett., 2016, 647, 150–156.
17. A. S. Ivanov, K. V. Bozhenko and A. I. Boldyrev, J. Chem. Theory Comput., 2012, 8, 135–140.
18. T. R. Galeev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2011, 13, 20549–20556.
19. G. J. Brendel, E. M. Marlett and L. M. Niebylski, Inorg. Chem., 1978, 17, 3589–3592.
20. B. Sakintuna, F. Lamari-Darkrim and M. Hirscher, Int. J. Hydrogen Energy, 2007, 32, 1121–1140.
21. A. N. Alexandrova and A. I. Boldyrev, J. Chem. Theory Comput., 2005, 1, 566–580.
22. A. N. Alexandrova, J. Phys. Chem. A, 2010, 114, 12591–12599.
23. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
24. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158.
25. P. Fuentealba, H. Preuss, H. Stoll and L. Von Szentpály, Chem. Phys. Lett., 1982, 89, 418–422.
26. A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829.
27. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571.
28. J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968.
29. B. M. Wong, D. Lacina, I. M. B. Nielsen, J. Graetz and M. D. Allendorf, J. Phys. Chem. C, 2011, 115, 7778–7786.
30. L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 126, 084108.
31. R. G. Pearson, Acc. Chem. Res., 1993, 26, 250–255.
32. P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1873.
33. D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217.
34. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revis. C.01, Gaussian, Inc., Wallingford CT, 2009.
35. http://www.chemcraftprog.com, chemcraft.
36. Ugo Varetto, Molekel 5.4, Swiss National Supercomputing Centre, Lugano (Switzerland).
37. A. L. Allred, J. Inorg. Nucl. Chem., 1961, 17, 215–221.
38. S. S. Batsanov, Neorg. Mater., 2001, 37, 871–885.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra01422h

---