Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Rectangular and hexagonal doping of graphene with B, N, and O: a DFT study†
Saif Ullah *a,
Akhtar Hussainb and
Fernando Satoa
*a,
Akhtar Hussainb and
Fernando Satoa
aDepartamento de Física, Instituto de Ciências Exatas, Campus Universitário, Universidade Federal de Juiz de Fora, Juiz de Fora, MG 36036-900, Brazil. E-mail: sullah@fisica.ufjf.br
bTPD, Pakistan Institute of Nuclear Science and Technology (PINSTECH), P.O. Nilore, Islamabad, Pakistan
First published on 14th March 2017
Abstract
First-principles density functional theory (DFT) calculations were carried out to investigate the rectangular and hexagonal doping of graphene with B, N, and O. In both of these configurations, though the dopants are incorporated at the same sublattices sites (A or B), the calculated values of the band gaps are very different with nearly the same amount of cohesive energies. In this study, the highest value of the band gap (1.68 eV) is achieved when a maximum of 4 O atoms are substituted at hexagonal positions, resulting in a lower cohesive energy relative to that of the other studied systems. Hexagonal doping with 3 O atoms is significantly more efficient in terms of opening the band gap and improving the structural stability than the rectangular doping with 4 O atoms. Our results show the opportunity to induce a higher band gap values having a smaller concentration of dopants, with better structural stabilities.
Introduction
Graphene is a single layer of sp2 hybridized carbon atoms arranged in a honeycomb lattice, and is the basic building block of all graphitic materials of every dimension (0D, 1D, and 3D).1–4 The extraordinary physical, electrical, and optical properties of graphene nominate it as a potential candidate for use in semiconductor electronic devices.3,5–7 The exceptional charge carrier mobility of graphene (106 cm2 V s−1) makes it very much desirable for use in semiconductor electronic devices.8Besides these distinctive properties, the one big hurdle is the zero gap character of graphene, which restricts its use in nanoelectronics. In this regard, the band gap engineering of graphene is necessary.9 Fortunately, we can overcome this issue in a number of ways. Graphene superstructures such as quantum dots,10,11 nanoribbons,12,13 and nanomeshes14 can address this problem by inducing a quantum confinement effect, which leads to the opening of a band gap around the Dirac point. Furthermore, one of the simple and efficient techniques to alter the electronic structure of graphene is substitutional doping where C atoms are replaced by impurity atoms. Graphene can be doped with Al, B, NO2, H2O, and F4-TCNQ to achieve p-type doping, while for n-type doping N and alkali metals are used as dopants.15–20 Graphene is usually doped with B and N atoms because these dopants are the neighbors of C. Moreover, by using B and N dopants, the 2D geometry of graphene is retained due to the nearly equal covalent radii of these atoms. Additionally, graphene can be doped with Be, co-doped with Be–B and Be–N, and molecular doping with BeO to change the electronic structure, significantly.21,22 Graphene has been doped with B, N, O, and F, in a previous study, to investigate the electronic properties of graphene, but this study was limited to one dopant atom only.17 A systematic study on the doping of graphene with B and N can be found in ref. 23. These authors studied different sites with varying concentrations of the dopants and found that, for maximum band gap opening in graphene, the dopants must be integrated at the same sublattices positions (A or B). In our recent study, we investigated two types of doping configuration of Be in graphene, namely rectangular and hexagonal.21 In that study, we discovered that, after the selection of a suitable dopant, in order to induce higher band gaps it is important not only to employ the dopants at the same sublattices sites (A or B), but also to choose specific sites (i.e. hexagonal configurations). To the best of our knowledge, these rectangular and hexagonal configurations are not reported in the literature for any atom(s) other than Be.
In this study, the doping of graphene with B, N, and O is investigated using a DFT study. We have chosen previously investigated rectangular and hexagonal configurations for our doped graphene systems to check the response of the electronic structures. The main theme of this study is to check the validity of our configurations for other atoms (B, N and O) except Be, and to obtain the optimum value of the band gap of graphene with the minimum number of dopants.
Computational details
First-principles density functional theory (DFT) calculations were performed using the SIESTA code.24 For electron–ion interactions, we used Troullier–Martins norm conserving pseudopotentials.25 The GGA = PBE level of theory was used for electron–electron interactions.26 The double zeta (DZ) basis set was selected and the orbital confining cut-off was set to 0.01 Ry. For higher doping concentrations (9.375–12.5%), we have performed VDW-DF27 calculations complemented by the double zeta basis set with polarization (DZP) to investigate the magnetic moment, if any. The mesh cut-off value was fixed to 200 Ry for our 4 × 4 graphene supercell with periodic boundary conditions. The z-axis was set to 14 Å to avoid interactions between the layers. The Brillouin zone was sampled with 30 × 30 × 1 Monkhorst–Pack k-points. The optimization procedure was done using a conjugate gradient algorithm until all of the forces were less than 0.01 eV Å−1. For the cohesive energy calculations, we used the following formula:| Ecoh = [Etot − niEi]/n, (i = C, B, N, and O) |
Ecoh is the cohesive energy per atom. Ei and Etot correspond to the energy of an individual element (the gas phase energy) in the same supercell and the total energy of the system, respectively. n represents the total number of atoms in the supercell.
Results and discussion
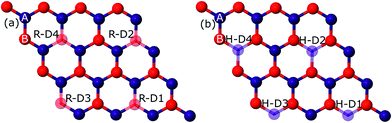
Primarily, we optimized our 4 × 4 graphene sheet to get a relaxed structure. The relaxed C–C bonds were found to be 1.44 Å in length, in agreement with prior studies.21–23,28 This relaxed geometry with the corresponding band structure is shown in Fig. S1 in the ESI.† This optimized graphene sheet was doped with B, N, and O atoms in rectangular and hexagonal configurations with increasing concentration, ranging from 3.125% to 12.5% (1–4 C atoms replaced by impurity atoms). In the rectangular configuration, the C atom(s) replaced by dopant(s) is (are) denoted by RD1–RD4 (hollow spheres) and in the hexagonal configuration these dopants are denoted by HD1–HD4, as can be seen from Fig. 1. The upper two dopants (R-D2, R-D4) in the rectangular configuration are shifted along the positive x-axis by 2.46 Å (which is the lattice constant of graphene) relative to H-D2 and H-D4 of the hexagonal configuration. The results so obtained are presented below.B-doping
Initially, one C atom is replaced with one B atom making the B concentration 3.125% in the host graphene. The geometry was fully relaxed to the required accuracy. The C–B bonds were enlarged to a value of 1.50 Å due to the larger covalent radius of B (85 pm) compared to that of C (75 pm). Due to the electron deficit character of B, the Fermi level underwent a downward shift of 0.78 eV from the Dirac point. The electronic band structure calculations show a band gap opening of 0.21 eV as can be seen in Fig. 2. All of these values were found to be in good agreement with the earlier findings.17,23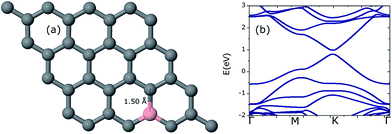 | ||
| Fig. 2 Optimized geometry of a 4 × 4 graphene sheet doped with a single B atom (a) along with the corresponding band structure graph (b). The Fermi level is set to a zero energy scale. | ||
After the satisfactory replication of these results, we started doping graphene with B at varying concentrations at the rectangular and hexagonal sites (Fig. 1). Their geometries, along with their band structures, can be seen in Fig. S2–S7 in the ESI.†
The C atoms in a graphene sheet consisting of 32 atoms are substituted with 1 to 4 B atoms in the rectangular configuration, which caused a linear increase in the band gap values, ranging from 0.21 to 0.55 eV (Fig. 3). This linear increase in the band gap with an increasing percentage of B-atoms can be achieved when all of the B-atoms are employed in the graphene sheet at the same sublattice sites (A or B).23 Moreover, the band gap values can be increased significantly if the B dopants are integrated at the hexagonal sites. By doping with 4 B atoms hexagonally, an abrupt increase in the value of the band gap can be seen as compared to rectangular doping with 4 B atoms. This is due to the fact that the B dopants actually make a 2 × 2 superlattice in graphene, which can be regarded as ideal hexagonal doping. Furthermore, these configurations (rectangular and hexagonal) led to the same geometry and structural stability, yet different band gap values are observed. Due to the larger covalent radius of B than of C, an expansion in the unit cell is observed for B doping. Spin polarized calculations reveal that only 4 B atom-doping of graphene at hexagonal sites induced a magnetic moment of 0.7 μB. These indicate the proficiency of hexagonal doping.
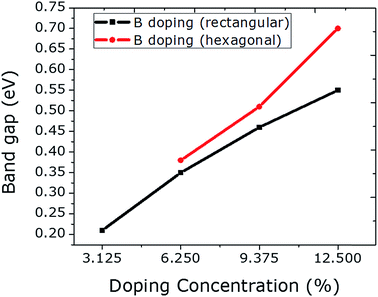 | ||
| Fig. 3 The relationship between B doping with increasing concentration at rectangular and hexagonal sites and the respective band gap values is plotted. | ||
N-doping
A N atom was doped into a graphene sheet and the C–N bonds were found to be 1.42 Å in length after structural optimization. As the N atom is electron-rich relative to the C atom, the Fermi level is raised by 0.78 eV. The same band gap value of 0.21 eV is observed as in the case of the single B atom. Fig. S7–S14 in the ESI† correspond to the N doping of graphene.The number of N atoms is increased in the graphene sheet from 1 to 4 in rectangular configurations. A linear rise in the band gap value is achieved (Fig. 4), which is similar to the B doping presented above. This linear rise was reported by Rani and Jindal23 when N atoms were doped into graphene at the same sublattices sites (A or B). The band gap values can be enhanced significantly by incorporating the N atoms at hexagonal sites, which is comparable to the result of hexagonal doping with B discussed above. Similar to B doping, a higher value for the band gap can be achieved by N doping hexagonally, which also tended to the same stability as that of rectangular doping. Furthermore, a negligibly small reduction in unit cell size is observed due to the smaller covalent radius of N than that of C. No magnetic moment was calculated for rectangular doping. However, hexagonal doping with 3 and 4 N atoms induced magnetic moments of 0.8 and 1.3 μB, respectively. The magnetic moment that arose from the 3 N atom hexagonal doping is greater than that from the 4 B atom hexagonal doping.
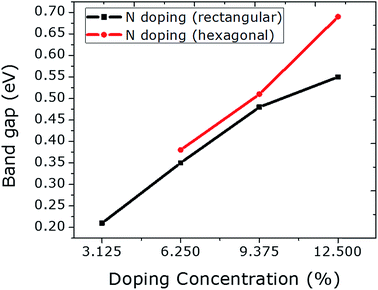 | ||
| Fig. 4 The relationship between N doping with increasing concentration at rectangular and hexagonal sites and the band gap values is plotted. | ||
O-doping
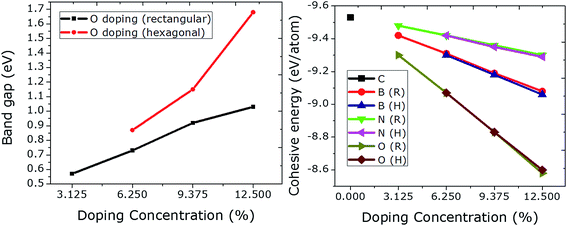
It is interesting to investigate the rectangular and hexagonal doping of graphene with O as O atom has two electrons more than C, which could be compared to the results obtained previously from Be doping (having two electrons less than C).21 Additionally, there is no such study regarding oxygen doping at specific sites in graphene. For this purpose, we doped graphene with a single atom of O initially. The optimized C–O bonds were found to be 1.49 Å in length, which is comparable to the value of 1.50 Å obtained before.17 The Fermi level is moved upward by 0.58 eV. This insertion of O in graphene induced a band gap opening of 0.57 eV, which is a bit higher than the value of 0.50 eV calculated by Wu et al.17The doping concentration of O in graphene is increased from 3.125 to 12.5% (1–4 O) in the rectangular configuration. A linear rise in band gap is observed with rectangular doping. However, an exponential rise in the band gap can be seen from the hexagonal doping of graphene with O. The value of the band gap is increased enormously from 1.03 to 1.68 eV just by choosing specific dopant sites (hexagonal). This huge increase occurs because the dopants form a 2 × 2 superlattice in the graphene, which can be considered as the ideal hexagonal doping configuration. This tendency of increasing the band gap linearly and exponentially is in agreement with Be doping with increasing doping concentration.21 Moreover, the size of the unit cell is found to be the same as that in pristine graphene even at a high dopant concentration (12.5%). No magnetic moment was observed for any case (rectangular or hexagonal) at any level of dopant concentration.
The effect of doping concentration on the structural stability is shown in Fig. 5 (right panel). The cohesive energies of N doped graphene are higher than those of B and O doped graphene. The lowest cohesive energies are plotted for O doping which at the same time give rise to higher values for the band gaps (max. value = 1.68 eV) when compared to B and N doping. An increase in the dopant concentration gives rise to a higher value of the band gap, and at the same time leads to a linear decrease in the cohesive energy. All of the results are summarized in Table 1.
| Dopants | Concentration (%) | Configuration | Cohesive energy (eV per atom) | Band gap (eV) |
|---|---|---|---|---|
| a The calculated value of the cohesive energy of graphene is −9.53 eV per atom. | ||||
| 1B | 3.125 | Rectangular | −9.42 | 0.21 |
| 2B | 6.25 | Rectangular | −9.31 | 0.35 |
| 2B | 6.25 | Hexagonal | −9.30 | 0.38 |
| 3B | 9.375 | Rectangular | −9.19 | 0.46 |
| 3B | 9.375 | Hexagonal | −9.18 | 0.51 |
| 4B | 12.5 | Rectangular | −9.08 | 0.55 |
| 4B | 12.5 | Hexagonal | −9.06 | 0.70 |
| 1N | 3.125 | Rectangular | −9.48 | 0.21 |
| 2N | 6.25 | Rectangular | −9.42 | 0.35 |
| 2N | 6.25 | Hexagonal | −9.42 | 0.38 |
| 3N | 9.375 | Rectangular | −9.36 | 0.48 |
| 3N | 9.375 | Hexagonal | −9.35 | 0.51 |
| 4N | 12.5 | Rectangular | −9.30 | 0.55 |
| 4N | 12.5 | Hexagonal | −9.29 | 0.69 |
| 1O | 3.125 | Rectangular | −9.30 | 0.57 |
| 2O | 6.25 | Rectangular | −9.07 | 0.73 |
| 2O | 6.25 | Hexagonal | −9.07 | 0.87 |
| 3O | 9.375 | Rectangular | −8.83 | 0.92 |
| 3O | 9.375 | Hexagonal | −8.83 | 1.15 |
| 4O | 12.5 | Rectangular | −8.58 | 1.03 |
| 4O | 12.5 | Hexagonal | −8.60 | 1.68 |
Conclusions
Electronic structure calculations for graphene doped with B, N, and O at rectangular and hexagonal sites are carried out using first-principles density functional theory (DFT). The dopant number is increased from 1–4 in a 4 × 4 graphene sheet. A linear increase in band gap values occurred due to the rectangular doping while an exponential rise in band gaps can be seen due to the hexagonal configuration of the dopants in the graphene. This difference in the band gaps obtained for different configurations is more prominent for O doping, which is comparable to Be doping21 as these atoms have two electrons more and fewer, respectively, than the C atom. The value of the band gap obtained from 3 O atoms doped at the hexagonal site is substantially greater than that when 4 O atoms are doped at the rectangular site, hence, providing the opportunity to induce a higher value of the band gap with better structural stability. Furthermore, for hexagonal doping with 4 B, 3 N, and 4 N atoms, we have observed magnetic moments at the VDW-DF/DZP level of theory. No magnetic moment was observed for O doping. This shows the supremacy of hexagonal site doping over rectangular site doping. Our results offer the possibility of getting a higher value of the band gap with a higher structural stability, due to a lower amount of dopants.Acknowledgements
We are thankful to the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), Fundação de Amparo à Pesquisa do Estado de Minas Gerais (FAPEMIG), Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES), and Financiadora de Estudos e Projetos (FINEP) for their financial support.References
- P. R. Wallace, Phys. Rev., 1947, 71, 622 CrossRef CAS.
- R. Saito, G. Dresselhaus and M. S. Dresselhaus, Physical Properties of Carbon Nanotubes, Imperial College Press, London, UK, 1998 Search PubMed.
- A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183 CrossRef CAS PubMed.
- A. H. C. Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109 CrossRef.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Gregorieve and A. A. Firsov, Science, 2004, 306, 666 CrossRef CAS PubMed.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 197, 438 Search PubMed.
- A. K. Geim, Science, 2009, 324, 1530 CrossRef CAS PubMed.
- E. V. Castro, H. Ochoa, M. I. Katsnelson, R. V. Gorbachev, D. C. Elias, K. S. Novoselov, A. K. Geim and F. Guinea, Phys. Rev. Lett., 2010, 105, 266601 CrossRef PubMed.
- K. S. Novoselov, Nat. Mater., 2007, 6, 720 CrossRef CAS PubMed.
- L. A. Ponomarenko, F. Schedin, M. I. Katsnelson, R. Yang, E. W. Hill, K. S. Novoselov and A. K. Geim, Science, 2008, 320, 356 CrossRef CAS PubMed.
- B. Trauzettel, D. V. Bulaev, D. Loss and G. Burkard, Nat. Phys., 2007, 3, 192 CrossRef CAS.
- M. Y. Han, B. Ozyilmaz, Y. Zhang and P. Kim, Phys. Rev. Lett., 2007, 98, 206805 CrossRef PubMed.
- X. Li, X. Wang, L. zhang, S. Lee and H. Dai, Science, 2008, 319, 1229 CrossRef CAS PubMed.
- J. Bai, X. Zhong, S. Jiang, Y. Huang and X. Duan, Nat. Nanotechnol., 2010, 5, 190 CrossRef CAS PubMed.
- P. A. Denis, Chem. Phys. Lett., 2010, 492, 251 CrossRef CAS.
- A. Lherbier, X. Blasé, Y.-M. Niquet, F. Triozon and S. Roche, Phys. Rev. Lett., 2008, 101, 036808 CrossRef PubMed.
- M. Wu, C. Cao and J. Z. Jiang, Nanotechnology, 2010, 21, 505202 CrossRef CAS PubMed.
- E. H. Hwang, S. Adam and S. D. Sarma, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 195421 CrossRef.
- O. Leenaerts, B. Partoens and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 125416 CrossRef.
- H. Pinto, R. Jones, J. P. Goss and P. R. Briddon, J. Phys.: Condens. Matter, 2009, 21, 402001 CrossRef CAS PubMed.
- S. Ullah, A. Hussain, W. A. Syed, M. A. Saqlain, I. Ahmad, O. Leenaerts and A. Karim, RSC Adv., 2015, 5, 55762 RSC.
- A. Hussain, S. Ullah and M. A. Farhan, RSC Adv., 2016, 6, 55990 RSC.
- P. Rani and V. K. Jindal, RSC Adv., 2013, 3, 802 RSC.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745 CrossRef CAS.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS PubMed.
- D. R. Cooper, B. D’Anjou, N. Ghattamaneni, B. Harack, M. Hilke, A. Horth, N. Majlis, M. Massicotte, L. Vandsburger, E. Whiteway and V. Yu, ISRN Condens. Matter Phys., 2012, 2012, 56 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra28837e |
| This journal is © The Royal Society of Chemistry 2017 |