Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Weak hydrogen bonding competition between O–H⋯π and O–H⋯Cl†
Hailiang Zhao,
Shanshan Tang,
Qun Zhang and
Lin Du *
*
Environment Research Institute, Shandong University, Shanda South Road 27, 250100 Shandong, China. E-mail: lindu@sdu.edu.cn
First published on 24th April 2017
Abstract
The weak intermolecular interaction between 2,2,2-trifluoroethanol (TFE) and 3-chloro-2-methyl-1-propene (CMP) has been investigated by gas phase FTIR spectroscopy and DFT calculations. CMP offers two hydrogen bond docking sites to the hydrogen bond donor: the chlorine atom (O–H⋯Cl) and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C π electron system (O–H⋯π). DFT calculations suggest that MeOH approaches CMP in five different orientations. The structural, energetic, and spectroscopic parameters of the most stable structures in each orientation were studied, and their binding energies range from −25.5 to −19.5 kJ mol−1. The docking to the π system is at least 1 kJ mol−1 more favored than the docking to the chlorine atom. The equilibrium constant for complexation (2.3 × 10−2) was determined from the experimental and calculated intensity of the OH-stretching transition. The Gibbs free energy of formation was found to be 9.3 kJ mol−1. The nature of the non-covalent interaction was analyzed with the atoms in molecules (AIM) method.
C π electron system (O–H⋯π). DFT calculations suggest that MeOH approaches CMP in five different orientations. The structural, energetic, and spectroscopic parameters of the most stable structures in each orientation were studied, and their binding energies range from −25.5 to −19.5 kJ mol−1. The docking to the π system is at least 1 kJ mol−1 more favored than the docking to the chlorine atom. The equilibrium constant for complexation (2.3 × 10−2) was determined from the experimental and calculated intensity of the OH-stretching transition. The Gibbs free energy of formation was found to be 9.3 kJ mol−1. The nature of the non-covalent interaction was analyzed with the atoms in molecules (AIM) method.
1. Introduction
The study of intermolecular interactions is of great interest since intermolecular bonding strongly affects the properties of substances.1 Hydrogen bonding is one of the most relevant and most studied intermolecular interactions in nature, governing molecular conformations and thus biochemical functionality. Hydrogen bonded complexes are fundamentally important for understanding the nature of the hydrogen bond phenomenon. Weak hydrogen bonds could form between an X–H donor and π- or Cl-electron acceptor. Understanding the nature of weak intermolecular interactions still remains a challenging problem.A number of theoretical and experimental investigations have considered X–H⋯π hydrogen bonding interactions in a variety of different molecular systems.2–6 The hydrogen bonded methanol–ethene complex, the most elementary example of weak intermolecular alcohol hydrogen bonding to a π system, has been studied recently with FTIR spectroscopy.2 The quantitative insights into O–H⋯π interactions obtained for methanol–ethene can help to advance the understanding of pre-reaction complexes in olefin epoxidation,7 hydroxyl radical reactions,8 electric field effects in O–H⋯π contacts4 and the subtle donor–acceptor balance in methanol–ethyne.3 The O–H⋯Cl hydrogen bond is less well investigated than O–H⋯π. In a previous study, hydrogen-bonded complexes of methanol with different proton accepting and proton donating molecules containing Cl, F, NH2, OH, OR, and COOH functional groups have been modeled using DFT with hybrid B3LYP and M05-2X functionals, recommended for modeling of system in which weak dispersion interactions are important.9
The hydrogen bonding acceptor molecules have one more docking site in some cases, hereby, there is a competition between different docking sites. Much attention has been paid on such competition for various hydrogen bonded complexes recently. Methanol is shown to engage two nearly equivalent solvation sites in 2,5-dimethylfuran, the electron-rich π cloud and the electron-deficient oxygen site.10 The OH group of methanol prefers to coordinate a 2,5-dimethylfuran molecule at its oxygen site, but largely because the methyl group simultaneously solvates the aromatic ring. The competing π solvation by the OH group is only marginally less stable but shows a significantly larger bathochromic shift in the experimental infrared spectrum.10 Similarly, anisole also can offer two attractive hydrogen bond acceptor sites to an incoming hydrogen bond donor: its oxygen atom and its delocalized π electron system. Infrared absorption spectroscopy in the OH stretching fundamental range applied to a cold supersonic jet expansion of anisole and methanol in helium shows that the oxygen binding site is preferred.11 Subsequently, the effect of ring methylation on the methanol–anisole complex has been studied.12 The subtle balance between the two structures can be varied in supersonic jets by one order of magnitude through single to triple methylation of the aromatic ring and introduction of a single tert-butyl substituent, as evidenced by infrared spectroscopy. It is interesting to investigate the competition of two docking sites in one molecule.
3-Chloro-2-methyl-1-propene (CMP) is a chlorinated derivative of highly reactive isobutene, due to a non-symmetrical character and the induction effect of the methyl group which raises the electron density at the double bond.13 In the present study, we choose to study complexes of 2,2,2-trifluoroethanol (TFE) as the hydrogen bond donor and CMP as the hydrogen bond acceptor to investigate the competition between the weak interactions of O–H⋯π and O–H⋯Cl. Detection of weak interactions such as O–H⋯π and O–H⋯Cl typically relies on the sensitive vibrational signature of the donor OH bond and the spectroscopic “red shift” that usually accompanies bond formation. FTIR spectra of the TFE–CMP complex were measured in the gas phase at room temperature, and the investigation of the structural, energetic, and spectroscopic parameters of the hydrogen bonded complexes was carried out by DFT calculations. Quantum theory of atoms in molecules (AIM) analysis was performed to understand the nature of weak interactions in the TFE–CMP complex.
2. Experimental section
CMP (97%) and TFE (99.5%) were supplied by Aladdin and Aldrich, respectively. All samples were purified and degassed with several freeze–pump–thaw cycles on a vacuum line (base pressure less than 1 × 10−4 Torr) before use. All vapor pressures were measured with Tamagawa CDG-800 pressure gauges. Infrared spectra of the TFE–CMP complex and monomers at room temperature were recorded with a Bruker Vertex 70 FTIR spectrometer. For all the spectra, a KBr beam splitter and a DLaTGS (deuterated lanthanum α alanine doped triglycine sulfate) detector were used. The interferograms were averaged over 128 scans with a spectral resolution of 1.0 cm−1. Gas phase infrared spectra were recorded using standard multi-reflection gas cell with 6 m optical path length (Infrared Analysis, Inc.). Before each measurement, we waited for at least 30 min to let the gas in the cell to reach equilibrium. The spectra analysis was performed with OPUS 7.2 and OriginPro 9.0 software.The chemicals were led into the glass cell on a vacuum line. In the experiments, the gas adsorption of TFE or CMP on the cell wall before measurement could reach 10%. The loss of chemicals during the process of preparing the gas mixture was another factor leading to the uncertainty on the pressures in the cell. Practically, a pressure “calibration” procedure was performed.14 We measured a pure TFE spectrum at a certain pressure (nominal) immediately after filling the vapor into the cell. In the spectral subtraction, a weighting factor was applied to the pure TFE spectrum so that the TFE transitions matched in regions where only TFE was absorbed. The product of the nominal TFE pressure to the weighting factor is the “real” TFE pressure in the cell. The pressures of CMP were also calibrated in this way. By doing this, the contribution of the TFE and CMP monomer spectrum can be completely cancelled from the spectrum of their mixture, and the residue spectrum is from the complex. The intensity enhancement of the OH-stretching fundamental in the complex makes it possible to observe the complex in the gas phase.
3. Computational methods
All the DFT calculations were carried out with Gaussian 09 (Revision E.01) program package.15 Various structures of the monomers (TFE, CMP) and the TFE–CMP complex were optimized with B3LYP-D3 using aug-cc-pVTZ basis set on all atoms. The B3LYP-D3 functional has been parameterized for describing dispersion interaction.16 The harmonic vibrational frequency calculations on the optimized geometries were performed at the same level of theory to ensure the structures at local minima and thus to evaluate the zero point vibrational energy (ZPVE). As suggested in our recent work, a “verytight” optimization convergence criterion and an “ultrafine” numerical integration grid were used for the DFT calculations to obtain reliable results.17 The “verytight” convergence criterion uses a very small cutoff (root mean square = 1 × 10−6 a.u.) on force constants calculations instead of the default cutoff (root mean square = 3 × 10−4 a.u.). Using this criterion not only ensures adequate convergence but, provides more reliable vibrational frequencies. When using “verytight” with DFT as is the case in this study, “int = ultrafine”, which uses a more accurate numerical integration grid, should be used as well. Such calculation should provide reasonably good frequencies and thus good thermochemical corrections to the electronic energies for the hydrogen bonded complexes.14 The binding energies (BEs) are defined as the difference between the energies of the complex and the sum of the monomers, and are corrected with ZPVE and basis set superposition error (BSSE). The BSSE was corrected with the popular counterpoise (CP) method.18 Besides, calculations at the MP2/aug-cc-pVTZ level have been carried out and compared with the B3LYP-D3 results. The geometries and interaction energies with MP2 methods were provided in ESI.† AIM analysis was carried out by utilizing the AIM2000 program package.4. Results and discussion
4.1. Geometric analysis
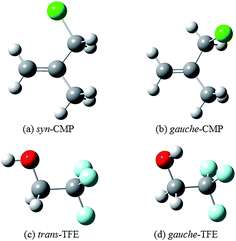
Two conformers of 3-chloro-2-methyl-1-propene (CMP) were found in the previous studies.19,20 The syn conformer (Fig. 1a) was 2.8 kJ mol−1 less stable than the gauche one (Fig. 1b) by molecular mechanics calculations.19 Meanwhile, the Raman band intensities as a function of temperature showed that the gauche conformer was dominated in liquid phase with an energetic preference of 2.5 ± 0.5 kJ mol−1.20 In this study, the gauche conformer was calculated to be 5.6 kJ mol−1 (B3LYP-D3/aug-cc-pVTZ) more stable than the syn one. These results suggested a gauche ⇌ cis conformational equilibrium, and both conformers were considered in this study. Moreover, the isolated gas phase TFE molecule has two conformers along the C–C–O–H frame (Fig. 1c and d): a trans-conformer (noted as t-) and a gauche-conformer (noted as g-). The gauche-conformer was calculated to be much more stable than the trans with a relative energy of 7.2 kJ mol−1 (B3LYP-D3/aug-cc-pVTZ). Our previous calculations showed that only gauche-TFE conformer was preferred upon complexation.21Hydrogen bonding competition occurs when the acceptor molecule has more than one docking site. Investigations of such competition can reveal the relative strength of the bonding abilities in the acceptor molecule. A competition between O–H⋯O and O–H⋯π docking sites has recently been reported for several hydrogen bonded complexes.22–25 The O–H⋯π docking is slightly more favored in supersonic jet expansions as compared with the O–H⋯O docking in the MeOH–anisole complex.23 However, O–H⋯O docking is preferred in the phenol–anisole and water–1,2-dimethoxybenzene.24,25 There are various ways where TFE can interact with CMP under consideration. One sort of interaction consists an O–H⋯π hydrogen bond in which the proton donating OH group approaches to the π system of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C group: (1) TFE reaches the C
C group: (1) TFE reaches the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C group on the same side as Cl in gauche-CMP (Fig. 2a); (2) TFE is close to the C
C group on the same side as Cl in gauche-CMP (Fig. 2a); (2) TFE is close to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C group on the opposite side as Cl in gauche-CMP (Fig. 2b); (3) TFE is towards to bonding the C
C group on the opposite side as Cl in gauche-CMP (Fig. 2b); (3) TFE is towards to bonding the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C group in syn-CMP (Fig. 2d). The second sort of interaction, O–H⋯Cl, involves the approach of the OH group of TFE toward the Cl atom: (4) TFE approaches Cl in gauche-CMP (Fig. 2c); (5) TFE comes to Cl in syn-CMP (Fig. 2e). Only the most stable structures in each binding pattern are discussed, and other high-lying structures are provided in the ESI (Fig. S1†).
C group in syn-CMP (Fig. 2d). The second sort of interaction, O–H⋯Cl, involves the approach of the OH group of TFE toward the Cl atom: (4) TFE approaches Cl in gauche-CMP (Fig. 2c); (5) TFE comes to Cl in syn-CMP (Fig. 2e). Only the most stable structures in each binding pattern are discussed, and other high-lying structures are provided in the ESI (Fig. S1†).
 | ||
| Fig. 2 The most stable structures of the TFE–CMP complexes obtained at the B3LYP-D3/aug-cc-pVTZ level. The dashed lines denote the O–H⋯π and O–H⋯Cl hydrogen bonds. | ||
Selected geometric parameters along with the changes in the OH and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond length upon complexation are given in Table 1. For an X–H proton donor molecule (X = a highly electronegative atom such as N, O, or F), the typical feature is the elongation of the X–H bond.26 The ΔrOH and ΔrC
C bond length upon complexation are given in Table 1. For an X–H proton donor molecule (X = a highly electronegative atom such as N, O, or F), the typical feature is the elongation of the X–H bond.26 The ΔrOH and ΔrC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C data for the O–H⋯π and O–H⋯Cl hydrogen bonded structures (Table 1) are all positive, indicating elongation behavior.27 For ΔrOH, the values of the O–H⋯π and O–H⋯Cl structures are similar, and they are in the range of 0.0036 to 0.0054 Å. This is close to a previous study on the H2O–aromatic ring (benzene, phenol, indole, and imidazole) complexes, where the two molecules interact with each other via O–H⋯π hydrogen bonding interactions and the ΔrOH of the H2O molecule upon complexation was obtained at 0.0007–0.0048 Å (MP2/6-31+G**).26 However, the ΔrOH of the traditional O–H⋯O hydrogen bonds was calculated to be much larger at 0.0079–0.0131 Å (B3LYP-D3/aug-cc-pVTZ) in alcohol (MeOH, EtOH, TFE)–ethylene oxide (EO) complexes.21 The ΔrOH is the largest in TFE-gauche-CMP (b) upon complexation. Moreover, the C
C data for the O–H⋯π and O–H⋯Cl hydrogen bonded structures (Table 1) are all positive, indicating elongation behavior.27 For ΔrOH, the values of the O–H⋯π and O–H⋯Cl structures are similar, and they are in the range of 0.0036 to 0.0054 Å. This is close to a previous study on the H2O–aromatic ring (benzene, phenol, indole, and imidazole) complexes, where the two molecules interact with each other via O–H⋯π hydrogen bonding interactions and the ΔrOH of the H2O molecule upon complexation was obtained at 0.0007–0.0048 Å (MP2/6-31+G**).26 However, the ΔrOH of the traditional O–H⋯O hydrogen bonds was calculated to be much larger at 0.0079–0.0131 Å (B3LYP-D3/aug-cc-pVTZ) in alcohol (MeOH, EtOH, TFE)–ethylene oxide (EO) complexes.21 The ΔrOH is the largest in TFE-gauche-CMP (b) upon complexation. Moreover, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds are also elongated by 0.0025 to 0.0035 Å for the formation of the O–H⋯π hydrogen bonded structures. The corresponding values for the O–H⋯Cl bonded structures are only about 0.0005 to 0.0007 Å. These results clearly imply that the O–H⋯π hydrogen bonding interactions have large influences on the C
C bonds are also elongated by 0.0025 to 0.0035 Å for the formation of the O–H⋯π hydrogen bonded structures. The corresponding values for the O–H⋯Cl bonded structures are only about 0.0005 to 0.0007 Å. These results clearly imply that the O–H⋯π hydrogen bonding interactions have large influences on the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond. For reference, calculations at the MP2/aug-cc-pVTZ level predict similar geometries as B3LYP-D3 method, but with slightly larger ΔrOH values and smaller intermolecular hydrogen bond distances (see in ESI†).
C bond. For reference, calculations at the MP2/aug-cc-pVTZ level predict similar geometries as B3LYP-D3 method, but with slightly larger ΔrOH values and smaller intermolecular hydrogen bond distances (see in ESI†).
| Structures | O–H⋯π/Cl | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
||
|---|---|---|---|---|
| ΔrOHa | rHBb | θc | ΔrC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Cd Cd |
|
a ΔrOH = rcomplex − rmonomer, is the change in the OH bond length upon complexation.b Intermolecular hydrogen bond distance.c Intermolecular hydrogen bond angle.d ΔrC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C = rcomplex − rmonomer, is the change in the C C = rcomplex − rmonomer, is the change in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond length upon complexation. C bond length upon complexation. |
||||
| TFE-gauche-CMP (a) | 0.0037 | — | — | 0.0025 |
| TFE-gauche-CMP (b) | 0.0054 | — | — | 0.0031 |
| TFE-gauche-CMP (c) | 0.0052 | 2.3675 | 150.2 | 0.0005 |
| TFE-syn-CMP (d) | 0.0046 | — | — | 0.0035 |
| TFE-syn-CMP (e) | 0.0036 | 2.4405 | 173.4 | 0.0007 |
The calculated BE, enthalpy of formation (ΔHθ298 K), and Gibbs free energy of formation (ΔGθ298 K) at the B3LYP-D3/aug-cc-pVTZ level for all structures are listed in Table 2. The calculated ZPVE could reach as large as 3.8 kJ mol−1. The BEs for the TFE–CMP structures are very close to each other. Complexes of t-butyl alcohol with cyclohexene, cyclopentene and norbornene were theoretically studied and the O–H⋯π hydrogen bonded complexes were found with BEs of −22.8 to −19.7 kJ mol−1 (B3LYP-D3/def2-TZVP).28 The BE of the O–H⋯π hydrogen bonded MeOH–ethene complex was calculated to be −11.0 kJ mol−1 (B2PLYP-D3BJ/VTZ).2 On the other hand, BE of the traditional O–H⋯O hydrogen bond was calculated to be −21.3 and −30.0 kJ mol−1 (B3LYP-D3/aug-cc-pVTZ) for MeOH–EO and TFE–EO (g), respectively.21 The traditional O–H⋯O hydrogen bond is stronger than the O–H⋯π hydrogen bond. The BEs indicate that TFE-gauche-CMP (Fig. 2a) is 2.8 kJ mol−1 more stable than the one on the opposite side as Cl (Fig. 2b), and only slightly more stable by 0.8 kJ mol−1 than the O–H⋯Cl TFE-gauche-CMP structure. The BEs demonstrate that the two TFE-syn-CMP structures are more stable than the three TFE-gauche-CMP structures. The O–H⋯π TFE-syn-CMP structure is also slightly more stable by 1.2 kJ mol−1 than the O–H⋯Cl TFE-syn-CMP. In either gauche-CMP or syn-CMP structures, we may notice that the O–H⋯π structure is more stable than the corresponding O–H⋯Cl structure. The MP2 calculated results show the same trend as the B3LYP-D3 method. The uncorrected BEs of MP2 are generally 3–5 kJ mol−1 more negative than the corresponding B3LYP-D3 values (see in ESI†).
| Structures | Type | BEb | ZPVE | BSSE | ΔHθ298 K | ΔGθ298 K | Kcalceq |
|---|---|---|---|---|---|---|---|
| a Obtained at the B3LYP-D3/aug-cc-pVTZ level; energies are in kJ mol−1.b BE corrected with ZPVE and BSSE. | |||||||
| TFE-gauche-CMP (a) | O–H⋯π | −22.3 | 2.9 | 0.9 | −20.5 | 16.0 | 1.6 × 10−3 |
| TFE-gauche-CMP (b) | O–H⋯π | −19.5 | 3.0 | 1.2 | −18.0 | 17.4 | 8.7 × 10−4 |
| TFE-gauche-CMP (c) | O–H⋯Cl | −21.5 | 3.2 | 1.0 | −20.0 | 17.9 | 7.3 × 10−4 |
| TFE-syn-CMP (d) | O–H⋯π | −25.5 | 3.8 | 1.1 | −24.5 | 16.1 | 1.5 × 10−3 |
| TFE-syn-CMP (e) | O–H⋯Cl | −24.3 | 3.3 | 1.1 | −23.0 | 15.5 | 1.9 × 10−3 |
4.2. Experimental and calculated OH-stretching spectra
The gas phase spectra of TFE–CMP were measured in the IR region (3200–3650 cm−1) at room temperature. The absorption bands of the complex are different from the bands of the monomers, due to the formation of hydrogen bonds. The spectra of TFE, CMP, and their mixture in the 3200–3650 cm−1 region measured with the 6 m path length cell are presented in Fig. S2 (ESI†). Difference spectroscopic method was used to observe changes in hydrogen bonding by subtraction of individual monomer spectra from the spectrum of their mixture (Fig. 3). Although small amount of the TFE–TFE dimer exists in the spectra of the mixture, the influence was minimized by subtracting the contribution of the dimer from the mixture spectra.29–32 The spectra in the OH-stretching region obtained with the 20 cm path length cell are very weak (Fig. S3 in ESI†). It can be noticed that stronger bands are formed at higher pressure (Fig. 3), and the contour of the complex bands is the same at different pressures. On the other hand, the integrated intensity of the vibrational bands of the complex is proportional to the partial pressure of the complex in the infrared absorption spectra. The integrated absorbance of the complex band is plotted against the product of the pressures of the monomers and the results are well reproduced by a linear fit (Fig. S4†). The integration region for TFE–CMP is 3525–3632 cm−1. Consequently, the straight line confirms the formation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex. The deconvolution fitting of the absorption bands of the complex has been carried out and the best fit would be fitting into one Lorentzian function (Fig. S5 in ESI†).
1 complex. The deconvolution fitting of the absorption bands of the complex has been carried out and the best fit would be fitting into one Lorentzian function (Fig. S5 in ESI†).
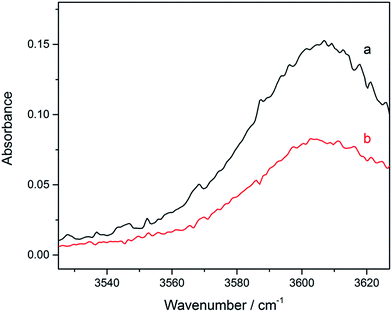 | ||
Fig. 3 Spectra of the TFE–CMP complex in the ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) OH band region. A 6 m path length cell was used. (a) 18 Torr TFE + 28 Torr CMP; (b) 15 Torr TFE + 20 Torr CMP. OH band region. A 6 m path length cell was used. (a) 18 Torr TFE + 28 Torr CMP; (b) 15 Torr TFE + 20 Torr CMP. | ||
The observed spectra for the TFE–CMP complex are in good agreement with previously published spectra of the TFE–EO and TFE–ethylene sulfide (ES) complexes.21 The red shift (Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ), an indication of the hydrogen bond strength, is obtained as the frequency difference between the associated and free OH-stretching vibrations. The observed OH-stretching fundamental transition frequencies of TFE and TFE–CMP were measured to be 3658 and 3606 cm−1, respectively. The red shift of the OH-stretching fundamental transition of TFE–CMP was obtained to be 52 cm−1. This result is in line with early studies of the O–H⋯π hydrogen bonding interactions: (i) the harmonic red shifts of the OH-stretching fundamental transition of t-butyl alcohol with cyclohexene, cyclopentene and norbornene were observed at 63 to 80 cm−1 in supersonic jet expansions;28 (ii) in an FTIR spectroscopic study of the MeOH–ethene complex, the red shift of the OH-stretching fundamental transition of MeOH was observed at 45 cm−1.2 As compared with the traditional O–H⋯O hydrogen bond, the red shift of the OH-stretching fundamental transition of TFE was observed at 155 cm−1 in TFE–EO (g) by FTIR.21 It shows that the traditional O–H⋯O hydrogen bond is stronger than the O–H⋯π hydrogen bond.
), an indication of the hydrogen bond strength, is obtained as the frequency difference between the associated and free OH-stretching vibrations. The observed OH-stretching fundamental transition frequencies of TFE and TFE–CMP were measured to be 3658 and 3606 cm−1, respectively. The red shift of the OH-stretching fundamental transition of TFE–CMP was obtained to be 52 cm−1. This result is in line with early studies of the O–H⋯π hydrogen bonding interactions: (i) the harmonic red shifts of the OH-stretching fundamental transition of t-butyl alcohol with cyclohexene, cyclopentene and norbornene were observed at 63 to 80 cm−1 in supersonic jet expansions;28 (ii) in an FTIR spectroscopic study of the MeOH–ethene complex, the red shift of the OH-stretching fundamental transition of MeOH was observed at 45 cm−1.2 As compared with the traditional O–H⋯O hydrogen bond, the red shift of the OH-stretching fundamental transition of TFE was observed at 155 cm−1 in TFE–EO (g) by FTIR.21 It shows that the traditional O–H⋯O hydrogen bond is stronger than the O–H⋯π hydrogen bond.
The calculated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and OH-stretching fundamental transition frequencies and the red shifts of the TFE–CMP structures are summarized in Table 3. The increase of intensity (fD/fM) of both the O–H⋯π and O–H⋯Cl bonded conformers was calculated to be 6–8 times stronger than that of the monomer. The red shifts of the OH-stretching fundamental transition were calculated in the range of 85–126 cm−1. In the gauche-CMP structures, the red shift of the OH-stretching fundamental transition with respect to the monomer in O–H⋯π structure (TFE-gauche-CMP (b), 126 cm−1) is greater than that in O–H⋯Cl structure (TFE-gauche-CMP (c), 115 cm−1). The same trend was obtained for the syn-CMP structures. The results imply that the O–H⋯π hydrogen bond is stronger than O–H⋯Cl. Moreover, the C
C and OH-stretching fundamental transition frequencies and the red shifts of the TFE–CMP structures are summarized in Table 3. The increase of intensity (fD/fM) of both the O–H⋯π and O–H⋯Cl bonded conformers was calculated to be 6–8 times stronger than that of the monomer. The red shifts of the OH-stretching fundamental transition were calculated in the range of 85–126 cm−1. In the gauche-CMP structures, the red shift of the OH-stretching fundamental transition with respect to the monomer in O–H⋯π structure (TFE-gauche-CMP (b), 126 cm−1) is greater than that in O–H⋯Cl structure (TFE-gauche-CMP (c), 115 cm−1). The same trend was obtained for the syn-CMP structures. The results imply that the O–H⋯π hydrogen bond is stronger than O–H⋯Cl. Moreover, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibrational transitions of the O–H⋯π bonded TFE–CMP structures were calculated to be red shifted by 8–12 cm−1 with respect to the corresponding CMP monomer, which is similar with the C
C stretching vibrational transitions of the O–H⋯π bonded TFE–CMP structures were calculated to be red shifted by 8–12 cm−1 with respect to the corresponding CMP monomer, which is similar with the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching transition: red shifts of 21–34 cm−1 were observed between phenol derivatives and methyl acetate/methyl chloroacetate in carbon tetrachloride solution by FTIR spectroscopy.33 The red shifts are caused by electronic charge released from the C
O stretching transition: red shifts of 21–34 cm−1 were observed between phenol derivatives and methyl acetate/methyl chloroacetate in carbon tetrachloride solution by FTIR spectroscopy.33 The red shifts are caused by electronic charge released from the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond to the hydrogen bond donor during the hydrogen bond formation.34 However, due to the very low intensity of the C
O bond to the hydrogen bond donor during the hydrogen bond formation.34 However, due to the very low intensity of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibrational band, it could not be recorded with FTIR in the present study.
C stretching vibrational band, it could not be recorded with FTIR in the present study.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and OH-stretching vibrational frequencies (cm−1), red shifts and calculated relative intensities in the most stable TFE–CMP structures at the B3LYP-D3/aug-cc-pVTZ level
C and OH-stretching vibrational frequencies (cm−1), red shifts and calculated relative intensities in the most stable TFE–CMP structures at the B3LYP-D3/aug-cc-pVTZ level
| Structures | Calculated O–H | Calculated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
Observed O–H | |||||
|---|---|---|---|---|---|---|---|---|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) |
Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) a a |
fD/fMb | ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) |
Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) a a |
fD/fMb | ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) |
Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) a a |
|
a Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) = = ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) monomer − monomer − ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) complex.b fD/fM represents the increase of intensity due to the complex formation. complex.b fD/fM represents the increase of intensity due to the complex formation. |
||||||||
| TFE-gauche-CMP (a) | 3714 | 90 | 6.1 | 1700 | 8 | 1.1 | 3606 | 52 |
| TFE-gauche-CMP (b) | 3678 | 126 | 7.9 | 1697 | 10 | 1.4 | ||
| TFE-gauche-CMP (c) | 3689 | 115 | 7.0 | 1706 | 2 | 0.9 | ||
| TFE-syn-CMP (d) | 3689 | 114 | 7.8 | 1709 | 12 | 1.2 | ||
| TFE-syn-CMP (e) | 3719 | 85 | 6.0 | 1719 | 3 | 0.9 | ||
4.3. Equilibrium constant for complex formation
The thermodynamic equilibrium constant (Keq) of the complexation between TFE and CMP at a certain temperature can be determined as following:
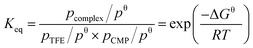 | (1) |
 | (2) |
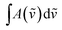 is the integrated absorbance in cm−1, l is the optical path length in meters and fcalc is the oscillator strength calculated at the B3LYP-D3/aug-cc-pVTZ level. The full band as the experimental intensity of the OH-stretching fundamental transition was used. This method has been widely used in similar studies.14,17,21,29,37–39
is the integrated absorbance in cm−1, l is the optical path length in meters and fcalc is the oscillator strength calculated at the B3LYP-D3/aug-cc-pVTZ level. The full band as the experimental intensity of the OH-stretching fundamental transition was used. This method has been widely used in similar studies.14,17,21,29,37–39
The TFE-syn-CMP (d) structure (O–H⋯π) is the most stable one based on the binding energy. Its oscillator strength (7.09 × 10−5) was used to determine the pressures of complex. A plot of pcomplex against pTFE × pCMP is shown in Fig. 4. The equilibrium constant (Keq) for the TFE–CMP complex is obtained from the slope of the least-square fitting of these data. The measured Keq at room temperature for TFE–CMP is 2.3 × 10−2. This value is smaller than the previously reported thermodynamic equilibrium constants of the MeOH–EO, EtOH–EO, and TFE–EO complexes (2.7 × 10−2, 2.9 × 10−2, and 3.0 × 10−1, respectively) determined with the same approach.21 The Keq value reveals that the hydrogen bonding in the TFE–CMP complex is weaker than the alcohol–EO complexes. The calculated equilibrium constants are significantly underestimated as compared to the measured value. The calculated thermodynamic equilibrium constants are strongly functional dependent. For example, for TFE–EO (g), the predicated values are 2.7 × 10−3, 1.6 × 10−2, and 5.5 × 10−2 with B3LYP, ωB97X-D and B3LYP-D3, respectively.21 The Gibbs free energies of formation (ΔGθexpt) can be obtained according to eqn (1). The ΔGθexpt of TFE–CMP was obtained to be 9.3 kJ mol−1. The ΔGθ298 K values in Table 2 are slightly overestimated by several kJ mol−1.
4.4. Topological analysis
The topological analysis was performed using the wavefunctions calculated at the B3LYP-D3/aug-cc-pVTZ level. The AIM plots of the TFE–CMP structures with bond critical points (BCPs), ring critical points (RCPs), cage critical points (CCPs) and electron density paths are shown in Fig. 5. The topological parameters, including electron density ρ(r), Laplacian ∇2ρ(r) at the BCPs, and change in atomic charge Δq(H) at the H atom are listed in Table 4. There are three criteria for a hydrogen bond: (i) the existence of a BCP; (ii) the electron density ρ(BCP) in the range of 0.002–0.040 a.u.; (iii) the Laplacian ∇2ρ(BCP) in the range of 0.014–0.139 a.u.40,41 The electron densities at the BCPs are in the range of 0.0113–0.0134 a.u. and the Laplacian ∇2ρ(BCP) of the structures is in the range of 0.0446–0.0645 a.u. for all the structures. All the values for the two types of bonds are within the hydrogen bond criteria along with the existence of BCPs (Fig. 5).| Structures | Type | Δq(H) | ρ(BCP) | ∇2ρ(BCP) |
|---|---|---|---|---|
| TFE-gauche-CMP (a) | O–H⋯π | 0.013 | 0.0113 | 0.0446 |
| TFE-gauche-CMP (b) | O–H⋯π | 0.018 | 0.0132 | 0.0496 |
| TFE-gauche-CMP (c) | O–H⋯Cl | 0.028 | 0.0134 | 0.0645 |
| TFE-syn-CMP (d) | O–H⋯π | 0.022 | 0.0128 | 0.0513 |
| TFE-syn-CMP (e) | O–H⋯Cl | 0.018 | 0.0117 | 0.0547 |
Due to the interference of the CF3 group in TFE, several types of hydrogen bonds formed in the TFE–CMP structures: O–H⋯π, O–H⋯Cl, C–H⋯O and C–H⋯F. Consequently, the AIM analysis indicates the existence of RCPs in TFE–CMP, with the formation of a multi-membered ring. Furthermore, CCPs are formed by these hydrogen bonds with O–H⋯π and O–H⋯Cl as the dominant interactions. The remaining interactions are weak non-covalent interactions known as cooperative hydrogen bonding interactions, which play an important role in determining the structure and properties of materials.42,43 In general, the cooperative hydrogen bond interactions make positive contribution to stabilize the structures. The formation of RCPs and CCPs stabilizes the complexes.
5. Conclusions
In summary, the hydrogen bonding interaction between TFE and CMP has been investigated by gas phase FTIR and dispersion-corrected DFT calculations. The competition between O–H⋯π and O–H⋯Cl binding sites were studied, with the π docking site is slightly favored over the Cl docking site by about 1 kJ mol−1 in binding energies, relatively larger changes of OH bond length and red shifts of the OH-stretching fundamental transition upon complexation. The red shift in the OH-stretching transition for the TFE–CMP complex was observed at 52 cm−1 by FTIR. AIM analysis shows that the electron densities and the Laplacian of the electron densities for the five most stable structures fall in the range of hydrogen bond.Acknowledgements
This work was supported by National Natural Science Foundation of China (21577080, 21407095, 91644214) and Shandong Provincial Natural Science Foundation, China (ZR2014BQ013, ZR2016BB36). We thank the High Performance Computing Center of Shandong University for providing high-performance computation.References
- C. A. Hunter, Angew. Chem., Int. Ed., 2004, 43, 5310–5324 CrossRef CAS PubMed.
- M. Heger, R. A. Mata and M. A. Suhm, Chem. Sci., 2015, 6, 3738–3745 RSC.
- K. V. J. Jose, S. R. Gadre, K. Sundararajan and K. S. Viswanathan, J. Chem. Phys., 2007, 127, 104501 CrossRef PubMed.
- M. Saggu, N. M. Levinson and S. G. Boxer, J. Am. Chem. Soc., 2011, 133, 17414–17419 CrossRef CAS PubMed.
- K. Mackeprang, S. D. Schroder and H. G. Kjaergaard, Chem. Phys. Lett., 2013, 582, 31–37 CrossRef CAS.
- R. Medel, M. Heger and M. A. Suhm, J. Phys. Chem. A, 2015, 119, 1723–1730 CrossRef CAS PubMed.
- A. Berkessel, J. A. Adrio, D. Huettenhain and J. M. Neudorfl, J. Am. Chem. Soc., 2006, 128, 8421–8426 CrossRef CAS PubMed.
- J. Daranlot, A. Bergeat, F. Caralp, P. Caubet, M. Costes, W. Forst, J. C. Loison and K. M. Hickson, ChemPhysChem, 2010, 11, 4002–4010 CrossRef CAS PubMed.
- S. K. Kolev, P. St Petkov, M. A. Rangelov and G. N. Vayssilov, J. Phys. Chem. A, 2011, 115, 14054–14068 CrossRef CAS PubMed.
- A. Poblotzki, J. Altnoeder and M. A. Suhm, Phys. Chem. Chem. Phys., 2016, 18, 27265–27271 RSC.
- M. Heger, J. Altnoeder, A. Poblotzki and M. A. Suhm, Phys. Chem. Chem. Phys., 2015, 17, 13045–13052 RSC.
- H. C. Gottschalk, J. Altnoeder, M. Heger and M. A. Suhm, Angew. Chem., Int. Ed., 2016, 55, 1921–1924 CrossRef CAS PubMed.
- M. Marek, M. Roman, D. Danica and S. Pokorný, Makromol. Chem., 1986, 187, 2337–2344 CrossRef CAS.
- L. Du, K. Mackeprang and H. G. Kjaergaard, Phys. Chem. Chem. Phys., 2013, 15, 10194–10206 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford, CT, USA, 2013 Search PubMed.
- L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688 RSC.
- L. Du, J. R. Lane and H. G. Kjaergaard, J. Chem. Phys., 2012, 136, 184305 CrossRef PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- S. H. Schei, Acta Chem. Scand., Ser. A, 1983, 37, 671–677 CrossRef.
- D. A. C. Compton, S. C. Hsi, H. H. Mantsch and W. F. Murphy, J. Raman Spectrosc., 1982, 13, 30–37 CrossRef CAS.
- S. Tang, H. Zhao and L. Du, RSC Adv., 2016, 6, 91233–91242 RSC.
- H. Sasaki, S. Daicho, Y. Yamada and Y. Nibu, J. Phys. Chem. A, 2013, 117, 3183–3189 CrossRef CAS PubMed.
- M. Heger, J. Altnoder, A. Poblotzki and M. A. Suhm, Phys. Chem. Chem. Phys., 2015, 17, 13045–13052 RSC.
- G. Pietraperzia, M. Pasquini, F. Mazzoni, G. Piani, M. Becucci, M. Biczysko, D. Michalski, J. Bloino and V. Barone, J. Phys. Chem. A, 2011, 115, 9603–9611 CrossRef CAS PubMed.
- J. T. Yi, J. W. Ribblett and D. W. Pratt, J. Phys. Chem. A, 2005, 109, 9456–9464 CrossRef CAS PubMed.
- S. Scheiner, T. Kar and J. Pattanayak, J. Am. Chem. Soc., 2002, 124, 13257–13264 CrossRef CAS PubMed.
- C. Yuan, H. Wu, M. Jia, P. Su, Z. Luo and J. Yao, Phys. Chem. Chem. Phys., 2016, 18, 29249–29257 RSC.
- R. Medel, M. Heger and M. A. Suhm, J. Phys. Chem. A, 2015, 119, 1723–1730 CrossRef CAS PubMed.
- A. S. Hansen, L. Du and H. G. Kjaergaard, Phys. Chem. Chem. Phys., 2014, 16, 22882–22891 RSC.
- A. S. Hansen, L. Du and H. G. Kjaergaard, J. Phys. Chem. Lett., 2014, 5, 4225–4231 CrossRef CAS PubMed.
- I. Bako, T. Radnai and M. C. B. Funel, J. Chem. Phys., 2004, 121, 12472–12480 CrossRef CAS PubMed.
- T. Scharge, D. Luckhaus and M. A. Suhm, Chem. Phys., 2008, 346, 167–175 CrossRef CAS.
- G. S. F. D'Alva Torres, C. Pouchan, J. J. C. Teixeira-Dias and R. Fausto, Spectrosc. Lett., 1993, 26, 913–922 CrossRef.
- M. Dulce, G. Faria, J. J. C. Teixeira-Dias and R. Fausto, J. Mol. Struct., 1991, 263, 87–94 CrossRef.
- R. S. Friedman and P. W. Atkins, Molecular Quantum Mechanics, Oxford University Press, Oxford, 5th edn, 2011 Search PubMed.
- B. J. Miller, L. Du, T. J. Steel, A. J. Paul, A. H. Soedergren, J. R. Lane, B. R. Henry and H. G. Kjaergaard, J. Phys. Chem. A, 2012, 116, 290–296 CrossRef CAS PubMed.
- L. Du and H. G. Kjaergaard, J. Phys. Chem. A, 2011, 115, 12097–12104 CrossRef CAS PubMed.
- S. Chung and M. Hippler, J. Chem. Phys., 2006, 124, 214316 CrossRef PubMed.
- M. Hippler, J. Chem. Phys., 2007, 127, 084306 CrossRef PubMed.
- U. Koch and P. Popelier, J. Phys. Chem., 1995, 99, 9747–9754 CrossRef CAS.
- S. J. Grabowski, J. Phys. Org. Chem., 2004, 17, 18–31 CrossRef CAS.
- S. Blanco, P. Pinacho and J. C. López, Angew. Chem., Int. Ed., 2016, 55, 1–6 CrossRef PubMed.
- A. S. Mahadevi and G. N. Sastry, Chem. Rev., 2016, 116, 2775–2825 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra00901a |
| This journal is © The Royal Society of Chemistry 2017 |