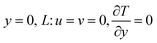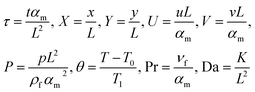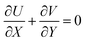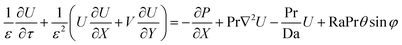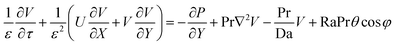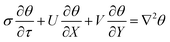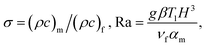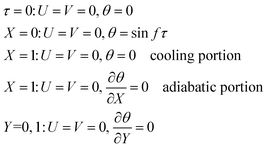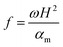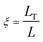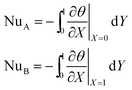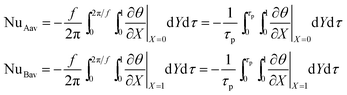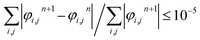DOI:
10.1039/C6RA28333K
(Paper)
RSC Adv., 2017,
7, 17519-17530
Numerical simulation of natural convection in an inclined porous cavity under time-periodic boundary conditions with a partially active thermal side wall
Received
17th December 2016
, Accepted 15th March 2017
First published on 21st March 2017
Abstract
Natural convection in an inclined porous cavity with positively or negatively inclined angles is studied numerically for time-periodic boundary conditions on the left side wall and partially active thermal boundary conditions on the right wall. The results show that a partially active thermal boundary condition on wall B can lead to heat transfer between two opposing vertical side walls. Temperature locations on wall B have significant effects on heat transfer of wall B, but weak effects on that of wall A. Compared with the uniform thermal boundaries, the non-uniform temperature distributions on wall B can reduce the oscillation amplitude of NuB. The absolute value of Nuav for the uniform boundary condition on wall B is highest when |φ| > 30° and the differences of Nuav between different boundary conditions on wall B decrease with the increasing of |φ|.
1. Introduction
Fluid flow and heat transfer of natural convection in a fluid-saturated porous medium has been a subject of considerable interest to scientists and researchers due to its wide range of geophysical and engineering applications such as geothermal systems, nuclear and chemical reactors, cooling of electronic devices, high performance building insulation, and solar power collectors. Representative studies in this field have been very well summarized in the books by and Pop and Ingham,1 Vafai2 and Nield and Bejan.3
In the past two decades, natural convection in a system with time oscillating boundary conditions has received much attention.4–16 Kazmierczak and Chinoda4 numerically studied the problem of laminar buoyancy-driven flow in a square cavity driven by a warm vertical wall, having a uniform surface temperature whose magnitude is changing sinusoidally with time. They found that the effect of the periodically changing wall temperature is felt only partially into the enclosure and, overall, the time-averaged heat transfer across the enclosure is rather insensitive to the time-dependent boundary condition. Lage et al.5 numerically and theoretically investigated natural convection in a two-dimensional square enclosure with one side cold and isothermal, and the other side heated with pulsating heat flux. Antohe et al.6,7 theoretically and numerically studied heat and momentum transport in a rectangular enclosure filled with clear fluid or fully saturated porous medium, under time-periodic horizontal heating. They found that the convection intensity within the enclosure increases linearly with heating amplitude for a wide range of parameters. Kwak et al.8 numerically investigated time-varying natural convection of an incompressible Boussinesq fluid in a sidewall-heated square cavity. The temperature at the cold sidewall Tc is constant, but at the hot sidewall a time-varying temperature condition is prescribed. Kwak et al.9,10 numerically investigated natural convection of an incompressible fluid in a square cavity which has a constant-temperature cold sidewall and an opposite hot sidewall with sinusoidally-varying temperature profile. It was found that a large-amplitude wall temperature oscillation causes an augmentation of the time-mean heat transfer rate. The maximum gain of the time-mean Nusselt number in the interior occurs at the resonance frequency, at which maximal fluctuations of the Nusselt number are found. The mechanism for resonant enhancement of the time-mean heat transfer is described. Chung et al.11 numerically studied finite-wall effect on buoyant convection in an enclosure with pulsating exterior surface temperature. The finite-wall effect on the shift of resonance frequency is discussed. The temperature oscillation at the interior surface of the solid wall is examined, and the convection-modified model is introduced to describe the alteration in the temperature contrast across the fluid portion. Sarris et al.12 numerically studied natural convection in a two-dimensional, rectangular enclosure with sinusoidal temperature profile on the upper wall and adiabatic conditions on the bottom and sidewalls, the applied sinusoidal temperature is symmetric with respect to the midplane of the enclosure. They found that the values of the maximum and the minimum local Nusselt number at the upper wall are shown to increase with increasing Rayleigh number. Bilgen et al.13 numerically investigated natural convection in enclosure with heating and cooling by sinusoidal temperature profiles on one side. Jha and Ajibade14 recently reported the effect of viscous dissipation on natural convection flow between vertical parallel plates with time-periodic boundary conditions. It was found that, in presence of viscous dissipation, fluids of relatively small Prandtl number has higher temperature than the channel plates and as such, heat is being transferred from the fluid to the plate. Huang et al.15,16 numerically studied conjugate conduction-natural convection in an enclosure with time-periodic sidewall temperature and inclination. They found that the total heat transfer rate of enclosure is dependent on the amplitude and period of the pulsating sidewall temperature. The heat transfer rate increases as the pulsating amplitude increases. They also investigated natural convection in a square enclosure induced by inner circular cylinder with time-periodic pulsating temperature and analyzed the influence of pulsating temperature on the unsteady fluid flow and heat transfer in the square enclosure.
A survey of the above exiting literatures has shown that most of these studies dealt with natural convection of fluid in an enclosure with time-periodic boundary conditions. However, studies of natural convection in a fluid-saturated porous medium system subject to the same boundary conditions are relatively scarce.17–22 Antohe and Lage17 theoretically and numerically studied the natural convection flow within a fluid saturated porous medium enclosure subjected to intermittent heating from the side (hot wall). They found that at the resonance frequency the fluid saturated porous medium system behaves as a dynamic thermal insulator in which the strong natural convection activity within the system, characterized by high amplitude heat flow oscillations. By two types of experimental methods, Kazmierczak and Muley18 experimentally investigated natural convection in a horizontal porous layer heated from below. It was found that the steady-state heat-transfer rate through the enclosure is greater in the porous layer containing a thin top fluid layer. The transient experiments showed that the cycle-averaged heat-transfer rate through the layer is different from its steady-state value when the bottom wall temperature oscillates. The heat transfer may increase or decrease, which depends strongly on the kind of upper surface condition.
It is worth noting that Kalabin et al.19 reported that the time-averaged Nusselt number is not zero for an inclined cavity with a sinusoidal wall temperature on one side of the wall and a constant average temperature on the opposing side. This system has no temperature difference between the opposing two side walls in a time-averaged sense and there is actually no heat transfer between the walls when these side walls are kept vertical. They found that the average Nusselt number takes a maximum value at an inclined angle of about φ = 54° and dimensionless frequency f = 20π for Grashof numbers (2 × 105 and Gr = 3 × 105). Their findings could be used for controlling the natural convection heat transfer rate. They studied cavity flow, but similar phenomena may be expected to occur in porous media. Wang et al.20,21 studied the natural convection in an inclined porous cavity with one side wall (upward facing) of oscillating temperature and the opposing side wall (downward facing) at constant average temperature. Numerical results were obtained for the values of the inclined angle 0° < φ < 80° and various values of dimensionless oscillating frequency. They found the time-averaged heat flux is always transferred from the upward-facing wall to downward-facing wall for a porous enclosure. They obtained the maximum heat flux at an inclined angle of 42.2° and the dimensionless frequency of 46.7π. They also studied the effects of positive/negative inclined angles of the cavity and various values of oscillation frequency on the natural convection heat transfer. Similar studies were also performed by Wang et al.22 They numerically investigated three-dimensional unsteady natural convections in an inclined porous cavity with time oscillating boundary conditions. It was found that, with proper selection of inclination angle and oscillation frequency, the natural convection heat transfer will be significantly improved and the maximal heat fluxes are finally obtained with the optimal combinations of f = 35π, α1 = 50, α2 = 45 when Ra = 106 and f = 40π, α1 = 45°, α2 = 45 when Ra = 107. Recently, natural convection heat transfer enhancement in an air filled square cavity periodically cooled from above was numerically investigated by Raji et al.23 They found that variable cooling temperatures could lead to a drastic change in the flow structure and the corresponding heat transfer, especially at specific low periods of the cold variable temperatures. This leads to a resonance phenomenon characterized by an important increase in heat transfer by about 46.1% compared to the case of a constant cold temperature boundary condition. Bhadauria et al.24 studied the effects of time-periodic thermal boundary conditions and internal heating on heat transport in a porous medium. The effects of internal Rayleigh number, amplitude and frequency of modulation, thermo-mechanical anisotropies, and Vadasz number on heat transport had been analyzed and depicted graphically. Wang et al.25 numerically investigated natural convection heat transfer of copper–water nanofluid in a square cavity with time-periodic boundary temperature. They found that the copper nanoparticles have a pronounced influence on the oscillating behaviors for the flow and temperature fields, as well as the average Nusselt number. The results indicated that the addition of copper nanoparticles causes a remarkable increase in time-averaged Nusselt number. Soto-Meca et al.26 numerically studied the heat and mass transfer performance of a double diffusive lid driven cavity under pulsating flow. They found that the pulsating flow regime is found to be an effective tool for improving the efficiency of heat and mass transfer applications. The results allow the characterization of the operation performance of high efficiency mass and heat transfer systems in the case of double diffusive mixed convection problems based on pulsating flow conditions.
A careful review of the existing literature reveals that there lacks fundamental information regarding the heat transfer characteristic of porous enclosure under time-periodic boundary conditions with partially active thermal side wall. In addition to natural convection in porous enclosures with uniform thermal boundaries, recently attention has been intensively paid to the cases with non-uniform temperature distributions on the walls.27–30 For example, heat transfer in partially opened enclosures filled with porous medium exists in some applications like, solar energy collection and cooling of electronic components, in which the active walls may be subject to abrupt temperature non-uniformities due to shading or other effects. The relative position of the hot and cold wall regions has significant effects on the fluid flow and heat transfer in the porous medium. Oztop et al.27 numerically investigated the steady natural convection in a partially opened enclosure filled with porous media using the Brinkman–Forchheimer model and the effects of pertinent parameters such as Grashof number, Darcy number, porosity, length of the heated wall and the location center of the opened cavity were examined. Sankar et al.28 reported a numerical investigation of the convective flow and heat transfer in a square porous cavity with partially active thermal walls. Five different heating and cooling zones are considered along the vertical walls while the remaining portions of the side walls as well as the top and bottom of the cavity are adiabatic. Wu et al.29,30 numerically studied natural convection in cavity filled with porous medium with partially and sinusoidal thermal active sidewalls under local thermal non-equilibrium conditions.
As well known, natural convection heat transfer in inclined cavities also has many important applications, such as solar energy collectors, double-glazed windows, car batteries, electronic cooling systems, and crystal growth.31 Basak et al.31–35 analyzed natural convection within inclined porous square cavities for various inclination angles via the heatline and entropy generation approaches and the strategic application of entropy generation concept for optimization of the natural convection in inclined porous square cavities. They also studied entropy generation during natural convection in a triangular enclosure with various configurations for the linearly heated inclined walls, and the heatline patterns during natural convection for different types of Dirichlet heatfunction boundary conditions. The enclosures with various shapes (square, curved, trapezoidal, tilted square and parallelogrammic) are considered with various thermal boundary conditions. Cho et al.36 numerically investigated natural convection heat transfer performance and entropy generation of Al2O3–water nanofluid in an inclined wavy-wall cavity. The simulations focus specifically on the effects of the cavity inclination angle, nanoparticle volume fraction. Kefayati et al.37 numerical simulated entropy generation of associated with the natural convection of non-Newtonian nanofluid using the Buongiorno's mathematical model in an inclined cavity. They found that the augmentation of the power-law index enhances various entropy generations in different Rayleigh numbers and inclined angles. The aim of present paper is to numerically investigate natural convection in an inclined porous cavity with positive or negative inclined angles for time-periodic boundary conditions on left side wall and partially active thermal boundary conditions on right wall. In the following sections, firstly, the physical models and mathematical formulations of the problem are given. Subsequently, a numerical simulation of the full governing equations is carried out to study the transport structures and heat transfer rate. The results from the numerical computations are then discussed in detail. Finally, the conclusions are given.
2. Mathematical formulation
The two-dimensional inclined enclosure under investigation is filled with a fluid-saturated porous medium. The schematic configuration of the problem is illustrated in Fig. 1, and six different simulated modes are shown in Fig. 2, with L denoting the side length of the square enclosure. Fig. 1a and b show a cavity that is tilted at a positive or negative angle φ with respect to the horizontal, respectively. The fluid is a Newtonian incompressible fluid (Pr = 1), and the porous medium is considered to be homogeneous and isotropic. Furthermore, the porous medium is assumed to be in local thermal equilibrium with the fluid.
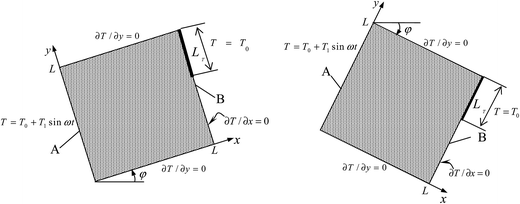 |
| | Fig. 1 Schematic of the dimensional physical problem. | |
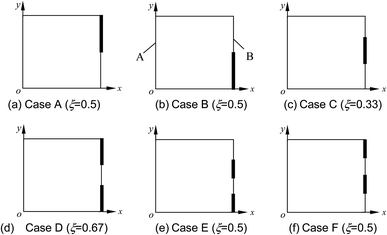 |
| | Fig. 2 Different partially active thermal locations (φ = 0°). | |
The temperature of right wall (wall B) of the cavity is partially kept constant at T0, while the remaining part of the right walls is insulated, the temperature of the opposing side wall (wall A) varies sinusoidally in time with a mean temperature T0. The other two walls of the cavity are adiabatic. The thermophysical properties of the fluid and the porous material are taken to be constant except for the density variation in the buoyancy force, which is treated by the Boussinesq approximation.
Lauriat and Prasad41 examined the relative importance of inertia and viscous forces on natural convection in porous media for a differentially heated vertical cavity. They found that there exists an asymptotic convection regime where the solution is independent of the permeability of the porous matrix, or the Darcy (Da) and Forchheimer (Fs) numbers. The higher the fluid Rayleigh number, Ra, the earlier this regime starts in terms of Da and Fs. The Brinkman-extended Darcy formulation used in the literature,41 which does not include the quadratic drag effect (i.e. Forchheimer term), is adopted for modeling the fluid flow in the porous medium, the governing equations for mass, momentum, and energy in two-dimensional, laminar flow are as follows.
| |
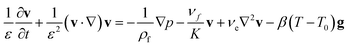 | (2) |
| |
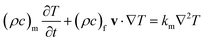 | (3) |
where
β is the fluid volumetric expansion coefficient,
g is the gravitational acceleration vector,
v represents the filtration velocity vector,
ρf is the fluid density,
νf is the fluid kinematic viscosity,
ε and
K are the porosity and permeability of the porous medium, respectively,
T stands for temperature,
t for time,
km is the stagnant thermal conductivity of porous medium, and
νe is the effective kinematic viscosity of the porous medium. The value of
νf is used as an approximate value of
νe,
i.e.,
νe =
νf, and this approximation provides good agreement with experimental data obtained by Lundgren.
38
In accordance with the present problem, the governing eqn (1)–(3) are subject to the following initial and boundary conditions:
| |
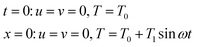 | (4a) |
| |
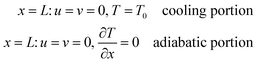 | (4b) |
| |
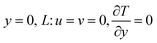 | (4c) |
It can be seen from eqn (4) that the temperature of wall A sinusoidally oscillates over an average value T0 with amplitude T1 and frequency ω.
Defining the following dimensionless variables,
| |
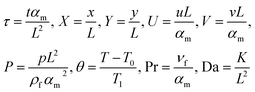 | (5) |
where Pr and Da are the Prandtl number and the Darcy number, respectively.
αm is the modified thermal diffusivity defined as
km = (
ρc)
f. The governing
eqn (1)–(3) can be written in the following dimensionless forms:
| |
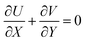 | (6) |
| |
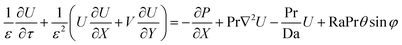 | (7) |
| |
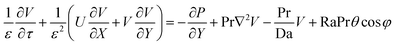 | (8) |
| |
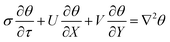 | (9) |
where
φ is the inclined angle of the cavity. The heat capacity ratio
σ and Rayleigh number Ra are defined as
| |
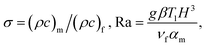 | (10) |
The corresponding dimensionless initial and boundary conditions are given by
| |
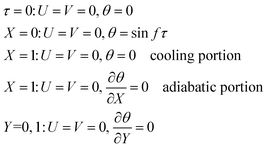 | (11) |
where
f is the dimensionless oscillating frequency of the boundary temperature and is defined as
| |
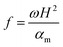 | (12) |
The ratio between length of cooling wall and height of cavity wall is defined as:
| |
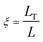 | (13) |
The geometrically averaged Nu at walls A and B are given as follows:
| |
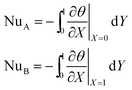 | (14) |
The time-averaged Nusselt number in one period along the oscillating temperature wall and constant temperature wall are defined as
| |
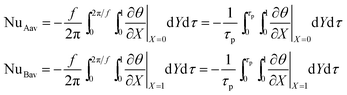 | (15) |
where
τp is the dimensionless period of the temperature oscillation and
τp = 2π/
f.
3. Numerical method
The dimensionless governing eqn (6)–(9) are solved using the SIMPLER algorithm outlined by Patankar.39 The convective terms are discretized by using the QUICK scheme reported by Hayase et al.,40 and a second-order central difference scheme is used for the diffusion terms. The resulting algebraic equations are solved by the tridiagonal matrix algorithm (TDMA).
The convergence of computations is declared at each time instant when the following criterion is satisfied:
| |
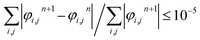 | (16) |
where
φ stands for
U,
V, and
θ;
n is an internal iteration number. Accuracy tests were performed using three sets of grids: 41 × 41, 51 × 51, and 61 × 61. The results indicate insignificant differences between the 51 × 51 and 61 × 61 grids as shown in Wang
et al.21 Therefore, for all computations in this paper, a 51(
X) × 51(
Y) staggered, non-uniform grid was employed. Grid stretching was made to cluster the mesh points near the boundary walls, where sharp gradients of velocity and temperature are expected. To validate the computer code, we solved the problem of two-dimensional natural convection in a vertical porous cavity as studied by Lauriat and Prasad.
41 The one vertical wall of the cavity is isothermally heated at
Th and the other vertical wall is cooled at constant temperature
Tc, while the horizontal walls are adiabatic. As shown in
Table 1, the detailed comparison of average Nusselt number predictions with the data obtained by Lauriat and Prasad
41 are listed in
ref. 21. These comprehensive verification efforts demonstrated the robustness and accuracy of the present numerical method, which can be attributed to the applying for simulation of natural convection in an inclined porous cavity displayed in
Fig. 1.
Table 1 Comparison of average Nusselt number predictions with the computed data of Lauriat and Prasad (1989) (Pr = 1)
| Ra |
Da |
ε |
Nu |
| Present |
Lauriat and Prasad41 |
| 108 |
10−4 |
0.4 |
25.75 |
25.70 |
| 108 |
10−6 |
0.4 |
3.102 |
3.06 |
| 107 |
10−6 |
0.1 |
1.073 |
1.07 |
| 109 |
10−6 |
0.4 |
13.34 |
13.22 |
| 103 |
10−2 |
0.4 |
1.02 |
1.02 |
4. Results and discussion
In this paper, the effects of partially active thermal location on wall B, positive/negative inclined angle and oscillating frequency on natural convection are mainly investigated, the Rayleigh, Darcy, and Prandtl numbers, porosity, and the heat capacity ratio are kept constant: Ra = 106, Da = 10−3, Pr = 1, ε = 0.6, and σ = 1. In this study, the time step is Δτ = 1 × 10−5. In order to obtain a standing oscillating solution independent of the initial state, 5–10 oscillating periods are needed to be calculated. Based on the above given conditions, numerical results are obtained for the values of the inclined angles φ = ±15°, ±30°, ±45°, ±60°, and ±75°, and the dimensionless oscillation frequency f = 20π, 60π, and 100π.
4.1. Flow and thermal fields
Fig. 3–8 show the time-dependent flow patterns and isotherms over the duration of the ninth period (τ = 0.8–0.9) for f = 20π and φ = 45°, respectively. The solid lines indicate the positive contour values, while the dashed lines indicate the negative contour values. It is evident from Fig. 3 that, due to asymmetric thermal boundary condition and inclined cavity, asymmetric flow field distribution appears in cavity, the streamlines vary in different patterns, and clockwise (solid lines) and counter clockwise (dots lines) rotatings exist simultaneously during one period. The flow patterns in cavity changes continuously during one period due to the variation of thermal boundary condition on left wall. Also, it can be seen from Fig. 3–8 that the forms of boundary conditions on wall B have significant effects on isotherms and flow patterns of porous cavity. Firstly, the flow pattern of porous cavity is quite complicated in one period, which varies with the change of the temperature of at wall A, the single clockwise cell occurs in the entire cavity during half cycle of the oscillation period. For another half cycle of the oscillation period, there are two circulations with same or inverse directions of rotation in the cavity because the instantaneous temperature of wall A is higher or lower than the constant average temperature. Secondly, it is interesting to find that, the position of vortex center near wall B move with the locations of wall B whose temperature is partially kept constant at T0, the number of vortex center near wall B equals the number of partially active thermal locations at τ = 0.875 (Fig. 6g and Fig. 8g) which indicates that the periodically cooled and thermal insulated by right wall (wall B) can lead to the fluid rise up from the portion of the heated part of left side wall and flow down along the right side wall with uniformly cooled boundary condition forming a rotating cell inside the cavity, and the number of rotating cell increases with increasing the number of heated section at left side wall.
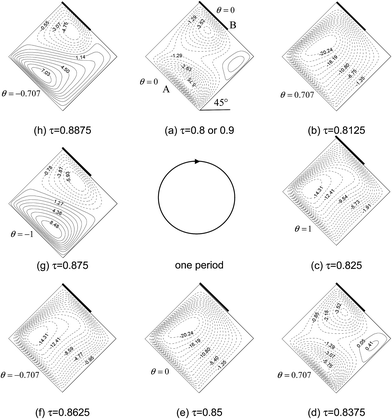 |
| | Fig. 3 Sequential plots of stream functions for case A during one period for f = 20π and φ = 45° at Ra = 106, Da = 10−3, Pr = 1, and ε = 0.6. | |
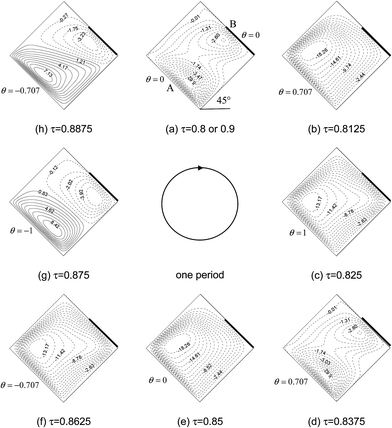 |
| | Fig. 4 Sequential plots of stream functions for case B during one period for f = 20π and φ = 45° at Ra = 106, Da = 10−3, Pr = 1, and ε = 0.6. | |
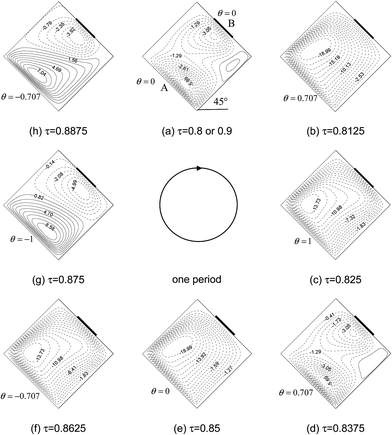 |
| | Fig. 5 Sequential plots of stream functions for case C during one period for f = 20π and φ = 45° at Ra = 106, Da = 10−3, Pr = 1, and ε = 0.6. | |
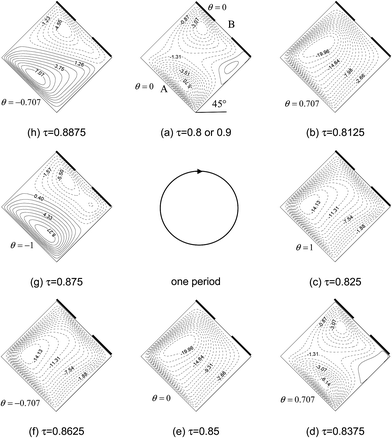 |
| | Fig. 6 Sequential plots of stream functions for case D during one period for f = 20π and φ = 45° at Ra = 106, Da = 10−3, Pr = 1, and ε = 0.6. | |
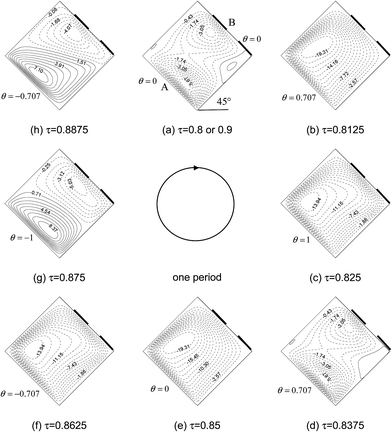 |
| | Fig. 7 Sequential plots of stream functions for case E during one period for f = 20π and φ = 45° at Ra = 106, Da = 10−3, Pr = 1, and ε = 0.6. | |
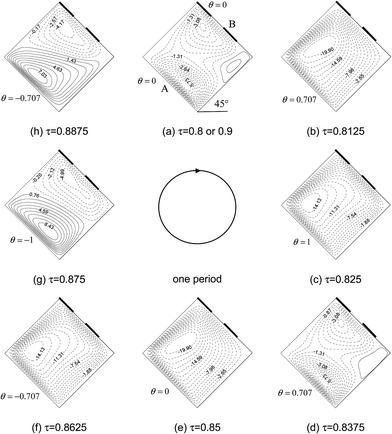 |
| | Fig. 8 Sequential plots of stream functions for case F during one period for f = 20π and φ = 45° at Ra = 106, Da = 10−3, Pr = 1, and ε = 0.6. | |
4.2. Effects of partially active thermal locations and positive/negative angles of inclination on heat transfer
In order to consider the effect of partially active thermal locations on heat transfer of porous cavity, the other boundary parameters are all kept constant as φ = 0°, f = 20π, Ra = 106, Da = 10−3, Pr = 1, ε = 0.6, and σ = 1. Fig. 9 shows the transient responses of the average Nusselt numbers for wall A (X = 0) and wall B (X = 1). As shown in Fig. 9, firstly, NuA and NuB fluctuate with the oscillation of temperature on wall A, which are not symmetrical about the lines NuA = 0 or NuB = 0. Compared with the simulation results of uniform thermal boundary condition as shown in Wang et al.,21 the time-averaged Nusselt number Nuav are not on the order of 10−8 when the right wall (wall B) of the cavity is partially kept constant at T0, as shown in Table 2, which indicates that partially active thermal boundary condition on wall B can lead to temperature difference between the opposing two side walls in a time-averaged sense and there is actually heat transfer between the walls when these side walls are kept vertical. It may be noted that partially thermal active wall leads to heat transfer area difference between vertical side walls, and the heat transfer balance is broken and heat transfer occurs between two vertical side walls of the porous cavity, the total heat transfer in cavity can be changed by non-uniform thermal boundary conditions. Secondly, the values of time-averaged Nusselt number Nuav are positive or negative for different boundary conditions on wall A of porous cavity, which indicates that different forms of partially active thermal locations at wall B provide different temperature distributions and lead to positive and negative total net heat flux between two vertical side walls of porous cavity.
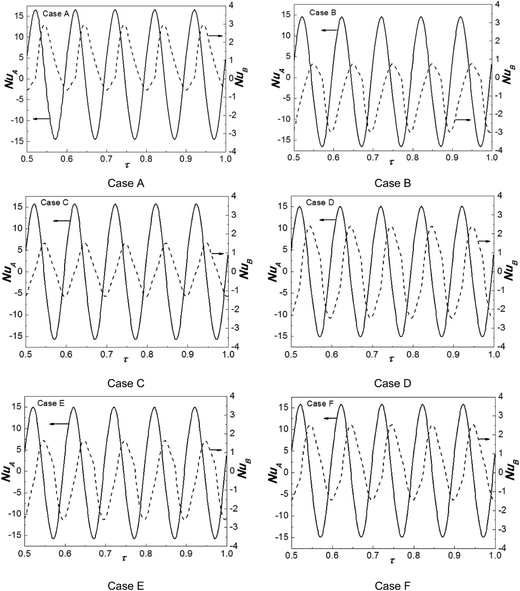 |
| | Fig. 9 Transient responses of the average Nusselt numbers for wall A (X = 0) and wall B (X = 1) for f = 20π, φ = 0°. | |
Table 2 Summary of the time-averaged Nusselt numbers for different partially active thermal locations (φ = 0°)
| |
Case A |
Case B |
Case C |
Case D |
Case E |
Case F |
Wang et al.21 |
| Nuav |
0.9177 |
−0.8796 |
0.0800 |
−0.0358 |
−0.3848 |
0.4280 |
2.23 × 10−8 |
Fig. 10 and 11 show transient responses of the average Nusselt numbers for wall A (X = 0) and wall B (X = 1) for f = 20π, φ = ±45° and ±60°. It can be seen that temperature locations on wall B have significant effects on the heat transfer of wall B, but weak on that of wall A. Compared with the uniform thermal boundaries, the non-uniform temperature distributions on wall B can reduce the oscillation amplitude of NuB due to the heat transfer boundary length of right wall shortens, the oscillation amplitude of NuB of case C is the minimal and which of case D is the maximum among seven kinds of boundary condition on wall B. It is due to that, with the increase of the value of side wall location, the natural convection is developed and enhanced along with the flow direction. The transient values of NuA and NuB present symmetrical distribution about the lines of NuA = 0 or NuB = 0.
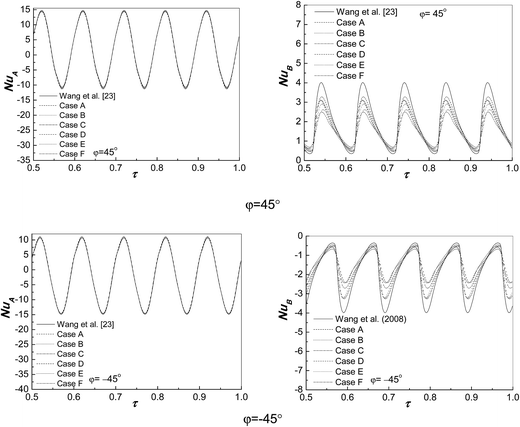 |
| | Fig. 10 Transient responses of the average Nusselt numbers for wall A (X = 0) and wall B (X = 1) for f = 20π, φ = 45° and φ = −45°. | |
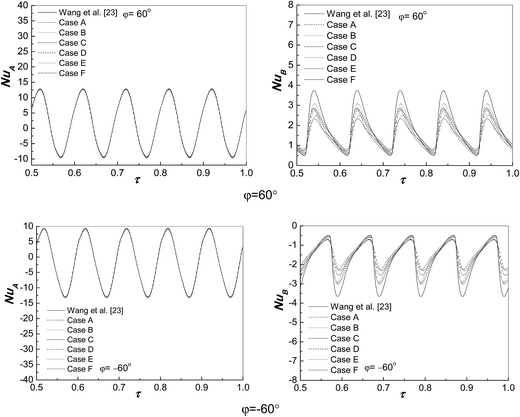 |
| | Fig. 11 Transient responses of the average Nusselt numbers for wall A (X = 0) and wall B (X = 1) for f = 20π, φ = 60° and φ = −60°. | |
Fig. 12 reflects the variations of time-averaged Nusselt number with positive or negative inclined angles for different partially thermal active locations and oscillating frequency at Ra = 106, Da = 10−3, Pr = 1, and ε = 0.6. The results show that the oscillating frequency has weak effect on the heat transfer of porous cavity. The time-average Nusselt number profile is symmetric about the center point of line Nuav = 0, which implies that positive/negative angles of inclination of porous cavity can change the heat flux direction in cavity. The time-average Nusselt numbers reach a maximum value at φ = ±45° for uniform temperature distribution on wall B, and reach maximum value at φ = ±25° for non-uniform temperature distribution on wall B. Also, the maximum value of Nuav for uniform boundary condition on wall B is higher than those of non-uniform boundary conditions. It can be observed that, the absolute value of Nuav for uniform boundary condition on wall B is highest when |φ| > 30°. When |φ| < 40°, the difference of Nuav between case A and case B becomes maximum. Obviously, the differences of Nuav between different boundary conditions on wall B decrease as increasing of |φ|, which reveals that the pattern of partially active thermal wall has weak effects on heat transfer behavior in porous cavity when the vertical walls of cavity become horizontally top or bottom walls (φ = ±90°). In these cases, the heat transfer in cavity is similar to that with stationary fluid and the heat transfer is due to pure conduction.
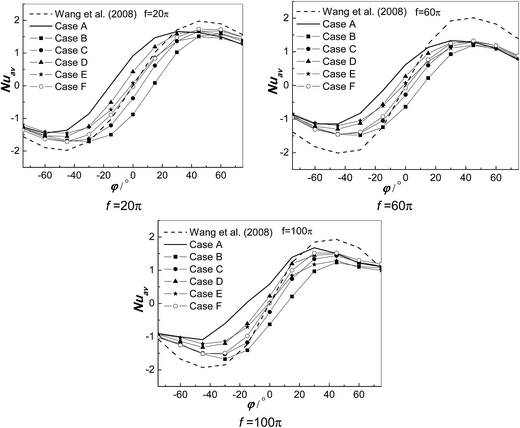 |
| | Fig. 12 Variations of time-averaged Nusselt number with positive or negative inclined angles for different partially active thermal locations and oscillation frequency at Ra = 106, Da = 10−3, Pr = 1, and ε = 0.6. | |
5. Conclusions
Natural convection in an inclined porous cavity with positive/negative inclined angles is numerical simulated for the case of one wall with the sinusoidal oscillating temperature and the opposing wall being partially thermal active. Main attention has been focused on the effect of the main factors, including the partially thermal active pattern on side wall, positive/negative angles of inclination and dimensionless oscillating frequency, on the fluid flow and heat transfer characteristics in porous cavity. Main conclusions are as follows.
(1) The transient responses in the average Nusselt numbers NuA and NuB fluctuate with the oscillation of temperature on wall A, which are not symmetrical about the line Y = 0. Partially active thermal boundary condition on wall B can lead to heat transfer between two opposing vertical side walls.
(2) Different forms of partially active thermal locations at wall B provide positive and negative total net heat flux of porous cavity. The temperature locations on wall B have significant effects on heat transfer of wall B, but weak on that on wall A.
(3) Compared with the uniform thermal boundaries, the non-uniform temperature distributions on wall B can reduce the oscillation amplitude of NuB. Compared with the NuB under other kind of boundary conditions on wall B, the oscillation amplitude of NuB of case C is minimal.
(4) The absolute value of Nuav for uniform boundary condition on wall B is highest when |φ| > 30°. When |φ| < 40°, the difference value of Nuav between case A and case B become maximum and the differences of Nuav between different boundary conditions on wall B decrease as increasing of |φ|.
Nomenclature
| c | Specific heat, J (kg−1 K−1) |
| Da | Darcy number |
| f | Dimensionless oscillation frequency, ωh2/ν |
| g | Gravitational acceleration, m s−2 |
| H | Side length of cavity, m |
| k | Thermal conductivity, W (m−1 K−1) |
| K | Permeability of the porous medium, m2 |
| NuA | Average Nusselt number computed over oscillating temperature wall |
| NuB | Average Nusselt number computed over constant temperature wall |
| Nuav | Time-averaged Nusselt number in one period |
| p | Pressure, Pa |
| P | Dimensionless pressure |
| Pr | Prandtl number |
| Q | Heat capacity of porous medium at temperature T |
| Ra | Rayleigh number |
| t | Time, s |
| T | Temperature, K |
| u, v | Velocity components along x and y axes, m s−1 |
| U, V | Non-dimensional velocity components |
| x, y | Cartesian coordinates, m |
| X, Y | Non-dimensional Cartesian coordinates |
Greek symbols
| αf | Thermal diffusivity of fluid, m2 s−1 |
| αm | Thermal diffusivity of porous medium, m2 s−1 |
| β | Coefficient of volume expansion, K−1 |
| ε | Porosity |
| θ | Dimensionless temperature |
| νe | Effective kinematic viscosity, m2 s−1 |
| νf | Kinematic viscosity of fluid, m2 s−1 |
| ρ | Density, kg m−3 |
| τ | Dimensionless time |
| τp | Dimensionless period of oscillation |
| σ | Heat capacity ratio |
| ω | Oscillation frequency, s−1 |
| φ | Inclined angle |
| ξ | Ratio between length of active thermal wall and height of cavity wall |
Superscript
subscripts
| A | Constant temperature wall |
| B | Oscillating temperature wall |
| f | Fluid |
| m | Fluid-saturated porous medium |
Acknowledgements
This work is supported by National Science Foundation of China (Grant No. 21476181), China Postdoctoral Science Foundation Funded Project (No. 2013M540768), China Postdoctoral Science Special Foundation (Grant No. 2015T81048) and Cyrus Tang Foundation.
References
- I. Pop and D. B. Ingham, Convective Heat Transfer: Mathematical and Computational Modelling of ViscousFluids and Porous Media, Pergamon, Oxford, 2001 Search PubMed.
- K. Vafai, Handbook of Porous Media, Marcel Dekker, New York, 2nd edn, 2005 Search PubMed.
- D. A. Nield and A. Bejan, Convection in Porous Media, Springer-Verlag, New York, 3rd edn, 2006 Search PubMed.
- M. Kazmierczak and Z. Chinoda, Buoyancy-Driven Flow in an Enclosure with Time Periodic Boundary Conditions, Int. J. Heat Mass Transfer, 1992, 35, 1507–1518 CrossRef CAS.
- J. L. Lage and A. Bejan, The Resonance of Natural Convection in an Enclosure Heated Periodically from the Side, Int. J. Heat Mass Transfer, 1993, 36, 2027–2038 CrossRef CAS.
- B. V. Antohe and J. L. Lage, Amplitude Effects on Convection Induced by Time-Periodic Horizontal Heating, Int. J. Heat Mass Transfer, 1996, 38, 1121–1133 CrossRef.
- B. V. Antohe and J. L. Lage, The Prandtl Number Effect on the Optimum Heating Frequency of an Enclosure Filled with Fluid or with a Saturated Porous Medium, Int. J. Heat Mass Transfer, 1987, 40, 1313–1323 CrossRef.
- H. S. Kwak and J. M. Hyun, Natural Convection in an Enclosure Having a Vertical Sidewall with Time- Varying Temperature, J. Fluid Mech., 1996, 329, 65–88 CrossRef.
- H. S. Kwak, K. Kuwahara and J. M. Hyun, Resonant Enhancement of Natural Convection Heat Transfer in a Square Enclosure, Int. J. Heat Mass Transfer, 1998, 41, 2837–2846 CrossRef.
- H. S. Kwak, K. Kuwahara and J. M. Hyun, Prediction of the Resonance Frequency of Natural Convection in an Enclosure with Time-Periodic Heating Imposed on One Sidewall, Int. J. Heat Mass Transfer, 1998, 41, 3157–3160 CrossRef CAS.
- K. H. Chung, H. S. Kwak and J. M. Hyun, Finite-Wall Effect on Buoyant Convection in an Enclosure with Pulsating Exterior Surface Temperature, Int. J. Heat Mass Transfer, 2001, 44, 721–732 CrossRef.
- I. E. Sarris, I. Lekakis and N. S. Vlachos, Natural Convection in a 2D Enclosure with Sinusoidal Upper Wall Temperature, Numer. Heat Transfer, Part A, 2002, 42, 513–530 CrossRef.
- E. Bilgen and Y. R. Ben, Natural Convection in Enclosure with Heating and Cooling by Sinusoidal Temperature Profiles on one Side, Int. J. Heat Mass Transfer, 2007, 50, 139–150 CrossRef.
- B. K. Jha and A. O. Ajibade, Effect of viscous dissipation on natural convection flow between vertical parallel plates with time-periodic boundary conditions, Comm. Nonlinear Sci. Numer. Simulat., 2012, 17, 1576–1587 CrossRef.
- Z. Huang, C. H. Zhang and G. Xi, Conjugate conduction-natural convection in an enclosure with time-periodic sidewall temperature and inclination, Int. J. Heat Fluid Flow, 2011, 32, 52–64 CrossRef.
- Z. Huang, W. Zhang and G. Xi, Natural convection in square enclosure induced by inner circular cylinder with time-periodic pulsating temperature, Int. J. Heat Mass Transfer, 2015, 82, 16–25 CrossRef.
- B. V. Antohe and J. L. Lage, A Dynamic thermal insulator: inducing resonance within a fluid saturated porous medium enclosure heated periodically from the side, Int. J. Heat Mass Transfer, 1994, 37, 771–782 CrossRef.
- M. Kazmierczak and A. Muley, Steady and transient natural convection experiments in a horizontal porous layer: the effects of a thin top fluid layer and oscillating bottom wall temperature, Int. J. Heat Fluid Flow, 1994, 15, 30–41 CrossRef CAS.
- E. V. Kalabin, M. V. Kanashina and P. T. Zubkov, Natural convection heat transfer in a square cavity with time-varying side-wall temperature, Numer. Heat Transfer, Part A, 2005, 621–631 CrossRef.
- G. Wang, Q. W. Wang, M. Zeng and H. Ozoe, Numerical study of natural convection heat transfer in an inclined porous cavity with time-periodic boundary conditions, Transp. Porous Media, 2008, 74, 293–309 CrossRef.
- G. Wang, Q. W. Wang, M. Zeng and H. Ozoe, Natural convection heat transfer in an inclined porous cavity under time-periodic boundary conditions with positive/negative inclined angles, J. Porous Media, 2008, 11(6), 541–555 CrossRef.
- Q. W. Wang, J. Yang, M. Zeng and G. Wang, Three-dimensional numerical study of natural convection in an inclined porous cavity with time sinusoidal oscillating boundary
conditions, Int. J. Heat Fluid Flow, 2010, 31, 70–82 CrossRef CAS.
- A. Raji, M. Hasnaoui, M. Firdaouss and C. Ouardi, Natural convection heat transfer enhancement in a square cavity periodically cooled from above, Numer. Heat Transfer, Part A, 2013, 63, 511–533 CrossRef CAS.
- B. S. Bhadauria, I. Hashim and P. G. Siddheshwar, Effects of time-periodic thermal boundary conditions and internal heating on heat transport in a porous medium, Transp. Porous Media, 2013, 97, 185–200 CrossRef CAS.
- G. Wang, X. Meng, M. Zeng, H. Ozoe and Q. W. Wang, Natural convection heat transfer of copper–water nanofluid in a square cavity with time-periodic boundary temperature, Heat Transfer Eng., 2014, 35(6–8), 630–640 CrossRef CAS.
- A. Soto-Meca, J. Serna and F. J. S. Velasco, Heat and mass transfer enhancement in a double diffusive mixed Convection lid cavity under pulsating flow, Comput. Chem. Eng., 2016, 94, 128–140 CrossRef CAS.
- H. F. Oztop, K. Al-salem, Y. Varol and I. Pop, Natural convection heat transfer in a partially opened cavity filled with porous media, Int. J. Heat Mass Transfer, 2011, 54, 2253–2261 CrossRef.
- M. Sankar, M. Bhuvaneswari, S. Sivasankaran and Y. h. Do, Buoyancy induced convection in a porous cavity with partially thermally active sidewalls, Int. J. Heat Mass Transfer, 2011, 54, 5173–5182 CrossRef.
- F. Wu, W. J. Zhou and X. X. Ma, Natural convection in a porous rectangular enclosure with sinusoidal temperature distributions on both side walls using a thermal non-equilibrium model, Int. J. Heat Mass Transfer, 2015, 85, 756–771 CrossRef.
- F. Wu, G. Wang and W. J. Zhou, A thermal nonequilibrium approach to natural convection in a square enclosure due to the partially cooled sidewalls of the enclosure, Numer. Heat Transfer, Part A, 2015, 67, 771–790 CrossRef CAS.
- A. K. Singh, S. Roy and T. Basak, Analysis of Bejan's heatlines on visualization of heat flow and thermal mixing in titled square cavity, Int. J. Heat Mass Transfer, 2012, 55, 2965–2983 CrossRef.
- P. Biswal, A. Nag and T. Basak, Analysis of thermal management during natural convection within porous tilted square cavities via heatline and entropy generation, Int. J. Mech. Sci., 2016, 115–116, 596–615 CrossRef.
- V. M. Rathnam, M. Roy and T. Basak, Analysis of entropy generation during natural convection in tilted triangular enclosures with various base angles, Numer. Heat Transfer, Part A, 2016, 69(12), 1332–1354 CrossRef.
- P. Biswal and T. Basak, Sensitivity of heatfunction boundary conditions on invariance of Bejan's heatlines for natural convection in enclosures with various wall heatings, Int. J. Heat Mass Transfer, 2015, 89, 1342–1368 CrossRef.
- A. K. Singh, T. Basak, A. Nag and S. Roy, Role of entropy generation on thermal management during natural convection in tilted porous square cavities, J. Taiwan Inst. Chem. Eng., 2015, 50, 153–172 CrossRef CAS.
- C. C. Cho, C. H. Chiu and C. Y. Lai, Natural convection and entropy generation of Al2 O3 –water nanofluid in an inclined wavy-wall cavity, Int. J. Heat Mass Transfer, 2016, 97, 511–520 CrossRef CAS.
- G. H. R. Kefayati, Nor Azwadi Che Sidik, Simulation of natural convection and entropy generation of non-Newtonian nanofluid in an inclined cavity using Buongiorno's mathematical model (Part II, entropy generation), Powder Technol., 2017, 305, 679–703 CrossRef CAS.
- T. S. Lundgren, Slow flow through stationary random beds and suspensions of spheres, J. Fluid Mech., 1972, 51, 273–299 CrossRef.
- S. V. Patankar, Numerical Heat Transfer and Fluid Flow, McGraw-Hill, New York, 1980 Search PubMed.
- T. Hayase, J. A. Humphery and R. Grief, A consistently formulated QUICK scheme for east and stable convergence using finite-volume calculation procedures, J. Comput. Phys., 1992, 98, 108–118 CrossRef.
- G. Lauriat and V. Prasad, Non-darcian effects on natural convection in a vertical porous enclosure, Int. J. Heat Mass Transfer, 1989, 32, 2135–2148 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a and
Gang Wangb
*a and
Gang Wangb