Effect of erbium concentration on the structural, optical and electrical properties of a Bi₄Ti₃O₁₂ system

Abstract

We have studied the influence of erbium doping on the optical and electrical properties of a Bi₄Ti₃O₁₂ compound. Bi_4−xEr_xTi₃O₁₂ (x = 0.0, 0.1, 0.2 and 0.3) samples are prepared by the solid state reaction method. X-ray diffraction (XRD) revealed that our samples are homogenous and crystallize in the orthorhombic system with the Fmmm space group. Absorbance measurement reveals that the peak intensity increases with increasing erbium concentrations and this behavior confirms the good homogeneity of the samples. DC-conductivity measurements show that all samples are characterized by a semiconductor behavior. It is found that electrical conductivity is reduced considerably with increasing erbium content up to x = 0.3. This is due to the decrease in oxygen vacancy density. For the free compound, dc-conductivity is characterized by the appearance of a saturation region at a specific temperature (T_sat = 480 K). For Er doped compounds, T_sat goes beyond 600 K. An AC-conductivity study shows that the conductivity is governed by the jump relaxation model (JRM) and conduction through grain boundaries. We found that the conductivity spectrum of the investigated materials obeys the Jonscher universal double power law. The deduced activation energy increases when increasing the erbium content from E_a = 467 meV for x = 0 to E_a = 670 meV for x = 0.3. Increasing the Er substitution reduces the frequency dispersion of the real part of the dielectric constant ε′. Also, the tan δ plot indicates that the investigated samples exhibit the characteristics of a relaxor dielectric.

---

1. Introduction

Recently, bismuth layer-structure ferroelectric (BLSF) materials have been attracting intensive attention from several research groups^1–3 due to their high Curie temperatures (T_C), exceptional thermal stability, excellent resistance to depolarization and fatigue, interesting crystal structures, strong anisotropic characters and peculiar electrical properties.^4–6 Also, BLSF compounds are environmentally friendly and are lead (Pb) free. Such properties open up wide potential applications in the electronics industry which include the manufacture of memory devices, sensors, pyroelectric detectors, displays, switching devices, etc.⁷

The bismuth titanate Bi₄Ti₃O₁₂ (BIT) is a BLSF element which generated special interest for light up-conversion, visible-light-driven photocatalytic and ferroelectric studies due to its excellent electrical, intensive optical properties and high stability under the harsh photocatalytic reaction conditions.⁸ BIT shows variety characteristics such as ferroelectric–paraelectric phase transition at the Curie temperature (T_C) of 675 °C. Usually, it crystallizes in the polar orthorhombic system.⁹ The BIT exhibits an anisotropy in its ferroelectricity and electrical conduction which are depending on its structural properties.¹⁰ Many studies reported that bismuth titanate compounds have often been synthesized by adding or substitution element in order to ameliorate its electrical properties.¹¹ The effect of introducing trivalent rare earth ions on the physical properties of diverses materials has been reported in the literature.^12,13 Among these ions, erbium is found to be a good dopant which affects optical properties.^14,15 Recently, it is found that erbium content modifies the electrical properties.³ It is noticed that the electrical properties show a continuous improvement with the increasing Er concentration. Such improvements in the electrical resistivity and reduction in dielectric losses are attributed to the suppression of the oxygen vacancy concentration. However, the correlation between optical and electrical properties is not investigated in detail. Accordingly, the present work presents the investigation of some physical properties of BIT ceramics. The latters have been doped with different erbium content in order to study their optical and electrical properties. Many techniques have been used for the preparation of BIT such as solid state reaction, sol–gel, hydrothermal, metal organic decomposition, coprecipitation and combustion.^16–20 It is well known that the solid–state reaction method is expected to be a potential candidate for preparation ceramics materials which is easy to prepare. Using such method, Er doped BIT samples are elaborated. Then, we report in this paper, the effect of erbium doping on the structural, optical and electrical properties of Bi₄Ti₃O₁₂ system.

2. Experimental details

The Bi_4−xEr_xTi₃O₁₂ (x = 0.0, 0.1, 0.2 and 0.3) samples are synthesized using high purity precursors: Bi₂O₃, TiO₂ and Er₂O₃ (purity > 99.9%) in the desired proportions. To prepare the samples, the conventional solid state reaction method at high temperature is used. The starting materials are weighted in the appropriate stoichiometric amounts then intimately mixed in an agate mortar. The powder is placed in an platinum crucible and calcined at 650 °C and 850 °C for 3 h. Then, the powder is mixed with 2 wt% polyvinyl alcohol (PVA) binder. The obtained product is pressed into pellets of about 1 mm of thickness. Pellets are sintered at 1050 °C for 3 h after various heat-treatments. The sample undergo several cycles of grinding–pelleting–sintering.²¹ Finally, these pellets are cooled from high temperature to room temperature following the cooling inertia of the furnace (∼8 h).^22,23 A great care has been taken over the preparation method, the physical properties depend strongly on the synthesis route and also on the cooling method.

Structural characterizations are carried out by means of X-ray diffraction at room temperature utilizing a powder diffractometer using CuKα radiation (λ = 1.5406 Å). Scanning is performed at room temperature in the diffraction angle range between 2θ = 5° and 80° with a step size of 0.016°. Structural analysis is carried out with Rietveld analysis using Fullprof program.^24,25 A scanning electron microscope (SEM) JEOL-JSM-5400 was used to observe the microstructure. Optical reflectance spectra of the films are obtained using an UV-Vis-NIR Shimadzu 3100 spectrophotometer equipped with an integrate sphere. A thin silver film is deposited through a circular mask of 6 mm of diameter on the both side of the pellet. A plane capacitor configuration is obtained and permits the investigation of electrical properties of the synthesized material. Measurements are conducted with an Agilent 4294A analyzer under vacuum and in dark with signal amplitude of 20 mV.

3. Results and discussion

3.1. X-ray diffraction

The Bi_4−xEr_xTi₃O₁₂ with x = 0, 0.1, 0.2, and 0.3 samples are investigated by X-ray powder diffraction analysis. The XRD patterns of Bi_4−xEr_xTi₃O₁₂ compounds registered at room temperature are depicted in Fig. 1a. The phase identification and structural analysis of samples are performed using the FullProf program^24,25 and it is found that the samples are crystallized in the orthorhombic structure with Fmmm space group. These patterns reveal the presence of Bi₂O₃ peaks as the minor secondary phase with space group I23 in addition to the primary phase of Bi_4−xEr_xTi₃O₁₂. This may be due to the mobility and segregation of particular bismuth at some places resulting in the formation of secondary phases during the process of calcination. This impurity is identified with X'Pert HighScore Plus software. Given the small concentration of the impurity, we assume that the secondary phase have a small influence on the microstructural development of Bi_4−xEr_xTi₃O₁₂ system and have a little effect on the subsequent measurements of physical properties. This secondary phase will have no effect on electrical conductivity as it should be exist as isolated crystallites very spaced. It is important to note that the Bi₂O₃ is known as an excellent ionic conductor (with ρ ≈ 1 Ω cm at 1073 K²⁶). Then, we investigate the electrical properties in the temperature range 80–700 K. Consequently, in this temperature range, the contribution of the impurity on the conductivity can be neglected. The structural refinement patterns including the observed and calculated profiles as well as the difference profile for the end members, Bi₄Ti₃O₁₂ and Bi_3.7Er_0.3Ti₃O₁₂, are depicted in Fig. 1. The calculated XRD patterns coincide with the observed patterns as shown in Fig. 1b and c. Summary of structural parameters and the unit cell values obtained for each sample are listed in Table 1. Due to the smaller ionic radius of erbium (0.88 Å) as compared to bismuth (1.03 Å), the unit cell should monotonically decreases. But, in this study, it is observed that the lattice parameters and the unit cell did not show significant monotonic changes. The observed results indicates that the presence of the impurity corroborate the influence of the secondary phase on the structural parameters.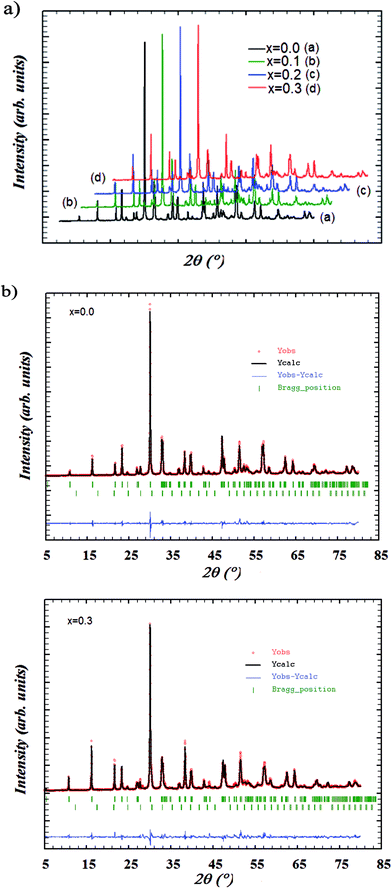

Fig. 1 (a) XRD patterns of Bi_4−xEr_xTi₃O₁₂ ceramics with (0.0 ≤ x ≤ 0.3). (b) X-ray powder diffraction patterns and refinement at room temperature for: (i) x = 0.0 and (ii) x = 0.3.

Table 1 Structural data obtained after Rietveld refinement for Bi_4−xEr_xTi₃O₁₂ (with 0.0 ≤ x ≤ 0.3)

compound	Symmetry	a (Å)	b (Å)	c (Å)	V (Å)^3
x = 0.0	Fmmm – orthorhombic	5.409(1)	5.446(4)	32.819(4)	966.869(1)
x = 0.1	Fmmm – orthorhombic	5.410(6)	5.447(8)	32.831(7)	967.745(1)
x = 0.2	Fmmm – orthorhombic	5.406(1)	5.441(1)	32.809(2)	965.078(9)
x = 0.3	Fmmm – orthorhombic	5.405(9)	5.442(4)	32.821(3)	965.627(7)

---

3.2. SEM observations

The pellets used for optical measurements were observed by SEM and typical images are shown in Fig. 2. The white grains are from the residual BaSO₄ (used in optical measurement) powder on the pellet surface. Otherwise, we note a compact compound with big size of grain elongated in one direction. This is due to the fact that the growth rate is higher in the direction perpendicular to the c-axis.²⁷ No precipitates or secondary phase were observed. Each pellet was cleaved and the cross section was observed. The images of Fig. 3 show plate-like morphology for all samples. The plate-like grains have a large area, indicating good crystallinity, and are of random orientation.²⁸ These images reveal also few pore and confirm the high density of the sample.

Fig. 2 SEM photographs of compounds with x = 0 and x = 0.2.

Fig. 3 Cross section morphology of the compounds obtained by SEM observation.

3.3. optical absorbance

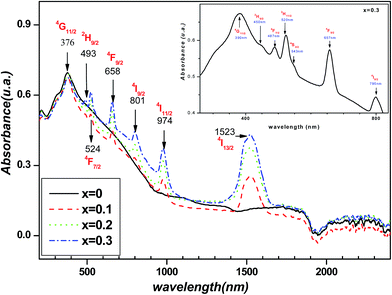
At room temperature, Fig. 4 shows the absorbance spectra, of the investigated compounds, in the range of wavelength between 200 and 2400 nm. For free erbium compound (x = 0.0), the absorbance increases when the wavelength increases from 200 to 376 nm, then, it decreases continually for the longer wavelength. When erbium is introduced several peaks appear in the spectra. These peaks correspond to the transition from the ground state ⁴I_15/2 to excited one. Both positions and attribution, of each peak, are indicated in the Fig. 4 and its inset. The peaks are situated on 1530, 970, 795, 657, 543, 520, 487, 450 and 390 nm and are attributed to the transition to excited states ⁴I_13/2, ⁴I_11/2, ⁴I_9/2, ⁴F_9/2, ⁴S_3/2, ²H_11/2, ⁴F_7/2, ²H_9/2 and ⁴G_11/2 respectively. Another peak should appear at 406 nm corresponding to the transition to the ⁴F_5/2 state. But, its position is situated in the large absorbance band of the matrix and it can be identified. These obtained spectra are similar to those obtained by Zannen et al.²⁹, in which the transition to ⁴I_13/2 was not explored. The peak intensity increases with the increase of the erbium content. As these spectra are recorded at the same conditions, this behavior means that the peak intensity is correlated to erbium content. Thus, the evolution of the intensity with erbium content is another indicator of the good homogeneity of the samples.

Fig. 4 Absorbance spectra of Bi_4−xEr_xTi₃O₁₂ ceramics with (0.0 ≤ x ≤ 0.3).

3.4. AC conductivity

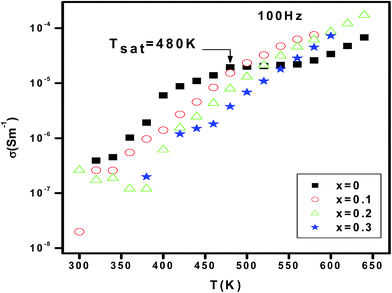
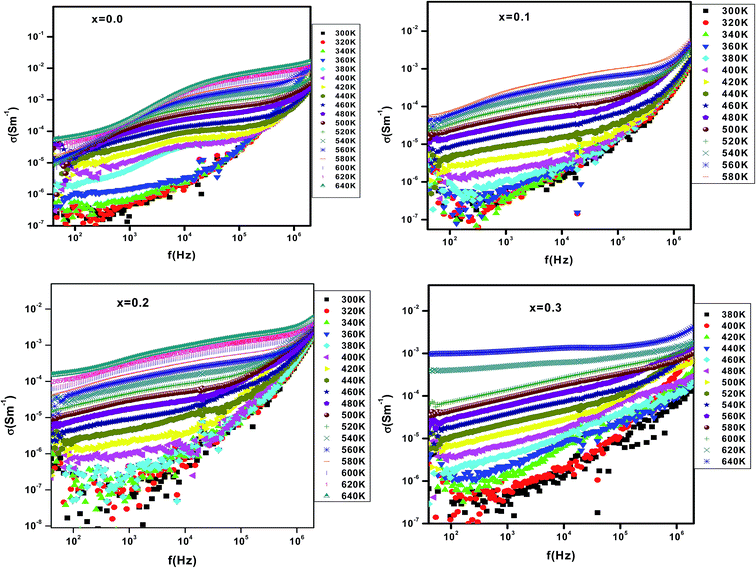
Fig. 5 shows the variation of the electrical conductivity versus temperature for different erbium concentrations. In the whole explored temperature range, Fig. 5 shows that dc-conductance increases with increasing temperature. Consequently, the material exhibits a semiconductor behavior. Also, the conductivity decreases when increasing erbium concentrations from x = 0.0 to x = 0.3 in the temperature range 300–480 K. In ferroelectric perovskite, the element substitution is related to the temperature dependence of conductivity. In such systems, oxygen vacancies are considered to be the most mobile charge carriers³⁰ and mostly in titanates. At higher temperatures, oxygen vacancies will be ionized and release electron which contribute to the conduction. These electrons can be trapped by Ti³⁺ ions or oxygen vacancies and it can be thermally activated. The value of activation energy can help on distinguishing which trap is efficient. When erbium content increases, the oxygen vacancies are seen to be reduced. As continuous decrease is observed in the measured dc-conductivity for a change in Er content from x = 0.0 to 0.3. For the parent compound, the appearance of a saturation region, at T_sat = 480 K, is observed. When Er is introduced, the T_sat goes beyond the value 480 K. The rise on such specific temperature is related to several effects. In fact, the density of free carriers increases while increasing temperature. The carriers acquired a sufficient thermal energy to exceed the encountered barrier. In addition, the thermal activation contributes to a reduction of the efficiency of the capture of charge traps. At T > 480 K and for the erbium free compound, we suggest that the available density of trapped charge is vanished, then, the saturation region appear at higher temperature. The increase of T_sat increases with introducing erbium can be related to the trapping of charge carriers by defects created by erbium. So, a higher thermal energy is needed to release such carriers. Then, the conductivity increase again and the appearance of the saturation region is expected over the explored temperature range.

Fig. 5 Temperature dependence of dc-conductivity of Bi_4−xEr_xTi₃O₁₂ ceramics with (0.0 ≤ x ≤ 0.3).

Fig. 6 shows the variation of conductivity versus frequency at different temperatures for x = 0.0, 0.1, 0.2 and 0.3. The conductivity spectrum possesses the following characteristics: (i) at low frequency, a plateau is observed and the conductivity increases with increasing temperature. Such observation indicates that conduction mechanism is thermally activated. (ii) At high temperature region, the conductivity plots are characterized by a change in the slope twice at low and high frequency. The variation of conductivity as a function of frequency is typical of a conductivity which is explained by the jump relaxation model (JRM)³¹ and conduction through grain boundaries.

Fig. 6 Conductivity spectra of Bi_4−xEr_xTi₃O₁₂ compounds with x = 0.0, 0.1, 0.2 and 0.3.

The JRM introduced by Funke and extended by Elliot,³² to account the ionic conduction in solids, is based on the existence of high probability for a jumping ion to jump back (unsuccessful hop). However, if the neighbourhood becomes relaxed with respect to the ion's position, the ion stays in the new site. In the low-frequency region, the conductivity is associated with successful hops. Beyond the low-frequency region, many hops are unsuccessful and as the frequency increases, more hops are unsuccessful. The change in the ratio of successful to unsuccessful hops results in dispersive conductivity. The JRM suggests that different activation energies are associated with unsuccessful and successful hopping processes. Applying JRM to the frequency response of ac conductivity, the experimental conductivity data are found to be described by the double power law proposed by Jonscher,³³

σ_ac = σ_dc + Aω^S1 + Bω^S2

where σ_ac is the total conductivity, σ_dc is the transitional hopping, giving the long-range electrical transport in the long time limit. The coefficient (A and B) and the angular frequency exponent (S1 and S2) are temperature and material intrinsic property dependent constants^34,35

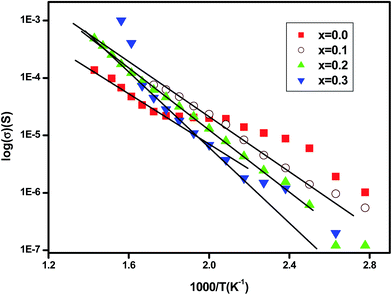
The dc conductivity is determined from the frequency independent region. Fig. 7 shows the variation of σ_dc against 1000/T. For oxide materials, the dc-conductivity is usually dependent upon the carrier concentration and mobility. At higher temperature, the conductivity follows the thermally activated transport of Arrhenius type described by the equation:

σ_dc = σ₀ exp(E_a/k_BT)

where σ₀, E_a, and k_B represent the pre-exponential term, the activation energy of the mobile charge carriers and Boltzmann's constant respectively. The activation energy is calculated from the linear portion of the plot of dc-conductivity versus 1000/T (Fig. 7).

Fig. 7 Plot of log(σ_dc) vs. 1000/T.

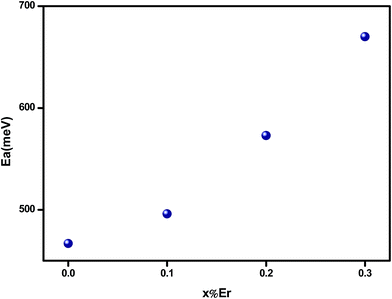
It is found that the activation energy increases with increasing erbium content as shown in Fig. 8. Thus, it can be assumed that the Er ion contributes indirectly in electrical conductivity. In ferroelectric perovskite,³⁰ at higher temperature, the ionization of oxygen vacancies creates conducting electrons which are easily thermally activated. The large values of activation energy and conductivity evolution suggest that the conduction at higher temperature region, for charge carriers, may be oxygen vacancies.³⁶ The rise in activation energy can be related to the reduction on motivating the oxygen vacancies jumping.¹

Fig. 8 Activation energy value for different erbium content.

3.5. Dielectric properties

In order to study the effect of substitution with erbium ion on dielectric properties, the variation of dielectric constant ε′ as a function of frequency, for all investigated samples, is shown in Fig. 9. It is observed that dielectric constant decreases with increasing frequency. Such behavior can be related to the contribution of different polarization types (interfacial, dipolar, atomic, ionic, and electronic).^37,38 At high frequency region, only dipolar and space charge polarization contribute to polarization leading to a decrease of the dielectric constant. At low frequency, the increase of the dielectric constant can be explained according to the Maxwell–Wagner polarization effect.^39,40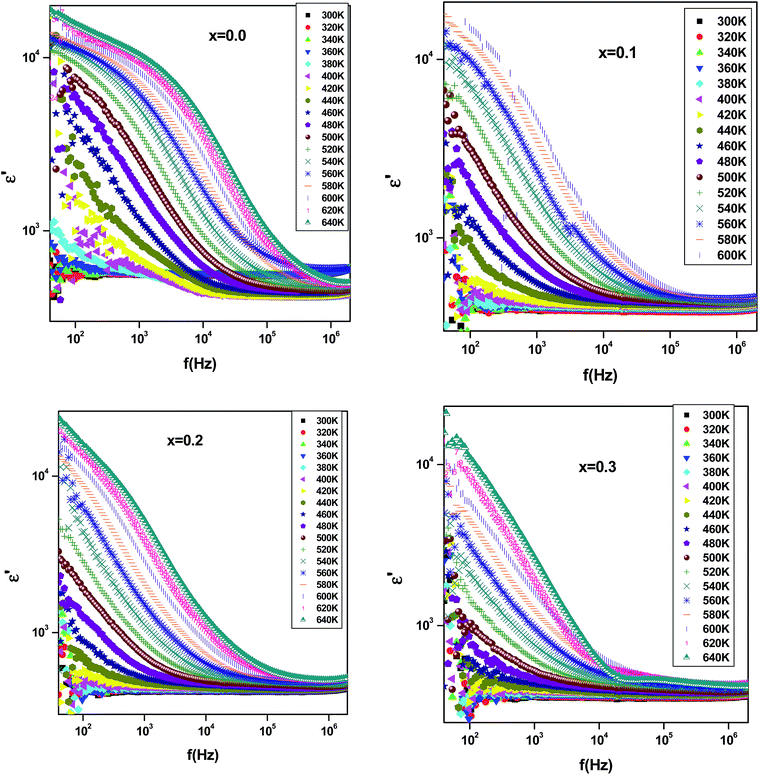

Fig. 9 Variation of dielectric constant (ε′) with frequency and temperature of Bi_4−xEr_xTi₃O₁₂ ceramics with (0.0 ≤ x ≤ 0.3).

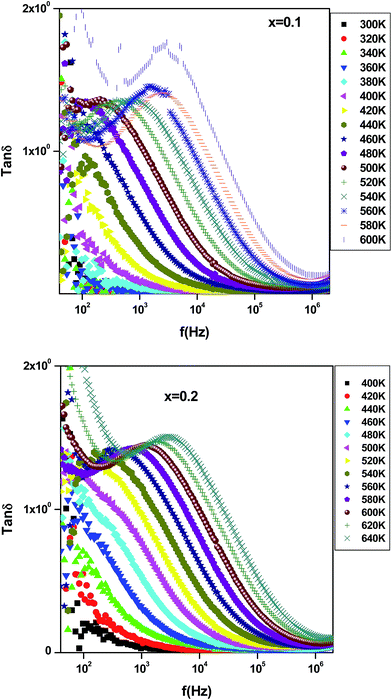
The increase of dielectric constant ε′ at low frequencies is associated to the heterogeneous conduction in the grain and grain boundary. The grain boundary region is characterized by a much higher resistivity. As shown in Fig. 10, the dielectric constant decreases with increasing Er content. In fact, this is attributed to the reduction in the A-site bismuth concentration and the reduction of oxygen vacancy concentration because the increasing of the substitution of Bi³⁺ by stable Er³⁺.⁴¹ The variation of tan δ as function of frequency and temperature is shown in Fig. 11. It is obvious that the dielectric loss increases with increasing temperature for all investigated samples. The tan δ plot shows a relaxation peak. The latter shifts toward high frequency side as temperature increases confirming the presence of dielectric relaxation in the material.⁴² Such relaxation can be explained by Maxwell–Wagner polarization.^39,40 The observed behavior indicates that the investigated samples exhibit a characteristic of relaxor dielectric.

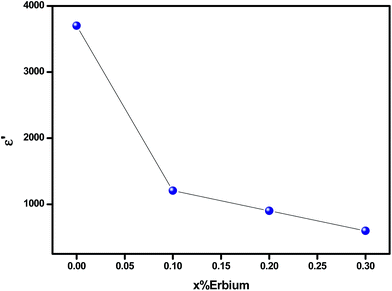Fig. 10 Dielectric constant (ε′) of Bi_4−xEr_xTi₃O₁₂ ceramics for different erbium content (at 520 K for 1 kHz).

Fig. 11 Plot of (tan δ) versus frequency of Bi_4−xEr_xTi₃O₁₂ at different temperatures.

4. Conclusion

We have investigated the structural, optical and electrical properties of polycrystalline Bi₄Ti₃O₁₂ where the bismuth was substituted by erbium. The X-ray diffraction analysis revealed that all samples exhibit orthorhombic Fmmm structure. The feature peak of erbium is observed in absorbance spectra and their intensities increase with erbium content. DC-conductivity measurements indicate that the materials exhibit a semiconductor behavior in the whole explored temperature range. A significant decrease in σ_dc is observed when introducing Er content. For undoped sample, a saturation region appeared at a specific temperature (T_sat = 480 K) in σ_DC (T) curves. For the Er doped compounds, T_sat go beyond 600 K. It is found that conduction process is thermally activated and the values of the deduced activation energy suggest the possibility of electrical conduction due to the mobility of oxide ions or oxide ion vacancies at higher temperature. Conduction mechanism is well described by the jump relaxation model and conduction through grain boundaries. The frequency dependence of conductance followed the Jonscher law. The increase of Er leads to the decrease of the dielectric dispersion ε′. The tan δ plot indicates the presence of dielectric relaxation in the materials.

Acknowledgements

The authors would like to thank Mr Mohammed Sghaier Ben Rguiga from ETAP Tunis for his help in SEM observation.

References

1. Y. Chen, Z. Pen, Q. Wang and J. Zhu, J. Alloys Compd., 2014, 612, 120.
2. F. Rehman, J. B. Li, M. S. Cao, Y. J. Zhao, M. Rizwan and H. B. Jin, Ceram. Int., 2015, 41, 14652.
3. R. Bokolia, O. P. Thakur, V. K. Raic, S. K. Sharma and K. Sreenivas, Ceram. Int., 2016, 42, 5718.
4. H. Yan, H. Zhang, R. Ubic, M. J. Reece, J. Liu, Z. Shen and Z. Zhang, J. Adv. Mater., 2005, 17, 1261.
5. L. Bellaiche and D. Vanderbilt, Phys. Rev. Lett., 1999, 83, 1347.
6. B. H. Park, B. S. Kang, S. D. Bu, T. W. Noh, J. Lee and W. Jo, Nature, 1999, 401, 682.
7. J. J. Wang, L. J. Feng, X. L. Chao, K. Zhao and A. J. Yan, Curr. Appl. Phys., 2013, 13, 1713.
8. Z. Chen, X. Jiang, C. Zhu and C. Shi, Appl. Catal., B, 2016, 199, 241.
9. J. F. Dorrian, R. E. Newnham and D. K. Smith, Ferroelectrics, 1971, 3, 17.
10. L. L. Wang, W. H. Maa, Y. F. Fang, Y. Zhang, M. K. Jia, R. P. Li and Y. P. Huang, Procedia Environ. Sci., 2013, 18, 547.
11. J. Konig, M. Spreitzer, B. Jancar, D. Suvorov, Z. Samardzija and A. Popovic, J. Eur. Ceram. Soc., 2009, 29, 1695.
12. F. Auzel, Chem. Rev., 2004, 104, 139–173.
13. L. F. Johnson, J. E. Guesic, H. J. Guggenheim, T. Kushida, S. Singh and L. G. Uitert, Appl. Phys. Lett., 1969, 15, 48–50.
14. J. Capobianco, F. Vetrone and J. Boyer, J. Phys. Chem. B, 2002, 106, 1181–1187.
15. H. Higushi, M. Takahashi, Y. Kawamoto, K. Kadono, T. Oshtsuki, N. Peyghambarian and N. Kitamura, Appl. Phys., 1998, 83, 19–27.
16. S. Madeswaran, N. V. Giridharan and R. Jayavel, Mater. Chem. Phys., 2003, 80, 23.
17. P. Pookmanee, P. Uriwilast and S. Phanichpant, Ceram. Interfaces, 2004, 30(7), 1913.
18. W. L. Liu, H. R. Xia, H. Han and X. Q. Wang, J. Mater. Sci., 2005, 40, 1827.
19. P. H. Xiang, Y. Kinemuchi, T. Nagaoka and K. Watari, Mater. Lett., 2005, 59(28), 3590.
20. O. Subohi, G. S. Kumar, M. M. Malik and R. Kurchania, Phys. B, 2012, 407, 3813.
21. A. Selmi, R. M'nassri, W. Cheikhrouhou-Koubaa, N. Chniba Boudjada and A. Cheikhrouhou, J. Alloys Compd., 2015, 619, 627.
22. N. Khare, D. P. Singh, H. K. Gupta, P. K. Siwach and O. N. Srivastava, J. Phys. Chem. Solids, 2004, 65, 870.
23. A. Selmi, R. M'nassri, W. Cheikhrouhou-Koubaa, N. Chniba Boudjada and A. Cheikhrouhou, Ceram. Int., 2015, 41, 7723.
24. H. M. Rietveld, A profile refinement method for nuclear and magnetic structures, Appl. Crystallogr., 1969, 2, 65.
25. T. Roisnel and J. Rodriguez-Carvajal, Computer Program FULLPROF, LLB-LCSIM, 2003.
26. T. Takahashi and H. Iwahara, Mater. Res. Bull., 1978, 13, 1447.
27. J. J. Wang, L. J. Feng, X. L. Chao, K. Zhao and A. J. Yan, Curr. Appl. Phys., 2013, 13, 1713–1717.
28. G. Parida and J. Beran, Ceram. Int., 2014, 40, 3139.
29. M. Zannen, H. Khemakhem, A. Kabadou and M. Es-Souni, J. Alloys Compd., 2013, 555, 56.
30. T. Badapanda, S. Sarangi, S. Parida, B. Behera, B. Ojha and S. Anwar, J. Mater. Sci.: Mater. Electron., 2015, 26, 3069.
31. K. Funke, Prog. Solid State Chem., 1993, 22, 111.
32. S. R. Elliot, Adv. Phys., 1987, 36, 135.
33. A. K. Jonscher, Nature, 1977, 267, 673.
34. W. Chen, W. Zhu, O. K. Tan and X. F. Chen, J. Appl. Phys., 2010, 108, 034101.
35. A. Pelaiz-Barranco, M. P. Gutierrez-Amador, A. Huanosta and R. Valenzuela, Appl. Phys. Lett., 1998, 73, 2039.
36. J. S. Kim, I. W. Kim, C. W. Ahn, T. K. Song, S. S. Kim, S. X. Chi, J. S. Bae and J. H. Jeong, Jpn. J. Appl. Phys., 2002, 41, 6785.
37. N. K. Singh, A. Panigrahi and R. N. P. Chaudhary, Mater. Lett., 2001, 50, 1.
38. T. Kar and R. N. P. Chaudhary, Mater. Sci. Eng., B, 2002, 90, 224.
39. J. Maxwell, Electricity and Magnetics, V 1, S 328, Oxford University Press, London, 1873.
40. K. Wagner, Ann. Phys., 1913, 40, 817.
41. R. Bokolia, O. P. Thakur, V. Rai, S. K. Sharma and K. Sreenivas, Ceram. Int., 2015, 41, 6055.
42. V. Hornebecq, C. Elissalde, V. Porokhonskyy, V. Bovtun, J. Petzelt, I. Gregora, M. Maglione and J. Ravez, J. Phys. Chem. Solids, 2003, 64, 471.

---