Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Gas-phase conformational preference of the smallest saccharide (glycolaldehyde) and its hydrated complexes with bridged hydrogen bonding†
Pengchao Wang,
Yongjun Hu *,
Huaqi Zhan and
Jiaxin Chen
*,
Huaqi Zhan and
Jiaxin Chen
MOE Key Laboratory of Laser Life Science & Institute of Laser Life Science, College of Biophotonics, South China Normal University, Guangzhou 510631, P. R. China. E-mail: yjhu@scnu.edu.cn; Fax: +86-20-85216052; Tel: +86-20-85217070
First published on 18th January 2017
Abstract
Glycoaldehyde (GA, HOCH2CHO) is the simplest sugar unit of the carbohydrates and the only sugar to have been detected in interstellar space to date. In the present report, the conformation of GA and its flexible hydrated complexes have been investigated in the gas phase by using mass-selected infrared (IR) spectroscopy based on vacuum-ultraviolet single photon ionization (118 nm). With the aid of theoretical calculations, the neutral GA bearing a ring-type intramolecular hydrogen bonding interaction was confirmed to be the dominant isomer in the gas phase. Moreover, the water molecules in the monohydrated complexes preferentially broke the intramolecular hydrogen bond and bridged the carbonyl oxygen and hydroxyl hydrogen of GA with two additional intermolecular H-bonds, revealing the “working rules” governing preferred binding. The theoretical results confirmed that the existence probability of the two lowest energy conformations stabilized by two intermolecular hydrogen bonds would be larger than that of the next two isomers with one intramolecular plus one intermolecular hydrogen bond. Structural investigation of hydrated GA conformers has revealed that the water molecules play the role of a bridge through intermolecular H-bonds, achieving selective population of specific GA molecular conformations. These results suggest that these hydrogen-bonded bridge structures in the hydrated complexes may provide good models for recognition in larger systems.
1. Introduction
Hydrogen bonding is a key component of carbohydrate molecular recognition and, more generally, in the maintenance of their preferred conformational structures. Intramolecular hydrogen bonds within the carbohydrate molecules, and intermolecular hydrogen bonds between carbohydrates and their neighboring molecules, such as water or noncovalently bound biomolecules, can compete or act together in bridged hydrogen-bonds to stabilize their conformations. This was also similar to other biomolecules and organometallics.1–5 Previous studies have identified that water does not simply work as a spectator solvent but also as an active participant in carbohydrate molecular recognition processes.6–12 In the past few decades, the infrared-ultraviolet (IR-UV) hole burning double resonance scheme spectrum of hydrated phenyl β-D-glucopyranoside revealed that the water locates close to the hydroxymethyl group, breaking the weakest pre-existing hydrogen bond to the bridged hydrogen-bonded conformation, and changing the preferred monomeric conformation of the hydroxymethyl group from gg to gt.13 However, it is unclear how the inserted water alters the conformation of the substrate and what governs the preferred binding sites in those hydrated carbohydrate complexes that do not contain a phenyl chromophore.GA is the simplest sugar unit of the carbohydrates and the only sugar to have been detected in interstellar space to date.14–16 Water, the most ubiquitous and fundamental solvent on earth, is a critical component in many physical and chemical processes in chemistry, biology, and geochemistry.17,18 A molecular-level understanding of the role of water as an active participant in this simplest sugar molecules is, therefore, of significant interest. More specifically, it's intriguing to understand why the water opts to locate close to the hydroxyl or carbonyl group in the GA–water complex. In this case, the molecules form a complex while maintaining the intramolecular hydrogen bonds, e.g., via stacking, or the intramolecular bonds are broken for the sake of intermolecular hydrogen bonding, or some intermediate form.
An alternative approach to studying the interaction of molecules is to prepare jet-cooled neutral molecular aggregates in the gas phase.19 These neutral molecules can be subjected to size- and state-specific spectroscopic investigations without suffering thermal effects and perturbations from their surrounding environment.20 Resonance-enhanced multiphoton ionization (REMPI) is a powerful technique with a wide range of potential applications, including double resonance IR-UV.21 However, these applications require the presence of a ultraviolet (UV) chromophore in the molecule and a sufficiently long-lived resonant intermediate electronic state, to allow for effective detection and monitor.22 These techniques are, therefore, inapplicable for unperturbed detection of species without a UV chromophore group. One way of circumventing this limitation is to use single photon ionization in the vacuum-ultraviolet (VUV) region, which has the advantage to detect aliphatic molecules. The recent development of vibrational spectroscopic techniques based on VUV photoionization and its subsequent combination with supersonic-jet expansion techniques (typically pulsed jets) have made it possible to observe the IR spectra of simple and fundamental molecular aggregates in their neutral states.23,24 This effective approach can provide the information of the geometric structures of molecules, clusters and their intermolecular interactions.19,25–29 Furthermore, the vibrational frequencies and intensities of IR absorption, such as modes involving OH, NH, and CH groups, are generally very sensitive probes of hydrogen bonding and other intra- and inter-molecular interactions, which make them excellent probes for investigation of detailed aspects of the structures of biologically relevant ions, radicals, and molecules.23
The structure of GA determined by intramolecular hydrogen bonding interaction was previously detected by conventional IR and Raman spectroscopy in the gas phase or in matrix isolation.30–32 The GA–water complex was studied by Fourier transform microwave spectroscopy, where only two lowest conformers referring to cis–cis-water-1 (CC-W-1) and cis–cis-water-2 (CC-W-2) conformer could be found in the gas phase.33 To comprehensively consider the existence of these conformers under isolated conditions without thermal effects and perturbations from their surrounding environment, mass selected optical spectroscopy, as a powerful method, was used herein to investigate gas-phase GA molecules and their hydrated complexes in a supersonic jet. It is worthy of further discussion for the more detailed information about structures of GA molecule compared with its hydrated complexes in the gas phase. Herein, we present direct evidence for the dominant conformer of neutral GA in the gas phase based on the results of IR plus VUV (118 nm) single photon ionization spectroscopy and density functional theory (DFT) calculations. Moreover, the role of water in the formation of monohydrated complex GA–water conformations in the gas phase is discussed.
2. Experimental setup and calculation methods
2.1 Experimental setup
IR spectra of neutral GA and GA–water were recorded based on the VUV photoionization detection. The experimental equipment was set up by our group and its details have been described elsewhere,34–38 and only a brief description is given here. A gaseous mixture of sample molecules and helium was expanded supersonically into the vacuum system through a pulsed valve (Parker General Valve series 9) with a pulse width of ca. 150 μm duration. Passing through a skimmer, the molecular beam interacted with pulsed IR and VUV light (ca. 10 ns) in the ionization region of the time-of-flight mass spectrometry (TOFMS), which is used for the detection of the generated ions. The TOFMS has been set to maximize the intensity of the higher masses by optimizing the time delay between the nozzle opening and the VUV laser triggering. GA and water were purchased from Aladdin-Reagent Company (Shanghai, China) and used without additional purification.The 118 nm VUV light is the ninth harmonic of the 1.064 μm fundamental radiation of a Nd3+/YAG laser. The 355 nm radiation from an Nd/YAG laser (third harmonic) is focused into a cell containing a Xe/Ar 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 mixture at 200 Torr total pressure. An MgF2 lens focuses the 118 nm light in the ionization region of the TOFMS and disperses the remaining 355 nm light. Tunable IR radiation output in the mid-IR range has a pulse energy of 3–5 mJ per pulse (2650–3850 cm−1), a time duration of ca. 10 ns, and a bandwidth of ca. 2 cm−1.
10 mixture at 200 Torr total pressure. An MgF2 lens focuses the 118 nm light in the ionization region of the TOFMS and disperses the remaining 355 nm light. Tunable IR radiation output in the mid-IR range has a pulse energy of 3–5 mJ per pulse (2650–3850 cm−1), a time duration of ca. 10 ns, and a bandwidth of ca. 2 cm−1.
The principle of IR plus VUV non-resonant ionization has been described previously.23 IR spectra of neutral monomer and its hydrated complexes were observed by size-selective IR spectroscopy with the VUV photoionization detection schemes, which are called the Non-Resonant Ion Dip IR Spectroscopy (NRIDip-IR). The IR pulse was introduced ca. 30 ns prior to the VUV ionization for spectroscopy of neutrals. Note that the VUV (non-resonant) photon energy (ca. 10.49 eV) is 0.29 eV above the ionization energy (IE) (GA = 10.20 eV) of the GA monomer.39 To measure the IR spectrum, the mass-selected ion intensity was monitored while the IR frequency was scanned. In the present measurements, IR spectra of sample molecules were obtained by monitoring their parent channels. The concentrations of sample molecules were controlled in order to prevent the formation of large cluster in the jet expansion.
2.2 Calculation methods
All the following theoretical calculations of the monomer and its hydrated complexes were performed with the GAUSSIAN 03 and GAUSSIAN 09 program packages.40,41 Geometry optimization of neutral molecules were calculated by the DFT and MP2 functional. The MP2 theoretical functional, which accounts for the electron correlation, can obtain more reliable results for correlation energies than the DFT method.42 Therefore, the geometry optimization and correlation energies of GA and GA–water were predicted by MP2/6-311++G(d,p). The ωB97X-D functional contains the empirical treatment of dispersion interactions and gives reliable non-covalent interactions for many systems, i.e., dimethyl ether dimer, tryptamine+–(N2)n and their hydrated complexes with satisfactory vibrational frequencies.43–47 Thus, the dispersion-corrected density functional theory calculations were performed at the unrestricted ωB97X-D/cc-pVTZ level to obtain vibrational energy of the GA and its hydrated complexes. The harmonic frequencies are scaled by a factor of 0.9415.43,44 For the hydrated complexes, natural bond orbital (NBO) analysis was also employed with the ωB97X-D functional and cc-pVTZ basis set.48 All relative energies were zero-point energy (ZPE)-corrected in the Gaussian program.40,41 The optimized structures and NBO diagrams were visualized using the GaussView 5 program.3. Results and discussion
3.1 Theoretical calculations about geometric parameters of glycolaldehyde and glycolaldehyde–water
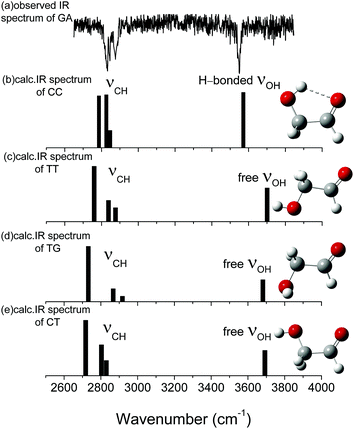
Fig. 1 shows the fully optimized geometries of the four most stable conformers of the GA and nine GA–water complex conformers. Compared with MP2/6-311++G(d,p), the conformers are more stable at ωB97X-D/cc-pVTZ level. So the final computational results were discussed at this level. Based on ab initio results, the simulated GA conformers include cis–cis (CC), trans–trans (TT), trans–gauche (TG) and cis–trans (CT) forms, where CC is the most stable conformer stabilized by an intramolecular H-bond between the hydrogen atom (7H) of the hydroxyl group and the oxygen atom (8O) from the carbonyl group. The TT (13.23 kJ mol−1) and TG (14.12 kJ mol−1) conformers are almost isoenergetic with the TT conformer being slightly lower in energy. The CT (21.22 kJ mol−1) conformer is the highest in energy of all four GA conformers and differs from CC by rotation of the OH (6O–7H) group. Compared with previous calculations, i.e., CC (0.0 kJ mol−1), TT (15.21 kJ mol−1), TG (15.43 kJ mol−1) and CT (22.19 kJ mol−1), at MP4 (SDTQ)/cc-pVQZ level, our theoretical predicted results are close to their results.49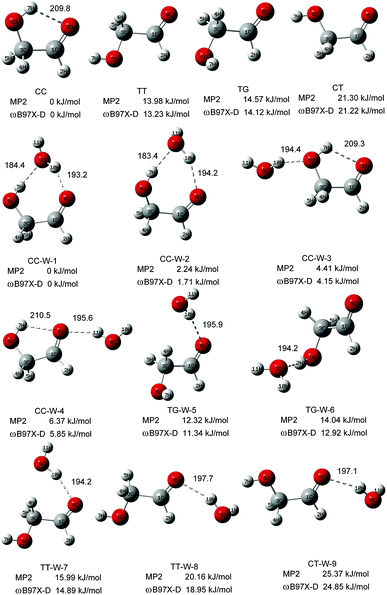 | ||
| Fig. 1 The stable structures and calculated relative energy of the GA and GA–water conformers at the ωB97X-D/cc-pVTZ and MP2/6-311+G(d,p) levels. The bond lengths are in picometers. | ||
In the nine GA–water complex conformers, water can serve as a hydrogen bond donor for the hydroxyl or carbonyl oxygen of GA, and it can also act as a hydrogen bond acceptor for the OH group. Their main structural parameters are list in Table 1. It should be noted that the four most stable conformers are associated with the CC conformer of the parent molecule and stabilized by two hydrogen bonds. However, the next five conformers, i.e., trans–gauche-water-5 (CC-W-5, 11.34 kJ mol−1), trans–gauche-water-6 (CC-W-6, 12.92 kJ mol−1), trans–trans-water-7 (CC-W-7, 14.89 kJ mol−1), trans–trans-water-8 (CC-W-8, 18.95 kJ mol−1), and cis–trans-water-9 (CC-W-9, 24.85 kJ mol−1), only contain one intramolecular hydrogen bond respectively. In CC-W-1 and CC-W-2 conformers, water broke the intramolecular hydrogen bond and bridged the carbonyl oxygen (8O) and hydroxyl hydrogen (7H) of CC by two additional intermolecular H-bonds. It can be found that the structures of the parent molecule in CC-W-1 and CC-W-2 conformers are changed in the 6O–7H group (dihedral angle 1C–3C–6O–7H changing from 0.0° to 49.7° and 48.9°, respectively). However, the difference between CC-W-1 and CC-W-2 conformers is mainly related to the position of the free 9O–11H water group with respect to 8O–1C (dihedral angle 11H–9O–8O–1C, equal to 128.1° and 256.3°, respectively). In addition, the free water plays a role of donor in cis–cis-water-3 (CC-W-3) conformer and bond to hydroxyl oxygen (6O) by intermolecular hydrogen bonding while the water bind to carbonyl oxygen (8O) in cis–cis-water-4 (CC-W-4) conformer. In contrast with the CC conformer, the most significant features of the four conformers are the reorientation of the 6O–7H hydroxyl group, moving from the plane into the direction of water to form a dihedral angle (1C–3C–6O–7H) of about 49.7° in CC-W-1 (48.9° in CC-W-2), with a dihedral angle (1C–3C–6O–7H) of about 359.4° in CC-W-3 (359.0° in CC-W-4). In the next five high energy conformers, the water serve as a hydrogen bond donor binding to carbonyl oxygen of parent molecule except the TG-W-6 conformer, in which the water acts as a hydrogen bond acceptor.
| CC | CC-W-1 | CC-W-2 | CC-W-3 | CC-W-4 | |
|---|---|---|---|---|---|
| 7H–9O or 7H–8O/pm | 209.8 | 184.4 | 183.4 | 209.3 | 210.5 |
| 8H–10O or 8O–11H/pm | 193.2 | 194.2 | 194.4 | 195.6 | |
| 8O–1C–3C–6O/deg | 0.0 | 348.5 | 348.7 | 0.6 | 0.3 |
| 1C–3C–6O–7H/deg | 0.0 | 49.7 | 48.9 | 359.4 | 359.0 |
| 11H–9O–8O–1C/deg | 128.1 | 265.3 | 116.8 | 185.5 |
| TG-W-5 | TG-W-6 | TT-W-7 | TT-W-8 | CT-W-9 | |
|---|---|---|---|---|---|
| 8H–10O/pm | 195.9 | 194.2 | 194.2 | 197.7 | 197.1 |
| 8O–1C–3C–6O/deg | 191.7 | 190.5 | 180.6 | 173.1 | 0.7 |
| 1C–3C–6O–7H/deg | 85.9 | 71.2 | 179.9 | 176.1 | 181.2 |
| 11H–9O–8O–1C/deg | 130.0 | 79.9 | 175.7 | 102.6 | 108.2 |
3.2 Experimental results
| Description | Experiment | Calculations | ||||
|---|---|---|---|---|---|---|
| Observed | Gas phaseb | Arc | CC (ha/anha) | CCd | CCd | |
| a Comparison with the experimental values obtained in gas phase and calculated wavenumbers at MP2/6-311++G(d,p) and CCSD(T)/cc-pVTZ level.b Taken from ref. 52.c Taken from ref. 53.d Taken from ref. 54. | ||||||
| OH stretch | 3548.2 | 3549 | 3542 | 3571.2/3538.1 | 3542 | 3570 |
| as. CH2 stretch | 2876.9 | 2881 | 2855 | 2846.9/2839.5 | 2876 | 2898 |
| CH2 twist and CH2 wag, ip OH bend | /2604.2 | 2649 | 2650 | |||
| CH2 twist and ip OH bend, CH2 wag | /2542.4 | 2503 | 2496 | |||
| The first overtone of CH2 scissor | /2874.6 | 2798 | 2913 | |||
| CH2 wag, ip OH bend and CH2 scissor | /2774.3 | 2882 | 2883 | |||
| s. CH2 stretch | 2845.3 | 2840 | 2895 | 2826.0/2824.3 | 2999 | |
| The first overtone of CH2 rock and ip CH bend | /2693.3 | 2794 | ||||
| ip OH bend, CH2 wag and CH2 wag, ip OH bend | /2623.9 | 2689 | 2681 | |||
| CH stretch | 2828.2 | 2820 | 2845 | 2786.1/2710.4 | 2822 | 2854 |
| The first overtone of CH2 wag, ip OH bend | /2821.5 | 2831 | 2816 | |||
| CH2 wag, ip OH bend and ip CH bend | /2691.9 | 2775 | 2767 | |||
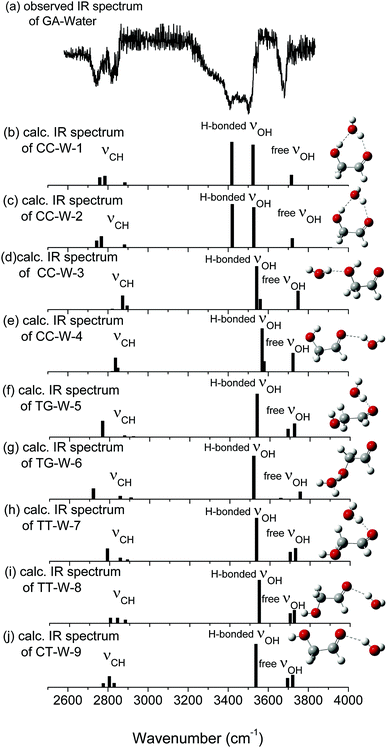
The calculated vibrational patterns and band positions of the two lowest energy conformations (CC-W-1 and CC-W-2) are both in good agreement with the experimental IR signature. Thus, the identities and structures of the CC-W-1 and CC-W-2 conformers in the neutral GA–water complexes could be confirmed. In the above conformers, the water molecule chooses the water-binding sites to form an intermolecular H-bonded bridge, which changes the orientation of the hydroxyl group. This was similar to the previous report for hydrated monosaccharides.1 In addition, the features, which relate to weak intermolecular and intramolecular H-bonds in the CC-W-3 and CC-W-4 conformers, are close to the peaks centered at 3529.0 cm−1 in the observed spectrum. This may explain why the relative intensity of the experimental characteristic peaks centered at 3529.0 cm−1 is slightly higher than those centered at 3442.1 cm−1.56 Therefore, the CC-W-3 and CC-W-4 conformers cannot be excluded in the neutral GA–water. The spectra of the next five high energy conformers aren't consistent with the observed spectrum in the OH region obviously. Therefore, these high energy conformers wouldn't exist in the beam of neutral GA–water, which confirms that only CC conformer exist in the molecular beam. Table 3 reports the frequencies of the experimental bands and the calculated vibrational transitions of the four most stable conformers in accord with experimental results. The calculated anharmonic frequencies are also richer in the CH regions due to the presence of multiple peaks associated with transitions to overtones and combination bands. Except for the usual bandshift, the harmonic frequencies differ less from its anharmonic counterpart in higher energy range. When anharmonic corrections are included, the calculated anharmonic frequencies get more close to the experimental position compared with harmonic frequencies. Additionally, Boltzmann distribution of the hydrated GA conformers based on the relative Gibbs free energy were calculated and shown in ESI.† From the table, it can be seen that the CC-W-1 and CC-W-2 conformers were the main dominant contributions (about 87.6%) while CC-W-3 and CC-W-4 conformers accounted for 12.3% in the gas phase. This implies that the probability of CC-W-1 and CC-W-2 existing is higher than those of CC-W-3 and CC-W-4. These results established that the water prefers to play the role of a bridge through hydrogen bonding rather than cooperativity, thus leading to a generalization of the rules for conformational selectivity in hydrated GA.
| Description | Experiment | Calculations | |||
|---|---|---|---|---|---|
| Observed | CC-W-1 (ha/anha) | CC-W-2 (ha/anha) | CC-W-3 (ha/anha) | CC-W-4 (ha/anha) | |
| Free OH stretch | 3700.5 | 3715.8/3683.6 | 3720.0/3701.5 | 3748.6/3714.2 | 3723.5/3702.8 |
| H-b. OH stretch | 3529.0 | 3523.9/3519.2 | 3527.6/3519.4 | 3560.0/3550.4 | 3579.1/3549.1 |
| H-b. OH stretch | 3442.1 | 3418.1/3416.1 | 3420.4/3411.9 | 3542.2/3534.1 | 3569.6/3542.3 |
| as. CH2 stretch | 2905.7 | 2884.4/2869.9 | 2882.7/2879.4 | 2895.6/2888.3 | 2849.5/2843.2 |
| CH2 twist and CH2 wag, ip OH bend | /2603.8 | /2605.6 | /2611.2 | /2613.5 | |
| CH2 twist and ip OH bend, CH2 wag | /2543.1 | /2541.7 | /2550.8 | /2548.4 | |
| The first overtone of CH2 scissor | /2874.2 | /2869.8 | /2880.9 | /2879.3 | |
| CH2 wag, ip OH bend and CH2 scissor | /2780.1 | /2780.3 | /2772.6 | /2773.5 | |
| s. CH2 stretch | 2870.9 | 2784.9/2772.3 | 2767.2/2759.3 | 2873.1/2868.4 | 2837.6/2829.3 |
| The first overtone of CH2 rock and ip CH bend | /2700.2 | /2698.4 | /2692.8 | /2691.9 | |
| ip OH bend, CH2 wag and CH2 wag, ip OH bend | /2623.8 | /2624.1 | /2631.4 | /2630.3 | |
| CH stretch | 2801.4 | 2759.1/2756.1 | 2743.8/2738.3 | 2822.0/2804.2 | 2821.2/2803.2 |
| The first overtone of CH2 wag, ip OH bend | /2820.8 | /2919.7 | /2835.8 | /2838.4 | |
| CH2 wag, ip OH bend and ip CH bend | /2692.6 | /2689.9 | /2705.3 | /2704.8 | |
3.3 Interaction energy obtained from natural bond orbital (NBO) analysis
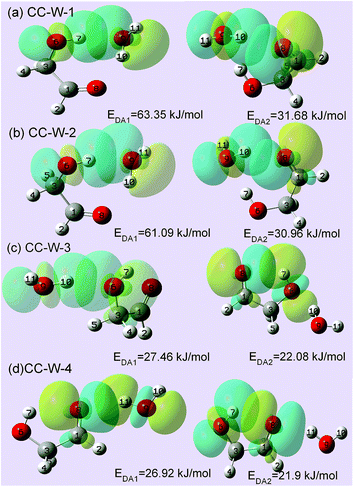
To substantiate the spectroscopy results and estimate the interaction strength, the stabilization energy gained from the hydrogen bond interaction was calculated at the level of ωB97X-D/cc-pVTZ for the hydrated complexes.57 Fig. 4 shows 3D overlap diagrams for the nS → σ*OH donor–acceptor interaction energy obtained from natural bond orbital (NBO) analysis for the four stable hydrated complexes.58 For each conformer, the more orbital overlap the nS → σ*OH donor–acceptor interaction obtained, the greater the magnitude of stabilization energy. The magnitude of the stabilization energy for the 6O–7H⋯9O hydrogen bond interaction is more than twice as large as for the 9O–10H⋯8O interaction in both CC-W-1 and CC-W-2 conformers. This result is consistent with the experimentally observed redshifts.59 However, the magnitude of the stabilization energy of the intermolecular H-bonded interaction is found to be close to that of the intramolecular H-bond in both CC-W-3 and CC-W-4 conformers. Moreover, this stabilization energy is slightly lower than that of 9O–10H⋯8O in the CC-W-1 and CC-W-2 conformers. Therefore, the stretch modes related to the latter three H-bonds mentioned above would have similar vibrational frequencies and their bands would overlap in the observed spectra at ca. 3529.0 cm−1.4. Conclusions
In conclusion, mass selected IR-VUV spectroscopy has been used to directly detect the isolated and hydrated conformers of GA. The results reveal that the CC conformer with a ring-type structure is the dominant conformer in the gas-phase for neutral GA. Although all four hydrated GA conformers (labeled CC-W-1, CC-W-2, CC-W-3, and CC-W-4 in this work) could coexist in the gas phase, water molecules preferentially insert into the intramolecular hydrogen bond to form a cyclic H-bonding bridge between the carbonyl and hydroxyl groups of the open CC conformers of GA (CC-W-1 and CC-W-2) by two additional intermolecular H-bonds. Structural investigation of hydrated GA conformers has revealed that water plays the role of a bridge through intermolecular H-bonds, achieving selective population of specific GA molecular conformations. The conclusions drawn from the mechanisms of flexible conformation can be extended to other carbohydrates and biomolecules.Acknowledgements
This work has been supported by NSFC (No. 11079020, 21273083, U1332132) grants and Guangdong-NSF grants (No. S2013010016551). The scientific research foundation for State Education Ministry, the foundation for introduction of talents by the universities in Guangdong Province, and the project under scientific and technological planning by Guangzhou City.References
- E. J. Cocinero, P. Carcabal and A. M. Rijs, Top. Curr. Chem., 2015, 364, 299–333 CrossRef CAS PubMed.
- E. C. Stanca-Kaposta, D. P. Gamblin, E. J. Cocinero, J. Frey, R. T. Kroemer, A. J. Fairbanks, B. G. Davis and J. P. Simons, J. Am. Chem. Soc., 2008, 130, 10691–10696 CrossRef CAS PubMed.
- J. B. G. Gluyas, A. N. Sobolev, E. G. Moore and P. J. Low, Organometallics, 2015, 34, 3923–3926 CrossRef CAS.
- T. D. Cook, S. N. Natoli, P. E. Fanwick and T. Ren, Organometallics, 2016, 35, 1329–1338 CrossRef CAS.
- J. Zhang, M.-X. Zhang, C.-F. Sun, M. Xu, F. Hartl, J. Yin, G.-A. Yu, L. Rao and S. H. Liu, Organometallics, 2015, 34, 3967–3978 CrossRef CAS.
- R. A. Jockusch, R. T. Kroemer, F. O. Talbot and J. P. Simons, J. Phys. Chem. A, 2003, 107, 10725–10732 CrossRef CAS.
- E. J. Cocinero, E. C. Stanca-Kaposta, E. M. Scanlan, D. P. Gamblin, B. G. Davis and J. P. Simons, Chem.–Eur. J., 2008, 14, 8947–8955 CrossRef CAS PubMed.
- J. P. Simons, B. G. Davis, E. J. Cocinero, D. P. Gamblin and E. C. Stanca-Kaposta, Tetrahedron: Asymmetry, 2009, 20, 718–722 CrossRef CAS.
- H. B. Xie, L. Jin, S. Rudic, J. P. Simons and R. B. Gerber, J. Phys. Chem. B, 2012, 116, 4851–4859 CrossRef CAS PubMed.
- L. Jin, J. P. Simons and R. B. Gerber, J. Phys. Chem. A, 2012, 116, 11088–11094 CrossRef CAS PubMed.
- N. Mayorkas, S. Rudic, E. J. Cocinero, B. G. Davis and J. P. Simons, Phys. Chem. Chem. Phys., 2011, 13, 18671–18678 RSC.
- N. Mayorkas, S. Rudić, B. G. Davis and J. P. Simons, Chem. Sci., 2011, 2, 1128–1134 RSC.
- P. Carcabal, R. A. Jockusch, I. Hunig, L. C. Snoek, R. T. Kroemer, B. G. Davis, D. P. Gamblin, I. Compagnon, J. Oomens and J. P. Simons, J. Am. Chem. Soc., 2005, 127, 11414–11425 CrossRef CAS PubMed.
- H. S. P. Müller, F. Schlöder, J. Stutzki and G. Winnewisser, J. Mol. Struct., 2005, 742, 215–227 CrossRef.
- J. M. Hollis, F. J. Lovas and P. R. Jewell, Astrophys. J., 2000, 540, 107–110 CrossRef.
- J. K. Jorgensen, C. Favre, S. E. Bisschop, T. L. Bourke, E. F. van Dishoeck and M. Schmalzl, Astrophys. J., Lett., 2012, 757, 4–9 CrossRef.
- W. Stumm and J. J. Morgan, Aquatic Chemistry, Chemical Equilibria and Rates in Natural Waters, Wiley, New York, 3rd edn, 1996 Search PubMed.
- P. M. Wiggins, Microbiol. Mol. Biol. Rev., 1990, 54, 432–449 CAS.
- M. Zhou, L. Andrews and C. W. Bauschlicher, Chem. Rev., 2001, 101, 1931–1962 CrossRef CAS PubMed.
- J. M. Lisy, J. Chem. Phys., 2006, 125, 132302–132320 CrossRef PubMed.
- M. P. Gaigeot and R. Spezia, Top. Curr. Chem., 2015, 364, 99–151 CrossRef CAS PubMed.
- A. M. Rijs and J. Oomens, Top. Curr. Chem., 2015, 364, 1–42 CrossRef CAS PubMed.
- Y. J. Hu, J. W. Guan and E. R. Bernstein, Mass Spectrom. Rev., 2013, 32, 484–501 CrossRef CAS PubMed.
- C. Y. Ng, M. A. Johnson and T. J. Martinez, Annu. Rev. Phys. Chem., 2014, 65, 197–224 CrossRef CAS PubMed.
- T. S. Zwier, Annu. Rev. Phys. Chem., 1996, 47, 205–241 CrossRef CAS.
- T. Ebata, A. Fujii and N. Mikami, Int. Rev. Phys. Chem., 1998, 17, 331–361 CrossRef CAS.
- U. Buck and F. Huisken, Chem. Rev., 2000, 100, 3863–3890 CrossRef CAS PubMed.
- M. A. Duncan, Int. Rev. Phys. Chem., 2003, 22, 407–435 CrossRef CAS.
- J. M. Lisy, J. Chem. Phys., 2006, 125, 132302 CrossRef PubMed.
- H. Niki, P. D. Maker, C. M. Savage and L. P. Breitenbach, Chem. Phys. Lett., 1981, 80, 499–503 CrossRef CAS.
- A. Aspiala, J. Murto and P. Sten, Chem. Phys., 1986, 106, 399–412 CrossRef CAS.
- J. Ceponkus, W. Chin, M. Chevalier, M. Broquier, A. Limongi and C. Crepin, J. Chem. Phys., 2010, 133, 094502–094506 CrossRef PubMed.
- J. R. Aviles-Moreno, J. Demaison and T. R. Huet, J. Am. Chem. Soc., 2006, 128, 10467–10473 CrossRef CAS PubMed.
- Y. J. Hu, H. B. Fu and E. R. Bernstein, J. Chem. Phys., 2006, 125, 154306 CrossRef CAS PubMed.
- Y. J. Hu, H. B. Fu and E. R. Bernstein, J. Phys. Chem. A, 2006, 110, 2629–2633 CrossRef CAS PubMed.
- Y. J. Hu, H. B. Fu and E. R. Bernstein, J. Chem. Phys., 2006, 125, 154305 CrossRef CAS PubMed.
- H. B. Fu, Y. J. Hu and E. R. Bernstein, J. Chem. Phys., 2006, 124, 024302 CrossRef CAS PubMed.
- Y. J. Hu, H. B. Fu and E. R. Bernstein, J. Chem. Phys., 2006, 124, 114305 CrossRef CAS PubMed.
- S. Maity, R. I. Kaiser and B. M. Jones, Faraday Discuss., 2014, 168, 485–516 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision C.02, Gaussian, Inc., Wallingford CT, 2004 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, revision C 01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- R. N. Pribble and T. S. Zwier, Science, 1994, 265, 75–79 CAS.
- K. Sakota, M. Schütz, M. Schmies, R. Moritz, A. Bouchet, T. Ikeda, Y. Kouno, H. Sekiya and O. Dopfer, Phys. Chem. Chem. Phys., 2014, 16, 3798 RSC.
- M. Schütz, K. Sakota, R. Moritz, M. Schmies, T. Ikeda, H. Sekiya and O. Dopfer, J. Phys. Chem. A, 2015, 119(39), 10035–10051 CrossRef PubMed.
- B. L. Yoder, K. B. Bravaya, A. Bodi, A. H. C. West, B. Sztáray and R. Signorell, J. Chem. Phys., 2015, 142, 114303 CrossRef PubMed.
- Y. K. Kang and B. J. Byun, Biopolymers, 2012, 97, 778–788 CrossRef CAS PubMed.
- A. Kinal and S. Sayhan, Int. J. Hydrogen Energy, 2016, 41, 392–400 CrossRef CAS.
- M. Xie, Y. Matsuda and A. Fujii, J. Phys. Chem. A, 2015, 119, 5668–5675 CrossRef CAS PubMed.
- M. L. Senent, J. Phys. Chem. A, 2004, 108, 6286–6293 CrossRef CAS.
- Y. Matsuda, K. Hoki, S. Maeda, K. I. Hanaue, K. Ohta and K. Morokuma, et al., Phys. Chem. Chem. Phys., 2012, 14, 712–719 RSC.
- J.-W. Shin and E. R. Bernstein, J. Chem. Phys., 2009, 130, 214306 CrossRef PubMed.
- P. Carbonniere and C. Pouchan, Theor. Chem. Acc., 2012, 131, 1183 CrossRef.
- M. Jetzki, D. Luckhaus and R. Signorell, Can. J. Chem., 2004, 82, 915 CrossRef CAS.
- J. Ceponkus, W. Chin, M. Chevalier, M. Broquier, A. Limongi and C. Crepin, J. Chem. Phys., 2010, 133, 094502 CrossRef PubMed.
- Y. J. Hu, H. B. Fu and E. R. Bernstein, J. Chem. Phys., 2006, 125, 154305–154310 CrossRef CAS PubMed.
- T. N. Wassermann, P. Zielke, J. J. Lee, C. Cezard and M. A. Suhm, J. Phys. Chem. A, 2007, 111, 7437–7448 CrossRef CAS PubMed.
- S. D. Schroder, J. H. Wallberg, J. A. Kroll, Z. Maroun, V. Vaida and H. G. Kjaergaard, J. Phys. Chem. A, 2015, 119, 9692–9702 CrossRef PubMed.
- E. D. Glendening, C. R. Landis and F. Weinhold, Adv. Rev., 2012, 2, 1–42 CAS.
- V. R. Mundlapati, S. Ghosh, A. Bhattacherjee, P. Tiwari and H. S. Biswal, J. Phys. Chem. Lett., 2015, 6, 1385–1389 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra26965f |
| This journal is © The Royal Society of Chemistry 2017 |