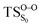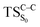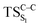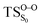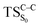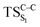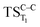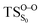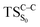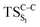A combined theoretical and experimental study on the mechanism of spiro-adamantyl-1,2-dioxetanone decomposition

Abstract

1,2-Dioxetanones have been considered as model compounds for bioluminescence processes. The unimolecular decomposition of these prototypes leads mainly to the formation of triplet excited states whereas in the catalysed decomposition of these peroxides singlet states are formed preferentially. Notwithstanding, these cyclic peroxides are important models to understand the general principles of chemiexcitation as they can be synthesised, purified and characterised. We report here results of experimental and theoretical approaches to investigating the decomposition mechanism of spiro-adamantyl-1,2-dioxetanone. The activation parameters in the unimolecular decomposition of this derivative have been determined by isothermal kinetic measurements (30–70 °C) and the chemiluminescence activation energy calculated from the correlation of emission intensities. The activation energy for peroxide decomposition proved to be considerably lower than the chemiluminescence activation energy indicating the existence of different reaction pathways for ground and excited state formation. These experimental results are compared with the calculations at the complete active space second-order perturbation theory (CASPT2), which reveal a two-step biradical mechanism starting by weak peroxide bond breakage followed by carbon–carbon elongation. The theoretical findings also indicate different transition state energies on the excited and ground state surfaces during the C–C bond cleavage in agreement with the experimental activation parameters.

---

1 Introduction

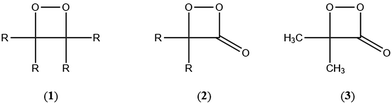
The simplest models for chemiluminescence (CL) and bioluminescence transformations are constituted by the thermal unimolecular decomposition of 1,2-dioxetanes (1) and 1,2-dioxetanones (2) and the mechanism of these transformations has been extensively studied by experimental and theoretical means.^1–3 Several hundreds of 1,2-dioxetane derivatives have been prepared and their properties studied, mainly the activation parameters and the singlet and triplet chemiexcitation quantum yields. Additionally, five 1,2-dioxetanone derivatives have been synthesised and only one derivative has been studied in detail, namely 4,4-dimethyl-1,2-dioxetanone (3), whose

unimolecular, as well as catalysed decomposition, has been considered by several research groups.^1–5 More recently, we reported experimental data on the catalysed decomposition of two new 1,2-dioxetanone derivatives, spiro-adamantyl-1,2-dioxetanone (4) and spiro-cyclopentyl-1,2-dioxetanone (5).⁶

The unimolecular decomposition of 1,2-dioxetanes and 1,2-dioxetanones leads, mainly, to the formation of triplet excited

carbonyl products, with quantum yields of up to 30%, whereas the singlet excited state formation is inefficient, reaching rarely up to 1%.^1–4 Peroxide derivatives with higher degree of substituents are more stable and possess higher quantum yields.^2,4,7

Two extreme pathways were suggested for this transformation; a concerted mechanism, first proposed by Turro,⁸ as well as a biradical path, initially formulated by Richardson.^9,10 The concerted mechanism is a single-step reaction process in which the C–C and O–O bonds dissociate simultaneously. The two-step biradical mechanism, however, implies that once the O–O bond is cleaved, the system enters a so-called entropic trapping region^11,12 of biradical nature where four singlet and triplet states are degenerated, then, the C–C rupture comes into action. Some of the obtained experimental data appear to be more compatible with the biradical mechanism. Although, the others can be better rationalised with a concerted transformation. Consequently, a “merged” reaction pathway, in which the O–O elongation is not fully completed when the C–C cleavage occurs, has been suggested maintaining the biradical nature of the process without formation of a biradical intermediate in a potential energy surface minimum.⁷ This mechanistic proposal appears to accommodate all (or at least most) of the available experimental data up to now. Although, generally no charge or electron transfer processes are considered in the unimolecular decomposition of cyclic peroxides, some recent work has pointed out a feasible importance of charge and electron spin transfer actions.¹³

During the last 10 years, significant efforts have been performed to understand the CL phenomenon with computational methodologies, by studying the decomposition mechanism of 1 and 2, in detail.^12,14,15 These ab initio findings, as well, confirm a step-wise biradical mechanism for 1, taking into account the time it takes to pass the entropic trapping region before complete thermal decomposition. According to these efforts, in contrast to singlet excited state formation, triplet excitation requires almost the same energy as the thermal decomposition to ground state products. However, the dissociation mechanism of 2, is not supported yet neither by ab initio¹⁵ nor DFT studies, due to the lack of molecular dynamics simulations.¹⁶

An open mechanistic question in the unimolecular 4-membered ring peroxide decomposition is if there are distinct reaction pathways for the formation of ground and excited state products, which possess different activation energies? Only a few experimental studies have addressed this question; Turro and co-workers have investigated the possibility of different transition states for the formation of ground state, triplet and singlet excited state products, measuring the isothermal and CL activation energies for the decomposition of tetramethyl-1,2-dioxetane and concluded that ground as well as excited state reaction occur all by a common transition state.¹⁷ In a study on the unimolecular decomposition of dimethyl-1,2-dioxetanone (3), Schmidt and Schuster have reported different activation energies for the formation of ground and excited state products.¹⁸ However, these results have been questioned by Turro and Chow, which report similar values for the ground and excited state activation parameters in the decomposition of this 1,2-dioxetanone derivative.¹⁹

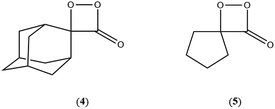
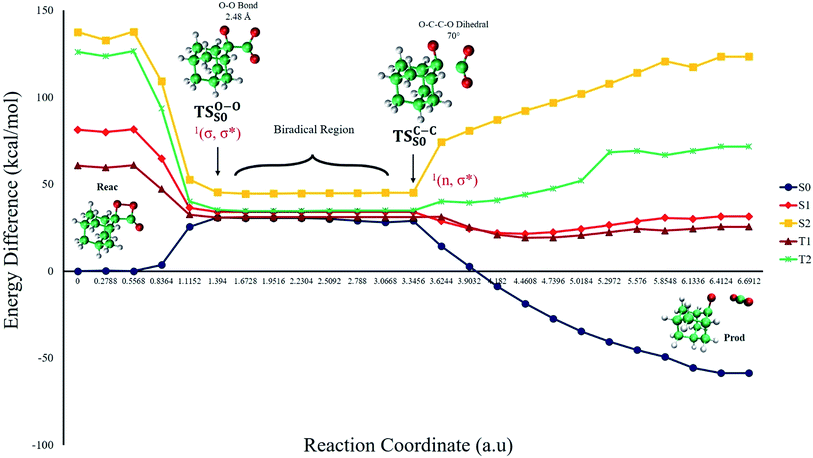
On the basis of the previous theoretical efforts with 1,2-dioxetane^12,14,20 and 1,2-dioxetanone,¹⁵ a two-step biradical mechanism in which the C₁–C₂ rupture occurs after terminating the O₁–O₂ fragmentation, can be expected for the decomposition of spiro-adamantyl-1,2-dioxetanone to adamantanone and CO₂ (see Fig. 1). The first step in the biradical mechanism is the O₁–O₂ cleavage (TS_S0), after that the system enters a biradical region in which four singlet and four triplet manifolds are degenerated. The next step of the reaction mechanism is the C₁–C₂ bond breakage (TS_S1,T1) which basically occurs along the lowest-lying excited states, since the TS corresponding the C₁–C₂ rupture is quite shallow on the ground state and hence difficult to compute.

Fig. 1 Decomposition mechanism of spiro-adamantyl-1,2-dioxetanone. Immediately after the O–O rupture (the first step), the system enters to a biradical region in which four singlet and four triplet manifolds are degenerated. After that, the C–C fragmentation comes into action and decomposes the system into two species of adamantanone and CO₂.

The aim of the present article is to report a qualitative and quantitative study on the electronically excited state formation of spiro-adamantyl-1,2-dioxetanone as a prototype. The spiro-adamantyl-1,2-dioxetanone was chosen as the model peroxide derivative for the experimental studies, as this has been shown before to be relatively stable and hence, can be conveniently purified by low-temperature recrystallization. The chemiexcitation quantum yields and the activation parameters of the unimolecular decomposition of this 1,2-dioxetanone derivative were determined and the results obtained compared to those extracted from theoretical calculations applying multiconfigurational strategies. Especially, the possible existence of different reaction pathways for ground and excited state formation was addressed by experimental and theoretical approaches. It is noteworthy that a theoretical study on a similar but larger system, 3-(2-spiro-adamantyl)-4-methoxy-4-(3-phosphoryloxy)-phenyl-1,2-dioxetane has been recently reported proposing a reversible charge transfer-initiated luminescence mechanism.²¹

2 Results

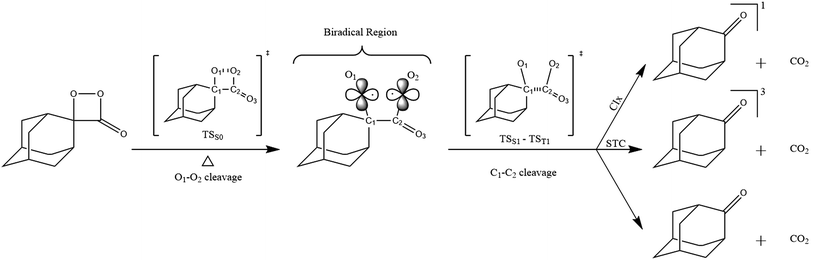
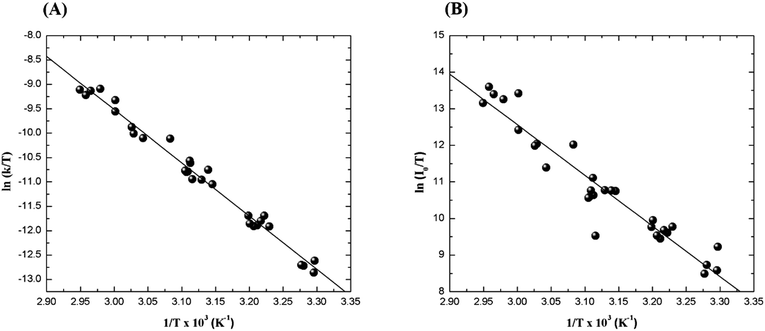
The relatively stable α-peroxylactone derivative, spiro-adamantyl-1,2-dioxetanone (4), was synthesized according to the published procedure, purified by low-temperature recrystallization and characterized by NMR spectroscopy as reported before.²² The kinetic assays on the decomposition of the 1,2-dioxetanone derivative 4 were performed in toluene as solvent. Initially, the singlet (Φ_S) and triplet quantum yields (Φ_T) in its unimolecular decomposition were determined, using two energy acceptors which are known to possess relatively high oxidation potentials and therefore should not lead to significant catalysed decomposition of the peroxide.^1–3 2,5-Diphenyloxazole (PPO, E^ox_p/2 = 1.46 V vs. SCE)^21,22 was used to determine the singlet quantum yields and 9,10-dibromoanthracene (DBA, E^ox_p/2 = 1.42 V vs. SCE),^23,24 which can act as a triplet energy acceptor due to the bromine heavy-atom effect,^1–3 was utilized to determine the triplet quantum yields. These quantum yields of electronically excited states formed in the decomposition of 4 are Φ_T = 1.0 ± 0.3 × 10⁻² E mol⁻¹ and Φ_S = 3.3 ± 0.3 × 10⁻⁵ E mol⁻¹, corresponding to a triplet to singlet ratio (Φ_T/Φ_S) of about 300, similar to that commonly observed in 1,2-dioxetane decomposition. The triplet quantum yield determined here is similar to that of Φ_T = 1.5% reported for the unimolecular decomposition of 4,4-dimethyl-1,2-dioxetanone (3), however, the singlet quantum yield is considerably lower than the one determined before for 3.^{1,3–5,18,19}

For the determination of the activation parameters for the unimolecular decomposition of 4, the decomposition kinetics in toluene were followed by the intensity of the direct CL emission, corresponding to 2-adamantanone fluorescence, in a temperature range of around 30 to 70 °C (Fig. 2). The kinetic curves give rise to the observed rate constants (k_obs) and the initial emission intensities (I₀), obtained by the first-order exponential fitting. The correlation of the decomposition rate constants with the temperature, according to Eyring plots, showed to be linear and allows the determination of the activation enthalpies (Δ^≠H) and entropies (Δ^≠S) (Fig. 3, Table 1). Using the I₀ values, instead of k_obs, in the Eyring plot, the activation enthalpy for the CL process (Δ^≠H_CL) can be obtained. This approach is based on the fact that the emission intensities correspond directly to a reaction rate, as these intensities depend on the decomposition rate constant, the 1,2-dioxetanone concentration and the emission quantum yield. Therefore, the emission intensities are proportional to the rate constant of the decomposition process leading to excited state formation and can be utilized to obtain the activation enthalpy of this process. However, as no rate constants are utilized for the correlation, it is not possible to obtain values for the activation entropy (Fig. 3, Table 1). The reported activation parameters are obtained from at least three independent rate constant measurements at each temperature. The error bars come from linear regression of rate constant values according to the Eyring equation, using error progression analysis for the calculation of the deviation in the Δ^≠S and Δ^≠G values.

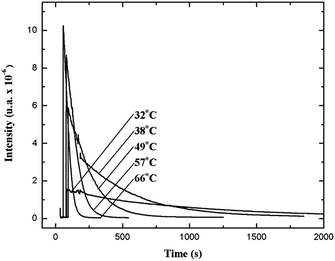Fig. 2 Kinetic emission intensity curves for the direct emission in the unimolecular decomposition of spiro-adamantyl-1,2-dioxetanone (4) (1.33 mmol L⁻¹) at different temperatures.

Fig. 3 Eyring correlation of (A) the rate constants (k) and (B) the initial emission intensities (I₀) with the temperature for the unimolecular decomposition of spiro-adamantyl-1,2-dioxetanone (4) (1.33 mmol L⁻¹).

Table 1 Activation parameters for the unimolecular decomposition of spiro-adamantyl-1,2-dioxetanone (4)

	Δ^≠H (kcal mol^−1)	Δ^≠S (cal mol^−1 K^−1)	Δ^≠G (25 °C) (kcal mol^−1)	Δ^≠HCL (kcal mol^−1)
Unimol. decomp.	21.7 ± 0.6	−1.1 ± 0.8	22.0 ± 0.5	28 ± 2

---

The activation data obtained clearly indicate that the CL activation enthalpy, obtained from the correlation of the initial emission intensities, is significantly higher than the “normal” isothermal activation enthalpy, obtained from the correlation of the observed decay rate constants. Interestingly, the activation entropy is close to zero, in agreement with the occurrence of a unimolecular process, thereby excluding significant participation of dark peroxide decomposition (Table 1).

2.1 Geometry optimization and activation energies

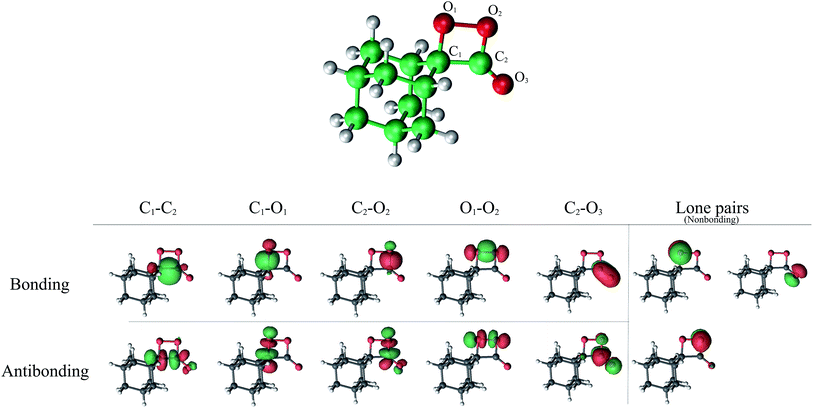
Considering the previous studies on 1,2-dioxetane,¹⁴ 1,2-dioxetanone¹⁵ and Dewar 1,2-dioxetane,²⁰ one can claim that these O–O bond breaking reactions occur via a two-step mechanism for most of the cases. This, however, has been illustrated in Section 3, applying the intrinsic reaction coordinate (IRC) calculations. In this reaction mechanism, first the O₁–O₂ cleavage takes place, after that the C₁–C₂ rupture comes into action. Taking into account the features of such mechanism, several transition structures can be characterized: the TS on the singlet ground state surface corresponding to the O₁–O₂ bond breakage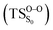 , from which the considered singlet and triplet excited states become degenerated with the S₀; the TS on the ground, first singlet and first triplet excited states corresponding to the C₁–C₂ cleavage (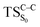, 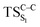and 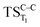, respectively).

In the present study, MS-CASPT2(10in8)/ANO-VDZP geometry optimizations were carried out and the most relevant geometrical parameters for the CL reaction of 4 are compiled in Table 2. In contrast to 1,2-dioxetane¹⁴ and other alkyl-substituted 1,2-dioxetanes,²⁵ where the O₁–C₁–C₂–O₂ dihedral angles are between 19 to 22 degrees, the starting geometry (Reac) has zero degree of the dihedral angle, whereas the C₁–C₂ and O₁–O₂ are more or less the same. The 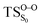has the similar dihedral angle (6.7°) which reveals a stretching of O₁–O₂ bond instead of a torsion of the O₁–C₁–C₂–O₂ dihedral angle for 1,2-dioxetanes that was stated to be responsible for the formation of an entropic trapping process and hence producing excited state species.¹² This difference is due to the conjugation effects caused by the C₂=O₃, that restricts the twisting around the C₁–C₂ bond. It is noteworthy that the found TS dihedral angle at the CASSCF method is close to zero (0.77°). These findings are consistent with the study of 1,2-dioxetanone by Liu et al. that characterized the optimized geometries to be effectively planner.¹⁵

Table 2 Geometrical parameters of important transition geometries on the ground and excited states optimized at MS-CASPT2(10in8)/ANO-L-VDZP level of theory

	Reac
Bond lengths (Å)
C1–C2	1.506	1.549	1.654	1.876
O1–O2	1.531	2.482	2.825	2.559
C2–O3	1.200	1.221	1.186	1.181
C1–O1	1.475	1.383	1.361	1.360
C2–O2	1.392	1.336	1.296	1.224
Angles (degree)
C1–C2–O3	139.4	128.8	110.6	116.2
O1–C1–C2	87.5	108.3	105.9	107.0
O2–C2–O3	127.1	119.5	127.9	140.4
Dihedral angle (degree)
O1–C1–C2–O2	0.00	6.76	70.1	1.82

---

Table 3 also compiles the relative energies of the optimized stationary points at the CASPT2 level of increasing accuracy as well as ZPVE and Gibbs free energy correction. The comparison of the relative energies showed that the CASSCF energies are affected by the dynamical correlation. For instance, in the 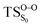structure the CASSCF underestimates the energy barrier by 12.8 kcal mol⁻¹, this is caused by the lack of dynamical correlation. This huge difference between CASSCF and CASPT2 energies convinced us to perform CASPT2 geometry optimization on the transition structures, in order to provide quantitatively accurate activation energies. However, the final results revealed that CASSCF method is accurate enough to optimize geometries of spiro-adamantyl-1,2-dioxetanone and it, therefore, was used for the IRC calculations. Unless stated otherwise, the energy values shown in this study are the MS-CASPT2(16in13)/ANO-L-VTZP.

Table 3 Relative energies (kcal mol⁻¹) of transition structures of the thermal decomposition of spiro-adamantyl-1,2-dioxetanone (4) optimized at MS-CASPT2 level of theory. DZ and TZ refer to the ANO-L-VDZP and ANO-L-VTZP basis sets, respectively

	MS-CASPT2(16in13)/TZ//MS-CASPT2(10in8)/DZ	ZPVE	Gibbs (298 K)
Reac	0.0	0.0	0.0
	30.98	29.98	30.43
	23.95	21.97	22.11
	28.77	26.79	26.93
	26.45	24.47	24.61

---

The ground state dissociation begins by surmounting a barrier height of 31 kcal mol⁻¹ (the rate-limiting step). After that, 23.9 kcal mol⁻¹ is required to cleave the C–C bond and lead to the products. Taking ZPVE corrections into account, however, decreases these values to 30.4 and 22.1 kcal mol⁻¹, respectively, due to bond dissociation. The bond dissociation causes a change in entropy of the reaction as well. The computed CL activation energy (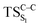) is 28.7 kcal mol⁻¹, which is more or less the same as the one obtained experimentally by kinetic studies (∼28 kcal mol⁻¹). These theoretical findings, both qualitatively and quantitatively support the manifestation of two different pathways; one with lower energy (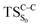) leading to the products, and one with higher energy (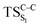) producing chemiexcitation products.

2.2 Ground state decomposition

The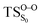 on the ground state potential energy surface (PES) was located and verified by vibrational frequency analysis at the CASSCF method. An imaginary frequency (409 cm⁻¹) corresponding to the O₁–O₂ stretching mode was discovered for the TS. A downward MEP at the MS-CASPT2//CASSCF/ANO-L-VDZP level of theory, starting from the optimized 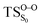, connects the reactant (Reac) and a minimum (Min^O–O) in the entropic trapping region where four singlet and four triplet states are degenerated (see Fig. 4). To be able to explain the different activation energies for ground and excited state decompositions obtained from experiment, a downward MEP search toward the product species was also performed from the 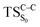(verified by an imaginary frequency of 485 cm⁻¹) and is illustrated in Fig. 4.

Fig. 4 Computed MS-CASPT2//CASSCF/ANO-L-VDZP energy profile on the S₀ surface started from the and continued by the . The region in which all the states are degenerated or nearly-degenerated are clearly shown from this TS structure.

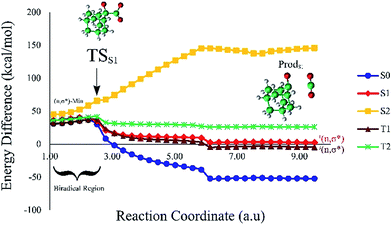
Based on the MEP, the mechanism for the thermal decomposition can be described. First, stretching the O₁–O₂ bond leads the molecule from the reactant to formation of the 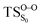. After that, the C₁–C₂ stretch begins and decomposes molecule to the products. At the 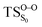of the MEP, the MS-CASPT2 energy gap between S₀, S₁ and T₁ manifolds are less than 4 kcal mol⁻¹, implying that there is a crossing where the adiabatic states strongly interact. The energetics at the 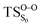reveals that the T₁ is slightly higher in energy than the S₀ (0.5 kcal mol⁻¹), which indicates the presence of an intersystem crossing (ISC) on top of the internal conical intersection (CIx) between S₀ and S₁. This is proven by the large SOC values obtained at MS-CASPT2(16in13) level, see ESI Table S5.† From these crossing points adiabatic transformations take place on the MEPs from ¹(σ,σ*) to ^1,3(n,σ*). This transformation does not break the planer symmetry and after the crossing point, the ^1,3(n,σ*) states more or less maintain the planer structure. However, once the molecule leaves the entropic trapping region, it twists around the O–C–C–O dihedral angle to form the 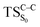which breaks the plane. This TS is the responsible for the C–C dissociation along the S₀ manifold.

2.3 Dissociation on the S₁ and T₁ manifolds

Due to the small energy gap between S₁ and T₁ structures, located at the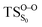 , this structure has been taken as starting geometry to optimize the 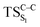and 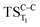. The relevance of the TS structures was verified by vibrational frequency analysis at the CASSCF method. An imaginary frequency (316 cm⁻¹) corresponding to the C₁–C₂ stretching mode was discovered for these TSs. After finding the TS structures, the downward MEPs along these states were computed at MS-CASPT2//CASSCF/ANO-L-VDZP. The IRC search on the second TS in both S₁ and T₁ states, connects the minimum on entropic trapping region (Min^O–O) to the excited adamantanone and a ground state CO₂ (see Fig. 5 and S1†). The first points along the MEPs indicate that all the states are nearly degenerated until the molecule arrives to the transition structure. The nature of the states in the 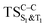region (2.79 au) is (n,σ*) and consequently, no change in the nature takes place after the TS along the IRC. The MEPs finally terminate in the excited adamantanone. As depicted in Fig. 5 and S1,† the energy profile for the T₁ manifold is essentially identical to the S₁ manifold, except that the T₁ is lower in energy than the S₁. However, finding the 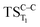and the corresponding MEP search lies beyond the scope of the present study (see ESI Fig. S1†).

Fig. 5 Computed MS-CASPT2//CASSCF/ANO-L-VDZP IRC on the S₁ state from the .

The MS-CASPT2//SA-CASSCF protocol did not significantly change the shape and relative positions of the ground and excited state MEPs optimized at the SA-CASSCF level. Although the SA-CASSCF(10in8) approach is not the most accurate method to describe this reaction mechanism in detail, it is quite safe to qualitatively interpret its reaction mechanism and to some extent quantitatively.

3 Discussion

To begin with, our obtained experimental activation parameters for spiro-adamantyl-1,2-dioxetanone decomposition as well as the reported values in the literature for all known 1,2-dioxetanone derivatives are compiled in Table 4. The activation enthalpies for the thermolysis of 1,2-dioxetanones are in the 11–22 kcal mol⁻¹ range (Table 4). The Gibbs free-energy values at 25 °C (Δ^≠G) show that 4 is the most stable 1,2-dioxetanone synthesized till now, while the peroxyoxalate reaction high-energy intermediate (HEI), 1,2-dioxetanedione (8),²⁴ remains the most unstable example of this class of cyclic peroxide (Table 4). Nonetheless, 4 is still more labile than the non-substituted 1,2-dioxetane (Δ^≠G = 23.2 kcal mol⁻¹),^7,26 thus accounting for the fact that the preparation and handling of these cyclic organic peroxides is not trivial.²²

Table 4 Compilation of activation parameters for the unimolecular decomposition of 1,2-dioxetanone derivatives

1,2-Dioxetanone	Δ^≠H (kcal mol^−1)	Δ^≠S (cal mol^−1 K^−1)	Δ^≠G^a (kcal mol^−1)	Δ^≠HCL (kcal mol^−1)
a At 25 °C.
Unimolecular decomposition
4^this work	21.7 ± 0.6	−1.1 ± 0.8	22.0 ± 0.5	28 ± 2
3 (ref. 3)	19.2 ± 0.2	−8.2 ± 0.5	21.6 ± 0.3	—
3 (ref. 4)	21.7 ± 0.3	0 ± 1	21.7	25.0 ± 0.1
3 (ref. 5)	21.7 ± 0.6	—	—	21.0 ± 0.8
6 (ref. 6)	18.8	−8.9	21.5	—
7 (ref. 5)	17.5 ± 0.1	−12.0 ± 0.2	21.1 ± 0.2	16.6 ± 1.3
10 (ref. 3)	13.7 ± 0.3	−24.1 ± 1.0	20.9 ± 0.5	—
9 (ref. 5)	19.3 ± 1.4	−4.85 ± 0.52	20.8 ± 1.4	16.6 ± 2.0
8 (ref. 7)	11.2 ± 0.4	−23.2 ± 0.8	18.2 ± 0.6	—

---

The activation entropies for the unimolecular decomposition of 1,2-dioxetanones vary from very negative (e.g., 10) to near-zero values (e.g., 4) (Table 4). For a unimolecular process, where two molecules of product are generated from one reactant molecule, Δ^≠S values should be around zero or positive, due to a higher degree of disorder in the TS. Negative Δ^≠S values for the unimolecular thermolysis of 1,2-dioxetanes have been interpreted as related to impurities-induced dark decomposition.^1,2,27 This rationale may be applied to explain the considerably low values for Δ^≠H of the derivatives 7 and 10, for whom highly negative activation entropy values were reported (Table 4); even so, the Δ^≠G values of these compounds fall within the expected range for the series.

For the chemiexcitation reaction the Δ^≠H_CL values are in some cases similar to the reaction enthalpies Δ^≠H (for the 1,2-dioxetanones 7 and 9) or significantly higher, as seen for peroxides 3 and 4 (Table 4). This Δ^≠H_CL > Δ^≠H observation may be associated with the existence of an impurity-catalysed dark decomposition (with no light emission), which possess a rate constant k_imp embedded to the experimentally determined k_obs value, a reaction path possibly with lower activation energy. This may be the case for the unimolecular decomposition of 1,2-dioxetanone 3, which shows highly negative Δ^≠S values. However, the observed Δ^≠S ≈ 0 for the spiro-adamantyl derivative 4 (Table 4) indicates that this supposed impurity-catalysed process is absent or non-significant, showing that the unimolecular decomposition of this peroxide occurred in a “cleaner” system. Therefore, this 5.8 kcal mol⁻¹ difference between Δ^≠H_CL and Δ^≠H for 4 may point towards the existence of two distinct pathways for unimolecular peroxide decomposition: one with a lower energy, leading to ground state products, and the other with a higher energy barrier producing chemiexcited products. This is in agreement with earlier observations made by Schmidt and Schuster,²⁸ who found a higher activation energy for the CL pathway in the unimolecular decomposition of 4,4-dimethyl-1,2-dioxetanone (3). However, in a subsequent work, Turro and Chow determined very similar activation parameters for the isothermal and CL pathway in the decomposition of the same cyclic peroxide derivative.²⁹

These contradictive results indicate the high inherent difficulties to work with this kind of highly unstable peroxide and to obtain reproducible and solid experimental data. The results reported here are more trustable as they were obtained with a derivative which is more stable and could be purified by low-temperature recrystallization and characterized by NMR spectroscopy. Furthermore, the low activation entropy measured for the unimolecular decomposition indicates that the reaction system does not contain any impurities like heavy metal atoms, which could induce dark catalysis. Therefore, we believe to have obtained experimental evidence, for the first time, that the two concurrent reaction pathways may exist in the unimolecular decomposition of spiro-adamantyl-1,2-dioxetanone, one leading to excited state formation and the other giving directly to ground state products. This important experimental observation led us to study the process also by theoretical means.

The theoretical evidences indicate that the CL mechanism of spiro-adamantyl-1,2-dioxetanone occurs as follows. First, an activation energy of 30.4 kcal mol⁻¹ corresponding to the O₁–O₂ cleavage is essential to enter the biradical region in which energy degeneracy takes place between lowest-lying four singlet and triplet states of the system. In this region, the singlet excited state is populated. Taking the significant amount of SOC into account, the population can also be transferred to the triplet excited state of the molecule. After that, a second activation energy related to the C₁–C₂ rupture (TS^C–C) is required to dissociate the molecule. The essential energy values to surmount this barrier height for the ground 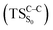and first singlet excited states 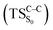are different. Our CASPT2 calculations clearly support a lower activation energy on the ground state (22.1 kcal mol⁻¹) than the singlet manifold (27 kcal mol⁻¹).

In summary, the theoretical calculations indicate that: (i) there is an extended biradical region in the decomposition of 4 on the ground state PES, where S₀, S₁ and T₁ states are degenerated, allowing the formation of singlet and triplet excited states; (ii) the transition state for the rate limiting O–O bond cleavage is the same for S₀, S₁ and T₁; (iii) on the ground state energy surface, an additional activation energy exists for C–C bond cleavage, therefore the decomposition process of 4 should be nominated as a biradical mechanism; (iv) an activation energy for C–C bond cleavage exists on the S₁ and T₁ excited state surfaces; indicating that singlet quantum yields (and also triplet quantum yields) should change with the temperature; (v) the S₁ PES is higher in energy than the T₁ PES, indication preferential formation of triplet state products.

These facts should now be related to the obtained experimental result: (a) formation of singlet as well as triplet excited states is observed in the thermal decomposition of 4, in agreement with (i); (b) the different activation energies for thermal decomposition and the chemiexcitation pathway would indicate different transition states for ground and excited state formation, contrarily to the theoretical results outlined in (ii), however, the observation of a higher energy PES for S₁ formation during C–C bond cleavage, shown in (iv), can explain the experimental results, as higher quantum yields should be expected at higher temperatures, leading to the measurement of a higher CL activation energy; (c) the difference in the experimental and calculated activation energies for thermal decomposition might be due to the fact that the former were obtained in toluene and the later calculated in vacuo;³⁰ (d) the experimentally observed (Φ_T/Φ_S) ratio of about 300 can be understood by the fact that the calculated triplet PES for C–C bond cleavage is lower in energy than the corresponding excited singlet PES.

Therefore, we can conclude that the theoretical calculations performed on this system are in excellent qualitative agreement with the experimental results obtained and also contribute to a more precise description of the decomposition mechanism of the model 1,2-dioxetanone derivative 4.

4 Methodology

4.1 Experimental section

Toluene for the kinetic CL assays was stirred overnight over EDTA, filtered, distilled, and then redistilled from metallic sodium; Rubrene (RUB) was used as received. spiro-Adamantyl-1,2-dioxetanone (4) was prepared and handled as described elsewhere.²² Peroxide solutions for the kinetic CL assays were stored in vials and kept at −78 °C during the experiments; their concentration was determined by an iodometric assay, as reported elsewhere. All glassware, including pipettes and micro syringes, was treated with EDTA solutions to remove traces of metal ions.

4.2 Kinetic chemiluminescence assays

Light emission time-profiles were recorded on a fluorescence spectrophotometer or a photon counter system for low intensity assays. A quartz cuvette containing the solvent or ACT solution is allowed to equilibrate thermally in the thermostated cell holder and the reaction initiated by addition of a small amount (typically 10 to 30 μL for a total volume of 2.00 mL) of peroxide stock solution, the CL emission intensity decay being registered for at least three half-lives. The equipment baseline emission intensity was discounted for all kinetic assays. The light emission time-profiles were fitted with a first-order exponential decay equation to determine the initial emission intensities (I₀, in E s⁻¹) and the observed rate constants (k_obs, in s⁻¹). The light emission intensity, registered in arbitrary units (a.u. s⁻¹), was converted to absolute light units (einstein s⁻¹) through calibration of the photomultiplier tube (PMT) using a modified version of the luminol standard method,²³ and considering the PMT wavelength sensibility. The fluorescence quantum yield of 2-adamantanone, determined in toluene, proved to show only slightly variation with the temperature (30 to 70 °C).

For the determination of chemiexcitation quantum yields, the decomposition of the peroxide 4 was performed in the presence of different concentrations of the energy acceptor ([PPO] = 5.0–50 mmol L⁻¹, ([DBA] = 0.50–5.0 mml L⁻¹) and the CL quantum yields determined at each energy acceptor concentration from the area under the emission intensity curves, obtained in absolute einstein (E) units by luminol calibration.²³ The quantum yields at infinite energy acceptor concentration (Φ^∞_S and Φ^∞_T), which correspond to the yield of singlet and triplet excited carbonyl compounds initially formed in peroxide decomposition, were determined from double reciprocal plots between the respective quantum yields and the energy acceptor concentration (1/Φ_S vs. [PPO] and 1/Φ_T vs. [DBA]) as described before.⁷

4.3 Computational chemistry

Geometry optimizations of the reactant and the transition states (TS) along the ground state (S₀), first singlet excited state (S₁) and first triplet state (T₁) as well as minimum energy path (MEP) calculations were performed at complete active space self-consistent filed (CASSCF) method,^31,32 with no symmetry constraints, in conjunction with the atomic natural orbital (ANO-L) basis set contracted to O,C[3s2p1d]/H[2s1p] (thereafter ANO-L-VDZP).³³ CASSCF provides a balanced description of different electronic states and correctly treats the multiconfigurational character of the wave functions, especially important when bonds are being broken or formed. A state average of four states with equal weights was considered for all CASSCF calculations. Subsequent single point state-specific (SS) complete-active-space second-order perturbation theory (CASPT2) energy calculations were carried out at the optimized CASSCF geometries, which includes dynamical correlation in the final energies. In these CASPT2 calculations the basis set was improved from double- to triple-ζ quality, O,C[4s3p2d1f]/H[3s2p1d] (thereafter ANO-L-VTZP),³⁴ following the CASPT2//CASSCF protocol employed in related studies. Furthermore, to benchmark whether the optimized geometries at CASSCF level are accurate, partial CASPT2 geometry optimizations using constrained numerical gradients and composite gradients³⁵ were performed in conjunction with ANO-L-VDZP basis set for the stationary points.

In order to analyse state-interaction effects of the CASPT2 wave functions, the multi-state (MS) approach³⁶ of the CASPT2 method was also used. The MS- and SS-CASPT2 approaches give rise to energy values with differences of lower than 1 kcal mol⁻¹. This is caused by the small off-diagonal elements of the effective Hamiltonian matrix in the MS calculations. Throughout the CASPT2 calculations, freezing the core orbitals of non-hydrogen atoms as well as a modification of the zero^th-order Hamiltonian, excluding the standard ionization potential electron affinity (IPEA) (with 0.0 value) were applied.³⁷ On the other hand, an imaginary level shift of 0.2 a.u. was used, in order to solve weakly interacting intruder-states problems.³⁸

The selection of a reasonable active space in the both CASSCF and CASPT2 calculations was done based on the described two-step mechanism. The required amount of electrons and orbitals expected for the CL process of spiro-adamantyl-1,2-dioxetanone are 16 electrons distributed in 13 orbitals, similar active space to the study of parent 1,2-dioxetanone applying CASSCF method,¹⁵ proved by 2-RDM method.³⁹ This selection corresponds to C₁–C₂, O₁–O₂, C₁–O₁, C₂–O₂ σ bonding and σ* antibonding, C₂=O₃ π bonding and π* antibonding as well as the three oxygen lone pairs orbitals (see Fig. 6). This active space was employed for computing the final energies of the stationary points at MS-CASPT2 approach (MS-CASPT2(16in13)). However, the geometry optimizations applying this active space, would be time- and CPU-demanding and therefore unaffordable, with respect to size of the system. On the other hand, not all of the above orbitals are significantly important throughout the reaction mechanism. For instance, for the first step of the reaction, the six orbitals corresponding to C₁–O₂, C₂–O₂ σ bonding and σ* antibonding as well as the O3 lone pair are doubly occupied and still intact. Hence, for the geometry optimizations and the MEP calculations, it is safe to exclude these orbitals from the active space. The accuracy of this approach was consequently confirmed by performing two test calculations using CAS(10in8) and CAS(16in13) in both reactant and .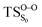

Fig. 6 Natural orbitals relevant in the decomposition of spiro-adamantyl-1,2-dioxetanone.

Four equally weighted roots were considered in the state average (SA)-CASSCF procedure for all the CASSCF computations. The final reported MEPs in the present study correspond to SA-CASSCF computations with the lowest-lying four singlet (S₀, S₁, S₂ and S₃) and four triplet (T₁, T₂, T₃, T₄) states.

Zero-point vibrational energy (ZPVE) and Gibbs free energy corrections were computed numerically at the SA(4)-CASSCF(10in8)/ANO-L-VDZP level of theory. Spin–orbit coupling (SOC) terms between singlet and triplet manifolds were calculated within the AMFI and CASSI frameworks^40,41 at the MS-CASPT2(16in13)/ANO-L-VTZP wave function over four singlet and four triplet states. A development version of the MOLCAS-8 quantum chemistry package suite was employed for all the calculations.⁴²

5 Conclusions

We have shown here that the experimentally determined activation parameters for the unimolecular and catalysed decomposition of spiro-adamantyl-1,2-dioxetanone indicate the occurrence of two different pathways for the formation of ground state and singlet exited state products. To better understand the differences between the pathways, theoretical calculations on the unimolecular decomposition using a multiconfigurational approach with dynamical correlation corrections have been performed. The corresponding results reveal a common transition state in the rate-limiting step for ground and excited state product formation. Notwithstanding, the transition state for the not-rate-limiting C–C bond cleavage step showed to possess different energies for ground and singlet excited state formation. Admittedly, the computed rate-limiting activation energy is overestimated compared to the experimental value. Although, the qualitative picture of the reaction mechanism is still in reasonable agreement with the experiment, if not in full agreement. This deviation can, however, be justified by the errors involved in the CASPT2 excitation energies using the IPEA correction, recently reported by Zobel et al.⁴³ In addition, to fully describe the process, the pivotal role of performing molecular dynamics calculations in solution is inevitable.

Consequently, the experimentally obtained data can be rationalized with the theoretical calculations, as these predict the temperature dependence of the quantum yields, with higher quantum yields expected for higher temperatures. This situation is equivalent to the observation of a higher activation enthalpy for the CL reaction, obtained from the temperature correlation of emission intensities.

Finally, the theoretical calculations indicate the occurrence of a biradical mechanism in the decomposition of 1,2-dioxetanone derivative 4 and explain the preferential formation of triplet excited carbonyl product.

Acknowledgements

PF and WJB are grateful to the Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) for the financial support under the 2015/02314-8 and 2014/22136-4 project numbers, respectively. IFG acknowledges financial support from the Swedish Research Council (Grant No. 2012-3910), the eSSENCE program and Uppsala University.

References

1. W. Adam and G. Cilento, Chemical and Biological Generation of Excited States, ed. W. Adam and G. Cilento, Academic Press, New York, 1982.
2. A. L. P. Nery and W. J. Baader, Quimiluminescência de Peróxidos Orgânicos: Geração de Estados Electronicamente Excitados na Decomposição de 1,2-dioxetanos, Quim. Nova, 2001, 24, 626–636.
3. W. J. Baader, C. V. Stevani and E. L. Bastos, Chemiluminescence of Organic Peroxides, in The Chemistry of Peroxides, ed. Z. Rappoport, Wiley & Sons, Chichester, 2006, vol. 2, pp. 1211–1278.
4. W. Adam, Thermal Generation of electronic Excitation with Hyperenergetic Molecules, Pure Appl. Chem., 1980, 52, 2591–2608.
5. G. B. Schuster and S. P. Schmidt, Chemiluminescence of Organic Compounds, Adv. Phys. Org. Chem., 1982, 18, 187–238.
6. F. H. Bartoloni, M. A. Oliveira, L. F. M. L. Ciscato, F. A. Augusto, E. L. Bastos and W. J. Baader, Chemiluminescence Efficiency of Catalyzed 1,2-Dioxetanone decomposition determined by steric effects, J. Org. Chem., 2015, 80, 3745–3751.
7. W. Adam and W. J. Baader, Effects of methylation on the thermal stability and chemiluminescence properties of 1,2-dioxetanes, J. Am. Chem. Soc., 1985, 107, 410–416.
8. (a) N. J. Turro and A. Davequet, Chemiexcitation Mechanisms – Role of Symmetry and Spin–Orbit Coupling in Diradicals, J. Am. Chem. Soc., 1975, 97, 3859–3862; (b) N. J. Turro and P. Lechtken, Thermal and Photochemical Generation of Electronically Excited Organic Molecules. Tetramethyl-1,2-Dioxetane and Naphthvalene, Pure Appl. Chem., 1973, 33, 363–367.
9. H. E. O'Neal and W. H. Richardson, Thermochemistry of 1,2-Dioxetane and its Methylated Derivatives. Estimation of Activation Parameters, J. Am. Chem. Soc., 1970, 92, 6553–6557.
10. W. H. Richardson and H. E. O'Neal, Thermochemistry adn Estimated Activation Parameters for the Thermal Decomposition of 1,2-Dioxetanedione, 4-tert-Butyo-1,2-Dioxetane-3-One and 4,4-Dimethyl-1,2-Dioxetane-3-One, J. Am. Chem. Soc., 1972, 94, 8665–8668.
11. S. De Feyter, E. W.-G. Diau, A. A. Scala and A. H. Zewail, Femtosecond dynamics of diradicals: transition states, entropic configurations and stereochemistry, Chem. Phys. Lett., 1999, 303, 249.
12. L. De Vico, Y.-J. Liu, J. W. Krogh and R. Lindh, Chemiluminescence of 1,2-Dioxetane. Reaction Mechanism Uncovered, J. Phys. Chem. A, 2007, 111(32), 8013–8019.
13. L. Pinto da Silva and J. C. G. Esteves da Silva, Mechanistic Study of the Unimolecular Decomposition of 1,2-Dioxetanedione, J. Phys. Org. Chem., 2013, 26, 659–663.
14. P. Farahani, D. Roca-Sanjuán, F. Zapata and R. Lindh, Revisiting the Nonadiabatic Process in 1,2-Dioxetane, J. Chem. Theory Comput., 2013, 9(12), 5404–5411.
15. F. Liu, Y.-J. Liu, L. De Vico and R. Lindh, Theoretical Study of the Chemiluminescent Decomposition of Dioxetanone, J. Am. Chem. Soc., 2009, 131(17), 6181–6188.
16. D. Roca-Sanjuán, D. A. Mazziotti, M. Lundberg and R. Lindh, Comment on Density Functional Theory Study of 1,2-Dioxetanone Decomposition in Condensed Phase, J. Comput. Chem., 2012, 33(26), 2124–2126.
17. H. C. Steinmetzer, A. Yekta and N. J. Turro, Chemiluminescence of tetramethyl-1,2-dioxetane. Measurement of activation parameters and rates of exceedingly slow reactions by a simple and nondestructive method. Demonstration of indistinguishable activation energies for generation of acetone singlets a, J. Am. Chem. Soc., 1974, 96, 282–284.
18. S. P. Schmidt and G. B. Schuster, Kinetics of unimolecular dioxetanone chemiluminescence. Competitive parallel reaction paths, J. Am. Chem. Soc., 1978, 100, 5559–5561.
19. N. J. Turro and M.-F. Chow, Chemiluminescence Thermolysis of alpha Peroxylactones, J. Am. Chem. Soc., 1980, 102, 5058–5064.
20. P. Farahani, M. Lundberg, R. Lindh and D. Roca-Sanjuán, Theoretical Study of the Dark Photochemistry of 1,3-Butadiene via the Chemiexcitation of Dewar Dioxetane, Phys. Chem. Chem. Phys., 2015, 17(28), 18653–18664.
21. L. Yue and Y.-J. Liu, Mechanism of AMPPD Chemiluminescence in a Different Voice, J. Chem. Theory Comput., 2013, 9, 2300–2312.
22. F. H. Bartoloni, M. A. Oliveira, F. A. Augusto, L. F. M. L. Ciscato, E. L. Bastos and W. J. Baader, Synthesis of Unstable Cyclic Peroxides for Chemiluminescence Studies, J. Braz. Chem. Soc., 2012, 23, 2093–2103.
23. C. V. Stevani, S. M. Silva and W. J. Baader, Studies on the Mechanism of the Excitation Step in Peroxyoxalate Chemiluminescence, Eur. J. Org. Chem., 2000, 2000, 4037–4046.
24. L. F. M. L. Ciscato, F. H. Bartoloni, E. L. Bastos and W. J. Baader, Direct Kinetic Observation of the Chemiexcitation Step in Peroxyoxalate Chemiluminescence, J. Org. Chem., 2009, 74, 8974–8979.
25. E. L. Bastos and W. J. Baader, Theoretical Studies on Thermal Stability of Alkyl-Substituted 1,2-Dioxetanes, ARKIVOC, 2007, 257–272.
26. W. Adam and W. J. Baader, 1,2-Dioxetane: Synthesis, Characterization, Stability and Chemiluminescence, Angew. Chem., Int. Ed. Engl., 1984, 23, 166–167.
27. A. K. Campbell, Chemiluminescence: Principles Applications in Biology and Medicine, Ellis Howard Ltd, Chichester, 1988.
28. W. Adam and O. Cueto, Cyclic Peroxide.81. Fluorescer-Enhanced Chemiluminescence of alpha. Peroxylactones via Electron Exchange, J. Am. Chem. Soc., 1979, 101, 6511–6515.
29. W. Adam and H. C. Steinmetzer, (1-Adamantyl)-a-Peroxylactone: Synthesis, Kinetics and Luminescence, Angew. Chem., Int. Ed., 1972, 11, 540–542.
30. L. Pinto da Silva, C. M. Magalhães and J. C. G. Esteves da Silva, Interstate Crossing-Induced Chemiexcitation Mechanism as the Basis for Imidazopyrazinone Bioluminescence, ChemistrySelect, 2016, 1, 3343–3356.
31. B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, A Complete Active Space SCF Method (CASSCF) Using a Density Matrix Formulated Super-CI Approach, Chem. Phys., 1980, 48, 157–173.
32. B. O. Roos, Ab Initio Methods in Quantum Chemistry Part 2, inAdvances in Chemical Physics, John Wiley and Sons, New York, 1987, pp. 399–446.
33. B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, Main Group Atoms and Dimers Studied with a New Relativistic ANO Basis Set, J. Phys. Chem. A, 2004, 108, 2851–2858.
34. D. Roca-Sanjuán, F. Aquilante and R. Lindh, Multiconfigurational Second-Order Perturbation Theory Approach to Strong Electron Correlation in Chemistry and Photochemistry, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(4), 585–603.
35. M. Stenrup, R. Lindh and I. F. Galván, Constrained Numerical Gradients and CompositeGradients: Practical Tools for Geometry Optimization andPotential Energy Surface Navigation, J. Comput. Chem., 2015, 36, 1698–1708.
36. J. Finley, P.-Å. Malmqvist, B. O. Roos and L. Serrano-Andrés, The Multi-state CASPT2 Method, Chem. Phys. Lett., 1998, 288, 299–306.
37. G. Ghigo, B. O. Roos and P.-Å. Malmqvist, A Modified Definition of the Zeroth-order Hamiltonian in Multiconfigurational Perturbation Theory (CASPT2), Chem. Phys. Lett., 2004, 396, 142–149.
38. N. Forsberg and P.-Å. Malmqvist, Multiconfigurational Perturbation Theory with Imaginary Level Shift, Chem. Phys. Lett., 1997, 274, 196–204.
39. L. Greenman and D. A. Mazziotti, Strong Electron Correlation in the Decomposition Reaction of Dioxetanone with Implications for Firefly Bioluminescence, J. Chem. Phys., 2010, 133, 164110.
40. Ò. Rubio-Pons, L. Serrano-Andrés and M. Merchan, A Theoretical Insight into the Photophysics of Acridine, J. Phys. Chem. A, 2001, 105, 9664–9673.
41. S. J. Strickler and R. Berg, A Relationship between Absorption Intensity and Fluorescence Lifetime of Molecules, J. Chem. Phys., 1962, 37, 814.
42. F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. Delcey, L. De Vico, I. F. Galván, N. Ferré, L. M. Frutos, M. Gagliardi, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P.-Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryasov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, Molcas 8: New Capabilities for Multiconfigurational Quantum Chemical Calculations Across the Periodic Table, J. Comput. Chem., 2016, 37, 506–541.
43. J. P. Zobel, J. J. Nogueira and L. González, The IPEA Dilemma in CASPT2, Chem. Sci., 2017, 8, 1482–1499.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates for the involved structures and their corresponding relative electronic energies, as well as, dissociation along the lowest-lying triplet manifold. See DOI: 10.1039/c6ra26575h

---