A probe of steric ligand substituent effects on the spin crossover of Fe(II) complexes

Abstract

Identifying and quantifying the individual factors affecting the temperature and properties of the spin crossover in transition metal complexes is a challenging task, because many variables are involved. While the most decisive factor is the crystal field imparted by ligands around the active metal center, some less common actors are intramolecular steric repulsions or non-covalent interactions. A series of three Fe(II) complexes of 1,3bpp derivatives of (2-(pyrazol-1-yl)-6-(1H-pyrazol-3-yl)pyridine) have been prepared and characterized crystallographically to probe these effects: [Fe(1,3bpp)₂](ClO₄)₂ (1), [Fe(met1,3bpp)₂](ClO₄)₂ (2) and [Fe(dimet1,3bpp)₂](ClO₄)₂ (3). The ligands exhibit none, one or two methyl substituents on the pyrazol-1-yl heterocycle. These groups exert a dramatic effect on the SCO temperature in the solid state, and, most significantly, in solution (with T_SCO (3) > T_SCO (1) > T_SCO (2)). Extensive DFT calculations have unveiled the origin of these effects which lie in the intramolecular non-covalent or steric interactions rather than resulting from crystal field effects.

---

Introduction

Octahedral transition metal complexes in the configurations d⁴ to d⁷ may be in two different spin states, depending on the energy of the t_2gvs. e_g orbital splitting in relation to the energy necessary for pairing two electrons within one d orbital. If both energies are comparable, the system is likely to exhibit spin crossover (SCO) phenomena following small external perturbations.^1–3 The ensuing spin transitions cause important changes not only to the magnetic properties, but also to the structure and to a number of physical properties.^4,5 For this reason, this phenomenon is considered as a promising entry into molecule-based switching materials for potential applications in nanotechnology.^6,7 Among the suitable metals, Fe(II) is especially interesting because the transition toggles the complex between a diamagnetic (S = 0) and a paramagnetic (S = 2) state, causes dramatic colour changes and leads to Fe-to-ligand bond distance variations of 10% or larger.^8,9 For a given metal ion, the temperature and dynamics of the SCO are affected by many factors, most often superimposed, dependent on the ligands,¹⁰ the crystal system,¹¹ intermolecular interactions^5,12,13 or secondary bonding interactions.^14–16 Many synthetic chemists are dedicating efforts to designing and creating complexes with the challenging goal of unveiling the specific influence of each factor, if possible with independence of any other effect. The many ways in which the specific nature of the ligands affects the thermodynamics of the SCO have been recently reviewed.¹⁰ This is best investigated, whenever possible, in solution rather than in the solid state, since the latter situation involves often the existence of solvatomorphs^17–26 and sometimes polymorphs,¹¹ usually affecting dramatically the SCO properties. Ligand field effects, as conveyed through the incorporation of ligand substituents, have been analysed extensively, leading to results that sometimes may appear conflicting.^27–30 Some of the earlier reports already point out to the difference between σ-donating and π-accepting properties of the ligands to explain the complexity of the substituent effects on the SCO properties.^30,31 Very recently, the study in solution of an extensive family of 1bpp/Fe(II) complexes (1bpp = 2,6-bis-(pyrazol-1-yl)-pyridine) featuring a variety of substituents on the central pyridine or on the pyrazole rings demonstrated the coexistence and the opposing effect of both, σ and π bonding properties, as well as their differing relative importance depending on the position of the substituent.³² Another way for substituents to influence the SCO temperature is through variations in intramolecular attractive or repulsive interactions resulting from the structural changes accompanying the spin transition. In the mentioned study, this is not the case since the substituents investigated are located at distal positions, thus not taking part in such interactions. Nonetheless, several ligand families have been shown experimentally to stabilize or even trap the high spin (HS) state of Fe(II) complexes by introducing a steric constraint to the shrinking bound to occur upon SCO to the low spin (LS) state.^33–37 This effect has also been rationalized through DFT calculations.^37,38 In much rarer cases, intramolecular interactions block or impede the transition to the HS state. This occurs in an Fe(II) scorpionate complex exhibiting a bulky group that exerts steric intra-ligand repulsion with the lengthening of the Fe–N bond distances accompanying the SCO.³⁹ It has also been suggested to happen with the cation [Fe(Me₄-1bpp)₂]²⁺ (Me₄-1bpp = 2,6-bis-(3,5-dimethylpyrazol-1-yl)-pyridine), as a result of the interaction of the methyl groups in position 5 of pyrazolyl with the central pyridine in the 1bpp core.¹⁰ The same effect was invoked to explain the decrease in the SCO temperature in an Fe(II) complex of an indazoylpyridine derivate.⁴⁰ We have now designed a ligand system to probe these two not ligand field related opposite effects within an analogous series of Fe(II) complexes. Thus, three ligands have been prepared (Scheme 1); 2-(pyrazol-1-yl)-6-(1H-pyrazol-3-yl)pyridine (1,3bpp),⁴¹ 2-(3-methylpyrazol-1-yl)-6-(1H-pyrazol-3-yl)pyridine (met1,3bpp) and 2-(3,5-dimethylpyrazol-1-yl)-6-(1H-pyrazol-3-yl)pyridine (dimet1,3bpp), showing zero, one and two methyl substituents on the pyrazol-1-yl rings. The corresponding homoleptic Fe(II) complexes [Fe(1,3bpp)₂](ClO₄)₂ (previously published,⁴¹1), [Fe(met1,3bpp)₂](ClO₄)₂ (2) and [Fe(dimet1,3bpp)₂](ClO₄)₂ (3) were prepared and their magnetic properties determined in the solid state and in solution. The results show that the methyl in position 3 favours the HS state compared to the unsubstituted system, and that the same substituent on position 5 favours the LS state, with a stronger incidence. These results have been fully rationalized and quantified with the help of DFT calculations in terms of inter- and intra-ligand interaction effects. The computational method has been used to investigate the potential analogue with only one methyl on position 5 (“4”), not accessible experimentally with our synthetic procedure. This has allowed confirming the observed trends and their interpretation.

Scheme 1 Molecular structure of ligands 1,3bpp, met1,3bpp and dimet1,3bpp.

Results and discussion

Synthesis

The ligands met1,3bpp and dimet1,3bpp were prepared in three steps using a procedure analogous to the synthesis of 1,3bpp.⁴¹ Thus, the appropriate substituted pyrazole ring was first coupled through one N atom to 2-acetyl-6-bromopyridine. The pyrazole with only one substituent couples through the less crowded nitrogen atom, leading ultimately to the ligand met1,3bpp with the substituent on position 3. This in fact prevents using this procedure to prepare met1,3bpp with the methyl on position 5. The product is then functionalized at the carbonyl end with N,N-dimethylformamide-dimethyl acetal into the corresponding 3-(dimethylamino)prop-2-en-1-one moiety which is readily converted by ring closure with hydrazine into the pyrazole-3-yl substituent of the central pyridine group, common to all the 1,3bpp ligands. The complex [Fe(1,3bpp)₂](ClO₄)₂ (1) was prepared as published by our group.⁴¹ It could be obtained following two distinct procedures as two different polymorphs, 1a and 1b (see below). Complexes [Fe(met1,3bpp)₂](ClO₄)₂ (2) and [Fe(dimet1,3bpp)₂](ClO₄)₂ (3) were obtained by direct reaction of the hydrated Fe(ClO₄)₂ salt with the met1,3bpp and dimet1,3bpp ligands, respectively, in the presence of a catalytic amount of ascorbic acid to prevent the oxidation of Fe(II) to Fe(III). Compound 2 was obtained from a reaction in absolute ethanol that produced a yellow solution, using hexane as the crystallization medium. The pair of solvents used to obtain 3 as red crystals are acetone and diethyl ether. The reaction with met1,3bpp using acetone/toluene produces a solvatomorph, [Fe(met1,3bpp)₂](ClO₄)₂·H₂O (2b), incorporating one molecule of water per complex unit (ESI†).

Description of the structures

The structure of complex 1 has been already described in a previous publication.⁴¹ This compound can be obtained following two different procedures as two polymorphs, 1a and 1b, showing two different organizations of the Fe(II) complex cations closely related to these observed for compounds 2 and 3, respectively (see below). The structure of the solvatomorph 2b is briefly described in the ESI (Table S1 and Fig. S1 and S2†).

[Fe(met1,3bpp)₂](ClO₄)₂ (2). The structure of 2 was determined at 100 K, on crystals that had turned red from their original yellow color at room temperature. Their solvent free lattice is found in the monoclinic space group C2/c. The asymmetric unit consists of one formula unit, with eight such moieties present in the unit cell. The complex cation features a distorted octahedral Fe(II) center coordinated to two met1,3bpp tris-imine ligands lying approximately perpendicular to each other (Fig. 1). As a result of the asymmetric character of the ligands, this complex is chiral, both enantiomers being present in the lattice, which is racemic. The average of the Fe–N bond distances is 1.96(4) Å, corroborating the LS state of the compound at this temperature. The spin state is also evident from the distortion parameters Σ and Θ,^42–44 which here amount to 93.2° and 367.8°, respectively, within the region expected for LS compounds.⁹

Fig. 1 Molecular representation of [Fe(met1,3bpp)₂](ClO₄)₂ (2) at 100 K with heteroatoms labelled. Only H atoms of N–H groups shown (in yellow). Dashed lines are H-bonds.

As expected in solvent free structures of Fe/bpp complexes with at least one pyrazol-3-yl ring per ligand, the ClO₄^– anions establish hydrogen bonding interactions with their N–H groups (Fig. 1). The complexes organize in the lattice as one of the polymorphs previously reported of compound 1 (1a).⁴¹ Thus, they are disposed as sheets containing arrays of [Fe(met1,3bpp)₂]²⁺ cations. Within the sheets, each complex interacts with two neighbours via two π⋯π and six C–H⋯π interactions. In between the sheets, each cation establishes a total of six weaker C–H⋯π contacts with two nearby congeners (Fig. 2). The parallel arrays within these layers alternate complexes of opposed coordination chirality and also two different orientations. The angle between complexes in these two orientations (measured using idealized planes of two equivalent ligands) is 41.40°. There are two types of (very similar) interlayer separations (Fig. S3†), 9.640 Å and 9.887 Å.

Fig. 2 Sheet organization of the cations in 2, emphasizing their two different orientations and the π⋯π and C–H⋯π interactions formed by each complex with its immediate neighbours within the sheet.

The structure of 2 was also determined at 300 K, on crystals that had turned pale yellow, as a result of a LS to HS conversion. Following the SCO and the thermal expansion, the unit cell experiences an isotropic growth (Table S2†), with a volume expansion of 5%, translating into an increase of the separation between layers of complex cations to 9.767 and 9.894 Å, respectively. Furthermore, the average Fe–N at this temperature is 2.16(2) Å, while the distortion parameters are Σ = 147.5° and Θ = 378.2°, respectively, confirming that at 300 K, the compound is in its HS configuration.

[Fe(dimet1,3bpp)₂](ClO₄)₂ (3). The molecular structure of 3 was determined at 100 and 298 K. At both temperatures, the lattice exhibits the monoclinic P2₁/n space group, the asymmetric unit coinciding with the empirical formula and the unit cell enclosing four such moieties. The complex cation [Fe(dimet1,3bpp)₂]²⁺ is analogous to that of 2, now with the ligand dimet1,3bpp (Fig. 3). The average of the Fe–N distances (1.95(4) Å at both temperatures) and the Σ/Θ distortion parameters (88.7/367.2° and 90.0/367.1° respectively) show that the Fe(II) centres are in the LS state at 100 and 296 K. Attempts to obtain the structure of 3 in the HS (>400 K, see below) were unsuccessful because of crystal damage. In the LS, the lattice is related to the layered organization of 2. One main difference is that within layers of complex cations, the chirality and orientations of the complexes are identical, whereas the handedness of the cations alternate in moving through adjacent layers. Within each sheet, each complex has four first neighbours, establishing four π⋯π and eight C–H⋯π interactions (Fig. 4). Interestingly, this particular arrangement is the same as that of the other polymorph of compound 1 (1b) also previously characterized.⁴¹

Fig. 3 Molecular representation of [Fe(dimet1,3bpp)₂](ClO₄)₂ (3) at 100 K with heteroatoms labelled. Only H atoms of N–H groups shown (in yellow). Dashed lines are H-bonds.

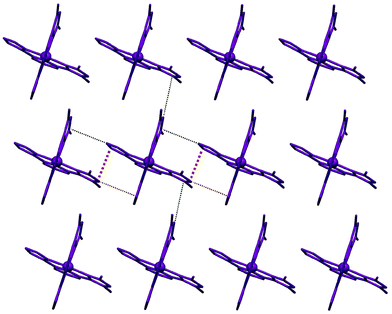Fig. 4 Sheet organization of the cations in 3, showing their sole orientation and the π⋯π and C–H⋯π interactions formed by each complex with its immediate neighbours within the sheet.

The layers feature separations (Fig. S4†) of 9.420/9.499 and 9.636/9.598 Å at both temperatures, respectively. In going from 100 K to 296 K, the cell dimensions experience an isotropic expansion purely of thermal origin, with a volume increase of 4%.

The homogeneity of the phases described above was established by means of powder X-ray diffraction (PXRD) methods. The purity and homogeneity of compound 1, in its two polymorphic forms, respectively, had been established previously using this method.⁴¹ For the cases of 2 and 3, PXRD experiments were also conducted. The results prove that in both cases the bulk material corresponds to the compound unveiled by single crystal X-ray diffraction (Fig. S5†).

Solid state magnetic and thermal properties

The influence of the methyl substituents on the SCO of the 1,3bpp/Fe(II) complexes was first assessed through bulk magnetic susceptibility measurements. Data from polycrystalline samples of 2 and 3 were collected between 5 and 400 K in the warming and cooling modes under a constant magnetic field (see the ESI†) and were compared to these from polymorphs 1a and 1b. All the results are displayed in Fig. 5 in the form of χ_MT vs. T plots (χ_M is the molar paramagnetic susceptibility). At low temperature, all complexes are essentially diamagnetic, with χ_MT values at 100 K ranging 0.06 to 0.17 cm³ K mol⁻¹. In all cases, an abrupt increase of χ_MT occurs upon warming up to nearly constant values of 3.01 (2), 3.26 (1a) and 3.4 cm³ Kmol⁻¹ (1b), while for 3 the product (2.64 cm³ K mol⁻¹) was still increasing at 400 K, the maximum temperature reached by the magnetometer. The high temperature values show that the Fe(II) centers reach the HS (S = 2), consistent with the data from SCXRD, and with the occurrence of SCO. The SCO profiles in the cooling mode are quasi-superimposable to these in the warming mode, indicative of the absence of hysteresis, even though the transitions of 2 and 1b are clearly more abrupt than those of 1a and 3 (see below). The various systems, in addition, exhibit dramatically different transition temperatures, with T_1/2 values of 183 (2), 278 (1a), 314 (1b) and 378 K (3). These observations are fully consistent with the temperature-dependence of the molar heat capacity. Indeed, anomalies are observed at temperatures coinciding with those of the SCO processes, which are very sharp, sharp and relatively broad, respectively, for 2, 1b and 1a/3 (Fig. 5, Fig. S6† and Table 1). The excess enthalpy and entropy associated with SCO, ΔH_SCO and ΔS_SCO (as derived from the excess heat capacity ΔC_p; Table 1 and the ESI†) give a qualitative measure of the cooperativeness of a SCO process. Here, the excess entropies turn out to be much larger than the electronic component R ln 5, which is indicative of significant coupling of the SCO with lattice phonons. These thermodynamic parameters are however affected by the temperature of the SCO processes, which varies dramatically in the present compounds. Therefore, a more quantitative measure of the cooperativity has been obtained by fitting the experimental ΔC_pvs. T data to the so-called domain model (see the ESI† for details).^45,46 The derived number of interacting molecules per domain, n, is similar for 1a and 3, and is 8.5 and 9.0, respectively, while for 1b it is about double, characteristic of the medium to high cooperative character of the SCO (values of n close to unity are expected for gradual SCO while values above 20 are found for strongly cooperative systems).^46–48 On the contrary, the very large n obtained for 2 (n = 128.7) ranges among the largest reported,⁴⁶ thus depicting a highly cooperative system. This is likely due to a strong coupling between the SCO and the induced structural modifications, in agreement with a sharp variation of cell parameters at the SCO. In fact, the anomaly in the C_pvs. T curve exhibits clearly two components (Fig. S7†), an extremely sharp peak on top of a broader feature, most likely reflecting both processes.

Fig. 5 Thermal SCO properties of compounds 1a, 1b, 2 and 3: χ_MT vs. T plots (top) and molar heat capacity at constant pressure as derived from DSC measurements (bottom). All data shown correspond to the warming mode.

Table 1 Thermodynamic parameters of compounds 1a, 1b, 2 and 3

	1a	1b	2	3
a Solid-state, from fit of ΔCpvs. T to the domain model (see the ESI). b Solid-state, from χMT vs. T. c Solution, from NMR (in solution, 1a and 1b become, to a very good approximation, the same system).
ΔHSCO (kJ mol^−1)	13.57	17.74	5.87	14.11
ΔSSCO (J mol^−1 K^−1)	48.7	56.8	31.7	38.0
n	8.5(1)	20.0(2)	128.7(3)	9.0(1)
T SCO (K)^a	278.8(3)	313.4(3)	182.1(1)	375.0(3)
T 1/2 (K)^b	278	314	184	378
T 1/2 (K)^c	262	262	232	281

---

While the substituents on the 1,3bpp ligand-core certainly have an impact on T_1/2, the marked disparity between polymorphs 1a and 1b (of about 40 K) demonstrates that the crystal packing alone is very influential. Thus, while solid-state measurements are essential to investigate the latter effects, especially on the cooperativity, this technique is not appropriate to quantify with independence the influence of the nature and location of the methyl substituents on the SCO temperature.

¹H-NMR spectroscopy

To identify the influence of the ligand on the temperature of the spin transition, excluding solid state effects, the best choice is the use of a solution methodology, such as NMR. The variable temperature paramagnetic susceptibility of a soluble substance may be calculated by this technique, using the Evans method.^49–51 The latter is based on the relationship between χ_M of a paramagnetic substance and the effect that it causes to the chemical shift of any species in solution. This effect is called the paramagnetic shift and it may be measured directly using a diamagnetic reference (such as TMS) by collecting the NMR spectrum with a coaxial tube made of two separate compartments that contain both, the solvent and the reference. One of the compartments must also contain the magnetic species in solution. The paramagnetic shift can thus be obtained directly from the composite spectrum, extracting the difference between the signals of the reference in both compartments. The room temperature ¹H NMR spectra of complexes 1, 2 and 3 (Fig. S8†) in CD₃OD show sets of paramagnetically shifted and broadened peaks lacking hyperfine splitting, consistent with the symmetry, number of protons and integration expected in each case (considering that the signals from the N–H groups are broadened beyond detection because of their proximity to Fe(II) and their ability to exchange). In these spectra, the remainder of the peaks is due to TMS, residual MeOH, H₂O and other solvents, in addition to the free ligand. In view of their stability in solution, the spectra of the three compounds at various temperatures were recorded between 193 and 300 K. The variations of the TMS paramagnetic shift (Table S6†) provide the temperature dependence of χ_M in solution for 1, 2 and 3. The corresponding plot of χ_MT vs. T (Fig. 6) reveals that the three complexes exhibit gradual SCO processes, with approximately T_1/2 values of (in K) of 232 (2), 262 (1) and 281 (3). These values are correlated with the temperatures obtained from bulk measurements, while the differences are ascribed to the contribution from solid-state effects. These can be very important, as illustrated by the almost 100 K difference in the SCO temperature shown by 3.

Fig. 6 χ _M T vs. T plots as derived from solution ¹H NMR spectra in d₄-MeOH of 1, 2 and 3 by employing the Evans method (see the text for details). Calculations have been performed from the temperature where the paramagnetic shift was large enough to be measured.

From the solution experiments, it is deduced that a methyl group at position 3 of the pyrazolyl ring stabilizes the HS state with respect to the LS state (thus reducing the SCO temperature). The presence of methyl groups on positions 3 and 5 leads to the opposite result, an increase of the SCO temperature. Therefore, a substituent on position 5 not only opposes the influence of the 3-methyl group but also has a dominant impact. This could be corroborated if the compound with only one methyl group on position 5 was accessible experimentally; however, it is not the case (see above). In any case, the above data demonstrate that the choice of the specific 1,3bpp derivate opens a means of tuning the SCO temperature. In order to rationalize the causes of the observed effects, in addition to investigating what would be the net impact of a hypothetical 5-methyl derivate, DFT calculations were performed.

DFT calculations

The relative stability of the HS and LS state formed in the gas phase was calculated by means of DFT+U+D2 for complexes 2 (3-methyl derivate), 3 (3,5-dimethyl derivate) and for a hypothetical 5-methyl derivate (“4”). The results were compared with those previously published for the bare complex cation of 1.³⁷ The energies of the optimized structures furnished the electronic contributions to the enthalpy difference existing between both states (ΔH_elec). The computed values (Table 2) are fully consistent with the experimental results. Thus, compared with ΔH_elec for complex 1, with a bare 1,3bpp ligand (of 11.9 kJ mol⁻¹), the effect of adding methyl groups depends drastically on the position of this substituent. When it is located at position 3 (complex 2), ΔH_elec diminishes by ca. 2.0 kJ mol⁻¹ (ΔH_elec = 9.9 kJ mol⁻¹) whereas adding it at position 5 (“4”) increases its value notably by 7.7 kJ mol⁻¹, up to ΔH_elec = 19.6 kJ mol⁻¹. The addition of two methyl substituents, one at each position, results in a value of ΔH_elec = 16.4 kJ mol⁻¹. This value is 4.5 kJ mol⁻¹ larger than that of 1, which is close to the combination of both individual effects, calculated separately for 2 and “4” (7.7–2.0 = 5.7 kJ mol⁻¹). It is clear that the opposite effects exerted by methyl groups at positions 3 and 5, respectively, partially cancel each other when both are present.

Table 2 Average energy of the two sets of 3d-orbitals for compounds 1–3 and “4”, energy difference between them (ΔE, in eV), and electronic enthalpy (ΔH, in kJ mol⁻¹)

	1	2	3	“4”
t2g	−1.48	−1.45	−1.41	−1.48
eg	2.26	2.28	2.31	2.28
ΔE	−3.74	−3.73	−3.72	−3.76
ΔH	11.9	9.9	16.4	19.6

---

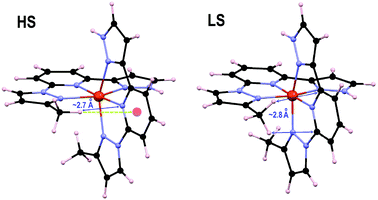
The origin of these ΔH_elec values was investigated by analyzing first the effect of the substituents on the t_2g and e_g orbitals of the Fe ion (Table 2) as was done recently on a family of 1bpp/Fe(II) complexes.³² Here, the addition of one (2 and “4”) or two (3) methyl substituents seems to destabilize the e_g orbitals (Table 2). However, a clear pattern is not observed for the t_2g set. In any case, the orbital energy splitting does not show any correlation with ΔH_elec; therefore, the effect of the methyl groups ascribed to the ligand field is at best, very minor. Indeed, the previously reported differences in ΔH_elec when changing two H atoms by two 4-methyl groups on 1bpp-pyrazoles (i.e., only causing ligand field effects) are less than one order of magnitude smaller than the values in Table 2.³² This indicates that the differences seen here must be associated, to a large extent, to inter- and/or intra-ligand interactions within the complex involving the methyl groups, linked to the changes in Fe–N distances occurring upon SCO. These effects contribute to ΔH_elec in two ways: (i) by causing a strain to the overall structure of the [Fe(1,3-bpp)₂]²⁺ core, and (ii) through direct inter- and intra-ligand interactions. In order to analyze the influence of the 3-methyl group, single-point calculations were performed on the optimized structures of 2^LS and 2^HS, after substituting the methyl group by an H atom, keeping the rest of the geometry untouched. These species, termed here 2^core, are equivalent to 1, but have different HS and LS nuclear configurations. The computed ΔH_elec for 2^core (12.9 kJ mol⁻¹) is ca. 1 kJ mol⁻¹ larger than for 1; therefore, the strain of the backbone caused by the substituent destabilizes the HS more than the LS state (thus, it opposes the observed overall effect for this substituent). Indeed, comparing the optimized geometries of 2 and 1 (Fig. S9 and S10†) reveals that the HS structures are much more distant from each other than the LS geometries. Specifically, in the HS, the plane of the 1,3bpp core exhibits a rotation of ∼10° around its N_pz–Fe–N_pz axis when moving from 1 to 2. This difference may be due to the steric effect of the 3-methyl, pushing the other ligand back, perhaps also favoring an attractive C–H⋯π interaction between the methyl group and the central pyridine of that ligand (see also Fig. 7). In fact, the optimized structure of 2 also shows a shorter Fe–N bond for the 1-pyrazole than for the 3-pyrazole ring, which could be due to such favorable contact. The difference between 2 and 2^core in terms of ΔH_elec must be then traced back to the direct interaction between the methyl group and the other ligand. Inspection of the optimized structures 2^HS and 2^LS shows that the former exhibits the closest contact between the 3-methyl group and the other 1,3bpp ligand of ca. 2.7 Å, with this substituent well positioned for the mentioned C–H⋯π contact. The contraction of the Fe(II) coordination sphere caused by the SCO to the LS state forces the methyl group to rotate and exhibit two closest C–H⋯π contacts with the other ligand (now of ca. 2.8 Å each), instead of one. The attractive interaction may not be now so favorable or have turned repulsive (the Fe–N bond distance is now shorter for the 3-pyrazole than for the 1-pyrazole ring). This would explain an overall stabilization of the HS state. The ca. 3 kJ mol⁻¹ difference in ΔH_elec between 2^core and 2 (12.9 vs. 9.9 kJ mol⁻¹) is in any case the consequence of going from an attractive inter-ligand interaction to a less favorable one.

Fig. 7 DFT+U+D2 optimized geometries of complex 2 in both spin states. The HS state structure (left) emphasizes the closest contact between the 3-methyl and the other ligand, as well as the possible C–H⋯π with that ligand. The LS state structure highlights the two closest inter-ligand interactions.

The individual effect of the methyl group at position 5 is studied by analyzing the hypothetical compound “4”. In analogy with the above procedure, we have used the methyl-free “4^core” complex to quantify (i) the strain of the [Fe(1,3-bpp)₂]²⁺ core and (ii) the direct intramolecular interactions. First, the comparison between “4^core” and 1 shows that the HS state is 4.7 kJ mol⁻¹ less stable in the former case (with ΔH_elec of 16.6 kJ mol⁻¹ in “4^core” compared to 11.9 kJ mol⁻¹ in 1). This must be traced back to the presence of the 5-methyl group causing the strain of the [Fe(1,3-bpp)₂]²⁺ core to accommodate part of the steric congestion between the 5-methyl and the central pyridine. Second, the difference between “4” (19.6 kJ mol⁻¹) and “4^core” quantifies the direct impact of the intraligand interactions associated with the 5-methyl (Fig. 8), which account for an effect of 3 kJ mol⁻¹ on ΔH_elec, thus completing the difference in ΔH_elec of 7.7 kJ mol⁻¹ between “4” and 1. Therefore, the stabilization of the LS state as a result of an intra-ligand repulsion is here shown and proved theoretically for the first time. This effect was invoked to explain the increase in the SCO temperature of the Fe(II) complex of an indazoylpyridine derivate,⁴⁰ but a subsequent computational analysis suggested that the HS vs. LS state stability was instead influenced by inter-ligand interactions altering the FeN₆ coordination sphere, and not by such steric hindrance.³⁷

Fig. 8 DFT+U+D2 optimized geometries of complex “4” in both spin states showing the closest contact between the 5-methyl and the central pyridine of the same ligand.

Experimental

Synthesis

The ligand 2-(pyrazol-1-yl)-6-(1H-pyrazol-3-yl)pyridine (1,3bpp) was synthesized as published,⁴¹ using a slight modification of a previously reported procedure.⁵² The corresponding complex [Fe(1,3bpp)₂](ClO₄)₂ (1) was prepared as previously published.⁴¹Caution: Perchlorate salts of metal complexes are potentially explosive. Only small quantities of material should be prepared and the samples should be handled with care.

1-(6-(3-Methylpyrazol-1-yl)pyridin-2-yl)ethanone. To a solution of 1-(6-bromopyridin-2-yl)ethanone (2.5 g, 12.5 mmol) in toluene (15 mL) were added, under a N₂ atmosphere, 3-methylpyrazole (1.53 g, 18.75 mmol), 1,10-phenanthroline monohydrate (0.5 g, 2.5 mmol), CuI (0.24 g, 1.25 mmol) and K₂CO₃ (1.9 g, 12.5 mmol). The resulting black mixture was heated to reflux and vigorously stirred overnight. After cooling to room temperature, ethyl acetate (20 mL) and water (20 mL) were added and the organic layer was isolated. The aqueous solution was extracted two additional times with ethyl acetate and the organic phases were recombined, washed with brine, dried with MgSO₄ and evaporated under vacuum to afford the product as a brown liquid (2.4 g, 96%). ¹H NMR (400 MHz, CDCl₃, ppm): δ 2.37 (s, 3H), 2.72 (s, 3H), 6.22 (d, J = 2.5 Hz, 1H), 7.91–7.77 (m, 2H), 8.05–8.02 (m, 1H), 8.45–8.42 (m, 1H).

1-(6-(3-Methylpyrazol-1-yl)-pyridin-2-yl)-3-(dimethylamino)-prop-2-en-1-one. N,N-Dimethylformamide-dimethyl acetal (2.5 mL, 24 mmol) was added to 1-(6-(3-methylpyrazol-1-yl)pyridin-2-yl)ethanone (2.4 g, 11.9 mmol) and the mixture was heated to reflux (120 °C) and stirred overnight. After cooling to room temperature, the resulting dark yellow solution was concentrated under vacuum to obtain the product as a brown powder (2.77 g, 91%). ¹H NMR (400 MHz, CDCl₃, ppm): δ 2.32 (s, 3H), 2.93 (s, 3H), 3.13 (s, 3H), 6.24–6.11 (m, 1H), 6.46–6.34 (m, 1H), 7.97–7.77 (m, 4H), 6.42 (m, 1H),8.46 (d, J = 2.0 Hz, 1H).

2-(3-Methylpyrazol-1-yl)-6-(1H-pyrazol-3-yl)pyridine (met1,3bpp). A large excess of hydrazine monohydrate (2.5 mL, 50 mmol) was added to a methanolic solution (25 mL) of 1-(6-(3-methylpyrazol-1-yl)-pyridin-2-yl)-3-(dimethylamino)prop-2-en-1-one (2.77 g, 10.8 mmol) and the mixture stirred and refluxed overnight. Subsequently, the resulting solution was cooled to room temperature, producing a pale yellow precipitate that was filtered, washed with water and diethyl ether and dried in air to afford the product as a white powder (1.5 g, 62%). ¹H NMR (400 MHz, CDCl₃, ppm): δ 2.33 (s, 1H), 6.22 (d, J = 2.5 Hz, 1H), 6.78 (s, 1H), 7.51 (s, 1H), 7.60 (d, J = 1.9 Hz, 1H), 7.83–7.72 (m, 1H), 8.45 (d, J = 2.4 Hz, 1H), 11.11–10.20 (m, 1H).

1-(6-(3,5-Dimethylpyrazol-1-yl)pyridin-2-yl)ethanone. To a solution of 1-(6-bromopyridin-2-yl)ethanone (2.25 g, 11.3 mmol) in toluene (5 mL) were added, under a N₂ atmosphere, 3,5-dimethylpyrazole (0.9 g, 9.36 mmol), 1,10-phenanthroline monohydrate (0.37 g, 1.9 mmol), CuI (0.1 g, 0.5 mmol) and K₂CO₃ (3.2 g, 23.15 mmol). The resulting dark brown mixture was heated to reflux and vigorously stirred overnight. After cooling to room temperature, ethyl acetate (20 mL) and water (20 mL) were added and the organic layer isolated. The aqueous solution was extracted two additional times with ethyl acetate and the organic phases were recombined, washed with brine, dried with MgSO₄ and evaporated under vacuum. Column chromatography (7 : 3 hexanes/ethyl acetate) provided 0.66 g (32% yield) of the title compound as a white solid. ¹H NMR (400 MHz, CDCl₃, ppm): δ 2.31 (s, 3H), 2.70 (s, 3H), 2.76 (s, 3H), 6.04 (s, 1H), 7.97–7.8 (m, 2H), 8.00–7.87 (m, 2H), 8.13 (dd, J = 7.8, 1.4 Hz, 1H).

1-(6-(3,5-Dimethylpyrazol-1-yl)-pyridin-2-yl)-3-(dimethylamino)prop-2-en-1-one. N,N-Dimethylformamide-dimethyl acetal (0.3 mL, 2.23 mmol) was added to 1-(6-(3,5-dimethylpyrazol-1-yl)-(1H-pyrazol-1-yl)pyridin-2-yl)ethanone (0.66 g, 3.1 mmol) and the mixture was heated to reflux (110 °C) and stirred overnight. After cooling to room temperature, the resulting dark yellow solution was concentrated under vacuum to yield the product as a pale brown solid (0.83 g, 87%). ¹H NMR (400 MHz, CDCl₃, ppm): δ 2.31 (s, 3H), 2.78 (s, 3H), 2.96 (s, 3H), 3.19 (s, 3H), 6.02 (s, 1H), 6.45 (d, J = 12.7 Hz, 1H), 8.02–7.86 (m, 4H).

2-(3,5-Dimethylpyrazol-1-yl)-6-(1H-pyrazol-3-yl)pyridine (dimet1,3bpp). An excess of hydrazine monohydrate (0.1 mL, 1.35 mmol) was added to an ethanolic solution (5 mL) of 1-(6-(3,5-dimethylpyrazol-1-yl)-pyridin-2-yl)-3-(dimethylamino)prop-2-en-1-one (0.72 g, 0.27 mmol) and the mixture was stirred and refluxed overnight. The resulting solution was cooled to room temperature and water (5 mL) was added. The organic phase was separated by decantation. The aqueous phase was extracted three times with CH₂Cl₂ (10 ml), and the organic layers were then combined, washed with brine, dried with MgSO₄ and evaporated under vacuum to afford the product as a pale brown solid (0.52 g, 80%). ¹H NMR (400 MHz, CDCl₃, ppm): δ 2.32 (s, 3H), 2.74 (s, 3H), 6.04 (s, 1H), 6.82 (d, J = 2.0, 1H), 7.6 (s, 1H), 7.66 (d, J = 2.1, 1H), 7.83–7.82 (m, 2H), 10.67 (s, 1H).

[Fe(met1,3bpp)₂](ClO₄)₂ (2). To a solution of Fe(ClO₄)₂·6H₂O (0.023 g, 0.065 mmol) and ascorbic acid (∼2 mg) in absolute ethanol (10 mL) was added dropwise a solution of met1,3bpp (0.027 g, 0.12 mmol) in absolute ethanol (10 mL). The resulting dark yellow solution was stirred for 40 minutes at room temperature. The solution was then filtered and layered with hexane (1 : 1 vol.). Yellow crystals of the product suitable for single crystal X-ray diffraction were obtained after 4 days. Yield: 43.2%. EA, calcd (%) for C₂₄H₂₂Cl₂FeN₁₀O₈ (found): C, 40.87 (41.04); H, 3.14 (3.01); N, 19.86 (19.06).

[Fe(dimet1,3bpp)₂](ClO₄)₂ (3). To a solution of Fe(ClO₄)₂·6H₂O (0.023 g, 0.065 mmol) and ascorbic acid (∼2 mg) in dry acetone (10 mL) was added dropwise a solution of 2met1,3bpp (0.029 g, 0.12 mmol) in dry acetone (10 mL). In this case, the resulting red solution was stirred for 40 minutes, filtered, and layered with diethyl ether. 3–4 days later, red crystals of the product of good quality for single crystal X-ray diffraction were obtained. Yield: 60.1%. EA, calcd (%) for C₂₆H₂₆Cl₂FeN₁₀O₈ (found): C, 42.59 (43.03); H, 3.57 (3.22); N, 19.10 (18.96).

Single-crystal X-ray diffraction

Data for 2 and 3 were collected on a Bruker APEXII QUAZAR diffractometer equipped with a microfocus multilayer monochromator with MoKα radiation (λ = 0.71073 Å), at 100 and 298/300 K for both compounds. Data for 2b were collected at 100 K on Beamline 11.3.1 at the Advanced Light Source, on a Bruker D8 diffractometer equipped with a PHOTON 100 CCD detector and using silicon (111) monochromated synchrotron radiation (λ = 0.7749 Å). Data reduction and absorption corrections were performed with SAINT and SADABS, respectively.⁵³ All structures were solved by intrinsic phasing with SHELXT⁵⁴ and refined by full-matrix least-squares on F² with SHELXL-2014.⁵⁵ The structure of 2b was refined as a 2-component twin, using a twin law found through PLATON.⁵⁶ The structure was first solved in P₁ on HKLF4 data and then transformed to the monoclinic Cc with PLATON/ADDSYM. All details can be found in CCDC 1534003–1534004 (2), 1534005 (2b) and 1534006–1534007 (3)† that contain the supplementary crystallographic data for this paper. Crystallographic and refinement parameters are summarized in Table S1† together with average Fe–N bond lengths and distortion parameters. Selected bond lengths and angles and intermolecular distances are given in Tables S2–S4.†

Physical measurements

Magnetic measurements. These measurements were performed with either an MPMS5 or an MPMS-XL SQUID magnetometer through the “Unitat de mesures Magnètiques” of the Universitat de Barcelona or the Servicio General de Apoyo a la Investigación-SAI, Universidad de Zaragoza. Diamagnetic corrections for the sample holder were applied as well as a correction for the diamagnetic contribution of the sample, as derived from Pascal's constants.

Differential scanning calorimetry (DSC). These experiments were done with a Q1000 calorimeter from TA Instruments equipped with the LNCS accessory. Calibration of the temperature and enthalpy scales was achieved with a standard sample of In, using its melting transition (156.6 °C, 3296 J mol⁻¹). Mechanically crimped Al pans with an empty pan as a reference were used. All reported data were obtained at a scanning rate of 10 K min⁻¹. Measurements on 2 were also done at scanning rates down to 0.5 K min⁻¹ to confirm that no hysteresis was present. For heat capacity, a synthetic sapphire was measured in the same temperature range. By comparison, an overall accuracy of 0.2 K for the temperature and up to 10% for the heat capacity was estimated over the whole studied temperature range.

Powder X-ray diffraction (PXRD). Patterns were recorded through the X-ray diffraction and fluorescence unit of the Servicio General de Apoyo a la Investigación-SAI, Universidad de Zaragoza, using a D-Max Rigaku diffractometer equipped with a Cu rotating anode and a graphite monochromator to select the Cu Kα_1,2 wavelength.

Computational details

All energy evaluations were performed on molecular geometries optimized in the HS and LS states using the Quantum Espresso package (QE),⁵⁷ the PBE + U functional with a Hubbard-like U parameter of 2.65 eV on the “d” orbitals of iron, the D2 correction of Grimme,⁵⁸ and Vanderbilt pseudopotentials.⁵⁹ The molecules were introduced in a cubic cell of 60 Bohr³ to isolate them from the virtual counterparts, which means that all calculations simulate gas-phase conditions. This has been done with the help of the Makov–Payne approximation to treat the charged unit cells.⁶⁰ The Hubbard term has been used to cure the incomplete cancellation of the electronic self-interaction in the PBE functional, which results in an unrealistic delocalization of orbitals.^61,62 The value U = 2.65 eV has been found to be adequate to describe ΔH_elec in FeN₆-based compounds.⁶³ The t_2g (and e_g) orbitals were identified by projecting the density of states on the Fe atom, and the values given in Table 1 correspond to the average value for the three (two) non-degenerate orbitals of the LS species of molecules 1–4.

Conclusions

By preparing a family of analogous [Fe(1,3′bpp′)₂](ClO₄)₂ complexes, with ‘bpp’ being non-substituted, 3-methyl or 3,5-dimethyl substituted 1,3-bis-pyrazolylpyridine ligands, it is shown that these remote substituents have a dramatic effect on the SCO temperature of the Fe(II) spin carrier. This influence is manifested on the solid-state thermal behaviour of the concerned systems and most significantly on their SCO in solution, where packing effects are absent. DFT calculations show that these dramatic effects are due to intramolecular steric or non-covalent interactions, which favour either the LS or the HS state, depending on the position of the substituent.

Acknowledgements

The authors thank the Generalitat de Catalunya for the prize ICREA Academia 2008 and 2013, and acknowledge the ERC for the Starting Grant StG-2010-258060 (GA), MINECO for grants MAT2014-53961-R (OR), MAT2015-70868-ERC (OR), CTQ2012-32247 (GA) and CTQ2015-68370-P (GA, CBM, RD), LabEx-Chemistry of Complex Systems for the post-doctoral grant ANR-10LABX-0026CSC (SV), the regional High-Performance Computing (HPC) center in Strasbourg for computational resources (SV) and the Avempace II Erasmus Mundus Action 2program for a PhD scholarship (MD). This research used resources of the Advanced Light Source, which is a DOE Office of Science User Facility under contract no. DE-AC02-05CH11231.

Notes and references

1. P. Gütlich, A. Hauser and H. Spiering, Angew. Chem., Int. Ed. Engl., 1994, 33, 2024–2054.
2. P. Gütlich, A. B. Gaspar and Y. Garcia, Beilstein J. Org. Chem., 2013, 9, 342–391.
3. P. Gütlich and H. A. Goodwin, in Spin Crossover in Transition Metal Compounds I, ed. P. Gütlich and H. A. Goodwin, Springer, Berlin, Heidelberg, 2004, pp. 1–47.
4. P. Gütlich, Y. Garcia and H. A. Goodwin, Chem. Soc. Rev., 2000, 29, 419–427.
5. M. A. Halcrow, Chem. Soc. Rev., 2011, 40, 4119–4142.
6. A. Bousseksou, G. Molnár, L. Salmon and W. Nicolazzi, Chem. Soc. Rev., 2011, 40, 3313–3335.
7. P. Gamez, J. Sánchez Costa, M. Quesada and G. Aromí, Dalton Trans., 2009, 7845–7853.
8. J. Olguin and S. Brooker, Coord. Chem. Rev., 2011, 255, 203–240.
9. G. A. Craig, O. Roubeau and G. Aromí, Coord. Chem. Rev., 2014, 269, 13–31.
10. M. A. Halcrow, Crystals, 2016, 6, 58.
11. J. Tao, R.-J. Wei, R.-B. Huang and L.-S. Zheng, Chem. Soc. Rev., 2012, 41, 703–737.
12. P. Guionneau, Dalton Trans., 2014, 43, 382–393.
13. M. Fumanal, F. Jiménez-Grávalos, J. Ribas-Ariño and S. Vela, Inorg. Chem., 2017, 56, 4474–4483.
14. Z. Ni and M. P. Shores, J. Am. Chem. Soc., 2009, 131, 32–33.
15. S. A. Barrett and M. A. Halcrow, RSC Adv., 2014, 4, 11240–11243.
16. M. C. Young, E. Liew, J. Ashby, K. E. McCoy and R. J. Hooley, Chem. Commun., 2013, 49, 6331–6333.
17. S. Bonnet, G. Molnár, J. S. Costa, M. A. Siegler, A. L. Spek, A. Bousseksou, W. T. Fu, P. Gamez and J. Reedijk, Chem. Mater., 2009, 21, 1123–1136.
18. R.-J. Wei, J. Tao, R.-B. Huang and L.-S. Zheng, Inorg. Chem., 2011, 50, 8553–8564.
19. W. Zhang, F. Zhao, T. Liu, M. Yuan, Z.-M. Wang and S. Gao, Inorg. Chem., 2007, 46, 2541–2555.
20. G. A. Craig, J. S. Costa, O. Roubeau, S. J. Teat and G. Aromí, Chem. – Eur. J., 2012, 18, 11703–11715.
21. J. S. Costa, S. Rodríguez-Jiménez, G. A. Craig, B. Barth, C. M. Beavers, S. J. Teat and G. Aromí, J. Am. Chem. Soc., 2014, 136, 3869–3874.
22. L. A. Barrios, C. Bartual-Murgui, E. Peyrecave-Lleixa, B. Le Guennic, S. J. Teat, O. Roubeau and G. Aromi, Inorg. Chem., 2016, 55, 4110–4116.
23. L. J. K. Cook, R. Kulmaczewski, O. Cespedes and M. A. Halcrow, Chem. – Eur. J., 2016, 22, 1789–1799.
24. R. G. Miller and S. Brooker, Chem. Sci., 2016, 7, 2501–2505.
25. S. Rodríguez-Jiménez, H. L. C. Feltham and S. Brooker, Angew. Chem., Int. Ed., 2016, 55, 15067–15071.
26. M. Steinert, B. Schneider, S. Dechert, S. Demeshko and F. Meyer, Angew. Chem., Int. Ed., 2014, 53, 6135–6139.
27. W. Phonsri, D. S. Macedo, K. R. Vignesh, G. Rajaraman, C. G. Davies, G. N. L. Jameson, B. Moubaraki, J. S. Ward, P. E. Kruger, G. Chastanet and K. S. Murray, Chem. – Eur. J., 2017, 23, 7052–7065.
28. H.-J. Lin, D. Siretanu, D. A. Dickie, D. Subedi, J. J. Scepaniak, D. Mitcov, R. Clérac and J. M. Smith, J. Am. Chem. Soc., 2014, 136, 13326–13332.
29. V. Martínez, A. B. Gaspar, M. C. Muñoz, G. V. Bukin, G. Levchenko and J. A. Real, Chem. – Eur. J., 2009, 15, 10960–10971.
30. J. G. Park, I.-R. Jeon and T. D. Harris, Inorg. Chem., 2015, 54, 359–369.
31. K. Nakano, N. Suemura, K. Yoneda, S. Kawata and S. Kaizaki, Dalton Trans., 2005, 740–743.
32. L. J. Kershaw Cook, R. Kulmaczewski, R. Mohammed, S. Dudley, S. A. Barrett, M. A. Little, R. J. Deeth and M. A. Halcrow, Angew. Chem., Int. Ed., 2016, 55, 4327–4331.
33. J. M. Holland, S. A. Barrett, C. A. Kilner and M. A. Halcrow, Inorg. Chem. Commun., 2002, 5, 328–332.
34. J. Elhaik, D. J. Evans, C. A. Kilner and M. A. Halcrow, Dalton Trans., 2005, 1693–1700.
35. A. Santoro, L. J. K. Cook, R. Kulmaczewski, S. A. Barrett, O. Cespedes and M. A. Halcrow, Inorg. Chem., 2015, 54, 682–693.
36. M. A. Hoselton, L. J. Wilson and R. S. Drago, J. Am. Chem. Soc., 1975, 97, 1722–1729.
37. C. Bartual-Murgui, S. Vela, O. Roubeau and G. Aromí, Dalton Trans., 2016, 45, 14058–14062.
38. S. Vela, C. Gourlaouen, M. Fumanal and J. Ribas-Ariño, Magnetochemistry, 2016, 2, 6.
39. P. Hamon, J.-Y. Thépot, M. Le Floch, M.-E. Boulon, O. Cador, S. Golhen, L. Ouahab, L. Fadel, J.-Y. Saillard and J.-R. Hamon, Angew. Chem., Int. Ed., 2008, 47, 8687–8691.
40. A. Santoro, L. J. Kershaw Cook, R. Kulmaczewski, S. A. Barrett, O. Cespedes and M. A. Halcrow, Inorg. Chem., 2015, 54, 682–693.
41. C. Bartual-Murgui, C. Codina, O. Roubeau and G. Aromí, Chem. – Eur. J., 2016, 22, 12767–12776.
42. P. Guionneau, M. Marchivie, G. Bravic, J.-F. Létard and D. Chasseau, J. Mater. Chem., 2002, 12, 2546–2551.
43. M. Marchivie, P. Guionneau, J.-F. Létard and D. Chasseau, Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 25–28.
44. P. Gütlich and H. A. Goodwin, Top. Curr. Chem., 2004, 233, 1–47.
45. M. Sorai and S. Seki, J. Phys. Chem. Solids, 1974, 35, 555–570.
46. M. Sorai, Y. Nakazawa, N. Nakano and Y. Miyazaki, Chem. Rev., 2013, 113, PR41–PR122.
47. O. Roubeau, M. Castro, R. Burriel, J. G. Haasnoot and J. Reedijk, J. Phys. Chem. B, 2011, 115, 3003–3012.
48. Z. Arcis-Castíllo, S. Zheng, M. A. Siegler, O. Roubeau, S. Bedoui and S. Bonnet, Chem. – Eur. J., 2011, 17, 14826–14836.
49. D. F. Evans, J. Chem. Soc., 1959, 2003–2005.
50. S. K. Sur, J. Magn. Reson., 1989, 82, 169–173.
51. D. H. Grant, J. Chem. Educ., 1995, 72, 39.
52. D.-W. Tan, J.-B. Xie, Q. Li, H.-X. Li, J.-C. Li, H.-Y. Li and J.-P. Lang, Dalton Trans., 2014, 43, 14061–14071.
53. G. M. Sheldrick, SAINT and SADABS, Brucker AXS Inc., Madison, Wisconsin, USA, 2012.
54. G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2015, 71, 3–8.
55. G. M. Sheldrick, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2015, 71, 3–8.
56. A. Spek, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2015, 71, 9–18.
57. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. d. Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
58. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
59. D. Vanderbilt, Phys. Rev. B: Condens. Matter, 1990, 41, 7892–7895.
60. G. Makov and M. C. Payne, Phys. Rev. B: Condens. Matter, 1995, 51, 4014–4022.
61. D. A. Scherlis, M. Cococcioni, P. Sit and N. Marzari, J. Phys. Chem. B, 2007, 111, 7384–7391.
62. A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Phys. Rev. B: Condens. Matter, 1995, 52, R5467–R5470.
63. S. Vela, M. Fumanal, J. Ribas-Ariño and V. Robert, Phys. Chem. Chem. Phys., 2015, 17, 16306–16314.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 1534003–1534007. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7qi00347a

---