Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Solute particle near a nanopore: influence of size and surface properties on the solvent-mediated forces†
Julien
Lam
 and
James F.
Lutsko
and
James F.
Lutsko
 *
*
Center for Nonlinear Phenomena and Complex Systems, Code Postal 231, Université Libre de Bruxelles, Boulevard du Triomphe, 1050 Brussels, Belgium. E-mail: jlutsko@ulb.ac.be
First published on 31st October 2017
Abstract
Nanoscopic pores are used in various systems to attract nanoparticles. In general the behaviour is a result of two types of interactions: the material specific affinity and the solvent-mediated influence also called the depletion force. The latter is more universal but also much more complex to understand since it requires modeling both the nanoparticle and the solvent. Here, we employed classical density functional theory to determine the forces acting on a nanoparticle near a nanoscopic pore as a function of its hydrophobicity and its size. A simple capillary model is constructed to predict those depletion forces for various surface properties. For a nanoscopic pore, complexity arises from both the specific geometry and the fact that hydrophobic pores are not necessarily filled with liquid. Taking all of these effects into account and including electrostatic effects, we establish a phase diagram describing the entrance and the rejection of the nanoparticle from the pore.
1 Introduction
Determining forces acting on a nanoparticle in the vicinity of a nanoscopic pore is of great scientific and industrial importance for a wide range of systems such as filtering membranes for water purification1–6 and porous solids made of cylindrical cavities employed as nucleants for selective crystallization.7–9 In biophysics, nanopores are used for protein unfolding,10–15 DNA sequencing16–21 and protein detection.22–26 In all these cases, controlling the solute behavior close to the pore entrance plays a major role in the success of the desired application and contributes to the ultimate goal of engineering systems to have specific properties.When studying this type of system, one major difficulty consists of modeling the depletion force accounting for the indirect role of solvent molecules. Depletion forces are observed in numerous fundamental processes such as colloidal self-assembly,27–30 protein stabilization in helix31,32 and the effective attraction between hydrophobic surfaces.33,34 Microscopically, depletion forces result from two effects: (a) at very short separations, solvent molecules are excluded from the gap between the macroscopic objects (particles, molecular chains and flat walls) thus generating a force; and (b) the formation of low-density phases in the gap between the objects due to capillary effects. The first contribution to the depletion force only depends on the geometry and the surface properties of the macroscopic objects whereas the second depends as well on the interaction between the surfaces and the solvent. These solvent-mediated interactions were thoroughly reviewed by Chandler35 and also by Berne et al.36 In general, many different model liquid solvents have been studied including hard sphere,27,37–44 Lennard-Jones potentials45–47 and also single point charge water.35,48–51 In addition, various specific geometries have been discussed in the literature such as biomolecules,52 two big spheres,27,37 two planar surfaces40,41,45 and a big sphere and a planar surface.37–39
However, despite its practical importance, the interaction between a nanoparticle and a nanoscopic pore has received less attention due to its inherent complexity. Previous works thoroughly studied the behavior of a large hard sphere in the vicinity of a rigid non-interacting wall and thus only focussed on entropic effects.42–44 In addition, the time scale for the nanoparticle entrance inside a pore was discussed recently for a spherical pore of a fixed size and hydrophobicity.53 In this paper, we aim at studying how the interplay between hydrophobicity and aspect ratio of the pore can induce the nanoparticle entrance or rejection. We model the liquid using a simple Lennard-Jones potential so as to describe the dominant effects of excluded volume and nontrivial energetics giving rise to wetting behaviour. Finite-temperature density functional theory54,55 (DFT) was employed to compute the equilibrium state including the fully (non-symmetry constrained) three dimensional density profile along with the free energy. We applied the model first to a nanoparticle interacting with a flat surface and inside an infinite cylinder. From these calculations, a capillary model is built to understand the mechanisms generating the depletion forces. Then, we focused on a system made of a solute in the vicinity of a nanoscopic pore for empty, filled and partially filled pores and we determined under which conditions the nanoparticle enters the pore. Moreover, we introduced functionalization of the surfaces modeled as electrostatic forces and show that when these are sufficiently high, the nanoparticle entrance can be activated even in conditions where the depletion forces would dictate otherwise. Finally, the influence of the nanoparticle hydrophobicity was studied in the last section. Our work contributes to the general understanding of solute infiltration within nanoscopic pores by providing a qualitative picture guiding the design of pores in terms of size, solvophobicity and chemical functionalization. In addition, the quantitative figures obtained in this work provide a basis for a coarse-graining of the solute–pore interactions. This should ultimately lead to simplifications of the multi-scale problems made of solvent/solute/pore.
2 Theory
2.1 Density functional theory
Our systems can be divided into three elements: the walls, the nanoparticle and the fluid. The walls and the nanoparticle are static and play the role of external potentials acting on the fluid. The local density of the fluid and the free energy of the entire system are calculated using classical Density Functional Theory. First, an energy functional is constructed as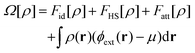 | (1) |
The ideal gas contribution is
 | (2) |
The molecules of the fluid interact via a pair potential, v(r), which we take to be a Lennard-Jones interaction that has been truncated at r = rc and shifted giving
| v(r) = vLJ(r) − vLJ(rc), r < rc | (3) |
 | (4) |
 | (5) |
Finally, the external potential ϕext(r) at any given point is the sum of the contributions from all of the walls and the nanoparticle.
We perform the calculations on a three dimensional grid. The fluid density is specified on the grid points and the free energy is minimized with respect to these values using conjugate gradients. The hard-sphere contributions require performing spherical integrals of the density and this is done using trilinear interpolation of the density and spherical t-designs.57 For some of our applications, we minimize at constant particle number, which is the integral of the density over all space, rather than at constant chemical potential. Technically, there are additional corrections that should be evaluated in this case58 but in practice it is known that these tend to be negligible for systems of the size considered here.
To carry out the numerical calculations, the density is discretized on a Cartesian lattice and the entire system is subject to periodic boundaries. Care was taken to extend the systems sufficiently in each direction so as to avoid self-interactions, etc. All calculations were carried out with 5 lattice points per unit of σ which is sufficiently small to perform calculations for large simulation boxes while retrieving quantitative agreement with finer discretizations.
2.2 Model
For the liquid/liquid interaction, the Lennard-Jones potential is parametrized by the length scale denoted σ and the energy parameter denoted εliq/liq. The cutoff is chosen equal to rc = 3σ. We worked at a temperature of kBT = 0.8εliq/liq which is located between the triple point and the critical temperature59 but we do not believe that this choice affects physics discussed below. In addition, the chemical potential is chosen higher than the one at liquid–vapor coexistence denoted, μcoex. Indeed, at room temperature and at atmospheric pressure, liquid water does not coexist with its vapor state. The pressure at coexistence is roughly Pcoex = 1/20Patm so in the DFT calculations, the chemical potential is chosen to reproduce this ratio of the pressure to its value at coexistence resulting in a supersaturation Δμ ≡ μ − μcoex = 0.27kBT.Solids are often represented by effective potentials such as the Steele potential60,61 and related models62 which are derived for simple geometries like planar walls. Here, we will address the complex geometry of a cylindrical pore so we have modeled our solids within an atomistic framework. In practice, the solid is represented by fixed particles disposed in a face-centered cubic (FCC) lattice with the (100) surface exposed to the fluid. The initial solid density is ρ = 1.09σ−3 which is the equilibrium, zero-temperature density for an FCC Lennard-Jones solid.63 For each calculation, the simulation box lengths are chosen to be commensurate with the initial lattice spacing of the wall and then readjusted to also be commensurate with the length scale of the DFT discretization used for the calculation. The lattice spacing is then modified to be a multiple of the final simulation box lengths which changes the solid density by a negligible amount (no more than 1%). The same truncated and shifted Lennard-Jones potential is used to model solid–liquid interactions. For simplicity and to reduce the number of parameters the length parameters for both interactions are taken to be equal. With such a model, the wettability represented by the contact angle, θ, is directly related to the ratio between the two Lennard-Jones energy parameters: ε* ≡ εwall/liq/εliq/liq. Details on the contact angle derivation can be found in the ESI, section 1.† In practice, for large values of ε*, liquid molecules are more attracted to the solid than to themselves and the solid is hydrophilic.
Initially, we take the nanoparticle to be a hard sphere particle of radius Rn thus avoiding considerations regarding the chemical nature of the solute to focus only on the depletion forces. Later, we discuss the effect of direct interactions between the nanoparticles and the walls. To fix the relevant length scales and to explain our choices of nanoparticle sizes, we note that a water molecule has a typical effective size (diameter) of about 0.275 nm while typical globular proteins such as Lysozyme have diameters of 3 or 4 nm so that the smallest nanoparticles of interest here have a diameter on the order of 10 water molecules and, hence, a radius of about Rn = 5σ.
3 Results
3.1 Depletion potential in the case of a flat wall and an infinite cylinder
 | ||
| Fig. 1 Liquid density profiles for a nanoparticle, Rn = 5σ, near a flat wall for various hydrophobicities: (a, d) ε* = 0.1 i.e. θ = 171°, (b, e) ε* = 0.3 i.e. θ = 95° and (c, f) ε* = 0.5 i.e. θ = 0°. The distance between the nanoparticle center and the wall is equal to 8σ + Rn for (a, b, c) and Rn for (d, e, f). Each image is of size 25σ × 25σ [see also ESI, section 2†]. | ||
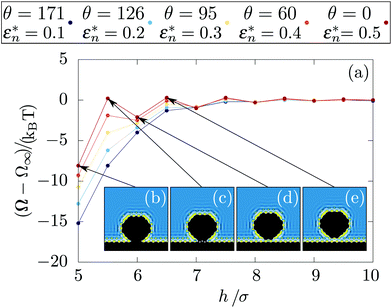
The free energy as a function of the nanoparticle/wall distance, denoted h, is shown in Fig. 2 for different contact angles and for two solute diameters. Far from the wall (h > Rn + 5σ), the free energy is constant and there is no effective interaction between the nanoparticle and the wall. Closer to the wall, the behaviour of the free energy depends on the degree of hydrophobicity. Qualitatively, two effects are at work. First, it is energetically costly for fluid to be in contact with a hydrophobic wall – alternatively, one can say that the fluid–wall surface tension increases with the degree of hydrophobicity. In this case, the presence of a nanoparticle near the wall allows for the formation of a region of vapor-like density which has a lower wall surface tension and therefore lowers the total free energy of the system. Second, the usual depletion force (effective attraction due to exclusion of the solvent) gives rise to an attractive interaction even for a purely hard-core interaction between the wall and the fluid.45 For this reason, the effective force on the nanoparticle does not become negative at the wetting transition (where the fluid–wall interaction becomes favored with respect to the vapor) but rather at higher degrees of hydrophilicity in which the fluid has an effectively negative wall surface tension thus overwhelming all other effects. Finally, the forces are higher when the nanoparticle is larger because more solvent molecules are influenced by the nanoparticle presence.
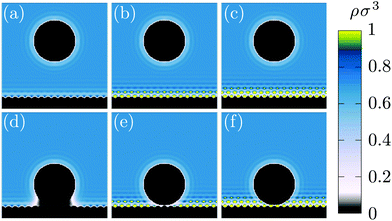
Infinite cylinder. In this case, the system is made of a large FCC crystal out of which all particles within the given diameter (Dcyl) are removed. The length of the cylinder is equal to 31σ and the periodic boundaries imply that it is effectively infinite in length. For the radial dimensions, the crystal size is chosen so that it has a width greater than rc. Both the density and free energy are computed as a function of the distance from the nanoparticle to the cylindrical wall. Fig. 3 shows typical density profiles obtained with the described geometry.
 | ||
| Fig. 3 Liquid density profiles for a nanoparticle, Rn = 5σ, inside a cylinder of diameter, Dcyl = 37.5σ for various hydrophobicity: (a,d) ε* = 0.1 i.e. θ = 171°, (b, e) ε* = 0.3 i.e. θ = 95° and (c, f) ε* = 0.5 i.e. θ = 0°. The distance between the nanoparticle center and the cylinder wall is equal to Dcyl/2 for (a, b, c) and Rn for (d, e, f). Each image is of size 40σ × 40σ [see also ESI, section 2†]. | ||
As shown in Fig. 4, similarly to the case of a flat wall, increasing the hydrophobicity leads to an increase of the solute attraction. In addition, the forces are higher inside smaller cylinders since layering is more present.
Capillary model. For both a flat wall and a cylinder, two regimes are observed: (i) far from the wall, the free energy is constant, (ii) close to the wall, the free energy decreases almost linearly. As evidenced by Fig. 1d and 3d, this abrupt transition results from the formation of a low-density gas-like phase between the wall and the nanoparticle. This suggests that a simple capillary model can be used to estimate the excess free energy when the nanoparticle approaches the wall. We approximate the gaseous volume as a cylinder stretching from the wall to the nanoparticle with a radius of r0 which is, in general, not equal to Rn. We assume the low-density fluid has the properties of the bulk gas phase and introduce γn,l/g, γw,l/g and ωl/g as respectively the nanoparticle–liquid/gas surface tensions, the wall–liquid/gas surface tensions and the bulk liquid/gas grand potential per unit of volume. Accordingly, the excess grand potential, Ω(h) − Ω(h → ∞), is given by:
 | (6) |
As shown in Fig. 2 and 4, the DFT results are in good qualitative and indeed semiquantitative agreement with predictions from the capillary model for both geometries. The slight shift can be due to the gaseous region approximated as a purely cylindrical geometry thus neglecting edge effects close to the nanoparticle and the wall. Similar results were also obtained using single point charge model for the liquid and with different geometries35,36,51 thus confirming the ability of our elementary model to capture most physical features underlying the hydrophobic interactions.
3.2 Depletion potential in the case of a cylindrical pore
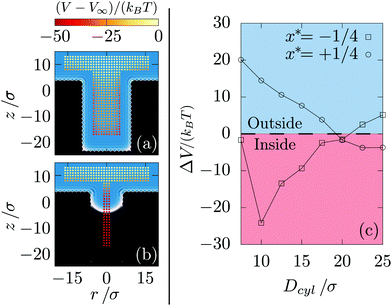
Nanoscopic pores are built using an FCC crystal out of which atoms located inside a cylinder of diameter denoted Dcyl and of height H = 25σ are removed. The distinction from the previously considered infinite cylinder is that the pore is terminated at one end by crystal an is open at the other end to the bulk fluid [see Fig. 6]. The height of the crystal is chosen to leave few layers of atoms below the pore and we fixed the width of the crystal equal to Dcyl + 26σ which is sufficient for the pore sizes considered here. Above the wall, the system is loaded with a 25σ liquid layer [see Fig. 6].Depletion potential. Then, calculations are run for a nanoparticle Rn = 5σ at various positions and for different pore properties (Dcyl, ε*). The aim is to measure the grand potential and determine whether or not the nanoparticle is more likely to enter the pore.
Fig. 6 shows the grand potential for various positions of the nanoparticle at different pore conditions. In general, free energy is minimum when the nanoparticle is at the bottom of the pore for two different reasons. On the one hand, compared to when the pore is empty and the nanoparticle is in the bulk fluid above, inserting the nanoparticle inside the pore effectively transfers liquid molecules to the bulk region. Thus, the free energy decreases since the system is supersaturated and so favors the bulk liquid state. On the other hand, when the pore is filled, the cylindrical depletion forces are larger than those of a flat wall (as shown in Fig. 4). Consequently, when the nanoparticle manages to enter the pore it is more likely to stay inside.
However, when it is outside the pore, the nanoparticle does not “know” that the free energy will be lower at the bottom of the pore: whether or not it enters will depend on the free energy gradients near the pore entrance. Thus, we compare the free energy at the pore entrance (radial position r < Dcyl/2) with that far from it (r = Dcyl/2 + 10σ). These two free energies are respectively denoted Ωin and Ωout and indicated in Fig. 6. When ΔΩ ≡ Ωin − Ωout > 0, the nanoparticle is more likely to stay close to the wall rather than entering inside the pore. Fig. 7 shows ΔΩ when changing the supersaturation, the pore size and its degree of hydrophobicity.
In summary, for pores much larger than the nanoparticle (Dcyl ≥ 2Rn = 10σ), the particle is only favored to enter the pore at sufficiently high hydrophobicity. For pores with diameters less than twice that of the nanoparticle, entrance is increasingly favored with decreasing pore size until the particle prefers the pore even near the wetting transition. Finally, for pores smaller than the nanoparticle (Dcyl = 7.5σ), hydrophilic walls provokes the nanoparticle rejection. There, the pore are filled with highly structured liquid [see ESI, section 5†] and the nanoparticle presence at the pore entrance generates frustration. When the walls are sufficiently hydrophobic, the pore is empty thus avoiding frustration. These trends are stronger at higher chemical potential (i.e., higher liquid density and pressure), probably due to stronger frustration of the fluid packing near the walls and nanoparticle. Surprisingly, at Dcyl = 7.5σ and θ = 171°, the nanoparticle is also rejected. There, the pore is empty and in general, increasing the hydrophobicity for an empty pore leads to an increase of the flat wall attraction while keeping the pore attraction constant [see ESI, section 6†].
3.3 Functionalization of the surfaces: the role of electrostatic effects
In addition to depletion forces, the nanoparticle can also interact with nanopores by means of electrostatic effects. The total free energy for a system with an explicit wall–nanoparticle interaction potential V(r) and the system without such a potential is simply that Ω = ΩV=0 + V(R) where R is the position of the center of the nanoparticle. Thus, our previous results can now be used to study the effect of such additional forces with little supplementary computation.In an electrolyte solution, electrostatic interactions can be approximated by a simplified screened Coulomb interaction:
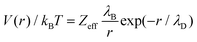 | (7) |
The calculated electrostatic contributions are added to the already obtained depletion energy. The phase diagram for nanoparticle inclusion can thus be modified for different interaction strengths [see Fig. 10]. First, adding attractive electrostatic energy allows for more conditions at which the nanoparticle can enter the pore. Then, repulsive electrostatic energy competes with the attractive depletion energy thus leading to more complex behaviors [see Fig. 10(e–h)]. Firstly, for small pores (Dcyl ≤ 15σ), adding a repulsive electrostatic energy simply rejects the nanoparticle. Secondly, for larger pores (17.5σ ≤ Dcyl ≤ 22.5σ), the repulsive contribution is higher at the flat wall that at the pore entrance. Therefore, the total free energy can be located at the pore entrance which should lead to the nanoparticle entrance. Yet, the repulsive contribution is so high that the pore becomes repulsive and the nanoparticle is rejected from both the flat wall and the pore. Thirdly, for the largest pores (Dcyl = 25σ) there is the emergence of a region for which the nanoparticle is neither attracted nor rejected. Indeed, while the overall energy are repulsive everywhere else, at the center (r = 0), the nanoparticle is too far from the wall to notice its influence and there is no forces.
3.4 Role of the nanoparticle hydrophobicity
For this final section, the nanoparticle is represented by 317 fixed particles located within a distance Rnano = 4σ disposed in an FCC lattice with a solid density ρ = 1.09σ−3. The truncated and shifted Lennard-Jones potential is also used to model nanoparticle–liquid interactions with the length scale and the energy parameters respectively denoted σ and εnano/liq. We define . Fig. 9a shows the results obtained for a flat wall. When both systems are hydrophobic, the results are qualitatively similar to those obtained with a hard sphere nanoparticle [see also ESI, section 7†]. However, for hydrophilic nanoparticles, the depletion potential shows oscillations when approaching the wall. As evidenced in Fig. 9(b–e), in these cases, the nanoparticle is microscopically structured because of the large hydrophilicity and its atomistic nature. Therefore, the observed oscillations originate from the confrontation between the structures near the wall and near the nanoparticle. Then, complexity should arise when changing the wall hydrophobicity and the orientation, crystal structure and size of the nanoparticle. Those effects will be the subject of a following article.
. Fig. 9a shows the results obtained for a flat wall. When both systems are hydrophobic, the results are qualitatively similar to those obtained with a hard sphere nanoparticle [see also ESI, section 7†]. However, for hydrophilic nanoparticles, the depletion potential shows oscillations when approaching the wall. As evidenced in Fig. 9(b–e), in these cases, the nanoparticle is microscopically structured because of the large hydrophilicity and its atomistic nature. Therefore, the observed oscillations originate from the confrontation between the structures near the wall and near the nanoparticle. Then, complexity should arise when changing the wall hydrophobicity and the orientation, crystal structure and size of the nanoparticle. Those effects will be the subject of a following article.
4 Conclusions
In summary, our work determined the depletion potential acting on a nanoparticle near a nanoscopic pore. The size and the surface properties were systematically varied. We performed fully three-dimensional DFT calculations to determine the equilibrium structure and free energy of the system for various positions of the nanoparticle and from this extracted information about the forces driving the particle into or away from the pore. The role of functionalization of the surfaces was also considered.We studied very specific features: (i) atomistic walls were used and crystalline patterning of the fluid near the wall was found for the first time in DFT and (ii) entrance edges playing a major role in the nanoparticle behavior. Depletion potentials were first computed for a flat wall and an infinite cylinder. We showed that the degree of hydrophobicity, the nanoparticle size but also the cylinder diameter can all increase the depletion potential. We constructed a well-defined thermodynamic model based on the capillary approximation. Reasonable agreement between the model and the DFT results shows that the model captures the main physical processes generating such a solvent mediated force. Consequently, for a coarse grain modeling, three main ingredients should be included: (i) the depletion energy is nearly linear with the distance, (ii) its onset is abrupt because it results from the emergence of a gaseous phase and (iii) its range is not larger than 5σ.
Next, the nanopore geometry was studied. The first complexity arises from the fact that the liquid state is not necessarily stable inside the pore channel. A first phase diagram allowed us to identify conditions for which the pore is filled with liquid. Thereafter, a nanoparticle is positioned in the vicinity of the pore entrance. When the pore is filled, results for the depletion potential are consistent with the more simple geometries previously discussed. When the pore is empty, the depletion forces are surprisingly larger. This results from an increase of the number of particles in the liquid state when moving the nanoparticle inside the gaseous phase. Finally, a phase diagram showing conditions driving the nanoparticle inside the pore was obtained. Remarkably, while it could be thought that large pores are necessary to carry the nanoparticle inside, we demonstrate that the contrary happens. Increasing hydrophobicity and decreasing the size of the pore play two major roles. On the one hand, it increases the direct depletion forces. On the other hand, it allowed for an empty pore to be stable thus generating an additional osmotic pressure. In the last section, electrostatic effects are added by means of a simple screened Coulomb interaction. We demonstrate that tuning the amount of charges, one can trigger the nanoparticle entrance even when depletion forces prescribe otherwise.
Our microscopic models incorporate generic physical effects such as excluded volume and long (but finite) ranged attraction. This is enough to give the usual phenomenology of fluid layering near a wall, hydrophobic–hydrophilic behavior, Young's law [see Fig. 2 in ESI, section 1†], a typical liquid–vapor phase diagram, etc. The mechanism behind the dominant solvent-mediated forces – namely, the formation of a meniscus of vapor for hydophobic surfaces – is also quite generic and so we expect the general result (that the solvent mediated forces have a range of about 5 solvent molecule diameters and that the energy varies linearly (and so that the forces are constant) as a function of distance from the surface) to hold for a wide variety of solvents. The only unknown quantity is, e.g., the value of the binding energy at zero separation. From our analytic model for flat wall, this value can be obtained by solving a simple set of algebraic equations [see eqn (10)–(12) in ESI, section 3†].
As a perspective, the numerical values and also the thermodynamic model obtained in this work describe quantitatively the role of solvent-mediated forces. Therefore, they can be used to avoid the modeling of liquid when studying a multi-scale system made of solvent/solute/pore. In the context of selective crystallization, our work also provides an important guideline for the rational design of porous materials. Especially, we show that depletion forces can drive the nanoparticle into the pore by tuning the solvent interactions and the size of the pore. As a result, one can avoid the construction of nanoparticle specific materials. Moreover, the use of electrostatic effects allows one to adjust the nanoparticle behavior. This can happen in particular by applying an electric field to generate surface charges on the pore.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work of JL was funded by the European Union's Horizon 2020 research and innovation program within the AMECRYS project under grant agreement no. 712965. That of JFL was funded by the European Space Agency under Contract No. ESA AO-2004-070.References
- P. Vandezande, L. E. Gevers and I. F. Vankelecom, Chem. Soc. Rev., 2008, 37, 365–405 RSC.
- X. Peng, J. Jin, Y. Nakamura, T. Ohno and I. Ichinose, Nat. Nanotechnol., 2009, 4, 353–357 CrossRef CAS PubMed.
- E. Gibbins, M. D'Antonio, D. Nair, L. S. White, L. M. F. dos Santos, I. F. Vankelecom and A. G. Livingston, Desalination, 2002, 147, 307–313 CrossRef CAS.
- A. F. Ismail, P. S. Goh, S. M. Sanip and M. Aziz, Sep. Purif. Technol., 2009, 70, 12–26 CrossRef CAS.
- J. Lee and R. Karnik, J. Appl. Phys., 2010, 108, 044315 CrossRef.
- S. Tseng, Y.-M. Li, C.-Y. Lin and J.-P. Hsu, Nanoscale, 2016, 8, 2350–2357 RSC.
- U. V. Shah, D. R. Williams and J. Y. Heng, Cryst. Growth Des., 2012, 12, 1362–1369 CAS.
- U. V. Shah, M. C. Allenby, D. R. Williams and J. Y. Heng, Cryst. Growth Des., 2012, 12, 1772–1777 CAS.
- U. V. Shah, J. V. Parambil, D. R. Williams, S. J. Hinder and J. Y. Heng, Powder Technol., 2015, 282, 10–18 CrossRef CAS.
- D. Rodriguez-Larrea and H. Bayley, Nat. Nanotechnol., 2013, 8, 288–295 CrossRef CAS PubMed.
- G. Oukhaled, J. Mathe, A.-L. Biance, L. Bacri, J.-M. Betton, D. Lairez, J. Pelta and L. Auvray, Phys. Rev. Lett., 2007, 98, 158101 CrossRef CAS PubMed.
- A. Brinker, G. Pfeifer, M. J. Kerner, D. J. Naylor, F. U. Hartl and M. Hayer-Hartl, Cell, 2001, 107, 223–233 CrossRef CAS PubMed.
- M. Pastoriza-Gallego, M.-F. Breton, F. Discala, L. Auvray, J.-M. Betton and J. Pelta, ACS Nano, 2014, 8, 11350–11360 CrossRef CAS PubMed.
- B. Luan, T. Huynh, J. Li and R. Zhou, ACS Nano, 2015, 10, 317–323 CrossRef PubMed.
- Z. Xu, S. Zhang, J. K. Weber, B. Luan, R. Zhou and J. Li, Nanoscale, 2016, 8, 12143–12151 RSC.
- A. C. Rand, M. Jain, J. M. Eizenga, A. Musselman-Brown, H. E. Olsen, M. Akeson and B. Paten, Nat. Methods, 2017, 14, 411 CrossRef CAS PubMed.
- M. D. Cao, S. H. Nguyen, D. Ganesamoorthy, A. G. Elliott, M. A. Cooper and L. J. Coin, Nat. Commun., 2017, 8, 14515 CrossRef CAS PubMed.
- D. Branton, et al. , Nat. Biotechnol., 2008, 26, 1146–1153 CrossRef CAS PubMed.
- L.-H. Yeh, M. Zhang, S. Qian and J.-P. Hsu, Nanoscale, 2012, 4, 2685–2693 RSC.
- Y. Zhang, G. Wu, W. Si, J. Ma, Z. Yuan, X. Xie, L. Liu, J. Sha, D. Li and Y. Chen, Nanoscale, 2017, 9, 930–939 RSC.
- J. Comer and A. Aksimentiev, Nanoscale, 2016, 8, 9600–9613 RSC.
- X. Zhang, Y. Wang, B. L. Fricke and L.-Q. Gu, ACS Nano, 2014, 8, 3444–3450 CrossRef CAS PubMed.
- M. Wanunu, S. Bhattacharya, Y. Xie, Y. Tor, A. Aksimentiev and M. Drndic, ACS Nano, 2011, 5, 9345–9353 CrossRef CAS PubMed.
- C. Shasha, R. Y. Henley, D. H. Stoloff, K. D. Rynearson, T. Hermann and M. Wanunu, ACS Nano, 2014, 8, 6425–6430 CrossRef CAS PubMed.
- E. C. Yusko, B. R. Bruhn, O. M. Eggenberger, J. Houghtaling, R. C. Rollings, N. C. Walsh, S. Nandivada, M. Pindrus, A. R. Hall, D. Sept, J. Li, D. S. Kalonia and M. Mayer, Nat. Nanotechnol., 2016, 12, 360–367 CrossRef PubMed.
- L. J. Steinbock, S. Krishnan, R. D. Bulushev, S. Borgeaud, M. Blokesch, L. Feletti and A. Radenovic, Nanoscale, 2014, 6, 14380–14387 RSC.
- S. Asakura and F. Oosawa, J. Chem. Phys., 1954, 22, 1255–1256 CrossRef CAS.
- Y. Mao, M. Cates and H. Lekkerkerker, Physica A, 1995, 222, 10–24 CrossRef CAS.
- B. Götzelmann, R. Evans and S. Dietrich, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 6785 CrossRef.
- A. Yodh, K.-H. Lin, J. C. Crocker, A. Dinsmore, R. Verma and P. Kaplan, Philos. Trans. R. Soc. London, Ser. A, 2001, 359, 921–937 CrossRef CAS.
- A. Maritan, C. Micheletti, A. Trovato and J. R. Banavar, Nature, 2000, 406, 287–290 CrossRef CAS PubMed.
- Y. Snir and R. D. Kamien, Science, 2005, 307, 1067–1067 CrossRef CAS PubMed.
- M. Azadi, A. V. Nguyen and G. E. Yakubov, Langmuir, 2015, 31, 1941–1949 CrossRef CAS PubMed.
- M. U. Hammer, T. H. Anderson, A. Chaimovich, M. S. Shell and J. Israelachvili, Faraday Discuss., 2010, 146, 299–308 RSC.
- D. Chandler, Nature, 2005, 437, 640 CrossRef CAS PubMed.
- B. J. Berne, J. D. Weeks and R. Zhou, Annu. Rev. Phys. Chem., 2009, 60, 85 CrossRef CAS PubMed.
- R. Dickman, P. Attard and V. Simonian, J. Chem. Phys., 1997, 107, 205–213 CrossRef CAS.
- R. Roth, B. Götzelmann and S. Dietrich, Phys. Rev. Lett., 1999, 83, 448 CrossRef CAS.
- C. Xiao, J. Guo and C. Li, EPL, 2005, 73, 443 CrossRef.
- K. Nygård, S. Sarman, K. Hyltegren, S. Chodankar, E. Perret, J. Buitenhuis, J. F. van der Veen and R. Kjellander, Phys. Rev. X, 2016, 6, 011014 Search PubMed.
- K. Nygård, Curr. Opin. Colloid Interface Sci., 2016, 22, 30–34 CrossRef.
- H. Mishima, H. Oshima, S. Yasuda, K.-I. Amano and M. Kinoshita, J. Chem. Phys., 2013, 139, 11B618_1 CrossRef PubMed.
- H. Mishima, H. Oshima, S. Yasuda, K.-I. Amano and M. Kinoshita, Chem. Phys. Lett., 2013, 561, 159–165 CrossRef.
- R. Hara, K.-I. Amano, M. Kinoshita and A. Yoshimori, J. Chem. Phys., 2016, 144, 105103 CrossRef PubMed.
- M. C. Stewart and R. Evans, J. Chem. Phys., 2014, 140, 134704 CrossRef CAS PubMed.
- B. Chacko, R. Evans and A. J. Archer, J. Chem. Phys., 2017, 146, 124703 CrossRef PubMed.
- A. Maciołek, A. Drzewiński and P. Bryk, J. Chem. Phys., 2004, 120, 1921–1934 CrossRef PubMed.
- X. Huang, C. J. Margulis and B. J. Berne, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 11953–11958 CrossRef CAS PubMed.
- B. S. Jabes, D. Bratko and A. Luzar, J. Phys. Chem. Lett., 2016, 7, 3158–3163 CrossRef CAS PubMed.
- A. J. Patel, P. Varilly, S. N. Jamadagni, H. Acharya, S. Garde and D. Chandler, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 17678–17683 CrossRef CAS PubMed.
- A. J. Patel, P. Varilly and D. Chandler, J. Phys. Chem. B, 2010, 114, 1632–1637 CrossRef CAS PubMed.
- Y.-K. Cheng and P. J. Rossky, Nature, 1998, 392, 696 CrossRef CAS PubMed.
- P. Tiwary, J. Mondal, J. A. Morrone and B. Berne, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 12015–12019 CrossRef CAS PubMed.
- R. Evans, Adv. Phys., 1979, 28, 143 CrossRef CAS.
- J. F. Lutsko, Adv. Chem. Phys., 2010, 144, 1 CrossRef CAS.
- R. Roth, R. Evans, A. Lang and G. Kahl, J. Phys.: Condens. Matter, 2002, 14, 12063 CrossRef CAS.
- R. Womersley, Efficient Spherical Designs with Good Geometric Properties, http://web.maths.unsw.edu.au/rsw/Sphere/EffSphDes/index.html, accessed: 2017-04-12.
- A. Gonzalez, J. A. White, F. L. Roman and R. Evans, J. Chem. Phys., 1998, 109, 3637 CrossRef CAS.
- E. A. Mastny and J. J. de Pablo, J. Chem. Phys., 2007, 127, 104504 CrossRef PubMed.
- W. A. Steele, Surf. Sci., 1973, 36, 317 CrossRef CAS.
- W. A. Steele, The Interaction of Gases with Solid Surfaces, Pergamon, Oxford, 1974 Search PubMed.
- D. W. Siderius and L. D. Gelb, J. Chem. Phys., 2011, 135, 084703 CrossRef PubMed.
- N. Ashcroft and N. Mermin, Solid State Physics, Saunders College, Philadelphia, 1976 Search PubMed.
- S. H. Behrens and D. G. Grier, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2001, 64, 050401 CrossRef CAS PubMed.
- W. Haynes, CRC Handbook of Chemistry and Physics, Taylor & Francis, 93rd edn, 2012 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: (1) Computation of the contact angle relationship with the energy parameter ε, (2) density profile, (3) geometrical expressions used to compute the depletion forces using a capillary model, (4) model to identify conditions at which the cylindrical pore is filled/empty, (5) comparison of density profiles for small hydrophilic pores and (6) nanoparticle inclusion for empty and filled pores (7) role of the nanoparticle hydrophobicity with a hydrophobic wall. See DOI: 10.1039/C7NR07218J |
| This journal is © The Royal Society of Chemistry 2017 |