Open Access Article
Open Access ArticleStatic and dynamic hidden symmetries of icosahedral viral capsids
Sergey B.
Rochal
 *a,
Olga V.
Konevtsova
a and
Vladimir L.
Lorman
b
*a,
Olga V.
Konevtsova
a and
Vladimir L.
Lorman
b
aFaculty of Physics, Southern Federal University, 5 Zorge str., 344090 Rostov-on-Don, Russia. E-mail: rochal_s@yahoo.fr
bLaboratoire Charles Coulomb, UMR 5221 CNRS and Université de Montpellier, pl. E. Bataillon, 34095 Montpellier, France
First published on 26th July 2017
Abstract
Viral shells self-assemble from identical proteins, which tend to form equivalent environments in the resulting assembly. However, in icosahedral capsids containing more than 60 proteins, they are enforced to occupy not only the symmetrically equivalent locations but also the quasi-equivalent ones. Due to this important fact, static and dynamic symmetries of viral shells can include additional hidden components. Here, developing the Caspar and Klug ideas concerning the quasi-equivalence of protein environments, we derive the simplest hexagonal tilings, that in principle could correspond to the local protein order in viral shells, and apply the resulting theory to nucleocytoplasmic large dsDNA viruses. In addition, analyzing the dynamic symmetry of the P22 viral shell, we demonstrate that the collective critical modes responsible for the protein reorganization during the procapsid maturation are approximately equivalent to the normal modes of the isotropic spherical membrane with O(3) symmetry. Furthermore, we establish the relationship between the dynamic symmetry of the P22 procapsid and the protein arrangement regularities that appear only in the mature capsid.
Introduction
By the middle of the last century, symmetry became the robust basis for the exploration and formulation of the fundamental principles of non-living nature. The symmetry determines the structural organization and dictates the dynamics of relatively simple physical and chemical nanoscale systems. In living organisms, which are incommensurably more complex than classical objects studied in physics and chemistry, the role of symmetry appears to be less significant. Nevertheless, symmetry in its different forms remains extremely important for viruses representing relatively simple systems that are intermediate between living and non-living forms.1 On the one hand, during the maturation,2–4 which usually occurs at the final stages of virus self-assembly, viral shells reconstruct their protein structures but preserve their initial icosahedral symmetry. On the other hand, the highly ordered viral capsid also contains a genome and therefore both mechanisms of host cell infection as well as virulence of viruses are strongly dependent on the structural organization of capsids.5–7 For these reasons, studying general (including symmetry) principles for determining the capsid structure and processes of viral shell reorganization presents a challenging task of great significance.In addition, many basic concepts established for viral capsids are also used in other fields of nanoscience: for applications in nanobiotechnology, e.g., controlled drug delivery and nanoparticle encapsulation; and for elucidating the design and development of antiviral strategies in the rapidly developing field of nanomedicine,8–10 and then all the way to the fundamental problems of nanophysics and nanochemistry.11,12
Capsids have been studied for more than 50 years. As early as 1962, Caspar and Klug (CK) understood that rotational icosahedral symmetry I is typical of viral shells and proposed the famous geometrical model of their structure.13 Proteins forming a capsid are most often identical to each other. So, in order to minimize the number of conformational states, which are necessary for a large number of identical protein units to establish chemical bonds between neighbors, CK modeled the viral shell with an additional (or hidden) local symmetry, which made environments of all identical proteins structurally similar or quasi-equivalent, effectively combining two seemingly incompatible concepts: global icosahedral symmetry and local translational order. The proposed model was based on smooth mappings of a specific periodic hexagonal structure onto the surface of a regular icosahedron. The proposed structure has P6 chiral symmetry and was constructed from proteins located in one system of equivalent points with the trivial symmetry.
The identification of a translation (h, k) of the hexagonal structure with an icosahedral edge allowed CK to match the planar hexagonal order with the icosahedral shell consisting of 20 regular triangles. CK showed that if the vertices of 60° sectors eliminated from the shell net are situated at the future 5-fold icosahedral axes, then it is possible to fit the hexagonal orders at the glued faces of the icosahedral shell perfectly. The resulting capsid structure allows “not to break the type of lattice chemical bonds”,13 because in addition to the conventional point symmetry, the obtained icosahedral shell preserves the symmetry of the planar hexagonal structure in a latent form. This latent symmetry converts symmetrically nonequivalent protein positions into quasi-equivalent ones.
The CK model imposes strong restrictions on both the number N of proteins in a capsid (N = 60T, where T = h2 + k2 + hk, and indices (h, k) are non-negative integers) and their space organization, in particular, imposing the fact that the capsid should consist of hexamers and pentamers.13 Indeed, the overwhelming majority of the structures of small- and medium-sized viral capsids is in full agreement with the CK model, but there are notable anomalous viral shells with the structural organization violating the model.14–19 For instance, the capsid of L–A virus is characterized by T = 2, which is impossible at integers h and k; the capsid of Dengue virus characterized by T = 3 and the capsids of other Flaviviridae (Zika virus, Yellow Fever virus, Western Nile virus, etc.) do not contain hexamers at all (in contrast to the viral shells described by the CK model). The capsids of nucleocytoplasmic large dsDNA viruses of Asfarviridae, Ascoviridae, Iridoviridae, Poxviridae, Mimiviridae, and Phycodnaviridae20–23 viral families also do not contain hexamers but instead have trimers and pentamers as their structural units (SUs). Although the latter capsids can still be characterized by the CK triangulation number T, it no longer coincides with the number of symmetrically nonequivalent protein orbits in the capsid and the famous equality N = 60T becomes invalid.
The existence of various viral capsids violating the CK model keeps attracting interest to the interpretation of their structures. The overwhelming majority of publications devoted to the anomalous viral shells endows the CK model as absolutely inapplicable to such capsids and propose much more complicated conceptions for their rationalization.24–31 For example, in ref. 24 the CK idea to map the planar 2D order onto the shell surface was completely rejected; instead the tiling approach typical of quasi-crystals was suggested. In the models of large and giant viral capsids only the regular icosahedron is ordinarily taken from the CK model.32–34 This icosahedron is not covered with a common hexagonal lattice. Instead, its neighboring faces are decorated with differently oriented (but symmetrically equivalent) trigonal patterns.
Recently, we modified the CK model and made it suitable to describe the anomalous capsids of small viruses.35 Both anomalous and ordinary small viral shells (with T ≤ 4) were obtained in the framework of the CK projection scheme due to the chiral mappings of the primitive hexagonal lattice (PHL) onto the regular icosahedral surface. In the modified model,35 the asymmetric proteins occupy all former PHL nodes, which obtain the trivial symmetry after the order transfer onto the icosahedral surface. This approach eliminates too strict symmetry restrictions of the CK theory and demonstrates that small viral shells possess PHL symmetry in a latent form. However, the question of whether there are other simple planar structures that can correspond to the order of proteins in other anomalous capsids is still unanswered.
In the first part of this article, generalizing the CK quasi-equivalence principle and developing further our approach,35 we deduce a very limited number of regular patterns that can underlay the protein order in various viral shells, which are unexplained in the framework of neither the original CK model13 nor the modified one.35 The obtained patterns (additional to the PHL) are the simplest hexagonal periodic tilings generated from the PHL by minimal multiplications of its unit cell. The tilings found describe, in particular, the local order of proteins in a wide variety of large and giant viral shells.
The static and dynamic symmetries of the P22 bacteriophage considered in the second part of this article are even more interesting. As is known,4,36 during the P22 bacteriophage maturation the initially spherical procapsid becomes faceted and its volume increases. Additionally, the hexamers deformed in the procapsid take the regular shape. All these features are common for maturation of numerous bacteriophages. Nevertheless, as we show here, this process in the P22 viral shell is characterized by two intriguing peculiarities. First, both the changes of the shell shape and the symmetrization of hexamers represent the procapsid collective critical modes that are almost equivalent to the normal ones of the isotropic spherical membrane with the O(3) symmetry. Second, the hidden dynamic symmetry revealing itself in the specific form of the procapsid critical modes is not the only one for the P22 viral shell. As a result of the maturation process, the local symmetry of the protein order in the mature capsid increases, giving rise to the structure that could be obtained directly by means of the symmetry allowed mapping of the honeycomb lattice onto the icosahedral surface. Thus, two hidden symmetries revealing themselves in the dynamics of procapsid critical modes and in the structural regularities of the mature capsid turn out to be mutually dependent.
Results and discussion
Simplest hexagonal periodic tilings and the structures of large and giant viral capsids
Considering the structures of small viral capsids, we have shown35 that the CK choice of the hexagonal structure (which is mapped onto the icosahedron surface in the CK model) is too specific because the mapping of any planar hexagonal structure onto the icosahedral surface breaks the local symmetry of the mapped positions. This symmetry breaking allows locating asymmetric proteins directly on the icosahedral surface at positions coinciding with those of the symmetry axes of the initial planar structure. The chiral mappings of PHL onto the icosahedral surface lead to structural models of small viral capsids both satisfying and contradicting the CK original theory.35 Since within the PHL framework it is possible to explain the organization of only a limited number of capsids, we start this section by the construction of other planar patterns suitable to model the protein order in other icosahedral viral shells.To get these structures, it is reasonable to use the well-known CK ideas, according to which the spatial organization of identical proteins in capsids should ensure the maximal equivalence of protein environments. For that purpose, the following conditions should be satisfied. First, only the presence of 6-fold axes in the periodic structures enables their smooth mapping onto the icosahedron surface, therefore, in order to construct the icosahedral capsids, it is reasonable to use the periodic structures with hexagonal symmetry. Second, the desired structures should be chiral since in achiral structures constructed from asymmetrical SUs both left-handed and right-handed units are required simultaneously. Third, due to the presence of identical proteins, the structures should include the only crystallographic position (not mandatory in general as in the CK approach) containing symmetrically equivalent nodes.
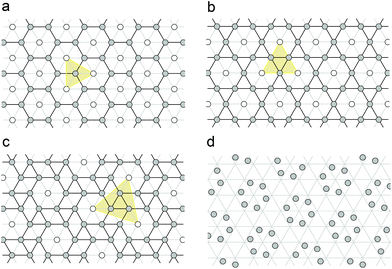
The CK structure13 satisfies all the conditions listed above. It has P6 symmetry and contains one general crystallographic position, which can be occupied by proteins directly before the mapping. However, there also exist three appropriate periodic hexagonal patterns with the positions of 6-fold, 3-fold and 2-fold local symmetries, respectively. The first of these structures is PHL, while two other ones are ordinarily called honeycomb lattice (HCL) and trihexagonal tiling (TT), which is also referred to as the Kagome lattice. All these three structures are closely related to each other. HCL and TT are easily obtained from PHL as a result of its unit cell multiplication by 3 and 4, accordingly (see Fig. 1a and b). To increase the generality of our approach, we decided to also consider snub trihexagonal tiling (STT) (shown in Fig. 1c) that appears in the case of the next symmetrically allowed multiplication of the PHL unit cell by 7. Let us note that due to the same geometrical reasons that cause the CK selection rules,13 the 6-fold symmetry is conserved if and only if the PHL unit cell is multiplied by Tm = h2 + k2 + hk, where (h, k) are integers. Therefore, above we listed all allowed tilings with Tm ≤ 7. Additionally, Fig. 1d demonstrates how the well-known CK structure is obtained from the STT one.
In the structures under consideration the squared length of a primitive translation is expressed as Ts = h2 + k2 + hk, where indices (h, k) are integers. For the structures depicted in Fig. 1a–c, the indices are (1, 1), (2, 0) and (2, 1), respectively. In all these three cases, the unit cell multiplication and corresponding symmetry lowering lead to the splitting of the PHL nodes into two regular crystallographic positions. One of them (denoted with empty circles) constitutes the PHL with an enlarged cell, while the second one (denoted with filled circles) forms the tilings, which are used for further investigation of capsid structures.
We now show how the capsid structures of the majority of nucleocytoplasmic large dsDNA viruses can be interpreted within the framework of the patterns depicted in Fig. 1a–c. We consider the virus group that infects eukaryotes and encompasses members of the Asfarviridae, Ascoviridae, Iridoviridae, Poxviridae, Mimiviridae, and Phycodnaviridae20–23 viral families. One of the most actively discussed representatives of this virus group is Paramecium Bursaria Chlorella Virus (PBCV-1), which is the member of the Phycodnaviridae viral family. According to the experimental data,32 the PBCV-1 capsid contains 5040 protein copies organized in 1680 trimers and 60 protein copies organized in pentamers. Centers of trimers and pentamers form a pseudo T = 169d quasi-equivalent lattice.32 One more member of the Phycodnaviridae family, Phaeocystis pouchetii virus (PpV01) with T = 219 (h = 7, k = 10)37 and Chilo iridescent virus (CIV)38 with T = 147 (h = 7, k = 7) of the Iridoviridae family have similar capsid organizations. The local structure of these capsids (as the ones of the majority of nucleocytoplasmic large dsDNA viruses) is commonly interpreted as the PHL, the nodes of which are decorated with trimers; each trimer consisting of 3 elongated monomers.32,34 Since each monomer, in turn, entails two domains, the trimers are often treated as pseudohexamers.
As we demonstrate below, the regularities of the local protein order in the above-mentioned capsids can be understood in the frame of the STT structure (see Fig. 1c). A comparison between the panels a–c of Fig. 2 demonstrates that the elongated monomers form three of each of the six STT edges of the hexagons’ sides. These edges are shown in Fig. 2a with double lines. Such arrangement of monomers decreases the symmetry of the capsid facets from P6 to P3. However, since monomers consist of two domains, the domain centers are located in the vicinity of the STT nodes (which are denoted by yellow circles). Thus, the trigonal order of facets turns out to be very close to the parent hexagonal one. Nevertheless, the symmetry lowering from P6 to P3 breaks the local translational order between the adjacent facets near the edges of the icosahedral shell as evidenced also by experiments.38
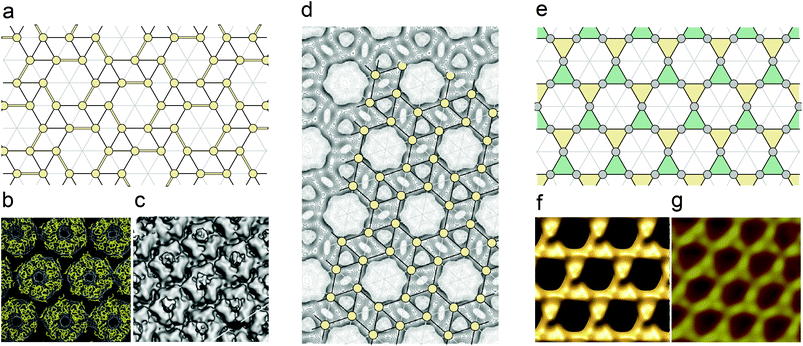 | ||
| Fig. 2 Hidden symmetry of the large and giant viral capsids. (a) Decoration of the snub trihexagonal tiling leading to its symmetry lowering from P6 to P3. To break the hexagonal symmetry some STT edges are drawn with the double lines. In the capsids of PBCV-132 and CIV,38 which are shown in panels (b) and (c), respectively, the monomers form these edges. In the frames of the proposed interpretation, each STT node (these nodes are denoted by yellow circles) is located near the center of one of domains, pair of which forms a monomer. (d) Protein density map of the Vaccinia virus scaffolding D13 on top of a membrane (modified from ref. 40). Snub hexagonal tiling is imposed on the density map. The nodes of this tiling (yellow circles) coincide with the most intensive maxima of the density map.40 (e) Interpretation of the Mimivirus capsid in terms of the trihexagonal tiling (shown in Fig. 1b). Coloring of triangles with yellow and green corresponds to the two sublattices of trimers discussed in the text. (f) Mimivirus viral shell surface simulated by using the homologous PBCV1 capsomer structure.33 (g) High-magnification AFM image of the Mimivirus surface.41 Comparison between panels (e–g) shows that the nodes of the trihexagonal tiling and the most protruding points on the capsid surface form very similar patterns. | ||
Although the capsid structures of the majority of nucleocytoplasmic large dsDNA viruses are similar and can be described in the same framework, there exist two known exceptions: the capsid of Mimivirus (Mimiviridae family)33 and the protein shell of the immature virion of Vaccinia virus (Poxviridae family).39,40 In both exceptional cases, trimers are located at the HCL nodes (denoted by filled circles in Fig. 1a) instead of the PHL ones. At the initial stage of the immature virion self-assembly, D13 proteins (which are not contained in the mature Vaccinia virion) form trimers with pseudohexagonal symmetry. Later these trimers self-assemble into a spherical shell that becomes brick-shaped during the maturation process. A surface representation of the Vaccinia virus scaffolding D13 on top of a membrane is shown in Fig. 2d, which is modified from ref. 40. The most intensive maxima of the 3D density map (the highest one is chosen for each protein molecule) coincide with the nodes of the superimposed STT (see this tiling shown in Fig. 1c). We believe that this coincidence convincingly demonstrates the hidden symmetry of the capsid under consideration.
In contrast with the spherical shell of immature Vaccinia virion, the giant shell of Mimivirus is characterized by strong icosahedral faceting. Nevertheless, according to ref. 34 and 40 the structures of the immature Vaccinia shell and the Mimivirus one are similar since in contrast to the majority of nucleocytoplasmic large dsDNA viruses, these shells are based on the HCL arrangement (instead of the PHL one). The HCL nodes are decorated with trimers, which are the SUs typical of all large and giant viral shells. However, apparently the Mimivirus capsid is not definitively resolved. Xiao et al.33 use a possible analogy with the structure of Paramecium bursaria chlorella virus-1 (PBCV-1) and claim that the HCL in the Mimivirus capsid is decorated with trimers in such a way that the order of the capsid facets has P6 symmetry. To satisfy this condition, the neighboring trimers located on the HCL nearest vertices should be mutually rotated by 60° with respect to one another. In contrast, Klose and Rossmann34 presume that all trimers inside one facet are parallel to each other (as is the case in the majority of nucleocytoplasmic large dsDNA viral capsids based on the PHL arrangement). The parallel orientation of all trimers inside the facet then decreases its symmetry down to P3. This symmetry lowering, in turn, should break the local translational symmetry between the trimers located near the icosahedron edges and this type of local order distortion is also confirmed experimentally.33 However, it is clear that the parallel orientation of all trimers (inside every facet) is not mandatory to obtain P3 symmetry. Conserving this symmetry, two types of symmetrically nonequivalent trimers (located in the nearest HCL nodes) can arbitrarily rotate around each other. Having no intention of proposing our own model of the Mimivirus shell, we stress that the ambiguities in the interpretation of this structure are not very essential. The CryoEM reconstruction data33 (see Fig. 2f) and the AFM images41 (see Fig. 2g) indicate strongly that in this capsid the most protruding points on the shell surface form a pattern, which is very close to the arrangement of the TT nodes (see this tiling in Fig. 2e). Returning to the Mimivirus shell models,33,34 let us clarify that in both of them the centers of protein trimers coincide with the centers of triangles forming the TT structure. As shown in Fig. 2e yellow and green triangles correspond respectively to the two sublattices of trimers (which are symmetrically equivalent in the model33 and are not in the other one34).
So, in spite of the fact that in both capsids of Vaccinia virus and Mimivirus trimers are located in the HCL nodes, a more detailed analysis reveals the different hidden symmetries underlying these shells, and the latent regularities of the protein arrangements in the considered capsids are described in terms of STT and TT structures, respectively.
Thus, the experimental data discussed above demonstrate that in a wide variety of large and giant viral capsids the hidden static symmetry reveals itself in the specific regular arrangements of the protein order (see Table 1). Depending on the capsid type, these arrangements can be interpreted in terms of the periodic trihexagonal or snub trihexagonal tilings, which can be found in patterns formed by the protein distribution functions or by the most protruding points on the capsid surfaces. We note also that the STT nodes have the trivial local symmetry and can be occupied by proteins (or their domains) without any symmetry caused restriction. In contrast, due to the 2-fold local symmetry of the TT nodes, the asymmetrical SUs can be located in them only after the tiling is transferred onto the icosahedral surface. Of course, the nodes mapped onto 2-fold icosahedron axes cannot be filled. This selection rule is, however, inessential for the Mimivirus capsid since in the considered models33,34 of this shell the proteins never coincide with the TT nodes.
| Virus | Family | Triangulation | Location of trimer centers | Hidden symmetry | Latent peculiarity in protein order |
|---|---|---|---|---|---|
| Paramecium bursaria chlorella virus (PBCV-1) | Phycodnaviridae | T = 169; h = 7, k = 8 | PHL | STT | Dimers are located along some of STT edges |
| Phaeocystis pouchetii virus (PpV01) | Phycodnaviridae | T = 219; h = 7, k = 10 | PHL | STT | Dimers are located along some of the STT edges |
| Chilo iridescent virus (CIV) | Iridoviridae | T = 147; h = 7, k = 7 | PHL | STT | Dimers are located along some of the STT edges |
| Immature virion of Vaccinia virus | Poxviridae | The capsid is not icosahedral | HCL | STT | STT is formed by the most intensive maxima of the protein density map |
| Mimivirus | Mimiviridae | 972 ≤ T ≤ 1200; h = 19 ± 1, k = 19 ± 1 | HCL | TT | TT nodes are the most protruding points on the capsid surface |
The next section is entirely devoted to the P22 viral shell, for which the restrictions imposed on the local symmetry of positions occupied by the asymmetrical proteins became essential. This viral shell is interesting for us since it exhibits two different hidden symmetries simultaneously. The first of them reveals the exceptional dynamics of the P22 procapsid critical modes, which are responsible for morphological changes of this viral shell during its maturation. The second latent symmetry appears only in the mature viral shell and leads to a more regular capsid structure that could be obtained directly by means of an appropriate mapping of the HCL tiling onto the icosahedral surface.
Hidden symmetries in the viral shell of bacteriophage P22
It is well known that the final stage of the virus formation is its maturation, giving rise to its ability to infect the host cell. The maturation is characterized by a series of significant, correlated changes in the procapsid structure. One of the most common features of this process, which is typical of a variety of viruses and widely discussed in the literature, is the change of the shell's shape from spherical to faceted.4,42,43 Along with the biochemical transformations, some purely physical phenomena play a significant role during the maturation process. Particularly, it was demonstrated that the main structural changes of the procapsid during its maturation can be described as the result of a condensation of several (critical) normal modes of the procapsid shell.44,45 This idea allows us to interpret the maturation process (or at least its early stages, when the formation of the chemical cross-linking bonds between the capsid's proteins, typical of the final stages, has not yet started) as a soft-mode phase transition in analogy to the structural phase transformations in crystals.46,47However, the capsids do not have the translational symmetry of crystals. Therefore, the analysis of normal modes in capsids is much more difficult. Following the standard procedure for the determination of normal modes, one can calculate and diagonalize the Hessian matrix of 3N dimensions, where N is the total number of the rigid SUs in the capsid.48 However, the selection of elastically coupled rigid SUs is not a completely reasonable approach, since the capsid's proteins consist of domains, which have a complex internal structure. While taking into account that the distinct atoms and their mutual interactions are more appropriate, it is also a much more complicated task due to the enormous number of atoms in any capsid and therefore a whole series of different models have been devoted to the calculation of the normal modes in capsids.49–52
An alternative methodology was proposed to apply the continuum approach to analyze different phenomena in capsids53–56 and we have also used this approach to study the maturation process in the bacteriophage HK97.57 We have shown that the experimentally observed rotation of pentamers and the symmetrization of hexamers, occurring during the maturation process in this bacteriophage, are approximately equivalent to the switching-off of the irreducible (with the wave number l = 6) shear field of an isotropic and homogeneous spherical shell.
The advantage of the continuum approach is that it leads to complex, but observable analytical solutions, which can be easily compared with the experimental data. Unfortunately, the continuum approximation by necessity idealizes the viral shell, treating it as isotropic and homogeneous. Consequently, the necessary conditions for the continuum approach to be applied to any system are such that the effective wavelengths of the modes which can be described within this approximation should be much larger than the distances between the adjacent SUs. Even if this condition is satisfied, there remains another open question: to what extent and in which particular cases is it justified to replace the icosahedral symmetry of the capsid by the continuous symmetry of the ideal sphere. In fact, this question leads further to another one, which can be ultimately answered only by analyzing experimental data: to what extent can the dynamic elastic properties of the viral shell be considered as spherically symmetric in the long-wavelength limit?
We leave the comparison with the experiment until the end of this section and first recall briefly the main facts about the linear dynamics and types of the normal modes existing in the isotropic spherical membrane. Earlier, both the dynamics of a spherical shell with a finite thickness53 and that of an infinitely thin membrane58 have been considered in the literature. The difference between these two models does not affect the possible types of modes, which can be classified in both cases according to the irreducible representations (IRs) of the spherical symmetry group O(3). This is not surprising since it is well-known that within the linear regime, every normal mode of any system is spanned by the single IR of the system's symmetry group, while the solutions of the linearized equations of motion are always the linear combinations of normal modes.
For a thin spherical shell, regardless of the model which describes its linear dynamics, the O(3) symmetry imposes very strict constraints on the possible normal modes. Three types of modes are ordinarily distinguished: bending, stretching and shear modes. The displacement fields corresponding to bending and stretching normal modes contain both the radial and tangent components, since the irreducible radial and tangent displacement fields with the same wave number l can be linearly coupled. The mode with the main contribution of the radial component is conventionally called the “bending” mode, while the mainly tangential mode is denoted as the “stretching” mode. In contrast, the shear modes have only a tangent component. For normal bending-stretching modes the displacement fields ulm(θ,φ) of the points on the spherical surface can be represented as:
| ulm(θ,φ) = AlmYlm(θ,φ)er + Blm grad‖Ylm(θ,φ), | (1) |
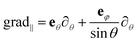 . All modes with the same l are (2l + 1) times degenerate and have the same frequency, which is determined by the parameters of the shell model. These parameters also define the ratio between the amplitudes Alm and Blm. As for the shear modes, the corresponding displacement fields have the following form:
. All modes with the same l are (2l + 1) times degenerate and have the same frequency, which is determined by the parameters of the shell model. These parameters also define the ratio between the amplitudes Alm and Blm. As for the shear modes, the corresponding displacement fields have the following form:| ulm(θ,φ) = Clm[er × grad‖Ylm(θ,φ)]. | (2) |
Normal modes with displacement fields (2) are also (2l + 1) times degenerate, so their frequencies do not depend on the m value. Note also that the parity Pr of functions Ylm(θ,φ) and that of the displacement fields (1) are the same: Pr = (−1)l, while for the shear fields (2)Pr = (−1)l+1. Therefore, the parities of bending–stretching and shear modes possessing the same wave number l are opposite and these modes are thus linearly uncoupled.
As is mentioned above, the symmetry of the procapsid is determined by the spatial distribution of the chiral protein molecules and is characterized by the rotation group of icosahedron I, which is the subgroup of the symmetry group of sphere O(3). The procapsid can therefore exhibits different types of normal modes and the application of eqn (1) and (2) for the description of procapsid dynamics needs further elucidation.
In contrast to the group O(3), which has an infinite number of IRs, the group I possesses only 5 IRs. As a result, several symmetrically different normal modes of the spherical membrane can contribute to only one normal mode of the procapsid. The standard methods to analyze the dynamics of systems related to the group–subgroup relationship allow constructing correlation dependencies between the modes of ideal spherical shells and those of icosahedral procapsids.53 According to the conventional group theory,53,59 the procapsid mode spanning the given IR of the group I, can include only those modes of the spherical membrane that are characterized by the symmetrically allowed IRs of the group O(3). After the symmetry restriction O(3) → I each allowed IR of the group O(3) should contain the given IR of the group I.
In the course of proteins’ reorganization during the procapsid-to-capsid reconstruction, the I symmetry of the viral shell is ordinarily conserved. Therefore, first of all, we are interested in the relationship between the totally symmetrical normal modes of procapsid and the normal modes of the spherical shell. Eqn (1) and (2) show that if some linear combination of spherical harmonics 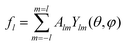 has I or Ih symmetry then the fields
has I or Ih symmetry then the fields
| ulr = erfl, | (3a) |
| ulstr = grad∥fl, | (3b) |
| ulshear = [er × grad∥fl], | (3c) |
The theory of irreducible functions fl was developed earlier.30,31 Here we note only that the so-called integrity basis of the symmetry group I consists of 4 invariants, which have 2nd, 6th, 10th and 15th degrees. In addition, the square of the latter invariant is a polynomial function of the three former ones and the invariant of the second degree is totally isotropic on the sphere surface. Based on these facts, the functions fl can be constructed only for those l values, which satisfy the following relation:
| l = 15k + 6i + 10j, | (4) |
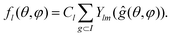 | (5) |
Here elements ĝ are 60 symmetry operations of the group I. For different m values, the sum in eqn (5) yields either zero or functions that differ only by the normalizing coefficient Cl. For example, we present the first allowed function f6, which in Cartesian coordinates has the following simple form:
| f6(x,y,z) = (y2 − z2τ2)(z2 − x2τ2)(x2 − y2τ2) + c, | (6) |
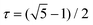 is the golden mean,
is the golden mean, 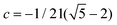 , and the radius-vector r = <x,y,z> of a point on a unit sphere is related in a standard way to θ and φ variables of the spherical coordinate system. It is also useful to show explicitly the function f15, which is used below to describe the deformation of the hexamers in the procapsid P22. In Cartesian coordinates this function reads:
, and the radius-vector r = <x,y,z> of a point on a unit sphere is related in a standard way to θ and φ variables of the spherical coordinate system. It is also useful to show explicitly the function f15, which is used below to describe the deformation of the hexamers in the procapsid P22. In Cartesian coordinates this function reads: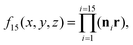 | (7) |
It is very important to note that any symmetric (with respect to the procapsid symmetry I) displacement of the spherical surface can be expanded into a series of fields (3). However, if and only if the hidden spherical symmetry indeed reveals itself in the totally symmetric normal mode of the procapsid, then the only one normal mode of the spherical membrane should give the main contribution to this procapsid mode. Since the main structural changes during the procapsid maturation can be described as a condensation of several totally symmetric normal modes of the procapsid shell,44,45 we can state in addition that if the procapsid dynamics indeed possesses the hidden spherical symmetry, then the protein reorganization during the procapsid maturation should be well described by only several (critical) fields (3) with particular values of l.
Below we proceed to the application of the above theoretical developments to study the morphological changes in viral shells upon their maturation. As we mentioned above, during the maturation of different bacteriophages (including bacteriophage P22) the procapsid shape changes from spherical to faceted. It is not difficult to verify that the appearance of this icosahedral faceting can be well described by the simplest radial critical field ur = erf6, which has the symmetry Ih (see Fig. 3). Also, it is very interesting to stress that two opposite signs of this radial field lead to both the icosahedral and dodecahedral shapes of the initially spherical membrane. While the capsids with the icosahedral faceting (similar to that of P22) are well known, there exists also a whole series of viruses which display the dodecahedral capsid shape. An example of this type is given by the pathogenic human Parvovirus B1960 (which is shown in Fig. 3d). It is surprising that the simplest critical function (6) catches the difference between icosahedron and dodecahedron in a very simple and straightforward way.
 | ||
| Fig. 3 (a and b) Spherical surface deformation by radial displacement fields proportional to the irreducible function f6 given by eqn (6). Amplitudes of the displacement fields in panels (a) and (b) have opposite signs. (c and d) Experimental realization of the capsid shapes induced by displacement fields (a) and (b). Icosahedral viral capsid of the bacteriophage P22 (see ref. 61) is shown in panel (c), while panel (d) demonstrates the viral capsid of the pathogenic human parvovirus B19 (see ref. 60) with the dodecahedral faceted shape. | ||
Upon the maturation changes in the procapsid shell of bacteriophage P22, the hidden symmetry O(3) clearly manifests itself not only in the appearance of faceting (similar shape changing is common for a lot of capsids), but also during the symmetrization of hexamers. Previously, for the case of bacteriophage HK 97,57 we showed that the switching-off of the irreducible shear field (which in terms of the developing theory reads as [er × grad f6]) is equivalent to the symmetrization of hexamers. Bacteriophage P22 has an analogous hidden dynamical symmetry that reveals itself in the other critical irreducible shear field u15shear = [er·grad f15]. This difference is possibly related to the fact that HK97 and P22 viruses belong to two different classes of phages.4 This difference can be justified by the following known fact. For HK97, the procapsid proteins are found in the solution only in the state of capsomers, which form a dynamical mixture of hexamers and pentamers.37,62 In contrast, the procapsid proteins of the bacteriophage P22 exist as monomers in the solution63,64 and consequently these viral shells are self-assembled in different pathways.
Fig. 3c shows the capsid of bacteriophage P22,65 which (as well as the previously mentioned capsid HK 97) consists of 420 proteins. However, in contrast to HK97, the structure of the mature capsid P22 has the hidden symmetry, which allows one to model the mature shell in terms of the HCL structure mapped onto the surface of a regular icosahedron. The positions of proteins in the mature capsid of P22 bacteriophage (see Fig. 4c modified from ref. 65) are marked by yellow dots, located in the most protruding points on the capsid surface. In addition to Fig. 4c, Fig. 4b helps to understand our interpretation of the capsid structure, since faceting of the spherical honeycomb lattice shown in Fig. 4b leads to the lattice shown in Fig. 4c.
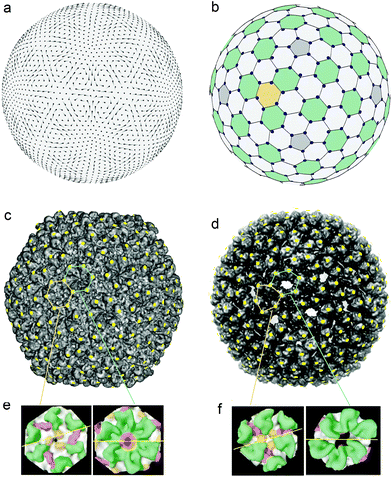 | ||
| Fig. 4 The reorganization of the viral shell of the bacteriophage P22 and the hidden symmetries becoming discernible during the maturation process. (a) The displacement field u15shear corresponding to the normal shear mode of a homogeneous and isotropic spherical shell. This is the simplest irreducible shear field with icosahedral symmetry Ih. Vectors of the field are given by line segments; the color intensity gradient of the segment indicates the field direction, while the segment length is proportional to the field amplitude. (b) The undistorted spherical honeycomb lattice formed from approximately regular hexagons and pentagons. The lattice nodes are shifted by the field u15shear and shown by the blue circles. (c) Experimental structure of the bacteriophage P22 capsid.65 The yellow dots marked on the structure are located at the most protruding points on the capsid surface. These dots form the 3D honeycomb lattice, which can be obtained due to the faceting of the spherical lattice shown in panel (b). (d) Experimental structure of the bacteriophage P22 procapsid.66 Yellow dots have the same angular coordinates as the blue circles in panel (b). These dots and the most protruding points at the procapsid surface practically coincide. (e) The local structure of the capsid: the arrangement of six proteins around the 3-fold axis (left panel) and the internal arrangement of the hexamer (right panel) are similar.36 This fact indirectly confirms the found hidden symmetry of the capsid. (f) Local structure of the procapsid: the arrangement of proteins around the 3-fold axis (left panel) and their arrangement in the deformed hexamer (right panel) are substantially different.36 | ||
The positions of proteins in the procapsid P22 (see its structure in Fig. 4d modified from ref. 66) can also be determined as the most protruding points on the immature shell surface. Then, by expanding the tangential part of the protein displacement fields into a series of irreducible mutually-orthogonal fields (3b) and –(3c), it is possible to conclude that the main contribution to the deformation of hexamers is due to the shear field u15shear. This fact is easily checked directly by comparison between panels (d) and (b) of Fig. 4. The latter panel shows both the undistorted spherical honeycomb lattice and its nodes (small blue circles) shifted by the field u15shear. In Fig. 4d the positions with the same angular coordinates are shown as small yellow dots, superimposed on the experimental structure of procapsid P22. Since the yellow dots and the most protruding points at the procapsid surface practically coincide, this demonstrates clearly that the field u15shear reproduces quite accurately the tangent shift of protein positions during the procapsid to capsid transformation. We can therefore state that the latent spherical symmetry reveals itself in the normal mode responsible for the symmetrization of the hexamers in the icosahedral protein nanoassembly. Let us stress that the field u15shear is the simplest even (with respect to the spatial inversion) irreducible icosahedral shear field of the spherical shell, while in the case of the procapsid HK97 the simplest odd field u7shear plays the analogous role in the hexamer symmetrization.57
In both the capsid and the procapsid of the bacteriophage P22 all 60 hexamers are symmetrically equivalent. Their centers coincide with 60 from 200 hexagonal tiles (highlighted by green color in Fig. 4b). From the comparison of Fig. 4c–f, it is evident that during the maturation process two symmetrically nonequivalent types of hexagonal tiles (the centers of the first-type tiles lie on the 3-fold icosahedron axes, while the second-type tiles are equivalent to hexamers in the CK model of this shell) obtain the regular hexagonal shape (shown in Fig. 4e) and this symmetrization increases the latent symmetry of the mature P22 shell. Thus, the dynamics of the procapsid critical modes and the structure of the mature capsid appear to be mutually dependent and the two hidden symmetries of this viral shell are therefore interrelated.
At the end of this section, we discuss in detail the general features of the viral shells with icosahedral symmetry and arrangements of proteins similar to that observed in the mature P22 capsid. Note that if such fullerene-type shell possesses icosahedral symmetry (as in the case of the P22 capsid), then it has 20Tf nodes, where the value Tf = hf2 + kf2 + hfkf is determined by the integer indexes (hf, kf) and in analogy with the CK theory defines the squared length of the icosahedron edge. Note also that if all nodes of the fullerene-type shell are filled with the asymmetrical SUs (as it happens in the P22 capsid), then the allowed values of Tf are limited. This restriction is due to the fact that asymmetric SUs cannot be located in sites with nontrivial local symmetry. Let us recall that 3-fold symmetry axes pass through all the nodes of the planar HCL. After the HCL mapping onto the icosahedron surface, the local symmetry of any node is conserved, if and only if this node is located on one of the global 3-fold symmetry axes of the icosahedron. In the fullerene-type icosahedral shells the global 3-fold symmetry axes always coincide either with the HCL nodes or with the centers of the hexagonal cells. The coincidence of the latter type occurs provided Tf is divisible by 3. Thus, only for those HCL mappings which satisfy the condition Tf mod 3 = 0, all nodes of the resulting shells lost the symmetry and become suitable for containing the asymmetrical SUs.
In addition, we make two other remarks. First, we stress that such shells have exactly the same number of general orbits as the capsids in the traditional CK model: T = Tf/3. For example, the capsid P22 is characterized by the simplest chiral fullerene-type shell with the minimal value of Tf divisible by 3: Tf = 21, <hf = 4, kf = 1>. The vertices of 60 hexagonal tiles (which are green in Fig. 4b) correspond to the locations of all the proteins which form the hexamers in the traditional CK interpretation (T = 7) of this capsid. Second, we note that the arrangement of nodes in the fullerene-type shells can in principle be achiral and in this case the shell acquires the chiral symmetry I only after filling its nodes with the asymmetrical chiral SUs. For instance, in the capsid protein structure of the Herpes simplex virus (T = 16, <h = 4, k = 0>; see Fig. 4 in ref. 67) one can easily recognize the fullerene-type achiral shell for which Tf = 48, <hf = 4, kf = 4>.
Conclusions
We presented a detailed study of the hidden static and dynamic symmetries of the icosahedral viral shells. The first of them is related to the structural peculiarities and conventional symmetry of the planar order underlying the protein arrangements in the capsids. As is known, the paradigmatic CK model13 treats the capsid shell as a regular icosahedron, smoothly covered with a specific planar hexagonal structure, which is formed from identical proteins located at equivalent points with the trivial local symmetry. The CK model implies that the capsids consist of pentamers and hexamers, while the protein order in the shells possesses latent symmetry elements originating from the conventional symmetry operations of the CK hexagonal structure. However, a lot of capsids violate the CK type of protein arrangement.14–23,32–34We considered such anomalous viral shells of the large and giant viruses and demonstrated that they can be modeled within the CK mapping scheme, provided that the hexagonal structures, which are mapped onto the icosahedron surface, are more symmetric than the CK one. Let us stress that the original CK theory treats such structures as prohibited since the nontrivial local symmetry of their crystallographic positions is incompatible with the protein asymmetry. However, the positions, which have nontrivial local symmetry on the plane, can lose it after the order is embedded onto the icosahedron surface, as it occurs if the mapped position is not located on the icosahedral axis. Thus, all such nonspecifically located positions become suitable for the proteins to occupy. Due to this fact, the PHL (the nodes of which have 6-fold symmetry on the plane) can underlie the local order of proteins in small viral capsids.35 Furthermore, developing the CK quasi-equivalence principle, we have found a very limited number of hexagonal patterns in addition to the PHL that in principle could correspond to the local order of proteins in viral shells. These structures are deduced from the PHL due to its unit cell multiplications by 3, 4 and 7, and represent the well-known honeycomb lattice, the trihexagonal tiling and the snub trihexagonal one, respectively. The positions in the first two patterns are located on 3- and 2-fold axes, and the third tiling is interesting because it yields the most regular arrangement of hexamers in the frame of the conventional CK hexagonal structure. Finally, the performed analysis shows that the hidden symmetry of protein organizations in a wide variety of large and giant capsids related to nucleocytoplasmic large dsDNA viruses can be understood in terms of the simple hexagonal tilings listed above. Perhaps, developing our ideas, one will be able to understand the principles of the structural organization of vaults,68 which are nanoscale ribonucleoprotein complexes having a form similar to capsids and present in most multicellular organisms.
It should also be emphasized that both the CK theory and the approach proposed in this article are based on the capsid nets of the icosahedral type. However, some exceptional capsids are not rationalized in this framework since their structures can be enfolded using the nets of the dodecahedral type only.28,69 Therefore neither the original CK theory13 nor its modifications proposed here and in ref. 35 are not applicable to such viral shells. Nevertheless, we would like to emphasize that this fact does not diminish in any way the importance of the CK pioneer theory,13 which successfully explains (even in its original form) the structure of most icosahedral viral shells.
Apparently, the prevalence of the CK-type capsids in nature is caused by the fact that the protein arrangement in them is very close to the periodic order of asymmetrical SUs which is possible on a plane. In contrast, the symmetrical hexagonal tilings considered can be decorated with asymmetrical SUs only on the icosahedral surface, where, obviously, an additional orientational ordering of SUs is needed. Due to this supplemental ordering, the resulting shell's structure is farther from the parent planar order, and consequently, the anomalous capsids are less common than those satisfying the CK theory.13 Although an analysis of the orientational ordering of SUs on the surface of anomalous capsids is beyond the scope of the present article, in future studies one could consider this problem using known approaches developed to study phase transitions in crystals.
The hidden dynamical symmetry of capsids elucidated in this article manifests itself in the maturation processes occurring at the final step of the virus self-assembly cycle. These processes are extremely important since they enable the mature viruses to acquire the ability to infect the host cell. The maturation of any viral shell is characterized by significant correlated changes in its structure. The shape of the shell very often varies from spherical to faceted, and sometimes hexamers, which are deformed in the procapsid, recover a more regular shape. The main structural changes during the maturation process can be described as a result of the condensation of several critical normal modes of the procapsid shell44,45,57 and we further developed and generalized this approach by showing that in some cases, despite the inhomogeneity and lower geometrical symmetry of procapsid, its normal modes (namely, those responsible for the faceting appearance and the change of the hexamers shape) can be quite close to certain normal modes of the homogeneous and more symmetric thin spherical membranes. We also formulated significant group-theory constraints on the types of such modes and proposed a simple way to calculate their explicit form. The hidden dynamical symmetries of HK97 and P22 bacteriophage shells were compared and for the latter case only the static and dynamic hidden symmetries appear to be closely related, since the maturation of the P22 capsid causes the displacement of its proteins approximately into the nodes of the more regular icosahedral shell based on the HCL structure. The resulting structure is the first one in a series of analogous fullerene-type chiral shells with all nodes available for decoration with asymmetric SUs.
As we have noted in the previous section, the hidden symmetry of protein order in mature Herpes simplex capsids can also be interpreted in terms of the HCL structure. However, in spite of the known fact that the protein reorganization during the Herpes simplex virus maturation is similar to the hexamer symmetrization occurring in bacteriophage shells,4 the hidden dynamic symmetry, corresponding to the reorganization process, is absent. As we have checked, for the shell of the Herpes simplex virus it is impossible to relate the hexamer symmetrization with a critical mode being simultaneously the normal mode of a spherical membrane. The Herpes capsid is more complex than the P22 and HK97 viral shells since it contains 3 types of nonequivalent hexamers. Therefore in future studies it would be interesting to search for hidden dynamic symmetry in large icosahedral viruses (with T > 7), where not all hexamers are symmetrically equivalent. It is very interesting to understand whether such capsids can exhibit this symmetry like it occurs in smaller bacteriophages HK97 and P22, where all hexamers are symmetrically equivalent.
Finally, the discovered peculiarities in the structural organization of large and giant viral shells and the established relations between the structural regularities and the dynamics of the critical normal modes in capsids of some bacteriophages can be easily generalized to the case of abiotic materials in the context of nanotechnology. This makes the proposed approach useful for a wide spectrum of scientific domains, from structural and physical virology to nanoscience and soft matter physics.
Author contributions
V. L. proposed to study the symmetry lowering due to the mapping of known hexagonal tilings upon the icocahedron surface. In addition, he revealed the hidden symmetry and latent features of protein arrangement in the Mimivirus capsid. O. K. studied the symmetry of P22 bacteriophage, made the computations and drew the figures. S. R. developed the mathematical fundamentals of the theory suggested and wrote this article.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
S. R. and O. K. are grateful to Rudolf Podgornik for his substantial assistance. After the sudden death of Vladimir Lorman, Rudolf Podgornik has kindly edited this article. S. R. and O. K. gratefully acknowledge financial support from the Russian Science Foundation, grant number 15-12-10004.Notes and references
- S. J. Flint, L. W. Enquist, V. R. Racaniello and A. M. Skalka, Principles of Virology: Molecular Biology, Pathogenesis, and Control, American Society Microbiology, Washington, 2000 Search PubMed.
- J. King and W. Chiu, in Structural Biology of Viruses, ed. W. Chiu, R. Burnett and R. Garcea, Oxford University Press, New-York, 1997, pp. 288–311 Search PubMed.
- J. F. Conway, W. R. Wikoff, N. Cheng, R. L. Duda, R. W. Hendrix, J. E. Johnson and A. C. Steven, Science, 2001, 292, 744–748 CrossRef CAS PubMed.
- D. Veesler and J. E. Johnson, Annu. Rev. Biophys., 2012, 41, 473–496 CrossRef CAS PubMed.
- A. C. Steven, J. B. Heymann, N. Cheng, B. L. Trus and J. F. Conway, Curr. Opin. Struct. Biol., 2005, 15, 227–236 CrossRef CAS PubMed.
- E. Pokidysheva, Y. Zhang, A. J. Battisti, C. M. Bator-Kelly, P. R. Chipman, C. Xiao, G. G. Gregorio, W. A. Hendrickson, R. J. Kuhn and M. G. Rossmann, Cell, 2006, 124, 485–493 CrossRef CAS PubMed.
- L. Li, S.-M. Lok, I.-M. Yu, Y. Zhang, R. J. Kuhn, J. Chen and M. G. Rossmann, Science, 2008, 319, 1830–1834 CrossRef CAS PubMed.
- L. Menéndez-Arias and F. Gago, Antiviral Agents: Structural Basis of Action and Rational Design, in Structure and Physics of Viruses, Springer, Berlin, Heidelberg, 2013, pp. 599–630 Search PubMed.
- J. Bárcena and E. Blanco, Design of novel vaccines based on virus-like particles or chimeric virions, in Structure and Physics of Viruses, Springer, Berlin, Heidelberg, 2013, pp. 631–665 Search PubMed.
- L. Sánchez-Sánchez, R. D. Cadena-Nava, L. A. Palomares, J. Ruiz-Garcia, M. S. T. Koay, J. J. M. T. Cornelissen and R. Vazquez-Duhalt, Enzyme Microb. Technol., 2014, 60, 24–31 CrossRef PubMed.
- J. N. Culver, A. D. Brown, F. Zang, M. Gnerlich, K. Gerasopoulos and R. Ghodssi, Virology, 2015, 479–480, 200–212 CrossRef CAS PubMed.
- F. Li and Q. Wang, Small, 2014, 10, 230–245 CrossRef CAS PubMed.
- D. L. D. Caspar and A. Klug, Cold Spring Harbor Symp. Quant. Biol., 1962, 27, 1–24 CrossRef CAS PubMed.
- H. Naitow, J. Tang, M. Canady, R. B. Wickner and J. E. Johnson, Nat. Struct. Biol., 2002, 9, 725–728 CrossRef CAS PubMed.
- I. Rayment, T. S. Baker, D. L. Caspar and W. T. Murakami, Nature, 1982, 295, 110–115 CrossRef CAS PubMed.
- R. C. Liddington, Y. Yan, J. Moulai, R. Sahli, T. L. Benjamin and S. C. Harrison, Nature, 1991, 354, 278–284 CrossRef CAS PubMed.
- R. J. Kuhn, W. Zhang, M. G. Rossmann, S. V. Pletnev, J. Corver, E. Lenches, C. T. Jones, S. Mukhopadhyay, P. R. Chipman, E. G. Strauss, T. S. Baker and J. H. Strauss, Cell, 2002, 108, 717–725 CrossRef CAS PubMed.
- S. Mukhopadhyay, B.-S. Kim, P. R. Chipman, M. G. Rossmann and R. J. Kuhn, Science, 2003, 302, 248–248 CrossRef CAS PubMed.
- J. E. Johnson, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 27–33 CrossRef CAS.
- L. M. Iyer, L. Aravind and E. V. Koonin, J. Virol., 2001, 75, 11720–11734 CrossRef CAS PubMed.
- L. M. Iyer, S. Balaji, E. V. Koonin and L. Aravind, Virus Res., 2006, 117, 156–184 CrossRef CAS PubMed.
- N. Yutin, Y. I. Wolf, D. Raoult and E. V. Koonin, Virol. J., 2009, 6, 223 CrossRef PubMed.
- P. Colson, X. De Lamballerie, N. Yutin, S. Asgari, Y. Bigot, D. K. Bideshi, X.-W. Cheng, B. A. Federici, J. L. Van Etten, E. V. Koonin, B. La Scola and D. Raoult, Arch. Virol., 2013, 158, 2517–2521 CrossRef PubMed.
- R. Twarock, J. Theor. Biol., 2004, 226, 477–482 CrossRef CAS PubMed.
- T. Keef, R. Twarock and K. M. Elsawy, J. Theor. Biol., 2008, 253, 808–816 CrossRef CAS PubMed.
- T. Keef and R. Twarock, J. Math. Biol., 2009, 59, 287–313 CrossRef CAS PubMed.
- T. Keef, J. P. Wardman, N. A. Ranson, P. G. Stockley and R. Twarock, Acta Crystallogr., Sect. A: Found. Crystallogr., 2013, 69, 140–150 CAS.
- O. V. Konevtsova, S. B. Rochal and V. L. Lorman, Phys. Rev. Lett., 2012, 108, 38102 CrossRef CAS PubMed.
- O. V. Konevtsova, V. L. Lorman and S. B. Rochal, Phys. Solid State, 2015, 57, 810–814 CrossRef CAS.
- V. L. Lorman and S. B. Rochal, Phys. Rev. Lett., 2007, 98, 185502 CrossRef CAS PubMed.
- V. L. Lorman and S. B. Rochal, Phys. Rev. B: Condens. Matter, 2008, 77, 224109 CrossRef.
- N. Nandhagopal, A. A. Simpson, J. R. Gurnon, X. Yan, T. S. Baker, M. V. Graves, J. L. Van Etten and M. G. Rossmann, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 14758–14763 CrossRef CAS PubMed.
- C. Xiao, Y. G. Kuznetsov, S. Sun, S. L. Hafenstein, V. A. Kostyuchenko, P. R. Chipman, M. Suzan-Monti, D. Raoult, A. McPherson and M. G. Rossmann, PLoS Biol., 2009, 7, e1000092 Search PubMed.
- T. Klose and M. G. Rossmann, Biol. Chem., 2014, 395(7–8), 711–719 CAS.
- S. B. Rochal, O. V. Konevtsova, A. E. Myasnikova and V. L. Lorman, Nanoscale, 2016, 8, 16976–16988 RSC.
- Z. Zhang, B. Greene, P. A. Thuman-Commike, J. Jakana, P. E. Prevelige, J. King and W. Chiu, J. Mol. Biol., 2000, 297, 615–626 CrossRef CAS PubMed.
- A. Fokine, P. G. Leiman, M. M. Shneider, B. Ahvazi, K. M. Boeshans, A. C. Steven, L. W. Black, V. V. Mesyanzhinov and M. G. Rossmann, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 7163–7168 CrossRef CAS PubMed.
- X. Yan, Z. Yu, P. Zhang, A. J. Battisti, H. A. Holdaway, P. R. Chipman, C. Bajaj, M. Bergoin, M. G. Rossmann and T. S. Baker, J. Mol. Biol., 2009, 385, 1287–1299 CrossRef CAS PubMed.
- M. W. Bahar, S. C. Graham, D. I. Stuart and J. M. Grimes, Structure, 2011, 19, 1011–1020 CrossRef CAS PubMed.
- J.-K. Hyun, C. Accurso, M. Hijnen, P. Schult, A. Pettikiriarachchi, A. K. Mitra and F. Coulibaly, PLoS Pathog., 2011, 7, e1002239 CAS.
- Y. G. Kuznetsov and A. McPherson, Microbiol. Mol. Biol. Rev., 2011, 75, 268–285 CrossRef CAS PubMed.
- C. M. Teschke and K. N. Parent, Virology, 2010, 401, 119–130 CrossRef CAS PubMed.
- J. E. Johnson, Curr. Opin. Struct. Biol., 2010, 20, 210–216 CrossRef CAS PubMed.
- F. Tama and C. L. Brooks, J. Mol. Biol., 2002, 318, 733–747 CrossRef CAS PubMed.
- F. Tama and C. L. Brooks, J. Mol. Biol., 2005, 345, 299–314 CrossRef CAS PubMed.
- T. Guérin and R. Bruinsma, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2007, 76, 61911 CrossRef PubMed.
- A. Aggarwal, J. Rudnick, R. F. Bruinsma and W. S. Klug, Phys. Rev. Lett., 2012, 109, 148102 CrossRef CAS PubMed.
- B. R. Brooks, D. Janezic and M. Karplus, J. Comput. Chem., 1995, 16, 1522–1542 CrossRef CAS.
- B. Roux and M. Karplus, Biophys. J., 1988, 53, 297–309 CrossRef CAS PubMed.
- T. Simonson and D. Perahia, Biophys. J., 1992, 61, 410–427 CrossRef CAS PubMed.
- J. F. Gibrat, J. Garnier and N. Go, J. Comput. Chem., 1994, 15, 820–837 CrossRef CAS.
- H. W. T. Van Vlijmen and M. Karplus, J. Chem. Phys., 2001, 115, 691–698 CrossRef CAS.
- M. Widom, J. Lidmar and D. R. Nelson, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2007, 76, 31911 CrossRef CAS PubMed.
- Z. Yang, I. Bahar and M. Widom, Biophys. J., 2009, 96, 4438–4448 CrossRef CAS PubMed.
- M. M. Gibbons and W. S. Klug, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2007, 75, 31901 CrossRef PubMed.
- W. H. Roos, R. Bruinsma and G. J. L. Wuite, Nat. Phys., 2010, 6, 733–743 CrossRef CAS.
- O. V. Konevtsova, V. L. Lorman and S. B. Rochal, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2016, 93, 52412 CrossRef CAS PubMed.
- S. B. Rochal, V. L. Lorman and G. Mennessier, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2005, 71, 21905 CrossRef CAS PubMed.
- J. P. Elliot and P. G. Dawber, Symmetry in physics, Macmillan, London, 1979 Search PubMed.
- B. L. Gurda, K. N. Parent, H. Bladek, R. S. Sinkovits, M. A. DiMattia, C. Rence, A. Castro, R. McKenna, N. Olson, K. Brown, T. S. Baker and M. Agbandje-McKenna, J. Virol., 2010, 84, 5880–5889 CrossRef CAS PubMed.
- D. P. Patterson, P. E. Prevelige and T. Douglas, ACS Nano, 2012, 6, 5000–5009 CrossRef CAS PubMed.
- Z. Xie and R. W. Hendrix, J. Mol. Biol., 1995, 253, 74–85 CrossRef CAS PubMed.
- M. T. Fuller and J. King, Biophys. J., 1980, 32, 381–401 CrossRef CAS PubMed.
- P. E. Prevelige, D. Thomas and J. King, Biophys. J., 1993, 64, 824–835 CrossRef CAS PubMed.
- J. Lucon, S. Qazi, M. Uchida, G. J. Bedwell, B. LaFrance, P. E. Prevelige and T. Douglas, Nat. Chem., 2012, 4, 781–788 CrossRef CAS PubMed.
- K. N. Parent, R. Khayat, L. H. Tu, M. M. Suhanovsky, J. R. Cortines, C. M. Teschke, J. E. Johnson and T. S. Baker, Structure, 2010, 18, 390–401 CrossRef CAS PubMed.
- J. B. Heymann, N. Cheng, W. W. Newcomb, B. L. Trus, J. C. Brown and A. C. Steven, Nat. Struct. Biol., 2003, 10, 334–341 CrossRef CAS PubMed.
- N. L. Kedersha, J. Cell Biol., 1990, 110, 895–901 CrossRef CAS PubMed.
- O. V. Konevtsova, V. V. Pimonov, V. L. Lorman and S. B. Rochal, J. Phys.: Condens. Matter, 2017, 29, 284002 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2017 |