Nanorattles with tailored electric field enhancement

Abstract

Nanorattles are metallic core–shell particles with core and shell separated by a dielectric spacer. These nanorattles have been identified as a promising class of nanoparticles, due to their extraordinary high electric-field enhancement inside the cavity. Limiting factors are reproducibility and loss of axial symmetry owing to the movable metal core; movement of the core results in fluctuation of the nanocavity dimensions and commensurate variations in enhancement factor. We present a novel synthetic approach for the robust fixation of the central gold rod within a well-defined box, which results in an axisymmetric nanorattle. We determine the structure of the resulting axisymmetric nanorattles by advanced transmission electron microscopy (TEM) and small-angle X-ray scattering (SAXS). Optical absorption and scattering cross-sections obtained from UV-vis-NIR spectroscopy quantitatively agree with finite-difference time-domain (FDTD) simulations based on the structural model derived from SAXS. The predictions of high and homogenous field enhancement are evidenced by scanning TEM electron energy loss spectroscopy (STEM-EELS) measurement on single-particle level. Thus, comprehensive understanding of structural and optical properties is achieved for this class of nanoparticles, paving the way for photonic applications where a defined and robust unit cell is crucial.

---

Introduction

After irradiation with light, collective coherent oscillation of the free electrons at noble metal nanoparticle surfaces results in an enhanced electromagnetic near-field. These intense local fields can coherently couple to adjacent metallic nanoparticles resulting in enhanced electromagnetic fields that can exceed the intensity of the exciting field by multiple orders of magnitude.^1,2 The optical response and the field enhancement can be tuned by varying the material properties, e.g., type of noble metal (mostly gold or silver), particle size, particle shape and, most importantly, inter-particle spacing.³ This optimization of the field enhancement is of vital importance in sensing applications because Raman scattering scales with the fourth power of the field strength,^4,5 and therefore, analyte sensitivity is determined by material properties.

Several strategies have been developed for creating particles with large and/or controlled field enhancement in solution. Kumacheva et al. used a photo-activated crosslinker to assemble gold nanorods tip-to-tip in solution, targeting advanced sensing and optoelectronic applications.⁶ Side-by-side assembly was achieved by Zhang et al., who developed a ligand-controlled self-assembly route based on feedback at a water/chloroform interface. In this work, the authors prepared nanorod dimers with a controlled offset to break the symmetry of light.⁷ Alternatively, DNA conjugation has been used extensively for precise assembly of nanorod dimers and nanospheres in solution to induce chiral plasmonic effects.^8–10 Recently, a high-yield strategy has also been introduced, using biomolecular interactions to directly fabricate colloidal assemblies with core-satellite architecture.^11,12 In many applications, however, uniform inter-particle distances and isotropic excitation conditions are essential for avoiding intensity fluctuations, and synthesis strategies targeted at improving the field enhancement homogeneity remain highly advantageous.

An alternative approach is core–shell synthesis aimed at generating field enhancement between the core and shell.¹³ The group of Nam et al. have shown strong field enhancement using DNA-tailorable nanoparticles with ultra-small interior gap in a spherical nanoparticle system for SERS applications.¹⁴ In order to obtain higher yield, the galvanic replacement process was then used by various groups to synthesize spherical,^13,15 cubic,^16,17 cuboidal,¹⁸ and octahedral¹⁹ plasmonic nanorattles, and exploit the improved sensitivity for catalytic applications and plasmonic sensors. In particular, the flat face-to-face contact at metal–insulator-metal contact points ensures larger and stronger region of field enhancement in comparison to curved particles.⁵ These rattle nanoparticles, however, incorporate a freely moveable core, and the undefined core position leads to variable gap dimensions and, as a result, multiple and broad plasmonic resonances appear. These limitations can be overcome by introducing axisymmetric fixation of the inner core to the outer box using state-of-the-art synthesis methods, such as anisotropic silver overgrowth of a gold core, while suppressing side reactions²⁰ combined with kinetically-controlled galvanic replacement reactions.^19,21 This approach ensures a constant and well-defined gap separation over the entire colloidal ensemble.

In this contribution, we demonstrate a novel synthetic approach for axisymmetric nanorattles, comprehensive structural (TEM, SAXS) and optical (UV-vis-NIR) characterization, as well as simulations of the optical properties with the finite difference time domain (FDTD) method. Finally, we demonstrate excellent agreement between the field enhancement predicted by FDTD and EELS mapping, paving the way for applications as plasmonic particles with high intrinsic field enhancement.

Results and discussion

Synthesis and ensemble-averaged characterization via small-angle X-ray scattering

The synthesis of axisymmetric nanorattles consists of three steps. First, single-crystalline gold nanorods are prepared using a protocol published by Vigderman and Zubarev.²² This synthesis utilizes the cationic surfactant cetyltrimethylammonium bromide (CTAB) and silver nitrate to direct the growth of seed particles into single-crystalline gold nanorods. Hydroquinone is used as a weak reducing agent to tune the growth kinetics, resulting in a nearly 100% shape yield and high ion-to-metal conversion. To further reduce the length dispersity, purification based on depletion forces was applied.^23–25 For this method, in dependency of an employed surfactant concentration, particle sizes and shapes can be targeted due to their different interaction areas. Thus, particles above a certain size are selectively flocculated, followed by sedimentation of those reversible flocculates. This way, the size dispersity of particle solutions can be reduced (for details, see ESI S1 and S2†). On the lateral faces of the gold nanorods, higher-index facets are exposed, while the tips feature low-index facets.²⁶

Chloride ions selectively stabilize {100} facets. Consequently, in the second step, silver can be overgrown selectively on the lateral facets using cetyltrimethylammonium chloride (CTAC) as a surfactant. This yields cuboidal shells forming gold@silver cuboids with {100} facets on each of the six faces.^21,27 The controlled overgrowth relies on the deceleration of the reaction kinetics utilizing a syringe pump to suppress side reactions, e.g. non-selective silver overgrowth in the longitudinal direction or secondary nucleation (previously described as living conditions).²⁰ Suppression of longitudinal growth is particularly critical for the present synthesis, as uncontrolled growth leads to variations in the core/shell geometry during the next synthesis step.

In the third step, galvanic replacement is carried out on gold@silver cuboids. For this synthesis, a binary surfactant mixture of CTAC and benzylhexadecyldimethylammonium chloride (BDAC) is used to efficiently slow down the reaction kinetics. The aromatic head group of BDAC reduces the diffusion rate of complexed ions toward the stabilized metal surface.²¹ Next, BDAC-complexed gold(III) chloride is continuously added at a rate below the kinetic reaction limit in order to suppress etching of the silver shell and favor galvanic replacement. During this process, gold(III) ions are reduced on the gold@silver cuboid surface forming a gold–silver alloy shell. For each reduced gold ion, three silver atoms are oxidized and removed, resulting in a cavity formed between the exterior gold–silver alloy shell and the inner gold nanorod core (eqn (1)).^19,28,29

Au³⁺ + 3Ag⁰ → Au⁰ + 3Ag⁺ (1)

Transmission electron microscopy (TEM) images of the respective nanoparticle geometries are presented in Fig. 1. Due to the controlled nature of the silver overgrowth, gold@silver particles with a well-defined cuboidal shape and, more importantly, a negligible elongation in longitudinal direction (∼2 nm per tip) are obtained. Consequently, the nanorod core is firmly bound to the outer alloy shell after galvanic replacement and, thus, accurately positioned and fixed in the center.

Fig. 1 Synthetic pathway toward axisymmetric nanorattles. In the TEM images, gold nanorods are overgrown with silver (gold@silver cuboids) to obtain axisymmetric nanorattles via subsequent galvanic replacement.

In order to obtain structural information representative of the many-particle ensemble (rather than an isolated fraction as for TEM), we performed small-angle X-ray scattering (SAXS), as summarized in Fig. 2A.¹²Fig. 2B shows the scattering profiles of the intermediate colloidal dispersions (gold nanorods, gold@silver cuboids), as well as the final axisymmetric nanorattles. The scattering response reveals defined form factor minima, which provide detailed information on the size range of different hierarchical levels and indicate the high uniformity of the particles’ sizes and shapes. Due to the complex three-dimensional structure of the cuboids and nanorattles, the scattering profiles were fitted using numerical modeling based on Debye's equation.³⁰ The broad parameter space (length, width, dispersity, and nanorattle wall thickness) was screened using a best fit approach, which includes the modeled scattering response of all realistic parameter combinations (for details, see ESI S3†). This comprehensive approach, based on experimental scattering response and best-fit modeling, reveals reliable morphological information concerning the quality of the plasmonic particle.

Fig. 2 Morphological characterization of the colloidal dispersion via small-angle X-ray scattering. (A) Schematic representation of the nanoparticle dimensions and morphology evaluated by three-dimensional modeling. The free parameters are represented by the respective data in the sketch. (B) Experimental scattering signatures (black dots) and simulations (red lines) for gold nanorods, gold@silver cuboids, and axisymmetric nanorattles.

For gold nanorods, the analytical model of a cylinder (see Fig. 2B) sufficiently describes the experimental scattering response. The nanorod width (mean = 11 nm) had a narrow distribution of 3.5% and the length (mean = 68 nm) were found to exhibit no noticeable dispersity. This high uniformity can be attributed to the efficient purification method applied after synthesis (see experimental part for more details). In the plasmonics community, monodispersity for a colloidal suspension is commonly defined as dispersity below 10%,³¹ which was achieved with ease in our approach utilizing additional purification.

For the model of the three-dimensional structure of the gold@silver cuboid, the previously determined parameters of the gold nanorod were held constant, and the dimensions of the silver shell were varied. Evaluation of the SAXS data yields a width of 31.5 ± 1.6 nm and a length of 72.2 ± 5.8 nm, indicating silver tip layer and a side layer thicknesses of 2.0 nm and 10.4 nm, respectively. In comparison to previous works,^21,27 we obtained gold@silver nanoparticles of high quality (dispersity below 10%) and even more importantly, with a tip elongation of only 2 nm, which is crucial for the fixation of the core in the next synthesis step.

The nanoparticle cavities are defined by the dielectric gap between the fixed rod core and the cuboid box. SAXS analysis of the axisymmetric nanorattles (Fig. 2) provides external dimensions of 77.2 ± 3.9 nm in length and 31.5 ± 3.6 nm in width. The high sensitivity of X-ray scattering to cavity dimensions is discussed in detail in the ESI S3.† From this analysis, the size of the internal gap could be precisely determined to be 8.1 ± 1.0 nm, corresponding to a shell thickness of 4.5 ± 0.5 nm at the side (long axis) and 5.5 ± 0.5 nm at the tips. A sufficient shell thickness is important to guarantee a spectral overlap between the plasmonic mode from the shell and the transversal mode from the gold nanorod core.³² Because the galvanic replacement is initiated by the formation of a hole in the silver shell (as described in detail by Liz-Marzán et al.^19,28), small structural defects were observed by TEM (Fig. 1). These structural defects were represented in the SAXS models by filling 9% of the cavity volume with diffuse silver scattering centers (see ESI S3F†). When considered as a whole, the SAXS measurements and models indicate that extraordinary low dispersity (<10%) was achieved, and the nanorattle cores were axisymmetrically fixed with an outstanding spatial precision below 1 nm, throughout the entire colloidal dispersion.

Plasmonic response via polarization-dependent UV-vis-NIR spectroscopy

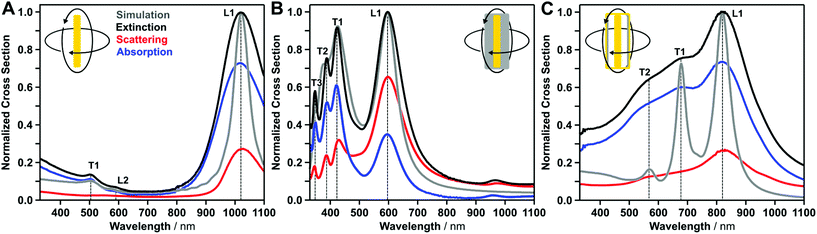
We experimentally analyzed the plasmonic properties of the colloidal dispersion by extinction, absorption and scattering UV-vis-NIR spectroscopy using an integrating sphere setup (Fig. 3). In order to model the UV-vis-NIR spectroscopic response, we used the geometric sizes obtained from SAXS evaluation and calculated the optical response using a time-domain electromagnetic modeling method.

Fig. 3 Numerical simulation of the ensemble-averaged geometric model and comparison with absorption, scattering and extinction UV-vis-NIR spectroscopy. Optical response for gold nanorods (A), gold@silver cuboids (B) and axisymmetric nanorattles (C) and numerical simulations (grey line). Cross-sections were calculated based on the morphology obtained from SAXS evaluation. Schematic inset indicates the degree of freedom in the solution based measurements. Extinction (black line) is defined as sum of absorption (blue line) and scattering (red line).

Gold nanorods exhibit one transversal dipolar mode (T1), a dominant longitudinal dipolar mode (L1), and a higher-order longitudinal mode (L2), which is in good agreement with observations from literature.^33–35 The transversal and longitudinal modes originate from excitation along the short and long axes of the nanoparticle, respectively. Importantly, an indication for high field enhancement is a dominant contribution in absorption cross section, consequently, we will distinguish between scattering and absorption. The scattering cross sections reveal that the energetically lowest longitudinal mode (L1) contributes more strongly to scattering than the energetically higher modes, which is also in good agreement with observations from the literature.^33–35 The positions of the plasmonic modes, as well as the intensity ratios are also in good agreement with the results from electromagnetic simulations, which were based on the geometric size information revealed by SAXS modeling.

The plasmonic properties of the gold@silver cuboids are dominated by their cuboidal silver shells. Three distinct transversal modes (T1–T3) and one longitudinal dipolar mode (L1) are present in the FDTD simulations and in the experimental measurements.^21,36 The number of transversal modes is directly correlated with edge rounding and/or corner sharpness, and theoretically, five cubic modes are possible.³⁷ To the best of our knowledge, a maximum of three modes have been observed experimentally for edge lengths smaller than 40 nm. FDTD simulations revealed an edge rounding (defined as radius of curvature scaled by edge length) smaller than 8% (see ESI S4†). All modes show a strong contribution to absorption, except the longitudinal mode. Due to the significantly greater polarizability of silver compared to gold, the longitudinal resonance shows a stronger contribution to scattering in the NIR region.

In the case of the axisymmetric nanorattles, two transversal (T1 and T2) modes and one longitudinal (L1) are excited. During the galvanic replacement process, the cuboidal silver shell is reduced to a dielectric gap covered by a cuboidal gold box. At the same time, the ultra-thin silver layer on the tips ensures a fixed gold rod at the center. Consequently, the nanocavity can be excited between the cuboidal box and the inner gold rod. A high field enhancement is expected within the gap region, which correlates with dominant contribution of absorption cross-section. We also observe multiple transversal modes, which will be described in more detail below. The electromagnetic modeling of axisymmetric nanorattles was performed in the same manner as for core–shell and rod particles based on the morphology obtained from SAXS measurements. Here we found good agreement in the energetic mode positions, but the electromagnetic modeling underestimates the resonance broadening. In literature, this resonance broadening was attributed to size and wall thickness variations.²³ In addition, broadening could also be connected to defects in the walls, however, due to the random nature of these wall defects (variation in size and position), they could not be included in the electromagnetic modeling. So far, we used conventional UV-vis-NIR spectroscopy to identify the plasmonic modes and assign transversal or longitudinal excitation based on their spectral position. In order to clarify the nature of the excitation, we conducted polarization-dependent measurements.

In order to orient the synthesized nanoparticles without electromagnetic coupling, a suspension of the surfactant-functionalized particles was mixed with a saturated aqueous polyvinyl alcohol (PVA) solution (Fig. 4).³⁸ Films of this suspension were prepared by evaporation of the water. The 1 mm thick films were cut into 10 × 50 mm² pieces, heated above the glass transition temperature (T_g ∼ 75 °C),³⁹ and uniaxially stretched by 200%. The resulting shear forces acting between polymer matrix and the anisotropic nanoparticles aligned the particles along the stretching axis, and after this process, polarization dependence could easily be observed with the bare eye. We used polarized UV-vis-NIR spectroscopy to characterize the macroscopically aligned samples, and we were experimentally able to distinguish between transversal and longitudinal modes for each nanoparticle type. Fig. 4 shows color changes for gold nanorods and gold@silver cuboids in the visible wavelength range. The axisymmetric nanorattles show minor differences in color by observation with the bare eye, which is expected due to the close vicinity of the transversal nanocavity modes and the longitudinal mode in the red to NIR wavelength range. Generally, the plasmonic resonances were red-shifted with respect to their positions in aqueous solution owing to the change of refractive index of the matrix (i.e., from water (n = 1.33) to PVA (n = 1.47 as measured by spectroscopic ellipsometry, see ESI S5† for more details)).⁴⁰

Fig. 4 Control over the anisotropic plasmonic properties by mechanical strain within a polymeric matrix. Embedding the rod-like nanoparticles in PVA matrices and subsequently stretching above the glass transition temperature results in macroscopic orientation of the anisotropic nanoparticles (schematically depicted in A). Polarization imaging and polarized UV-vis-NIR spectroscopy reveal the separate excitation of the transversal (green) and the longitudinal (purple) plasmonic modes for gold nanorods (B), gold@silver cuboids (C), and axisymmetric nanorattles (D).

For polarization-dependent UV-vis-NIR spectroscopy, we must define two excitation possibilities: electric field vector parallel and perpendicular to the stretching axis. Perpendicular excitation of the gold nanorods leads to a transversal mode at 510 nm (T1) only. For parallel excitation, the higher-order dipolar mode at 605 nm (L2) and the dipolar longitudinal mode at 1095 nm (L1) are observable (Fig. 4B). The measurements indicate near-perfect alignment of the gold nanorods with a dichroic ratio of 0.97 (for details see ESI†). For gold@silver cuboids, three resonances at 448 nm, 401 nm, and 348 nm (T1–3) were found during the polarization dependent measurement, corresponding to the experimentally-observed cubic modes (see also the discussion in the FDTD modelling section). For parallel excitation, only the longitudinal dipolar resonance (L1) at 670 nm was observed. For this excitation state, weak plasmonic modes were also present in the UV region, which match the cubic modes from perpendicular excitations. For the axisymmetric nanorattles, extinction along the stretching axis shows a pronounced plasmon resonance at 911 nm. For perpendicular excitation, two cavity modes (T1 at 690 nm, and T2 at 600 nm) could be clearly identified.

Near-field plasmonic properties via EELS mapping and FDTD modeling

Upon excitation, each of the particle types features distinct electromagnetic properties (Fig. 5A). The local distribution of surface charges, field enhancements, effective areas, and strengths are closely correlated with the respective particle shape and composition. To compare the electric field enhancements, we integrated the electric field along the beam direction and normalized these values by the integrated distance. Gold nanorods, for example, have a rather weak electric field enhancement along the cylindrical shaped rod for transversal excitation. For longitudinal excitation, the field enhancement is pronounced at the tips, as can be also identified also from the corresponding distribution of surface charges. This field concentration is increased for gold@silver cuboids as a result of the sharp edges and inclusion of plasmonically-active silver as a shell material. For axisymmetric nanorattles, a nanocavity is present and a confined electric field is observed within the dielectric cavity volume (transversal excitation). Surface charge calculations reveal the nature of the nanocavity mode. Here, the shell induces the mirror charge into the core material. These observations are in agreement with results reported in literature.^21,41 A similar nanocavity signature is obtained for the longitudinal mode, however, this signature is less pronounced due to the electrical contact between the core and the shell at the tips of the internal gold nanorods.

Fig. 5 Surface charge distribution and electric-field enhancement of the different plasmonic nanoparticles. (A) Nature of the plasmonic modes and integrated electric field distributions (integrated in z-direction) of the energetically lowest transversal and longitudinal plasmonic modes. The plasmonic modes were excited perpendicular and parallel to the long axes of the nanoparticles at the wavelength of the corresponding plasmonic resonance. Integrated electric field enhancement for longitudinal (B) and transversal excitation (C) (integrated in y–z and x–z, respectively, and normalized to the integrated distance and area).

In order to compare and to quantify the cavity resonance with the resonances of gold nanorods and gold@silver cuboids, we integrated the electric field along the beam direction (z-axis) and lateral directions (x-axis or y-axis, respectively). Using this integration method (shown in Fig. 5), we plotted the plasmonic resonances as cross-sections corresponding to the transversal and longitudinal excitation. In these cross-section plots, two properties of the plasmonic modes could be identified: (I) the highest field enhancement occurs at the metallic–dielectric interface, and (II) the electric field decays exponentially into the dielectric material and environment. For the longitudinal cross-section (electric field vector parallel to y-axis), the field enhancement is most significant at the sharp corners. Excitations of the transversal modes (electric field vector parallel to x-axis) reveal significant differences for the various nanoparticle types. Especially for the axisymmetric nanorattles, we observed a dominant field enhancement in the gap region, which exceeds the field enhancement of the shell-environment by multiple times. More importantly, the field enhancement is even stronger than that of the longitudinal mode. In summary, these electromagnetic modeling methods present solid theoretical support for the characteristic surface charge signature and strong field enhancement factor of the cavity mode only observed for axisymmetric nanorattles.

Finally, to experimentally establish the morphological shape and field enhancement within the gap region, we analyzed the axisymmetric nanorattles by electron tomography in high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) mode, and we supported these measurements with STEM energy dispersive X-ray spectroscopy (STEM-EDS) and STEM electron energy loss spectroscopy (STEM-EELS) mapping (Fig. 6). The investigations of the morphology (HAADF-STEM), accompanied by elemental analysis, reveal the composition of the outer shell to be an alloy of silver and gold, which is in good agreement with SAXS evaluation (details in ESI S6,† as well as literature).²⁸ For all analyzed nanorattles, a fixed gold rod covered by a gold box was observed. Artifacts, such as bridging between box and core were attributed to incomplete galvanic replacement and included in the SAXS evaluation. The STEM-EELS analysis of the nanorattles allowed detection of the near-field plasmonic features (Fig. 6D and ESI S7–9†). The STEM-EELS results are in good agreement with those from UV-vis-NIR spectroscopy, where three plasmonic modes could be observed. Deviations in mode positions, however, were observed and attributed to interactions with the thin carbon substrate used for EELS measurements, which is not accounted for in our simulations.⁴² Further details can be found in the ESI S9.† Mapping of the near-field by EELS allows quantification of the spatial field enhancement of plasmonic modes.⁴³ At low energy losses (1.5 eV–2.0 eV, 620 nm–827 nm), the longitudinal dipolar mode (L1) of the nanorattle is excited. Energy losses ranging from 2.5 eV to 3.0 eV (413 nm–496 nm) identify the first-order transversal cavity mode (T1). Here, the electric field is homogeneously distributed inside the cavity. At energy losses between 3.0 eV–3.5 eV (354 nm–413 nm), the higher-order transversal mode (T2) is excited, showing a weaker field enhancement inside the cavity. The transversal response is superposed by the bridging defects between core and box. Consequently, the plasmonic properties observed on the single particle level can be transferred to the macroscopic level and vice versa.

Fig. 6 Structural and electromagnetic characterization of an individual nanorattle. HAADF-STEM image of a nanorattle (A), STEM-EDS elemental maps revealing the distribution of Au and Ag in the structure (B) three-dimensional (3D) representation of the reconstructed volume of the nanorattle shown in A, (C) revealing the lateral separation between inner core and shell. STEM-EELS mappings (D) at distinct energies show electric field enhancement inside of the cavity.

Conclusion

Using a galvanic replacement process, we synthesized a nanoparticle structure where a metallic nanorod core is fixed at the small facets of a nanobox shell with defined dielectric spacer. This structure shows strong field enhancement in the particles inner cavity, which is homogenous for all particles. This field enhancement critically depends on the particle's morphology, especially on the axially-symmetric fixation of the gold nanorod to the gold nanobox and the dimensions of the box. Since our protocol allows controlling these parameters with nanoscale accuracy, the field enhancement can be efficiently tailored. For sensing and catalytic applications, a uniform wall thickness is important to ensure efficient coupling of light to the plasmonic cavity. The tailored optical properties were confirmed by comprehensive structural (TEM, SAXS) and optical (polarized UV-vis-NIR) characterization. Moreover, electromagnetic simulations were used to verify the consistency of the model and quantify the electric field enhancement. A reliable and up-scalable synthesis method of an axisymmetric nanorattle is a first step toward novel photonic meta-surfaces, which obtain their optical properties from the collective excitation of the assembled unit cells.^44,45 The geometric design of the unit cell is the key for such structures, which can be subsequently arranged by self-assembly to potentially exploit their collective optical effects.^46,47 Thus, our approach adds a novel element to the toolbox of plasmonic metamaterials.

Experimental

Materials

CTAB (99%) was purchased from Merck chemicals. CTAC, HAuCl₄·3H₂O (99.9%), silver nitrate (99.9999%), sodium borohydride (99%), hydroquinone (HQ, 99%), and PVA (M_w 70–100 kg mol⁻¹) were purchased from Sigma Aldrich. L-(+)-Ascorbic acid (AA, 99.5%) was purchased from Grüssing GmbH. BDAC was purchased from Molekula. All chemicals were used without further purification. All solutions, except HAuCl₄, were prepared immediately before use. Glassware was cleaned with aqua regia prior to use. Water was purified using a Milli-Q system (Millipore). The final resistivity was 18.2 MΩ cm.

Seed synthesis

CTAB solution (5 mL, 0.2 M) was mixed with 5 mL of an aqueous 1 mM HAuCl₄ solution (43.4 μL of a 0.11518 M HAuCl₄ solution was added to 5 mL of water). 600 μL of 0.01 M NaBH₄ solution was quickly added while stirring vigorously, resulting in a brownish yellow solution. Stirring was continued for 2 min, then the seed solution was kept at room temperature for up to 30 minutes until use.

Synthesis of gold nanorods

36.45 g CTAB was dissolved in 1000 mL of purified water (f.c.: 0.1 M). 4.341 mL of 0.11518 M HAuCl₄ solution (f.c.: 0.5 mM) and 5 mL of 0.1 M AgNO₃ solution were added (f.c.: 0.5 mM). After at least 5 min, 50 mL of 0.1 M HQ solution (f.c.: 5 mM) was added while stirring. 2 min later, 24 mL of the as-prepared seed solution was added (3 batches of seed solution were mixed). Before characterization, the gold nanorod suspension was kept at 32 °C for at least 48 h.

Purification of gold nanorods

In a graduated cylinder, 11.33 g of CTAC (0.0354 mol) were dissolved in 88 mL purified water. 140 mL of the as-prepared gold nanorod dispersion was centrifuged for 30 min at 8500 rcf to decrease the volume to 12 mL. The resulting gold nanorod dispersion was mixed with the CTAC solution (f.c.: CTAC: 0.354 M, CTAB: 0.012 M). The colloidal solution was left to settle for 21 h before 95 mL of the supernatant, having a light reddish brown color, was decanted. The remaining 5 mL of the solution, containing a brown sediment, was diluted with 5 mL of Milli-Q water (f.c.: CTAC: 0.177 M, CTAB: 0.006 M). 24 h after the last agitation, the brown supernatant was separated from the brown sediment. This final sediment was used for further growth reactions.

Synthesis of gold@silver cuboids with an Ag/Au ratio of 15

35 mL of the as-prepared gold nanorod solution was centrifuged for 30 min at 8500 rcf and decanted, to reduce to volume to 5 mL. The 5 mL gold nanorod dispersion was diluted with 25 mL of a 10 mM CTAC solution. This process was repeated six times. The concentration of gold in the final solution was 0.193 mmol L⁻¹ as measured utilizing the interband absorption at a wavelength of 400 nm.³³ 100 mL of this gold nanorod solution was used in the synthesis of 1 : 15 Au@Ag cuboids. Using a syringe pump with two identical syringes, 25 mL of a 0.1 M AgNO₃ solution and 25 mL of a 0.4 M AA solution were added to the gold nanorod solution, while it was heated to a temperature of 60 °C. The syringes were each set to deliver 250 μL h⁻¹ (0.15 mol Ag per mol Au per h) in two steps of 12.5 mL each. All containers, syringes and tubes were shielded from ambient light to prevent solution degradation. The resulting deep green Au@Ag cuboid dispersions were centrifuged (35 min, 3500 rcf) and washed with a 10 mM CTAC solution.

Synthesis of nanorattle particles using a syringe pump setup

10 mL of Au@Ag cuboids with a Ag/Au ratio of 15 in CTAC were diluted with 80 mL of purified water and 10 mL of 0.1 M BDAC-solution. For a stoichiometric replacement of 40% of the silver, 30.3 mL of a 0.125 mM HAuCl₄-solution, containing 10 mM BDAC, were added using a syringe pump. The first two milliliters were added over the course of one hour, the remaining 28.3 mL were added over three hours. For different stoichiometric replacement percentages, the total quantity of added HAuCl₄ solution was varied.

Preparation of PVA films containing metal nanoparticles

7.5 g of PVA (90 kg mol⁻¹) was dissolved in 92.5 g of purified water (7.5 wt%). For each PVA film, 5 mL of the corresponding particle solution was added to 20 mL of PVA solution. After thorough mixing, the solutions were transferred into a petri dish and degassed in a desiccator under high vacuum until the solution was free of trapped air. The petri dish was then placed on a hot plate and heated to 90 °C. To slow down evaporation, the petri dish was covered with a watch glass, leaving a small gap for moisture to escape.

Electron microscopy characterization

Standard transmission electron microscopy measurements were performed with a Zeiss LEO 922 OMEGA EFTEM with an acceleration voltage of 200 kV. For TEM analysis of nanoparticles, 1 mL of nanoparticle solution was concentrated to 100 μL via centrifugation and washed twice to reduce the surfactant concentration below the critical micelle concentration. Subsequently, 4 μL of this solution was dried on 300 mesh copper grid with an approximately 3 nm carbon film.

HAADF-STEM images, electron tomography series, STEM-EDS elemental maps and STEM-EELS plasmon maps were acquired using an aberration-corrected cubed FEI Titan electron microscope operated at 120 kV and equipped with a monochromator, yielding an energy resolution of 0.12 eV. For the acquisition of the tomography series, a Fischione model 2020 single tilt tomography holder was used, and the series were acquired manually within a tilt range from −74° to +70° using a tilt increment of 2°. The reconstruction of the series was performed using the simultaneous iterative reconstruction technique (SIRT), implemented in the ASTRA toolbox.⁴⁸ For the acquisition of the STEM-EDS elemental maps, a ChemiSTEM system was used,⁴⁹ and quantification was performed using ESPIRT software. To analyze the EELS data sets, we used the EELSModel software.⁵⁰ The thickness of the C support was approximately 3 nm.

UV-vis-NIR spectroscopy

UV-vis-NIR spectra were recorded on a Cary 5000 spectrophotometer (Agilent, USA) equipped with a diffuse reflection accessory (DRA) for absorption spectroscopy and a universal measurement accessory (UMA) for polarization dependent spectroscopy. Determination of the extinction, absorption and reflection contributions was performed as described elsewhere.¹²

Small-angle X-ray scattering (SAXS)

All SAXS data reported here were measured using a “Double Ganesha AIR” (SAXSLAB, Denmark). The X-ray source of this laboratory-based system is a rotating anode (copper, MicoMax 007HF, Rigaku Corporation, Japan) providing a parallel beam at λ = 0.154 nm. The measurements were done on samples contained in 1 mm glass capillaries (Hilgenberg, code 4007610, Germany) at room temperature, and the transmitted intensity data were recorded by a position sensitive detector (PILATUS 300 K, Dectris). To cover the range of scattering vectors between 0.02–5.0 nm⁻¹, different detector positions were used. The circularly averaged data were normalized to incident beam, sample thickness and measurement time before subtraction of the solvent. All measurements were put on an absolute scale by standard less absolute intensity calibration.

Electromagnetic simulations (FDTD)

Simulations of extinction/absorbance/scattering spectra, induced magnetic and electric fields, surface charge distributions and current flow were performed using the commercial software FDTD Solutions (ver. 8.11.422) from Lumerical Solutions Inc. A total-field scattered-field source was used for the interaction with light and with a moving dipole source for the comparison with EELS measurements. For EELS simulations, the model and scripts of Nordlander and coworkers were used with a meshing of the electron trajectory in 750° × 2° nm steps.⁴² For the dielectric properties of silver, a CRC approximation by Hagemann et al. was used, while for the properties of gold, data from Johnson and Christy was used.^51,52 For each material, a RMS error of 0.2 or lower was given. Two meshes were used for the simulation: for the empty space, a mesh size of 2 nm was used, while the particle was meshed with a size of 0.5 nm. To determine the field distributions, charge density and current flow, the model was simulated at the wavelengths of the absorption maxima of the corresponding plasmonic modes. Electric field enhancement distributions were integrated along the incident k-vector and the related cross-sections further integrated to the plane of incidence of the electric field of the incident light source. All simulations reached a convergence of 10⁻⁵ before reaching 300 fs simulation time. For the best simulation stability, the mesh area was chosen to be at least 100 nm larger than the modeled structure in all three spatial directions.

Acknowledgements

This study was funded by the European Research Council under grant Template-assisted assembly of METAmaterials using MECHanical instabilities (METAMECH) ERC-2012-StG 306686. This work was also supported by the Deutsche Forschungsgemeinschaft (DFG) within the Cluster of Excellence ‘Center for Advancing Electronics Dresden’ (cfaed). M. T. wants to acknowledge funding by the Elite Network of Bavaria, the Bavarian Ministry of State according to the Bavarian elite promotion act (BayEFG), as well as the Alexander von Humboldt Foundation for a Feodor-Lynen Research Fellowship. S. B. acknowledges financial support from the European Research Council (Starting Grant No. COLOURATOM 335078) and T. A. acknowledges funding from the Research Foundation Flanders (FWO, Belgium) through a postdoctoral grant. We thank Ken Harris from the National Research Council Canada for valuable discussion of the manuscript.

References

1. E. Hao and G. C. Schatz, J. Chem. Phys., 2003, 120, 357–366.
2. D. C. Marinica, A. K. Kazansky, P. Nordlander, J. Aizpurua and A. G. Borisov, Nano Lett., 2012, 12, 1333–1339.
3. M. Rycenga, C. M. Cobley, J. Zeng, W. Li, C. H. Moran, Q. Zhang, D. Qin and Y. Xia, Chem. Rev., 2011, 111, 3669–3712.
4. R. A. Alvarez-Puebla and L. M. Liz-Marzán, Small, 2010, 6, 604–610.
5. R. Kodiyath, S. T. Malak, Z. A. Combs, T. Koenig, M. A. Mahmoud, M. A. El-Sayed and V. V. Tsukruk, J. Mater. Chem. A, 2013, 1, 2777.
6. A. Lukach, K. Liu, H. Therien-Aubin and E. Kumacheva, J. Am. Chem. Soc., 2012, 134, 18853–18859.
7. S. Yang, X. Ni, X. Yin, B. Kante, P. Zhang, J. Zhu, Y. Wang and X. Zhang, Nat. Nanotechnol., 2014, 9, 1002–1006.
8. C. A. Mirkin, R. L. Letsinger, R. C. Mucic and J. J. Storhoff, Nature, 1996, 382, 607–609.
9. W. Ma, H. Kuang, L. Wang, L. Xu, W. S. Chang, H. Zhang, M. Sun, Y. Zhu, Y. Zhao, L. Liu, C. Xu, S. Link and N. A. Kotov, Sci. Rep., 2013, 3, 1934.
10. A. Kuzyk, R. Schreiber, Z. Fan, G. Pardatscher, E.-M. Roller, A. Hogele, F. C. Simmel, A. O. Govorov and T. Liedl, Nature, 2012, 483, 311–314.
11. S. N. Sheikholeslami, H. Alaeian, A. L. Koh and J. A. Dionne, Nano Lett., 2013, 13, 4137–4141.
12. R. P. Höller, M. Dulle, S. Thomä, M. Mayer, A. M. Steiner, S. Förster, A. Fery, C. Kuttner and M. Chanana, ACS Nano, 2016, 10, 5740–5750.
13. J. A. Fan, K. Bao, L. Sun, J. Bao, V. N. Manoharan, P. Nordlander and F. Capasso, Nano Lett., 2012, 12, 5318–5324.
14. D.-K. Lim, K.-S. Jeon, J.-H. Hwang, H. Kim, S. Kwon, Y. D. Suh and J.-M. Nam, Nat. Nanotechnol., 2011, 6, 452–460.
15. N. Gandra, C. Portz and S. Singamaneni, Adv. Mater., 2014, 26, 424–429.
16. Y. Ma, W. Li, E. C. Cho, Z. Li, T. Yu, J. Zeng, Z. Xie and Y. Xia, ACS Nano, 2010, 4, 6725–6734.
17. J.-E. Park, S. Kim, J. Son, Y. Lee and J.-M. Nam, Nano Lett., 2016, 16, 7962–7967.
18. Y. Khalavka, J. Becker and C. Sönnichsen, J. Am. Chem. Soc., 2009, 131, 1871–1875.
19. L. Polavarapu, D. Zanaga, T. Altantzis, S. Rodal-Cedeira, I. Pastoriza-Santos, J. Pérez-Juste, S. Bals and L. M. Liz-Marzán, J. Am. Chem. Soc., 2016, 138, 11453–11456.
20. M. Mayer, L. Scarabelli, K. March, T. Altantzis, M. Tebbe, M. Kociak, S. Bals, F. J. García de Abajo, A. Fery and L. M. Liz-Marzán, Nano Lett., 2015, 15, 5427–5437.
21. M. Tebbe, C. Kuttner, M. Mayer, M. Maennel, N. Pazos-Pérez, T. A. Koenig and A. Fery, J. Phys. Chem. C, 2015, 119, 9513–9523.
22. L. Vigderman and E. R. Zubarev, Chem. Mater., 2013, 25, 1450–1457.
23. K. Park, H. Koerner and R. A. Vaia, Nano Lett., 2010, 10, 1433–1439.
24. L. Scarabelli, M. Coronado-Puchau, J. J. Giner-Casares, J. Langer and L. M. Liz-Marzán, ACS Nano, 2014, 8, 5833–5842.
25. K. Nakamura, T. Oshikiri, K. Ueno, Y. Wang, Y. Kamata, Y. Kotake and H. Misawa, J. Phys. Chem. Lett., 2016, 7, 1004–1009.
26. E. Carbó-Argibay, B. Rodríguez-González, S. Gómez-Graña, A. Guerrero-Martínez, I. Pastoriza-Santos, J. Pérez-Juste and L. M. Liz-Marzán, Angew. Chem., Int. Ed., 2010, 49, 9397–9400.
27. S. Gómez-Graña, B. Goris, T. Altantzis, C. Fernández-López, E. Carbó-Argibay, A. Guerrero-Martínez, N. Almora-Barrios, N. López, I. Pastoriza-Santos, J. Pérez-Juste, S. Bals, G. Van Tendeloo and L. M. Liz-Marzán, J. Phys. Chem. Lett., 2013, 4, 2209–2216.
28. B. Goris, L. Polavarapu, S. Bals, G. Van Tendeloo and L. M. Liz-Marzán, Nano Lett., 2014, 14, 3220–3226.
29. X. Zhuo, X. Zhu, Q. Li, Z. Yang and J. Wang, ACS Nano, 2015, 9, 7523–7535.
30. P. Debye, Ann. Phys., 1915, 351, 809–823.
31. N. G. Bastús, F. Merkoçi, J. Piella and V. Puntes, Chem. Mater., 2014, 26, 2836–2846.
32. Z. A. Combs, S. T. Malak, T. König, M. A. Mahmoud, J. L. Chávez, M. A. El-Sayed, N. Kelley-Loughnane and V. V. Tsukruk, Part. Part. Syst. Charact., 2013, 30, 1071–1078.
33. L. Scarabelli, A. Sanchez-Iglesias, J. Perez-Juste and L. M. Liz-Marzan, J. Phys. Chem. Lett., 2015, 6, 4270–4279.
34. X. Ye, C. Zheng, J. Chen, Y. Gao and C. B. Murray, Nano Lett., 2013, 13, 765–771.
35. B. Nikoobakht and M. A. El-Sayed, Chem. Mater., 2003, 15, 1957–1962.
36. B. A. Glatz, M. Tebbe, B. Kaoui, R. Aichele, C. Kuttner, A. E. Schedl, H. W. Schmidt, W. Zimmermann and A. Fery, Soft Matter, 2015, 11, 3332–3339.
37. S. Zhang, K. Bao, N. J. Halas, H. Xu and P. Nordlander, Nano Lett., 2011, 11, 1657–1663.
38. J. Pérez-Juste, B. Rodríguez-González, P. Mulvaney and L. M. Liz-Marzán, Adv. Funct. Mater., 2005, 15, 1065–1071.
39. Z. H. Mbhele, M. G. Salemane, C. G. C. E. van Sittert, J. M. Nedeljković, V. Djoković and A. S. Luyt, Chem. Mater., 2003, 15, 5019–5024.
40. S. Mahendia, A. K. Tomar, P. K. Goyal and S. Kumar, J. Appl. Phys., 2013, 113, 073103.
41. M. Mayer, M. Tebbe, C. Kuttner, M. J. Schnepf, T. A. Konig and A. Fery, Faraday Discuss., 2016, 191, 159–176.
42. Y. Cao, A. Manjavacas, N. Large and P. Nordlander, ACS Photonics, 2015, 2, 369–375.
43. A. L. Koh, K. Bao, I. Khan, W. E. Smith, G. Kothleitner, P. Nordlander, S. A. Maier and D. W. McComb, ACS Nano, 2009, 3, 3015–3022.
44. W. Fan, S. Zhang, B. Minhas, K. J. Malloy and S. R. J. Brueck, Phys. Rev. Lett., 2005, 94, 033902.
45. S. P. Burgos, R. de Waele, A. Polman and H. A. Atwater, Nat. Mater., 2010, 9, 407–412.
46. S. Gómez-Graña, J. Pérez-Juste, R. A. Alvarez-Puebla, A. Guerrero-Martínez and L. M. Liz-Marzán, Adv. Opt. Mater., 2013, 1, 477–481.
47. T. Thai, Y. Zheng, S. H. Ng, H. Ohshima, M. Altissimo and U. Bach, Nanoscale, 2014, 6, 6515–6520.
48. W. van Aarle, W. J. Palenstijn, J. De Beenhouwer, T. Altantzis, S. Bals, K. J. Batenburg and J. Sijbers, Ultramicroscopy, 2015, 157, 35–47.
49. P. Schlossmacher, D. Klenov, B. Freitag and H. Von Harrach, Microsc. Today, 2010, 18, 14–20.
50. J. Verbeeck and S. Van Aert, Ultramicroscopy, 2004, 101, 207–224.
51. H. J. Hagemann, W. Gudat and C. Kunz, J. Opt. Soc. Am., 1975, 65, 742–744.
52. P. B. Johnson and R. W. Christy, Phys. Rev. B: Solid State, 1972, 6, 4370–4379.

---

Footnotes

† Electronic supplementary information (ESI) available: Further experimental details, optical data, electromagnetic simulations and detailed information about the SAXS fitting procedure. See DOI: 10.1039/c7nr02952g

‡ These authors have contributed equally.

§ Current address: Department of Chemistry, University of Toronto, 80 St. George Street, Toronto, M5S 3A6, Ontario, Canada.

---