Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
An efficient genetic algorithm for structure prediction at the nanoscale
Tomas
Lazauskas
 *,
Alexey A.
Sokol
*,
Alexey A.
Sokol
 and
Scott M.
Woodley
and
Scott M.
Woodley
University College London, Kathleen Lonsdale Materials Chemistry, Department of Chemistry, 20 Gordon Street, London WC1H 0AJ, UK. E-mail: t.lazauskas@ucl.ac.uk
First published on 23rd January 2017
Abstract
We have developed and implemented a new global optimization technique based on a Lamarckian genetic algorithm with the focus on structure diversity. The key process in the efficient search on a given complex energy landscape proves to be the removal of duplicates that is achieved using a topological analysis of candidate structures. The careful geometrical prescreening of newly formed structures and the introduction of new mutation move classes improve the rate of success further. The power of the developed technique, implemented in the Knowledge Led Master Code, or KLMC, is demonstrated by its ability to locate and explore a challenging double funnel landscape of a Lennard-Jones 38 atom system (LJ38). We apply the redeveloped KLMC to investigate three chemically different systems: ionic semiconductor (ZnO)1–32, metallic Ni13 and covalently bonded C60. All four systems have been systematically explored on the energy landscape defined using interatomic potentials. The new developments allowed us to successfully locate the double funnels of LJ38, find new local and global minima for ZnO clusters, extensively explore the Ni13 and C60 (the buckminsterfullerene, or buckyball) potential energy surfaces.
1. Introduction
In the search for new tunable materials, in recent years, there has been growing interest in nanoclusters that show a strong correlation between their size, morphology, and physical and chemical properties.1 Nanoclusters, or small nanoparticles, have typical dimensions below 2–5 nm, a size regime where current experimental techniques are insufficient for accurate and comprehensive structure characterisation. Vitally, it is where computational approaches can usefully complement and aid experimental studies. Moreover, the atomic structure for an optimal value of a property of interest can be predicted and thus the theory can guide a rational design of future materials.The computational task of structure prediction requires global optimisation (GO) algorithms as well as suitable algorithms to assess configurations. It is generally assumed that nanoclusters adopt the lowest energy configurations under ambient conditions and initial models are typically of nanoclusters with a fixed composition, isolated in vacuo,2 and under athermal conditions. The predicted lowest energy structures can then be employed in models that include the substrate or surrounding medium added, and/or at different pressures and temperatures.
GO algorithms are employed to identify locally stable structures on the energy landscape,3i.e. the global minimum (GM) and higher energy local minima (LM). The most popular methods include evolutionary algorithms,4–11 which mimic processes of natural selection and procreation, Swarm algorithms, inspired by the processes from the nature,12–14Monte Carlo basin hopping,15–17 and random sampling.18–20 In particular, when applied to nanoclusters, these techniques exploit standard local optimisation routines.
There are a number of research groups that have developed appropriate software for tackling the challenge of structure prediction.4,14,15,21–32 Here, the KLMC software suite, or Knowledge Led Master Code,10,33 is developed to utilise massively parallel computer platforms and third-party computational chemistry software to perform statistical sampling and systematic searches for local and global minima on energy landscapes. Automation within KLMC alleviates manual, repetitive and mundane computational tasks typically required in simple task farming, global optimisation techniques and statistical sampling. The Genetic Algorithm (GA) module within KLMC has already been exploited to predict the plausible structures of nanoclusters of binary heteropolar compounds,10i.e. local minima of ZnO, MgO, KF, and CdSe,10 on energy landscapes defined using two levels of theory: interatomic potentials (IP) (as implemented within GULP34,35) and density functional theory (DFT) (as implemented within FHI-aims36), respectively.
In this article, we report significant developments to KLMC and demonstrate its improved performance on predicting atomic structures of four chemically different systems. New developments in the GA module address the well-known issue of creating and maintaining structural diversity within the GA population of nanoclusters. The power of this approach is demonstrated by searching for atomic structures of LJ38; an example of a challenging double funnel energy landscape.
In particular, new tools to compare structures topologically enable a more efficient route to determine duplicate structures that can be replaced with unique candidates. The redeveloped and optimised algorithm is employed to predict LM nanoclusters for ZnO, C, and Ni, by searching the energy landscape defined using interatomic potentials for ionic, covalent and metallic interactions, respectively.
In the next section, we provide a detailed description of new tools and improvements in the KLMC GA methodology. The application of the redeveloped KLMC GA module to the four chemically diverse systems is presented in section 3. We conclude this paper with a summary of methodological developments and analysis of the chosen applications.
2. Methods
2.1. The KLMC genetic algorithm
The general idea behind a genetic algorithm is to mimic the process of natural selection. It is an iterative process which employs techniques inspired by evolution, including selection, crossover, and mutation. Here selection biases the choice towards better candidates from the population and survival. Procreation of new candidates is achieved using a crossover algorithm, combined with a mutation algorithm, which is analogous to the biological mutation of DNA. The iterative process evolves candidates towards a better solution and is continued until a predetermined number of iterations are reached or the solution satisfies a predetermined fitness level (i.e. in our case – a target energy). A detailed flowchart of the GA implemented within the KLMC software suite is given in Fig. 1.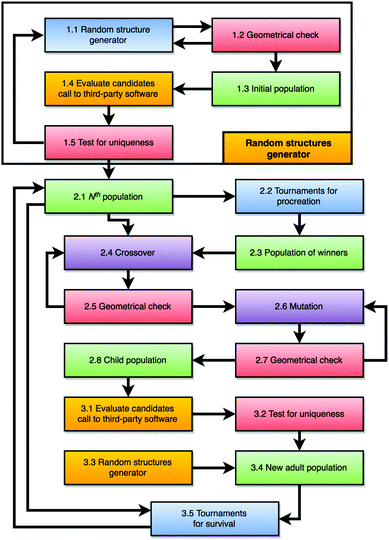 | ||
| Fig. 1 Flow chart of the enhanced KLMC's GA. Colour mapping as previously:10 blue and purple – original and enhanced actions undertaken by KLMC, respectively; orange – parallelised action; green – main result; and red – new functionality. | ||
In this study, we employ a Lamarckian approach, in which each new candidate configuration is relaxed to a local energy minimum. Only LM configurations are, therefore, compared during selection. Our GA implementation starts by creating an initial population of candidates (Step 1.3). Each candidate is composed of a predefined set of randomly distributed atoms (Step 1.1) and undergoes a geometrical evaluation (Step 1.2) to check whether the atoms are not too close (any interatomic distances within a tolerance based on ionic and covalent radii) and that each nanocluster is not fragmented. If a candidate fails the initial geometrical evaluation, a new set of randomized atomic coordinates are generated and evaluated. After the initial population is generated, all candidates are optimised (Step 1.4), duplicates are removed (Step 1.5) and process is repeated until the population reaches the user defined size. On the next stage, the current population is passed on (Step 2:1) to be evolved.
The evolution process is repeated for a specified number of iterations or until no new unique candidate configuration has been generated for a predefined number of iterations. During each evolutionary iteration, a new population is created by the application of crossover and mutation procedures to the pairs of configurations from the previous population. Selected candidate structures for the crossover operation are traditionally called parents and the outcome, possibly after the mutation operation (Step 2.6) has been applied, are called children. The crossover procedure is applied n times to generate n new configurations. In our implementation, each new configuration is created by mixing the structural information from both “father” and “mother” configurations. Tournaments (Step 2.2) are simulated, in order to select the candidates for fatherhood in the crossover procedure. Each tournament is biased towards selecting a better candidate from a random subgroup taken from the current population (Step 2.3). In this study: the best candidate (lowest energy structure) in a subgroup wins; a different subgroup is created for the selection of each father; the size of each subgroup is half that of the population and may contain any candidate multiple times. In contrast, the mother configurations are randomly selected from the current GA population.
Mutation is an application of a small Monte Carlo step (random atomic displacements of less than 1.8 Å, i.e. 10% less than the typical bond length). It is applied to each child configuration (Step 2.6). The inclusion of the mutation operation helps to introduce new structural features and improve the diversity in the population while retaining the main structural motif of the parent; the magnitude of the displacement controls the degree of the introduced disruption. This algorithm is especially useful when the structures of the current population are all similar, possibly all from the same superbasin, or when the same structure is chosen for the mother and father.
The structures created by the crossover and mutation operators form the children population (Step 2.8), where upon each child is structurally relaxed to its local energy minimum (Step 3.1) using third-party software. The relaxation is analogous to the maturing process (a child becoming an adult).
Before forming a new adult population, all the duplicate structures are replaced by random structures using the random structure generator (Step 3.3), ensuring that the population is filled with valid unique configurations.
The constructed and randomly generated structures, after relaxation, form a new adult population (Step 3.4), which then competes to survive with the adults from the current population (Step 2.1). Thus further drives the evolution in the desired direction and to constrains the size of the GA population. Only the fittest (lowest energy) structures are selected for the new GA population (Step 3.5), to which the next GA iteration is applied.
In the simulations using our previous GA implementation,10 it was observed that the population was prone to losing diversity and a significant fraction of the CPU time, or effort, was wasted in optimising configurations to the LM already evaluated. Therefore, we have enhanced our GA by implementing: a new filter, a geometrically based pre-screener, for all new candidates earmarked for relaxation; new routines designed to improve the diversity in the population; and new methods for identifying duplicates (identical candidates).
2.2. Geometrical prescreening
A geometrical prescreener has been implemented to identify structures that are likely to fail to converge to a desirable LM during the computationally expensive local optimisation and therefore discarded. The implemented geometrical prescreener is much quicker to complete than a local optimisation, and consists of three checks which are performed on a structure.The first is employed to identify clusters that contain at least two atoms that are physically too close to each other. In theory, all interatomic distances are calculated and then compared to a minimum radial cut-off, rmin. In practice, once one interatomic distance is found to be too small the remaining interatomic distances are not calculated. Moreover, as the Cartesian coordinates are known, only if the absolute values of all the components of Rij, a vector separating atoms i and j, are below the cut-off, will KLMC compute |Rij|2 and compare to rmin2, thus avoiding many products and all square root procedures. In our simulations, rmin depends on the species of the pair and a user defined scaling factor, λmin. For like species, rmin = 2λminrcovi, where rcovi is the covalent radius of the atom i. Otherwise rmin = λmin(rioni + rionj), where rioni, j is the ionic radius of atoms i and j, respectively. For metals, appropriate metallic radii should be used instead.
The second check is performed to ensure that the nanocluster is not fragmented and is as follows: all N atoms of the nanocluster are given two labels: an atom number and a fragment number. Initially all the atoms are considered as individual fragments having matching atom and fragment labels running from 1 to N and the fragment number is updated after computing the coordination of each atom in the structure. More precisely, for every atom m a check is performed with a pre-defined radial cut-off (rmax) against all the other atoms with non-matching fragment labels. If two atoms have different fragment numbers and are within rmax, all atoms labelled with the higher fragment number are re-labelled with the lower fragment number of the two atoms. When the check for the atom m is completed, if the number of atoms with the fragment number m is one, then there are at least two fragments in the nanocluster, and the algorithm can be stopped. If the check is continued and performed on all the atoms, the number of unique fragment numbers is equal to the number of fragments in the nanocluster. To save computational time, a similar procedure described for the first check is replicated here: if possible, comparison between an interatomic distance r and the radial cut-off rmax is achieved by comparing components of r2 with rmax2.
An alternative cheaper algorithm for testing fragmentation is also available (check three). Although more robust, it does not determine the number of fragments. Here, KLMC searches for atoms with a coordination number of zero using the rmax cut-off; if found, the nanocluster is rejected and there is no need to perform the previous, more extensive check. In practice, the algorithm to compute the coordination number of all atoms has been adapted for this task to reduce the computational effort; the algorithm ends as soon as one atom is found to have a coordination number of zero, and the determination of the coordination of each atom is also terminated once the search has found one atom within its coordination sphere and the search is not computed for any atom already found to be coordinated to an atom already checked.
The value of rmax is calculated using the same method employed to calculate rmin (see check one), but using λmax instead of λmin. The optimal choice of λmin and λmax is system dependent.
These checks are an efficient way of discarding structures, which also are likely to take a very long time or even fail to converge in any type of an iterative self-consistent procedure, thus reducing computational effort. The geometrical prescreener is applied when a new structure is generated randomly (Step 1.2) or as a result of crossover (Step 2.5) and mutation (Step 2.7). If the prescreener discards a structure, a new one is created in the same way as the discarded one, i.e. if mutation is rejected then the mutation operator is applied again to the original crossovered configuration, whereas if crossover is rejected, the crossover operator is repeated using the same parents. In both cases, there is a maximum number of attempts (100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 as optimised in our previous study and is system independent) for crossover and mutation per new candidate structure, after which the unsuccessful crossover and mutation is replaced by a newly generated random structure. If the latter fails, the current population size is reduced by one.
000 as optimised in our previous study and is system independent) for crossover and mutation per new candidate structure, after which the unsuccessful crossover and mutation is replaced by a newly generated random structure. If the latter fails, the current population size is reduced by one.
2.3. Move classes
As mentioned above, ensuring and maintaining the diversity of the population is a challenging task, but necessary, otherwise the performance of the GA will deteriorate. The new structural features can be created during crossover (Step 2.4) and mutation (Step 2.6) operations. First we consider the crossover operator.Previously in KLMC,10 a conventional three-dimensional routine was used to split parent structures into pairs of different fragments: parent nanoclusters are randomly rotated about a random axis, then each split into two fragments; joining the fragments from two parents will produce the child nanocluster. By performing multiple tests on small size structures that form two-dimensional configurations, it has been observed that this routine tends to generate 3D child structures, which failed or were difficult to optimize. Therefore, a new routine has been added to determine the dimensionality of the parents and the crossover operation modified for one- and two-dimensional structures.
In particular, the frame of reference for each cluster is redefined in order to align the centre of the cluster to a common origin for all clusters and the principal axes of each cluster with the same Cartesian axes, using the tensor of inertia. Therefore, once displaced and rotated, one- and two-dimensional clusters will therefore, once displaced and rotated, only have atoms on the x-axis and in the xy-plane, respectively. Then, to determine the dimensionality of a cluster, KLMC checks whether all atoms are within a set tolerance of the x-axis for linear structures and, if not, within the same tolerance from the xy-plane for planar structures. A default tolerance value of 0.8 Å was chosen, as it is shorter than the length of a typical bond but also allows for some corrugations or curvature in the cluster and, moreover, proved suitable for all the systems considered here. If two planar structures are found, for example, then the crossover routine will randomly rotate each parent cluster about the z-axis, rather than any random axis before splicing together fragments from each to form a new child structure with the same composition as either parent. For linear parents, no additional random rotation is applied.
It is essential to maintain structural diversity in the population, to ensure the effectiveness of the crossover operator. Traditionally, this is achieved by the application of the mutation operator to introduce new structural features. Hence KLMC supports the standard phenotype mutation operator that randomly perturbs (small random displacements) a random subset of atoms. As each new configuration is immediately relaxed (the Lamarckian approach), then this mutation operator must apply a large enough Monte Carlo step to escape its current energy basin. To overcome the problems with the traditional operator, we have implemented three new mutation operations (or move classes): self-crossover, expansion–contraction and atom exchange. One mutation move class is applied to each cluster configuration produced by the crossover routine.
The probability of each mutation move class, including the standard Monte Carlo step, is set by the user before the GA simulation is started. The new mutation operators are:
• Self-crossover – a crossover operation is performed using the same structure for both parents, but with a random rotation applied to just one parent.
• Expansion–contraction – the nanocluster's coordinates are rescaled by a random factor within a user defined range.
• Atom exchange – for compounds, a random subset of atoms are swapped.
2.4. Uniqueness
The success of the crossover operator requires a good diversity of structural features within the population, thus maintaining diversity is an important task in any evolutionary algorithm. We have implemented a Lamarckian based algorithm, which is more prone to kill diversity than a Darwinian approach by an unwanted proliferation within the population of just one configuration.† Different configurations within the same catchment area on the energy landscape will relax to the same LM. As duplicate structures are removed, then a population of a finite size is more likely to contain a more diverse set of structural types (i.e. structures from different energy basins).As the Lamarckian population only contains LM (or at least stationary point) structures, a finite energy difference between two fully relaxed clusters implies two different LM. The reverse is not necessarily true, and, in practice, tolerances within the routines used to refine each cluster to a LM can cause a small non-zero energy difference between two structures of the same LM energy basin. Improving the tolerances will make each refinement more costly and extremely wasteful if the resulting LM is already found or much higher in energy than those already within the population and therefore is likely to be discarded in the next stage. Moreover, the chosen model (energy definition) may itself not be that accurate, thus only an approximate LM is required.
The energy differences between the nearest-neighbour energy-ranked LM are typically greater for better ranked, small nanoclusters. In the previous study of nanoclusters composed of up to 24 atoms,10 most duplicate structures were distinguished by comparing their energies. Two different LM structures with the same energy (typically left and right hands of enantiomers) were found by conducting independent runs of KLMC.
Ideally, all unique LM that fall within a certain energy range above the GM should be found during one GA run. Moreover, we are interested in bigger nanoclusters, which, unfortunately, are not only more expensive to refine but also typically have a higher density of LM with respect to energy, and degeneracy (different LM with the same energy) is more likely. For big clusters, relying on only comparing energies in order to distinguish duplicates becomes more of a liability for both computational cost (if tolerances in refinements improved) and success at finding all low energy LM (unique LM removed by mistake). Hence, we have implemented a number of new algorithms for identifying identical structures.
There are a number of algorithms in the literature that have been designed to recognise similar structures and/or measure the degree of similarity.37–39 Although these solutions are comprehensive, the associated computational costs are also high, while information which is not necessary for the current objective is also generated by these procedures.
We have implemented two new test routines within KLMC for comparing structures. The first test determines how similar two clusters are by assuming that similar clusters should have similar principal moments of inertia (which are computed using the zheevj3 routine40). Initially their effective sizes, as characterised by the trace of the tensor for the moment of inertia (I), are compared. If the difference between the two traces is below a user defined threshold, a further comparison is made using the following similarity metric:
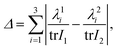 | (1) |
Our second test is employed to identify duplicate structures, rather than how similar two structures are. KLMC achieves this by exploiting a more robust algorithm, which is implemented within the NAUTY software package (No AUTomorphisms, Yes?) written by McKay and Piperno.41 Previously, similar approaches have been successfully implemented for topological analyses of point defects42 and identification of similar defect clusters43 in bulk systems.
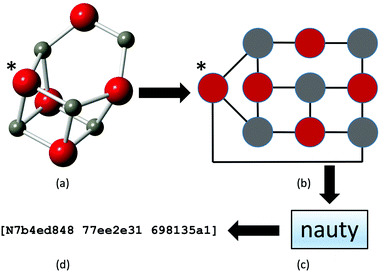
NAUTY tackles the problem of computing automorphism between graphs with an option to produce canonical labelling for them. Using NAUTY, a graph can be canonically labelled by three 8-digit hexadecimal numbers, forming a unique character string, or a fingerprint, thus providing a very quick and robust way to compare graphs.
In our work we use this functionality of NAUTY in the following way: we assume that each cluster's configuration can be represented as a coloured graph (Fig. 2(a) and (b)), where each atom is treated as a vertex and its colour is determined by the atom's element (as a one-to-one map). In particular, the vertex colour depends on the number of unique elements in the system studied, thus binary, ternary, and quaternary compounds will have vertices of 2, 3, and 4 different colours, respectively. Next we identify the edges of a graph by analysing the interatomic distances. If the distance between two atoms (vertices) i and j is less than rgij, then we assume that there is an edge between them (it can be thought of as a bond between two atoms).
The graph depends on the chosen value of rgij, which were kept fixed during our simulations to ensure that NAUTY will generate a unique fingerprint (Fig. 2(c) and (d)). These fingerprints are easily compared to identify duplicates that need to be removed from the population.
Thus, we have developed and implemented a number of new algorithms into the KLMC GA module with an aim of maintaining and improving diversity in the evolutionary process. We will demonstrate next the application of the redeveloped software to the study of four chemically diverse nanocluster systems.
Ideally, a comparison with other structure prediction software that implements a genetic or evolutionary algorithm4,8,22,28,31,32,44,45 would be useful. However, a fair comparison requires a level playing field, i.e. collaboration of authors from each code, as carried out in previous studies,27,46 which is beyond the scope of the current work.
3. Applications
3.1. Systems
The new version of our GA in KLMC was tested on the nanoclusters of four different types of systems: a Lennard-Jones model system LJ38; an ionic compound (ZnO)n, n = 1–32; a metal Ni13; and a covalently bonded molecule C60. For each system, the energy is defined at a semiclassical level using IPs as implemented in GULP34,35. KLMC uses GULP not only to compute the energy and interatomic forces, but also to relax new cluster configurations to the LM.For the 38-atom Lennard-Jones clusters, the standard Lennard-Jones potential, with σ = ϵ = 1, was used.
For zinc oxide, a formal charge model was employed with additional energy contributions from Buckingham and Lennard-Jones (LJ) IPs with potential parameters values taken from a previous study.47 In this study we use two models: during the GA searches, the potential energy surface (PES) is calculated using a rigid ion model (RM) and afterwards the RM LM were refined to the LM on the Shell Model (SM) PES. The SM is not as robust as the RM, but does include electronic polarization effects.
For nickel nanoclusters, the IP parameters for the embedded atom model were taken from the Database of Published Interatomic Potential Parameters,48 where the original Tight Binding (TB) many-body IPs49 were reproduced as a combination of a modified embedded-atom method model and a Born–Mayer repulsive term.
For the carbon clusters we have employed a Tersoff's bond-order potential, which has successfully modelled small fullerene structures.50 For some of our GA searches for C60 we also used an artificial atom at the centre of the simulation box, in order to guide the search away from dense, rather than bubble-like carbon structures.
3.2. Parameters of GA simulations
Here, we present the set of parameters that were used in our simulations. We have used fixed values for rgij (graph radii for evaluating the fingerprint values) of 2.5, 3.4, 1.6, and 1.9 Å for ZnO, Ni, LJ38, and C systems, respectively. These are proportional to the respective bond lengths. For the geometrical prescreening, the scaling factors are λmin = 0.6 and λmax = 1.25. These values were chosen to avoid constraining the simulations to a certain configurational subspace and to reject systems that are physically (chemically) impossible. We do not expect a user of KLMC to change these values when the landscape is defined using interatomic potentials as the sensitivity of these parameters, in our experience, only become really important when electronic structure methods are employed.For all simulations, 80% of the structures from the crossover operation were mutated using one of the mutation move classes, chosen at random with probability weights: 20% – self-crossover, 10% – atom exchange, 10% – expansion, 10% – contraction, and 50% – random displacement. The scaling factors for the expansion and contraction are 1.8% and 0.8% respectively.
The simulation box size, population size and the number of generations were dependent upon the size of the nanocluster. For (ZnO)n, n = 1–32, these parameters increased with respect to n, taking values between 4.0–12.0 Å, 20–140, and 100–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, respectively. For Ni13 we used 5.0 Å, 200, and 200, for LJ38, 8.0 Å, 100, and 10
000, respectively. For Ni13 we used 5.0 Å, 200, and 200, for LJ38, 8.0 Å, 100, and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, and for C60, 8.0 Å, 200, and 10
000, and for C60, 8.0 Å, 200, and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.
000.
For our local geometry optimisations, we have chosen tolerances on energy, atomic forces and atomic coordinates to ensure that, the energy, measured in eV per cluster, is converged to at least seven decimal places, which has been considered essential to maintain structural diversity in previous global optimisation studies39 and also ensures the correct ranking of local minimum candidate structures.
Different convergence criteria were used for the problems with known solutions and those with unknown solutions. For known solutions, the simulations were terminated once these targeted structures had been found with a reasonable statistical reproducibility. For simulations with no known target structure, in particular the larger ZnO clusters, the optimum (or minimum) number of GA iterations, m, without generating a new unique configuration that would indicate that the search has been successfully completed is generally unknown. With no convergence criteria, when the search has successfully completed more GA iterations are typically performed to gain confidence in the current structural predictions so unfortunately a much larger value for m is typically used. Minimising m can easily lead to missing low energy configurations.
It is not necessary to minimise m for small system sizes, however, for GA runs on our larger systems, we define two subsets of the current population: the first subset, U1, includes the lowest energy LM (which, by definition includes the tentative GM), and the second subset, U2, is composed of the next lowest energy LM, where U1 + U2 ≤ population size and U1/U2 = 0.2. The simulation is deemed to be converged when no new unique structures appear within subset U2 during ten consecutive GA iterations (m = 10). Towards the end of a GA run, monitoring changes to subset U2, rather than U1, is a more robust procedure as changes to subset U2 are more likely given (see below) the exponential growth with energy in the number of unique LM structures within an accessible energy range.
3.3. The double-funnel problem of the 38-atom Lennard-Jones cluster
Although as mentioned, the difficulty of exploring a landscape depends on the number of degrees of freedom (determined by the size of the cluster), it also depends on the complexity of the potential energy landscape. There are particular cases when the GM of a smaller cluster is much more difficult to locate than the GM of a larger cluster on the same energy landscape. An example of such a phenomenon is the 38-atom Lennard-Jones cluster (LJ38) double funnel problem; the two lowest energy LM are located in very differently sized funnels, with the GM residing in the narrower of the two. The nature of this puzzle has been clarified by representing this energy landscape with a connectivity graph51 of the energies for all LM and the lowest energy barriers that separate them. Let us consider a typical Monte Carlo simulation on such a landscape. In search for a low energy LM starting from a random point on the landscape, a random walker, that performs a sequence of small Monte Carlo steps, perhaps following the Metropolis algorithm, would proceed to escape from a current LM most likely in the direction of a small energy barrier to a neighbouring LM. If the new LM has a lower energy, then the walker is unlikely to return to the original LM. Once within a certain region of the landscape, the walker is thus funnelled towards the GM of that region. The ease of finding the true GM therefore depends on the relative size of the catchment area of the funnel containing it. Funnels occupying a relatively small fraction of the energy landscape require extensive exploration, for example using very many walkers, making it computationally very expensive. Hence, such systems are perfect for testing the efficiency of global optimisation algorithms. More recently ideas of niching have become more popular to direct the search into a desired funnel, a method which benefits from knowing how to distinguish which funnel you are in.52,53 Here, we concentrate on developing an approach that does not use such prior knowledge.The complex energy landscape of LJ38 has a double-funnel shape, where one funnel contains the fcc truncated octahedron (GM) and the other funnel contains the incomplete Mackay icosahedron (LM2).
This PES was extensively studied by several groups51,54–56 using different approaches, including Monte Carlo Basin Hopping. These and most of the other studies addressing the funnelling landscapes conclude that some sort of a biased (imposed preference) method is needed in order to efficiently explore such PES that contain multiple funnels. Thus, we have chosen the LJ38 case as one of the examples to investigate the performance of our improved unbiased GA.
We have performed 50 independent searches for the LJ38 double funnels using our GA implementation with the simulation parameters given in the subsection 3.2. For this particular system we chose to analyse how quickly the two funnels can be located and what is the success rate of finding them is within 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 GA iterations. We have observed that the second lowest energy structure, the incomplete Mackay icosahedron, was found during all our simulations. In fact, averaging over the 50 GA runs, only a fifth of the 10 000 GA iterations were required. The distribution graph of the GA iteration when the LM2 was found for the first time is given in Fig. 3(a), with the mean value of 1861.16, standard deviation of 1896.46, skewness of 1.60 and kurtosis of 2.02. Similarly in Fig. 3(b) we present the results for the GM structure, which has been found 6 times out of 50 after a fairly high number of iterations.
000 GA iterations. We have observed that the second lowest energy structure, the incomplete Mackay icosahedron, was found during all our simulations. In fact, averaging over the 50 GA runs, only a fifth of the 10 000 GA iterations were required. The distribution graph of the GA iteration when the LM2 was found for the first time is given in Fig. 3(a), with the mean value of 1861.16, standard deviation of 1896.46, skewness of 1.60 and kurtosis of 2.02. Similarly in Fig. 3(b) we present the results for the GM structure, which has been found 6 times out of 50 after a fairly high number of iterations.
As can be seen in Fig. 4, the energy distributions of the lowest energy structures of the simulations that found the GM (red lines) and the ones that did not (blue lines) are very similar. Moreover, the top seven structures (excluding the GM) have been generated during all the simulations, thus indicating that the improved algorithm is able to find all local minima (that are probably within the larger funnel containing LM2) and, given enough GA iterations, the GM that is within the narrower funnel. Fig. 3 and 4 show how complicated the PES is in this particular case, but nonetheless unbiased GA in KLMC 2.0 was able to locate both double funnels, whereas previous studies51,54,55 employed a biased preference method during the searches.
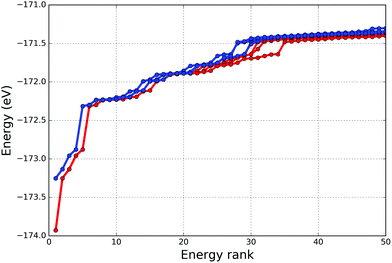 | ||
| Fig. 4 The energies of the lowest energy structures from simulations that were able to find the GM and LM2 (red lines) and the ones that were able to find the LM2 but not the GM (blue lines). | ||
3.4. Performance of the GA on (ZnO)24
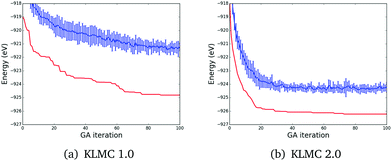
In order to evaluate the performance of our new GA implemented in KLMC, we initially concentrated on (ZnO)24, a system which was previously investigated using KLMC and other software.2,47,57 We chose (ZnO)24 as our representative system, as it has many metastable LM configurations, the tentative GM configuration is accepted with a high confidence level, and it is not too computationally expensive to generate statistics for. We have performed 10 GA simulations using KLMC with and without the newly added enhancements and every GA simulation was run for 100 GA steps.GA convergence tests for the two versions of the code are presented in Fig. 5. The red line shows the mean energy evolution, as a function of the number of GA cycles, of the lowest energy structure, averaged over the ten independent runs. Within the first twenty GA iterations, the energy curve is much steeper for KLMC 2.0, which was able to find lower energy candidate structures more quickly than its counterpart KLMC 1.0. The energies obtained with KLMC 2.0 are also significantly lower, and the GM was always found. In contrast, KLMC 1.0 found the GM in only three out of the ten simulations within the given 100 GA steps.
The blue line in Fig. 5 presents the evolution of the mean energy of the twenty lowest energy structures within a GA simulation averaged over the ten GA simulations. The blue line is also much closer to the red for KLMC 2.0 indicating that the new version of GA was also better at finding more LM. This is also the cause of the smaller error bars for KLMC 2.0, which implies that it was able to find more structures which have similar energies than KLMC 1.0. This is important, as it indicates a much healthier, evolving population of competitive candidates, rather than one strong candidate amongst much weaker competitors. As the number of possible candidate structures increases with the number of formula units, there will be a high number of LM with similar energies. Different structures may have very similar energies, which would not be recognised if the simple energy criterion is used. The resultant population, therefore, is forced to span over a wider energy range. By using topological analysis, KLMC 2.0 is able to remove duplicates based on their configurations.
In conclusion, the new more rigorous geometrical prescreening, the greater variety of mutation move classes and a check for uniqueness based on the topological analysis improved the GA diversity and convergence significantly.
3.5. (ZnO)n, n = 1–32
ZnO nanoclusters have been studied extensively2,47,57–71 and most of the studies report that the larger LM structures typically resemble bubbles and nanotubes. As we have access to the data published by Al-Sunaidi et al.,47 and as it is the first and only systematic study that also includes the low energy metastable (ZnO)n configurations up to n = 32, we have used these results as our benchmark. Our tentative GM and lowest metastable LM structures are typically lower in energy or at least comparable with the cluster configurations reported previously. Here we repeat this study using our enhanced KLMC GA with the same local optimisers to search for LMs on the same PES. We report only those results that differ from the ones published by Al-Sunaidi et al.47 Previous results are labelled using the notation from the original publication, i.e. lower/upper case letters indicate the rank with regard to RM/SM, respectively, whereas any missing LM found by KLMC 2.0 are marked with a star after the size number.For n < 24, all the previously reported structures were found at the end of the GA simulations. When the energy difference between isomers is relatively small, the ranking is more sensitive to the choice of the energy landscape, the definition of which includes the cut-offs applied to short-range interactions. In the previous work, additional LJ r−12 terms were added to penalize any unphysically short interatomic distances and to increase the robustness of the cost function used by the GA. This is no longer deemed necessary as the implemented geometrical prescreeners remove such clusters. Thus, there are a number of cases where the LM found on the RM PES have a slightly different ranking from that previously reported, e.g. for n = 12, cluster 12d has a lower energy than 12c (labelled 12*c and 12*d), and our isomer of 12h, which was labelled 12j, has a lower energy than 12i and is approximately 0.001 eV higher in energy than 12h.
Nonetheless, after the refinement to SM LM, the configurations of the top six SM LM for n = 12 from both studies were identical. There were, however, a few minor changes in SM energy, which is most likely caused by the different levels of tolerance used during the optimisation.
For bigger clusters, we have found a number of LM that were previously missed. Two new tentative GM, as measured using the SM, were found. In both cases, n = 24 (Fig. 6(a)) and n = 27 (Fig. 6(c)), a capped-nanotube, or barrel configuration. The barrel configuration for the 24*A(b) structure is capped at each end by a hexagon and three tetragons, with one capped ends rotated out of phase about the axis of the barrel by 45°. This configuration could be seen as an extension of the 18A(a) barrel structure with the rolled hexagonal sheet extended by six ZnO dimers. 24*A(b) is 0.37 eV lower in energy (SM) than the previously reported GM 24A(c). This result explains the unusual findings in ref. 47 for n = 24, which contradicted the generally observed trend for ZnO nanoclusters with octagonal faces being less stable than structures without them. By extending the 18A(a) structure's hexagonal pattern by another six dimers, a previously unreported larger nanotube 30*B(h) can be formed with the same symmetry as 24*A(b) as shown in Fig. 6(g).
 | ||
| Fig. 6 SM and LM structures of (ZnO)n, n = 24–32 that were not reported in the previous study.47 Labels include the number of hexagonal–tetragonal–octagonal faces and the point group symmetry of the LM. | ||
As ranking may change when the SM is switched to a more accurate electronic structure based model, it is important to find all low energy LM that are at least thermodynamically accessible. For n = 30, as mentioned, we also found a lower energy configuration for the second lowest energy LM (SM), labelled 30*B(h). Using the RM, it is the eighth lowest energy structure found by KLMC 2.0, but switching to the SM, its stability improves, and is only 0.04 eV higher in energy than the GM.
We also found another new low energy isomer for n = 30 (Fig. 6(f)); another perfect bubble formed of twenty six hexagons and six tetragons. Comparing only bubbles of twenty six hexagons and six tetragons, the 30*E(d) configuration has the highest SM energy of the 26-6 isomers, whereas the 30*B(h) has the highest RM energy.
Similar to the 24*A(b) structure, the 27*A(d) structure is also a barrel, but unlike the 24*A(b), the hexagonal ends are in phase. Other barrels of this type include 21A(a), 15A(a), and 9A(a). The 27*A(d) SM structure is our tentative GM, with a SM energy that is 0.26 eV lower than the previously reported GM, 27*B(b).
A new nanotube-like structure 32*C(a) was also found for n = 32 (Fig. 6(h)), which is the RM GM and ranked third using the SM. 32*C(a) is a wider version of 24B(a) and 16C(c), with each barrel capped with octagons that are in antiphase (45° rotation) to each other. As with the hexagon terminated nanotubes, there also exist barrels with octagonal caps that are in phase also exist: 28*E(b), 20*A(a), and 12*F(d).
The ranking of larger hexagon capped nanotubes is improved when switching from the RM to the SM. The opposite is observed for the octagon terminated nanotubes, for which a better RM rank is found than that of SM. Currently, we are investigating larger clusters.
We were also able to find new isomers for n = 25, 25*C(c), and n = 28, 28*B(c) and 28*C(d), Fig. 6(b), (d), and (e), respectively, where 25*C(c) is an enantiomer of 25C(d). Switching Zn and O atoms results in a slight difference in energy. For n = 28, two new configurations, which are enantiomers of each other, were found with very low energies that were not reported in the previous study. With the SM, these structures are ranked second and third and form an intermediate configuration between a bubble and nanotube, which we refer to as a capsule. Each end of this capsule is terminated with three tetragons and three hexagons.
To test the reproducibility of the predicted structures from our new algorithm, we choose to perform ten independent GA simulations for the following sizes: n = 20, 24, 27, 28, 30, and 32. These sizes were chosen to represent a “good” spread, starting from less complicated n = 20, to significantly more challenging cases of n = 27, 30, and 32, in which the barrel structures form.
In Table 1, with "we report at which iteration (N), the GM was found during a GA search on the RM PES, and “*” marks the selected cases, for which we show an average N over ten simulations.
| n | N | n | N |
|---|---|---|---|
| 11 | 0 | 22 | 42 |
| 12 | 1 | 23 | 13 |
| 13 | 1 | 24 | 33* |
| 14 | 1 | 25 | 359 |
| 15 | 1 | 26 | 497 |
| 16 | 3 | 27 | 96* |
| 17 | 3 | 28 | 400* |
| 18 | 3 | 29 | 1335 |
| 19 | 7 | 30 | 590* |
| 20 | 15* | 31 | 3544 |
| 21 | 9 | 32 | 196* |
In general, the GM for small size clusters (n < 24) was found very quickly. For n > = 20, the correlation between n and N becomes more apparent: the task of finding the GM typically becomes more computationally demanding as n increases. Similar size dependencies of the success rates are presented in the previous work,47 where an onset of lower success rates occurred at n = 17. Thus, the new improved GA implementation is both more robust and remains efficient for larger systems.
The lowest energy structures are perfect bubbles that exhibit only tetragonal and hexagonal faces. The perfect bubbles, whose structure has been discussed in detail,47 exhibit structural motifs, including tetragonal rings, that is not present in the ground state bulk structure of wurtzite ZnO, but is known as a part of a hypothetical body-centred tetragonal phase, with a low calculated energy of formation.72–74 If the largest faces in a perfect bubble are hexagonal, then according to Euler's rule there will only be six tetragonal faces. A certain degree of disorder can be present as the actual location of the tetragonal faces with respect to each other can vary to an ever greater extent as the bubble size increases. Octagonal faces are another type of topological defect, which can result from converting two hexagonal faces to one octagonal and one tetragonal face or, producing two coordinated sites, the result of bond breaking along a shared edge between a tetragonal and a hexagonal face. Either process results in a further increase of possible bonding arrangements on the surface of a bubble and therefore the computational challenge in modelling this system originates from the number of structural motifs that the energy landscape produces by rearranging the octagonal, hexagonal and tetragonal faces on the surface of a structure, which increases with the system size. As the clusters grow, there emerges another structural motif of low energy defected bubbles with atoms inside. To illustrate this behaviour, we have plotted the density of states (Fig. 7) for the lowest 1000 energy structures of the n = 30 system.
As the density of states plot indicates, the majority of the structures are those with the octagonal faces and atoms within the bubbles. The energy penalty per atom for such defective systems compared to the GM is minimal (∼0.07 eV) which makes the search on this energy landscape more difficult as the cluster size grows. Nonetheless, the unbiased KLMC 2.0 GA algorithm was able to cope with such complicated PES. Moreover, the GA in KLMC 2.0 was quicker to converge and found missing LM, including new tentative global minima.
One advantage of studying ionic systems with formal charges is the intrinsic Coulomb ordering that emerges both in the short and long ranges, which severely reduces the number of plausible candidate structures. Next we consider Ni13, the stability of which is determined by short-range many-body interactions.
3.6. The magic of Ni13
Nickel is a ferromagnetic late transition metal with an open d-shell, which is widely studied using both simple interatomic potentials and DFT. Nickel has gained its popularity among research studies due to its applications in catalysis and hydrogen chemisorption. Both atomic structure and stability, and the electronic and magnetic properties of Ni clusters have been reported.70,75–83 Typically, in non-global optimization studies, Ni13 is assumed to adopt the ideal Platonic icosahedral configuration of Ni13 (Fig. 9(a)). The lowest energy structure on the DFT landscape has, however, been reported as a pentagonal bipyramid.82 The icosahedral structure in that study was found to be 0.46 eV above the GM, and ranked fifth. As the ranking proves to be crucially sensitive to the level of theory, it is very important to consider a complete set of the lowest energy LM and not only the GM.Using our new GA in KLMC, we have performed a search on the TB PES.49 It was estimated that at least 988 LM exist for clusters of LJ13.84 Due to the nature of the TB potential, the TB PES is more complex and has more LM than two body LJ PES. Thus, in Fig. 8, we focus on showing the density of states of the last (200th) GA generation in the subset and focus on the 2 eV energy range above the GM, which includes previously reported low DFT energy configurations from previous studies by Chou et al.81 and Lu et al.82
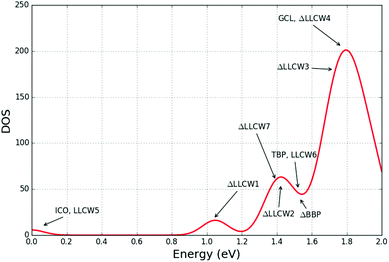 | ||
| Fig. 8 The DOS graph of the unique Ni13 LM clusters found using the new GA implementation in KLMC; annotations on the graph indicate which energy region a particular structure is in; prefix Δ marks the structure which is similar to (a distorted version of) a previously reported structure; notation LLCWm indicates structures presented in ref. 82, where m marks its ranking. | ||
Four structures – icosahedral (ICO), triangular biplanar (TBP), buckled biplanar (BBP) and garrison-cap layer (GCL) – that were reported in the study81 on LDA and GGA, were also found by us on the TB PES. These configurations are shown in Fig. 9. Other reported LDA and GGA LM configurations, such as cuboctahedral (FCC), decahedral (DEC), body-centered cubic (BCC), hexagonal close packed (HCP) and cagelike (CAG) were not found on the TB PES during our simulations. Although some LM, including ICO and TBP (Fig. 9(a) and (b)) match well with those previously reported, on the other hand, others, for example, ΔBBP and ΔGCL, Fig. 9(c) and (d), were found to become slightly distorted (where Δ labels structures, which are similar to those reported previously).
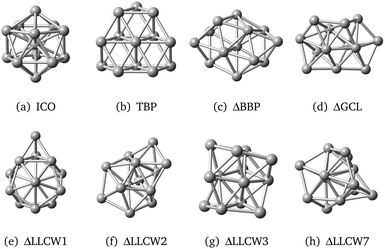 | ||
| Fig. 9 Ni13 LM cluster configurations found using the new GA in KLMCs, which were reported elsewhere.81,82 Prefix Δ marks the structure which is similar to (a distorted version of) a previously reported structure; notation LLCWm indicates structures presented in ref. 82, where m marks its GGA ranking. | ||
The missing FCC, DEC, BCC, HCP, BBP, and GCL configurations were constructed by hand and optimised using GULP to the LM on the TB PES. Structures FCC, DEC, BCC and HCP proved to be unstable and transformed to the ICO structure during the relaxation, whereas configurations BBP and GCL lowered their symmetry and adopted the ΔBBP and ΔGCL LM configurations, already found by our GA.
Comparison with GGA LM configurations82 shows that only a subset of Ni13 structures matched: their fourth, fifth, and sixth lowest energy structures correspond to our ΔGCL, ICO and TBP configurations. The eighth lowest GGA energy LM, FCC structure, was not found as a LM on the TB PES as it relaxes to the ICO structure.
Allowing for small distortions, other matches between their GGA LM and TB LM found during our GA search were identified. Examples are shown in Fig. 9(e)–(h), and are named LLCWn, where n stands for the GGA energy rank reported in the paper by Lu et al.82 KLMC was able to determine a match by comparing their fingerprints (see section 2.4).
Curiously, employing the many-body potentials for nickel significantly eases the global search on the potential energy landscape compared to the much simpler Lennard-Jones form. The stark contrast can be immediately seen comparing our GA simulations of LJ38 and Ni38 presented in Fig. 3. Using the TB IPs49 we were able to locate the two lowest energy structures from the LJ38 PES in ten attempts practically always within the first few hundreds GA iterations; however, the incomplete Mackay icosahedron is not the second lowest energy structure but third. We conclude that many-body interactions in the case of nickel proved to be powerful and selective in organising the energy landscape and effectively reducing the search space.
To summarize, KLMC 2.0 was able to find the stable and meta-stable LM on the TB PES that matched those on the DFT PES and therefore proved to be effective at exploring the TB PES for Ni13 LM configurations. These can be further refined using a higher level of theory to investigate their structural, energetic, magnetic and other properties.
3.7. C60
In the chemistry of carbon, the discovery of the small fullerene cage clusters has been one of the most exciting developments.85 They have a spherical cage structure and physical and chemical properties, which are exploited in different applications, including electronics,86 due to the superconducting phases; optics,87 due to the optical limiting properties; biomedical technology,88etc.We have applied our new GA algorithm to optimise the geometry of the C60 nanocluster. Previously, a similar study4 was carried out, which highlighted that one of the biggest challenges for a GA was the avoidance of getting trapped in certain configurations. By studying the same system and investigating the evolutionary process of the C60 in more detail, we have looked to see which processes are more influential during the search for lower energy configurations.
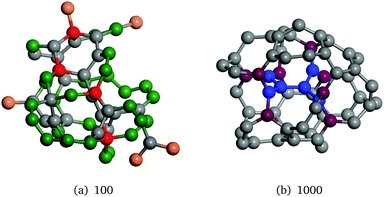
In our first attempt, we have performed ten independent GA runs of 1000 iterations, each population consisting of 100 members, which is comparable to our successful GA runs on the ZnO system of similar size. In the first GA population, there are already chemically sensible structures but with some clearly unfavourable features, in particular, undercoordinated terminal atoms (Fig. 10(a)). At the end of these simulations, the lowest energy LM formed shell structures filled with small clusters, as shown in Fig. 10(b).
These findings are reminiscent of the problem encountered in the structure prediction of nanoporous materials, with semi-covalent semi-ionic frameworks, e.g. zeolites. One of the most successful solutions has been the introduction of the hard and soft boundary exclusion/inclusion zones.89,90 Building on that experience we have fixed at the centre of the simulation box an artificial atom with a short-range repulsive potential to carbon atoms (choice of parameters explained in section 3.1). Ten simulations using the soft spherical exclusion zone and ten unconstrained simulations will be compared below.
In Fig. 11 we plot the energy evolution during one of our C60 simulations with an artificial atom, which illustrates the most common features of the GA simulations. Here, we report the twenty lowest isomer energies; the GM configuration is that of the buckyball, a spherical fullerene molecule.
 | ||
| Fig. 11 Energies of C60 configurations within the population that is evolved by a GA that targets the GM. Here the red line represents the average energy of the presented configurations. | ||
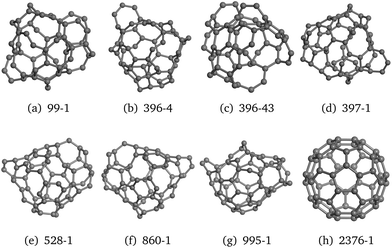
The evolutionary process starts from random configurations, which during the first GA steps optimise to more chemically inert structures, as can be seen by the initial steep energy drop followed by a gentle slope persisting for about 300 GA iterations. Around the 100th generation a lower energy configuration is found (Fig. 12(a)), which remains the lowest energy structure for a few hundred iterations, until around the 400th GA generation a new lower energy cluster is found (Fig. 12(d)). During these couple of hundred steps, even though the energy of the lowest energy configurations did not change, the lowest twenty configurations have improved – the spread became tighter and the average energy decreased.
The new configuration (Fig. 12(d)) was created by a crossover operation between LM configurations ranked 4 and 43 from the previous generation (Fig. 12(b) and (c) respectively) followed by a random mutation operation. Then the evolutionary process successfully continues until (GA generation 528) another configuration is found (Fig. 12(e)). It remains the lowest energy configuration for another couple of hundreds of GA iterations.
The first successful attempt to improve this latter configuration happens when a self-crossover operation was applied, thus resulting in a lower energy structure shown in Fig. 12(f). It helped to evolve a new series of energetically more stable structures. Around the 1000th GA generation, the new lowest energy configuration (Fig. 12(g)) resembles the buckyball shape, although with several defects and handles. During this simulation, the latter configuration was the lowest energy structure for more than one thousand GA iterations, during which even more similar energy structures were found, but not lower. This configuration remained the lowest energy structure for more than one thousand GA iterations, until a self-crossover operation was performed on it, which ended up in a slightly lower energy structure and a step closer to the buckyball configuration (Fig. 12(h)).
To gain a better insight into why the GM on this PES is so hard to find, we have followed the evolution of the twenty lowest energy structures. The lowest energy structure, GM, is a buckyball and the higher energy LM structures have some irregularities. The perfect buckyball configuration is formed by twelve pentagonal and twenty hexagonal rings, where no two pentagonal rings share an edge. Any deviation from this structural configuration, i.e. a defect, increases the system's energy and makes it less energetically stable. The most common defect observed was a pair of pentagonal rings sharing an edge and the second lowest energy structure has two pairs of them (Fig. 13(a)). Another common defect is an eight-atom ring, which is formed by breaking the shared edge between two pentagonal rings as shown in Fig. 13(c). The other LM out of the mentioned twenty have a combination of paired pentagonal rings, up to five, and/or an eight-atom ring.
The same defects appear at the end of all our simulations, with and without an artificial repulsive atom. During our simulations, three out of ten simulations with an artificial atom (Fig. 14(a)) were able to find the twenty lowest energy LM structures. Although none of the simulations without an artificial atom (Fig. 14(b)) have yet found the buckyball configuration, three simulations are very likely to converge to it relatively soon. Moreover, simulations with an artificial atom clearly converge much faster and have lower average energies than their counterparts without the atom. Both types of simulations have similar trends of having regions where average energy decreases slowly and regions where it drops very quickly, when a new tentative GM is found. Furthermore, we can see that the simulations, which have converged, have a very similar energy range of the twenty lowest energy structures, and it is slightly greater than that of the simulations that did not converge.
Comparing the results of the simulations with an artificial repulsive atom and without, we were not able to see similar intermediate states, as they produce different intermediate configurations. Again, this indicates that the PES has an enormous amount of LM and every simulation follows its individual path.
4. Conclusions
We have implemented and tested a new version of KLMC's population based global optimisation module. The focus was on improving the Lamarckian evolutionary algorithm, as applied to finding low energy LM structures for nanoclusters. The improvements included: implementing geometrical pre-screening routines, new mutation move classes, and algorithms for locating and removing duplicate structures within a population.Four different systems were used to check the effects on the performance of KLMC: LJ38, (ZnO)1–32, Ni13, and C60.
We show that the double-funnel problem of the 38-atom Lennard-Jones cluster can be successfully addressed with an unbiased approach, which shows the power of the new method to predict large size clusters on a complicated PES.
The new LM structures found for (ZnO)24 showed that we not only significantly improved the convergence speed but also increased the success rate of finding the target structures.
KLMC successfully reproduces previous results47 for (ZnO)n, n = 1–32, found missing LM and improved on the tentative GM for n ≥ 24. The missing LM were typically nanotubes. The discovery of low energy quasi 1D structures demonstrates the success of the new move classes introduced in KLMC 2.0.
The results from the Ni13 study show the importance of having IPs that can describe the system of interest, i.e. can reproduce the LM for all sought after isomers of a nanocluster. Importantly for this study, KLMC was able to find all the known and targeted LM configurations on the TB PES.
As the results from the C60 simulations indicate, the number of LM increases rapidly with the number of atoms and the GM can be contained in a relatively small energy basin, thus challenging to find. As expected, using soft boundary exclusion zones helps to target particular structural motifs or architectures, in our case bubble configurations. Unbiased algorithms still prove successful, even though much less efficient at finding the GM. This poses a question of whether new move classes should be explored in addressing the GA search on larger systems – cf. ref. 11. The difficulty in identifying the narrow funnel in the double funnel LJ38 problem and the success of the soft exclusion zone applied to the location of the buckminster fullerene on the C60 buckminster fullerene on the Tersoff's-potentials landscape suggest the urgency in the development of new, learn-on-the-fly, biasing algorithms which will be able to identify key structural features that can be targeted in future strategies of global optimisation.
This study has proven that the improved Lamarckian evolutionary algorithm with the focus on maintaining the structure diversity within KLMC is more robust than its predecessor and is a powerful tool for the structure prediction of nanoclusters.
Acknowledgements
The authors thank M. R. Farrow, C. R. A. Catlow, A. A. Al-Sunaidi and J. C. Schön for their useful comments in the course of this project and their preliminary studies, and EPSRC for funding (grant numbers EP/I03014X and EP/K038958). This work made use of the facilities of ARCHER, the UK's National High Performance Computing service, access to which was obtained from an MCC membership, which itself is supplied by EPSRC (grant number EP/L000202), and UCL Faraday and Grace High Performance Computing facilities, and UCL Research Computing Platforms services.References
- S. M. Woodley and R. Catlow, Nat. Mater., 2008, 7, 937–946 CrossRef CAS PubMed.
- C. R. A. Catlow, S. T. Bromley, S. Hamad, M. Mora-Fonz, A. A. Sokol and S. M. Woodley, Phys. Chem. Chem. Phys., 2010, 12, 786–811 RSC.
- S. Heiles and R. L. Johnston, Int. J. Quantum Chem., 2013, 113, 2091–2109 CrossRef CAS.
- D. Deaven and K. Ho, Phys. Rev. Lett., 1995, 75, 288–291 CrossRef CAS PubMed.
- Y. Zeiri, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1995, 51, 2769–2772 CrossRef.
- C. Roberts and R. L. Johnston, Phys. Chem. Chem. Phys., 2001, 3, 5024–5034 RSC.
- S. Darby, T. V. Mortimer-Jones, R. L. Johnston and C. Roberts, J. Chem. Phys., 2002, 116, 1536–1550 CrossRef CAS.
- A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704 CrossRef PubMed.
- C. W. Glass, A. R. Oganov and N. Hansen, Comput. Phys. Commun., 2006, 175, 713–720 CrossRef CAS.
- M. R. Farrow, Y. Chow and S. M. Woodley, Phys. Chem. Chem. Phys., 2014, 16, 21119–21134 RSC.
- J. Zhao, R. Shi, L. Sai, X. Huang and Y. Su, Mol. Simul., 2016, 7022, 1–11 Search PubMed.
- R. C. Eberhart and Y. Shi, IEEE Trans. Evolutionary Computation, 2004, 8, 201–203 CrossRef.
- R. Poli, D. Bratton, T. Blackwell and J. Kennedy, IEEE Trans. Evolutionary Computation, 2007, 1955–1962 Search PubMed.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter, 2010, 82, 1–8 Search PubMed.
- D. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 101, 5111–5116 CrossRef CAS.
- D. J. Wales and H. A. Scheraga, Science, 1999, 285, 1368–1372 CrossRef CAS PubMed.
- M. A. Zwijnenburg and S. T. Bromley, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 1–9 CrossRef.
- C. J. Pickard and R. J. Needs, Nat. Mater., 2008, 7, 775–779 CrossRef CAS PubMed.
- C. J. Pickard and R. J. Needs, J. Phys.: Condens. Matter, 2011, 23, 053201 CrossRef PubMed.
- J. M. McMahon, Phys. Rev. B: Condens. Matter, 2011, 84, 1–4 Search PubMed.
- S. M. Woodley, P. D. Battle, J. D. Gale, C. Richard and A. Catlow, Phys. Chem. Chem. Phys., 1999, 1, 2535–2542 RSC.
- R. L. Johnston, Dalton Trans., 2003, 4193 RSC.
- J. Cheng and R. Fournier, Theor. Chem. Acc., 2004, 112, 7–15 CrossRef CAS.
- G. Rossi and R. Ferrando, Chem. Phys. Lett., 2006, 423, 17–22 CrossRef CAS.
- A. A. Al-Sunaidi, A. A. Sokol, C. R. A. Catlow and S. M. Woodley, J. Phys. Chem. C, 2008, 112, 18860–18875 CAS.
- L. Cheng, Y. Feng, J. Yang and J. Yang, J. Chem. Phys., 2009, 130, 214112 CrossRef PubMed.
- S. E. Schönborn, S. Goedecker, S. Roy and A. R. Oganov, J. Chem. Phys., 2009, 130, 144108 CrossRef PubMed.
- J. M. Dieterich and B. Hartke, Mol. Phys., 2010, 108, 279–291 CrossRef CAS.
- M. Haertelt, A. Fielicke, G. Meijer, K. Kwapien, M. Sierka and J. Sauer, Phys. Chem. Chem. Phys., 2012, 14, 2849 RSC.
- S. Neelamraju, J. C. Schön, K. Doll and M. Jansen, Phys. Chem. Chem. Phys., 2012, 14, 1223–1234 RSC.
- Z. Chen, X. Jiang, J. Li, S. Li and L. Wang, J. Comput. Chem., 2013, 34, 1046–1059 CrossRef CAS PubMed.
- M. Chen and D. A. Dixon, J. Chem. Theory Comput., 2013, 9, 3189–3200 CrossRef CAS PubMed.
- S. M. Woodley, J. Phys. Chem. C, 2013, 117, 24003–24014 CAS.
- J. D. Gale, J. Chem. Soc., Faraday Trans., 1997, 93, 629–637 RSC.
- J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291–341 CrossRef CAS.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196 CrossRef CAS.
- B. Helmich and M. Sierka, J. Comput. Chem., 2012, 33, 134–140 CrossRef CAS PubMed.
- R. Hundt, J. C. Schön, S. Neelamraju, J. Zagorac and M. Jansen, J. Appl. Crystallogr., 2013, 46, 587–593 CrossRef CAS PubMed.
- A. Sadeghi, S. A. Ghasemi, B. Schaefer, S. Mohr, M. A. Lill and S. Goedecker, J. Chem. Phys., 2013, 139, 184118 CrossRef PubMed.
- J. Kopp, Int. J. Mod. Phys. C, 2008, 19, 13 Search PubMed.
- B. D. McKay and A. Piperno, J. Symb. Comput., 2014, 60, 94–112 CrossRef.
- F. El-Mellouhi, N. Mousseau and L. J. Lewis, Phys. Rev. B: Condens. Matter, 2008, 78, 1–4 CrossRef.
- T. Lazauskas, Ph.D. thesis, Loughborough University, 2014.
- S. M. Woodley, A. A. Sokol and C. R. A. Catlow, Z. Anorg. Allg. Chem., 2004, 630, 2343–2353 CrossRef CAS.
- M. Sierka, Prog. Surf. Sci., 2010, 85, 398–434 CrossRef CAS.
- A. R. Oganov, J. C. Schon, M. Jansen, S. M. Woodley, W. W. Tipton and R. G. Hennig, Modern Methods of Crystal Structure Prediction, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2010, pp. 223–2231 Search PubMed.
- A. A. Al-Sunaidi, A. A. Sokol, C. R. A. Catlow and S. M. Woodley, J. Phys. Chem. C, 2008, 112, 18860–18875 CAS.
- Database of Published Interatomic Potential Parameters, http://www.ucl.ac.uk/klmc/Potentials/.
- F. Cleri and V. Rosato, Phys. Rev. B: Condens. Matter, 1993, 48, 22–33 CrossRef CAS.
- P. A. Marcos, J. A. Alonso, A. Rubio and M. J. López, Eur. Phys. J. D, 1999, 6, 221–233 CrossRef CAS.
- J. P. K. Doye, M. A. Miller and D. J. Wales, J. Chem. Phys., 1999, 110, 6896 CrossRef CAS.
- B. Hartke, J. Comput. Chem., 1999, 20, 1752–1759 CrossRef CAS.
- U. Buck, C. C. Pradzynski, T. Zeuch, J. M. Dieterich and B. Hartke, Phys. Chem. Chem. Phys., 2014, 16, 6859–6871 RSC.
- J. P. Neirotti, F. Calvo, D. L. Freeman and J. D. Doll, J. Chem. Phys., 2000, 112, 10340–10349 CrossRef CAS.
- S. Goedecker, J. Chem. Phys., 2004, 120, 9911–9917 CrossRef CAS PubMed.
- M. T. Oakley, R. L. Johnston and D. J. Wales, Phys. Chem. Chem. Phys., 2013, 15, 3965–3976 RSC.
- M. Zhao, Y. Xia, Z. Tan, X. Liu and L. Mei, Phys. Lett. A, 2007, 372, 39–43 CrossRef CAS.
- A. C. Reber, S. N. Khanna, J. S. Hunjan and M. R. Beltrán, Chem. Phys. Lett., 2006, 428, 376–380 CrossRef CAS.
- B. Wang, S. Nagase, J. Zhao and G. Wang, J. Phys. Chem. C, 2007, 111, 4956–4963 CAS.
- B. Wang, X. Wang, G. Chen, S. Nagase and J. Zhao, J. Chem. Phys., 2008, 128, 144710 CrossRef PubMed.
- Z. Zhou, Y. Li, L. Liu, Y. Chen, S. B. Zhang and Z. Chen, J. Phys. Chem. C, 2008, 112, 13926–13931 CAS.
- X. Cheng, F. Li and Y. Zhao, J. Mol. Struct.: THEOCHEM, 2009, 894, 121–127 CrossRef CAS.
- J. M. Azpiroz, E. Mosconi and F. D. Angelis, J. Phys. Chem. C, 2011, 115, 25219–25226 CAS.
- C. Caddeo, G. Malloci, F. De Angelis, L. Colombo and A. Mattoni, Phys. Chem. Chem. Phys., 2012, 14, 14293 RSC.
- E. V. Trushin, I. L. Zilberberg and A. V. Bulgakov, Phys. Solid State, 2012, 54, 859–865 CrossRef CAS.
- G. Malloci, L. Chiodo, A. Rubio and A. Mattoni, J. Phys. Chem. C, 2012, 116, 8741–8746 CAS.
- I. A. Sarsari, S. J. Hashemifar and H. Salamati, J. Phys.: Condens. Matter, 2012, 24, 505502 CrossRef PubMed.
- C. Szakacs, E. Merschrod S. and K. Poduska, Computation, 2013, 1, 16–26 CrossRef.
- W. Pipornpong, B. Kaewruksa and V. Ruangpornvisuti, Struct. Chem., 2015, 27, 773–784 CrossRef.
- A. Fernando, K. L. D. M. Weerawardene, N. V. Karimova and C. M. Aikens, Chem. Rev., 2015, 115, 6112–6216 CrossRef CAS PubMed.
- R. Łazarski, M. Sierka, J. Heinzelmann, A. Koop, R. Sedlak, S. Proch and G. F. Ganteför, J. Phys. Chem. C, 2015, 119, 6886–6895 Search PubMed.
- C. R. A. Catlow, S. A. French, A. A. Sokol, A. A. Al-Sunaidi and S. M. Woodley, J. Comput. Chem., 2008, 29, 2234–2249 CrossRef CAS PubMed.
- B. J. Morgan, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 1–4 Search PubMed.
- D. Zagorac, J. C. Schön, J. Zagorac and M. Jansen, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 1–13 CrossRef.
- F. Reuse and S. Khanna, Chem. Phys. Lett., 1995, 234, 77–81 CrossRef CAS.
- S. K. Nayak, S. N. Khanna, B. K. Rao and P. Jena, J. Phys. Chem. A, 1997, 101, 1072–1080 CrossRef CAS.
- B. V. Reddy, S. K. Nayak, S. N. Khanna, B. K. Rao and P. Jena, J. Phys. Chem. A, 1998, 5639, 1748–1759 CrossRef.
- H. M. Duan, X. G. Gong, Q. Q. Zheng and H. Q. Lin, J. Appl. Phys., 2001, 89, 7308–7310 CrossRef CAS.
- V. G. Grigoryan and M. Springborg, Phys. Rev. B: Condens. Matter, 2004, 70, 18–22 CrossRef.
- T. Futschek, J. Hafner and M. Marsman, J. Phys.: Condens. Matter, 2006, 18, 9703–9748 CrossRef CAS.
- J. P. Chou, H. Y. T. Chen, C. R. Hsing, C. M. Chang, C. Cheng and C. M. Wei, Phys. Rev. B: Condens. Matter, 2009, 80, 1–10 Search PubMed.
- Q. L. Lu, Q. Q. Luo, L. L. Chen and J. G. Wan, Eur. Phys. J. D, 2011, 61, 389–396 CrossRef CAS.
- M. Y. Yu, W. X. Wang and S. G. Chen, Mater. Sci. Forum, 2014, 809–810, 406–411 CrossRef.
- J. A. Northby, J. Chem. Phys., 1987, 87, 6166 CrossRef CAS.
- H. W. Kroto, A. W. Allaf and S. P. Balm, Chem. Rev., 1991, 91, 1213–1235 CrossRef CAS.
- R. B. King, J. Chem. Inf. Model., 1999, 39, 180–191 CrossRef CAS.
- Y.-P. Sun, J. E. Riggs and B. Liu, Chem. Mater., 1997, 9, 1268–1272 CrossRef CAS.
- Z. Liu, J. T. Robinson, S. M. Tabakman, K. Yang and H. Dai, Mater. Today, 2011, 14, 316–323 CrossRef CAS.
- S. M. Woodley, C. R. A. Catlow, P. D. Battle and J. D. Gale, Chem. Commun., 2004, 22 RSC.
- S. M. Woodley, P. D. Battle, J. D. Gale, C. Richard and A. Catlow, Phys. Chem. Chem. Phys., 2004, 6, 1815 RSC.
Footnote |
| † For example, if on mutation the best structure relaxes back to the original structure, then this structure and its copy will become the best at surviving and procreating. The best structure is then also more likely to be chosen as both parents, thus children may also relax to the same structure. With an ever increasing likelihood of crossover and mutation creating more duplicates of the best structure, only one unique structure will quickly fill the population during further GA cycles. Such an avalanche effect should be avoided. |
| This journal is © The Royal Society of Chemistry 2017 |