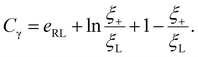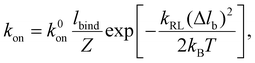Kinetics of receptor-mediated endocytosis of elastic nanoparticles†
Xin
Yi
 and
Huajian
Gao
*
and
Huajian
Gao
*
School of Engineering, Brown University, Providence, Rhode Island 02912, USA. E-mail: huajian_gao@brown.edu
First published on 25th November 2016
Abstract
It is now widely recognized that mechanical properties play critical roles in the cell uptake of nanomaterials. Here we conduct a theoretical study on the kinetics of receptor-mediated endocytosis of elastic nanoparticles that is limited by receptor diffusion, specifically focusing on how the uptake rate depends on the nanoparticle stiffness and size, membrane tension and binding strength between membrane receptors and ligands grafted on the nanoparticle surface. It is shown that, while soft nanoparticles are energetically less prone to full wrapping than stiff ones, the wrapping of the former is kinetically faster than that of the latter. Spherical and cylindrical elastic nanoparticles show dramatic differences in the effect of stiffness on the uptake rate. Additional theoretical analysis is performed to investigate the role of the stochastic receptor–ligand binding in the endocytosis of elastic nanoparticles. The relation between the uptake efficiency and uptake proneness is discussed. This study provides new insight into the elasticity effects on cell uptake and may serve as a design guideline for the controlled endocytosis and diagnostics delivery.
1 Introduction
Cell uptake of nanoparticles is of fundamental importance not only to the understanding of biological functions such as nutrient uptake but also to a broad range of applications including drug delivery, biomedical imaging, virology and nanoparticle hazard prevention.1 Over the past decade, it has become well established through both theoretical and experimental investigations that endocytosis of nanoparticles strongly depends on particle size,2–7 shape6–16 and surface physiochemical properties.16–20 A number of recent studies have also been performed to explore the effects of the stiffness of nanomaterials on the proneness,15,21–25 kinetic rate24,26–31 and pathways25,26 of particle internalization.For cell uptake of elastic nanoparticles via receptor-mediated membrane wrapping, theoretical analysis, molecular dynamics simulations and experimental studies showed that stiff nanoscale vesicles or capsules, require less adhesion energy than soft ones to complete the wrapping process,15,21–23 indicating a stiffness effect on the energetic proneness of cell uptake of nanoparticles. For example, stiffness-enhanced uptake has been observed in the interaction between lipid-covered polymeric nanoparticles of radius 40 nm and HeLa as well as endothelial cells.23 There have also been studies on the stiffness effect on the cell uptake rate of nanoparticles with different sizes and material compositions.24,26–32 However, there exist apparent inconsistencies and even contradictions in the literature. For example, phagocytosis of stiff microparticles by bone-marrow-derived macrophages exhibits higher efficiency than soft ones.24 Hydrogel nanoparticles with radius around 80 nm show strong stiffness-dependent uptake by murine RAW 264.7 macrophages.26 Nanoparticles of an intermediate Young's modulus EY (35 kPa to 135 kPa) are internalized at higher rates of uptake than softer (EY of 18 kPa) and stiffer (EY of 210 kPa) particles.26 Stiffness effects have also been identified in uptake by HepG2 cells of hydrogel nanoparticles with a radius of 400 nm and a compression modulus from 15 kPa to 150 kPa, but in these cases softer nanoparticles exhibit higher uptake rates than stiffer ones.27 As the particle stiffness is reduced, microsized polymer capsules have been observed to undergo a faster entry into HeLa cells.28,29 In contrast, stiffer hydrogel nanoparticles of radius 100 nm exhibit an enhanced integrated rate of membrane binding and uptake in their interaction with macrophages, epithelial and endothelial cells.30 Moreover, the effects of nanoparticle stiffness on their intracellular accumulation rate and distribution have been investigated.26–29 A recent study based on molecular dynamics simulations demonstrates that soft vesicular nanoparticles undergo a faster membrane wrapping process than stiff ones.31 Thus, although it is clear that the stiffness of nanoparticles has pronounced influences on their interaction with cells, the results from different experiments and simulation studies are not all consistent and the underlying mechanisms are still not fully clear. This calls for further investigations at a fundamental level.
Receptor-mediated endocytosis is one of the most important and best characterized cellular uptake pathways. Here we present the first theoretical model on the kinetics of receptor-mediated endocytosis of elastic nanoparticles, focusing on how the rate of uptake depends on the nanoparticle stiffness and size, membrane tension and binding strength between membrane receptors and ligands grafted on the nanoparticle surface. In this study, we assume that the receptors diffusing along the cell membrane bind instantly to the ligand-coated nanoparticle upon contact. It will be shown that, while soft nanoparticles are energetically less prone to full wrapping than stiff ones, the wrapping of the former is kinetically faster than that of the latter in the diffusion-limited case considered here. Spherical and cylindrical elastic nanoparticles show dramatically different behaviors with respect to the kinetic effects of stiffness. We have also performed case studies to demonstrate the effects of stochastic receptor–ligand binding on endocytosis. The interplay between energetic proneness and the kinetic rate of wrapping may rationalize the apparent controversies in the literature.
2 Model and methods
2.1 Process of receptor-mediated endocytosis
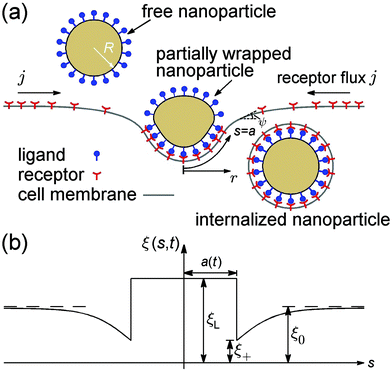
Consider an initially flat cell membrane of a finite size containing mobile receptors wrapping around an elastic spherical nanoparticle coated with compatible ligands (Fig. 1). We assume that the ligands on the nanoparticle surface are immobile and uniformly distributed at a density of ξL, whereas the receptors on the cell membrane are mobile, and can diffuse in the plane of the membrane until they bind specifically with the ligands on the nanoparticle. Before the nanoparticle comes in contact with the cell membrane, the receptors are assumed to be uniformly distributed at density ξ0, which is usually much smaller than ξL. Once the contact starts, each ligand within the contact region is assumed to bind with a receptor. Therefore, the receptor density within the contact region is raised from ξ0 to ξL, i.e., the same density as that of ligands on the nanoparticle. The receptor–ligand binding lowers the free energy of interaction, and causes the membrane to wrap around the nanoparticle at the cost of reduced configurational entropy due to receptor immobilization and increased elastic deformation energy in both the nanoparticle and membrane. Driven by the free energy reduction induced by receptor–ligand binding, the contact region expands as neighboring receptors are drawn to the contact edge by diffusion, which results in a local depletion of receptors in the vicinity of the contact region. The resulting gradient of receptor density in turn induces global receptor diffusion toward the binding site. As long as the free energy reduction associated with receptor–ligand binding can compensate for the energy cost mentioned above, the wrapping process continues until the nanoparticle is fully wrapped (Fig. 1). The wrapping time t is counted from the moment of contact (t = 0) until the state of full wrapping (t = tw), with tw defined as the total wrapping time.To model the wrapping process, we propose a model that accounts for both the kinetics of receptor diffusion and deformation of the wrapped nanoparticle and cell membrane. The kinetic part is based on a mathematical model initially developed for cell spreading33 but later generalized for the receptor-mediated endocytosis of rigid spherical and cylindrical nanoparticles with simplified receptor diffusion equations and membrane deformation configurations.2,3 The elastic nanoparticle is modeled as a deformable vesicle. Experimental studies indicate that the time scale of membrane equilibrium is less than one second,34 while cell uptake of nanomaterials is usually limited by receptor diffusion with a time scale in the range of tens of seconds to tens of minutes.6 This dramatic difference in the time scale suggests that the vesicular nanoparticle and cell membrane are essentially in a static equilibrium state on the time scale of receptor diffusion. In other words, the configurations of the vesicle and membrane can be determined by minimizing the free energy of the system at each time step of the wrapping process.21 Axisymmetric configurations will be assumed throughout the analysis.
2.2 Deformation of the particle–membrane system
We first describe the continuum modeling on the axisymmetric deformation of the elastic nanoparticle and cell membrane. During the wrapping process, the elastic deformation energy of the nanoparticle and cell membrane is expressed in terms of the Canham–Helfrich functional as21,47,50 | (1) |
 . It turns out to be useful to introduce the following normalized membrane tension,
. It turns out to be useful to introduce the following normalized membrane tension,![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 2σR2/κm, = 2σR2/κm, |
Variation of the energy functional in eqn (1) gives rise to a set of equations that govern the equilibrium configurations of the nanoparticle and cell membrane once the contact area is known at each time step associated with receptor diffusion.21 We adopt a shooting method to numerically determine the axisymmetric shapes of the nanoparticle and membrane corresponding to the lowest energy.21 The shapes shown in Fig. 1a are determined from the tangent angle ψ(s,t) with geometric relations ∂r/∂s = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ and ∂z/∂s = sin
ψ and ∂z/∂s = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ, where ψ = ψ(s,t) is the tangent angle with the arc length s defined along the cell membrane and measured from the bottom pole (s = 0) and the wrapping time t counted from the moment of contact (t = 0); r = r(s,t) and z = z(s,t) are the r- and z-coordinates of the adopted coordinate system in Fig. 1a, respectively.
ψ, where ψ = ψ(s,t) is the tangent angle with the arc length s defined along the cell membrane and measured from the bottom pole (s = 0) and the wrapping time t counted from the moment of contact (t = 0); r = r(s,t) and z = z(s,t) are the r- and z-coordinates of the adopted coordinate system in Fig. 1a, respectively.
2.3 Kinetics of receptor diffusion
Next we focus on the kinetics of receptor diffusion occurring in the cell membrane, which is characterized by the evolution of receptor density ξ(s,t) and could be determined by solving a deterministic moving boundary problem. The arc length of the contact region is denoted by a(t). At t = 0, a(0) = 0 and ξ(s,0) = ξ0. Conservation of the total number of receptors requires | (2) |
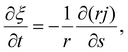 | (3) |
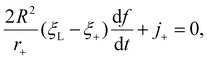 | (4) |
The diffusive flux of receptors, j = j(s,t), is assumed to be prescribed according to Fick's first law as35
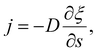 | (5) |
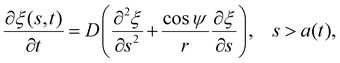 | (6) |
To obtain the total wrapping time tw from the moment of initial contact until the state of full wrapping with the wrapping degree f = 1, we evaluate the wrapping rate df/dt as a function of r+, ξ+ and j+ based on eqn (4), where r+ is determined as a function of f by the shooting method. As j+ = −D(∂ξ/∂s)|s = a+, the key step in obtaining tw lies with finding ξ+ and ξ(s,t) at a given f, following a power balance between elastic deformation and receptor diffusion as follows.
The total free energy of the system F(t), consisting of the energy of receptor–ligand binding, configurational entropy of receptors, and elastic deformation energy of the cell membrane and nanoparticle, is written as
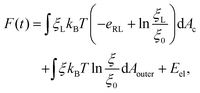 | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ξL/ξ0) and kBT
ln(ξL/ξ0) and kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ξ/ξ0) are the free energy per receptor associated with the loss of configurational entropy of the bound and free receptors, respectively.
ln(ξ/ξ0) are the free energy per receptor associated with the loss of configurational entropy of the bound and free receptors, respectively.
Differentiation of F(t) in eqn (7) with respect to time t results in
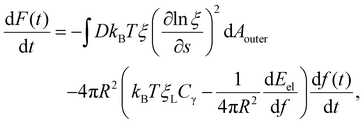 | (8) |
The integral term in eqn (8) represents the rate of energy dissipation associated with receptor transport along the cell membrane.2,33 By balancing the rate of free energy reduction in the wrapping process with the rate of energy dissipation during receptor transport, the second term in eqn (8) must vanish so that
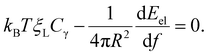 | (9) |
This equation allows ξ+(t) to be determined at a given f.
Once the receptor density profile at a point of time (t = t0) during the initial stage of contact is known, we can determine ξ(s,t) at any following time t > t0 by solving the diffusion eqn (6)via the finite difference method, using ξ+(t) to determine j+(t) in eqn (5), and then obtaining the wrapping rate df/dt from ξ+(t), j+(t) and r+(t) through eqn (4). This is a typical procedure in solving a deterministic moving boundary problem.
The receptor density ξ(s,t0) at the initial stage of contact can be determined approximately as follows. At this stage, the contact size is much smaller than the membrane size and the outer free membrane is almost flat. Therefore, the membrane at that moment can be approximately regarded as a flat membrane of an infinite size and the diffusion eqn (6) can be reduced to ∂ξ/∂t = D∂2ξ/∂s2 over a(t0) < s < ∞, which can be solved analytically as (ref. 2)
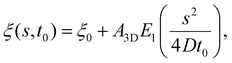 | (10) |
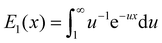 is the exponential integral and A3D is a constant of integration. This solution satisfies the axisymmetric diffusion equation and the boundary condition ξ(s,0) = ξ0 and ξ(s,t0) → ξ0, j(s,t0) → 0 as s → ∞. As nanoparticles of different stiffnesses display almost the same configuration at the initial stage of contact, the corresponding conservation condition eqn (4) can be approximated by (ξL − ξ+)da/dt + j+ = 0, the same form as that in the case of a rigid nanoparticle. Substituting the solution in eqn (10) into the above conservation equation results in
is the exponential integral and A3D is a constant of integration. This solution satisfies the axisymmetric diffusion equation and the boundary condition ξ(s,0) = ξ0 and ξ(s,t0) → ξ0, j(s,t0) → 0 as s → ∞. As nanoparticles of different stiffnesses display almost the same configuration at the initial stage of contact, the corresponding conservation condition eqn (4) can be approximated by (ξL − ξ+)da/dt + j+ = 0, the same form as that in the case of a rigid nanoparticle. Substituting the solution in eqn (10) into the above conservation equation results in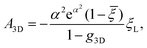 | (11) |
![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) = ξ0/ξL and g3D = α2eα2E1(α2), α being a constant to be determined. It follows that ξ+ = (
= ξ0/ξL and g3D = α2eα2E1(α2), α being a constant to be determined. It follows that ξ+ = (![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) − g3D)(1 − g3D)−1ξL. Substituting eqn (10) and (11) and ξ+ into eqn (9), the constant α can be determined from
− g3D)(1 − g3D)−1ξL. Substituting eqn (10) and (11) and ξ+ into eqn (9), the constant α can be determined from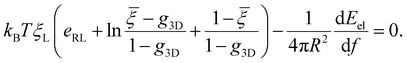 | (12) |
Once α is known, ξ(s,t0) at the initial stage of contact is fully defined by eqn (10). With the knowledge of ξ(s,t0), ξ+(t), the configurations of the nanoparticle and cell membrane, and the diffusion eqn (6), we can proceed to determine the wrapping rate df/dt through eqn (4). Following the above procedure of solving the deterministic moving boundary problem, the total wrapping time is then obtained as 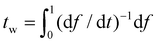 .
.
2.4 Particle wrapping induced by stochastic receptor–ligand binding
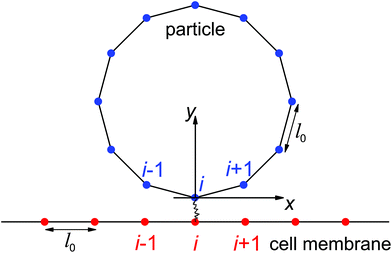
In the present study, we focus on the receptor-mediated endocytosis in which the rate of the particle wrapping is kinetically limited by the diffusional aggregation of receptors in the membrane to the cell–particle binding site, and the wrapping process is modeled as a deterministic moving boundary problem. An implicit assumption is that if the association rate of receptor–ligand bonds is high enough, the bond formation between a ligand and its complementary receptor would enable particle wrapping by the deformed cell membrane. To demonstrate the validity of this implicit assumption, we performed additional studies on the wrapping of a two-dimensional particle via stochastic receptor–ligand binding in the Cartesian coordinate system (x,y). A brief description of the modeling is provided here, and corresponding numerical results are presented in the Results section.The two-dimensional vesicular particle of circumference 2πR is discretized into Np elements of equal length (Fig. 2). The bending energy of the particle and cell membrane could be expressed as 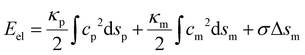 , where ci (i = p, m) is the curvature, si is the arc length and Δsm is the difference between the total length of the membrane and its projection on the horizontal axis. The curvature c is calculated from c2 = y2,xx/(1 + y2,xx)3 with y,xx ≡ d2y/dx2. The constraint of a fixed particle circumference is enforced by a harmonic energy penalty term
, where ci (i = p, m) is the curvature, si is the arc length and Δsm is the difference between the total length of the membrane and its projection on the horizontal axis. The curvature c is calculated from c2 = y2,xx/(1 + y2,xx)3 with y,xx ≡ d2y/dx2. The constraint of a fixed particle circumference is enforced by a harmonic energy penalty term 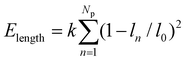 , where k is the penalty coefficient (taken as 103 in our simulations), ln is the length of the n-th element and l0 is the initial element length of a free circular vesicular particle. In a similar manner, the cell membrane is discretized into Nm elements of a reference length l0.
, where k is the penalty coefficient (taken as 103 in our simulations), ln is the length of the n-th element and l0 is the initial element length of a free circular vesicular particle. In a similar manner, the cell membrane is discretized into Nm elements of a reference length l0.
In this stochastic modeling, the ligands and receptors are immobile and uniformly distributed along the particle surface and cell membrane at the nodes of elements (blue and red dots in Fig. 2). The receptor–ligand bonds are modeled as linear springs of stiffness kRL and rest length lb. A bond is formed as the distance between the ligand and its complementary receptor is within a binding radius lbind. The elastic energy stored in a closed bond of length change Δlb is Eb = kRL(Δlb)2/(2kBT) with Δlb > 0 for a stretched closed bond. According to Kramer's theory,37,38 the dissociation rate koff of a closed bond is
koff = k0off![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[kRLΔlbxb/(kBT)], exp[kRLΔlbxb/(kBT)], |
where k0on is the reference association rate and the partition function Z is
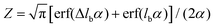 with
with 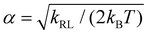 and erf being the error function.
and erf being the error function.
Here we employ Monte Carlo simulations based on the Metropolis algorithm to capture the deformation of the particle–membrane system and the Gillespie algorithm for the stochastic bonding and breaking of receptor–ligand bonds, respectively. The total deformation energy of the system includes the bending energy of the particle and cell membrane, the elastic energy stored in the closed receptor–ligand bonds, and energy penalty terms enforcing the length constraints of the particle and membrane. In the initial configuration, a flat cell membrane is located at y = −lb and a circular vesicular particle is centered at x = 0 and y = R as illustrated in Fig. 2. We are interested in particle wrapping after the initial attachment and nucleation of receptor–ligand domains.41 The ligand located at the bottom pole of the particle is assumed to bind its complementary receptor. The nodes of the discretized particle surface undergo random displacements to mimic thermally excited shape fluctuations. A new particle configuration is accepted or rejected according to the Metropolis algorithm. A similar scheme is employed in determining the cell membrane configuration, which is subjected to a periodic boundary condition in the x-direction. A single Monte Carlo sweep for the particle and cell membrane configurations consists of Np + Nm attempted random node displacements, in which self-contact and penetration between the particle surface and cell membrane is avoided. The first-reaction method of the Gillespie algorithm is then employed to determine when and where bond association/dissociation would occur in the new system configuration determined by the previous Monte Carlo sweep.39,40 Bond kinetics is monitored by updates of the bond binding state and elastic energy stored in closed bonds. The system configuration and stochastic binding events are recorded from the initial state as indicated in Fig. 2 until a dynamic equilibrium state of partial- or full-wrapping is achieved. The number of closed bonds as a function of elapsed wrapping time is provided in the Results section, and the following values have been adopted: R = 64 nm, Np = 80, Nm = 120, kRL = 0.25 pN nm−1, lbind = 1 nm, lb = 11 nm, k0on/k0off = 500, and ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 0.5.
= 0.5.
3 Results
The derivative of elastic energy dEel/df in eqn (9) and (12) and the r-coordinate of the contact edge rc in eqn (4) are plotted as functions of the wrapping degree f in Fig. 3a and b, respectively. With the knowledge of these variables and following the numerical scheme for obtaining df(t)/dt discussed in the preceding section, we can then obtain f(t) and the total wrapping time tw.In general, a smaller particle–membrane stiffness ratio κp/κm gives rise to a more flattened nanoparticle with a larger rc and consequently a longer contact circumference in the early- and mid-stages of wrapping, as shown in Fig. 3b. Also, during the late stage of wrapping, the contact edge becomes rather insensitive to particle stiffness (Fig. 3b). Since the rate of receptor diffusion is proportional to the length of the contact edge, the wrapping of a softer nanoparticle can thus be expected to be kinetically faster than that of a stiffer one. This is confirmed through numerical analysis in the following.
Depending on the types of cells, the receptor diffusivity D typically ranges from 0.01 μm2 s−1 to 1 μm2 s−1.42–45 The receptor density ξ0 can vary considerably from hundreds to thousands of receptors per square μm. For example, it was reported that ξ0 ≈ 1300 μm−2 for human leukemia CCRF-CEM cells and ξ0 ≈ 550 μm−2 for HeLa cervical cancer cells.46 The ligand density ξL also varies in a wide range depending on the nanoparticle type. For instance, while ξL ≈ 7 × 103 μm−2 for Semliki Forest virus (of radius 30 nm and 80 spikes on the surface)47 and HIV-1 (of radius 50 nm and 219 gp120 proteins on the surface),48ξL can vary from 3 × 103 μm−2 to 2 × 104 μm−2 for engineered nanoparticles.49 Therefore, the ratio ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) = ξ0/ξL could fall in the range of 0.025 to 0.5. The radius of the initial flat circular membrane is assumed to be L = 10 μm. A typical set of parameter values used in our calculations is summarized in Table 1.
= ξ0/ξL could fall in the range of 0.025 to 0.5. The radius of the initial flat circular membrane is assumed to be L = 10 μm. A typical set of parameter values used in our calculations is summarized in Table 1.
| κ m (kBT) | D (μm2 s−1) | e RL | ξ L ( μm−2) |
![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) = ξ0/ξL = ξ0/ξL |
|---|---|---|---|---|
| 20 | 0.1 | 15 | 5 × 103 | 0.025 |
Taking these typical parameter values, the wrapping degree f is determined and shown in Fig. 4 as a function of the normalized time tξLD for different κp/κm at ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 0.5,
= 0.5, ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) = 0.025 and R = 200 nm. If the process of membrane wrapping is modeled as an expansion of an effective contact area of receptor–ligand adhesion on a flat membrane, the receptor diffusion equation reduces to the classical two-dimensional (2D) isotropic plane diffusion and
= 0.025 and R = 200 nm. If the process of membrane wrapping is modeled as an expansion of an effective contact area of receptor–ligand adhesion on a flat membrane, the receptor diffusion equation reduces to the classical two-dimensional (2D) isotropic plane diffusion and 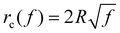 . In that case, the wrapping rate df/dt is a linear function of t as shown in ref. 2. In the current case where the slope of rc(f) in Fig. 3b is smaller than that of the classical 2D plane diffusion case, the wrapping rate df/dt decreases as wrapping proceeds. At a given f, df/dt should be proportional to rc. Since rc is insensitive to κp/κm at f < 0.15 (Fig. 3b), so is df/dt in this range (Fig. 4). As f becomes larger, a soft nanoparticle exhibits a larger rc in the mid-stage of wrapping and a slightly smaller rc in the late stage of wrapping, compared to a stiff nanoparticle of the same size (Fig. 3b). Therefore, compared to the reference case of a stiff particle, the wrapping of a soft nanoparticle becomes kinetically faster during the mid-stage of wrapping and slightly slower in the late-stage of wrapping, leading to a smaller total wrapping time as indicated in Fig. 4.
. In that case, the wrapping rate df/dt is a linear function of t as shown in ref. 2. In the current case where the slope of rc(f) in Fig. 3b is smaller than that of the classical 2D plane diffusion case, the wrapping rate df/dt decreases as wrapping proceeds. At a given f, df/dt should be proportional to rc. Since rc is insensitive to κp/κm at f < 0.15 (Fig. 3b), so is df/dt in this range (Fig. 4). As f becomes larger, a soft nanoparticle exhibits a larger rc in the mid-stage of wrapping and a slightly smaller rc in the late stage of wrapping, compared to a stiff nanoparticle of the same size (Fig. 3b). Therefore, compared to the reference case of a stiff particle, the wrapping of a soft nanoparticle becomes kinetically faster during the mid-stage of wrapping and slightly slower in the late-stage of wrapping, leading to a smaller total wrapping time as indicated in Fig. 4.
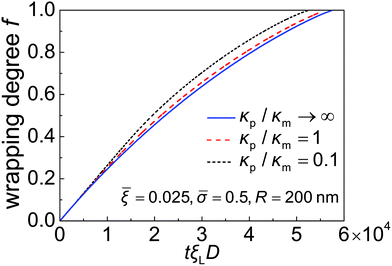 | ||
Fig. 4 Wrapping degree f as a function of the normalized time tξLD for different values of the nanoparticle–membrane stiffness ratio κp/κm at ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 0.5, = 0.5, ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) = 0.025 and R = 200 nm. = 0.025 and R = 200 nm. | ||
Due to the limited number of ligands and the finite strength of ligand–receptor binding energy, there exists a minimum radius of the nanoparticle R3Dmin below which the bending energy of the cell membrane as well as the deformation energy of the nanoparticle prohibits the wrapping process and reduces the wrapping speed to zero (α → 0). By assuming that eqn (10)–(12) are valid at R = R3Dmin and letting α → 0, the minimum wrapping radius R3Dmin can be obtained from eqn (12) as
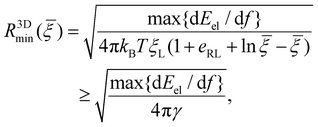 | (13) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) {dEel/df} represents the maximum value of dEel/df. A larger R3Dmin is required at a weaker binding strength eRLkBT and a smaller ligand density ξL. The equality in eqn (13) only holds at
{dEel/df} represents the maximum value of dEel/df. A larger R3Dmin is required at a weaker binding strength eRLkBT and a smaller ligand density ξL. The equality in eqn (13) only holds at ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) = 1, which is physiologically irrelevant in the current study. As the last term in the above equation can be regarded as the minimum nanoparticle radius obtained from the free energy minimization of the total elastic deformation energy and adhesion energy,21,47,50eqn (13) indicates that R3Dmin obtained based on the kinetic model of receptor diffusion is slightly larger than that derived from a free energy analysis in which the densities of ligands and mobile receptors are assumed to be equal and no receptor diffusion is considered. Since max{dEel/df} increases as κp decreases (Fig. 3a), eqn (13) also indicates that R3Dmin increases as κp decreases, as shown in Fig. 5. In other words, larger sizes are required for cell uptake of softer particles. This is consistent with our previous studies on the phase diagrams of cell uptake of elastic nanoparticles,15,21,22 where it was shown that cell uptake of softer nanoparticles requires larger normalized adhesion energy
= 1, which is physiologically irrelevant in the current study. As the last term in the above equation can be regarded as the minimum nanoparticle radius obtained from the free energy minimization of the total elastic deformation energy and adhesion energy,21,47,50eqn (13) indicates that R3Dmin obtained based on the kinetic model of receptor diffusion is slightly larger than that derived from a free energy analysis in which the densities of ligands and mobile receptors are assumed to be equal and no receptor diffusion is considered. Since max{dEel/df} increases as κp decreases (Fig. 3a), eqn (13) also indicates that R3Dmin increases as κp decreases, as shown in Fig. 5. In other words, larger sizes are required for cell uptake of softer particles. This is consistent with our previous studies on the phase diagrams of cell uptake of elastic nanoparticles,15,21,22 where it was shown that cell uptake of softer nanoparticles requires larger normalized adhesion energy ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) ≡ 2γR2/κm ∼ R at a given normalized membrane tension
≡ 2γR2/κm ∼ R at a given normalized membrane tension ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) ≡ 2σR2/κm.
≡ 2σR2/κm.
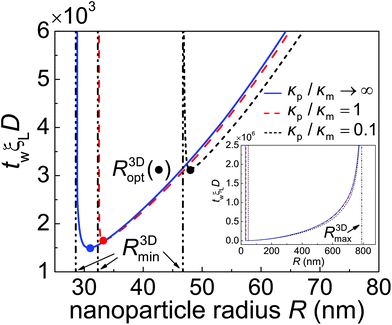 | ||
Fig. 5 The normalized total wrapping time twξLD as a function of the nanoparticle radius R for different values of the particle–membrane stiffness ratio κp/κm at ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 0.5 and = 0.5 and ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) = 0.025. R3Dmin and R3Dmax (inset) represent the minimum and maximum radii of a particle that can be wrapped according to eqn (13) and (14), respectively. R3Dopt, marked by solid circles, denotes the optimal wrapping radius at minimum wrapping time. = 0.025. R3Dmin and R3Dmax (inset) represent the minimum and maximum radii of a particle that can be wrapped according to eqn (13) and (14), respectively. R3Dopt, marked by solid circles, denotes the optimal wrapping radius at minimum wrapping time. | ||
Limited by the number of receptors (πL2ξ0) available to bind ligands (4πR2ξL) on the nanoparticle, the maximum wrapping radius R3Dmax is
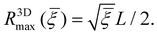 | (14) |
As indicated in eqn (13) and (14), the size range of wrapping particles (R3Dmin, R3Dmax) becomes broader as ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) increases. By comparing eqn (13) and (14), one can immediately see that full wrapping cannot take place unless the receptor density ratio
increases. By comparing eqn (13) and (14), one can immediately see that full wrapping cannot take place unless the receptor density ratio ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) exceeds a critical value
exceeds a critical value ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) c which can be determined from R3Dmin(
c which can be determined from R3Dmin(![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) c) = R3Dmax(
c) = R3Dmax(![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) c).
c).
Fig. 5 shows the normalized total wrapping time twξLD as a function of the nanoparticle radius R for different values of the particle–membrane stiffness ratio κp/κm at ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 0.5 and
= 0.5 and ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) = 0.025. As κp/κm decreases, so does tw for R > R3Dopt. The ratio of tw between a soft particle with κp/κm = 0.1 and a rigid one is about 0.9. Further numerical analysis indicates that the time ratio decreases as
= 0.025. As κp/κm decreases, so does tw for R > R3Dopt. The ratio of tw between a soft particle with κp/κm = 0.1 and a rigid one is about 0.9. Further numerical analysis indicates that the time ratio decreases as ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) increases. This stiffness-dependent kinetic effect on wrapping is due to the deformation of elastic nanoparticles and could be understood as follows. In general, the rate of wrapping mediated by receptor diffusion is proportional to the length of the contact edge. Since a softer nanoparticle is deformed into a more flattened configuration with a larger rc (Fig. 3b) as well as a longer contact circumference in a wide range of f, there is little surprise that it also undergoes a faster wrapping process compared to a stiffer particle. A stiffer particle has smaller R3Dmin and R3Dopt. As shown in Fig. 5 and S1 in the ESI,† the difference between R3Dmin and R3Dopt is around 1 nm to 3 nm. Moreover, for a nanoparticle of given stiffness, there is a range from R3Dmin to R < R3Dopt in which the wrapping time tw of that particle is larger than tw of a softer nanoparticle.
increases. This stiffness-dependent kinetic effect on wrapping is due to the deformation of elastic nanoparticles and could be understood as follows. In general, the rate of wrapping mediated by receptor diffusion is proportional to the length of the contact edge. Since a softer nanoparticle is deformed into a more flattened configuration with a larger rc (Fig. 3b) as well as a longer contact circumference in a wide range of f, there is little surprise that it also undergoes a faster wrapping process compared to a stiffer particle. A stiffer particle has smaller R3Dmin and R3Dopt. As shown in Fig. 5 and S1 in the ESI,† the difference between R3Dmin and R3Dopt is around 1 nm to 3 nm. Moreover, for a nanoparticle of given stiffness, there is a range from R3Dmin to R < R3Dopt in which the wrapping time tw of that particle is larger than tw of a softer nanoparticle.
As predicted by eqn (13) and (14), the wrapping process cannot be completed for nanoparticles with radius R < R3Dmin or R > R3Dmax. There is an optimal particle radius R3Dopt, which is slightly larger than R3Dmin, at which the total wrapping time tw is the smallest. The optimal nanoparticle size stems from the competition between thermodynamic driving force and receptor diffusion kinetics. For nanoparticles of radius smaller than R3Dopt, the elastic deformation energy of the system plays a dominant role in reducing the driving force for wrapping and leads to an increased wrapping time. For nanoparticles of radius larger than R3Dopt, the thermodynamic driving force for wrapping is only weakly related to the elastic energy of the system. In this situation, wrapping a larger nanoparticle requires more receptors to diffuse to a larger binding region, hence a longer wrapping time is induced (Fig. 5). These observations are all qualitatively consistent with the previous kinetic wrapping model for a rigid nanoparticle.2 To explore the effects of binding energy on tw, numerical calculations at eRL = 10 and 25 are carried out and presented in Fig. S1.† A comparison between Fig. 5 and S1 in the ESI† shows that a larger binding energy leads to smaller R3Dmin, R3Dopt and smaller optimal total wrapping time. Further numerical analysis indicates that both the optimal nanoparticle radius and optimal total wrapping time decrease as ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) increases, since larger
increases, since larger ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) means relatively stronger effective adhesion energy and less receptors are required to diffuse toward the wrapped nanoparticle.2
means relatively stronger effective adhesion energy and less receptors are required to diffuse toward the wrapped nanoparticle.2
Note that our calculations on the total wrapping time tw for different values of the particle–membrane stiffness ratio κp/κm and particle radius R are performed at the same normalized membrane tension ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) (≡2σR2/κm) instead of a varying membrane tension σ. To explore the possible effects of membrane tension on tw, numerical calculations at
(≡2σR2/κm) instead of a varying membrane tension σ. To explore the possible effects of membrane tension on tw, numerical calculations at ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) are carried out (see Fig. S2†). A comparison between Fig. 5 and S2† shows that a larger membrane tension leads to a larger R3Dmin. This is consistent with eqn (13), since max{dEel/df} increases as the membrane tension increases.21 It is also demonstrated that the membrane tension plays a negligible role in the control of cell uptake rate for R > R3Dopt, with indistinguishable influence on R3Dmax, as suggested in eqn (14).
are carried out (see Fig. S2†). A comparison between Fig. 5 and S2† shows that a larger membrane tension leads to a larger R3Dmin. This is consistent with eqn (13), since max{dEel/df} increases as the membrane tension increases.21 It is also demonstrated that the membrane tension plays a negligible role in the control of cell uptake rate for R > R3Dopt, with indistinguishable influence on R3Dmax, as suggested in eqn (14).
To demonstrate that high-affinity receptor–ligand binding facilitates particle wrapping by the deformed cell membrane, we performed case studies on the wrapping of two-dimensional particles through stochastic receptor–ligand binding at different particle–membrane stiffness ratios κp/κm at ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 0.5. In each study, a particle with radius R = 64 nm is uniformly coated with 80 ligands, the ratio between the reference association rate and spontaneous dissociation rate is k0on/k0off = 500, and the bending stiffness of the membrane is considered to be κm = 20 kBT. Fig. 6 shows the trajectories of closed bonds during particle wrapping. The results indicate that particles of different rigidities could be fully wrapped through binding reactions between ligands and receptors. Moreover, a stiffer particle achieves full internalization slightly faster than a softer particle in the wrapping process regulated by stochastic binding between immobile receptors and ligands. The underlying reason can be understood as follows. During the wrapping process, the distance near the contact edge between the surface of a softer particle and cell membrane is larger than that in the case of a stiffer particle. Therefore, the (re)binding rate is lower and dissociation rate is higher in the uptake of a softer particle, which in turn results in slower full internalization for the softer particle. In the diffusion-limited uptake under consideration, the uptake rate is dominated by receptor diffusion and the softer particle undergoes faster entry, as indicated in Fig. 5. Details of the stochastic modeling can be found in subsection 2.4.
= 0.5. In each study, a particle with radius R = 64 nm is uniformly coated with 80 ligands, the ratio between the reference association rate and spontaneous dissociation rate is k0on/k0off = 500, and the bending stiffness of the membrane is considered to be κm = 20 kBT. Fig. 6 shows the trajectories of closed bonds during particle wrapping. The results indicate that particles of different rigidities could be fully wrapped through binding reactions between ligands and receptors. Moreover, a stiffer particle achieves full internalization slightly faster than a softer particle in the wrapping process regulated by stochastic binding between immobile receptors and ligands. The underlying reason can be understood as follows. During the wrapping process, the distance near the contact edge between the surface of a softer particle and cell membrane is larger than that in the case of a stiffer particle. Therefore, the (re)binding rate is lower and dissociation rate is higher in the uptake of a softer particle, which in turn results in slower full internalization for the softer particle. In the diffusion-limited uptake under consideration, the uptake rate is dominated by receptor diffusion and the softer particle undergoes faster entry, as indicated in Fig. 5. Details of the stochastic modeling can be found in subsection 2.4.
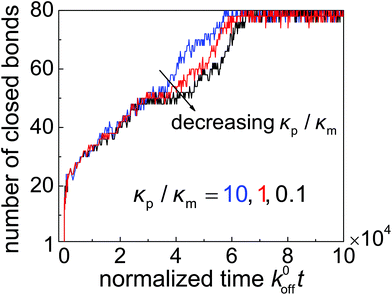 | ||
Fig. 6 Number of closed bonds as a function of the normalized wrapping time k0offt for different values of the nanoparticle–membrane stiffness ratio κp/κm at ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 0.5. = 0.5. | ||
4 Discussion
Our theoretical analysis indicates that the rate of receptor-mediated endocytosis depends on the nanoparticle stiffness, in particular, while soft nanoparticles are energetically less prone to wrapping than stiff ones,15,21,22 they exhibit higher uptake rates once the wrapping becomes energetically favorable. Since similar deformation configurations and elastic energy profiles are observed in the wrapping of solid nanocapsules,22 the same conclusions are expected to be also applicable for soft solid nanocapsules. These results can help understand some of the confusing and seemingly conflicting experimental observations in the literature. In particular, the stiffness-dependent rate of cell uptake is consistent with recent experimental observations27–29 and molecular dynamics simulations,31 in which it is reported that hydrogel nanoparticles,27 polymer microcapsules28,29 and vesicular nanoparticles31 undergo faster cell entry with decreasing particle stiffness. As the adhesive receptor–ligand interaction used in molecular dynamics simulations is typically based on instant reaction potentials such as the Lennard-Jones potential without the kinetic effect of receptor–ligand binding,10,11,31 it can be expected that our theoretical analysis on the uptake of elastic particle is consistent with molecular dynamics simulations.31 Since a softer particle can be more easily deformed into a flattened configuration in the early- and mid-stage of wrapping by the cell membrane,21,22 the enhanced cell–particle interaction causes the percentage of cells bound with softer particles to be higher than that with stiffer ones during the early incubation period.29In our previous21 and present theoretical analysis, the internalized elastic nanoparticle is modeled as an elastic vesicular nanoparticle (e.g., liposome) to facilitate the simplest possible description of particle deformation in the wrapping process, and the mobility of ligands embedded in the vesicular membrane is not taken into account. This approximation is not unreasonable in the case of high ligand surface density and low fluidity of liposomal membranes. In the case of relatively low ligand concentration and high membrane fluidity, the mobility of ligands plays an important role and could even dominate the wrapping process.31,51,52 Recent molecular dynamics simulations demonstrate that at a low surface density the ligand molecules would diffuse and finally aggregate into a single binding domain full of receptor–ligand bonds. Consequently, the formation of a ligand-free domain leads to an incomplete cell uptake.31,52 In comparison with liposomes, polymersomes are a class of artificial polymer vesicles that exhibit similar bending properties to lipid vesicles but are of orders of magnitude higher membrane lysis tension and larger membrane viscosity.53 Therefore, the ligands on the polymersomes could be regarded as immobile during the uptake and polymersomes (coated with immobilized ligands) can serve as an ideal example of soft particles considered in our model.
As indicated in our theoretical analysis, the stiffness effect on the cell uptake rate of spherical nanoparticles is mainly due to the different contact circumferences for different particle stiffness. A long contact circumference enhances receptor diffusion and promotes efficient full internalization. In a two-dimensional case where an elastic cylindrical nanoparticle is wrapped by the cell membrane, the length of contact edge is independent of the particle stiffness, suggesting that the uptake rate of two-dimensional particles should be stiffness-insensitive if the state of full wrapping is defined as f = 1. This is indeed confirmed in Fig. S3a.† If the full wrapping is defined as a state where the left and right sides of the cell membrane touch each other above the nanoparticle, the wrapping of a stiff nanoparticle would be faster than a soft one due to a shorter wrapping length required for the full wrapping (Fig. S4b†).
Besides the stiffness effect on the rate of cell uptake, our previous studies based on the free energy show that softer nanoparticles require stronger adhesion energy to achieve successful internalization,15,21,22 which means that soft nanoparticles are energetically less prone to full wrapping than stiff ones. Here the uptake proneness is used to characterize the tendency of an elastic nanoparticle to be fully internalized.15,21,22 Other properties remaining the same, soft particles are less likely to enter a cell than stiff ones. In this sense, uptake proneness is a concept associated with free energy and cannot be employed to describe time related quantities such as the wrapping time. In Fig. 5, S2 and S4,† the minimum wrapping radius falls into the category of uptake proneness; while the wrapping time is associated with the uptake rate.
5 Conclusions
A theoretical model of receptor-mediated endocytosis limited by receptor diffusion has been developed to describe the kinetic process of a cell membrane wrapping around an elastic nanoparticle via diffusional aggregation of receptors in the membrane to the cell–particle binding site. A key assumption in the model is that the membrane–nanoparticle system is able to instantaneously reach its equilibrium (i.e. minimum energy) configuration at the time scale of receptor diffusion during the wrapping process. The most important result is that, while soft nanoparticles are energetically less prone to wrapping than stiff ones, they exhibit higher uptake rates once the wrapping becomes energetically favorable.It was shown that the higher uptake rate of a softer nanoparticle results from enhanced receptor diffusion as a result of larger contact area between the membrane and particle at the early- and mid-stages of the wrapping process. There is an optimal particle size corresponding to the shortest wrapping time. Both the optimal particle radius and the wrapping time decrease as the receptor-to-ligand density ratio ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) increases. The minimum particle radius required for full internalization increases as the particle stiffness decreases; while the maximum particle radius that still allows full wrapping is insensitive to particle stiffness. Further calculations indicated that membrane tension plays an important role in the control of minimum particle radius but has a negligible effect on the wrapping rate. Unlike the uptake of spherical nanoparticles where softer particles lead to a faster internalization rate, cylindrical soft nanoparticles exhibit either the same or lower uptake rates compared with stiff ones, depending on the definition of full wrapping. Two-dimensional case studies on particle wrapping induced by stochastic receptor–ligand association/dissociation confirm that receptor–ligand bond formation could enable the wrapping of an elastic particle by a deformed membrane. These results indicate that tailoring particle elasticity can be an appealing way to control cell uptake.
increases. The minimum particle radius required for full internalization increases as the particle stiffness decreases; while the maximum particle radius that still allows full wrapping is insensitive to particle stiffness. Further calculations indicated that membrane tension plays an important role in the control of minimum particle radius but has a negligible effect on the wrapping rate. Unlike the uptake of spherical nanoparticles where softer particles lead to a faster internalization rate, cylindrical soft nanoparticles exhibit either the same or lower uptake rates compared with stiff ones, depending on the definition of full wrapping. Two-dimensional case studies on particle wrapping induced by stochastic receptor–ligand association/dissociation confirm that receptor–ligand bond formation could enable the wrapping of an elastic particle by a deformed membrane. These results indicate that tailoring particle elasticity can be an appealing way to control cell uptake.
In the present study, we have focused our attention on the kinetic process of a cell membrane wrapping around an elastic particle that is limited by the diffusion of receptors in the membrane. In a general case of cell uptake, receptor diffusion and receptor–ligand binding could play equally important roles in the uptake kinetics. Future work will be aimed at developing a more sophisticated theoretical modeling approach considering the coupling of receptor diffusion, system deformation, thermal fluctuation of the cell membrane and stochastic binding. Our current analysis can also serve as a foundation for future studies taking into account non-specific interactions between the cell membrane and nanoparticles,18 cell membrane roughness induced by thermal fluctuation,54 shape effects of nanoparticles,6,8,9,13 motility of ligands in vesicular nanoparticles,31,51 and other endocytic pathways24,26,55 such as phagocytosis in which actin reconfiguration plays an important role during the uptake.
Acknowledgements
This work was supported by the National Science Foundation (Grants CBET-1344097 and CMMI-1562904).References
- I. Canton and G. Battaglia, Chem. Soc. Rev., 2012, 41, 2718–2739 RSC.
- H. Gao, W. Shi and L. B. Freund, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 9469–9474 CrossRef CAS PubMed.
- G. Bao and X. R. Bao, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 9997–9998 CrossRef CAS PubMed.
- S. Zhang, J. Li, G. Lykotrafitis, G. Bao and S. Suresh, Adv. Mater., 2009, 21, 419–424 CrossRef CAS PubMed.
- T. Yue and X. Zhang, ACS Nano, 2012, 6, 3196–3205 CrossRef CAS PubMed.
- B. D. Chithrani and W. C. W. Chan, Nano Lett., 2007, 7, 1542–1550 CrossRef CAS PubMed.
- H. Jin, A. Daniel, A. D. Heller, R. Sharma and M. S. Strano, ACS Nano, 2009, 3, 149–158 CrossRef CAS PubMed.
- P. Decuzzi and M. Ferrari, Biophys. J., 2008, 94, 3790–3797 CrossRef CAS PubMed.
- S. E. A. Gratton, P. A. Ropp, P. D. Pohlhaus, J. C. Luft, V. J. Madden, M. E. Napier and J. M. DeSimone, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 11613–11618 CrossRef CAS PubMed.
- R. Vácha, F. J. Martinez-Veracoechea and D. Frenkel, Nano Lett., 2011, 11, 5391–5395 CrossRef PubMed.
- X. Shi, A. von dem Bussche, R. H. Hurt, A. B. Kane and H. Gao, Nat. Nanotechnol., 2011, 6, 714–719 CrossRef CAS PubMed.
- Y. Li, T. Yue, K. Yang and X. Zhang, Biomaterials, 2012, 33, 4965–4973 CrossRef CAS PubMed.
- S. Dasgupta, T. Auth and G. Gompper, Nano Lett., 2014, 14, 687–693 CrossRef CAS PubMed.
- X. Yi and H. Gao, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2014, 89, 062712 CrossRef PubMed.
- X. Yi, X. Shi and H. Gao, Nano Lett., 2014, 14, 1049–1055 CrossRef CAS PubMed.
- H.-M. Ding and Y.-Q. Ma, Small, 2015, 11, 1055–1071 CrossRef CAS PubMed.
- Y. Li, M. Kröger and W. K. Liu, Nanoscale, 2015, 7, 16631–16646 RSC.
- P. Decuzzi and M. Ferrari, Biomaterials, 2007, 28, 2915–2922 CrossRef CAS PubMed.
- M. Massignani, C. LoPresti, A. Blanazs, J. Madsen, S. P. Armes, A. L. Lewis and G. Battaglia, Small, 2009, 5, 2424–2432 CrossRef CAS PubMed.
- H.-M. Ding and Y.-Q. Ma, Biomaterials, 2012, 33, 5798–5802 CrossRef CAS PubMed.
- X. Yi, X. Shi and H. Gao, Phys. Rev. Lett., 2011, 107, 098101 CrossRef PubMed.
- X. Yi and H. Gao, Soft Matter, 2015, 11, 1107–1115 RSC.
- J. Sun, L. Zhang, J. Wang, Q. Feng, D. Liu, Q. Yin, D. Xu, Y. Wei, B. Ding, X. Shi and X. Jiang, Adv. Mater., 2015, 27, 1402–1407 CrossRef CAS PubMed.
- K. A. Beningo and Y. L. Wang, J. Cell Sci., 2002, 115, 849–856 CAS.
- Y. Li, X. Zhang and D. Cao, Nanoscale, 2015, 7, 2758–2769 RSC.
- X. Banquy, F. Suarez, A. Argaw, J.-M. Rabanel, P. Grutter, J.-F. Bouchard, P. Hildgen and S. Giasson, Soft Matter, 2009, 5, 3984–3991 RSC.
- W. Liu, X. Zhou, Z. Mao, D. Yu, B. Wang and C. Gao, Soft Matter, 2012, 8, 9235–9245 RSC.
- R. Hartmann, M. Weidenbach, M. Neubauer, A. Fery and W. J. Parak, Angew. Chem., Int. Ed., 2015, 54, 1365–1368 CrossRef CAS PubMed.
- H. Sun, E. H. H. Wong, Y. Yan, J. Cui, Q. Dai, J. Guo, G. G. Qiao and F. Caruso, Chem. Sci., 2015, 6, 3505–3514 RSC.
- A. C. Anselmo, M. Zhang, S. Kumar, D. R. Vogus, S. Menegatti, M. E. Helgeson and S. Mitragotri, ACS Nano, 2015, 9, 3169–3177 CrossRef CAS PubMed.
- T. Yue and X. Zhang, Soft Matter, 2013, 9, 559–569 RSC.
- A. C. Anselmo and S. Mitragotri, Adv. Drug Delivery Rev. DOI:10.1016/j.addr.2016.01.007.
- L. B. Freund and Y. Lin, J. Mech. Phys. Solids, 2004, 52, 2455–2472 CrossRef.
- C. K. Haluska, K. A. Riske, V. Marchi-Artzner, J.-M. Lehn, R. Lipowsky and R. Dimova, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15841–15846 CrossRef CAS PubMed.
- J. Faraudo, J. Chem. Phys., 2002, 116, 5831–5841 CrossRef CAS.
- D. Leckband and J. Israelachvili, Q. Rev. Biophys., 2001, 34, 105–267 CrossRef CAS PubMed.
- G. I. Bell, Science, 1978, 200, 618–627 CAS.
- P. Hanggi, P. Talkner and M. Borkovec, Rev. Mod. Phys., 1990, 62, 251–342 CrossRef.
- T. Erdmann and U. S. Schwarz, Phys. Rev. Lett., 2004, 92, 108102 CrossRef CAS PubMed.
- J. Qian, J. Wang and H. Gao, Langmuir, 2008, 24, 1262–1270 CrossRef CAS PubMed.
- T. Bihr, U. Seifert and A.-S. Smith, Phys. Rev. Lett., 2012, 109, 258101 CrossRef PubMed.
- J. Sloan-Lancaster, J. Presley, J. Ellenberg, T. Yamazaki, J. Lippincott-Schwartz and L. E. Samelson, J. Cell Biol., 1998, 143, 613–624 CrossRef CAS PubMed.
- D. P. Felsenfeld, D. Choquet and M. Sheetz, Nature, 1996, 383, 438–440 CrossRef CAS PubMed.
- A. Kusumi, C. Nakada, K. Ritchie, K. Murase, K. Suzuki, H. Murakoshi, R. S. Kasai, J. Kondo and T. Fujiwara, Annu. Rev. Biophys. Biomol. Struct., 2005, 34, 351–378 CrossRef CAS PubMed.
- C. M. Finnegan, S. S. Rawat, E. H. Cho, D. L. Guiffre, S. Lockett, A. H. Merrill Jr. and R. Blumenthal, J. Virol., 2007, 81, 5294–5304 CrossRef CAS PubMed.
- Y. Chen, A. C. Munteanu, Y.-F. Huang, J. Phillips, Z. Zhu, M. Mavros and W. Tan, Chem. – Eur. J., 2009, 15, 5327–5336 CrossRef CAS PubMed.
- M. Deserno, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2004, 69, 031903 CrossRef PubMed.
- S. X. Sun and D. Wirtz, Biophys. J., 2006, 90, L10–L12 CrossRef CAS PubMed.
- D. R. Elias, A. Poloukhtine, V. Popik and A. Tsourkas, Nanomed.: Nanotech. Biol. Med., 2013, 9, 194–201 CrossRef CAS PubMed.
- R. Lipowsky and H.-G. Döbereiner, Europhys. Lett., 1998, 43, 219–225 CrossRef CAS.
- D. Almeda, Investigating the Effect of Liposomal Membrane Fluidity and Antibody Lateral Mobility on Endothelial Cell Targeting, Ph.D. Thesis, Harvard University, February 2014 Search PubMed.
- V. Schubertová, F. J. Martinez-Veracoechea and R. Vácha, Soft Matter, 2015, 11, 2726–2730 RSC.
- R. Dimova, U. Seifert, B. Pouligny, S. Förster and H.-G. Döbereiner, Eur. Phys. J. E: Soft Matter Biol. Phys., 2002, 7, 241–250 CrossRef CAS.
- J. Hu, R. Lipowsky and T. R. Weik, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15283–15288 CrossRef CAS PubMed.
- D. M. Richards and R. G. Endres, Biophys. J., 2014, 107, 1542–1553 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: For the case of spherical elastic nanoparticles, two supplemental figures on the wrapping time as a function of particle radius at zero and a higher finite membrane tension. Technical details and several supplemental figures about the uptake kinetics of cylindrical elastic nanoparticles. See DOI: 10.1039/C6NR07179A |
| This journal is © The Royal Society of Chemistry 2017 |