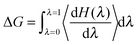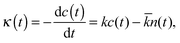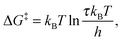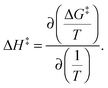Which fullerenols are water soluble? Systematic atomistic investigation

Abstract

Fullerenols are hydroxylated fullerenes, C₆₀(OH)_n, where n can be up to 40 depending on the method of synthesis. Fullerenols are considered for biomedical applications, thanks to their antioxidant activities. Aqueous solubilities of fullerenols are essential to efficiently deliver them to living bodies. We hereby report the hydration thermodynamics of fullerenols C₆₀(OH)₈, C₆₀(OH)₁₆, C₆₀(OH)₂₄, C₆₀(OH)₃₆, and C₆₀(OH)₄₄ and correlate them to the solute–solvent hydrogen bonding using classical molecular dynamics simulations. Two types of hydrogen bonds were detected: O(hydroxyl)–H(water) and H(hydroxyl)–O(water), whose parameters are well comparable. The most favorable hydration free energy was observed for C₆₀(OH)₃₆, whereas the hydration of C₆₀(OH)₄₄ is clearly less efficient, in spite of a larger number of hydroxyl groups. The beneficial action of each hydroxyl group decreases with their quantity within the fullerenol molecule increases. Hydrogen bonds were characterized (life times, geometries, and thermodynamics) in accordance with the Luzar–Chandler theory. Our systematic analysis of fullerenols identified the most suitable compositions to be used in the emerging biomedical applications.

---

Introduction

The first fullerene observation was reported three decades ago thereby launching an era of nanotechnologies.¹ The electron–nuclei potential energy of fullerene is well above the global minimum for the all-carbon compounds, which corresponds to graphite. Nevertheless, fullerenes were shown to exhibit a remarkable kinetic stability, making their versatile applications possible.^2–9 The highly curved surface of small fullerenes, including C₆₀, results in their high electronic polarizability and high reactivity. In most cases, fullerenes tend to act as electrophiles. Fullerenes aim to decrease their surface strain that corresponds to making their double bonds saturated. The most studied reactions involving fullerenes are hydrogenation, hydroxylation, both electrophilic and nucleophilic additions, carbene and radical addition, and pericyclic reactions.^10–13

A particular research interest is presently directed towards polyhydroxylated fullerenes,^14,15 called fullerenols or fullerols, due to their aqueous solubility, whereas most fullerene derivatives remain poorly soluble. Relatively aggressive conditions are required to obtain fullerenols, e.g. dilute sulfuric acid or dilute sodium hydroxide, hydrogen peroxide, etc. The maximum confirmed number of OH-groups per C₆₀ is 40, using hydroxide peroxide and heating. The authors of the corresponding work reported an excellent aqueous solubility of such fullerenols at pH = 7 of 58.9 g L⁻¹.¹⁶ Alternative polar groups were also used to adjust solubilities of fullerenes, while partially retaining beneficial physical chemical and electronic properties of pristine defect-free fullerenes. Carboxyfullerenes, C₆₀(CH–COOH)_n, where n = 2…6, bisphosphonate-, pyrazolino-, and amino-derivatives, C₆₀(NH₂)_n, where n = 3–5, were described.^16–20 Carboxylation can be used to modulate solubility and polarity,^21,22 but significant coverage of the fullerene surface has not been achieved yet. It is also unclear how many [double bond splayed left]CH–COOH groups can be grafted without undermining the stability of the backbone.

Rivelino and co-workers²³ used all-electron density functional theory (DFT) to investigate the stability, electronic properties, infrared and Raman absorption vibrational spectra, elastic and inelastic depolarization ratios of fullerenols as a function of the hydroxylation degree. Changes in the electronic properties were correlated to the number of hydroxyl groups. Tao and co-workers²⁴ found that the relative stability of the C₂₀-based fullerenols depends on the distribution of the OH-groups on the fullerene surface. The formation of C₂₀(OH)₈ from C₂₀ and 8 OH-groups is energetically favorable. Interestingly, the authors claim low reactivity of C₂₀(OH)₈, whereas pristine C₂₀ is known to be reactive. This theoretical study relied on hybrid DFT. Sardenberg and co-workers²⁵ considered fullerenols in the context of prospective free-radical sponges, antioxidants, and photosensitizers using eletrochemical impedance in aqueous solution. Fullerenols were shown to act as very weak acids, based on direct pH measurements. Maciel and co-authors investigated the thermodynamic properties of the fullerenol C₆₀(OH)₂₄ by means of molecular dynamics and thermodynamic integration and correlated the results with those for the hydrophobic C₆₀ molecule.²⁶

Fullerenols are considered in the context of biomedical applications nowadays.²⁷ For instance, fullerenols were reported to act against neurodegenerative diseases, likely due to their antioxidant activity.²⁸ Fullerenols based on endohedral metallofullerenes exhibit even more versatile biofunctionalities, opening an avenue for new and unexpected developments.^25,27,29 Li and co-workers³⁰ demonstrated the use of isoelectric focusing to separate different fractions of fullerenols based on their differing electronegativities. The authors assessed cytotoxicities of their fullerenols to be low. It was, however, noted that the highest negative charge densities in fullerenols might damage the DNA. Therefore, purification of the crude fullerenols is essential prior to their applications in biomedicine.³⁰

In the present work, we report a systematic hydration study of fullerenols, C₆₀(OH)_n, where n = 8, 16, 24, 36, and 44 (Fig. 1). By characterizing H-bonding and the associated thermodynamics between water molecules and fullerenols, we – for the first time – correlate their hydration thermodynamics with the number of hydroxyl groups grafted onto the surface. We used a peculiar geometry of C₆₀(OH)₈ due to the previous evidence that the hydroxyl group islands are more favorable than the even distribution of the same number of OH-groups.³¹

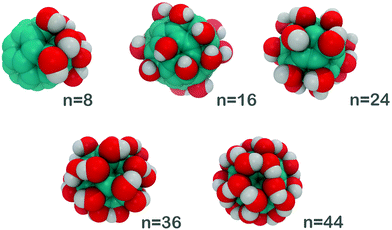Fig. 1 Optimized (local-minimum) molecular geometries (in scale) of the simulated fullerenols C₆₀(OH)_n, n = 8, 16, 24, 36, and 44.

Methodology

Each fullerenol molecule was surrounded by ca. 1500 water molecules in the cubic unit cell with periodic boundary conditions following the minimum-image convention. The TIP3P potential was used to reproduce interactions of water molecules.³² Reference geometries of fullerenols were determined by DFT calculations at the B3LYP/6-31G(d,p) level of theory.^33,34 Partial electrostatic charges were determined according to the CHelpG scheme (electrostatic potential fitting).³⁵ The Lennard-Jones parameters of the OPLS/AA force field for the sp² carbon, hydroxyl oxygen and hydroxyl hydrogen were used.³⁶ This procedure was applied previously having provided adequate results for polyhydroxyfullerene C₆₀(OH)₂₄.²⁶ The models of water and fullerenols were developed by following fully compatible procedures and can be used together without further adjustment. Reference optimized geometries, as well as CHelpG partial charges, are available in the ESI.†

MD simulations were conducted in the constant temperature constant pressure ensemble. The constant temperature was maintained by the velocity rescaling³⁷ with a relaxation time of 0.1 ps. The constant pressure, 1 × 10⁵ Pa, was maintained using a Parrinello–Rahman barostat³⁸ with a time constant of 1.0 ps and a compressibility constant of 4.5 × 10⁻⁵ bar⁻¹. The lengths of all covalent bonds involving hydrogen atoms were fixed by the LINCS algorithm.³⁹ Electrostatics beyond the pairwise cut-off, 1.2 nm, was represented using the particle mesh Ewald method.⁴⁰ The Lennard-Jones (12, 6) potential was modified, the switch method, between 1.1 and 1.2 nm for the van der Waals interactions to vanish completely at the cut-off distance. The equations-of-motion were integrated with a time-step of 2.0 fs, while the coordinate frames and the thermodynamic quantities were recorded every 50 time-steps.

Step-wise decoupling of the solute molecule from the explicit solvent environment was used to calculate the free energy, ΔG, of hydration of each simulated fullerenol:

where H is the parameterized empirical Hamiltonian and λ is a coupling parameter. λ = 1 corresponds to the fully solvated fullerenol, whereas λ = 0 corresponds to the non-interacting solute and solvent. Singularities were avoided by using soft-core potentials. The decoupling of both interaction terms, Coulomb and Lennard-Jones, simultaneously at the thermodynamic integration leads to an unphysical behaviour, due to the elimination of electron–electron repulsions. Therefore, two series of MD simulations were performed: (1) decoupling of the electrostatic interactions, but retaining Lennard-Jones interactions and (2) decoupling of the Lennard-Jones interactions, to remove the remaining interactions between the solute and the solvent. To decouple the Coulomb interactions, we used 25 values from λ = 1 until λ = 0, with all states spaced uniformly, λ = 0.04. 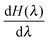The decoupling of the Lennard-Jones interactions involves high at λ ≪ 1, thus Δλ = 0.02 was used from λ = 0.24 to λ = 0. In turn, Δλ = 0.04 was used from λ = 1 to λ = 0.24. For every λ, the MD system was equilibrated during 500 ps. The productive simulations of 5000 ps were used to accumulate .

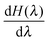The hydrogen bonds existing between fullerenol and water were investigated in accordance with the Luzar–Chandler theory.⁴¹ This theory defines a binary autocorrelation function, h(t), which phenomenologically describes the formation and breakage of the H-bond between two neighbouring molecules. h(t) = 1 corresponds to existence of H-bond, whereas h(t) = 0 designates no H-bond. The rate of the HB breakage is given by:

where the autocorrelation function c(t) stands for the probability of H-bond existence at time t and n(t) stands for the probability that the previously existing H-bond is ruined, despite molecules remaining within the H-bond distance. The inverse of k is defined as H-bond life time, τ = 1/k. The free energy alteration associated with the breaking of H-bond is, consequently, related to the H-bond life time by the Eyring relation:
where h and k_B are the Planck and Boltzmann constants, respectively, and T is the absolute temperature. The enthalpy alteration associated with the H-bond breakage is provided by the van't Hoff equation:

The entropy alteration is evaluated as:

ΔS^‡ = (ΔH^‡ − ΔG^‡)/T.

The calculation of ΔH^‡ requires independent sets of simulations at 290, 300, and 310 K to numerically obtain the derivative of ΔG^‡.

MD simulations and subsequent analysis were performed in the GROMACS 5.0 program.⁴² PACKMOL was used to generate Cartesian coordinates for initial molecular configurations.⁴³ Visual Molecular Dynamics (VMD, version 1.9.2) was used to visualize MD trajectories and prepare molecular graphics.⁴⁴

Results and discussion

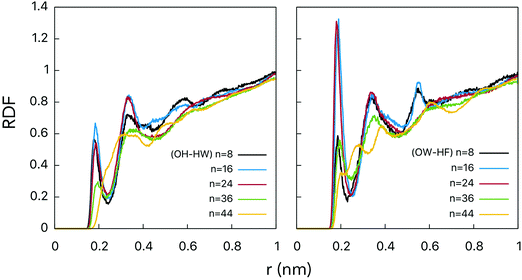
The hydroxyl groups grafted onto the fullerene surface behave qualitatively the same way as in alcohols. Two types of H-bonds connect water and fullerenol (Fig. 2): (1) the oxygen atom of fullerenol with the hydrogen atom of water and (2) the hydrogen atom of fullerenol with the oxygen atom of water. The H-bond constitutes the most important solute–solvent interaction in the aqueous solutions of fullerenols. The length of both types of H-bond is equal to ca. 0.19 nm (Fig. 3). This corresponds to a substantially strong bond, which is beneficial for fullerenol hydration. The second and third peaks can also be distinguished on the computed radial distribution functions (RDFs), suggesting that fullerenols get involved into the liquid-state network of the water molecules. Consequently, each fullerenol can be seen as a polywater molecule, which does not introduce crucial alterations into the bulk water structure. The RDF of C₆₀(OH)₄₄ appears qualitatively different. The first peak is poorly defined, 0.2–0.4 nm, and the longer-range structure is essentially absent. The origin of such a behavior will be discussed upon consideration of the H-bonds below.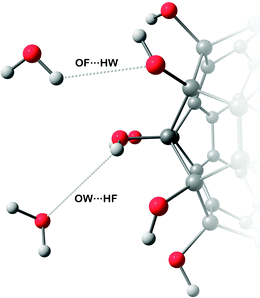

Fig. 2 Two types of H-bonds formed in the fullerenol solutions in water based on the classical MD simulations.

Fig. 3 RDFs between the oxygen and hydrogen belonging to fullerenol and water molecules. Right: OW–HF corresponds to oxygen of water and hydrogen of fullerenol. Left: OH–HW corresponds to oxygen of fullerenol and hydrogen of water.

RDFs for the centers-of-mass (COMs) of the water molecules and fullerenols are given in Fig. 4 providing important information on the solute–solvent closest-approach distance as a function of the number of the OH-groups. Indeed, visible differences were detected for different fullerenol compositions. The smallest distances, r_min at which RDF(r) ≠ 0, were observed in the case of n = 8 and n = 44. In turn, the most probable COM–COM distances were observed with n = 16 and n = 24. In C₆₀(OH)₈ and C₆₀(OH)₄₄, the OH-groups are located close enough to one another being able to form specific intramolecular OH interactions, which will be not classified here as hydrogen bonds by not meeting the conventional geometric criteria (Table 1). Since the OH-groups are oriented towards one another on the surfaces of these fullerenols (Fig. 1), a significant fraction of the neighboring water molecules remain undercoordinated. Consequently, a larger OH–OH spacing is likely to be beneficial in the solvation context.

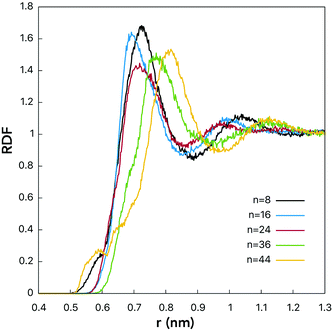Fig. 4 RDFs computed for centers-of-mass of fullerenol and water molecules. See the legend for line designation.

Table 1 Coulomb, Lennard-Jones, and total pairwise interaction energies of fullerenols and water, total number of intermolecular water–fullerenol hydrogen bonds and intramolecular fullerenol–fullerenol OH interactions; the last column shows the diffusion coefficients (in 10⁻⁵ cm² s⁻¹) of each fullerenol

n(OH)	U Coul, kJ mol^−1	U LJ, kJ mol^−1	U TOTAL, kJ mol^−1	# inter-H-bonds	# intra-OH interactions	D C60(OH)n, 10^−9 m^2 s^−1
a Molecular dynamics simulations.^26
0	0.0	−231 ± 10	−231 ± 10	0	0	1.27^a
8	−302 ± 31	−239 ± 19	−541 ± 36	9	2	0.58 ± 0.30
16	−417 ± 41	−220 ± 20	−637 ± 45	20	0	0.92 ± 0.16
24	−1020 ± 88	−107 ± 33	−1128 ± 94	36	2	0.35 ± 0.11
36	−901 ± 54	−181 ± 26	−1082 ± 60	31	7	0.32 ± 0.12
44	−669 ± 55	−186 ± 28	−855 ± 62	19	13	0.22 ± 0.08

---

Fullerenol–water pairwise interaction energies (Table 1) provide further insights into the role of the number of OH-groups. The Coulomb energy increases from n = 0 to n = 24, with the sharpest increment observed between n = 16 and n = 24. Further attachment of the OH-groups results in smaller Coulomb energy and smaller total pairwise energy. The maximum Coulomb energy coincides with the minimum LJ energy, since H-bonding is maintained by the dipole–dipole interactions. C₆₀(OH)₃₆ and C₆₀(OH)₄₄ engender a substantial quantity of the intramolecular OH interactions (Table 1). As expected, electrostatic binding plays a systematically more significant role in the fullerenol hydration, as compared to the van der Waals interactions. The total number of H-bonds generally decreases translation self-diffusion (Table 1). Interestingly, C₆₀(OH)₁₆ diffuses substantially faster than C₆₀(OH)₈, whose OH-groups form a compact island.

H-bond life times in C₆₀(OH)₈, C₆₀(OH)₁₆, C₆₀(OH)₂₄, and C₆₀(OH)₃₆ are comparable, being in line with their activation free energies (Table 2). However, C₆₀(OH)₄₄ stands out of the row with 44–47 ps. We believe that it is caused by slow diffusion of this fullerenol, 0.22 × 10⁻⁹ m² s⁻¹, and a significant number of intramolecular OH interactions, which get incorporated into a genuine network of liquid water. The H-bond activation free energy is determined by the favorable entropic factor and the unfavorable enthalpic factor (Table 3). Overall, the thermodynamics of H-bonding in the fullerenol–water solutions indicate similarity of the existing H-bonds, irrespective of the number of OH-groups in fullerenols.

Table 2 H-bond life time and activation Gibbs free energy of hydrogen bonding for both types of H-bonds in the simulated fullerenol–water MD systems at 300 K. OF–HW stands for the bond between the oxygen atom of fullerenol and the hydrogen atom of water. OW–HF stands for the bond between the hydrogen atom of fullerenol and the oxygen atom of water

n(OH)	OF–HW atom pair		OW–HF atom pair
	τ, ps	ΔG^‡, kJ mol^−1	τ, ps	ΔG^‡, kJ mol^−1
8	8	10	9	10
16	3	7	5	8
24	8	10	9	10
36	12	11	8	10
44	47	14	44	14

---

Table 3 Activation Gibbs free energy ΔG^‡, enthalpic factor ΔH^‡, and entropic factor −TΔS^‡ (kJ mol⁻¹) under standard conditions describing hydrogen bonding of both types in aqueous solutions of fullerenols. OF–HW stands for the H-bond formed by the oxygen atoms of fullerenol and the hydrogen atoms of water. OW–HF stands for the H-bond Hformed by the hydrogen atoms of fullerenol and the oxygen atoms of water

n(OH)	OF–HW atom pair		OW–HF atom pair
	ΔH^‡	−TΔS^‡	ΔH^‡	−TΔS^‡
8	26	−16	25	−15
16	20	−12	21	−12
24	23	−14	24	−14
36	28	−17	30	−20
44	28	−14	30	−16

---

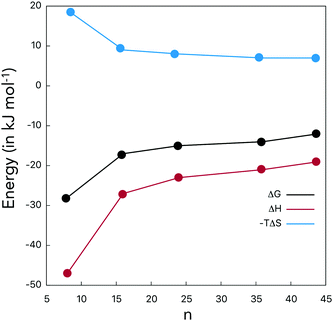
The hydration thermodynamic potentials are provided in Table 4, and Fig. 5 identifies the hydration benefit brought in by a single OH-group. The solute–solvent H-bonding leads to the highly favorable enthalpic factors, while the entropic factors are not favorable and smoothly increase as the number of OH-groups in fullerenols increases. All hydration free energies are below zero. The hydration potentials should not be confused with the H-bond thermodynamics (Tables 2 and 3), which were computed in accordance with the Luzar–Chandler theory.

Table 4 Standard hydration thermodynamic potentials (in kJ mol⁻¹) of fullerenols and corresponding normalized values (divided by n): Gibbs free energy ΔG, enthalpic factor ΔH, entropic factor −TΔS, given per mole of respective fullerenols

n(OH)	ΔG	ΔG/n,	ΔH	ΔH/n	−TΔS	−TΔS/n
8	−224	−28	−374	−47	150	19
16	−278	−17	−427	−27	150	9
24	−354	−15	−540	−23	186	8
36	−512	−14	−762	−21	249	7
44	−508	−12	−833	−19	325	7

---

Fig. 5 Standard hydration thermodynamic potentials (Gibbs free energy, enthalpic factor, and entropic factor) of fullerenols. The potentials were normalized by the number of the hydroxyl groups, n, in fullerenols for a more straightforward comparison.

Normalization with respect to the number of OH-groups reveals that the hydration of C₆₀(OH)₈, −28 kJ mol⁻¹, is the most successful one. C₆₀(OH)₈ has a high dipole moment under vacuum, 3.0 D. As the number of OH-groups increases, dG/n(OH) smoothly decreases reaching −12 kJ mol⁻¹ in C₆₀(OH)₄₄. Thus, the role of each OH-group decreases when their quantity increases. Intramolecular OH interactions, to a certain extent, prevent intermolecular H-bonding. The computed absolute hydration free energies are in concordance with the available solubility data.¹⁶

Conclusions

In the present work, we systematically described hydration thermodynamics of fullerenols using pairwise-potential-based MD simulations and comprehensive analysis of the MD trajectories. The identified hydration regularities were correlated to the number of H-bonds and the solute–solvent interaction energies. The fullerenol C₆₀(OH)₃₆ was found to exhibit the most favorable hydration free energy, −512 kJ mol⁻¹. Grafting of more than 36 hydroxyl groups per C₆₀ backbone is unlikely useful, giving rise to a significant number of intramolecular OH interactions, which naturally conflict with the solute–solvent H-bonds. C₆₀(OH)₈, with OH-groups forming a compact island, constitutes an interesting possibility. In this case, a fairly small number of OH-groups result in a substantially negative hydration energy, ΔG = −224 kJ mol⁻¹. It will be a challenge to synthesize such a molecule. The impact of one OH-group is highest in C₆₀(OH)₈ and decreases smoothly from C₆₀(OH)₁₆ to C₆₀(OH)₄₄. The H-bond life times are similar for C₆₀(OH)₈, C₆₀(OH)₁₆, C₆₀(OH)₂₄, and C₆₀(OH)₃₆, but grow drastically from C₆₀(OH)₃₆ to C₆₀(OH)₄₄. The reported physical insights guide a choice of most soluble fullerenols, which are therefore most suitable for biomedical applications.

Acknowledgements

Partial financial assistance was obtained from CNPq, CAPES, and FAPESP. We are delighted to thank the Neumann Supercomputing Center for its continuous dedicated service.

References

1. H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163.
2. S. E. Zhu, F. Li and G. W. Wang, Chem. Soc. Rev., 2013, 42, 7535–7570.
3. A. Mohajeri and A. Omidvar, Phys. Chem. Chem. Phys., 2015, 17, 22367–22376.
4. A. Montellano, T. Da Ros, A. Bianco and M. Prato, Nanoscale, 2011, 3, 4035–4041.
5. Y. J. He and Y. F. Li, Phys. Chem. Chem. Phys., 2011, 13, 1970–1983.
6. E. E. Fileti, J. Phys. Chem. B, 2014, 118, 12471–12477.
7. L. Pospisil, M. Gal, M. Hromadova, J. Bulickova, V. Kolivoska, J. Cvacka, K. Novakova, L. Kavan, M. Zukalova and L. Dunsch, Phys. Chem. Chem. Phys., 2010, 12, 14095–14101.
8. R. Long, Y. Dai and B. B. Huang, J. Phys. Chem. Lett., 2013, 4, 2223–2229.
9. A. V. Akimov, C. Williams and A. B. Kolomeisky, J. Phys. Chem. C, 2012, 116, 13816–13826.
10. H. Singh and M. Srivastava, Energy Sources, 1995, 17, 615–640.
11. J. Theobald, M. Perrut, J. V. Weber, E. Millon and J. F. Muller, Sep. Sci. Technol., 1995, 30, 2783–2819.
12. A. Astefanei, O. Nunez and M. T. Galceran, Anal. Chim. Acta, 2015, 882, 1–21.
13. A. Andreoni, L. Nardo, M. Bondani, B. Z. Zhao and J. E. Roberts, J. Phys. Chem. B, 2013, 117, 7203–7209.
14. S. Zanzoni, A. Ceccon, M. Assfalg, R. K. Singh, D. Fushman and M. D'Onofrio, Nanoscale, 2015, 7, 7197–7205.
15. Z. Z. Wang, Z. H. Lu, Y. L. Zhao and X. F. Gao, Nanoscale, 2015, 7, 2914–2925.
16. K. Kokubo, K. Matsubayashi, H. Tategaki, H. Takada and T. Oshima, ACS Nano, 2008, 2, 327–333.
17. Z. P. Jiang, Y. Zhang, L. B. Gan and Z. M. Wang, Tetrahedron, 2008, 64, 11394–11403.
18. O. Amelines-Sarria and V. A. Basiuk, J. Comput. Theor. Nanosci., 2009, 6, 73–79.
19. J. L. Delgado, N. Martin, P. de la Cruz and F. Langa, Chem. Soc. Rev., 2011, 40, 5232–5241.
20. F. F. Contreras-Torres, E. V. Basiuk, V. A. Basiuk, V. Meza-Laguna and T. Y. Gromovoy, J. Phys. Chem. A, 2012, 116, 1663–1676.
21. J. Wang, P. Liu, Z. Li, W. Qi, Y. Lu and W. S. Wu, Materials, 2013, 6, 4168–4185.
22. S. Q. Zhou, J. Y. Ouyang, P. Golas, F. Wang and Y. Pan, J. Phys. Chem. B, 2005, 109, 19741–19747.
23. R. Rivelino, T. Malaspina and E. E. Fileti, Phys. Rev. A, 2009, 79, 013201.
24. X. J. Li, X. H. Yang, L. M. Song, H. J. Ren and T. Z. Tao, Struct. Chem., 2013, 24, 1185–1192.
25. R. B. Sardenberg, C. E. Teixeira, M. Pinheiro and J. M. A. Figueiredo, ACS Nano, 2011, 5, 2681–2686.
26. C. Maciel, E. E. Fileti and R. Rivelino, Chem. Phys. Lett., 2011, 507, 244–247.
27. E. Y. Zhang, C. Y. Shu, L. Feng and C. R. Wang, J. Phys. Chem. B, 2007, 111, 14223–14226.
28. J. J. Yin, F. Lao, P. P. Fu, W. G. Wamer, Y. L. Zhao, P. C. Wang, Y. Qiu, B. Y. Sun, G. M. Xing, J. Q. Dong, X. J. Liang and C. Y. Chen, Biomaterials, 2009, 30, 611–621.
29. Z. Y. Chen, Y. Liu, B. Y. Sun, H. Li, J. Q. Dong, L. J. Zhang, L. M. Wang, P. Wang, Y. L. Zhao and C. Y. Chen, Small, 2014, 10, 2362–2372.
30. J. Li, M. Y. Zhang, B. Y. Sun, G. M. Xing, Y. Song, H. L. Guo, Y. A. Chang, Y. H. Ge and Y. L. Zhao, Carbon, 2012, 50, 460–469.
31. J. G. Rodríguez-Zavala and R. A. Guirado-López, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 075411.
32. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
33. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
34. C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
35. C. M. Breneman and K. B. Wiberg, J. Comput. Chem., 1990, 11, 361–373.
36. W. L. Jorgensen, D. S. Maxwell and J. TiradoRives, J. Am. Chem. Soc., 1996, 118, 11225–11236.
37. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
38. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7192.
39. B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463.
40. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10099.
41. A. Luzar and D. Chandler, Nature, 1996, 379, 55–57.
42. S. Pronk, S. Pall, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854.
43. L. Martinez, R. Andrade, E. G. Birgin and J. M. Martinez, J. Comput. Chem., 2009, 30, 2157–2164.
44. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6nj02813f

---