Body-centred cubic packing of spheres – the ultimate thermotropic assembly mode for highly divergent dendrons†
Xiaohong
Yao
a,
Liliana
Cseh
ab,
Xiangbing
Zeng
c,
Min
Xue
a,
Yongsong
Liu
a and
Goran
Ungar
*ac
aDepartment of Physics, Zhejiang Sci-Tech University, Xiasha College Park, Hangzhou 310018, China
bInstitute of Chemistry, Timisoara of Romanian Academy, Timisoara – 300223, Romania
cDepartment of Materials Science and Engineering, University of Sheffield, Sheffield S1 3JD, UK
First published on 27th September 2016
Abstract
We have synthesized sodium tris(alkoxy)benzoates in which one of the three alkyl chains branches further into three C18H37 chains. These AB5 hyperbranched minidendrons melt directly into a body-centred cubic (BCC) mesophase formed by spherical “micelles”. In contrast, their non-branched counterparts display various mesophases before they turn into BCC upon heating. This agrees with the predictions from a numerical geometric model that relates the shape of the molecular wedge to the type of mesophase they adopt. The spheres were found to shrink in volume upon heating and expand upon cooling, as molecules, in some cases nearly half of them, are ejected and reintegrated in the spheres. The ejection of dendrons is caused by their lateral thermal expansion. The BCC appears to be the ultimate mesophase for the extremely divergent wedges such as the hyperbranched minidendrons. In dendrons with chains of unequal length, the sphere size is fixed by the shorter chains, the longer ones back-folding or interdigitating to effectively widen the wedge. This new understanding of their assembly will help in designing new dendrons, e.g. for better encapsulation of guest molecules.
Conceptual insightsWhile there is a vast amount of literature, and even a Nobel prize, on understanding how rod-like mesogens form nematic and smectic liquid crystal phases, there is remarkably little on understanding the physical principles of self-assembly of tapered or wedge-shaped mesogens, even though the experimentally accumulated information has now become very substantial. Tapered molecules, including dendrons, form primarily columnar and cubic mesophases and, on their own or attached to other functional molecular moieties, they probably account for the majority of thermotropic self-assembled systems today. Virtually all designs of such compounds have so far been empirically based. In contrast, here we use an approach based on a quantitative geometrical model that relates the shape of the molecules and the mode of their self-assembly. The model prompted us to prepare “hyperbranched” minidendrons with the shape of a highly divergent “exponential” wedge. They were found to display the body-centred cubic mesophase. This appears to be the ultimate thermotropic assembly mode of highly divergent wedges. The compounds indeed assemble as the model predicts, and disassemble and reassemble thermally in a way compatible with the model. Among other outcomes of this work, the adopted principle of highly divergent wedges should help obtain better vehicles for encapsulation of different molecular species. |
Taper-shaped molecules that possess a degree of amphiphilicity often exhibit liquid crystal (LC) phases with 2-D or 3-D periodicity. The majority of such compounds so far have been dendrons and “minidendrons”, typically containing an aromatic core and flexible terminal alkyl or oligo(ethylene oxide) chains.1–5 Taper-shaped mesogens, including dendrons, are some of the most fundamental and widespread building blocks in supramolecular chemistry. They have been attached to moieties such as organic semiconductors,6,7 ionic conductors,8–12 crown ethers,13,14 donor–acceptor complexes,15,16 polymers,17–19 peptides,20 and nanoparticles,21,22etc. This way “dendronized” functional materials may be created that can be used in a variety of potential applications.23 The most common supramolecular objects that such dendrons or dendronized compounds form are columns and spheres. When the tapered molecules are fan-shaped, i.e. when they can easily fit in a plane, the compound is likely to form a columnar phase. Oversimplified, the pizza-slice-like molecules self-assemble into disks (“pizzas”) which, in turn, stack on top of each other and form columns which, finally, assemble on a 2-D lattice, usually hexagonal. However, if the peripheral chains have a cross-section larger than would fit in a plane, such tapered molecules adopt a conical shape. The cones then assemble into spheres which, in turn, pack on 3-D lattices.24
Fan shape induced columnar organization, often due to the attachment of alkoxyphenyl, or Percec-type dendrons,1 can be usefully exploited in many ways, e.g. in forming 1-D electronic6,7 and ionic8–12 conductors, in encapsulating light-emitting polymers,25 and forming artificial ionic channels, etc. Temperature-induced transition from columns to spheres can be used e.g. to create a thermal switch, whereby an ionically or electronically conducting columnar molecular wire would split into isolated spherical fragments at a pre-set temperature and break the circuit.26 A spherical assembly can also in principle be used to encapsulate and isolate molecules such as organic light emitters to prevent radiationless energy transfer. But this development has been hampered by the high sensitivity of supramolecular thermotropic micelles to insertion of any larger entity at the thin end of the molecular wedge, thereby effectively reducing the taper and reverting the spheres to columns. A better fundamental understanding of the spherical assembly of tapered molecules is keenly needed. There are also remarkably few theoretical or simulation studies on the subject.27,28
The lattices formed by the supramolecular spheres, or micelles, are the same as those found in metals and alloys, albeit on a length-scale an order of magnitude larger, with inter-sphere spacing typically of the order of 2–4 nm.29 Wedge-shaped compounds have been found to exhibit the following micellar LC phases: the cubic phase with Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n symmetry and 8 spheres in a unit cell, known in metallurgy as A15;30,31 the tetragonal P42/mnm phase (the “σ-phase”) with 30 spheres;32 the body-centred cubic (BCC), space group Im
n symmetry and 8 spheres in a unit cell, known in metallurgy as A15;30,31 the tetragonal P42/mnm phase (the “σ-phase”) with 30 spheres;32 the body-centred cubic (BCC), space group Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m with only 2 spheres per cell;17,33 and the aperiodic dodecagonal liquid quasicrystals (LQCs).34 Recently compiled statistics on the occurrence of these phases24 based on the data in ref. 1 are summarized in Table 1. The Pm
m with only 2 spheres per cell;17,33 and the aperiodic dodecagonal liquid quasicrystals (LQCs).34 Recently compiled statistics on the occurrence of these phases24 based on the data in ref. 1 are summarized in Table 1. The Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n cubic phase is found to be by far the most common, observed in 84% of all appearances of micellar phases, and 55% of all LC phases are detected in such compounds, including the columnar and smectic phases. On the other hand, the simplest micellar phase, the BCC, is the least represented, showing up in only 2% of micellar cases.
n cubic phase is found to be by far the most common, observed in 84% of all appearances of micellar phases, and 55% of all LC phases are detected in such compounds, including the columnar and smectic phases. On the other hand, the simplest micellar phase, the BCC, is the least represented, showing up in only 2% of micellar cases.
| Configuration at rootc | Cubic (A15) (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n) n) |
Tetragonal (σ) (P42/mnm) | Dodecagonal quasicrystal | BCC (Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
|---|---|---|---|---|
| a Percentages are relative to the total number of occurrences of micellar 3-D phases. b Phases occurring in the same compound at different temperatures are also counted. c Substitution at the exterior side of the phenyl ring that is closest to the apex of the dendron: AB3 = 3,4,5-, AB2 ortho = 3,4- and AB2 meta = 3,5-substitution. | ||||
| AB3 | 50 (94%) | 0 | 2 (4%) | 1 (2%) |
| AB2 ortho | 42 (91%) | 3 (7%) | 1 (2%) | 0 |
| AB2 meta | 7 (37%) | 7 (37%) | 4 (11%) | 1 (3%) |
| Total | 99 (84%) | 10 (8%) | 7 (6%) | 2 (2%) |
Table 1 also points to some interesting correlations between the molecular architecture and the phase type, e.g. there is a large preference for the narrow apex ortho AB2 dendrons to form the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n phase in contrast to the wider apex meta AB2 dendrons which show, if anything, a slight preference for the dodecagonal phase and its close approximant the σ-phase. In this communication we concentrate on the BCC phase. At first sight it is indeed surprising that this simple packing is the rarest. In fact, however, there is a group of compounds where the BCC is well represented, i.e. the 3,4,5-tris(alkoxy)benzoate salts of alkali metals or their sulfonate equivalents, as well as some other such AB3 “minidendrons”, including those attached to a polymer backbone.17,35–38 These can be regarded as 1st generation dendrons; when the alkyl chains are dodecyl or longer, they all display LC phases of which the BCC occurs at the highest temperatures. All of these salts also form other stable LC phases at lower temperatures. In order to understand this behaviour we first discuss a semiquantitative geometric model that relates the molecular shape to the packing mode of the spherical micelles. Since the model predicts that increased branching should stabilize the BCC, we decided to test our model by synthesising new “hyperbranched” alkoxybenzoate salts and test our model's predictions. From a practical viewpoint, if we want to encapsulate guest species into the micelles, thereby inevitably reducing the effective taper angle, we need to start with a wedge as highly tapered as possible in the first place. The second objective is to explore what happens when the terminal chains are not all of the same length, as they have been in most, if not all, of the previously reported studies.
n phase in contrast to the wider apex meta AB2 dendrons which show, if anything, a slight preference for the dodecagonal phase and its close approximant the σ-phase. In this communication we concentrate on the BCC phase. At first sight it is indeed surprising that this simple packing is the rarest. In fact, however, there is a group of compounds where the BCC is well represented, i.e. the 3,4,5-tris(alkoxy)benzoate salts of alkali metals or their sulfonate equivalents, as well as some other such AB3 “minidendrons”, including those attached to a polymer backbone.17,35–38 These can be regarded as 1st generation dendrons; when the alkyl chains are dodecyl or longer, they all display LC phases of which the BCC occurs at the highest temperatures. All of these salts also form other stable LC phases at lower temperatures. In order to understand this behaviour we first discuss a semiquantitative geometric model that relates the molecular shape to the packing mode of the spherical micelles. Since the model predicts that increased branching should stabilize the BCC, we decided to test our model by synthesising new “hyperbranched” alkoxybenzoate salts and test our model's predictions. From a practical viewpoint, if we want to encapsulate guest species into the micelles, thereby inevitably reducing the effective taper angle, we need to start with a wedge as highly tapered as possible in the first place. The second objective is to explore what happens when the terminal chains are not all of the same length, as they have been in most, if not all, of the previously reported studies.
In order to explain why spherical supramolecular dendrimers pack on different lattices, the average radial distribution functions of volume dV/dr have been calculated for different 3-D lattices with spherical motifs.32,39 These functions give the ideal shapes of wedge-shaped molecules that would fill the unit cell of a given phase perfectly uniformly. The spheres of radius r are allowed to grow simultaneously from their centres. Let vi(r) be that part of sphere i which does not overlap with another sphere. The graphs in Fig. 1 show the averaged functions dV/dr, where 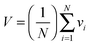 is the mean volume V, and N is the number of spheres in the unit cell. Before the spheres impinge on one another, all curves are parabolae, since the surface of a sphere is A(r) = dV/dr ∝ r2. But once they clash, the ascent of dV/dr either slows down (Pm
is the mean volume V, and N is the number of spheres in the unit cell. Before the spheres impinge on one another, all curves are parabolae, since the surface of a sphere is A(r) = dV/dr ∝ r2. But once they clash, the ascent of dV/dr either slows down (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n and tetragonal) or starts to drop (BCC, FCC, and simple cubic). Eventually dV/dr decreases to zero when all the space is filled. The shape of dV/dr beyond the first clash is different for different lattices. In Fig. 1 we also show the dV/dr curve for the hexagonal columnar (Colh) phase. Here the cylinders rather than spheres grow from their central axis; thus dV/dr is linear with r before the cylinders clash.
n and tetragonal) or starts to drop (BCC, FCC, and simple cubic). Eventually dV/dr decreases to zero when all the space is filled. The shape of dV/dr beyond the first clash is different for different lattices. In Fig. 1 we also show the dV/dr curve for the hexagonal columnar (Colh) phase. Here the cylinders rather than spheres grow from their central axis; thus dV/dr is linear with r before the cylinders clash.
 | ||
Fig. 1 Radial distribution of volume functions dV/dr for different micellar phases: face-centred cubic (FCC), BCC, Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n, P42/mnm (Tetrag) and simple cubic, as well as for the hexagonal columnar phase (Hex, Colh). The curves have been normalized to the same total volume of a micelle (disk in the case of Colh). The abscissa scale is in arbitrary units. For explanations of the insets, see the text (cf.ref. 32 and 39). n, P42/mnm (Tetrag) and simple cubic, as well as for the hexagonal columnar phase (Hex, Colh). The curves have been normalized to the same total volume of a micelle (disk in the case of Colh). The abscissa scale is in arbitrary units. For explanations of the insets, see the text (cf.ref. 32 and 39). | ||
A way to relate the dV/dr functions to the molecular shape is to imagine the conical molecule (inset α in Fig. 1) rolled out flat into a parabolic (r2) fan as schematically drawn in inset β in Fig. 1. The ideal envelope of the molecular fan for each phase is represented by the corresponding dV/dr, with r = 0 at the acute apex of the molecule. The rectangle in inset β indicates the limited region of dV/dr shown in the diagram.
The dV/dr distribution for BCC differs from those for Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n and P42/mnm in that it has a slightly higher peak and a shorter tail. This change in molecular envelope is expected to occur at increasing temperatures due to the lateral thermal expansion of the flexible chains requiring a higher dV/dr peak, and the longitudinal contraction of the chains requiring a shorter dV/dr tail. The dV/dr curves for the Pm
n and P42/mnm in that it has a slightly higher peak and a shorter tail. This change in molecular envelope is expected to occur at increasing temperatures due to the lateral thermal expansion of the flexible chains requiring a higher dV/dr peak, and the longitudinal contraction of the chains requiring a shorter dV/dr tail. The dV/dr curves for the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n and P42/mnm phases are similar to each other, and indeed the two phases have often been found to appear interchangeably.
n and P42/mnm phases are similar to each other, and indeed the two phases have often been found to appear interchangeably.
The two “close packed” structures, FCC and the hexagonal close packing (HCP), share the same dV/dr curve. Neither phase has yet been reported in thermotropic tapered compounds. The likely reason is the presence of large octahedral in addition to the small tetrahedral interstices. To reach the centres of the former, a long stretched chain is needed – see the long tail of the dV/dr curve for FCC. One can speculate that to form the FCC or HCP phase the dendron would have to have perhaps one of the chains very long to match the long tail of the dV/dr. Possibly it may also need one or two short branches in addition to comply with the high peak of the FCC curve.
The divergence of the wedge-shaped molecule can be approximated in general by using dV/dr = krp. A rough guide to the phase type that such wedge-shaped molecules would form is given as follows.24p ≈ 0: smectic; 0 < p < 1: bicontinuous cubic; p ≈ 1: columnar; p ≈ 2: micellar (cubic or other symmetries). Fig. 1 suggests that, as a crude approximation, the value of p also plays a part in determining which of the micellar phases is likely to be adopted by the compound, a higher p favouring the BCC and a lower p favouring the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n phase.
n phase.
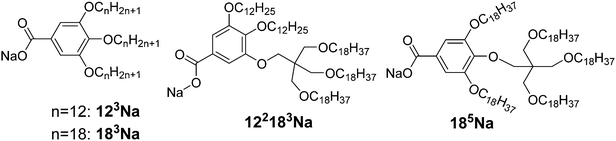
Here we explore the high end of p and try to make the wedge more “exponential”, i.e. make its width increase more steeply at larger r. Sodium salts 122183Na and 185Na were thus synthesised, each having one of their three alkoxy chains carrying a further three-way branching point based on pentaerythritol (see Scheme 1). A small branching group is used instead of the usual bulkier phenyl group to keep the wedge narrow near the root (small r), and thus increase the divergence p. The asymmetric compound 122183Na has the branched chain at the 3-position, and the symmetric compound 185Na at the 4-position. Furthermore, while in 185Na the five chains are similar in length, in 122183Na they differ in length considerably. These compounds were obtained via Williamson ether synthesis and the tris(alkyloxy)pentaerythritol intermediate was attached to the aromatic group via the Mitsunobu reaction. The synthesis is given in the ESI.† For comparison the AB3 Na salts 123Na and 183Na, with three unbranched C12H25 and C18H37 chains respectively, have also been prepared; their synthesis has been described previously.36Table 2 gives the phase sequence of the compounds on first heating, as obtained using DSC and X-ray diffraction.
| Compound | Phases and transition temperatures (°C) |
|---|---|
a k = crystal, Colr = rectangular columnar, Colh = hexagonal columnar, Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n and BCC = cubic, iso = isotropic liquid. n and BCC = cubic, iso = isotropic liquid.
|
|
| 123Na | k 70 Colr 91 Colh 110 Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n 220 BCC decomp n 220 BCC decomp |
| 183Na | k 84 Colh 104 BCC decomp |
| 122183Na | k 39 BCC 200 iso |
| 185Na | k 55 BCC decomp (>270) |
Fig. 2 shows the small-angle X-ray diffraction (SAXD) curves of the mesophases as a function of temperature, recorded during the heating of compounds 123Na and 185Na. Equivalent SAXD scans for the other compounds are shown in the ESI† (Fig. S2). All compounds show 2D or 3D liquid crystal phases above the crystal melting point. In accordance with previous studies of tris(alkoxy)benzoates,36123Na and 183Na start with the Colh phase and end up in the BCC phase (space group Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). In contrast, the hyperbranched compounds 122183Na and 185Na melt directly into the BCC phase. Once having reached it, all compounds except 122183Na remain in the BCC phase until at least 270 °C, where heating runs were interrupted for fear of decomposition. As an exception, 122183Na transforms to a disordered isotropic liquid at 200 °C, as is clear from Fig. S2b (ESI†). There is no detectable associated endotherm, meaning that the transition entropy is extremely low. In all cases the phase sequence is reversed on cooling. The diffraction intensities were used to reconstruct the electron density map of the BCC unit cell (Fig. 3b), which clearly shows the spherical maxima at the corners and at the centre of the cell, marking the positions of the aromatic + ionic cores of the micelles. The low density continuum is uniformly filled with the alkyl chains, as indicated by the uniformly green colour in the map.
m). In contrast, the hyperbranched compounds 122183Na and 185Na melt directly into the BCC phase. Once having reached it, all compounds except 122183Na remain in the BCC phase until at least 270 °C, where heating runs were interrupted for fear of decomposition. As an exception, 122183Na transforms to a disordered isotropic liquid at 200 °C, as is clear from Fig. S2b (ESI†). There is no detectable associated endotherm, meaning that the transition entropy is extremely low. In all cases the phase sequence is reversed on cooling. The diffraction intensities were used to reconstruct the electron density map of the BCC unit cell (Fig. 3b), which clearly shows the spherical maxima at the corners and at the centre of the cell, marking the positions of the aromatic + ionic cores of the micelles. The low density continuum is uniformly filled with the alkyl chains, as indicated by the uniformly green colour in the map.
The phase sequence Colh → Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n → BCC with increasing T for 123Na can be understood with reference to Fig. 1, by noting the increasingly higher peak and shorter tail of the corresponding dV/dr curves. That is, the Colh curve is suitable for linear wedges, such as those found at lower temperatures in 123Na and 183Na, when their alkyl chains are mainly extended with few gauche conformers. At higher T and increasing gauche content, the chains expand laterally and contract longitudinally. A fan-cone transformation occurs in these two compounds, triggering the columnar – cubic phase transition. If the molecule was confined to a plane, this would be equivalent to a transition from the linear to the parabolic fan (see inset β in Fig. 1), thus requiring the change to a phase structure with a parabolic rather than linear dV/dr. As the chain ends of 123Na in the Pm
n → BCC with increasing T for 123Na can be understood with reference to Fig. 1, by noting the increasingly higher peak and shorter tail of the corresponding dV/dr curves. That is, the Colh curve is suitable for linear wedges, such as those found at lower temperatures in 123Na and 183Na, when their alkyl chains are mainly extended with few gauche conformers. At higher T and increasing gauche content, the chains expand laterally and contract longitudinally. A fan-cone transformation occurs in these two compounds, triggering the columnar – cubic phase transition. If the molecule was confined to a plane, this would be equivalent to a transition from the linear to the parabolic fan (see inset β in Fig. 1), thus requiring the change to a phase structure with a parabolic rather than linear dV/dr. As the chain ends of 123Na in the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n phase continue to expand laterally upon further heating, a dV/dr function with an even higher peak and a shorter tail is required, and hence the Pm
n phase continue to expand laterally upon further heating, a dV/dr function with an even higher peak and a shorter tail is required, and hence the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n transforms into the BCC phase. In comparison, however, the longer chains of 183Na require such an additional lateral space already at a lower T, which explains why this compound bypasses the Pm
n transforms into the BCC phase. In comparison, however, the longer chains of 183Na require such an additional lateral space already at a lower T, which explains why this compound bypasses the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n phase altogether.
n phase altogether.
Turning our attention to the new hyperbranched salts, the fact that they only show the BCC phase is indeed what the dV/dr analysis predicted. Already at a low T their wide aliphatic brushes require the dV/dr shape associated with the BCC phase. Their wide end is believed to be made even wider by the well-known preference for alkyl chain ends to adopt gauche conformations.40 Hence these compounds do not show any other LC phase but the BCC.
As the temperature is increased, the BCC phase continues. It would appear that no other packing mode offers a better alternative for highly divergent molecules, i.e. a dV/dr with a higher peak and a shorter tail. This would explain why BCC persists over a range of 200 K or more in most benzoate salts. However, this does not prevent the dendrons from continuing to expand laterally and contract longitudinally with increasing T. Evidence can be found in the plots of BCC unit cell volume vs. T in Fig. 3a. The cell volume, and hence the volume of the spheres, decrease on heating for all compounds studied, particularly steeply for 183Na and 185Na; in the latter case the micelle volume nearly halves in the measured T range. Our explanation of this remarkable behaviour is in that, as the solid angle Ω of the conical molecule increases, the number of molecules μ = 4π/Ω, required to complete a sphere, decreases. Furthermore, longitudinal contraction of the chains also means that distant interstices can no longer be reached by the chain ends. Hence in order to fill the space, the lengthscale of the structure must contract. The thermal effect is equivalent to the thermal shrinkage of rubber, an entropically driven phenomenon.41
The thermal shrinkage of the spheres does not imply volume shrinkage of the material. As the compounds are made up mainly of alkyl chains, we have assumed the thermal expansivity to be close to that of liquid n-alkane C16H34.42 Estimating the density at room temperature to be approximately 0.95 g cm−3 based on previous measurements,35,36 and using the measured cell volumes and computed densities (see ESI,† Tables S3 and S4), we calculated μ, the number of molecules per sphere, at the low and high ends of the measured BCC range for all compounds studied – see the numbers in boxes in Fig. 3a. The spheres made up of appropriate numbers of cones are schematically shown as insets (i)–(v) in Fig. 3a. As T increases, the surplus dendrons are evidently continuously expelled from the spherical micelles, while at the same time new micelles are formed from the ejected molecules. The largest drop in μ occurs in 185Na, from 20.4 to 11.4. A similarly high rate of dendron ejection is also seen in 185Na. This complex process of disassembly and reassembly of micelles is reversible, as illustrated by the data on unit cell expansion on cooling for 122183Na (empty circles in Fig. 3a). Some hysteresis is evident at the relatively high applied cooling rate (10 K min−1). The re-integration of dendrons on cooling is a somewhat slower process than that of their ejection and regrouping on heating.
Thermal contraction of the unit cell has been observed, and ejection of surplus dendrons postulated, also in the case of the columnar phase.35,38,43 However, in that case contraction is only two-dimensional, and one needs to ascertain that a compensating expansion along the column axis does not occur. In fact, when the dendrons were covalently attached to a polymer backbone and prevented from leaving the column, the macroscopic fibre was found to extend longitudinally upon heating, in contrast to the usual longitudinal thermal shrinkage of the polymer fibres.43 In free minidendrons, where molecular spacing along the column axis was measured using X-rays, molecular ejection was confirmed as the most likely explanation of lateral shrinkage.35,38 Nevertheless, there can be no better proof of continuous and reversible thermal disassembly and reassembly than is provided in the case of 3D cubic structures, where thermal shrinkage occurs along all three dimensions, and molecular ejection and reintegration is the only possible mechanism. The presently studied hyperbranched minidendrons provide so far the most compelling examples of this process.
In Fig. 3e we show dV/dr curves in a real scale (nm and nm2 units) for the actual compounds studied here. As mentioned above, these curves represent the effective wedge shapes of the rolled-out molecules (inset β in Fig. 1). Fig. 3e shows graphically the actual widening and longitudinal contraction of the wedges upon heating from the lowest (dashed curves) to the highest T (solid curves). These are particularly prominent in 185Na and 183Na. The curves for 123Na also illustrate graphically the equivalent change occurring isothermally upon the transition from Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n to BCC (cf. dot-dash and solid green curves). Note that the end points of the curves in Fig. 3e (the length of the wedge) are directly related to the height of the curves in Fig. 3a. A further unexpected and counterintuitive finding revealed in Fig. 3a and e is that the size of the micelles of 122183 is exactly the same as that of 123Na, i.e. that the extra pentaerythritol branch with three long C18 chains replacing a single C12 chain made no difference to the length of the molecule and the size of the micelle. The reason for this can be gathered by comparing the solid blue and green curves in Fig. 3e; it shows that all the extra material in 122183Na went into doubling the width of the wedge, rather than extending it. This suggests that the sphere diameter is determined by the shorter chains, the long chains presumably folding back, being highly conformationally disordered or partially interdigitated – see the schematics in insets (vi) and (vii) in Fig. 3a and the molecular models in Fig. 3c and d. This illustrates how the molecular conformation adapts to the space filling requirement of the superstructure.
n to BCC (cf. dot-dash and solid green curves). Note that the end points of the curves in Fig. 3e (the length of the wedge) are directly related to the height of the curves in Fig. 3a. A further unexpected and counterintuitive finding revealed in Fig. 3a and e is that the size of the micelles of 122183 is exactly the same as that of 123Na, i.e. that the extra pentaerythritol branch with three long C18 chains replacing a single C12 chain made no difference to the length of the molecule and the size of the micelle. The reason for this can be gathered by comparing the solid blue and green curves in Fig. 3e; it shows that all the extra material in 122183Na went into doubling the width of the wedge, rather than extending it. This suggests that the sphere diameter is determined by the shorter chains, the long chains presumably folding back, being highly conformationally disordered or partially interdigitated – see the schematics in insets (vi) and (vii) in Fig. 3a and the molecular models in Fig. 3c and d. This illustrates how the molecular conformation adapts to the space filling requirement of the superstructure.
We note that although the dV/dr curves give a compelling rationale for many observed features of sequence, structure and size of micellar dendron phases, they should not be considered as the only factors involved. However, it is conspicuous that even if the differences in the dV/dr functions are rather subtle, as e.g. for the BCC and Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n phases, in all compounds where both phases appear, the BCC is invariably the high-T phase. Such a clear-cut distinction does not exist between the Pm
n phases, in all compounds where both phases appear, the BCC is invariably the high-T phase. Such a clear-cut distinction does not exist between the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n and the tetragonal σ-phase, where the dV/dr functions are very similar indeed.1,35,36
n and the tetragonal σ-phase, where the dV/dr functions are very similar indeed.1,35,36
Conclusions
We have prepared the first examples of “hyperbranched minidendrons” of the AB5 type and shown that the BCC structure provides what seems to be the ultimate mode of thermotropic spherical assembly for highly divergent dendrons. The dV/dr-based analysis was shown to be very useful in rationalizing the observed phase behaviour. The thermal shrinkage of the supramolecular aggregates via molecular ejection and reassembly has been confirmed beyond doubt, with an unprecedented extent of shrinkage recorded in the 185Na compound. The unexpected behaviour of minidendron 122183Na with mixed longer and shorter chains, forming micelles of exactly the same size as 123Na, is attributed to back-folding of the added long chains. These results help improve our general understanding of the complex self-assembly behaviour of taper-shaped molecules. We also believe that producing highly divergent dendrons like the hyperbranched ones in this study will allow larger guest molecules to be encapsulated into spherical dendron-based shells.Acknowledgements
We acknowledge funding from NFSC China (21274132 and 21544009), Zhejiang Natural Science Foundation (LY15B020007), the Science Foundation of Zhejiang Sci-Tech University (14062016-Y), the joint NSF-EPSRC PIRE program “RENEW” (EP/K034308) and the Leverhulme Trust (RPG-2012-804). G. U. and L. C. are grateful, respectively, for the awards of State Specially Recruited Expert and High-End Foreign Expert, both from the Government of China. For help with the synchrotron SAXS experiments we thank Prof. N. Terrill at I22, Diamond Light Source, UK.References
- B. M. Rosen, C. J. Wilson, D. A. Wilson, M. Peterca, M. R. Imam and V. Percec, Chem. Rev., 2009, 109, 6275–6540 CrossRef CAS PubMed.
- B. Donnio, S. Buathong, I. Bury and D. Guillon, Chem. Soc. Rev., 2007, 36, 1495–1513 RSC.
- C. Tschierske, Angew. Chem., Int. Ed., 2013, 52, 8828–8878 CrossRef CAS PubMed.
- T. Kato, N. Mizoshita and K. Kishimoto, Angew. Chem., Int. Ed., 2006, 45, 38–68 CrossRef CAS PubMed.
- H.-J. Sun, S. Zhang and V. Percec, Chem. Soc. Rev., 2015, 44, 3900–3923 RSC.
- F. Würthner, C. Thalacker, S. Diele and C. Tschierske, Chem. – Eur. J., 2001, 7, 2245–2253 CrossRef.
- Z. An, J. Yu, B. Domercq, S. C. Jones, S. Barlow, B. Kippelen and S. R. Marder, J. Mater. Chem., 2009, 19, 6688–6698 RSC.
- G. Ungar, S. V. Batty, V. Percec, J. Heck and G. Johansson, Adv. Mater. Opt. Electron., 1994, 4, 303–313 CrossRef CAS.
- T. Ichikawa, M. Yoshio, A. Hamasaki, T. Mukai, H. Ohno and T. Kato, J. Am. Chem. Soc., 2007, 129, 10662–10663 CrossRef CAS PubMed.
- M. Peterca, V. Percec, A. E. Dulcey, S. Nummelin, S. Korey, M. Ilies and P. A. Heiney, J. Am. Chem. Soc., 2006, 128, 6713–6720 CrossRef CAS PubMed.
- C. S. Pecinovsky, E. S. Hatakeyama and D. L. Gin, Adv. Mater., 2008, 20, 174–178 CrossRef CAS.
- B. Soberats, M. Yoshio, T. Ichikawa, X. B. Zeng, S. Taguchi, H. Ohno, F. Liu, G. Ungar and T. Kato, J. Am. Chem. Soc., 2015, 137, 13212–13215 CrossRef CAS PubMed.
- G. Johansson, V. Percec, G. Ungar and D. Abramic, J. Chem. Soc., Perkin Trans. 1, 1994, 447–459 RSC.
- A. Schultz, S. Laschat, A. Saipa, F. Gießelmann, M. Nimtz, J. L. Schulte, A. Baro and B. Miehlich, Adv. Funct. Mater., 2004, 14, 163–168 CrossRef CAS.
- V. Percec, M. Glodde, T. K. Bera, Y. Miura, I. Shiyanovskaya, K. D. Singer, V. S. K. Balagurusamy, P. A. Heiney, I. Schnell, A. Rapp, H.-W. Spiess, S. D. Hudson and H. Duan, Nature, 2002, 419, 384–388 CrossRef CAS PubMed.
- X.-H. Zhang, A. Grant, S. Ellinger, S. A. Odom, D. Sweat, D. B. Tanner, A. G. Rinzler, S. Barlow, J.-L. Bredas, B. Kippelen, S. R. Marder and J. R. Reynolds, J. Am. Chem. Soc., 2009, 131, 2824–2826 CrossRef PubMed.
- D. J. P. Yeardley, G. Ungar, V. Percec, N. M. Holerca and G. Johansson, J. Am. Chem. Soc., 2000, 122, 1684–1689 CrossRef CAS.
- Y. Tsuda, R. Kuwahara and J.-M. Oh, Trans. Mater. Res. Soc. Jpn., 2004, 29, 267–271 CAS.
- A. Grotzky, E. Atamura, J. Adamcik, P. Carrara, P. Stano, F. Mavelli, T. Nauser, R. Mezzenga and A. D. Schluter, Langmuir, 2013, 29, 10831–10840 CrossRef CAS PubMed.
- V. Percec, A. E. Dulcey, M. Peterca, P. Adelman, R. Samant, V. S. K. Balagurusamy and P. A. Heiney, J. Am. Chem. Soc., 2007, 129, 5992–6002 CrossRef CAS PubMed.
- B. Donnio, P. Garcia-Vazquez, J.-L. Gallani, D. Guillon and E. Terazzi, Adv. Mater., 2007, 19, 3534–3539 CrossRef CAS.
- K. Kanie, M. Matsubara, X. B. Zeng, F. Liu, G. Ungar, H. Nakamura and A. Muramatsu, J. Am. Chem. Soc., 2012, 134, 808–811 CrossRef CAS PubMed.
- X. Feng, M. E. Tousley, M. G. Cowan, B. R. Wiesenauer, S. Nejati, Y. Choo, R. D. Noble, M. Elimelech, D. L. Gin and C. O. Osuji, ACS Nano, 2014, 8, 11977–11986 CrossRef CAS PubMed.
- G. Ungar, F. Liu and X. B. Zeng, Thermotropic Cubic Liquid Crystal Phases, Other 3D Phases and Quasicrystals, in Handbook of Liquid Crystals, ed. J. W. Goodby, P. J. Collings, T. Kato, C. Tschierske, H. F. Gleeson and P. Raynes, VCH_Wiley, Weinheim, 2014, ch. 7, vol. 5, pp. 363-436 Search PubMed.
- B. P. Hoag and D. L. Gin, Liq. Cryst., 2004, 31, 185–199 CrossRef CAS.
- B.-K. Cho, A. Jain, S. M. Gruner and U. Wiesner, Science, 2004, 305, 1598–1601 CrossRef CAS PubMed.
- P. Ziherl and R. D. Kamien, J. Phys. Chem. B, 2001, 105, 10147–10158 CrossRef CAS.
- Y. Y. Li, S. T. Lin and W. A. Goddard, J. Am. Chem. Soc., 2004, 126, 1872–1885 CrossRef CAS PubMed.
- G. Ungar and X. B. Zeng, Soft Matter, 2005, 1, 95–106 RSC.
- V. S. K. Balagurusamy, G. Ungar, V. Percec and G. Johansson, J. Am. Chem. Soc., 1997, 119, 1539–1555 CrossRef CAS.
- K. Borisch, S. Diele, P. Göring, H. Müller and C. Tschierske, Liq. Cryst., 1997, 22, 427–443 CrossRef CAS.
- G. Ungar, Y. S. Liu, X. B. Zeng, V. Percec and W. D. Cho, Science, 2003, 299, 1208–1211 CrossRef CAS PubMed.
- C. H. M. Weber, F. Liu, X. B. Zeng, G. Ungar, N. Mullin, J. K. Hobbs, M. Jahr and M. Lehmann, Soft Matter, 2010, 6, 5390–5396 RSC.
- X. B. Zeng, Y. S. Liu, G. Ungar, V. Percec, A. E. Dulcey and J. K. Hobbs, Nature, 2004, 428, 157–160 CrossRef CAS PubMed.
- G. Ungar, V. Percec, M. N. Holerca, G. Johansson and J. A. Heck, Chem. – Eur. J., 2000, 6, 1258–1266 CrossRef CAS.
- V. Percec, M. N. Holerca, S. Uchida, W.-D. Cho, G. Ungar, Y. Lee and D. J. P. Yeardley, Chem. – Eur. J., 2002, 8, 1106–1117 CrossRef CAS.
- U. Beginn, L. Yan, S. N. Chvalun, M. A. Shcherbina, A. Bakirov and M. Möller, Liq. Cryst., 2008, 35, 1073–1093 CrossRef CAS.
- M.-H. Yen, J. Chaiprapa, X. B. Zeng, Y. S. Liu, L. Cseh, G. H. Mehl and G. Ungar, J. Am. Chem. Soc., 2016, 138, 5757–5760 CrossRef CAS PubMed.
- K. Kanie, M. Matsubara, X. B. Zeng, F. Liu, G. Ungar, H. Nakamura and A. Muramatsu, J. Am. Chem. Soc., 2012, 134, 808–811 CrossRef CAS PubMed.
- G. Zerbi, R. Magni, M. Gussoni, K. H. Moritz, A. Bigotto and S. Dirlikov, J. Chem. Phys., 1981, 75, 3175–3194 CrossRef CAS.
- We note that some reduction in the unit cell volume has also been observed on heating the bicontinuous cubic LC phases – see S. Kutsumizu, H. Mori, M. Fukatami, S. Naito, K. Sakajiri and K. Saito, Chem. Mater., 2008, 20, 3675–3687 CrossRef CAS . However, in that case the cause of the contraction is more complex as thermal increase in twist angle between successive molecular layers tends to shorten the distance between network junctions, causing additional unit cell contraction – see C. Dressel, F. Liu, M. Prehm, X. B. Zeng, G. Ungar and C. Tschierske, Angew. Chem., Int. Ed., 2014, 53, 13115–13120 CrossRef PubMed.
- R. A. Orwoll and P. J. Flory, J. Am. Chem. Soc., 1967, 89, 6814–6822 CrossRef CAS.
- J.-K. Kwon, S. N. Chvalun, J. Blackwell, V. Percec and J. A. Heck, Macromolecules, 1995, 28, 1552–1558 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6nh00155f |
| This journal is © The Royal Society of Chemistry 2017 |


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
