 Open Access Article
Open Access ArticleSolar-driven alumina calcination for CO2 mitigation and improved product quality†
Dominic
Davis‡
 a,
Fabian
Müller‡
a,
Fabian
Müller‡
 b,
Woei L.
Saw
b,
Woei L.
Saw
 c,
Aldo
Steinfeld
c,
Aldo
Steinfeld
 *b and
Graham J.
Nathan
*b and
Graham J.
Nathan
 *a
*a
aSchool of Mechanical Engineering, Centre for Energy Technology, The University of Adelaide, South Australia 5005, Australia. E-mail: graham.nathan@adelaide.edu.au
bDepartment of Mechanical and Process Engineering, ETH Zürich, 8092 Zürich, Switzerland. E-mail: aldo.steinfeld@ethz.ch
cSchool of Chemical Engineering, Centre for Energy Technology, The University of Adelaide, South Australia 5005, Australia
First published on 10th May 2017
Abstract
We report on the first-of-a-kind experimental demonstration of the calcination of alumina with concentrated solar thermal (CST) radiation at radiative fluxes up to 2190 suns using a 5 kW novel solar transport reactor. Aluminium hydroxide was calcined at nominal reactor temperatures over the range 1160–1550 K to yield chemical conversions of up to 95.8% for nominal residence times of approximately 3 s. Solar energy conversion efficiencies of up to 20.4% were achieved. The mean pore diameter and specific surface area of the solar-generated alumina with the greatest chemical conversion were 5.8 nm and 132.7 m2 g−1, respectively, which are higher values than are typical for industrial alumina production. In addition, the product is dominated by the γ-phase, which is desirable for the downstream processing to aluminium. This suggests that CST can improve the quality of alumina over existing fossil fuel based processes though a combination of a high heating rate and avoided contamination by combustion products. Furthermore, the solar-driven process has the potential to avoid the discharge of combustion-derived CO2 emissions for the calcination stage of the conventional Bayer process, which is typically 165 kg-CO2 per tonne-alumina.
1 Introduction
The use of concentrated solar thermal energy (CST) for high-temperature thermal processing of minerals has the potential to reduce reliance on fossil fuels and hence also to reduce greenhouse gas (GHG) emissions.1,2 The calcination stage of alumina refining with the Bayer process is potentially well suited to the application of CST because it is a highly endothermic process that proceeds at ∼1273 K, which is readily achievable with solar tower technology. In addition, the calcination process is not sensitive to some ingress of air, which raises the possibility that direct irradiation of particles may be achievable without the need for a window to completely seal a solar reactor. However, the technical feasibility of this process is yet to be evaluated experimentally. The overall objective of this investigation is therefore to assess and demonstrate the technical feasibility of alumina calcination with direct irradiation via CST.Alumina is an intermediate product in the production of aluminium and is also a product in its own right. Alumina refining accounts for approximately 27% of the primary energy used in aluminium production, over 90% of which is provided by the combustion of fossil fuels.3 A total of 115.2 million tonnes of alumina was produced globally in 2015 at an average energy intensity of 11.9 GJ per tonne-alumina, representing a significant contribution to GHG emissions.4 Calcination is the last step of the Bayer process, which heats the hydrated alumina (aluminium hydroxide or gibbsite, Al(OH)3) from the precipitation stage, to drive off the water of hydration and form anhydrous alumina (aluminium oxide, Al2O3). It is an energy-intensive process, which has historically been conducted with the use of fossil fuels and a rotary-kiln.5 However, since the oil crisis of the 1970s, with the resulting increase in the cost of fuels, stationary calciners (circulating fluidised bed, gas suspension and fluid-flash calciners) have been favoured over rotary-kilns due to their significantly reduced fuel consumption.6,7 The process heat requirements of modern industrial calciners and estimated resulting CO2 emissions (calculated from the combustion of methane) are now approximately 3 GJ per tonne-alumina and 165 kg-CO2 per tonne-alumina product, respectively, for which the predominant fuel is natural gas.8,9 Today, the increasing cost of fuels continues to be a driver for technological development of more fuel efficient alumina calciner technology.10 With the price of natural gas forecast to increase in some locations such as Australia,9 and with the global need to reduce GHG emissions, there is strong incentive to seek alternative energy sources such as CST for process heat.11 This provides the motivation for the present investigation.
The calcination of alumina is a thermal decomposition chemical reaction, which proceeds endothermically according to the following reaction:
 | (1) |
Modern plants typically process alumina (generally in the gibbsite form) within flash calciners using particles of ∼100 μm in diameter transported in a gas suspension through the reactor with residence times on the order of a few seconds. A solar reactor that processes powders of similar size to a flash calciner is the solar vortex transport reactor. This employs a vortex flow to transport particles in suspension through an irradiation zone where they undergo high heating rates to drive a thermochemical reaction. Direct solar irradiation of such a suspension of reacting particles is an efficient means of heat transfer to the reactants.12–15 Furthermore, the temperature at which alumina calcination takes place in the Bayer process, 1273–1373 K, is readily achievable in current commercially available solar tower concentrators11 and is significantly less than the 1750 K that has been achieved previously in the solar vortex transport reactor used for solar gasification.16 The potential for alumina to be calcined with CST has been assessed with a packed bed of boehmite (an aluminium oxyhydroxide) in a crucible positioned at the focal plane of a Fresnel concentrator by Padilla et al.17 They reported 75% conversion after 10 minutes of exposure to solar radiation concentrated to 2644 suns and full conversion with exposure time of 90 minutes.17 However to date, no assessments have been reported for the calcination of gibbsite in a practical reactor under conditions relevant to flash calcination. The industrial gibbsite calcination process shares similarities with the calcination of limestone, which takes place at ∼1150 K and has previously been demonstrated with the application of CST.18–21 This demonstration has been performed with direct irradiation in a cavity-receiver transporting a flow of entrained particles,18 which suggests that it may also be suitable for alumina calcination. It is also noteworthy that the alumina calcination process is sensitive to the gas-phase composition, which is one reason that natural gas is a preferred fuel for alumina production.22,23 The application of CST to the calcination process has the potential to further improve product quality by eliminating the possibility of contamination with combustion products and by reducing the significance of back-reactions from the presence of H2O, which is a product of combustion. While these reasons suggest that the alumina calcination process is potentially well suited to solar processing, its technical feasibility cannot be determined by implication. Due to the complex, coupled nature of the process, it is necessary to assess this experimentally with a prototype solar reactor.
When gibbsite is calcined, the solid reactant evolves through various intermediate materials, including the monohydrated aluminium oxyhydroxide and several transition phases of alumina before the final, thermodynamically stable α-alumina is formed at temperatures in the range 1375–1450 K.23,24 Both the type of intermediate transition aluminas that are formed and their relative presence in the alumina product depend particularly on the heating rate, particle size and the presence of water vapour in the reaction atmosphere.25 Studies have previously proposed the gibbsite reaction pathways according to these parameters,23,24,26 the consensus of which is as follows:
(a) Fine gibbsite particles (<10 μm) decompose via χ-Al2O3, an amorphous alumina, followed by κ-Al2O3 before reaching the final α-Al2O3 phase;
(b) Coarse gibbsite particles (>100 μm) decompose via the intermediate aluminium oxyhydroxide, boehmite (AlO(OH)). Upon further heating this progressively decomposes to γ-, δ-, and θ-Al2O3, before reaching the α-Al2O3 phase; and
(c) Gibbsite which undergoes the high heating rates of flash calcination (4700–15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K s−1) thermally decomposes initially to the amorphous χ-Al2O3 as in pathway (a) before crossing over to pathway (b) and progressively forming γ-, δ-, θ-Al2O3, and finally the α-Al2O3 phase.
000 K s−1) thermally decomposes initially to the amorphous χ-Al2O3 as in pathway (a) before crossing over to pathway (b) and progressively forming γ-, δ-, θ-Al2O3, and finally the α-Al2O3 phase.
The formation of the intermediate species, boehmite, occurs in the range 380–575 K and is favoured by rapid heating of coarse gibbsite particles, such that there is a high local water vapour pressure within the large gibbsite particles.23 For the case where the gibbsite particles are small enough for the water of hydration to be released without the increase of internal pressure, boehmite does not evolve.23 Its formation is also favoured by high water vapour pressures in the transport air, as is typical of combustion gases in alumina refinery calciners.24,27 On the basis that the use of CST will avoid the presence of H2O as a combustion product, it can be deduced that the substitution of combustion with CST will inhibit the formation of boehmite. This would be beneficial because boehmite contains structural hydroxyls that degrade product quality for alumina smelting. The transition aluminas are characterised by their large internal porosity and resulting large surface area. They are thus useful for smelting and as catalysts. In contrast, the highly ordered and stable crystalline structure of the α-alumina phase makes it suitable for use in abrasives, refractories and ceramics.26 The present investigation focusses on the refining of alumina for the purpose of smelting to produce primary aluminium. A study conducted by Whittington & Ilievski24 suggests that the majority of refinery-prepared smelter grade aluminas (SGAs) reacts via χ-Al2O3 (pathway c) to feature large proportions of the γ-Al2O3 phase. The phase composition of numerous SGAs has previously been determined with quantitative X-ray diffraction (XRD) analysis to reveal that the product from stationary calciners comprises 60–90% γ-Al2O3 content while that from rotary-kiln calciners comprises 60–70% γ-Al2O3 content.24 This was corroborated by Wind & Raahauge,28 who reported that in an industrial gas suspension calcination system only 3–8% boehmite content was found in the pre-calcination stages, and by Perander et al.,29 who found that refinery-produced SGA was dominated by the γ-Al2O3 phase. On this basis it can be anticipated that the high heating rates inherent with solar processing will favour reaction pathway (c) to form predominantly γ-Al2O3. However, there is a need to assess the validity of this deduction by experiment.
The fraction of residual water in the alumina product is another important measure of product quality. This is because residual water has the propensity to drive the adverse formation of hydrogen fluoride gas during the downstream aluminium smelting process.30 It is important that alumina is calcined to a sufficient extent for the residual water content to be in the range 0.69–0.95 wt%.31 Alumina water content can be present in both a chemically-bound state (as in the case of aluminium hydroxides, Al(OH)3 and AlO(OH)) and in a physically-adsorbed state. It has been found that both types of moisture in alumina contribute to hydrogen fluoride formation in the downstream smelting process although the physically-adsorbed moisture is more easily removed from alumina at low temperatures below 473 K, while chemically-bound moisture requires higher temperatures. The present investigation at laboratory-scale features a single pass of gibbsite particles through the solar reactor. There is thus a need to determine the maximum extent of conversion (minimum moisture content) that can be achieved with a single pass. There is also a further need to assess the partitioning of any residual water within the alumina product into these two types.
Two crucial measures of alumina product quality are its mean pore size and specific surface area (SSA). This is because, for the subsequent smelting process, the alumina serves not only as the feedstock but also as the material with which hydrogen fluoride (and other fluorine compounds) from smelter gases are removed (via a dry-scrubbing process).28 The SSA and mean pore size are the primary indicators of the adsorption capacity of alumina, so that product quality is enhanced both by a larger SSA and a larger mean pore size.32 Specifically, the subsequent process of aluminium smelting requires that the characteristic pore diameter of the alumina be an order of magnitude larger than the hydrogen fluoride molecule (having a van der Waals diameter of 0.36 nm).32 This is to ensure high adsorption of the hydrogen fluoride in the dry-scrubbing process used in aluminium production. Previous investigations have determined that, during the calcination of gibbsite through the transition alumina, the SSA of the material increases rapidly to a maximum (>300 m2 g−1) at about 673 K, due to its microporous structure (average pore size <2 nm). With higher temperatures, the extent of calcination increases, causing the average pore size to increase and the SSA to decrease and generate a mesoporous structure. Hence the final α-alumina has the lowest SSA of the various alumina phases,6,7,23,33 and there is a trade-off between the desire to obtain both a low residual water content and a high SSA.29,34 It has been proposed, however, that under rapid heating, such as tends to occur with flash calcination, the structural rearrangement of the gibbsite calcination sequence can be decoupled from the water removal.33 The high heating rates possible with directly irradiated CST therefore offer the potential to produce alumina with both favourable residual moisture content and favourable microstructural properties. There is thus a need to confirm whether or not this potential benefit can be realised in practice through testing with a small scale solar reactor.
To meet these needs, the primary aim of this paper is to provide an insight into whether or not the solar-driven calcination of alumina is technically feasible. Specifically, the present investigation aims to obtain detailed understanding of the influence of key experimental parameters on the extent to which alumina may be calcined in a solar vortex transport reactor. It particularly aims to assess the influence of particle residence time and reactor temperature on the alumina product quality and to relate the performance of a laboratory-scale reactor to a full-scale device. It also aims to assess the impact of solar processing on the alumina moisture content and the alumina microstructure (mean pore size and specific surface area), which are primary measures of product quality, and to deduce the transition alumina reaction pathway.
2 Experimental methodology
2.1 Solar reactor
The solar vortex transport reactor is shown schematically in Fig. 1. This configuration was developed previously for the gasification of petroleum coke16 and the cracking of natural gas.35 It consists of a 200 mm-long, 100 mm-diameter ceramic lined cylindrical cavity-receiver, enclosed by a 210 mm-long, 120 mm-diameter Inconel 601 shell and a water-cooled aluminium frustum with a 3 mm-thick transparent fused quartz window. The flow of transport air and suspended Al(OH)3 particles is confined to the cavity-receiver and is directly exposed to concentrated solar radiation entering through a 50 mm-diameter aperture, with an apparent absorptivity estimated to exceed 93%.36 The window is cooled and protected from particle deposition by two injected air flows: one entering radially through a circular gap directed over the internal face of the window (with flow rate 2–4 Ln min−1), and a second through four tangential nozzles on the frustum (with flow rate 1–2 Ln min−1). The combination of the two purge flows suppresses the migration of particles into the frustum region. The vortex transport gas flow of synthetic air was generated by two tangentially arranged nozzles at the top (2–7 Ln min−1 air flow) and the bottom (2–7 Ln min−1 air flow) of the cavity and 30 mm behind the aperture. The particles were fed to the reactor through the tangential nozzle at the top of the cavity. | ||
| Fig. 1 Schematic diagram of (a) the axial cross section; and (b) the front view of the solar vortex transport reactor. | ||
2.2 Reactants
Aluminium hydroxide particles in the gibbsite form with a purity of 99% were used as the reactant. Fig. 2 presents the particle size distribution of the Al(OH)3, whose mean was 15.5 μm as determined with laser scattering (HORIBA LA-950). The SSA of the particles was found to be 1.3 m2 g−1, determined with Brunauer–Emmett–Teller method (BET, Belsorp-max). Particles were entrained and fed using a fluidised bed feeder designed to operate over the range 1–2 g min−1. Two streams of air were used to control the feeding of the Al(OH)3 particles, one entering through a sintered plate at the bottom of the feeder fluidising the particles, and a second flow passing through a horizontal 5 mm-diameter carrier tube, which is aligned approximately 30 mm below the top of the static particle bed. A 1 mm hole in the upper surface of the carrier tube was used to entrain particles into the carrier tube air flow. The gibbsite mass feed rate was monitored online with weight scales (Kern FKB).2.3 Experimental arrangement
The experimental arrangement is shown in Fig. 3. Measurements were performed with the High-Flux Solar Simulator of ETH Zurich, which comprises an array of 7 high-pressure Xenon arcs, each close-coupled with truncated ellipsoidal specular reflectors. This provides an external source of intense thermal radiation – mostly in the visible and IR spectra – that closely approximates the heat transfer characteristics of highly concentrating solar optical systems. The solar radiative input power,![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) s, was measured optically with a Lambertian target and a calibrated CCD camera.
s, was measured optically with a Lambertian target and a calibrated CCD camera. ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) s was varied over the range 2.1–4.3 kW, which corresponds to mean solar concentration ratios, C, through the aperture in the range 1070–2190 suns (1 sun = 1 kW m−2). Temperatures were measured with type-K thermocouples at locations shown in Fig. 1. A reference nominal reactor temperature, Treactor, was measured with an Al2O3-shielded thermocouple located within the cavity as shown in Fig. 1. The nominal wall temperature, Twall, was calculated as the average of seven thermocouples located on the outside of the Inconel shell (r = 61 mm), covered with insulation, at various z–φ locations: (50 mm, 0°); (115 mm, 0°; 90°; 180°; 270°); (190 mm, 0°; 180°). The total transport air normal flow rate,
s was varied over the range 2.1–4.3 kW, which corresponds to mean solar concentration ratios, C, through the aperture in the range 1070–2190 suns (1 sun = 1 kW m−2). Temperatures were measured with type-K thermocouples at locations shown in Fig. 1. A reference nominal reactor temperature, Treactor, was measured with an Al2O3-shielded thermocouple located within the cavity as shown in Fig. 1. The nominal wall temperature, Twall, was calculated as the average of seven thermocouples located on the outside of the Inconel shell (r = 61 mm), covered with insulation, at various z–φ locations: (50 mm, 0°); (115 mm, 0°; 90°; 180°; 270°); (190 mm, 0°; 180°). The total transport air normal flow rate, ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) air,n, was controlled with electronic flow controllers (Bronkhorst HI-TEC). Dry synthetic air was used as the transport air with normal flow rates,
air,n, was controlled with electronic flow controllers (Bronkhorst HI-TEC). Dry synthetic air was used as the transport air with normal flow rates, ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) air,n, in the range 12.0–20.0 Ln min−1. Additionally, the gibbsite particle nominal residence time, τ, within the reactor was calculated from the cavity volume, V, and the total volumetric flow rate of transport air and gas product,
air,n, in the range 12.0–20.0 Ln min−1. Additionally, the gibbsite particle nominal residence time, τ, within the reactor was calculated from the cavity volume, V, and the total volumetric flow rate of transport air and gas product, ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) air (
air (![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) air,n corrected for reactor temperature). The
air,n corrected for reactor temperature). The ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) air input of the present investigation led to τ = 1.38–3.40 s. The similar value of nominal residence time in the present experimental facility to that of an industrial device despite three orders of magnitude smaller volume is attributed in part to much smaller ratio of the diameter of the inlet pipe to that of the reactor and, in part, to different methods of determining residence time. The Stokes number of the particles was calculated to be, Sk = 0.19, where:37
air input of the present investigation led to τ = 1.38–3.40 s. The similar value of nominal residence time in the present experimental facility to that of an industrial device despite three orders of magnitude smaller volume is attributed in part to much smaller ratio of the diameter of the inlet pipe to that of the reactor and, in part, to different methods of determining residence time. The Stokes number of the particles was calculated to be, Sk = 0.19, where:37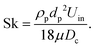 | (2) |
Since Sk ≪ 1, it is reasonable to assume that the residence time of the particles is equal to that of the gas. The Al(OH)3 particles were fed to the reactor with constant feeder conditions at ambient temperature and at mass flow rates, ṁAl(OH)3, in the range 0.55–2.53 g min−1. The particle to air volume fraction, ϕ, was controlled over the range 0.35 × 10–5–1.66 × 10–5 with changes to either ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) air or ṁAl(OH)3, and is defined as:
air or ṁAl(OH)3, and is defined as:
 | (3) |
The product particles were collected in a settling chamber downstream from the reactor. The water vapor concentration in the outlet air, ṁH2O, was measured online, downstream from the settling chamber, with a dew point sensor (Vaisala DMT346). Additionally, for one experimental run the water vapour partial pressure in the reactor was controlled by adding steam to the air flow of the second tangential inlet with an electric steam generator (Bronkhorst F- 201C). The steam was injected with a mass flow rate of ṁsteam = 1.17 g min−1 corresponding to a vapour partial pressure of 68.6 mbar. Measurements were taken at approximately steady-state and isothermal (to within 26 K) conditions, which follows a period of pre-heating to the desired temperature. Operating parameters were averaged over the duration of reactant particle feeding. A summary of the operating conditions of the 19 nominally steady-state experimental runs is provided in Table 1.
| # |
![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) s [W]
s [W] |
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) air,n [Ln min−1]
air,n [Ln min−1] |
ṁ steam [g min−1] | ṁ Al(OH)3 [g min−1] | T reactor [K] | T wall [K] | ϕ [—] | τ [s] |
|---|---|---|---|---|---|---|---|---|
| 1 | 2285 | 20.03 | — | 1.12 | 1259 | 1114 | 0.57 × 10–5 | 1.74 |
| 2 | 2108 | 20.03 | — | 0.73 | 1213 | 1020 | 0.40 × 10–5 | 1.91 |
| 3 | 3642 | 20.03 | — | 0.95 | 1479 | 1246 | 0.43 × 10–5 | 1.56 |
| 4 | 2132 | 20.03 | — | 0.84 | 1226 | 934 | 0.51 × 10–5 | 2.08 |
| 5 | 2316 | 12.03 | — | 1.35 | 1258 | 1122 | 1.13 × 10–5 | 2.81 |
| 6 | 2117 | 12.03 | — | 1.39 | 1161 | 928 | 1.40 × 10–5 | 3.40 |
| 7 | 3773 | 12.03 | — | 1.45 | 1454 | 1272 | 1.07 × 10–5 | 2.47 |
| 8 | 2291 | 20.03 | — | 2.07 | 1230 | 1106 | 1.06 × 10–5 | 1.72 |
| 9 | 2211 | 20.03 | — | 1.33 | 1216 | 977 | 0.77 × 10–5 | 1.97 |
| 10 | 4224 | 20.03 | — | 1.98 | 1421 | 1258 | 0.89 × 10–5 | 1.51 |
| 11 | 3730 | 12.03 | — | 2.32 | 1480 | 1311 | 1.66 × 10–5 | 2.33 |
| 12 | 3383 | 17.03 | — | 1.26 | 1414 | 1227 | 0.68 × 10–5 | 1.84 |
| 13 | 3492 | 12.03 | — | 1.75 | 1408 | 1219 | 1.35 × 10–5 | 2.55 |
| 14 | 4262 | 19.85 | — | 2.53 | 1551 | 1371 | 1.05 × 10–5 | 1.38 |
| 15 | 3766 | 16.03 | — | 1.06 | 1456 | 1254 | 0.60 × 10–5 | 1.92 |
| 16 | 2362 | 16.03 | — | 1.14 | 1208 | 1051 | 0.76 × 10–5 | 2.29 |
| 17 | 2198 | 16.03 | — | 0.55 | 1179 | 943 | 0.41 × 10–5 | 2.58 |
| 18 | 3965 | 20.03 | — | 1.35 | 1459 | 1284 | 0.59 × 10–5 | 1.50 |
| 19 | 3832 | 20.03 | 1.17 | 0.85 | 1439 | 1262 | 0.35 × 10–5 | 1.43 |
2.4 Product characterisation
Representative samples were taken from the collected particles in the settling chamber for post-experimental analyses of the following parameters: the loss on ignition (LoI) determined from the relative mass change during thermogravimetric analysis (TGA, Netzsch STA 409 CD); the particle morphology imaged by scanning electron microscopy (SEM, Philips XL30); the phases present in the sample by X-ray diffraction data (XRD, Rigaku MiniFlex 600 diffractometer), and the product microstructure, which was in turn evaluated by measurement of both SSA with the Brunauer–Emmett–Teller method (BET, Belsorp-max) and pore size distribution with the Barrett–Joyner–Halenda method (BJH, Belsorp-max).Fig. 4 presents the relative mass changes for the reactant Al(OH)3 and for a representative solar-processed sample collected from the settling chamber as a function of the TGA reference temperature, TTGA. This shows that the Al(OH)3 begins to decompose at about 500 K, following which the mass loss increases to a maximum of 34.6 wt% corresponding to the complete conversion of Al(OH)3 to Al2O3. Fig. 4 also shows that a small quantity of adsorbed moisture from the cooled, solar-processed alumina sample is released during its re-heating from ambient temperature to 423 K. The mass of this process can be quantified by the mass “Loss on Ignition” (LoI) in the temperature range: 298–423 K, denoted here as LoIads. The further mass loss of the solar-processed alumina from its heating to higher temperatures corresponds to the mass percentage of unreacted Al(OH)3 in the solar-processed alumina. The LoI over this second range, 423–1273 K is denoted as LoIX, and is used in the present investigation to calculate the overall molar conversion of Al(OH)3 to Al2O3, X, according to:
 | (4) |
3 Results & discussion
3.1 Steady-state operation
The operational conditions for the 19 nominally steady-state experimental runs listed in Table 1 resulted in Treactor = 1161–1551 K and Twall = 928–1371 K.§ The solar energy conversion efficiency, η, of the solar calcination process is defined to account for the energy required for the endothermic calcination process, as well as the sensible heating of the reaction products and the transport air, as follows: | (5) |
Here the sensible heat of the transport air is included in the useful energy because an industrial flash calcination process recovers the majority of such sensible heat through downstream heat exchangers, which are also used to pre-heat the particles. That is, the present solar reactor needs to both heat and react the particles, while they enter an industrial reactor hot. The performance indicators, X and η were measured to be in the range X = 84.8–95.8% and η = 8.8–20.4%, respectively. In terms of product quality parameters, the measured values of loss on ignition of adsorbed moisture were LoIads = 5.9–14.1%, the measured values of SSA were found to be in the range 132.7–226.6 m2 g−1 and the mean pore size was measured to be in the range dpore = 2.54–5.75 nm.
Fig. 5 presents the outputs from a typical experimental run (#9). Plotted are the temporal variations of ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) s, Treactor, Twall, ṁAl(OH)3, and ṁH2O. When the desired Twall was reached and steady temperatures were measured, the particle feeding was turned on. The period, 21–35 min, is considered to be nominally steady-state.
s, Treactor, Twall, ṁAl(OH)3, and ṁH2O. When the desired Twall was reached and steady temperatures were measured, the particle feeding was turned on. The period, 21–35 min, is considered to be nominally steady-state.
3.2 Extent of calcination and efficiency
Fig. 6a presents the dependence of X on Twall for all experimental runs with four different values of![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) air,n. It is evident that the reactor temperature has a controlling influence on the extent of conversion, so that an increase in Twall results in greater X. It can also be seen that a maximum chemical conversion of 95.8% was obtained for Twall = 1371 K. Despite this temperature being within the range typical of industrial flash calciners (1273–1373 K),11 the conversion was below 100%. This can be attributed both to the much smaller scale of the reactor in the present study relative to industrial-scale calciners and to the additional stages in industrial calcination systems, incorporating both particle preheating stages and a holding vessel, which together reduce the temperature rise and/or residence time required for full conversion. Fig. 6b presents the dependence of X on τ for three Twall. This shows that X is increased by an increase in τ, although the influence is relatively weak in comparison with that of Twall. The trend of increasing X with longer τ is also consistent with well-established understanding of the alumina calcination reaction.23,24 The slightly stronger influence of Twall than that of τ is further evident from results of experimental run 14 with Twall = 1371 K, which featured the greatest X despite having the shortest τ = 1.38 s.
air,n. It is evident that the reactor temperature has a controlling influence on the extent of conversion, so that an increase in Twall results in greater X. It can also be seen that a maximum chemical conversion of 95.8% was obtained for Twall = 1371 K. Despite this temperature being within the range typical of industrial flash calciners (1273–1373 K),11 the conversion was below 100%. This can be attributed both to the much smaller scale of the reactor in the present study relative to industrial-scale calciners and to the additional stages in industrial calcination systems, incorporating both particle preheating stages and a holding vessel, which together reduce the temperature rise and/or residence time required for full conversion. Fig. 6b presents the dependence of X on τ for three Twall. This shows that X is increased by an increase in τ, although the influence is relatively weak in comparison with that of Twall. The trend of increasing X with longer τ is also consistent with well-established understanding of the alumina calcination reaction.23,24 The slightly stronger influence of Twall than that of τ is further evident from results of experimental run 14 with Twall = 1371 K, which featured the greatest X despite having the shortest τ = 1.38 s.
Fig. 7 presents the dependence of η on ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) air (corrected for reactor temperature), for four different values of Twall. A maximum energy efficiency of 20.4% was achieved for this reactor. It can be seen that η increases with a reduction in Twall because both the conduction and re-radiation losses depend on the reactor wall temperature. It can also be seen that, for a given value of Twall, η increases with an increase in
air (corrected for reactor temperature), for four different values of Twall. A maximum energy efficiency of 20.4% was achieved for this reactor. It can be seen that η increases with a reduction in Twall because both the conduction and re-radiation losses depend on the reactor wall temperature. It can also be seen that, for a given value of Twall, η increases with an increase in ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) air. This implies that an increase in the flow rate of air and particles causes a greater fraction of the radiation to be absorbed by the reactant and transport air than by the walls, which increases the ratio of useful heat to losses. The values of η for this reactor are low relative to industrial-scale reactors but are comparable with those from other laboratory-scale reactors.16,20 This is because the ratio of internal surface area to internal volume of the reactor decreases with an increase in scale, causing a greater fraction of energy to be absorbed by the reactants and transport air relative to the walls of the reactor, which increases efficiency consistent with the results from Fig. 7. In addition, large scale industrial reactors are designed with heat integration and heat recovery systems to minimise heat losses and maximise efficiency.
air. This implies that an increase in the flow rate of air and particles causes a greater fraction of the radiation to be absorbed by the reactant and transport air than by the walls, which increases the ratio of useful heat to losses. The values of η for this reactor are low relative to industrial-scale reactors but are comparable with those from other laboratory-scale reactors.16,20 This is because the ratio of internal surface area to internal volume of the reactor decreases with an increase in scale, causing a greater fraction of energy to be absorbed by the reactants and transport air relative to the walls of the reactor, which increases efficiency consistent with the results from Fig. 7. In addition, large scale industrial reactors are designed with heat integration and heat recovery systems to minimise heat losses and maximise efficiency.
 | ||
Fig. 7 The energy efficiency, η (defined in eqn (5)), of the present solar calcination reactor as a function of the volumetric flow rate of transport air, ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) air, for four different wall temperatures, Twall. See Table 1 for details. air, for four different wall temperatures, Twall. See Table 1 for details. | ||
3.3 Product quality: residual moisture
Fig. 8 presents the LoIads as a function of ϕ for four different values of Twall. It can be seen that, for each value of Twall, the LoIads increases with ϕ. This can be explained by the increase in the concentration of water vapour, the gas-phase product of the reaction, due to an increase in volumetric loading of particles. That is, an increase in the partial pressure of water vapour in the reactor increases the resistance to the release of water into the gas phase. It can also be seen that Twall has a second order influence on the LoIads, so that the highest Twall = 1311 ± 60 K resulted in the lowest values of LoIads. | ||
| Fig. 8 Mass percentage of adsorbed moisture, LoIads, in the product from the solar reactor as a function of the particle to air volume fraction, ϕ (defined in eqn (3)), for four different wall temperatures, Twall, for experimental runs 1 to 17. | ||
Table 2 presents the influence of the addition of steam (ṁsteam = 1.17 g min−1) to the transport air flow on LoIads, X, and η, with all other operating conditions maintained nominally constant. It can be seen that the additional steam input, resulting in a water vapour partial pressure of 68.6 mbar, has a significant influence on the amount of surface moisture adsorbed by the alumina product, consistent with the trends in Fig. 8. More specifically, the LoIads was found to increase from 5.91% (run #18) to 7.99% (run #19). This can be explained by the increase in the partial pressure of water vapour in the transport air, which inhibits the diffusion of chemically-released water vapour into the gas phase. It also favours an increase in the readsorption of water vapour onto the surface of the alumina particle. For reference, the partial pressure of water vapour generated by the complete combustion of methane with 10% excess air is calculated to be 176.7 mbar, which is more than twice the 68.6 mbar used in the present experiment. Because methane is the dominant component of natural gas, which is the most common fuel used for industrial flash calciners, this implies that removing H2O from combustion by solar calcination has the potential to provide a significant benefit to product quality by reducing the partial pressure of the gas-phase moisture. It can also be noted from Table 2, that the increase of the partial pressure of water vapour has no significant influence on X or η for the present conditions.
| ṁ steam/ṁair | # | LoIads | X | η |
|---|---|---|---|---|
| [—] | [wt%] | [mol%] | [%] | |
| 0 | 18 | 5.91 | 94.5 | 14.0 |
| 0.045 | 19 | 7.99 | 94.0 | 14.2 |
3.4 Product quality: alumina microstructure
Fig. 9 presents SEM micrographs of the solid alumina product from experimental runs (a) #4 (Twall = 934 K), (b) #11 (Twall = 1311 K), (c) #14 (Twall = 1371 K), and (d) #19 (Twall = 1262 K). It is clear that slit-shaped pores have formed in the particles, whose width increases with the value of Twall. From previous work, this can be deduced to result from the calcination reaction mechanism, in which the structural hydroxyls (–OH) that hold gibbsite layers together are released rapidly as water during the calcination process, causing the gibbsite layers to split and form slit-shaped pores.6,39Fig. 10 presents the mean pore diameter, dpore, and the total specific pore volume, Vpore, of the solar processed alumina as a function of X. It can be seen that both dpore and Vpore increase with an increase in X, consistent with both the SEM micrographs (Fig. 9) and the previous assessments for non-solar calcination by Perander et al.6 For X = 95.8%, dpore reaches up to 5.8 nm for run 14. It can also be seen from a comparison with reported mean pore sizes of typical SGAs produced with industrial flash calciners (presented as the open symbols in Fig. 10),28,32,34 the solar process generates larger values of dpore for a given value of X than does the conventional process. Extrapolation suggests that dpore will continue to increase with X, so that solar-processed alumina has potential to achieve a larger mean pore size than the majority of conventionally-processed aluminas, noting the exception for two SGAs with pore size larger than 8 nm. It should also be recalled that the solar-processed alumina has been calcined with residence times in the order of a few seconds. This contrasts the industrial process, which also includes both a preheating stage and a holding vessel to provide additional residence time for pore growth. That is, the solar process generates a higher product quality by this measure than does the conventional processing, indicating potential to improve hydrogen fluoride adsorption capacity in the downstream dry-scrubbing process.
 | ||
| Fig. 10 Mean pore diameter, dpore, and total specific pore volume, Vpore, of the solar-produced aluminas as a function of the extent of chemical conversion, X, for experimental runs 1 to 17. Also shown with open symbols are the typical mean pore diameter of nine SGAs produced with industrial calciners as reported in the literature.28,32,34 | ||
Fig. 11 presents the measured values of SSA for the solar-produced alumina as a function of X. The figure shows that SSA is nearly constant (mostly in the range 168–190 m2 g−1) for lower values of X in the range 85–92%, but then decreases with further increases in X to the minimum of 132.7 m2 g−1 for X = 95.8%. The present values of SSA are significantly greater than previously reported values of SGA produced industrially, as shown in Fig. 11.28 Nevertheless, more data are required before a reliable comparison with the industrial data can be made, owing to the different values of X for the experimental and industrial data, which is associated with the difference in scale of the facilities.
 | ||
| Fig. 11 Specific surface area, SSA, of the present solar-produced aluminas as a function of the extent of chemical conversion, X, for experimental runs 1 to 17. Also shown is the typical X and SSA product quality properties of SGA calcined in an industrial gas suspension calciner.28 | ||
3.5 Product quality: X-ray diffraction analysis
Fig. 12 presents a series of XRD spectra of alumina powder samples produced with different values of Twall, but at constant![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) air,n = 20 Ln min−1 (ϕ = 0.40 × 10–5–1.06 × 10–5). For the case with Twall = 934 K, the presence of unconverted reactant can be seen from the discrete diffraction peaks corresponding to gibbsite, notably from the two peaks of greatest intensity at 2θ = 18.3° and 20.3°. For higher values of Twall the discrete diffraction peaks of gibbsite reduce in intensity and are replaced by the more diffuse diffraction peaks of the transition alumina. The presence of some residual gibbsite in the alumina samples, which each combine many alumina particles, indicates that a fraction of the particles did not reach sufficient temperature for long enough to convert all of the original gibbsite. Given the wide size distribution of the particles, it is likely that the residual gibbsite is preferentially partitioned in the larger particles, which require the longest residence time for complete conversion. However, further work will be required to verify this. For Twall = 1020 K and 1114 K a broad diffuse peak at 2θ = 42.8° can be seen, which corresponds to the χ-Al2O3 phase.23,24,40 For Twall = 1258 K and 1371 K the χ-Al2O3 peak is not present and the dominant diffuse diffraction peaks occur at 2θ = 19.4°, 31.9°, 37.6°, 39.3°, 45.7°, 60.6°, and 66.7° corresponding to γ-Al2O3. This is corroborated by an additional analysis of the samples by Fourier Transform Infrared Spectroscopy (not shown), which found that the spectra from the solar-processed alumina samples are characterised by a broad distribution without sharp peaks. This is consistent with the alumina having a complex disordered structure, which is typical of χ-Al2O3 and γ-Al2O3.41,42 It should also be noted that the XRD results from the two cases with the highest Twall feature small discrete peaks corresponding to α-Al2O3 (2θ = 25.6°, 35.1°, 43.3°, and 57.5°), indicating that the particles reached the temperature at which α-Al2O3 forms (1375–1450 K). Although it is difficult to quantify the relative presence of the transition aluminas due to their diffuse diffraction peaks,6,29 it is clear that γ-Al2O3 is the predominant phase produced during solar calcination, while small amounts of the α-Al2O3 phase were also observed. This is consistent with published results from refinery-produced aluminas, in which the dominant alumina phase is also γ-Al2O3, while α-Al2O3 makes up 2–9% (see Table 3).31 Taken together, these results imply that high temperature solar calcination favours the reaction pathway of χ- to γ- to α-Al2O3 (pathway c23,24,26).
air,n = 20 Ln min−1 (ϕ = 0.40 × 10–5–1.06 × 10–5). For the case with Twall = 934 K, the presence of unconverted reactant can be seen from the discrete diffraction peaks corresponding to gibbsite, notably from the two peaks of greatest intensity at 2θ = 18.3° and 20.3°. For higher values of Twall the discrete diffraction peaks of gibbsite reduce in intensity and are replaced by the more diffuse diffraction peaks of the transition alumina. The presence of some residual gibbsite in the alumina samples, which each combine many alumina particles, indicates that a fraction of the particles did not reach sufficient temperature for long enough to convert all of the original gibbsite. Given the wide size distribution of the particles, it is likely that the residual gibbsite is preferentially partitioned in the larger particles, which require the longest residence time for complete conversion. However, further work will be required to verify this. For Twall = 1020 K and 1114 K a broad diffuse peak at 2θ = 42.8° can be seen, which corresponds to the χ-Al2O3 phase.23,24,40 For Twall = 1258 K and 1371 K the χ-Al2O3 peak is not present and the dominant diffuse diffraction peaks occur at 2θ = 19.4°, 31.9°, 37.6°, 39.3°, 45.7°, 60.6°, and 66.7° corresponding to γ-Al2O3. This is corroborated by an additional analysis of the samples by Fourier Transform Infrared Spectroscopy (not shown), which found that the spectra from the solar-processed alumina samples are characterised by a broad distribution without sharp peaks. This is consistent with the alumina having a complex disordered structure, which is typical of χ-Al2O3 and γ-Al2O3.41,42 It should also be noted that the XRD results from the two cases with the highest Twall feature small discrete peaks corresponding to α-Al2O3 (2θ = 25.6°, 35.1°, 43.3°, and 57.5°), indicating that the particles reached the temperature at which α-Al2O3 forms (1375–1450 K). Although it is difficult to quantify the relative presence of the transition aluminas due to their diffuse diffraction peaks,6,29 it is clear that γ-Al2O3 is the predominant phase produced during solar calcination, while small amounts of the α-Al2O3 phase were also observed. This is consistent with published results from refinery-produced aluminas, in which the dominant alumina phase is also γ-Al2O3, while α-Al2O3 makes up 2–9% (see Table 3).31 Taken together, these results imply that high temperature solar calcination favours the reaction pathway of χ- to γ- to α-Al2O3 (pathway c23,24,26).
| SVR at laboratory-scale | SVR scaled to industrial-scale | |
|---|---|---|
| (a) Operational parameter comparison | ||
![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) s
s
|
5 kW | 50 MW |
| A S/V | 31.9 m−1 | 0.319 m−1 |
| τ | 1.38 s | 138 s |
| Solar-processed alumina (run #14) | Ref. 24, 29 and 33 | Ref. 28 | Ref. 31 | Ref. 32 | Ref. 34 | |
|---|---|---|---|---|---|---|
| (b) Product quality comparison | ||||||
| LoI1273 | 1.20 wt% | 0.7–0.8 wt% | 0.69–0.95 wt% | 0.3–1.5 wt% | 0.72–1.05 wt% | |
| α-Al2O3 content | Small amounts | 3–6 wt% | 2–9 wt% | 2–20 wt% | 3.9–8.1 wt% | |
| Gibbsite content | Small amounts | <0.1 wt% | <0.1 wt% | 0.56–2.65 wt% | ||
| Dominant alumina phase | γ-Al2O3 | γ-Al2O3 | γ-Al2O3 | |||
| SSA | 132.7 m2 g−1 | 73–81 m2 g−1 | 72–80 m2 g−1 | 68–80 m2 g−1 | 68.1–76.1 m2 g−1 | |
| d pore | 5.8 nm | 6.6–8.8 nm | 4.6–5.8 nm | 5.7–11.2 nm | ||
Fig. 13 presents XRD spectra of solar-processed alumina samples produced with a range of values of Twall for ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) air,n = 12 Ln min−1 (ϕ in the range 1.07 × 10–5–1.66 × 10–5). As for Fig. 12, the samples produced at lower temperatures have discrete diffraction peaks corresponding to gibbsite, which also implies the presence of unreacted gibbsite. The general trend is that the intensity of these peaks decreases with an increase in both Twall and X. The exception to this is the alumina sample processed with Twall = 1219 K, which exhibits gibbsite diffraction peaks with lower intensity than those of the two alumina samples processed with higher temperature. It should also be noted from Fig. 13 that the only clearly visible discrete diffraction peaks of gibbsite for the cases with low Twall are those at 2θ angles of 18.3° and 20.3°. In contrast, numerous discrete gibbsite peaks are visible for the alumina samples produced with low values of Twall and larger values of
air,n = 12 Ln min−1 (ϕ in the range 1.07 × 10–5–1.66 × 10–5). As for Fig. 12, the samples produced at lower temperatures have discrete diffraction peaks corresponding to gibbsite, which also implies the presence of unreacted gibbsite. The general trend is that the intensity of these peaks decreases with an increase in both Twall and X. The exception to this is the alumina sample processed with Twall = 1219 K, which exhibits gibbsite diffraction peaks with lower intensity than those of the two alumina samples processed with higher temperature. It should also be noted from Fig. 13 that the only clearly visible discrete diffraction peaks of gibbsite for the cases with low Twall are those at 2θ angles of 18.3° and 20.3°. In contrast, numerous discrete gibbsite peaks are visible for the alumina samples produced with low values of Twall and larger values of ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) air,n (Fig. 12). The evolution of χ-Al2O3 at Twall = 928 K and Twall = 1122 K and the subsequent evolution of γ-Al2O3 is evident for both the lower and higher values
air,n (Fig. 12). The evolution of χ-Al2O3 at Twall = 928 K and Twall = 1122 K and the subsequent evolution of γ-Al2O3 is evident for both the lower and higher values ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) air,n = 12 Ln min−1 and
air,n = 12 Ln min−1 and ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) air,n = 20 Ln min−1. However, diffraction peaks corresponding to the intermediate aluminium oxyhydroxide, boehmite, are also visible in the XRD traces of Fig. 13. The diffraction peaks at 2θ values of 14.5° and 28.2° also correspond to boehmite and are particularly evident from the samples calcined with Twall = 1219 K and 1311 K. For the sample calcined at Twall = 1311 K, the species that can be observed are unreacted gibbsite, boehmite and, most predominantly, γ-Al2O3. This indicates that, under these conditions, the calcination reaction follows both the χ- to γ- to α-Al2O3 pathway (pathway c as in Fig. 12) and the boehmite to γ- to α-Al2O3 pathway (pathway b23,24,26). The same particle size distribution was used throughout the present investigation, suggesting that the boehmite formation is attributable to the increased concentration of water vapour in the immediate presence of the reacting gibbsite particles due to the lower value of
air,n = 20 Ln min−1. However, diffraction peaks corresponding to the intermediate aluminium oxyhydroxide, boehmite, are also visible in the XRD traces of Fig. 13. The diffraction peaks at 2θ values of 14.5° and 28.2° also correspond to boehmite and are particularly evident from the samples calcined with Twall = 1219 K and 1311 K. For the sample calcined at Twall = 1311 K, the species that can be observed are unreacted gibbsite, boehmite and, most predominantly, γ-Al2O3. This indicates that, under these conditions, the calcination reaction follows both the χ- to γ- to α-Al2O3 pathway (pathway c as in Fig. 12) and the boehmite to γ- to α-Al2O3 pathway (pathway b23,24,26). The same particle size distribution was used throughout the present investigation, suggesting that the boehmite formation is attributable to the increased concentration of water vapour in the immediate presence of the reacting gibbsite particles due to the lower value of ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) air,n, which can be deduced to increase ϕ.
air,n, which can be deduced to increase ϕ.
3.6 Projection to a 50 MW solar vortex transport reactor and comparison of the product quality with the conventional process
Table 3a presents the ratio of internal surface area to internal volume of the reactor, AS/V, the thermal input of solar radiation,![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) s, and the nominal particle residence time, τ, for the case of greatest conversion in the present investigation. Predicted values for the 50 MW industrial scale are also shown, where the scale up procedure assumes constant C, constant ϕ, constant input velocity, geometric similarity and constant η (i.e. that ṁAl(OH)3 scales linearly with thermal input). The resulting scale up proportionality relationships are AS/V ∝
s, and the nominal particle residence time, τ, for the case of greatest conversion in the present investigation. Predicted values for the 50 MW industrial scale are also shown, where the scale up procedure assumes constant C, constant ϕ, constant input velocity, geometric similarity and constant η (i.e. that ṁAl(OH)3 scales linearly with thermal input). The resulting scale up proportionality relationships are AS/V ∝ ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) s−1/2 and τ ∝
s−1/2 and τ ∝ ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) s1/2. The assumption of constant input velocity is reasonable because the minimum velocity is set by the need to transport particles, while higher values are undesirable to avoid erosion. The assumption of constant efficiency is conservative because the 100-fold reduction in AS/V with the increase in scale will result in a significant reduction in relative heat losses.43Table 3a shows that, with these assumptions, the constant-velocity scale up results in a 100-fold increase in τ. Even though this represents an over-estimate of the increase in residence time because the scale-up process would also increase the relative diameter of the inlet gas stream, this is more than offset by the addition of the pre-heater and the holding vessel in the industrial process. That is, scale-up can be expected to increase X and/or reduce the value of Treactor relative to the present laboratory-scale investigation.
s1/2. The assumption of constant input velocity is reasonable because the minimum velocity is set by the need to transport particles, while higher values are undesirable to avoid erosion. The assumption of constant efficiency is conservative because the 100-fold reduction in AS/V with the increase in scale will result in a significant reduction in relative heat losses.43Table 3a shows that, with these assumptions, the constant-velocity scale up results in a 100-fold increase in τ. Even though this represents an over-estimate of the increase in residence time because the scale-up process would also increase the relative diameter of the inlet gas stream, this is more than offset by the addition of the pre-heater and the holding vessel in the industrial process. That is, scale-up can be expected to increase X and/or reduce the value of Treactor relative to the present laboratory-scale investigation.
Table 3b presents the parameters used to characterise the product quality for the present alumina product with greatest X (run #14), together with typical properties of SGA produced in industrial flash calciners as reported in the literature.24,28,29,31–34 This shows that the minimum LoI1273 of 1.20% achieved in the present investigation is somewhat higher than the typical value of alumina produced in industrial flash calciners. However, given that extent of conversion increases with τ, it can be deduced that the LoI1273 would decrease to <1% with scale up of the solar reactor, which would comply with industrial requirements.28 Furthermore, the additional incorporation of the preheating stages and holding vessels employed in current industrial processes, which provide sufficient residence time to achieve both a high conversion and a high surface area, can be expected to allow the solar reactor to be operated at lower temperature.28 It can also be seen that the dominant alumina phase of the present solar product is γ-Al2O3 with small amounts of α-Al2O3, which is consistent with that found in industrial processes. However, traces of gibbsite were also found from the XRD in the present samples of calcined solar alumina, which implies a poorer quality than is required for SGA. On the other hand, the SSA of the solar-processed alumina was found to be much higher than typical for SGA, which is consistent with the small scale, since SSA is expected to decrease with an increase in conversion. Of particular note is that the mean pore size of the solar-calcined alumina is in the upper range of industrially-produced alumina. This represents a benefit from solar calcination of alumina over conventional combustion-driven calcination.
4 Conclusions
The first-of-a-kind demonstration of the thermochemical calcination of alumina with concentrated solar thermal radiation has been undertaken with a solar vortex transport reactor. This shows that it is technically possible to calcine alumina without combustion and its concomitant CO2 emissions, at least during those periods when the solar resource is available. The extent of chemical conversion from aluminium hydroxide to aluminium oxide was found to increase with the solar radiative power input, and hence also with the reactor temperature, to a value of up to 95.8% in this small laboratory reactor (4.3 kW of solar radiative power and an average reactor wall temperature of 1371 K). The reactor temperature was found to be the dominant experimental variable controlling the extent of solar calcination. It was also found that an increase in the nominal particle residence time has a secondary influence, also increasing the extent of conversion. Solar energy conversion efficiencies of up to 20.4% were measured for this small scale reactor, on the basis that both the sensible and chemical heat are included as the useful heat, which is consistent with the high level of heat recovery from industrial processes. A higher reactor temperature results in a drop in efficiency, due to greater re-radiation and conduction losses. It is expected, however, that the extent of calcination and energy efficiency will increase with the scale up of a solar vortex transport reactor, allowing for lower reactor temperatures due to the longer particle residence time and relatively lower heat losses associated with larger scale reactors.Product quality assessments of the solar-calcined alumina provide strong evidence that solar calcination can result in improved quality alumina, relative to conventional industrially-calcined alumina. The addition of steam (to a water vapour partial pressure of 68.6 mbar) to the reactor transport gas flow resulted in an increase in the amount of adsorbed moisture (from 5.91% to 7.99%). This implies that the use of solar calcination, which avoids the production of steam by combustion, can reduce the amount of surface-adsorbed moisture in the alumina product (which is deleterious to alumina smelting). Consistent with this, the amount of moisture adsorbed by the alumina surface also depends on the particle to air volume fraction. This is because an increase in the partial pressure of water vapour, resulting from an increase in particle to air volume fraction, was found to inhibit diffusion of the water vapour into the transporting air phase.
The alumina microstructure analysis provided further evidence of the improved product quality from solar calcined alumina. The conditions producing a conversion of 95.8% were associated with a specific surface area of 132.7 m2 g−1 and critically, a mean pore diameter of 5.8 nm. The mean pore size of the solar-produced alumina was found to increase with the extent of conversion and can be expected to increase further with scale-up. The solar-produced aluminas of the present investigation are characterised by a relatively large specific surface area and mesoporous structure (with large pore sizes), which is desirable for increased hydrogen fluoride adsorption required for the downstream dry-scrubbing process in aluminium smelting.
The X-ray diffraction analysis revealed that the alumina produced with concentrated solar thermal energy is typically characterised by a high fraction of γ-Al2O3 phase and a low fraction of α-Al2O3. This is consistent with published results from refinery-produced aluminas. Furthermore, the transition pathway was found to be consistent with that associated with high heating rates.23,24,26 That is, the gibbsite is deduced to primarily decompose via the amorphous χ-alumina before reaching γ-alumina (pathway c of ref. 23, 24 and 26). Significantly, the cases with highest particle volume fraction (ϕ > 10–5), which are associated with greatest partial pressure of water vapour from the calcination reaction, were found to exhibit some decomposition of the gibbsite via boehmite before reaching γ-alumina and higher order transition aluminas.
Nomenclature
| A S | Reactor internal surface area [m2] |
| C | Solar concentration ratio (1 sun = 1 kW m−2) |
| D c | Reactor cavity internal diameter [m] |
| d p | Mean particle diameter [μm] |
| d pore | Mean pore diameter [nm] |
| ΔḢ | Rate of enthalpy change of a species [W] |
Δ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) ° ° | Standard enthalpy of reaction [kJ mol−1] |
| LoI | Loss on ignition [wt%] |
| m | Mass of a species/sample [g] |
| ṁ | Mass flow rate of a species [g min−1] |
| n | Number of moles of a species [mol] |
![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) s
s
| Solar radiative power input [W] |
| r | Radial coordinate [mm] |
| Sk | Stokes number |
| T | Temperature [K] |
| U in | Transport air inlet velocity [m s−1] |
| V | Reactor internal volume [m3] |
| V pore | Total specific pore volume [cm3 g−1] |
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif)
| Total gas volumetric flow rate |
| X | Chemical conversion [mol%] |
| z | Horizontal coordinate [mm] |
| η | Solar energy conversion efficiency [%] |
| θ | XRD incident angle [°] |
| μ | Dynamic viscosity [kg m−1 s−1] |
| ρ | Density [kg m−3] |
| τ | Nominal particle residence time [s] |
| ϕ | Particle to air volume fraction |
| φ | Angular coordinate [°] |
Subscripts
| 1273 | Over the temperature range 573–1273 K |
| ads | Of adsorbed moisture, evaluated over the range 298–423 K |
| air | Of air (making up the transport gas flow) |
| Al(OH)3 | Of aluminium hydroxide (gibbsite) feed particles |
| Al2O3 | Of aluminium oxide (alumina) produced |
| calcination | Of the calcination reaction |
| H2O | Of evolved water vapour |
| n | At normal conditions (273 K, 1 atm) |
| p | Of the particle |
| products | Of the reaction products |
| reactant | Of the reactant |
| reactor | Of the reactor cavity |
| steam | Of additional steam (into the transport gas flow) |
| TGA | Reference TGA temperature |
| wall | Of the reactor wall |
| X | Over the range for determining X, evaluated over the range 423–1273 K |
Superscripts
| T R | Evaluated at reactor cavity temperature |
| o | Evaluated at standard conditions |
Abbreviations
| BET | Brunauer–Emmett–Teller |
| BJH | Barrett–Joyner–Halenda |
| CCD | Charge-coupled device |
| CST | Concentrated solar thermal |
| GHG | Greenhouse gas |
| ISO | International Organization for Standardization |
| SEM | Scanning electron microscope |
| SGA | Smelter grade alumina |
| SSA | Specific surface area |
| TGA | Thermogravimetric analysis |
| XRD | X-ray diffraction |
Acknowledgements
We gratefully acknowledge the financial support by the Swiss State Secretariat for Education, Research and Innovation (Grant No. 16.0183) and the European Union's Horizon 2020 research and innovation programme (Project INSHIP – Grant No. 731287). This program has been supported by the Australian Government through the Australian Renewable Energy Agency (ARENA) program (Grant 1-USO034), and by the Australian Research Council (Grant DP150102230). The views expressed herein are not necessarily the views of the Australian Government, and the Australian Government does not accept responsibility for any information or advice contained herein. We are also grateful for the provision of an Australian Government Research Training Program Scholarship.References
- B. C. McLellan, G. D. Corder, D. P. Giurco and K. N. Ishihara, J. Cleaner Prod., 2012, 32, 32–44 CrossRef.
- J. G. J. Olivier, G. Janssens-Maenhout, M. Muntean and J. A. H. W. Peters, Trends in global CO2 emissions: 2015 report, PBL Netherlands Environmental Assessment Agency, The Hague, European Commission, Joint Research Centre, Ispra, 2015 Search PubMed.
- The International Aluminium Institute, Statistics, http://www.world-aluminium.org/statistics/, (accessed 4 December, 2016).
- K. Kermeli, P.-H. ter Weer, W. Crijns-Graus and E. Worrell, Energy Effic., 2015, 8, 629–666 CrossRef.
- F. Williams and H.-W. Schmidt, Light Met., 2012, 135–140 CAS.
- L. M. Perander, Z. D. Zujovic, T. F. Kemp, M. E. Smith and J. B. Metson, JOM, 2009, 61, 33–39 CrossRef CAS.
- B. E. Raahauge, Light Met., 2015, 73–78 CAS.
- B. Jenkins and C. Bertrand, IFRF Combustion J., 2001 Search PubMed , 200110.
- K. Lovegrove, S. Edwards, N. Jacobson, J. Jordan, J. Petersheim, J. Rutowitz, H. Saddler, M. Watt and J. Wyder, Renewable energy options for Australian industrial gas users, Report ITP/A0142, Australian Renewable Energy Agency, 2015.
- C. Klett and L. Perander, Light Met., 2015, 79–84 CAS.
- T. Eglinton, J. Hinkley, A. Beath and M. Dell'Amico, JOM, 2013, 65, 1710–1720 CrossRef.
- D. Hirsch and A. Steinfeld, Chem. Eng. Sci., 2004, 59, 5771–5778 CrossRef CAS.
- R. Bertocchi, Trans. ASME: J. Sol. Energy Eng., 2002, 124, 230–236 CrossRef CAS.
- L. A. Dombrovsky, W. Lipiński and A. Steinfeld, J. Quant. Spectrosc. Radiat. Transfer, 2007, 103, 601–610 CrossRef CAS.
- D. Mischler and A. Steinfeld, J. Heat Transfer, 1995, 117, 346–354 CrossRef CAS.
- A. Z'Graggen, P. Haueter, D. Trommer, M. Romero, J. C. de Jesus and A. Steinfeld, Int. J. Hydrogen Energy, 2006, 31, 797–811 CrossRef.
- I. Padilla, A. Lopez-Delgado, S. Lopez-Andres, M. Alvarez, R. Galindo and A. J. Vazquez-Vaamonde, Sci. World J., 2014, 2014, 825745 Search PubMed.
- A. Steinfeld, A. Imhof and D. Mischler, Trans. ASME: J. Sol. Energy Eng., 1992, 114, 171–174 CrossRef CAS.
- A. Meier, E. Bonaldi, G. M. Cella, W. Lipiński and D. Wuillemin, Sol. Energy, 2006, 80, 1355–1362 CrossRef CAS.
- V. Nikulshina, M. Halmann and A. Steinfeld, Energy Fuels, 2009, 23, 6207–6212 CrossRef CAS.
- G. Flamant, D. Hernandez, C. Bonet and J.-P. Traverse, Sol. Energy, 1980, 24, 385–395 CrossRef CAS.
- H. P. Wang, B. G. Xu, P. Smith, M. Davies, L. DeSilva and C. Wingate, J. Phys. Chem. Solids, 2006, 67, 2567–2582 CrossRef CAS.
- K. Wefers and C. Misra, Oxides and hydroxides of aluminum, Report 19, Alcoa, 1987.
- B. Whittington and D. Ilievski, Chem. Eng. J., 2004, 98, 89–97 CrossRef CAS.
- B. K. Gan, I. C. Madsen and J. G. Hockridge, J. Appl. Crystallogr., 2009, 42, 697–705 CrossRef CAS.
- V. J. Ingram-Jones, R. C. T. Slade, T. W. Davies, J. C. Southern and S. Salvador, J. Mater. Chem., 1996, 6, 73–79 RSC.
- J. Rouquerol, F. Rouquerol and M. Ganteaume, J. Catal., 1975, 36, 99–110 CrossRef CAS.
- S. Wind and B. E. Raahauge, Light Met., 2013, 155–162 CAS.
- L. M. Perander, Z. D. Zujovic, T. Groutso, M. M. Hyland, M. E. Smith, L. A. O'Dell and J. B. Metson, Can. J. Chem., 2007, 85, 889–897 CrossRef CAS.
- C. Sommerseth, K. S. Osen, C. Rosenkilde, A. J. Meyer, L. T. Kristiansen and T. A. Aarhaug, Light Met., 2012, 827–832 CAS.
- S. Wind, C. Jensen-Holm and B. E. Raahauge, Light Met., 2010, 757–764 Search PubMed.
- L. M. Perander, PhD thesis, The University of Auckland, 2010.
- J. Metson, T. Groutso, M. Hyland and S. Powell, Light Met., 2006, 89–93 CAS.
- L. M. Perander, M. A. Stam, M. M. Hyland and J. B. Metson, Light Met., 2011, 285–290 CAS.
- G. Maag, G. Zanganeh and A. Steinfeld, Int. J. Hydrogen Energy, 2009, 34, 7676–7685 CrossRef CAS.
- J. R. Howell, R. Siegel and M. P. Mengüç, Thermal radiation heat transfer, CRC press, 5th edn, 2011 Search PubMed.
- J. J. Derksen, S. Sundaresan and H. E. A. van den Akker, Powder Technol., 2006, 163, 59–68 CrossRef CAS.
- M. M. Hyland, A. R. Gillespie and J. B. Metson, Light Met., 1997, 113–117 CAS.
- J. de Boer, The structure and properties of porous materials, 1958, pp. 68–94 Search PubMed.
- T. Kogure, J. Am. Ceram. Soc., 2004, 82, 716–720 CrossRef.
- A. Boumaza, L. Favaro, J. Ledion, G. Sattonnay, J. B. Brubach, P. Berthet, A. M. Huntz, P. Roy and R. Tetot, J. Solid State Chem., 2009, 182, 1171–1176 CrossRef CAS.
- L. Favaro, A. Boumaza, P. Roy, J. Lédion, G. Sattonnay, J. Brubach, A. Huntz and R. Tétot, J. Solid State Chem., 2010, 183, 901–908 CrossRef CAS.
- A. Z'Graggen and A. Steinfeld, Int. J. Hydrogen Energy, 2008, 33, 5484–5492 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7gc00585g |
| ‡ The first two authors have contributed equally to this work. |
| § X, η and XRD results are presented as functions of Twall rather than Treactor due to the greater number of thermocouples contributing to the mean measurement and the lesser influence of direct irradiation on the thermocouple reading. |
| This journal is © The Royal Society of Chemistry 2017 |








