Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Selective hydrogenation of CO on Fe3S4{111}: a computational study
Alberto
Roldan
 * and
Nora H.
de Leeuw
* and
Nora H.
de Leeuw
School of Chemistry, Cardiff University, Main Building, Park Place, CF10 3AT, Cardiff, UK. E-mail: roldanmartineza@cardiff.ac.uk
First published on 8th November 2016
Abstract
Fischer–Tropsch (FT) synthesis has been a recursive method to form valuable molecules from syngas. Metal surfaces have been extensively studied as FT catalysts; among them, iron presents several phases under reaction conditions, oxides and carbides, as active sites for the FT and reverse water gas shift reaction. We present CO reduction on an iron sulfide phase with spinel structure, Fe3S4, also considering the pathways where C–O dissociates leaving CHx species on the surface, which may feed longer aliphatic chains via the FT process. We analysed the thermodynamic and kinetic availability of each step leading to O and OH species co-adsorbed on the surface as well as the formation of H2O from the hydrogenation of the alcohol group in the molecule. This detailed analysis led to energy profiles on both active sites of the surface, and we conclude that this Fe3S4 surface is highly selective towards the formation of methanol, in full agreement with experimental results. These findings point out that the C–C bond formation on greigite takes place through a hydroxycarbene FT mechanism.
Introduction
Fischer–Tropsch (FT) synthesis has been the subject of intense investigation for many decades as it gives access to industrially important chemicals from simple inorganic molecules (CO and H2).1–3 It is considered one of the most attractive routes to convert syngas into liquid fuels and chemicals, which consists of mainly paraffins and olefins, and low levels of oxygenates including alcohols, aldehydes, ketones and acids.4 Traditionally, four types of chain growth mechanisms have been proposed: the carbene mechanism,5 the hydoxycarbene mechanism,6 the CO-insertion mechanism,7 and the CH2-insertion mechanism.8The mechanism for methanol synthesis on metal catalysts has been extensively investigated with both experimental9–11 and theoretical methods,11–13 in part because it is considered to be an important alternative fuel for future transportation needs, either for methanol fuel cells or for the on-board generation of H2 for proton-exchange membrane fuel cells.14,15 Comparing the formation enthalpies of methanol and methane, fully reduced compounds, it is obvious that the latter is thermodynamically more favourable and therefore should hinder the formation of methanol. Methane is generated through the C–O bond fission, which may take place in adsorbed intermediate species (CHxO and CHxOH) somewhere along the CO hydrogenation pathway.13,16 Indeed, minor CHx species have been detected in methanol decomposition on metal surfaces, particularly at high pressures,17 while they may desorb rather than react under ultra-high vacuum conditions.18 Among the catalysts containing metals, iron-based catalysts have considerable merits due to their potential activity for the water–gas shift (WGS) reaction as well as their high FT activity and low cost.3,19 The catalytic performance of these catalysts have been examined drawing the conclusion that several carbide and oxide phases are present under working conditions, among them Fe3O4.20–25
A sulfide isomorphic to Fe3O4, greigite, has recently showed low turnover to electro-reduce CO2 to small molecules, methanol among them.26 However, the presence of S on FT catalysts has been considered as a poison, which raises the queries of the actual mechanism and the role of sulfur in the sulfide catalysts. In this work, we account for the lack of CH4 in the experimental analysis and provide evidence of the selectivity of Fe3S4 between hydrogenation pathways from CO to CH3OH and CHx on the surface, for this is crucial to complete and understand the intricate reaction networks that can be intercrossed at any stage of the reaction.
Computational details
Periodic plane-wave DFT calculations were performed using the Vienna ab initio simulation package (VASP),27,28 the Perdew–Wang 91 functional29 within the spin interpolation formula of Vosko et al.,30 and a kinetic energy of 600 eV to expand the plane-waves of the Kohn–Sham valence states.31 The inner electrons were represented by the projector-augmented wave (PAW) pseudopotentials considering also non-spherical contributions from the gradient corrections.32 All the calculations include the long-range dispersion correction approach by Grimme,33 which is an improvement on pure DFT when considering large polarizable atoms.34–39 We have used the global scaling factor parameter optimized for PBE, (s6 = 0.75). The optimisation thresholds were 10−5 eV and 0.03 eV Å−1 for the electronic and ionic relaxation, respectively. The Brillouin zone was sampled by a Γ-centred k-point mesh generated through a Monkhorst–Pack grid of 5 × 5 × 1 k-points, which ensures electronic and ionic convergence.40 In order to improve the convergence of the Brillouin-zone integrations, partial occupancies were determined using the tetrahedron method with Blöch corrections smearing with a set width for all calculations of 0.02 eV.The greigite unit cell consists of eight Fe3S4 subunits with a cubic lattice parameter of ∼9.8 Å (ref. 41 and 42) which is close to the calculated parameter resulting from the cell optimization (9.671 Å). The inverse thio-spinel arrangement is reflected by the formula AB2S4, where there are two possible locations for the Fe ions: tetrahedral sites (A), filled by Fe3+ ions, and octahedral sites (B), where both Fe3+ and Fe2+ ions co-exist.43–49 The initial magnetic moment of the slab was described by a high spin distribution in both types of Fe with antiparallel orientation as reported previously,50,51 which results in a ferromagnetic material.43,44,46–48,52–54 For an accurate treatment of the electron correlation in the localized d-Fe orbital, we have used the U approximation55,56 (Ueff = 1 eV),49,54,57 which improves the description of localized states in this type of systems where standard LDA and GGA functionals fail.58 The orbital spin-splitting in the valence region results in localized outermost 3d-electrons and in ordered magnetism45,59,60 in good agreement with experimental evidence.50,51 We have prepared the Fe3S4{111} surface as a slab model by cutting the bulk structure with the METADISE code,61 which considers periodicity in the plane direction and provides the atomic layer stacking resulting in non-dipolar reconstructions.62 The slab contains 56 atoms (24 Fe and 32 S) per unit cell exposing an area of 81.0 Å2 and a thickness of sufficient size to relax the two uppermost layers (four Fe3S4 units), keeping the bulk structure frozen at the bottom. We added a vacuum width of 12 Å between periodic slabs, big enough to avoid interaction between periodic images. The molecules in the gas phase were relaxed in an asymmetric box of 15 × 16 × 17 Å3.
We employed the improved dimer method (IDM), to find the transition states.63,64 We defined the adsorption energy as the difference between the isolated species and the combined system. The activation energy (EA) of a certain step is the energy required to surmount the potential barrier characteristic of the transition state. We have defined this energy barrier as the difference between the initial state and transition state energy for the forward process. The reaction energy (ER) of each step is calculated as the total energy difference between the final state (product(s)) and the initial state (reactant(s)).
Results and discussion
Greigite (Fe3S4) is an inverse spinel-structured material whose particles produced in hydrothermal synthesis expose {001} and {111} surfaces.26 We focused on the active {111} surface and, due to the presence of non-equivalent Fe ions, it has two distinct terminations depending on the relative FeA position with respect to the uppermost sulfur layer. The most stable termination contains two adsorption sites, FeA and FeB, originally occupying tetrahedral and octahedral bulk positions.65 The top S layer has a bulk-like structure consisting of rows along the [0−11] direction with rhombohedral packing.We have explored the adsorption of reactants and products on Fe3S4{111}. While CO adsorbs on FeA and FeB with a binding energy of −0.68 and −1.07 eV respectively, the adsorption of CH3OH is 20% weaker and CH4 does not chemisorb. Hence, all the CH4 molecules produced from the CO reduction will desorb from the surface leading to an overall exothermic process driven by the production of H2O. The co-adsorption of CO and four H ad-atoms is also higher in energy than adsorbed CH3OH (ΔE = 0.6 eV), indicating a favourable process.
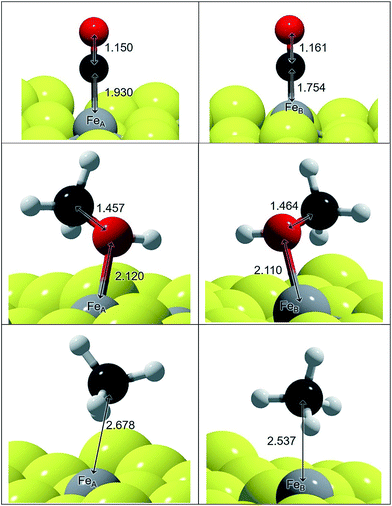
We have represented the optimised structures of CO and CH3OH in Fig. 1 and displayed the C–O and Fe–C distances. The C–O distances in the adsorbed states on FeA and FeB are 1–2% longer than in isolated CO and CH3OH molecules respectively. The molecules are placed practically on top of the metal sites at a distance according to their binding energy: the distances on FeA are longer than on FeB, indicating a weaker bond. The elongation of the C–O bond is also reflected in the νC–O stretching mode, which changes by ∼100 and ∼50 cm−1 for CO and CH3OH respectively compared to the gas phase molecules.
While the redox property of the surface determines the capacity to transfer electrons to the adsorbates, the acid–base character controls the gain and loss of hydrogens and therefore the yields of hydrogenation products. We have explored the co-adsorption and reaction of CO and H ad-atoms on the Fe3S4{111} surface leading to competition between hydrogenation and C–O fission.
The adsorption of these species on transition metal surfaces has been previously investigated leading to a wide range of data. Using a similar methodology to the one we employed here, CO adsorption is reported between −0.23 and −3.21 eV (corresponding to Cu and Pd respectively),13 while on oxides such as Fe3O4{111} the adsorption energies are −1.09 and −1.94 eV on FeA and FeB respectively,66 which are stronger than on the sulfide counterpart. These reports also indicated a C–O stretching red-shift, in agreement with our calculations, except that on pure metals it is considerably lower (∼1900 cm−1).12 Methanol adsorbs on top of fcc metals with an ideal surface releasing ∼0.5 eV, while methoxy was found to be unstable on Pt{111}.67,68 On Fe3O4{111}, the adsorption of CH3OH is weaker than of CO, which is similar to what we found on the thio-spinel, Fe3S4{111}, where the EB difference between CH3OH and CO is ∼0.1 eV.17 This is due to the fact that Fe3O4 is reluctant to modify its electronic structure while the sulfide has a milder ionic character.50
Adsorption of HxCOH and HxCO surface species (x = 0–3)
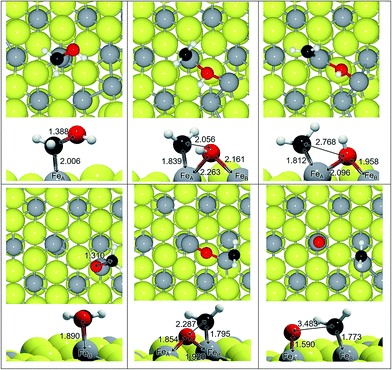
We have adsorbed the species involved in the generation of CH3OH and characterised the most stable configurations (see Table 1). We found progressive changes between the different species along the reduction process: (i) the C–O distance increases by 0.3 Å, which on average is only 0.06 Å shorter in HxCO than in the HxCOH species (∼1.392 Å), (ii) the Fe–C distance also increases by >1 Å, and (iii) the C–O stretching vibrational mode shifts by ∼1000 cm−1. All these changes are related to the change in carbon orbital hybridisation from sp1 to sp3. It is noticed that the saturation of the C by hydrogens makes the molecule bind to the surface through the O(H). This implies charge transfer from the surface and makes the distances and frequencies lay slightly out from the trend line, as in the case of H2CO (q = −0.5e) and more drastically in the Fe–C distance for the methoxy bonded through the oxygen (q = −0.35e). The relative stability of the intermediates is expressed in Table 1 by the energy difference between the intermediate in question, and the CO with the corresponding number of hydrogens on the Fe3S4{111} surface. It shows that although the formation of CH3OH is thermodynamically favourable, there are less favourable intermediates making the process less likely, especially on FeA.| Label | Adsorbate | Site | ΔE (eV) | d C–O (Å) | d Fe–C (Å) | ν C–O (cm−1) |
|---|---|---|---|---|---|---|
| a1 | CO | FeA | 0.00 | 1.157 | 1.864 | 2049 |
| a2 | HCO | 0.55 | 1.201 | 1.940 | 1747 | |
| a3 | HCOH | 0.79 | 1.319 | 1.822 | 1273 | |
| a4 | H2CO | 1.30 | 1.443 | 2.006 | 895 | |
| a5 | H2COH | 0.20 | 1.388 | 2.006 | 1131 | |
| a6 | H3CO | 0.01 | 1.446 | 3.550 | 962 | |
| a7 | H3COH | −0.55 | 1.457 | 3.132 | 962 | |
| b1 | CO | FeB | 0.00 | 1.163 | 1.749 | 2026 |
| b2 | HCO | 0.63 | 1.178 | 1.763 | 1940 | |
| b3 | HCOH | 0.89 | 1.330 | 1.781 | 1265 | |
| b4 | H2CO | 0.07 | 1.131 | 2.054 | 1288 | |
| b5 | H2COH | 0.55 | 1.396 | 1.997 | 1119 | |
| b6 | H3CO | −0.16 | 1.406 | 3.017 | 1085 | |
| b7 | H3COH | −0.57 | 1.464 | 2.981 | 944 |
Although the CH3OH formation from CO is still a matter of discussion, it is well documented on fcc metals. Cu showed good catalytic performance to reduce CO though most of the reaction intermediates (those in Table 1) adsorb weakly or endothermically.69 This is not the case for heavier metals, of which the general trend is that adsorption weakens in line with the C-orbitals hybridisation,13i.e. the greater hybridisation the weaker the adsorption. The geometrical changes taking place on the different species, such as the increase in bond length and red-shift of the C–O stretching vibrational mode, are also common features.12
Dissociation of HxCOH and HxCO species (x = 0–3)
We have studied the C–O scission of each intermediate species lying on FeA and FeB taking into account that the products may be displaced to a nearby Fe site; for instance, the C–O splitting of H2COH adsorbed on FeA, leads to CH2 remaining on FeA while OH binds both FeA and FeB, see Fig. 2. Once the C–O bond is completely dissociated, the CHx species lie an average of 0.4 Å closer to Fe than before dissociation. This short distance is also a consequence of the electrophilic character of the co-adsorbed O and OH groups, which withdraw electrons from nearby atoms; a co-adsorbed O ad-atom makes the Fe–C distance 0.09 Å shorter than a co-adsorbed hydroxyl on FeA, while it remains practically invariable on FeB (ΔdFe–C = 0.01 Å).Table 2 summarises the activation and reaction energies for the direct C–O scission. On FeA sites, the reaction energy (ER) related to C–O bond breaking is (i) endothermic (ER > 1 eV) for a2, a3 and a5 species, (ii) slightly endothermic (0 < ER > 1 eV) for methoxy (a6), and (iii) exothermic (ER < 0 eV) for formaldehyde (a4) and methanol (a7). Nevertheless, the high energy barriers indicate that the process is kinetically hindered and the C–O scission is unlikely; the lowest EA is for H2CO but still above 1 eV. The electronic and geometrical differences between sites make FeB behave differently: the process is endothermic for all the intermediates and ER is lower than 1 eV only for H3COH, while all the energy barriers are well above 1.5 eV.
| Label | Site | Reactants → products | E A (eV) | E R (eV) |
|---|---|---|---|---|
| R1 | FeA | HCO → CH + O | 3.91 | 2.08 |
| R2 | HCOH → CH + OH | 2.79 | 1.56 | |
| R3 | H2CO → CH2 + O | 1.27 | −0.55 | |
| R4 | H2COH → CH2 + OH | 1.84 | 1.50 | |
| R5 | H3CO → CH3 + O | 2.46 | 0.48 | |
| R6 | H3COH → CH3 + OH | 1.87 | −0.19 | |
| R7 | FeB | HCO → CH + O | 4.34 | 3.48 |
| R8 | HCOH → CH + OH | 1.72 | 1.69 | |
| R9 | H2CO → CH2 + O | 2.97 | 2.56 | |
| R10 | H2COH → CH2 + OH | 2.17 | 1.02 | |
| R11 | H3CO → CH3 + O | 2.52 | 1.72 | |
| R12 | H3COH → CH3 + OH | 2.32 | 0.69 |
The energy data in Table 2 shows that breaking the C–O bond is unfavourable under mild conditions. Although the activation and reaction energies have been found to be much smaller on pure metallic systems such as Pd{111},13 they follow a similar trend, showing the C–O splitting to be more favourable on HCOH and H2COH intermediates.
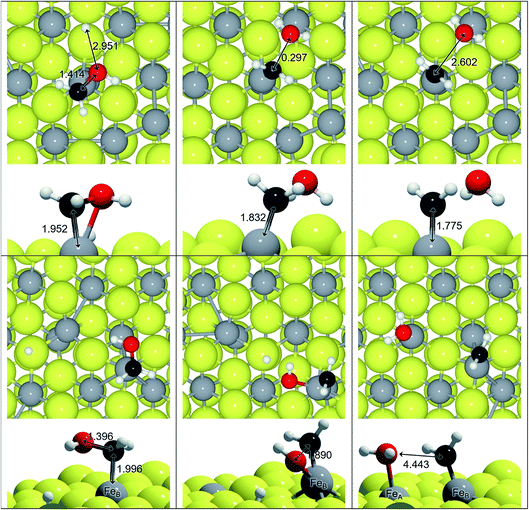
We have explored an alternative mechanism for C–O bond breaking driven by H2O generation, which is schematically represented in Fig. 3. Table 3 contains the activation and reaction energies for that process on FeA and FeB, respectively. The energy trends show decreasing values as the number of hydrogens in the molecule is increased, i.e. the C-orbital hybridisation changes from sp1 to sp3. In spite of this, the process is endothermic and kinetically unfavourable.
| Site | Reactants → products | E A (eV) | E R (eV) | |
|---|---|---|---|---|
| R13 | FeA | HCOH + H → CH + H2O | 1.71 | 0.77 |
| R14 | H2COH + H → CH2 + H2O | 0.93 | 0.72 | |
| R15 | H3COH + H → CH3 + H2O | 1.75 | −0.22 | |
| R16 | FeB | HCOH + H → CH + H2O | 2.46 | 2.06 |
| R17 | H2COH + H → CH2 + H2O | 1.75 | 0.63 | |
| R18 | H3COH + H → CH3 + H2O | 1.98 | −0.15 |
Among the different reaction mechanisms explored, only R3 and R6 are exothermic. Despite this, they are kinetically disabled and therefore the presence of CHx groups should be very scarce on Fe3S4{111}. Fig. 4 shows the energy profile for the reduction of CO to methanol (black lines) and the different paths studied describing the C–O dissociations for the direct and H2O driven pathways (red and blue lines, respectively). Most of these pathways are hindered by the high energy barrier, however, we noticed that for HxCO(H) species with x > 2, the dissociation of the C–O bond requires the same or less energy than some steps undertaken during the CO reduction. Therefore, if the system has enough energy to overcome the barrier of producing HxCO(H) intermediates, the C–O dissociation is accessible and some pathways become competitive, e.g. R4, R6, R11, R12, R14, R15, R17 and R18.
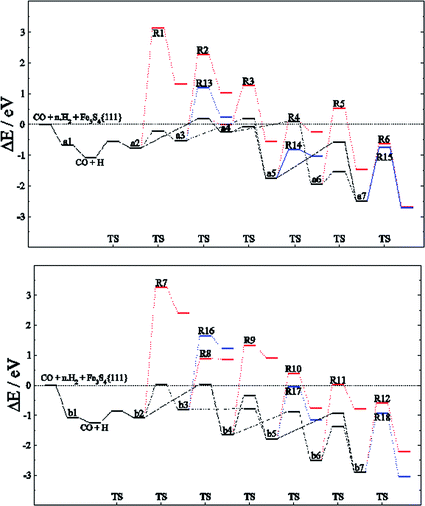 | ||
| Fig. 4 Energy profile for the reduction mechanism of CO to CH3OH (black line) on FeA (top) and FeB (bottom) sites of Fe3S4{111} considering the direct scission of C–OHx bond (red line) and its dissociation assisted by an H ad-atom leading to H2O (blue line). Intermediates and C–O dissociation reactions are labelled according to Tables 1–3. | ||
The reaction network for CH3OH formation on FeA may take place through HxCO and HxCOH intermediates; nonetheless, the path for the formation of a6 from a4 requires more energy to overcome the transition energy than that leading to a5. However, R14 is more kinetically feasible leading to CHx + H2O, although the process is thermodynamically unfavourable. Thus, a5 (H2COH) is crucial for the production of methanol, the desorption of which is >1 eV below the H3C–OH scission energy barriers. On the other hand, the C–O dissociations on FeB have a higher energy barrier: the stabilisation of b4 means that both H3CO and H3COH will be formed, the latter desorbing from the catalyst prior to dissociation. These results are in full agreement with the fact that CH4 molecules were not detected during the experiments using gas-chromatography and 1H-NMR techniques.26
Conclusions
We have studied systematically the competitive reactions of CO hydrogenation and C–O dissociation on both adsorption sites, FeA and FeB, of Fe3S4{111}. All the calculations were performed using DFT+U, including the long-range dispersion forces. We found a correlation of the C–O bond strength with the C orbital hybridization according to the bond distances and vibrational analysis, which is similar to the trends reported on metals and metal oxides. The examination of relative energies between the reactants and intermediates showed that although the reactions leading to the formation of methanol and methane are thermodynamically favorable, driven by the high energy of the H2 molecules (and the formation of H2O), it is necessary to overcome a reaction barrier. There are intermediates of higher energy, HCOH and H2CO, that determine the formation of products, especially on FeA. The lower energy reaction pathway leads exclusively to methanol through HCOH on FeA while both the HCOH and H2CO intermediates are of competing stability in the reaction mechanism on FeB. Thus, the C–O scission is generally an endothermic or kinetically disabled process under mild conditions on Fe3S4{111}; for this reason, this surface presents a selective CO reduction towards a low level of oxygenated molecules while iron oxides may lead to totally reduced molecules.Acknowledgements
We acknowledge the Engineering & Physical Sciences Research Council (grant EP/K035355/1 and EP/K035355/2) for funding. This work made use of the ARCHER facilities, the UK's national high-performance computing service, which is provided by UoE HPCx Ltd at the University of Edinburgh, Cray Inc. and NAG Ltd, funded by the Office of Science and Technology through EPSRC's High End Computing Programme and provided via our membership of the HPC Materials Chemistry Consortium (EPSRC EP/L000202). The authors also acknowledge the use of the UCL Legion High Performance Computing Facility and the Advanced Research Computing @ Cardiff (ARCCA) at Cardiff University, and associated support services, in the completion of this work. All data created during this research is openly available from the University of Cardiff Research Portal at http://doi.org/10.17035/d.2016.0011347963.References
- C. K. Rofer-DePoorter, Chem. Rev., 1981, 81, 447–474 CrossRef CAS.
- J. J. C. Geerlings, J. H. Wilson, G. J. Kramer, H. P. C. E. Kuipers, A. Hoek and H. M. Huisman, Appl. Catal., A, 1999, 186, 27–40 CrossRef CAS.
- M. E. Dry, Catal. Today, 2002, 71, 227–241 CrossRef CAS.
- A. Y. Khodakov, W. Chu and P. Fongarland, Chem. Rev., 2007, 107, 1692–1744 CrossRef CAS PubMed.
- F. Fischer and H. Tropsch, Ber. Dtsch. Chem. Ges., 1926, 59, 830–831 CrossRef.
- J. T. Kummer and P. H. Emmett, J. Am. Chem. Soc., 1953, 75, 5177–5183 CrossRef CAS.
- A. Y. Krylova, Solid Fuel Chem., 2014, 48, 22–35 CrossRef CAS.
- P. M. Maitlis, R. Quyoum, H. C. Long and M. L. Turner, Appl. Catal., A, 1999, 186, 363–374 CrossRef CAS.
- I. A. Fisher and A. T. Bell, J. Catal., 1997, 172, 222–237 CrossRef CAS.
- J. Nerlov and I. Chorkendorff, J. Catal., 1999, 181, 271–279 CrossRef CAS.
- M. Behrens, F. Studt, I. Kasatkin, S. Kühl, M. Hävecker, F. Abild-Pedersen, S. Zander, F. Girgsdies, P. Kurr, B.-L. Kniep, M. Tovar, R. W. Fischer, J. K. Nørskov and R. Schlögl, Science, 2012, 336, 893 CrossRef CAS PubMed.
- L. C. Grabow and M. Mavrikakis, ACS Catal., 2011, 1, 365–384 CrossRef CAS.
- R. García-Muelas, Q. Li and N. López, ACS Catal., 2015, 5, 1027–1036 CrossRef.
- A. K. Avcı, Z. İ. Önsan and D. L. Trimm, Top. Catal., 2003, 22, 359–367 CrossRef.
- D. R. Palo, R. A. Dagle and J. D. Holladay, Chem. Rev., 2007, 107, 3992–4021 CrossRef CAS PubMed.
- S. Lin, J. Ma, X. Ye, D. Xie and H. Guo, J. Phys. Chem. C, 2013, 117, 14667–14676 CAS.
- M. Baumer, J. Libuda, K. M. Neyman, N. Rosch, G. Rupprechter and H.-J. Freund, Phys. Chem. Chem. Phys., 2007, 9, 3541–3558 RSC.
- S. K. Desai, M. Neurock and K. Kourtakis, J. Phys. Chem. B, 2002, 106, 2559–2568 CrossRef CAS.
- D. Santos-Carballal, A. Roldan, R. Grau-Crespo and N. H. de Leeuw, Phys. Chem. Chem. Phys., 2014, 16, 21082–21097 RSC.
- M. D. Shroff, D. S. Kalakkad, K. E. Coulter, S. D. Kohler, M. S. Harrington, N. B. Jackson, A. G. Sault and A. K. Datye, J. Catal., 1995, 156, 185–207 CrossRef CAS.
- R. J. O'Brien, L. Xu, R. L. Spicer and B. H. Davis, Energy Fuels, 1996, 10, 921–926 CrossRef.
- Q.-L. Hao, F.-X. Liu, H. Wang, J. Chang, C.-H. Zhang, L. Bai, H.-W. Xiang, Y.-W. Li, F. Yi and B.-F. Xu, J. Mol. Catal. A: Chem., 2007, 261, 104–111 CrossRef CAS.
- M. Ding, Y. Yang, J. Xu, Z. Tao, H. Wang, H. Wang, H. Xiang and Y. Li, Appl. Catal., A, 2008, 345, 176–184 CrossRef CAS.
- M. Luo, H. Hamdeh and B. H. Davis, Catal. Today, 2009, 140, 127–134 CrossRef CAS.
- L. A. Cano, M. V. Cagnoli, J. F. Bengoa, A. M. Alvarez and S. G. Marchetti, J. Catal., 2011, 278, 310–320 CrossRef CAS.
- A. Roldan, N. Hollingsworth, A. Roffey, H. U. Islam, J. B. Goodall, C. R. Catlow, J. A. Darr, W. Bras, G. Sankar, K. B. Holt, G. Hogarth and N. H. de Leeuw, Chem. Commun., 2015, 51, 7501–7504 RSC.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- N. D. Mermin, Phys. Rev., 1965, 137, 1441–1443 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. Irrera, A. Roldan, G. Portalone and N. H. De Leeuw, J. Phys. Chem. C, 2013, 117, 3949–3957 CAS.
- N. Y. Dzade, A. Roldan and N. H. de Leeuw, J. Chem. Phys., 2013, 139, 124708 CrossRef CAS PubMed.
- S. S. Tafreshi, A. Roldan, N. Y. Dzade and N. H. de Leeuw, Surf. Sci., 2014, 622, 1–8 CrossRef CAS.
- S. Haider, A. Roldan and N. H. de Leeuw, J. Phys. Chem. C, 2013, 118, 1958–1967 Search PubMed.
- N. Dzade, A. Roldan and N. de Leeuw, Minerals, 2014, 4, 89–115 CrossRef CAS.
- F. Zhang, J. D. Gale, B. P. Uberuaga, C. R. Stanek and N. A. Marks, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 054112–054117 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- J. M. D. Coey, M. R. Spender and A. H. Morrish, Solid State Commun., 1970, 8, 1605–1608 CrossRef CAS.
- M. R. Spender, J. M. D. Coey and A. H. Morrish, Can. J. Phys., 1972, 50, 2313–2326 CrossRef CAS.
- D. J. Vaughan and J. A. Tossell, Phys. Chem. Miner., 1983, 9, 253–262 CrossRef CAS.
- D. J. Vaughan and J. A. Tossell, Am. Mineral., 1981, 66, 1250–1253 CAS.
- D. J. Vaughan and J. R. Craig, Am. Mineral., 1985, 70, 1036–1043 CAS.
- K. K. Surerus, M. C. Kennedy, H. Beinert and E. Munck, Proc. Natl. Acad. Sci. U. S. A., 1989, 86, 9846–9850 CrossRef CAS.
- M. J. Dekkers, H. F. Passier and M. A. A. Schoonen, Geophys. J. Int., 2000, 141, 809–819 CrossRef.
- M. J. Dekkers and M. A. A. Schoonen, Geophys. J. Int., 1996, 126, 360–368 CrossRef.
- L. Chang, B. D. Rainford, J. R. Stewart, C. Ritter, A. P. Roberts, Y. Tang and Q. W. Chen, J. Geophys. Res.: Solid Earth, 2009, 114, 1–10 Search PubMed.
- A. Roldan, D. Santos-Carballal and N. H. de Leeuw, J. Chem. Phys., 2013, 138, 204712–204716 CrossRef CAS PubMed.
- D. Santos-Carballal, A. Roldan, R. Grau-Crespo and N. H. de Leeuw, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 195106 CrossRef.
- D. J. Vaughan and M. S. Ridout, J. Inorg. Nucl. Chem., 1971, 33, 741–746 CrossRef.
- M. Braga, S. K. Lie, C. A. Taft and W. A. Lester, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 10837–10851 CrossRef CAS.
- L. Chang, A. P. Roberts, Y. Tang, B. D. Rainford, A. R. Muxworthy and Q. Chen, J. Geophys. Res., 2008, 113, 1–16 CrossRef.
- V. I. Anisimov, M. A. Korotin, J. Zaanen and O. K. Andersen, Phys. Rev. Lett., 1992, 68, 345–348 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- A. J. Devey, R. Grau-Crespo and N. H. de Leeuw, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 195126–195133 CrossRef.
- I. D. R. Moreira, F. Illas and R. L. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 155102–155116 CrossRef.
- D. J. Vaughan and J. A. Tossell, Am. Mineral., 1981, 66, 1250–1253 CAS.
- D. Rickard and G. W. Luther, Chem. Rev., 2007, 107, 514–562 CrossRef CAS PubMed.
- G. W. Watson, E. T. Kelsey, N. H. deLeeuw, D. J. Harris and S. C. Parker, J. Chem. Soc., Faraday Trans., 1996, 92, 433–438 RSC.
- P. W. Tasker, J. Phys. C: Solid State Phys., 1979, 12, 4977–4984 CrossRef CAS.
- G. Henkelman and H. Jonsson, J. Chem. Phys., 1999, 111, 7010–7022 CrossRef CAS.
- A. Heyden, A. T. Bell and F. J. Keil, J. Chem. Phys., 2005, 123, 224101–224115 CrossRef PubMed.
- A. Roldan and N. H. de Leeuw, Proc. R. Soc. London, Ser. A, 2016, 472 Search PubMed.
- G. S. Parkinson, Surf. Sci. Rep., 2016, 71, 272–365 CrossRef CAS.
- B. A. Sexton, Surf. Sci., 1981, 102, 271–281 CrossRef CAS.
- E. M. Karp, T. L. Silbaugh, M. C. Crowe and C. T. Campbell, J. Am. Chem. Soc., 2012, 134, 20388–20395 CrossRef CAS PubMed.
- A. A. Peterson, F. Abild-Pedersen, F. Studt, J. Rossmeisl and J. K. Norskov, Energy Environ. Sci., 2010, 3, 1311–1315 CAS.
| This journal is © The Royal Society of Chemistry 2017 |