Holistic computational structure screening of more than 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h2_char_2009.gif) 000 candidates for solid lithium-ion conductor materials†
000 candidates for solid lithium-ion conductor materials†
Austin D.
Sendek
 a,
Qian
Yang
b,
Ekin D.
Cubuk
c,
Karel-Alexander N.
Duerloo
c,
Yi
Cui
c and
Evan J.
Reed
*c
a,
Qian
Yang
b,
Ekin D.
Cubuk
c,
Karel-Alexander N.
Duerloo
c,
Yi
Cui
c and
Evan J.
Reed
*c
aDepartment of Applied Physics, Stanford University, Stanford, CA 94305, USA
bInstitute for Computational and Mathematical Engineering, Stanford University, Stanford, CA 94305, USA
cDepartment of Materials Science and Engineering, Stanford University, Stanford, CA 94305, USA. E-mail: evanreed@stanford.edu
First published on 1st December 2016
Abstract
We present a new type of large-scale computational screening approach for identifying promising candidate materials for solid state electrolytes for lithium ion batteries that is capable of screening all known lithium containing solids. To be useful for batteries, high performance solid state electrolyte materials must satisfy many requirements at once, an optimization that is difficult to perform experimentally or with computationally expensive ab initio techniques. We first screen 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831 lithium containing crystalline solids for those with high structural and chemical stability, low electronic conductivity, and low cost. We then develop a data-driven ionic conductivity classification model using logistic regression for identifying which candidate structures are likely to exhibit fast lithium conduction based on experimental measurements reported in the literature. The screening reduces the list of candidate materials from 12
831 lithium containing crystalline solids for those with high structural and chemical stability, low electronic conductivity, and low cost. We then develop a data-driven ionic conductivity classification model using logistic regression for identifying which candidate structures are likely to exhibit fast lithium conduction based on experimental measurements reported in the literature. The screening reduces the list of candidate materials from 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831 down to 21 structures that show promise as electrolytes, few of which have been examined experimentally. We discover that none of our simple atomistic descriptor functions alone provide predictive power for ionic conductivity, but a multi-descriptor model can exhibit a useful degree of predictive power. We also find that screening for structural stability, chemical stability and low electronic conductivity eliminates 92.2% of all Li-containing materials and screening for high ionic conductivity eliminates a further 93.3% of the remainder. Our screening utilizes structures and electronic information contained in the Materials Project database.
831 down to 21 structures that show promise as electrolytes, few of which have been examined experimentally. We discover that none of our simple atomistic descriptor functions alone provide predictive power for ionic conductivity, but a multi-descriptor model can exhibit a useful degree of predictive power. We also find that screening for structural stability, chemical stability and low electronic conductivity eliminates 92.2% of all Li-containing materials and screening for high ionic conductivity eliminates a further 93.3% of the remainder. Our screening utilizes structures and electronic information contained in the Materials Project database.
Broader contextWith the model and results presented herein, we present a new approach for the discovery of solid electrolytes with the potential to identify the next generation of high-performance LIB solid electrolytes from thousands of candidates. The development of new solid electrolytes could ease a plethora of concerns over the safety, stability, energy density, and cycle life of commercial LIBs. Additionally, the development of new solid electrolytes could facilitate the development of structural batteries for the weight- and volume-sensitive applications of electric aircraft and spacecraft. Furthermore, this screening approach allows for inclusion of additional requirements, including environmental concerns like earth abundance. The potential impact of a highly stable new solid material with liquid-like lithium conduction cannot be overstated: solid-state LIBs stand to improve on the safety, performance, and lifetime of our state-of-the-art energy storage technology, and in doing so help to realize an electrified future with less dependence on fossil fuels. |
1. Introduction
Lithium ion batteries (LIBs) show great promise as a superior energy storage technology for an array of applications, including mobile devices and electric vehicles. However, a critical performance and safety issue facing commercial LIBs is the use of liquid electrolytes. In most LIBs, the electrolyte is liquid, consisting of a lithium salt dissolved in an organic solvent;1 this type of electrolyte is cheap and exhibits high lithium ionic conductivity, which enables high power output from the cell. However, such solvents also enable or directly cause many safety and performance problems, including potential ignition of the flammable solvent when the cell is short-circuited by mechanical puncturing,2 reactions with the electrode that harm capacity and overall performance,3,4 and catastrophic pressure build-ups from thermally-induced solvent vaporization.1 Lithium-based batteries with solid electrolytes hold promise as safer, higher energy density and longer-lasting alternatives to conventional liquid electrolyte batteries by permitting the use of high voltage cathodes by limiting side reactions, easing flammability concerns, and suppressing dendrite growth.5 However, the principal design challenge with solid electrolytes is their lower ionic conductivities, typically many orders of magnitude below those of liquids (∼10−2 S cm−1).6The materials community has spent decades employing a largely guess-and-check approach to the search for new solid electrolytes. During this period, only a handful of materials with room temperature (RT) lithium conductivity comparable to liquids7–9 has been identified. However, high ionic conductivity is not the only requirement for a solid electrolyte; these materials should also exhibit a wide electrochemical stability window, negligible electronic conductivity, robust chemical stability, and low cost. Searching for high ionic conductivity solids is a considerable challenge in itself—and has been the main focus of many years of work—but navigating the many-dimensional space of these additional material requirements is even more difficult, and the unstructured nature of the search has resulted in slow progress.
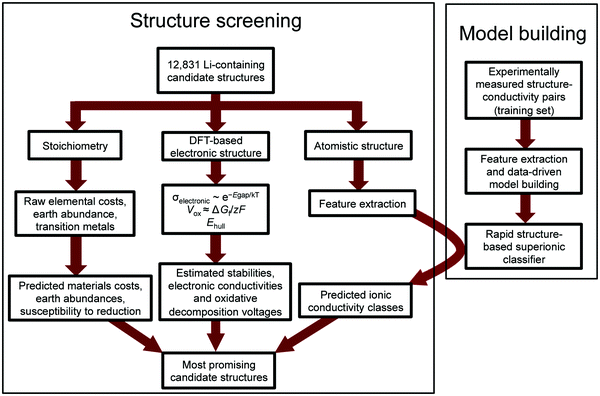
The number of known lithium-containing compounds is in the tens of thousands, the vast majority of which are untested and some of which may be excellent conductors. Here we present an improved method for searching the high dimensional space of technological constraints for promising materials by screening large datasets of electronic structure information contained in the Materials Project (MP) database.10 We first search for materials satisfying several prerequisite requirements (i.e. other than ionic conductivity), and we then utilize decades of available experimental data to build a rapidly calculable ionic conductivity classification model to look for the most likely superionic materials among these remaining candidates. The speed of the model is approximately 5–6 orders of magnitude faster than calculating ionic conductivity with DFT-based or experimental approaches, enabling screening of over 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 candidate Li-containing solids in a matter of minutes. Our approach is described in the flow chart in Fig. 1.
000 candidate Li-containing solids in a matter of minutes. Our approach is described in the flow chart in Fig. 1.
This statistical learning-based ionic conductivity classification approach seeks to objectively identify non-obvious information in the crystal structure that is highly correlated to ionic conductivity. This approach identifies generalized trends among all crystal structures, rather than limiting the search to a specific family or characteristic of conductors as in previous work;11,12 this is accomplished by compiling a diverse training set of structures. By using the existing data, the resulting model may be interpreted as a Bayesian prior on structure–property correlations for fast ion conduction; it can guide future studies in making the best guesses possible with the limited available data, and it is expected to be better than random trial-and-error. Additionally, this approach is more robust against human investigator bias, as it objectively reveals which, if any, of a set of hypotheses provide the best predictive power. The important information emerges automatically as the model learns. We utilize a data-driven predictor approach because electronic structure-based calculations of ionic conductivity often require computationally expensive energy barrier calculations, a currently insurmountable hurdle for screening over 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 materials. Applications of statistical learning techniques for understanding and screening materials have been small but steadily growing in popularity. These include efforts to predict the structures of hypothetical ternary oxides,13 identify new high Curie temperature piezoelectrics,14 predict thermodynamic stability,15 investigate chemical compound space,16 assist hydrothermal synthesis methods,17 and screen liquid electrolytes.18–21
000 materials. Applications of statistical learning techniques for understanding and screening materials have been small but steadily growing in popularity. These include efforts to predict the structures of hypothetical ternary oxides,13 identify new high Curie temperature piezoelectrics,14 predict thermodynamic stability,15 investigate chemical compound space,16 assist hydrothermal synthesis methods,17 and screen liquid electrolytes.18–21
2. Screening for constraints other than ionic conductivity
From the MP database, we obtain DFT-calculated atomistic and electronic structure information for each of the 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831 Li-containing candidate materials: the equilibrium atom positions, the band gap, the energy above the convex hull, and the Gibbs free energy of formation utilizing the MP's Python module Pymatgen.22 For this study, we consider only structures containing lithium; this makes up 19.2% of the 66
831 Li-containing candidate materials: the equilibrium atom positions, the band gap, the energy above the convex hull, and the Gibbs free energy of formation utilizing the MP's Python module Pymatgen.22 For this study, we consider only structures containing lithium; this makes up 19.2% of the 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 840 total structures in the MP database. We then compile data for four prerequisite criteria: electronic conduction, oxidative decomposition voltage, structural stability, and materials cost.
840 total structures in the MP database. We then compile data for four prerequisite criteria: electronic conduction, oxidative decomposition voltage, structural stability, and materials cost.
2.1 Electronic conductivity
In a battery, electronic conduction across the electrolyte must be minimal. To ensure low electronic conductivity, we screen for large band gap materials. The relationship between band gap and electronic conductivity for an intrinsic (n = p) crystalline semiconductor23 can be approximated as,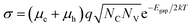 | (1) |
2.2 Structural stability
The energy above the convex hull Ehull quantifies the difference between the zero-temperature lattice energy of all phases and the most stable phase, Ehull. For a given compound, we assume those structures in the database with Ehull > 0 eV per atom to be unstable or metastable and discard them from the screening.2.3 Stability against oxidation at cathode
An additional requirement for solid electrolytes is a wide electrochemical stability window. Electrolytes with low stability against oxidation can react at the cathode and form high resistance interfacial layers that limit ionic current. A wide stability window is an important consideration in the search for promising ion conductors, as low activation energies for ion diffusion correlate with small magnitude (i.e. closer to zero) formation energies, and these small formation energies typically correlate with enhanced chemical reactivity. This constraint is quite restrictive and renders many superionic lithium conductors with low decomposition voltages unusable as standalone electrolytes in LIBs, e.g. Li3P. Sometimes the reaction products are highly ionically conductive and allow for normal operation, but without knowing the reaction products a priori we search for materials that are unlikely to react in the first place.Recent advances have been made in predicting the stability against oxidation at the cathode during discharge by computationally building phase diagrams with DFT.25 For increased efficiency, we estimate upper bounds on the oxidation potential using the DFT-computed formation energies ΔGf given in the MP database. Formation energies are defined with respect to the elemental constituents of the material:
 | (2) |
Although we do not know a priori the mechanism or energetics of the oxidation, we do know that the reaction is endergonic with energy ΔGox, pushed up the energy landscape by the cathode voltage, and results in a lithium-deficient product at the interface. A complete oxidation would have the following form:
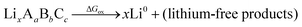 | (3) |
An energetic upper bound on this endergonic step would be complete phase segregation of the electrolyte into its elemental constituents. We might think of this decomposition as an intermediate step in a complete oxidation:
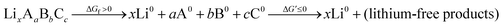 | (4) |
Since the reaction is endergonic, ΔGox = ΔGf + ΔG′ ≤ ΔGf; thus the formation energy is an upper bound on the oxidation energy. The Nernst equation provides the voltage required to drive an electrochemical reaction with energy E: V = zFE. With this we can calculate an upper bound oxidative decomposition voltage Ṽox on the true voltage for this reaction Vox (with respect to Li/Li+), from the known formation energy:
| Ṽox = ΔGf/xF | (5) |
In the ESI,† Fig. S1 we plot several examples of Ṽoxversus Vox as calculated rigorously with DFT in ref. 25 and confirm that Ṽox is an upper bound on Vox. Given that a typical cathode voltage is around 4 V vs. Li/Li+ or higher, we screen for materials with an estimated upper bound decomposition voltage of Ṽox > 4 V.
2.4 Stability against reduction at Li metal anode
Solid electrolyte materials must also remain stable against the low voltage of the anode. An ideal solid electrolyte will be stable down to 0 V vs. Li/Li+, thus enabling the usage of high energy density lithium metal anodes. Structures with transition metal atoms present are particularly susceptible to reactions with lithium, as the transition metals have many stable oxidation states. To improve the likelihood of chemical stability versus Li metal, we define a Boolean variable T which indicates if a transition metal is present in the stoichiometry (T = 1) or not (T = 0).The electrochemical stability windows provided in ref. 25 show that no materials with transition metals present achieve stability against Li metal, i.e. T = 0 is a necessary but not sufficient condition for Vred = 0. Thus to improve the likelihood of discovering materials stable against Li metal, we screen for materials with T = 0.
2.5 Cost
From a practical perspective, cost is a significant issue as well. An aggressive per-area cost target26 for electrolyte and/or separator materials is $10 per m2. As a rough estimate for materials cost, we consider the approximate per-mass costs of the raw elements in the material based on the prices of their commonly traded forms (sourced from Wikipedia27) and calculate a per-area cost for each material in US dollars (USD), assuming a 10 μm thickness. This serves to provide some sense for whether a material might feasibly ever reach the $10 per m2 cost target. We do not screen on cost but we provide it for all materials. The reference values for raw materials costs are given in Table S1 (ESI†).2.6 Earth abundance
Another practical constraint is the earth abundance of the constituent atoms in a material. To filter for stoichiometries with highly abundant atoms, we compile an abundance index IA for each structure based on the abundance ranking of the individual atoms. Each atom in the unit cell is assigned a score from 1 to 92 reflecting its rank in abundance in the earth's crust,28 and the overall material abundance index IA is simply the score of the least abundant atom in the unit cell. The atomic abundance ranks are given in Table S1 (ESI†). Although we calculate the earth abundance index for each candidate material, we do not use this as a screening criterion.3. Ionic conductivity screening
3.1 Training set
We compiled a training set of 40 crystal structures and reported experimentally measured ionic conductivity values available in the literature. These structures and ionic conductivity values are listed in Table 1. The atomic crystalline structures we employ for these 40 materials were downloaded from the Inorganic Crystal Structure Database (ICSD)85 which contains experimentally derived measurements. The work of Raccuglia et al.17 demonstrates the value of learning on negative examples; this supports our inclusion of many poor conductors in the training set. This is a relatively small set of available data from which to build a predictive model, and it is not clear a priori that there is sufficient information available to do so. The chances are best if good candidates for underlying physics are known, i.e. good features can be chosen.| Composition | RT bulk ionic conductivity (S cm−1) | Ionic conductivity ref. | Structure ref. |
|---|---|---|---|
| LiLa(TiO3)2 | 1 × 10−3 | 17 | 29 |
| Li9.81Sn0.81P2.19S12 | 5.5 × 10−3 | 30 | 30 |
| Li10Ge(PS6)2 | 1.4 × 10−2 | 7 | 31 |
| Li10.35Si1.35P1.65S12 | 6.5 × 10−3 | 30 | 30 |
| Li14ZnGe4O16(2) | 1.0 × 10−6 | 32 | 33 and 34 |
| Li2Ca(NH)2 | 6.4 × 10−6 | 35 | 36 |
| Li2Ge7O15 | 5.0 × 10−6 | 37 | 38 |
| Li2NH | 2.5 × 10−4 | 35 | 39 |
| Li2S | 1.0 × 10−13 | 40 | 41 |
| Li13.6Si2.8S1.2O16 | 6.0 × 10−7 | 42 | 43 |
| Li14Ge2V2O16 | 7.0 × 10−5 | 44 | 45 |
| Li15Ge3V2O4 | 6.03 × 10−6 | 46 | 47 |
| Li14.8Ge3.4W0.6O4 | 4.0 × 10−5 | 46 | 47 |
| Li3Fe2P3O12 | 1.0 × 10−7 | 48 | 49 |
| Li3N | 5.75 × 10−4 | 50 | 51 |
| Li3P | 1.0 × 10−3 | 8 | 52 |
| γ-Li3PS4 | 3.0 × 10−7 | 53 | 54 |
| Li3Sc2P3O12 | 1.0 × 10−10 | 55 | 56 |
| βII-Li3VO4 | 4.4 × 10−8 | 57 | 58 |
| Li4B7O12Cl | 1.0 × 10−7 | 59 | 59 |
| Li4BN3H10 | 2.0 × 10−4 | 60 | 61 |
| γ-Li4GeO4 | 3.1 × 10−12 | 37 | 62 |
| Li4SiO4 | 2.4 × 10−10 | 37 | 63 |
| Li5La3Bi2O12 | 2.0 × 10−5 | 64 | 64 |
| Li5La3Nb2O12 | 8.0 × 10−6 | 65 | 66 |
| Li5La3Ta2O12 | 1.5 × 10−6 | 65 | 66 |
| Li5NI2 | 1.5 × 10−7 | 67 | 68 |
| Li6BaLa2Ta2O12 | 4.0 × 10−5 | 69 | 70 |
| Li6FeCl8 | 1.0 × 10−4 | 71 | 72 |
| Li6NBr3 | 1.5 × 10−7 | 67 | 73 |
| Li6SrLa2Ta2O12 | 7.0 × 10−6 | 69 | 70 |
| Li7La3Zr2O12 | 3.5 × 10−4 | 74 | 75 |
| Li7P3S11 | 4.1 × 10−3 | 9 | 76 |
| LiAlH4 | 2.0 × 10−9 | 77 | 78 |
| LiAlSiO4 | 1.4 × 10−5 | 79 | 80 |
| LiBH4 | 2.0 × 10−8 | 60 | 81 |
| LiI | 1.0 × 10−6 | 42 | 82 |
| LiNH2 | 4.0 × 10−10 | 35 | 83 |
| α′-LiZr2P3O12 | 5.0 × 10−8 | 84 | 84 |
From these atomistic structures, we compute 20 features that characterize the local atomic arrangements and chemistry of the crystals. These features are chosen to be plausible candidates for exhibiting some correlation with ionic conductivity. These features depend only on the positions, masses, electronegativities, and atomic radii of the atoms, and therefore require minimal effort for computation. Conversely, building features from electronic structure requires computationally expensive simulations and quickly becomes intractable given the large number of candidate materials to screen. A list of our 20 features and their individual Pearson correlations with ionic conductivity for the structures in the training set is given in Table 2. The reference values we use for building the features are given in Table S1 (ESI†). For descriptions on how to calculate these 20 features given the reference values, see ESI,† Section S1. For reference, the feature values of lithium iodide and lithium phosphide are provided in the ESI,† Table S2.
| Feature | Pearson correlation coefficient | Training data standard deviation | Training data mean | Normalized regression coefficient | |
|---|---|---|---|---|---|
| a These features are averaged over the relevant parameter: bonds, atoms, Li–Li pathways, etc. | |||||
| 1 | Volume per atoma | 0.20 | 4.582 | 13.342 | 0 |
| 2 | Standard deviation in Li neighbour count | 0.22 | 1.430 | 1.766 | 0 |
| 3 | Standard deviation in Li bond ionicity | −0.04 | 0.274 | 0.858 | 0 |
| 4 | Li bond ionicitya | −0.18 | 0.372 | 1.403 | 0 |
| 5 | Li neighbour counta | −0.19 | 6.393 | 21.359 | 0 |
| 6 | Li–Li bonds per Li | 0.06 | 4.432 | 6.218 | +0.817 |
| 7 | Bond ionicity of sublattice | −0.28 | 0.330 | 0.978 | −1.323 |
| 8 | Sublattice neighbour counta | −0.13 | 7.087 | 20.660 | 0 |
| 9 | Anion framework coordination | −0.06 | 2.202 | 10.073 | −1.028 |
| 10 | Minimum anion–anion separation distancea (Å) | 0.09 | 0.708 | 3.395 | 0 |
| 11 | Volume per anion (Å3) | −0.01 | 35.131 | 36.614 | 0 |
| 12 | Minimum Li–anion separation distance (Å) | 0.20 | 0.288 | 2.072 | +2.509 |
| 13 | Minimum Li–Li separation distance (Å) | −0.10 | 0.746 | 2.730 | −1.619 |
| 14 | Electronegativity of sublatticea | −0.16 | 0.306 | 2.780 | 0 |
| 15 | Packing fraction of full crystal | 0.16 | 0.173 | 0.465 | 0 |
| 16 | Packing fraction of sublattice | 0.19 | 0.186 | 0.234 | 0 |
| 17 | Straight-line path widtha (Å) | 0.07 | 0.247 | 0.852 | 0 |
| 18 | Straight-line path electronegativitya | −0.29 | 0.707 | 2.535 | 0 |
| 19 | Ratio of features (4) and (7) | −0.03 | 0.719 | 1.611 | 0 |
| 20 | Ratio of features (5) and (8) | −0.18 | 0.152 | 1.057 | 0 |
| Constant term | — | — | — | −1.944 | |
The 20 features are chosen based on physical intuition and previous proposals and reports in the literature.86–90 We limit the feature pool to the 20 described here in order to enable exhaustive combinatorial searches of feature space (Discussed in Section 3.2), which become prohibitive beyond 20 features. Although many of the features we use have some correlation with ionic conductivity, none of the Pearson correlation coefficients are larger than ±0.3 and thus no features individually form a robust design criterion across all structure types. However, it is possible that a linear combination of features can build a model with better predictive power than a single feature alone. We again do not know a priori which or how many features are important, but we can identify them using combinatorial model building and statistical validation techniques.
Several of the training set structures from the ICSD are given with fractional atomic occupancies due to disorder. Since the feature extraction process maps one structural configuration to one feature vector but many different configurations are feasible, in this case the features are ambiguous. We treat these cases with a probabilistic approach, described in ESI† Section S2.
With these techniques we identify a distinct subset of features that define a model capable of predicting superionic behaviour and illuminating the structure–property relationship from a new perspective.
3.2 Model selection
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) :
: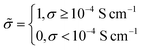 | (6) |
Under this classification scheme, 27.5% of the training set materials (11 of 40) are considered superionic. With this transformation we then classify the training set structures with an expression of the form:
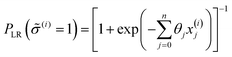 | (7) |
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (i) ∈ {0,1}, to be the class with greater likelihood, i.e.
(i) ∈ {0,1}, to be the class with greater likelihood, i.e. ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (i) = 1 and material i is predicted superionic if PLR ≥ 50%; and
(i) = 1 and material i is predicted superionic if PLR ≥ 50%; and ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (i) = 0 and material i is not predicted superionic if PLR < 50%. Although the physics governing ionic conduction is certainly more complicated than a linear sum of atomistic features, we seek to build a model that captures some of this important information despite its relative simplicity.
(i) = 0 and material i is not predicted superionic if PLR < 50%. Although the physics governing ionic conduction is certainly more complicated than a linear sum of atomistic features, we seek to build a model that captures some of this important information despite its relative simplicity.
Next we perform feature selection, where we identify a subset of the 20 features that builds the best predictor. Using a large number of features (compared to the number of data points) can result in overfitting, in which the quality of the training set fit is high, but the predictive power is poor. Using too few features can result in underfitting, where both the fit to the training set and the predictive power are poor.
To identify the optimal set of features to use in the feature reduction process, we use LR to build an ensemble of all possible models and compute predictive performance of each model. Due to the relatively small number of M = 40 materials and N = 20 features in our full data set, we can build a model from every possible combination of features for a total of 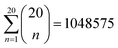 models. For each model, we fit the feature data to the ionic conductivity classes, calculate the training misclassification rate (TMR) between the predicted and observed values, and the cross-validated misclassification rate (CVMR) through leave-one-out cross-validation (LOOCV).91 The TMR is given by:
models. For each model, we fit the feature data to the ionic conductivity classes, calculate the training misclassification rate (TMR) between the predicted and observed values, and the cross-validated misclassification rate (CVMR) through leave-one-out cross-validation (LOOCV).91 The TMR is given by:
 | (8) |
Here we make use of the indicator function 1{X}, which evaluates to 1 if the argument X is true and 0 if X is false. The argument of the indicator function in eqn (8) is true if the model prediction ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (i) does not equal the observed class
(i) does not equal the observed class ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) (i). Thus eqn (8) counts the number of misclassified materials and divides it by the total number of materials, M.
(i). Thus eqn (8) counts the number of misclassified materials and divides it by the total number of materials, M.
The CVMR is calculated in a similar way, but with the model prediction ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (i) replaced by
(i) replaced by ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (i)LOO. In LOOCV, we systematically remove data point i, rebuild the model on the remaining N − 1 points, and then classify the removed point on this rebuilt model. The model prediction for material i built on all data points except i is
(i)LOO. In LOOCV, we systematically remove data point i, rebuild the model on the remaining N − 1 points, and then classify the removed point on this rebuilt model. The model prediction for material i built on all data points except i is ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (i)LOO. As before, if PLR ≥ 0.5, we set
(i)LOO. As before, if PLR ≥ 0.5, we set ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (i)LOO = 1, and if PLR < 0.5 we set
(i)LOO = 1, and if PLR < 0.5 we set ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (i)LOO = 0.
(i)LOO = 0.
 | (9) |
The CVMR serves as a metric for the quality of the predictive capacity of the model and we expect it to be high in regions of under- and overfitting.92 Since each prediction is made on a material that has been removed from the training set, the cross validation error captures the predictive power of the model on unseen data. Models that are overfit to the training data, for example, will have low training errors and high cross validation errors since the model cannot extrapolate outside the training data.
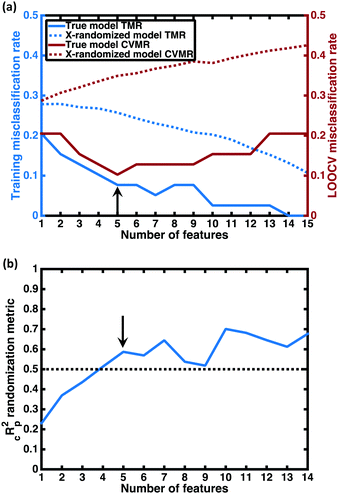
For each number of features n, where 1 ≤ n ≤ N, we identify which single model of the 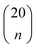 possible models gives the lowest CVMR value. The TMR and CVMR values of these highest-performing models are plotted against n as solid lines in Fig. 2(a). Note the CVMR is high at low n and high n, representing regions of underfitting and overfitting, respectively. The TMR declines steadily as expected. We identify a 5-feature model with minimal CVMR. This model has a TMR of 10%, meaning it misclassifies four of the 40 training points; the CVMR of 10% means four of the 40 training points are also misclassified in LOOCV. This cross validation error suggests the model will perform with approximately 90% accuracy on unseen data.
possible models gives the lowest CVMR value. The TMR and CVMR values of these highest-performing models are plotted against n as solid lines in Fig. 2(a). Note the CVMR is high at low n and high n, representing regions of underfitting and overfitting, respectively. The TMR declines steadily as expected. We identify a 5-feature model with minimal CVMR. This model has a TMR of 10%, meaning it misclassifies four of the 40 training points; the CVMR of 10% means four of the 40 training points are also misclassified in LOOCV. This cross validation error suggests the model will perform with approximately 90% accuracy on unseen data.
Some additional insight into the degree of statistical significance can be obtained by considering the false positive predictions of the models, i.e. the fraction of predicted superionics that are actually non-superionic. In performing the LOO cross-validation on the training set, we find that the true model classifies 11 training set materials as superionic while only 9 actually are, giving a false positive appearance rate of 2/11 = 18%. In performing X-randomization with n = 5, we find a false positive appearance rate of 75%. Given the 27.5–72.5% split between superionic and poor conductor classes in our training data, we would expect that guessing the class label without any information—essentially flipping a coin to determine the class—would give a false positive approximately 72.5% of the time, close to the X-randomized rate we observe. Thus the false positive appearance rate with our predictive model—the metric that is arguably more relevant than the total CVMR for setting expectations for in-depth studies on the most promising compounds—is also four times better than the X-randomized case. This suggests our model may be four times more likely to correctly predict a superionic material than random guessing.
To quantify the superiority of the model versus random noise, we calculate a modified version of the standard 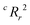 parameter employed in data-driven studies,91 given by,
parameter employed in data-driven studies,91 given by,
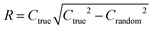 | (10) |
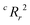 value, the better the performance than chance. The
value, the better the performance than chance. The 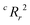 value for each minimum-CVMR n-feature model is shown in Fig. 2(b). The optimal LR model as determined by LOOCV has an
value for each minimum-CVMR n-feature model is shown in Fig. 2(b). The optimal LR model as determined by LOOCV has an  value of 0.59, exceeding the threshold of 0.5 for predictive models.91
value of 0.59, exceeding the threshold of 0.5 for predictive models.91
Due to the significant computational expense behind performing the entire combinatorial model building process a statistically important amount of times for many different random X matrices, we compare the true n-feature model results to the performance of a model with n columns of random noise. Without performing the full model building process on 20 columns of random noise, there could be some selection bias93 that may make the randomized case perform worse than it could be. We performed three runs of the full X-randomized model building process, and although it was probably not enough to be statistically sound (ref. 93 suggests at least ten and preferably 100 realizations), the  values were close to or greater than the threshold of 0.5, suggesting that even when controlling for selection bias the predictive power of the true model is still significantly stronger than chance.
values were close to or greater than the threshold of 0.5, suggesting that even when controlling for selection bias the predictive power of the true model is still significantly stronger than chance.
The most robust test of predictive power would normally be to break the training data into separate training, cross-validation, and test sets, and use the test set to assess the predictive capability. However, a thinning of the 40 available data points used for training here has the potential to increase predictive errors for such a small data set. Therefore, we opt to use the entire data set for training in this work and use the LOO CVMR score as a proxy for test error.92 There is potential for the LOO CVMR misclassification rate to be lower than a test set misclassification rate, and one might expect the LOO false positive rate of 18% to be optimistic. There are other reasons why this is likely to be optimistic, described in Discussion Section 4.3 below. In this work, we make the best guesses possible, which are likely to be better than random guessing. As the amount of experimental data increases in the future, more robust model building and validation will become possible.
3.3 Model performance
From the results of the model-building algorithm, we identify an optimal LR model with five features that can classify the training set materials with 10% cross-validated error. This unique model corresponds to the minimum in the CVMR plot, Fig. 2(a). Five features versus the 40 training examples keeps the model over the convention of a minimum 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio between data points and features to avoid overfitting.91 The LR model has the form of eqn (7), where
1 ratio between data points and features to avoid overfitting.91 The LR model has the form of eqn (7), where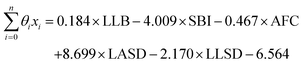 | (11) |
LLB is the average number of lithium neighbours for each lithium (feature 6); SBI is the average sublattice bond ionicity (feature 7), AFC is the average anion–anion coordination number in the anion framework (feature 9), LASD is the average shortest lithium–anion distance in angstroms (feature 12), and LLSD is the average shortest lithium–lithium distance in angstroms (feature 13). The performance of this model on the training data and the cross-validated data is shown in Fig. 3.
The signs of the coefficients provide some intuition on the crystal characteristics that encourage fast ion conduction. Eqn (11) says ionic conductivity increases in crystals where lithium has many neighbouring lithium atoms (θLLB > 0) at short distance away (θLLSD < 0). Covalent sublattices are preferred over ionic sublattices (θSBI < 0), which likely implies a more uniform electron distribution along conduction pathways. Lower anion–anion coordinations in the anion framework tend to improve conductivity (θAFC < 0), as do larger Euclidean distances separating the lithium and anion atoms at equilibrium (θLASD > 0). To assess the relative importance of the features, we can compare the magnitude of the coefficients when the feature data are mean-centred and normalized by their standard deviations (means and standard deviations are given in Table 2). In this case, eqn (11) becomes 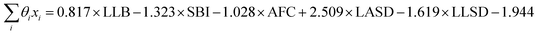 . This shows that, for example, small increases in the equilibrium lithium–anion distance make larger improvements to ionic conductivity than similar increases in the lithium–lithium bond number.
. This shows that, for example, small increases in the equilibrium lithium–anion distance make larger improvements to ionic conductivity than similar increases in the lithium–lithium bond number.
Wang et al. claim the anionic component of the sublattice should be in the low-coordination bcc arrangement to facilitate fast ion conduction.90 There appears to be evidence for this in the appearance of feature AFC in eqn (11) with a negative coefficient, implying that lower coordination anion frameworks (e.g. bcc or cubic) are preferred to high coordination ones (e.g. fcc or hcp). However, we note that this feature is only one of five in eqn (11), suggesting that it is only one of several important criteria for superionic behaviour. This likely stems from the broad set of training structures considered here beyond the sulphides considered by Wang et al. This suggests the anion geometry is perhaps not a universal predictor in itself across the full space of materials; this latter point is reinforced by the small (but still negative) single feature conductivity correlation of −0.06 in Table 2.
That θLLB > 0 also meshes with the conventional wisdom that higher dimensional conductors are better conductors; materials with many Li–Li connections are likely to possess many-dimensional conduction pathways and vice versa.
The inclusion of the feature SBI with a negative coefficient in eqn (11) highlights a paradox in the design of inorganic solid electrolytes: high sublattice ionicity generally leads to greater formation energy and therefore improved electrolytic stability, but it decreases ionic conductivity. This former trend can be seen in recent high-throughput electrochemical window calculations for Li conductors,25 where the width of the window increases with increasing anion electronegativity. An ideal solid electrolyte material, we might conclude, should have a strongly bonded, ionic sublattice far from the lithium conduction pathways; the pathways, however, should be dominated by covalent character so lithium can break and reform bonds with minimal energy penalty.
It is possible and perhaps likely that the specific correlations identified here are not causal, i.e. some of these features in the model may merely reflect the importance of some other aspect not included in the total feature space. The relevant identified features could change upon introduction of additional features that better describe the relevant physics. In fact, inclusion of a feature that is an exact model for ionic conductivity should result in a one-feature model that does an error-free job of predicting, barring noise in the experimental training data. Fig. 2 indicates that no single feature provides predictive power, indicating that none of the features provide an independent and complete description of the relevant physics of ion conduction in our training set. In the absence of an exact feature we need to employ a combination of many features, selected by learning on a diverse training set of structures. More data will enable better learning over an inexact feature space; according to the law of large numbers, the distribution over feature space should become increasingly apparent as more structures are sampled. Furthermore, these features have some correlation with each other; for example, the strongest correlation among the five features in eqn (11) is between features LLB and LLSD, with a Pearson correlation coefficient of −0.515. However, given the computational ease of calculating these five features, utilizing features with somewhat redundant information is acceptable.
Eqn (11) represents a novel design criterion for high conductivity lithium materials applicable to any periodic crystalline structure. Next, we employ this model for screening known lithium containing crystals.
3.4 Confidence metrics for screening
To apply these design criteria to the search for new superionic lithium conductors, we perform feature extraction for all 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831 lithium-containing materials in the Materials Project database and then predict superionic conductivity using the LR model. Since we expect the accuracy of these predictions to vary over a wide range, we consider three independent confidence metrics for each prediction. The first is the output of the predictor function PLR, the probability of belonging to the positive class. A larger value of PLR corresponds to a more confident prediction; the material is further from the “crossover” region of space where PLR = 50% shown in Fig. 3.
831 lithium-containing materials in the Materials Project database and then predict superionic conductivity using the LR model. Since we expect the accuracy of these predictions to vary over a wide range, we consider three independent confidence metrics for each prediction. The first is the output of the predictor function PLR, the probability of belonging to the positive class. A larger value of PLR corresponds to a more confident prediction; the material is further from the “crossover” region of space where PLR = 50% shown in Fig. 3.
The second metric is a distance-based metric d, which captures the distance in n-dimensional data space between the test material and the centroid of the training set. To account for the shape of the training data in this space, we normalize the Euclidean distance to the centroid by the variance of the data along each direction using Principal Component Analysis (PCA).94 Thus, for a given Euclidean distance, data points in regions of high training set data variance have a smaller d value, and vice versa. Smaller d values are desirable, as a smaller d indicates that the data point is nearer to the region in which the model was built and therefore that the prediction involves less extrapolation. In order to capture the relative distance from the training set, we normalize each screened material's d value by the mean d value of the materials in the training set.
The third confidence metric is a prediction error ε. This error is defined as the leave-one-out error (LOO error), equal to the standard deviation of PLR for a given material from systematically removing each data point from the training set, one at a time, and rebuilding the optimal model. In a statistical learning sense, this represents the magnitude of change in PLR we might expect to see when one additional data point is added to or removed from the training set. Small values are desirable, as this indicates a stable model for which additional information is unlikely to give significantly different results. Large values indicate the data point is in an unstable regime of data space where the model may be less reliable.
We note the inclusion of prediction confidence metrics highlights the strength of the data-driven approach: we know when the model predictions are most reliable and when they are questionable. This is more difficult for structure–property models that are not data-driven but rather derived exclusively from physical intuition and approximation. In the screening step, we accept only the highest PLR materials, and provide the values of d, ε and A although we do not screen on these confidence metrics. These three metrics are used after screening to indicate confidence in the PLR prediction value for each promising material.
4. Results and discussion
4.1 Screening results
We apply the following constraints in our prerequisite screening: Egap ≥ 1 eV, Ṽox ≥ 4 V, Ehull = 0 eV per atom and T = 0. We also discard any materials with elements with undefined electronegativity values (see Table S1, ESI†). These constraints cut the number of candidate materials down from 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831 to 317, a reduction of 92.2%. By far, the strictest constraint is structural stability Ehull = 0 eV per atom; only 11.5% (1472) of structures satisfy this requirement. Of the remaining 1472 structures, 43.2% (636) do not have transition metals, while 52.5% (773) have Egap ≥ 1 eV and 54.6% (803) have upper bound oxidation voltages of 4 V or higher. Although we do not screen on raw materials cost, we note that 72.0% (9240) of all materials have a raw materials cost of $10 per m2 or less per 10 μm thickness, as do 42.1% (619) of all stable structures.
831 to 317, a reduction of 92.2%. By far, the strictest constraint is structural stability Ehull = 0 eV per atom; only 11.5% (1472) of structures satisfy this requirement. Of the remaining 1472 structures, 43.2% (636) do not have transition metals, while 52.5% (773) have Egap ≥ 1 eV and 54.6% (803) have upper bound oxidation voltages of 4 V or higher. Although we do not screen on raw materials cost, we note that 72.0% (9240) of all materials have a raw materials cost of $10 per m2 or less per 10 μm thickness, as do 42.1% (619) of all stable structures.
Since the 317 structures satisfying all prerequisite criteria may be too many to explore exhaustively, we then apply the ionic conductivity screening to these candidate materials, screening for high superionic probability. Overall, the PLR values of these materials are low, as we might expect given the rarity of superionic conductors; the mean PLR value is 10.0% and the standard deviation is 21.1%. Thus, the number of materials truly predicted to be superionic (PLR > 50%) is few—only 21. These 21 most promising candidate materials and their performance metrics are provided in Table 3.
| MPID | Chemical formula | P LR | d | ε | A | E gap | Ṽ ox | USD/m2 (10 μm thick) | I A | Related study |
|---|---|---|---|---|---|---|---|---|---|---|
| a These materials require significant model extrapolations and are considered low confidence predictions. In all instances except mp-866665, this extrapolation is due to the mixed anion effect; see Section 4.3 for discussion. b LiCl is a known false positive; it is a poor RT ion conductor. Through our statistical analysis we expect approximately 18% of positive predictions to be false positives. | ||||||||||
| mp-554076 | BaLiBS3 | 0.589 | 1.049 | 0.048 | 1 | 2.153 | 9.697 | 23 | 38 | |
| mp-532413 | Li5B7S13 | 0.897 | 1.228 | 0.024 | 1 | 3.553 | 5.454 | 42 | 38 | 95 |
| mp-569782a | Sr2LiCBr3N2 | 1.000 | 6.852 | 0.000 | 0 | 3.973 | 13.968 | 16 | 45 | |
| mp-558219 | SrLi(BS2)3 | 0.518 | 1.556 | 0.114 | 1 | 2.91 | 13.964 | 38 | 38 | |
| mp-15797 | LiErSe2 | 0.543 | 1.505 | 0.056 | 1 | 1.615 | 6.778 | 170 | 67 | |
| mp-29410 | Li2B2S5 | 0.994 | 1.855 | 0.003 | 1 | 2.538 | 4.895 | 29 | 38 | 95 |
| mp-676361 | Li3ErCl6 | 0.655 | 0.974 | 0.042 | 1 | 5.211 | 7.794 | 70 | 44 | 96 and 97 |
| mp-643069a | Li2HIO | 0.652 | 2.081 | 0.079 | 0 | 4.319 | 4.054 | 2.40 | 60 | |
| mp-19896 | Li2GePbS4 | 0.604 | 1.063 | 0.090 | 1 | 2.265 | 4.591 | 13 | 54 | 90 |
| mp-7744a | LiSO3F | 1.000 | 4.097 | 0.000 | 0 | 5.792 | 13.446 | 10 | 34 | |
| mp-22905b | LiCl | 0.837 | 1.381 | 0.031 | 1 | 6.25 | 4.214 | 0.94 | 34 | 98 |
| mp-34477 | LiSmS2 | 0.89 | 1.33 | 0.028 | 1 | 1.921 | 8.536 | 6.50 | 40 | |
| mp-676109 | Li3InCl6 | 0.656 | 1.013 | 0.058 | 1 | 3.373 | 6.215 | 5.50 | 63 | 96 and 97 |
| mp-559238 | CsLi2BS3 | 0.812 | 1.642 | 0.055 | 1 | 3.094 | 4.798 | 160 | 49 | |
| mp-866665a | LiMgB3(H9N)2 | 1.000 | 5.149 | 0.000 | 0 | 6.511 | 11.222 | 30 | 38 | |
| mp-8751 | RbLiS | 0.775 | 1.279 | 0.051 | 1 | 2.745 | 4.22 | 240 | 34 | |
| mp-15789 | LiDyS2 | 0.901 | 1.339 | 0.025 | 1 | 1.935 | 8.736 | 9.20 | 39 | |
| mp-15790 | LiHoS2 | 0.899 | 1.327 | 0.025 | 1 | 1.965 | 8.749 | 300 | 55 | |
| mp-15791 | LiErS2 | 0.899 | 1.319 | 0.025 | 1 | 2.008 | 8.761 | 190 | 44 | |
| mp-561095a | LiHo3Ge2(O4F)2 | 0.984 | 3.247 | 0.009 | 0 | 4.163 | 53.18 | 370 | 55 | |
| mp-8430 | KLiS | 0.76 | 1.243 | 0.052 | 1 | 3.057 | 4.348 | 14 | 34 | |
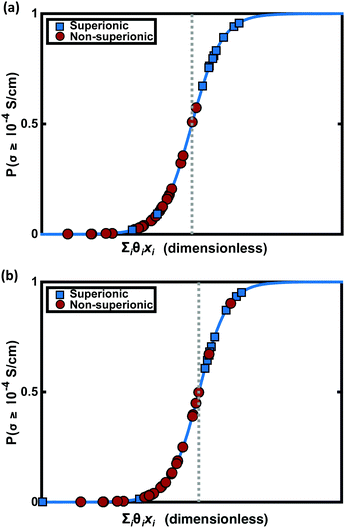
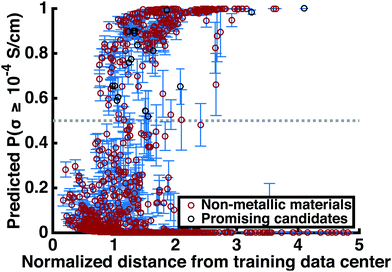
This step reduces the remaining compounds down by 93.3%, an overall reduction of 99.8%. Strengthening the constraints can shorten this list of promising compounds down to an arbitrarily small number. Table 3 includes many structures that have not yet been studied experimentally. Fig. 4 shows the superionic probabilities PLRversus d values for the 1054 stable, non-metallic structures plotted in red, with the 21 most promising candidates plotted in black.
In order to provide more high-scoring candidates from the screening process, we list in the ESI,† Table S3 the 56 additional materials that result from screening with less stringent requirements: PLR ≥ 0.5, Egap ≥ 0.5 eV, Ṽox ≥ 3 V, T = 0, and Ehull ≤ 0.1 eV per atom.
Had we screened these 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831 structures with the ionic conductivity model alone, the number of candidate materials would have been reduced only to 1408 materials (89.0% reduction). This suggests that the prerequisite constraints are more stringent as screening criteria than the ionic conductivity constraints.
831 structures with the ionic conductivity model alone, the number of candidate materials would have been reduced only to 1408 materials (89.0% reduction). This suggests that the prerequisite constraints are more stringent as screening criteria than the ionic conductivity constraints.
4.2 Ionic conductivity model performance
Since the available data is a bare minimum upon which one might expect to build a predictive model, the conductivity screening approach here should be considered as the best available fashion in which to thin the candidate pool in the absence of more information. It is expected to be better than random guesses.The LR model identifies 6.6% of the materials passing the prerequisite screening as superionic (and 10.8% of all Li-containing materials) if we only enforce the strict ionic conductivity prediction requirement, PLR > 50%. This is smaller than the 27.5% superionicity of the training set. While the true fraction of stable, large-gap superionic materials is unknown, it is likely to be lower than the 27.5% pulled from the literature here because authors are more likely to report good conductors than bad ones. Therefore, it is encouraging that the proportion of superionics that our model identifies in the MP database is much lower than 27.5%.
Because our screening is designed around battery applications, our prerequisite screening may be discarding otherwise notable materials that the model correctly identifies as superionic. Understanding the performance of the ionic conductivity model is important to guiding future improvements of the screening approach (not to mention that these superionic materials may be useful for other applications), and thus we provide a table of the materials that the model most confidently predicts as superionic, even though they may not satisfy the prerequisite criteria. Thirty-four materials meet the criteria PLR > 95%, d < 1.5, and Ehull = 0 eV per atom; they are provided in the ESI,† Table S4.
4.3 Possible sources of error
We note that the ionic conductivity values reported in the literature are largely from sintered polycrystalline samples, where the microstructure may play a role in determining the ionic conductivity.99 For the purposes of our analysis, we take the reported values to be representative of the bulk ionic conductivity. This highlights the importance of characterizing and reporting the grain size in future experimental studies in order to improve our understanding of structure–property correlations for ionic conductivity. An additional possible source of error might be that we build the ionic conductivity predictor on experimentally observed structures, but screen structures in the MP database that have been lattice-relaxed with DFT, which can change lattice constants by up to several per cent. This will introduce false positives into the screening if the ionic conductivity model predicts superionic behaviour in the screened DFT structures, but not in the true experimentally observed structures. This may be particularly relevant in layered structures like the lithium lanthanide sulphide structures in Table 3, with van der Waals interactions that are not well modelled by semi-local DFT.A possible source of error is introduced in the application of our model via ambiguities of the definition of the anion species in the lattice. The values of two of the model features, AFC and LASD, are dependent on how the anion in the lattice is defined. Some structures have mixed anion species with similar electronegativity, e.g. LiSO3F. When the convention of designating the anion as the most electronegative atom is applied, features AFC and LASD are computed with respect to F, without considering O. This leads to small values of AFC and large values of LASD, increasing the PLR value. These cases should be treated as low confidence predictions; this uncertainty is captured by the large d values of these materials.
The most significant source of error is likely the small amount of training data. As more data is added to this set, the likelihood of learning on chance correlations will decrease.
4.4 Classification threshold effects
The choice to partition the training data into two classes based on the threshold value of σ = 10−4 S cm−1 reflects engineering constraints for battery applications. However, this threshold value plays an important role in the performance of the classifier. As the threshold value approaches the median training set ionic conductivity of σ = 5 × 10−6 S cm−1, the training set becomes evenly split between positive (high ionic conductivity) and negative (low ionic conductivity) classes. To observe the effect of a different conductivity threshold value, we perform the combinatorial model building process again for a variety of cutoff values. We also perform X-randomization to assess the quality of these models. This analysis is provided in the ESI,† Section S4. We confirm that a perfect binary separation of the positive and negative examples does not appear at a different cutoff, and that our chosen cutoff of 10−4 S cm−1 does a satisfactory job of balancing the concerns of model performance and usefulness for battery applications.4.5 Comparison to known fast ion conductors
Our screening identifies several structures known for fast lithium conduction that were not included in the training set of structures. The ultimate measure of any predictive model is how it performs on data outside the training set; the set of screened materials functions as a test (hold-out) set for the model. By cross-checking with the literature and identifying several correct predictions including Li3OCl, the chloride spinels, and lithiated silicon and germanium (discussed below), we build confidence that our model performs well outside the training set and will be successful in identifying new superionic solids.A notable model prediction is for the anti-perovskite structure Li3OCl, first discovered in 2012 and exhibiting an experimentally observed RT ionic conductivity of up to 8.5 × 10−4 S cm−1.100 The model calculates the superionic probability to be 56%, thus making this a correct prediction. Since there are no structures that a human interpreter might judge “similar” to Li3OCl in the training set, this prediction represents a successful abstraction of superionic characteristics across diverse conductor structures. However the calculated Ṽox value of 3.438 V is below the screening threshold of 4 V, so Li3OCl is excluded from the final list of promising materials in Table 3, although it is given in Table S3 (ESI†).
Notable in Table 3 is the lithium–metal–halogen type structure Li3InCl6. Although an ionic conductivity for Li3InCl6 is not reported to our knowledge, the isomorphic Li3InBr6−xClx (0 < x < 3) forms a known fast lithium conductor with a reported RT ionic conductivity96,97 in the range 5 × 10−5–2 × 10−3 S cm−1 (Li3InBr6 is not in the MP database). The similar structure Li3ErCl6 is also classified as superionic, although the higher materials cost of Er makes this a less attractive candidate. Li6ErBr6 has a PLR value of 47.5%, excluding it from Table 3. Also of note in Table 3 are the lithium thioborates Li5B7S13 and Li2B2S5. These structures also do not appear in the literature, although lithium thioborate glasses in the B2S3–Li2S–LiI system were proposed as solid electrolyte materials in 1983 and have been observed to exhibit a RT ionic conductivity as high as 10−3 S cm−1.95
Another promising predicted superionic is Li6MgBr8, known in the literature for fast ion conduction.101 The model predicts the likelihood of superionic behaviour as 88%, but it is excluded from the final list of promising candidates in Table 3 due to the low Ṽox value of 3.856 V. It is, however, listed in the Table S3 (ESI†).
An apparent false positive in Table 3 is LiCl, which is a poor RT conductor (∼10−9 S cm−1) although it performs well at high temperature (10−3 S cm−1 at 500 °C).98 Our analysis in Section 3.2 implies that we might expect at least four (18%) of these 21 predicted positive materials to be false negatives. To our knowledge, none of the other candidates in Table 3 have been studied as solid electrolyte materials, although several have been studied for other unrelated properties.
A noteworthy class of materials that do not make the final cut are the chloride spinels,102 Li2MCl4 (M = Cd, Mg, Mn), with PLR values of 18.0%, 17.0%, and 17.4%, respectively. The chloride spinels exhibit experimentally observed RT ionic conductivities of up to 10−5 S cm−1;103 notably high, but below our superionic threshold of 10−4 S cm−1 and thus the predicted negative classification is accurate. However, our model predicts the bromide spinel structures Li2MnBr4 and Li2MgBr4 to be superionic. The most significant reason for the discrepancy in the predictions between the bromides and chlorides is that the Li–Li separation distances in the bromide are smaller, giving the bromide a LLB value of 4 versus a value of 1 for the chlorides. However, experimental work shows Li2MnBr4 has a RT ionic conductivity slightly lower than its chloride counterpart,104 thus making this classification incorrect. This issue reflects the difficulty in choosing a proper cut-off radius for the LLB descriptor since it introduces an unavoidable discontinuity in feature values; e.g. if the cut-off radius of 4 Å were instead 3.8 Å, both the bromide and the chloride would be correctly classified.
Experimental105 and computational106,107 work has reported that highly lithiated silicon and germanium exhibits superionic lithium conduction. Li21Si5 and Li15Ge4 both have high confidence predictions of 98.4% (d = 1.283) and 97.8% (d = 1.299) respectively, as shown in Table S4 (ESI†). These are metallic and low oxidation potential materials so they are not suitable electrolytes, but our superionic model provides a correct prediction of their high lithium conductivities.
Fast ion conductors with otherwise poor electrolyte performance (e.g. Li3P) do not appear in Table 3, as the prerequisite screening criteria make the list more targeted to electrolyte materials than previous ion conductor screening studies.90,108,109
Two families that have more than one compound in Table 3 and Table S3 (ESI†) are the lithium lanthanide chalcogenides, LiLnX2, and the ternary alkali metal chalcogenides ALiX. These materials have not been examined as ion conductors to our knowledge, but both possess a promising property for highly stable ion conductors: ionic bonding character away from lithium and less ionic bonding character with lithium. In the former material this is due to the Li intercalation in the van der Waals gap; in the latter it stems from more complex structural features detailed in recent electronic structure studies.110
4.6 Comparisons to previous screening work
Many of the candidate materials listed in Table 3 and Table S3 (ESI†) are different from those presented in previous screening studies. Screening for sulphides with high predicted ionic conductivity based on anionic packing in ref. 90 is reported to return promising structures including Li10Ge(PS6)2, Li7P3S11, Li3AsS3, LiGaS2, LiZnPS4, and Li2GePbS4. These first three materials are eliminated by our Vox estimates of 3.2 V, 3.5 V, and 2.8 V, respectively. LiGaS2 and LiZnPS4 both have predicted decomposition voltages (Vox = 5.4 V and 7.3 V, respectively) above our screening cutoff of 4 V, but our model does not classify these two as superionics (PLR = 35% and 1%, respectively). The former has a small (high confidence) d value of 1.1, but the latter has a large (low confidence) d value of 2.16 and is outside the domain of applicability (A = 0) due to the large lithium–lithium separation distances.Recent work108 in screening for fast lithium conductors with the bond-valence algorithm111–113 has focused on oxides, which we find rarely exhibit the structural characteristics required by our model for high superionic probability prediction. Of the 495 stable oxide structures we screen, only 1.6% of them (8) have PLR > 50%, and only 3 of these 8 satisfy all screening requirements, although these all have another anion present and thus large d values (see Table 3). There are two superionic oxides in our training set: LiLa(TiO3)2 and Li7La3Zr2O12.
It follows that several of the materials satisfying the bond valence screening are not predicted to exceed our 10−4 S cm−1 threshold, including e.g. Li2Te2O5 and Li2SO4. Others are eliminated in our screening process due to instability (Ehull > 0 eV), e.g. LiB3O5 and Li6Si2O7. Several others are eliminated due to low estimated decomposition voltage, e.g. Li2O and Li5AlO4. LiAlSiO4 is predicted to be a promising conductor by the bond-valence method but is included in our training set as a negative example due to its experimentally measured ionic conductivity of 1.4 × 10−5 S cm−1.
4.7 A clear roadmap for the future of screening
We discover that the prerequisite engineering requirements are more stringent in cutting down the list of candidate materials than the ionic conductivity requirement. This statement assumes that the materials in the MP database are representative of the universe of Li-containing materials. Previous solid lithium conductor screening studies have either screened exclusively on ionic conductivity (ref. 90 and 109) or have screened on ionic conductivity and then calculated the band gap for the most promising candidates (ref. 108). Our results suggest that future materials design and screening may be most fruitful by placing more importance on screening for phase stability, high band gaps and wide electrochemical stability windows.An exciting aspect of this statistical approach that distinguishes it from DFT alone and current experimental approaches is that it provides a clear path forward toward identifying the best ion conductors. New data points can be readily incorporated into the model to improve its accuracy, potentially leading to a test set if enough data are available in the future. We expect a test set to provide an improved bound on understanding the predictive capability. Data points that will have the most impact on constraining the model can be readily identified by sparse regions in feature space; in this case the existing training set and model can function as a Bayesian prior in guiding the next round of data generation. Although the comparison to random shows our features have predictive power, better features that more accurately reflect the physics can be incorporated to improve the model. The misclassification rate is already relatively low for the present model, but better features are expected to reduce the total number of features required. An exact model for conductivity comprises a one-feature model.
The approach here also points up the need for scientists to report not just the best conductors, but the mediocre and poor conductors also. Including more poor conductors (<10−8 S cm−1) in the training set is likely to make significant improvements, especially in predicting materials in the low conductivity regime. To that end, the authors invite investigators to share their RT ionic conductivity measurements of poor Li conductors. As mentioned above, it also highlights the importance of characterizing the grain size and other variables that serve as unquantified error in the present model.
5. Conclusions
By screening the Materials Project database for materials that satisfy battery technological requirements of low electronic conductivity, robust stability, and low cost we reduce the number of candidate solid Li electrolyte materials from 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831 to approximately 300. By leveraging the limited existing data on lithium ion conductors in the literature, we develop a predictive model and several confidence metrics to provide a means for identifying the highest-confidence superionic conductivity predictions and thus a method for shortening this list to the 21 best candidates plus tens of additional notable candidates.
831 to approximately 300. By leveraging the limited existing data on lithium ion conductors in the literature, we develop a predictive model and several confidence metrics to provide a means for identifying the highest-confidence superionic conductivity predictions and thus a method for shortening this list to the 21 best candidates plus tens of additional notable candidates.
Interestingly, we find that among the materials in the Materials Project database, the prerequisite screening limits the number of candidate structures much more than the ionic conductivity screening, and thus we emphasize that future work in solid electrolyte design and discovery must take these prerequisite performance requirements into account. The identification of untested materials satisfying the screening requirements is exciting, but that only 21 of the 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831 starting materials satisfy all these requirements suggests that it is naturally and inherently difficult to perform the many-property optimization across structure space needed for high electrolyte performance.
831 starting materials satisfy all these requirements suggests that it is naturally and inherently difficult to perform the many-property optimization across structure space needed for high electrolyte performance.
Identification of the generalizable microscopic features that give rise to fast ion conduction has been a difficult problem to solve; using statistical learning techniques we discover correlations leading to better than random predictions of the best ionic conductors in a diverse training set. While there are clearly correlations, the small size of the available experimental data makes the accuracy of these generalizations challenging to precisely predict. The model proposed here will only improve in time as more experimental data is reported and better features are proposed. We expect that the model described here will change, potentially significantly, as more data becomes available.
Toward this goal, we recommend the experimental community to characterize and report the grain size in the polycrystalline samples for which ionic conductivity is measured, as this is likely to affect the outcome of the ionic conductivity measurement and can therefore influence the accuracy of structure-based models. With a clear path forward to improvement, we present the superionic classification models described here as the first step towards a robust data-driven model for pinpointing promising solid electrolyte structures.
Acknowledgements
A. D. S. acknowledges funding from the Stanford University Office of Technology Licensing Fellowship through the Stanford Graduate Fellowship program and the TomKat Center for Sustainable Energy. The authors acknowledge useful questions and comments from Prof. Stefan Adams of the National University of Singapore. The authors also thank Peter Attia, Matt van den Berg, William Gent, Yuan Shen, and Yao Zhou for their many helpful contributions.References
- S. S. Zhang, J. Power Sources, 2006, 162, 1379–1394 CrossRef CAS.
- U. von Sacken, E. Nodwell, A. Sundher and J. R. Dahn, J. Power Sources, 1995, 54, 240–245 CrossRef CAS.
- J. Vetter, P. Novák, M. R. Wagner, C. Veit, K.-C. Möller, J. O. Besenhard, M. Winter, M. Wohlfahrt-Mehrens, C. Vogler and A. Hammouche, J. Power Sources, 2005, 147, 269–281 CrossRef CAS.
- D. Aurbach, J. Power Sources, 2000, 89, 206–218 CrossRef CAS.
- C. Monroe and J. Newman, J. Electrochem. Soc., 2005, 152, A396–A404 CrossRef CAS.
- V. Aravindan, J. Gnanaraj, S. Madhavi and H.-K. Liu, Chem. – Eur. J., 2011, 17, 14326–14346 CrossRef CAS PubMed.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682–686 CrossRef CAS PubMed.
- G. Nazri, Solid State Ionics, 1989, 34, 97–102 CrossRef CAS.
- A. Hayashi, K. Minami, F. Mizuno and M. Tatsumisago, J. Mater. Sci., 2008, 43, 1885–1889 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 11002 CrossRef.
- R. Jalem, M. Nakayama and T. Kasuga, J. Mater. Chem. A, 2014, 2, 720–734 CAS.
- K. Fujimura, A. Seko, Y. Koyama, A. Kuwabara, I. Kishida, K. Shitara, C. A. J. Fisher, H. Moriwake and I. Tanaka, Adv. Energy Mater., 2013, 3, 980–985 CrossRef CAS.
- G. Hautier, C. C. Fischer, A. Jain, T. Mueller and G. Ceder, Chem. Mater., 2010, 22, 3762–3767 CrossRef CAS.
- P. V. Balachandran, S. R. Broderick and K. Rajan, Proc. R. Soc. A, 2011, 467, 2271–2290 CrossRef CAS PubMed.
- B. Meredig, A. Agrawal, S. Kirklin, J. E. Saal, J. W. Doak, A. Thompson, K. Zhang, A. Choudhary and C. Wolverton, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 94104 CrossRef.
- O. A. von Lilienfeld, Int. J. Quantum Chem., 2013, 113, 1676–1689 CrossRef CAS.
- P. Raccuglia, K. C. Elbert, P. D. F. Adler, C. Falk, M. B. Wenny, A. Mollo, M. Zeller, S. A. Friedler, J. Schrier and A. J. Norquist, Nature, 2016, 533, 73–76 CrossRef CAS PubMed.
- C. Schütter, T. Husch, V. Viswanathan, S. Passerini, A. Balducci and M. Korth, J. Power Sources, 2016, 326, 541–548 CrossRef.
- T. Husch and M. Korth, Phys. Chem. Chem. Phys., 2015, 17, 22596–22603 RSC.
- C. Schütter, T. Husch, M. Korth and A. Balducci, J. Phys. Chem. C, 2015, 119, 13413–13424 Search PubMed.
- X. Qu, A. Jain, N. N. Rajput, L. Cheng, Y. Zhang, S. P. Ong, M. Brafman, E. Maginn, L. A. Curtiss and K. A. Persson, Comput. Mater. Sci., 2015, 103, 56–67 CrossRef CAS.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- M. A. Green, J. Appl. Phys., 1990, 67, 2944–2954 CrossRef CAS.
- M. K. Y. Chan and G. Ceder, Phys. Rev. Lett., 2010, 105, 196403 CrossRef CAS PubMed.
- W. D. Richards, L. J. Miara, Y. Wang, J. C. Kim and G. Ceder, Chem. Mater., 2016, 28, 266–273 CrossRef CAS.
- B. D. McCloskey, J. Phys. Chem. Lett., 2015, 6, 4581–4588 CrossRef CAS PubMed.
- Wikipedia Free Encycl., 2016.
- Wikipedia Free Encycl., 2016.
- R. Jimenez, A. Rivera, A. Varez and J. Sanz, Solid State Ionics, 2009, 180, 1362–1371 CrossRef CAS.
- S. Hori, S. Taminato, K. Suzuki, M. Hirayama, Y. Kato and R. Kanno, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2015, 71, 727–736 CAS.
- A. Kuhn, J. Köhler and B. V. Lotsch, Phys. Chem. Chem. Phys., 2013, 15, 11620–11622 RSC.
- P. G. Bruce and A. R. West, J. Electrochem. Soc., 1983, 130, 662–669 CrossRef CAS.
- H. Y.-P. Hong, Mater. Res. Bull., 1978, 13, 117–124 CrossRef CAS.
- I. Abrahams, P. G. Bruce, A. R. West and W. I. F. David, J. Solid State Chem., 1988, 75, 390–396 CrossRef CAS.
- W. Li, G. Wu, Z. Xiong, Y. P. Feng and P. Chen, Phys. Chem. Chem. Phys., 2012, 14, 1596–1606 RSC.
- S. Bhattacharya, G. Wu, C. Ping, Y. P. Feng and G. P. Das, J. Phys. Chem. B, 2008, 112, 11381–11384 CrossRef CAS PubMed.
- B. E. Liebert and R. A. Huggins, Mater. Res. Bull., 1976, 11, 533–538 CrossRef CAS.
- H. Völlenkle, A. Wittmann and H. Nowotny, Monatshefte Für Chem. Chem. Mon, 1970, 101, 46–56 CrossRef.
- K. Ohoyama, Y. Nakamori, S. Orimo and K. Yamada, J. Phys. Soc. Jpn., 2005, 74, 483–487 CrossRef CAS.
- Z. Lin, Z. Liu, N. J. Dudney and C. Liang, ACS Nano, 2013, 7, 2829–2833 CrossRef CAS PubMed.
- A. Claassen, Recl. Trav. Chim. Pays-Bas, 1925, 44, 790–794 CrossRef.
- R. D. Shannon, B. E. Taylor, A. D. English and T. Berzins, Electrochim. Acta, 1977, 22, 783–796 CrossRef CAS.
- A. N. Fitch, B. E. F. Fender and J. Talbot, J. Solid State Chem., 1984, 55, 14–22 CrossRef CAS.
- H. Hosono, Y. Mishima, H. Takezoe and K. J. D. MacKenzie, Nanomaterials: Research Towards Applications, Elsevier, 2006 Search PubMed.
- I. Abrahams and P. G. Bruce, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 696–701 CrossRef.
- I. Abrahams, P. G. Bruce, W. I. F. David and A. R. West, Acta Crystallogr., Sect. B: Struct. Sci., 1989, 45, 457–462 CrossRef.
- E. I. Burmakin, V. I. Voronin and G. S. Shekhtman, Russ. J. Electrochem., 2003, 39, 1124–1129 CrossRef CAS.
- A. K. Ivanov-Shits and I. V. Murin, Solid State Ion, St Petersburg St Petersburg State Univ., 2000, vol. 1 Search PubMed.
- S. Patoux, C. Wurm, M. Morcrette, G. Rousse and C. Masquelier, J. Power Sources, 2003, 119–121, 278–284 CrossRef CAS.
- W. Li, G. Wu, C. M. Araújo, R. H. Scheicher, A. Blomqvist, R. Ahuja, Z. Xiong, Y. Feng and P. Chen, Energy Environ. Sci., 2010, 3, 1524–1530 CAS.
- A. Rabenau and H. Schulz, J. Less-Common Met., 1976, 50, 155–159 CrossRef CAS.
- Y. Dong and F. J. DiSalvo, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2007, 63, i97–i98 CAS.
- M. Tachez, J.-P. Malugani, R. Mercier and G. Robert, Solid State Ionics, 1984, 14, 181–185 CrossRef CAS.
- K. Homma, M. Yonemura, T. Kobayashi, M. Nagao, M. Hirayama and R. Kanno, Solid State Ionics, 2011, 182, 53–58 CrossRef CAS.
- X. Xu, Z. Wen, X. Yang and L. Chen, Mater. Res. Bull., 2008, 43, 2334–2341 CrossRef CAS.
- T. Suzuki, K. Yoshida, K. Uematsu, T. Kodama, K. Toda, Z.-G. Ye, M. Ohashi and M. Sato, Solid State Ionics, 1998, 113–115, 89–96 CrossRef CAS.
- X. Song, M. Jia and R. Chen, J. Mater. Process. Technol., 2002, 120, 21–25 CrossRef CAS.
- R. D. Shannon and C. Calvo, J. Solid State Chem., 1973, 6, 538–549 CrossRef CAS.
- W. Jeitschko, T. A. Bither and P. E. Bierstedt, Acta Crystallogr., Sect. B: Struct. Sci., 1977, 33, 2767–2775 CrossRef.
- M. Matsuo, A. Remhof, P. Martelli, R. Caputo, M. Ernst, Y. Miura, T. Sato, H. Oguchi, H. Maekawa, H. Takamura, A. Borgschulte, A. Züttel and S. Orimo, J. Am. Chem. Soc., 2009, 131, 16389–16391 CrossRef CAS PubMed.
- P. A. Chater, W. I. F. David, S. R. Johnson, P. P. Edwards and P. A. Anderson, Chem. Commun., 2006, 2439 RSC.
- R. Hofmann and R. Hoppe, Z. Für Anorg. Allg. Chem, 1987, 555, 118–128 CrossRef CAS.
- W. H. Baur and T. Ohta, J. Solid State Chem., 1982, 44, 50–59 CrossRef CAS.
- R. Murugan, W. Weppner, P. Schmid-Beurmann and V. Thangadurai, Mater. Sci. Eng., B, 2007, 143, 14–20 CrossRef CAS.
- V. Thangadurai, H. Kaack and W. J. F. Weppner, J. Am. Ceram. Soc., 2003, 86, 437–440 CrossRef CAS.
- E. J. Cussen, Chem. Commun. Camb. Engl, 2006, 412–413 RSC.
- P. Hartwig, W. Weppner, W. Wichelhaus and A. Rabenau, Angew. Chem., Int. Ed. Engl., 1980, 19, 74–75 CrossRef.
- H. Sattlegger and H. Hahn, Naturwissenschaften, 1964, 51, 534–535 CrossRef CAS.
- V. Thangadurai and W. Weppner, Adv. Funct. Mater., 2005, 15, 107–112 CrossRef CAS.
- W. G. Zeier, S. Zhou, B. Lopez-Bermudez, K. Page and B. C. Melot, ACS Appl. Mater. Interfaces, 2014, 6, 10900–10907 CAS.
- H. D. Lutz, P. Kuske and K. Wussow, Z. Für Anorg. Allg. Chem, 1987, 553, 172–178 CrossRef CAS.
- E. Riedel, D. Prick, A. Pfitzner and H. D. Lutz, Z. Für Anorg. Allg. Chem, 1993, 619, 901–904 CrossRef CAS.
- R. Marx and R. M. Ibberson, J. Alloys Compd., 1997, 261, 123–131 CrossRef CAS.
- R. Murugan, V. Thangadurai and W. Weppner, Angew. Chem., Int. Ed., 2007, 46, 7778–7781 CrossRef CAS PubMed.
- C. A. Geiger, E. Alekseev, B. Lazic, M. Fisch, T. Armbruster, R. Langner, M. Fechtelkord, N. Kim, T. Pettke and W. Weppner, Inorg. Chem., 2011, 50, 1089–1097 CrossRef CAS PubMed.
- H. Yamane, M. Shibata, Y. Shimane, T. Junke, Y. Seino, S. Adams, K. Minami, A. Hayashi and M. Tatsumisago, Solid State Ionics, 2007, 178, 1163–1167 CrossRef CAS.
- H. Oguchi, M. Matsuo, T. Sato, H. Takamura, H. Maekawa, H. Kuwano and S. Orimo, J. Appl. Phys., 2010, 107, 96104 CrossRef.
- N. Sklar and B. Post, Inorg. Chem., 1967, 6, 669–671 CrossRef CAS.
- I. D. Raistrick, C. Ho and R. A. Huggins, Mater. Res. Bull., 1976, 11, 953–957 CrossRef CAS.
- V. Tscherry, H. Schulz and F. Laves, Z. Für Krist. – Cryst. Mater, 2015, 135, 175–198 Search PubMed.
- J.-P. Soulié, G. Renaudin, R. Černý and K. Yvon, J. Alloys Compd., 2002, 346, 200–205 CrossRef.
- D. Fischer, A. Müller and M. Jansen, Z. Für Anorg. Allg. Chem, 2004, 630, 2697–2700 CrossRef CAS.
- J. B. Yang, X. D. Zhou, Q. Cai, W. J. James and W. B. Yelon, Appl. Phys. Lett., 2006, 88, 41914 CrossRef.
- M. Catti, S. Stramare and R. Ibberson, Solid State Ionics, 1999, 123, 173–180 CrossRef CAS.
- A. Belsky, M. Hellenbrandt, V. L. Karen and P. Luksch, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 364–369 CrossRef.
- S. Hull, Rep. Prog. Phys., 2004, 67, 1233 CrossRef CAS.
- R. C. Agrawal and R. K. Gupta, J. Mater. Sci., 1999, 34, 1131–1162 CrossRef CAS.
- M. Avdeev, V. B. Nalbandyan and I. L. Shukaev, in Solid State Electrochemistry I, ed. V. V. Kharton, Wiley-VCH Verlag GmbH & Co. KGaA, 2009, pp. 227–278 Search PubMed.
- R. A. Huggins, Advanced Batteries, Springer US, Boston, MA, 2009 Search PubMed.
- Y. Wang, W. D. Richards, S. P. Ong, L. J. Miara, J. C. Kim, Y. Mo and G. Ceder, Nat. Mater., 2015, 14, 1026–1031 CrossRef CAS PubMed.
- K. Roy, S. Kar and R. N. Das, A Primer on QSAR/QSPR Modeling, Springer International Publishing, Cham, 2015 Search PubMed.
- G. James, D. Witten, T. Hastie and R. Tibshirani, An Introduction to Statistical Learning, Springer, 1st edn, 2013 Search PubMed.
- C. Rücker, G. Rücker and M. Meringer, J. Chem. Inf. Model., 2007, 47, 2345–2357 CrossRef PubMed.
- H. Abdi and L. J. Williams, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2010, 2, 433–459 CrossRef.
- H. Wada, M. Menetrier, A. Levasseur and P. Hagenmuller, Mater. Res. Bull., 1983, 18, 189–193 CrossRef CAS.
- Y. Tomita, H. Matsushita, K. Kobayashi, Y. Maeda and K. Yamada, Solid State Ionics, 2008, 179, 867–870 CrossRef CAS.
- K. Yamada, K. Kumano and T. Okuda, Solid State Ionics, 2006, 177, 1691–1695 CrossRef CAS.
- R. Court-Castagnet, C. Kaps, C. Cros and P. Hagenmuller, Solid State Ionics, 1993, 61, 327–334 CrossRef CAS.
- G. M. Christie and F. P. F. van Berkel, Solid State Ionics, 1996, 83, 17–27 CrossRef CAS.
- Y. Zhao and L. L. Daemen, J. Am. Chem. Soc., 2012, 134, 15042–15047 CrossRef CAS PubMed.
- M. Schneider, P. Kuske and H. D. Lutz, Z. Für Naturforschung B, 1993, 48, 1–6 CrossRef CAS.
- H. D. Lutz, W. Schmidt and H. Haeuseler, J. Phys. Chem. Solids, 1981, 42, 287–289 CrossRef CAS.
- R. Kanno, Y. Takeda and O. Yamamoto, Mater. Res. Bull., 1981, 16, 999–1005 CrossRef CAS.
- R. Kanno, Y. Takeda, O. Yamamoto, C. Cros, W. Gang and P. Hagenmuller, J. Electrochem. Soc., 1986, 133, 1052–1056 CrossRef CAS.
- N. Ding, J. Xu, Y. X. Yao, G. Wegner, X. Fang, C. H. Chen and I. Lieberwirth, Solid State Ionics, 2009, 180, 222–225 CrossRef CAS.
- C.-Y. Chou and G. S. Hwang, J. Power Sources, 2014, 263, 252–258 CrossRef CAS.
- E. D. Cubuk and E. Kaxiras, Nano Lett., 2014, 14, 4065–4070 CrossRef CAS PubMed.
- R. Xiao, H. Li and L. Chen, J. Materiomics, 2015, 1, 325–332 CrossRef.
- N. A. Anurova, V. A. Blatov, G. D. Ilyushin, O. A. Blatova, A. K. Ivanov-Schitz and L. N. Dem'yanets, Solid State Ionics, 2008, 179, 2248–2254 CrossRef CAS.
- T. Seddik, R. Khenata, A. Bouhemadou, D. Rached, D. Varshney and S. Bin-Omran, Comput. Mater. Sci., 2012, 61, 206–212 CrossRef CAS.
- S. Adams, J. Power Sources, 2006, 159, 200–204 CrossRef CAS.
- S. Adams and J. Swenson, Phys. Rev. Lett., 2000, 84, 4144–4147 CrossRef CAS PubMed.
- S. Adams, Solid State Ionics, 2000, 136–137, 1351–1361 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ee02697d |
| This journal is © The Royal Society of Chemistry 2017 |