Large d–d luminescence energy variations in square-planar bis(dithiocarbamate) platinum(II) and palladium(II) complexes with near-identical MS4 motifs: a variable-pressure study†
Stéphanie
Poirier
,
Feriel
Rahmani
and
Christian
Reber
 *
*
Département de chimie, Université de Montréal, Montréal, Québec H3C 3J7, Canada. E-mail: christian.reber@umontreal.ca
First published on 28th March 2017
Abstract
We present the variable-pressure luminescence spectra of crystals of isostructural palladium(II) and platinum(II) complexes with bis-N-benzyl-N′-3-methylpyridyldithiocarbamate (bmpDTC) ligands. The d–d luminescence band maxima Emax for these complexes are compared to others with different peripheral substituents on the dithiocarbamate ligands in the solid state. The comparison reveals significant variations of Emax despite very similar metal coordination geometries. Emax varies by 3000 cm−1 and 1300 cm−1 among four dithiocarbamate complexes of platinum(II) and palladium(II), respectively. Variations of Emax with pressure reveal the effects of intermolecular M⋯H–C interactions on several complexes. ΔEmax/ΔP values are negative for the bmpDTC complexes, unprecedented in the dithiocarbamate family. Static orientation and pressure-induced movement of the C–H bonds involved in intermolecular interactions have a significant effect on Emax and ΔEmax/ΔP, with a stronger impact on platinum(II) complexes than on their palladium(II) analogs.
Introduction
Square-planar complexes with d8 metal centers are an important class of luminophores.1–4 Significant variations of the luminescence properties can be achieved by variation of ligands and through metal–metal interactions,2,5–8 resulting in luminescence throughout the UV-vis to near IR wavelength range.1,2 This wavelength tunability is relevant for OLED applications.3,9,10 The luminescence spectra are sensitive to structural changes in the local environment of the emitting complex, induced by variations of pressure,11 temperature,12 or exposure to solvent vapors,13,14 making them potential sensors.15The simplest luminescence spectra involve d–d transitions. Ligand-field theory predicts identical energies if ligands, metal–ligand distances and L–M–L angles are identical. Different ligands lead to variations according to the spectrochemical series.16,17 This is illustrated by the comparison of luminescence maxima Emax for crystalline K2[PtBr4] and K2[PtCl4] at approximately 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 (800 nm)18 and 12
500 cm−1 (800 nm)18 and 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 cm−1 (780 nm),18 respectively, with Emax higher by 300 cm−1 for the stronger-field chloride ligands. The square-planar coordination geometry enables intermolecular interactions due to the empty coordination sites above and below the MX4 plane.1–4 Molecular crystals can be used to obtain experimental insight on both molecular luminescence properties and weak intermolecular interactions. Such interactions define many properties of chemical systems.19–22 In inorganic complexes, M⋯H–C interactions have been reported based on crystal structures,20,23,24 identified according to the established distance range of 2.3 to 2.9 Å and specific shifts of 1H NMR peaks23 in solution, the latter being limited to intramolecular effects and not applicable to intermolecular interactions in solids. Precise H positions are experimentally difficult to obtain from X-ray diffraction, leading to significant uncertainties. Intermolecular distances at ambient conditions do not lead to quantitative understanding of intermolecular interactions.25–27 In addition, these weak interactions are challenging to characterize with electronic structure calculations,26 illustrating the need for detailed experimental results.
800 cm−1 (780 nm),18 respectively, with Emax higher by 300 cm−1 for the stronger-field chloride ligands. The square-planar coordination geometry enables intermolecular interactions due to the empty coordination sites above and below the MX4 plane.1–4 Molecular crystals can be used to obtain experimental insight on both molecular luminescence properties and weak intermolecular interactions. Such interactions define many properties of chemical systems.19–22 In inorganic complexes, M⋯H–C interactions have been reported based on crystal structures,20,23,24 identified according to the established distance range of 2.3 to 2.9 Å and specific shifts of 1H NMR peaks23 in solution, the latter being limited to intramolecular effects and not applicable to intermolecular interactions in solids. Precise H positions are experimentally difficult to obtain from X-ray diffraction, leading to significant uncertainties. Intermolecular distances at ambient conditions do not lead to quantitative understanding of intermolecular interactions.25–27 In addition, these weak interactions are challenging to characterize with electronic structure calculations,26 illustrating the need for detailed experimental results.
A promising new approach involves the use of variable pressure on the solid samples to shorten M⋯H–C distances and gain experimental insight on characteristic spectroscopic shifts.25 Variable pressure is used to induce small structural variations leading to significant spectroscopic changes.28–30 We have recently shown that M⋯H–C interactions can be experimentally characterized by luminescence spectroscopy at variable pressure,31 with significantly wider variations occurring than in vibrational spectroscopy. It is advantageous that luminescence is observed only from the lowest excited state, according to Kasha's rule, eliminating problems due to overlapping bands.32 For many square-planar complexes, increasing pressure shifts Emax to higher energies, a consequence of metal–ligand bond compression. This is easily understood from ligand-field theory and orbital characteristics: shorter metal–ligand bonds lead to stronger destabilization of the LUMO, with M–S σ* character, than of the HOMO with π* character, resulting in positive ΔEmax/ΔP values.33,34 A series of complexes with chelating ligands have been studied and average trends have been determined for this effect, giving an average ΔEmax/ΔP value of +12 ± 2 cm−1/kbar for the shift of d–d luminescence transitions.31 Deviations from this average allow us to identify the effects of M⋯H–C interactions, yielding additional quantitative information beyond intermolecular distances from crystal structures at ambient conditions. These interactions have a significant impact on the luminescence energy, even though they are weaker than metal–ligand bonds.
We present isostructural palladium(II) and platinum(II) complexes with bis-N-benzyl-N′-3-methylpyridyldithiocarbamate (bmpDTC) ligands, showing M⋯H–C interactions from a CH2 group of a neighbouring ligand in the crystal structure. Surprising differences to other dithiocarbamate complexes with variable substituents but similar metal coordination geometry are observed. An important variation of Emax by 3000 cm−1 at ambient conditions is measured for platinum(II) dithiocarbamates. The variation observed for the palladium(II) analogs is smaller by a factor of two. We use luminescence spectroscopy at variable pressure to understand the differences.
Experimental
Synthesis
Pt(N-benzyl-N′-3-methylpyridyldithiocarbamate)2 ([Pt(bmpDTC)2]) and Pd(N-benzyl-N′-3-methylpyridyldithiocarbamate)2 ([Pd(bmpDTC)2]) were synthesized according to literature procedures.35 All reagents and solvents were used as received, without further purification.Metal chloride (0.0721 g of PtCl2 and 0.0575 g of PdCl2) was dissolved in a minimum (about 125 mL for PtCl2 and 70 mL for PdCl2) of dimethylsulfoxide (DMSO). Four equivalents (0.0432 g) of sodium hydroxide (NaOH) were dissolved in a minimum (about 25 mL) of ethanol 95%, with crushing and heating. An excess of carbon disulfide (0.3 mL) was added to the solution of sodium hydroxide. Two equivalents of the amine (0.1 mL, 0.1071 g) in the form of liquid N-nicotinylbenzylamine were mixed to the solution of sodium hydroxide to form the ligand in the form of N-benzyl-N′-3-methylpyridyldithiocarbamate. A powder (yellow for [Pt(bmpDTC)2], orange for [Pd(bmpDTC)2]) precipitates from the combination of N-benzyl-N′-3-methylpyridyldithiocarbamate solution and metal solution. The powder is filtered and washed with diethyl ether. Single crystals were obtained by slow cooling of the solutions in acetone. The crystals were collected with a yield of 58% for [Pt(bmpDTC)2] and 22% for [Pd(bmpDTC)2].
X-ray crystallography
Single crystals of C28H26N4PdS4 and C28H26N4PtS4 were mounted on a loop fiber and diffraction data was collected with a Bruker Venture Metaljet diffractometer equipped with a Photon 100 CMOS Detector, a Helios MX optics and a Kappa goniometer. The crystal-to-detector distance was 4.0 cm, and the data collection was carried out in 1024 × 1024 pixel mode. The crystals were kept at 295 K during data collection. Using Olex2,36 the structures were solved with the XT37 structure solution program using Direct Methods and refined with the XL38 refinement package using least squares minimization. The full structure was determined for C28H26N4PtS4 at 295 and 150 K. Only the unit cell parameters were measured for C28H26N4PdS4 to confirm the published structure.35Spectroscopy
Luminescence and Raman spectra of [Pt(bmpDTC)2] and [Pd(bmpDTC)2] were measured using a Renishaw InVia spectrometer with a Leica imaging microscope. Excitation wavelengths of 488 nm (argon ion laser) for luminescence measurements and of 785 nm (diode laser) for Raman measurements were used. A gas-flow microcryostat LINKAM system was used to vary the temperature of the sample. A gasketed diamond-anvil cell (DAC, High-Pressure Diamond Optics) was used to apply increasing pressure on the samples. Crystals were loaded in a steel gasket filled with Nujol oil added for pressure-transmitting. Ruby was added in the gasket in order to calibrate pressure.39 The spectrometer is calibrated with a tungsten lamp and luminescence spectra are corrected for system response.Results
Fig. 1 shows the structure of [Pt(bmpDTC)2] measured at room temperature. Crystallographic data are presented in Table 1. The structure is similar to the published palladium(II) analog,35 as compared in Table 2. These square-planar complexes have an inversion center and a MS4 motif with in-plane S–M–S angles of approximately 75° due to the chelating dithiocarbamate (DTC) ligands,12,35,40–42 summarized in Table 3 for platinum(II) bis-di(o-pyridyl)dithiocarbamate [Pt(dopDTC)2],40 platinum(II) and palladium(II) bis-diethyldithiocarbamate [M(EDTC)2],41 platinum(II) and palladium(II) bis-dimethyldithiocarbamate [M{(CH3)2DTC}2]12,31 and palladium(II) bis-pyrrolidine-N-dithiocarbamate [Pd(PDTC)2].41 M–S bond lengths also fall within the typical range of DTC values presented in Table 3, with values of approximately 2.32 Å for platinum(II) and 2.34 Å for palladium(II). In both [M(bmpDTC)2] complexes, short contacts between the metal and a hydrogen atom from a CH2 group of a neighbouring ligand are present, with an intermolecular distance of 2.81 Å for platinum(II) and 2.79 Å for palladium(II). Other square-planar d8 DTC complexes have been reported to show M⋯H–C interactions,35,43,44 such as complexes with methyl substituents on the dithiocarbamate ligands with intermolecular M⋯H–C distances of 2.99 Å for [Pt{(CH3)2DTC}2]40 and 2.92 Å for [Pd{(CH3)2DTC}2].31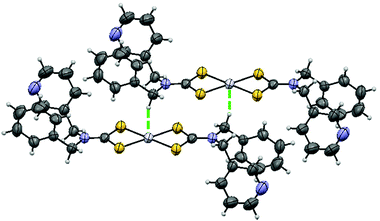 | ||
| Fig. 1 Crystal structure of [Pt(bmpDTC)2]. The thermal ellipsoids are shown at 50% probability. The Pt⋯H–C interaction is visualized by the green dotted line. | ||
| Temperature (K) | 295 | 150 |
|---|---|---|
| Empirical formula | C28H26N4PtS4 | C28H26N4PtS4 |
| M (g mol−1) | 741.86 | 741.86 |
| Temperature/K | 295 | 150 |
| Crystal system | Triclinic | Triclinic |
| Space group |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
| a/Å | 6.4927(15) | 6.4423(2) |
| b/Å | 10.115(3) | 10.0534(3) |
| c/Å | 11.568(3) | 11.5378(3) |
| α/° | 75.520(14) | 74.9490(10) |
| β/° | 79.620(13) | 80.0000(10) |
| γ/° | 72.223(13) | 71.4280(10) |
| Volume/Å3 | 696.0(3) | 680.67(3) |
| Z | 1 | 1 |
| ρ calc/g cm−3 | 1.770 | 1.810 |
| μ/mm−1 | 8.471 | 8.661 |
| F(000) | 364.0 | 364.0 |
| Crystal size/mm3 | 0.15 × 0.1 × 0.09 | 0.15 × 0.1 × 0.09 |
| Radiation | GaKα (λ = 1.34139) | GaKα (λ = 1.34139) |
| 2Θ range for data collection/° | 6.91 to 122.896 | 6.936 to 121.346 |
| Index ranges | −8 ≤ h ≤ 8, −13 ≤ k ≤ 13, −14 ≤ l ≤ 14 | −8 ≤ h ≤ 8, −13 ≤ k ≤ 13, −14 ≤ l ≤ 14 |
| Reflections collected | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 836 836 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 728 728 |
| Independent reflections | 3198 [Rint = 0.0466, Rsigma = 0.0226] | 3122 [Rint = 0.0443, Rsigma = 0.0187] |
| Data/restraints/parameters | 3198/0/169 | 3122/0/169 |
| Goodness-of-fit on F2 | 1.065 | 1.168 |
| Final R indexes [I ≥ 2σ(I)] | R 1 = 0.0407, wR2 = 0.1048 | R 1 = 0.0281, wR2 = 0.0672 |
| Final R indexes [all data] | R 1 = 0.0421, wR2 = 0.1063 | R 1 = 0.0283, wR2 = 0.0673 |
| Largest diff. peak/hole/e Å−3 | 1.66/−0.56 | 1.79/−0.68 |
| [Pt(bmpDTC)2] | [Pd(bmpDTC)2]35 | |
|---|---|---|
| Bond (Å) | ||
| M–S1 | 2.318(1) | 2.339(3) |
| M–S2 | 2.318(2) | 2.333(3) |
| S1–C | 1.729(5) | 1.749(7) |
| S2–C | 1.726(5) | 1.717(8) |
| C–N | 1.314(8) | 1.31(1) |
| N–C2 | 1.471(7) | 1.50(1) |
| N–C3 | 1.468(7) | 1.48(1) |
| Angles (°) | ||
| S1–M–S2 | 74.98(5) | 75.69(7) |
| S1–C1–S2 | 109.6(3) | 111.6(4) |
| Intermolecular distances (Å) | ||
| M⋯Ha–Ca | 2.8142(7) | 2.788(3) |
| M⋯Ca | 3.692(5) | 3.683(9) |
| M⋯Hb–Cb | 3.3417(8) | 3.473(4) |
| M⋯Cb | 3.989(5) | 4.118(9) |
| M⋯N | 3.912(4) | 3.973(7) |
| M⋯C | 4.500(5) | 4.557(8) |
| M⋯S1 | 5.165(2) | 5.124(6) |
| M⋯S2 | 5.478(2) | 5.584(6) |
| M⋯H–C (plane) | 4.047(1) | 4.055(5) |
| M⋯C (plane) | 4.528(7) | 4.53(1) |
| Metal | Ligand | ΔEmax /ΔP (cm−1/kbar) | Shortest intermolecular M⋯H–C (Å) | M–S1 (Å) | M–S2 (Å) | S1–M–S2 (°) | S1–M–S1 (°) | Ref. |
|---|---|---|---|---|---|---|---|---|
| Pt(II) | EDTC | +15 | 3.0581 | 2.321(2) | 2.314(2) | 75.22(6) | 180.00(6) | 54 |
| bmpDTC | −8 ± 3 | 2.8142(7) | 2.318(1) | 2.318(2) | 74.98(5) | 180.00(5) | This work | |
| (CH3)2DTC | +44 ± 5 | 2.9919(1) | 2.3290(8) | 2.3126(8) | 75.13(3) | 180.00(3) | 12 | |
| dopDTC | +11 ± 1 | 3.193(1) | 2.322(4) | 2.330(6) | 74.7(2) | 174.0(2), 176.3(2) | 40 | |
| Pd(II) | EDTC | +9 | 41 | |||||
| PDTC | +13 | 2.9457(4) | 2.353(2) | 2.343(2) | 75.69(8) | 180.00(8) | 41 | |
| bmpDTC | −2 ± 1 | 2.788(3) | 2.339(3) | 2.333(3) | 75.69(7) | 180.00(7) | This work | |
| (CH3)2DTC | +32 ± 3 | 2.9216(8) | 2.337(1) | 2.309(1) | 75.52(3) | 180.00(3) | 12 | |
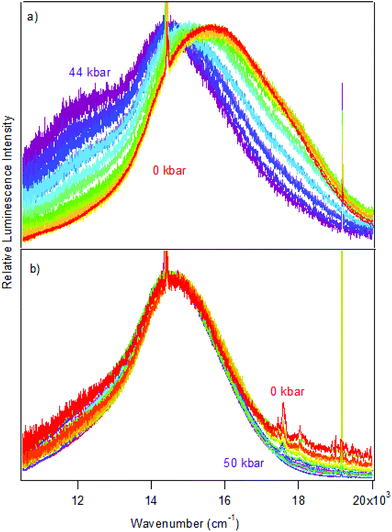
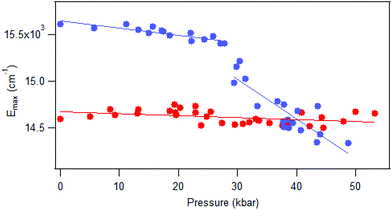
Luminescence spectra measured on crystals at variable pressure are presented in Fig. 2. Broad bands are observed, which is typical for the d–d transitions reported for dithiocarbamate complexes.42 For [Pt(bmpDTC)2], the luminescence maximum at ambient pressure appears at approximately 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cm−1 and shifts to lower energy as pressure increases. Two ΔEmax/ΔP values are measured in two different pressure ranges: −8 ± 1 cm−1/kbar from 0 to 28 kbar and −42 ± 6 cm−1/kbar from 28 to 49 kbar, as seen in Fig. 3. To the best of our knowledge, these are the first negative ΔEmax/ΔP values measured for platinum(II) dithiocarbamate complexes, as documented in Table 3, strongly deviating from the average ΔEmax/ΔP value of +12 ± 2 cm−1/kbar. The intensity of the luminescence spectra decreases significantly with increasing pressure, as seen in Fig. S1,† leading to the higher noise on the low-energy side of the spectra at pressures above 30 kbar in Fig. 2 where spectra are plotted with matching maximum intensities. This decreasing luminescence intensity at high pressure is a common phenomenon for crystalline samples, caused by increasingly efficient non-radiative relaxation processes. Energy transfer from excited molecules to pressure-induced defects acting as deep traps occurs, with both the number of defects and the efficiency of the energy transfer increasing with pressure. The intensity decrease does not affect the width of the luminescence bands, as illustrated by the constant full-widths at half-maximum (FWHM) in Fig. S2.†
600 cm−1 and shifts to lower energy as pressure increases. Two ΔEmax/ΔP values are measured in two different pressure ranges: −8 ± 1 cm−1/kbar from 0 to 28 kbar and −42 ± 6 cm−1/kbar from 28 to 49 kbar, as seen in Fig. 3. To the best of our knowledge, these are the first negative ΔEmax/ΔP values measured for platinum(II) dithiocarbamate complexes, as documented in Table 3, strongly deviating from the average ΔEmax/ΔP value of +12 ± 2 cm−1/kbar. The intensity of the luminescence spectra decreases significantly with increasing pressure, as seen in Fig. S1,† leading to the higher noise on the low-energy side of the spectra at pressures above 30 kbar in Fig. 2 where spectra are plotted with matching maximum intensities. This decreasing luminescence intensity at high pressure is a common phenomenon for crystalline samples, caused by increasingly efficient non-radiative relaxation processes. Energy transfer from excited molecules to pressure-induced defects acting as deep traps occurs, with both the number of defects and the efficiency of the energy transfer increasing with pressure. The intensity decrease does not affect the width of the luminescence bands, as illustrated by the constant full-widths at half-maximum (FWHM) in Fig. S2.†
The luminescence maxima of [Pd(bmpDTC)2] show a smaller shift to lower energy than for the platinum(II) analog, with a ΔEmax/ΔP value of −2 ± 1 cm−1/kbar as shown in Fig. 3. Its luminescence maximum at ambient pressure is at 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cm−1, lower in energy by approximately 1000 cm−1 than for the platinum(II) analog. The full-width at half-maximum (FWHM) is also lower than for the platinum(II) complex, with values of 2700 cm−1 and 4200 cm−1, respectively. These bandwidths are similar to values reported for other dithiocarbamate and thiocyanate complexes, between 2500 cm−1 for palladium(II) and 4000 cm−1 for platinum(II).41
600 cm−1, lower in energy by approximately 1000 cm−1 than for the platinum(II) analog. The full-width at half-maximum (FWHM) is also lower than for the platinum(II) complex, with values of 2700 cm−1 and 4200 cm−1, respectively. These bandwidths are similar to values reported for other dithiocarbamate and thiocyanate complexes, between 2500 cm−1 for palladium(II) and 4000 cm−1 for platinum(II).41
Raman spectra at variable pressure and temperature are shown in Fig. S3–S6.† The overall peak pattern stays constant, with broader peaks at higher temperature or pressure. We can use the published calculated spectra of [Pd{(CH3)2DTC}2]31 to assign matching peaks of [Pd(bmpDTC)2], namely those at 344 and 412 cm−1 assigned to the Pd–S asymmetric and symmetric stretching modes, respectively, and 892 and 1000 cm−1 to the symmetric and asymmetric C–S stretching modes. The stretching modes of the ligands are at approximately the same frequencies for the platinum(II) analog, but Pt–S stretching are expected to appear at higher energies. Peak maxima shift gradually to higher frequency with increasing pressure. The asymmetric C–S stretching frequency is presented in Fig. S7,† with shifts of +0.18 ± 0.01 cm−1/kbar and +0.22 ± 0.01 cm−1/kbar for [Pd(bmpDTC)2] and [Pt(bmpDTC)2], respectively. Broadening of the peaks with increasing pressure is also observed. A typical width changes from 5.6 to 8.1 cm−1 for [Pt(bmpDTC)2] and from 4.3 to 8.2 cm−1 for [Pd(bmpDTC)2], from ambient pressure to approximately 50 kbar for the same vibrational mode. This broadening is documented in the literature,45 attributed to crystal defects, and was previously reported for other dithiocarbamate complexes.41 The absence of any discontinuity in the pressure- or temperature-induced shifts of the peak maxima is evidence for the absence of phase transitions for both complexes, in particular for [Pt(bmpDTC)2] in the pressure range where the slope of the variable-pressure luminescence maxima changes in Fig. 3.
Discussion
According to the spectrochemical series, complexes with identical metal centers and ligator atoms are expected to show very similar ligand-field splittings and d–d transition energies. For square-planar complexes, the splitting can be precisely measured with luminescence spectroscopy. The luminescence energy for palladium(II) complexes is expected to be lower than for platinum(II) complexes, as documented by the Emax values in Fig. 4. The coordination geometries of all dithiocarbamate complexes compared in Fig. 4 are very similar and therefore only a small variation of the d–d transition energy is expected. The observed luminescence maxima at ambient pressure vary more among dithiocarbamate complexes than for complexes with different ligands, as summarized in Table S1.†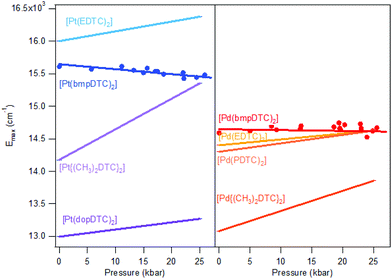 | ||
| Fig. 4 Comparison of ΔEmax/ΔP slopes for dithiocarbamate complexes of platinum(II) (left) and palladium(II) (right). Points represent luminescence maxima of Fig. 2. Lines are traced from ΔEmax/ΔP and Emax at ambient pressure from the literature. | ||
For platinum(II) complexes, a variation of Emax by approximately 3000 cm−1 is shown in Fig. 4, corresponding to a variation by 23%, induced only by varying the substituents on the periphery of the dithiocarbamate ligands. This is surprisingly high in view of the Emax variation by only 2% between K2[PtBr4] and K2[PtCl4] resulting from the different ligands. Even changing from a Br− ligand to a SCN− ligand induce a lower Emax variation of 17% than the difference observed among DTC complexes, as compared with K2[Pt(SCN)4], with a Emax of 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650 cm−1.46 Modification on the substituent on the periphery of ligands is not expected to induce higher energy changes than variation of the ligands itself, as supported by the spectrochemical series. The palladium(II) dithiocarbamate analogs show a lower Emax variation of 1300 cm−1 (12%) than their platinum(II) counterparts. This is also a more important variation of Emax than the one induced by variation of halide ligands between K2[PdBr4]47 and K2[PdCl4],47 which induce a 2% variation. The Emax variation for palladium(II) in DTC complexes is of the same order of magnitude as the change from K2[PdBr4] to (n-Bu4N)2[Pd(SCN)4],48 which is of 14%.
650 cm−1.46 Modification on the substituent on the periphery of ligands is not expected to induce higher energy changes than variation of the ligands itself, as supported by the spectrochemical series. The palladium(II) dithiocarbamate analogs show a lower Emax variation of 1300 cm−1 (12%) than their platinum(II) counterparts. This is also a more important variation of Emax than the one induced by variation of halide ligands between K2[PdBr4]47 and K2[PdCl4],47 which induce a 2% variation. The Emax variation for palladium(II) in DTC complexes is of the same order of magnitude as the change from K2[PdBr4] to (n-Bu4N)2[Pd(SCN)4],48 which is of 14%.
DFT calculations of the lowest-energy absorption maximum on single molecules of square-planar complexes show quantitatively comparable variations, indicating that the spectrochemical series theory is applicable to square-planar complexes.49 For instance, the calculated differences between absorption maxima are 900 cm−1 (10%) between [PtBr4]2− and [PtCl4]2− and 1500 cm−1 (16%) between [PtBr4]2− and [Pt(SCN)4]2−. For palladium(II), a 9% variation is calculated between [PdBr4]2− and [Pd(SCN)4]2−.49 In contrast, the surprising variation of Emax observed within the dithiocarbamate family can not be explained by the spectrochemical series. Clearly, other factors than the nature of the metal and ligator atoms have to be taken in account to understand the variation occurring in these complexes.
An important factor involved in the d–d luminescence energy of a single complex is the local symmetry at the metal site. The dithiocarbamate platinum(II) complex with the lowest Emax value (13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) in Fig. 4 is [Pt(dopDTC)2]. The substituents on the ligand of this complex induce a small distortion of the square-plane resulting in a τ4 value50 of 0.04, in contrast to all the other square-planar complexes analyzed here which have a τ4 value of 0 and perfect inversion symmetry. The τ4 value is the geometry index for ML4 complexes varying from square-planar (τ4 = 0) to tetrahedral (τ4 = 1), and is defined by:
000 cm−1) in Fig. 4 is [Pt(dopDTC)2]. The substituents on the ligand of this complex induce a small distortion of the square-plane resulting in a τ4 value50 of 0.04, in contrast to all the other square-planar complexes analyzed here which have a τ4 value of 0 and perfect inversion symmetry. The τ4 value is the geometry index for ML4 complexes varying from square-planar (τ4 = 0) to tetrahedral (τ4 = 1), and is defined by:
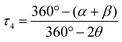 | (1) |
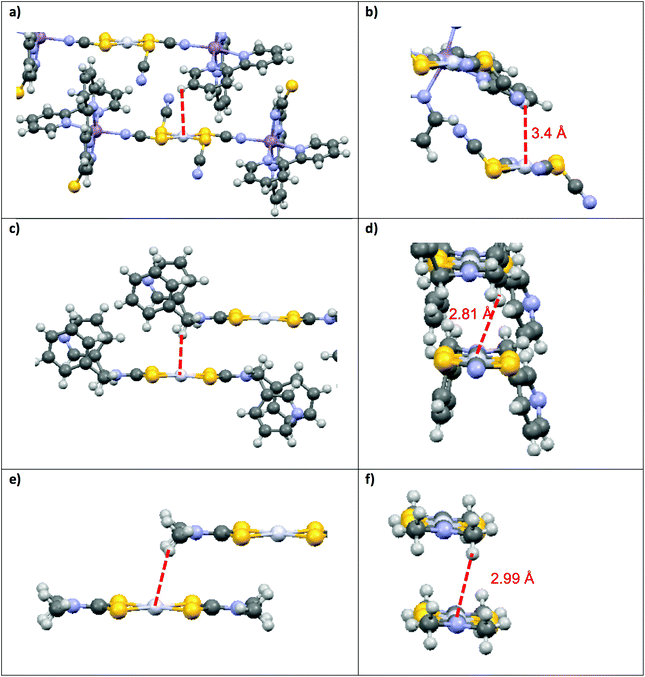
This structural distortion contributes to the variation of Emax values, but is not applicable to DTC complexes with perfect inversion symmetry. Their differences in Emax are due to external effects, such as M⋯H–C interactions. The highest Emax value reported in Fig. 4 for a square-planar platinum(II) DTC complex is 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 for [Pt(EDTC)2].41 In its crystal packing, there is no interaction with the metal since the closest C–H bond is poorly aligned, with a M⋯H distance of 3.06 Å. The HOMO–LUMO energy difference is therefore entirely due to the molecular structure, without additional contributions from intermolecular interactions. For the [Pt(bmpDTC)2] complex, the Emax value is 15
000 cm−1 for [Pt(EDTC)2].41 In its crystal packing, there is no interaction with the metal since the closest C–H bond is poorly aligned, with a M⋯H distance of 3.06 Å. The HOMO–LUMO energy difference is therefore entirely due to the molecular structure, without additional contributions from intermolecular interactions. For the [Pt(bmpDTC)2] complex, the Emax value is 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cm−1, lower in energy than for [Pt(EDTC)2]. A weak M⋯H–C interaction perpendicular to the MS4 plane is assumed (Fig. 5), as reported for the palladium(II) analog.35 Interaction with the dz2 orbital usually induces a destabilization of the HOMO level, decreasing the luminescence energy, in agreement with the lower Emax than for [Pt(EDTC)2]. The [Pt{(CH3)2DTC}2]12 complex shows an even lower Emax value of approximately 14
600 cm−1, lower in energy than for [Pt(EDTC)2]. A weak M⋯H–C interaction perpendicular to the MS4 plane is assumed (Fig. 5), as reported for the palladium(II) analog.35 Interaction with the dz2 orbital usually induces a destabilization of the HOMO level, decreasing the luminescence energy, in agreement with the lower Emax than for [Pt(EDTC)2]. The [Pt{(CH3)2DTC}2]12 complex shows an even lower Emax value of approximately 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1, indicating a more destabilized HOMO and, thus, a stronger M⋯H–C interaction. Even if the intermolecular Pt–H distance of 2.99 Å for [Pt{(CH3)2DTC}2] is longer than for [Pt(bmpDTC)2] with 2.81 Å, the alignment is more favorable to overlap with the dz2 electron density, as seen in Fig. 5d and f, rationalizing the different Emax values. For the palladium(II) complexes, Emax values at ambient pressure for [Pd(bmpDTC)2], [Pd(EDTC)2],41 and [Pd(PDTC)2]41 are very similar, within 300 cm−1, as shown in Fig. 4 and Table S1.† Both [Pd(EDTC)2] and [Pd(PDTC)2] show no short M⋯H–C distances in their crystal structure nor adequate alignment. [Pd(bmpDTC)2] shows a very similar Emax value, indicating that the reported35 Pd⋯H–C interaction is not strong enough at ambient pressure to significantly influence the HOMO energy of this complex. The Emax value alone is therefore not sufficient to identify the presence of M⋯H–C interactions in this system even though there is evidence from the crystal structure. The [Pd{(CH3)2DTC}2]12 complex shows Emax at 13
200 cm−1, indicating a more destabilized HOMO and, thus, a stronger M⋯H–C interaction. Even if the intermolecular Pt–H distance of 2.99 Å for [Pt{(CH3)2DTC}2] is longer than for [Pt(bmpDTC)2] with 2.81 Å, the alignment is more favorable to overlap with the dz2 electron density, as seen in Fig. 5d and f, rationalizing the different Emax values. For the palladium(II) complexes, Emax values at ambient pressure for [Pd(bmpDTC)2], [Pd(EDTC)2],41 and [Pd(PDTC)2]41 are very similar, within 300 cm−1, as shown in Fig. 4 and Table S1.† Both [Pd(EDTC)2] and [Pd(PDTC)2] show no short M⋯H–C distances in their crystal structure nor adequate alignment. [Pd(bmpDTC)2] shows a very similar Emax value, indicating that the reported35 Pd⋯H–C interaction is not strong enough at ambient pressure to significantly influence the HOMO energy of this complex. The Emax value alone is therefore not sufficient to identify the presence of M⋯H–C interactions in this system even though there is evidence from the crystal structure. The [Pd{(CH3)2DTC}2]12 complex shows Emax at 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, lower in energy by approximately 1400 cm−1 than for complexes with no interaction, indicative of stronger Pd⋯H–C interactions in this complex. For the platinum(II) complexes, the corresponding difference is 1800 cm−1 between [Pt(EDTC)2] and [Pt{(CH3)2DTC}2]. The platinum(II) dithiocarbamate complexes show bigger variations of Emax due to M⋯H–C interactions than their palladium(II) analogs.
000 cm−1, lower in energy by approximately 1400 cm−1 than for complexes with no interaction, indicative of stronger Pd⋯H–C interactions in this complex. For the platinum(II) complexes, the corresponding difference is 1800 cm−1 between [Pt(EDTC)2] and [Pt{(CH3)2DTC}2]. The platinum(II) dithiocarbamate complexes show bigger variations of Emax due to M⋯H–C interactions than their palladium(II) analogs.
Variable-pressure luminescence spectra allow us to characterize the impact of intermolecular interactions by comparing the ΔEmax/ΔP values for the compounds discussed here by determining deviations from the +12 ± 2 cm−1/kbar average. For [M(bmpDTC)2] complexes, shifts to lower energy are observed, which is unusual for dithiocarbamate complexes, as documented in Table 3. The only other dithiocarbamate complex with such a shift to lower energy is [Pd{(CH3)2DTC}2] in the 50 to 85 kbar range with a ΔEmax/ΔP value of −31 ± 8 cm−1/kbar.31 Only one other palladium(II) complex with a negative ΔEmax/ΔP value is known: [Pd{PyCHC(C3F7)O}2],51 a complex with chelating ligands with O and N ligator atoms, with a ΔEmax/ΔP value of −15 ± 7 cm−1/kbar, again due to an Pd⋯H–C interaction. Several negative ΔEmax/ΔP values have been reported for platinum(II) complexes, namely for Mx[Pt(CN)4]·mH2O,5 showing values from −320 to −140 cm−1/kbar caused by efficient overlap of dz2 orbitals of neighbouring platinum(II) ions. A relevant example is [Pt(SCN)2{(μ-SCN)Mn(NCS)(bipy)2}2],52 with a ΔEmax/ΔP value of −99 cm−1/kbar due to Pt⋯H–C interactions illustrated in Fig. 5a and b. Negative values of ΔEmax/ΔP arise from extended destabilization of the HOMO as pressure increases by shortening of the intermolecular distances. This comparison of ΔEmax/ΔP values places [M(bmpDTC)2] complexes intermediate between complexes without interaction (ΔEmax/ΔP of +12 ± 2 cm−1/kbar) and complexes with strong M⋯H–C interactions (−99 cm−1/kbar). In the crystal structures of the [M(bmpDTC)2] complexes, the hydrogen atom is slightly misaligned with the metal, as seen in Fig. 5c and d, leading to a weaker M⋯H–C interaction. The difference is striking compared to the much better M⋯H alignment for [Pt(SCN)2{(μ-SCN)Mn(NCS)(bipy)2}2], illustrated in Fig. 5a and b.
The [M{(CH3)2DTC}2] complexes in Fig. 5e and f show ΔEmax/ΔP values of +44 ± 5 cm−1/kbar (ref. 31 and 40) for the platinum(II) complex and +32 ± 3 cm−1/kbar (ref. 31) for its palladium(II) analog from ambient pressure to 25 kbar, higher values of ΔEmax/ΔP than the average +12 ± 2 cm−1/kbar. These high positive shifts are due to a loss of a M⋯H–C interaction as pressure increases. In these compounds, the CH3 substituent can rotate around the N–C bond, leading to a likely reorientation of the C–H bonds as pressure increases. This reorientation can strengthen or weaken the M⋯H–C interaction with pressure. In a structure where the carbon is part of a bulky cyclic ligand substituent, such as in [Pt(SCN)2{(μ-SCN)Mn(NCS)(bipy)2}2], changes in the orientation of the C–H bond are restricted unless the whole molecule moves, making this an unlikely rearrangement. As pressure increases, the distance between interacting atoms decreases, resulting in a stronger M⋯H–C interaction and a negative ΔEmax/ΔP value of −99 cm−1/kbar. In the [M(bmpDTC)2] compounds, the interaction originates from a CH2 group, an intermediate situation in terms of possible reorientation of C–H bonds. Rotation of the C–N bond is formally possible, but strongly limited by the bulky substituents, allowing only small reorientations for the CH2 group. The small negative ΔEmax/ΔP values of −8 ± 1 cm−1/kbar for [Pt(bmpDTC)2] and −2 ± 1 cm−1/kbar for [Pd(bmpDTC)2] indicate that the M⋯H–C interaction is still present in these complexes as pressure increases, as ΔEmax/ΔP is lower than the +12 ± 2 cm−1/kbar, but the position of the C–H bonds is not optimal for the interaction, leading to the low absolute ΔEmax/ΔP values. M⋯H–C interactions lead to lower Emax values at ambient conditions, but pressure-induced shifts of Emax towards lower energy can not be reliably predicted based only on the maxima at ambient conditions. These shifts depend on the orientation and mobility of the C–H bonds involved. Luminescence measurements at variable pressure reveal additional information, as shown by the comparison of M⋯H–C interactions involving mobile CH3 groups, less mobile CH2 groups in the bmpDTC complexes and immobile C–H bonds on bulky aromatic ligand fragments.
Since the crystal structures of [Pd(bmpDTC)2] and [Pt(bmpDTC)2] complexes are identical, with similar densities of 1.527 g cm−3 and 1.770 g cm−3, respectively, comparable decreases of intermolecular distances as well as identical variations of Emax with pressure are expected. Significantly different ΔEmax/ΔP values are observed for the palladium(II) and platinum(II) complexes, indicating effects of different magnitude for the two metal centers. [Pt(bmpDTC)2] shows two different ΔEmax/ΔP slopes with a more negative trend at pressures above 28 kbar, typical for a stronger interaction. This is not the case for the palladium(II) analog, where ΔEmax/ΔP stays close to zero across the full pressure range studied, evidence for a weak interaction. These differences indicate that, over the same pressure range, stronger intermolecular interactions occur in the crystalline platinum(II) complex than in its palladium(II) analog. The same qualitative trend is observed for the [M{(CH3)2DTC}2] complexes, illustrating the influence of the metal ion on M⋯H–C interactions. Palladium(II) and platinum(II) have similar ionic radii53 of 0.64 Å and 0.60 Å, respectively. In square-planar complexes, they also show similar metal–ligand bond lengths. It is, however, important to keep in mind that the 4d and 5d radial wave functions are different. In the direction perpendicular to the coordination plane, the main electron density arises from the d orbitals only, with the 4d function for palladium(II) extending significantly less than the 5d function for platinum(II). This difference qualitatively rationalizes the stronger negative shifts for platinum(II) complexes observed in the same pressure range as for palladium(II).
Conclusion
Luminescence maxima of isostructural square-planar complexes are strongly influenced by the crystalline environment and the possibility of intermolecular interactions. Square-planar complexes with dithiocarbamate ligands show surprising variations of the luminescence band maximum Emax. By studying both Emax at ambient conditions and the variation ΔEmax/ΔP, it is possible to measure the impact of intermolecular interactions on the metal-centered luminescence spectrum, and to compare similar complexes. Luminescence maxima of platinum(II) complexes are more strongly affected by M⋯H–C interactions than those of isostructural palladium(II) analogs, illustrating a stronger influence of intermolecular interactions for the 5d metal complexes, a likely consequence of different radial electron density distributions. Structural features also influence the strength of M⋯H–C interactions, critically depending on the alignment and the mobility of the C–H bonds involved in the interaction.Acknowledgements
We thank the Natural Sciences and Engineering Research Council (NSERC, Canada) and Fonds de recherche du Québec – Nature et technologies (FRQNT) for research grants, for graduate scholarships to S. P and for an undergraduate research fellowship to F. R.References
- V. W. W. Yam, V. K. Au and S. Y. Leung, Chem. Rev., 2015, 115, 7589–7728 CrossRef CAS PubMed.
- A. Aliprandi, D. Genovese, M. Mauro and L. De Cola, Chem. Lett., 2015, 44, 1152–1169 CrossRef CAS.
- J. Gareth Williams, S. Develay, D. Rochester and L. Murphy, Coord. Chem. Rev., 2008, 252, 2596–2611 CrossRef CAS.
- W. Paw, S. D. Cummings, M. Adnan Mansour, W. B. Connick, D. K. Geiger and R. Eisenberg, Coord. Chem. Rev., 1998, 171, 125–150 CrossRef CAS.
- G. Gliemann and H. Yersin, Struct. Bonding, 1985, 62, 87–153 CrossRef CAS.
- M. L. Deda, M. Ghedini, I. Aiello, T. Pugliese, F. Barigelletti and G. Accorsi, J. Organomet. Chem., 2005, 690, 857–861 CrossRef CAS.
- B. Ma, J. Li, P. I. Djurovich, M. Yousufuddin, R. Bau and M. E. Thompson, J. Am. Chem. Soc., 2005, 127, 28–29 CrossRef CAS PubMed.
- C. Y.-S. Chung and V. W. W. Yam, Chem. Sci., 2013, 4, 377–387 RSC.
- R. C. Evans, P. Douglas and C. J. Winscom, Coord. Chem. Rev., 2006, 250, 2093–2126 CrossRef CAS.
- B. Ma, P. I. Djurovich, S. Garon, B. Alleyne and M. E. Thompson, Adv. Funct. Mater., 2006, 16, 2438–2446 CrossRef CAS.
- H. D. Takagi, K. Noda, S. Itoh and S. Iwatsuki, Platinum Met. Rev., 2004, 48, 117–124 CrossRef CAS.
- S. Poirier, P. Guionneau, D. Luneau and C. Reber, Can. J. Chem., 2014, 92, 958–965 CrossRef CAS.
- S. Kishi and M. Kato, Mol. Cryst. Liq. Cryst., 2002, 379, 303–308 CrossRef CAS.
- K. Li, Y. Chen, W. Lu, N. Zhu and C. M. Che, Chem. – Eur. J., 2011, 17, 4109–4112 CrossRef CAS PubMed.
- Q. Zhao, F. Li and C. Huang, Chem. Soc. Rev., 2010, 39, 3007–3030 RSC.
- R. Tsuchida, Bull. Chem. Soc. Jpn., 1938, 13, 388–400 CrossRef CAS.
- W. Moffitt and C. J. Ballhausen, Annu. Rev. Phys. Chem., 1956, 7, 107–136 CrossRef CAS.
- H. Yersin, H. Otto, J. I. Zink and G. Gliemann, J. Am. Chem. Soc., 1980, 102, 951–955 CrossRef CAS.
- M. Mitani, T. Nakano and T. Fujita, Chem. – Eur. J., 2003, 9, 2396–2403 CrossRef CAS PubMed.
- L. M. Epstein and E. S. Shubina, Coord. Chem. Rev., 2002, 231, 165–181 CrossRef CAS.
- P. J. Chirik, N. F. Dalleska, L. M. Henling and J. E. Bercaw, Organometallics, 2005, 24, 2789–2794 CrossRef CAS.
- W. I. Sundquist, D. P. Bancroft and S. J. Lippard, J. Am. Chem. Soc., 1990, 112, 1590–1596 CrossRef CAS.
- M. Brookhart, M. L. Green and G. Parkin, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6908–6914 CrossRef CAS PubMed.
- J. Sassmannshausen, Dalton Trans., 2012, 41, 1919–1923 RSC.
- W. Scherer, A. C. Dunbar, J. E. Barquera-Lozada, D. Schmitz, G. Eickerling, D. Kratzert, D. Stalke, A. Lanza, P. Macchi, N. P. M. Casati, J. Ebad-Allah and C. Kuntscher, Angew. Chem., Int. Ed., 2015, 127, 2535–2539 CrossRef.
- M. Lein, Coord. Chem. Rev., 2009, 253, 625–634 CrossRef CAS.
- W. Yao, O. Eisenstein and R. H. Crabtree, Inorg. Chim. Acta, 1997, 254, 105–111 CrossRef CAS.
- C. Reber, J. K. Grey, E. Lanthier and K. A. Frantzen, Comments Inorg. Chem., 2005, 26, 233–254 CrossRef CAS.
- J. C. Zahner and H. G. Drickamer, J. Chem. Phys., 1961, 35, 1483 CrossRef CAS.
- C. Reber, C. Sonneville, S. Poirier, N. Bélanger-Desmarais, W. B. Connick, S. Chatterjee, P. Franz and S. Decurtins, in RSC Specialist Periodical Reports: Spectroscopic Properties of Inorganic and Organometallic Compounds, ed. J. Yarwood, R. Douthwaite and S. B. Duckett, The Royal Society of Chemistry, 2014, vol. 45, pp. 260–273 Search PubMed.
- S. Poirier, E. Tailleur, H. Lynn and C. Reber, Dalton Trans., 2016, 45, 10883–10886 RSC.
- M. Kasha, Discuss. Faraday Soc., 1950, 9, 14 RSC.
- K. L. Bray, in Topics in Current Chemistry, 2001, vol. 213, pp. 1–94 Search PubMed.
- J. W. Kenney, in Optoelectronic Properties of Inorganic Compounds, ed. M. Roundhill and J. P. Fackler Jr, Springer, USA, 1999, pp. 231–268, DOI:10.1007/978-1-4757-6101-6.
- A. N. Gupta, V. Kumar, V. Singh, K. K. Manar, M. G. B. Drew and N. Singh, CrystEngComm, 2014, 16, 9299–9307 RSC.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2015, 71, 3–8 CrossRef PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- G. J. Piermarini, S. Block, J. D. Barnett and R. A. Forman, J. Appl. Phys., 1975, 46, 2774 CrossRef CAS.
- S. Poirier, R. J. Roberts, D. Le, D. B. Leznoff and C. Reber, Inorg. Chem., 2015, 54, 3728–3735 CrossRef CAS PubMed.
- C. Genre, G. Levasseur-Thériault and C. Reber, Can. J. Chem., 2009, 87, 1625–1635 CrossRef CAS.
- D. C. Onwudiwe, J. N. Mugo, M. Hrubaru and E. Hosten, J. Sulfur Chem., 2014, 36, 36–47 CrossRef.
- M. K. Yadav, G. Rajput, L. B. Prasad, M. G. B. Drew and N. Singh, New J. Chem., 2015, 39, 5493–5499 RSC.
- A. Husain, S. A. A. Nami, S. P. Singh, M. Oves and K. S. Siddiqi, Polyhedron, 2011, 30, 33–40 CrossRef CAS.
- J. K. Grey, M. Marguerit, I. S. Butler and C. Reber, Chem. Phys. Lett., 2002, 366, 361–367 CrossRef CAS.
- I. Hidvegi, W. Tuszynski and G. Gliemann, Chem. Phys. Lett., 1981, 77, 517–519 CrossRef CAS.
- Y. Pelletier and C. Reber, Inorg. Chem., 1997, 36, 721–728 CrossRef CAS.
- J. K. Grey, I. S. Butler and C. Reber, J. Am. Chem. Soc., 2002, 124, 9384–9385 CrossRef CAS PubMed.
- E. Lanthier, C. Reber and T. Carrington, Chem. Phys., 2006, 329, 90–98 CrossRef CAS.
- L. Yang, D. R. Powell and R. P. Houser, Dalton Trans., 2007, 955–964, 10.1039/b617136b.
- S. Poirier, L. Czympiel, N. Belanger-Desmarais, S. Mathur and C. Reber, Dalton Trans., 2016, 45, 6574–6581 RSC.
- G. Levasseur-Thériault, C. Reber, C. Aronica and D. Luneau, Inorg. Chem., 2006, 45, 2379–2381 CrossRef PubMed.
- R. D. Shannon, Acta Crystallogr., Sect. C: Struct. Chem., 1976, 32, 751–767 Search PubMed.
- A. T. Baker and M. T. Emett, Aust. J. Chem., 1992, 45, 429–434 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Table of published luminescence band maxima Emax for square-planar platinum(II) and palladium(II) complexes, variable-pressure luminescence spectra, variable-pressure full-width at half-maximum (FWHM), variable-pressure and variable-temperature Raman spectra, cif file for [Pt(bmpDTC)2] at 150 and 295 K. CCDC 1527919 and 1527920. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7dt00545h |
| This journal is © The Royal Society of Chemistry 2017 |