Preparation and characterization of metastable trigonal layered MSb₂O₆ phases (M = Co, Ni, Cu, Zn, and Mg) and considerations on FeSb₂O₆

Abstract

MSb₂O₆ compounds (M = Mg, Co, Ni, Cu, Zn) are known in the tetragonal trirutile forms, slightly distorted monoclinically with M = Cu due to the Jahn–Teller effect. In this study, using a low-temperature exchange reaction between ilmenite-type NaSbO₃ and molten MSO₄–KCl (or MgCl₂–KCl) mixtures, these five compositions were prepared for the first time as trigonal layered rosiaite (PbSb₂O₆)-type phases. Upon heating, they irreversibly transform to the known phases via amorphous intermediates, in contrast to previously studied isostructural MnSb₂O₆, where the stable phase is structurally related to the metastable phase. The same method was found to be applicable for preparing stable rosiaite-type CdSb₂O₆. The formula volumes of the new phases show an excellent correlation with the ionic radii (except for M = Cu, for which a Jahn–Teller distortion is suspected) and are 2–3% larger than those for the known forms although all coordination numbers are the same. The crystal structure of CoSb₂O₆ was refined via the Rietveld method: P3̄1m, a = 5.1318(3) Å, and c = 4.5520(3) Å. Compounds with M = Co and Ni antiferromagnetically order at 11 and 15 K, respectively, whereas the copper compound does not show long-range magnetic order down to 1.5 K. A comparison between the magnetic behavior of the metastable and stable polymorphs was carried out. FeSb₂O₆ could not be prepared because of the 2Fe²⁺ + Sb⁵⁺ = 2Fe³⁺ + Sb³⁺ redox reaction. This electron transfer produces an additional 5s² shell for Sb and results in a volume increase. A comparison of the formula volume for the stable mixture FeSbO₄ + 0.5Sb₂O₄ with that extrapolated for FeSb₂O₆ predicted that the trirutile-type FeSb₂O₆ can be stabilized at high pressures.

---

1. Introduction

Preparation of a new crystal form for a well-known composition is challenging and very interesting because it can provide new properties and improve our understanding of the composition-structure–property relations. Recently, using a low-temperature ion-exchange reaction, a new form of MnSb₂O₆, isostructural with rosiaite PbSb₂O₆, was prepared and its magnetic properties and thermal transformations were studied.¹ In this structure, magnetic cations are arranged in trigonal layers that antiferromagnetically order at low temperatures, forming spin-frustrated triangles.

In this study, the same preparative approach was expanded to the entire MSb₂O₆ family (M = Mg, Fe, Co, Ni, Cu, Zn, and Cd) and the magnetic properties of the new phases with M = Ni, Co, and Cu were studied. A total of five of the seven listed compositions, with M = Mg, Co, Ni, Cu, and Zn, are known to crystallize in the tetragonal trirutile-structure type,² which is slightly monoclinically distorted for M = Cu due to the Jahn–Teller effect, whereas CdSb₂O₆ is found in the rosiaite form.³ MSb₂O₆ compounds with a partially filled d subshell (M = Co, Ni, and Cu) have attracted attention due to their magnetic properties,^4–13 whereas antimonates with nonmagnetic ions (M = Mg, Zn, and Cd) may be interesting as photocatalysts,^14,15 transparent conductors,¹⁶ and/or sensors.^17–19 Initially, FeSb₂O₆ was also reported to exist in the trirutile form; however, later studies showed that the mineral known as FeSb₂O₆ is actually FeSbO₄ (Fe_1/2Sb_1/2O₂) with disordered rutile-type structure.²⁰ An attempt to prepare FeSb₂O₆via solid-state reactions of Sb₂O₃ and FeSO₄·7H₂O at 1000 °C in air was made and a mixture of FeSbO₄ and Sb₂O₄ was obtained.²⁰ This result is explained by the oxidation of Fe²⁺ in air and does not preclude an attempted preparation in an inert atmosphere at much lower temperatures.

2. Experimental

2.1. Sample preparation and analysis

Only reagent-grade starting materials were used. NaSbO₃ was prepared at 550–850 °C from a stoichiometric mixture of dried Sb₂O₃, Na₂CO₃, and NaNO₃, as previously reported,^1,21 and its phase purity was confirmed via powder X-ray diffraction (XRD). MSO₄·xH₂O (M = Fe, Co, Ni, Cu, Zn, and Cd) was dried at 400 °C (in flowing argon atmosphere for FeSO₄). Subsequently, NaSbO₃, MSO₄, and KCl were carefully mixed using a mortar and pestle at the molar ratio of approximately 1 : 2.5 : 5, providing a five-fold excess of MSO₄ against the stoichiometric amount. For M = Cd, a double excess was also tested, with a 1 : 1 : 2 ratio of NaSbO₃, CdSO₄, and KCl. In some instances, half of the KCl was substituted with KBr to further lower the solidus temperature.

For M = Mg, this approach was inapplicable due to the excessively high eutectic temperature of the MgSO₄–KCl join, 665 °C.²² Therefore, a MgCl₂–KCl mixture was used instead.

The mixtures were heated for various periods at various temperatures in air (except for M = Fe, for which a CO₂ atmosphere was used), cooled, washed with warm water, dried, and examined via XRD.

The elemental composition of the samples was estimated using an electron microprobe (INCA ENERGY 450/XT) equipped with an X-Act ADD detector based on an electron microscope VEGA II LMU (Tescan) operated at the accelerating voltage of 20 kV. No potassium was detected; however, some samples showed a non-zero sodium content. The molar ratios M/Sb and Na/Sb were averaged on 8–11 points in each sample.

2.2. Diffraction studies

XRD was performed using Cu Kα radiation by an ARL X'TRA diffractometer equipped with a solid-state Si(Li) detector eliminating Co and Fe fluorescence and other undesired wavelengths (although sometimes very weak reflections from CuK_β and WL_α radiations were observed). Rietveld refinements were performed using the GSAS + EXPGUI suite.^23,24

Neutron diffraction experiments were carried out via the cold neutron two-axis diffractometer G4.1 located at ORPHEE reactor, Laboratory Léon Brillouin, Saclay, France. The wavelength of the incident monochromatic neutrons was 2.426 Å. Neutron diffraction data were obtained in the 2θ range from 6.0 to 85.9° with the step of 0.1°. The measurements were carried out using the special Orange cryostat for neutron research. The sample was placed in a cylindrical vanadium container having a diameter of 6 mm. The diffraction pattern was treated by the Rietveld method using the FullProf suite.²⁵

2.3. Magnetic measurements

The magnetic properties (temperature dependencies of the magnetic susceptibility and magnetization isotherms) of the MSb₂O₆ (M = Co, Ni, and Cu) samples in the temperature range from 2 to 350 K under a magnetic field up to 9 T were measured using Quantum Design MPMS-7T and VSM option of the Quantum Design PPMS-9T devices. The electron spin resonance spectra at room temperature were obtained using an X-band ESR spectrometer CMS 8400 (ADANI) (f ≈ 9.4 GHz, B ≤ 0.7 T). The effective g-factors of the samples were calculated with respect to an external reference for the resonance field. BDPA (a,g-bisdiphenyline-b-phenylallyl), g_ref = 2.00359, was used as the reference material.

3. Results and discussion

3.1. Preparation, identification, and phase transformations

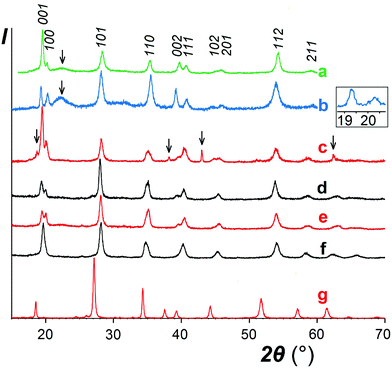
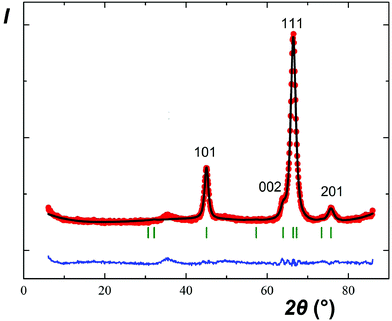
As expected, reactions of NaSbO₃ with low-melting mixtures of MSO₄ (M = Co, Ni, Cu, and Zn) or MgCl₂ with KCl (or KCl–KBr) resulted in formation of five new trigonal layered phases of the rosiaite type (Table 1, Fig. 1). However, this required careful selection of the temperature and duration, typically in the ranges of 420–500 °C and 40–80 minutes. The lower limits were determined by the solidus temperature of the salt mixture and incomplete reaction, whereas the higher limits were determined by the MSb₂O₆ transformation to the stable form. Moreover, the results were also dependent on the total mass of the reaction mixture. Because the furnace temperature was set only slightly higher than the solidus temperature, complete melting of the salt mixture required considerable time, especially long with large batches. To prepare 1–2 g of the desired product in one stage, a 5–10 g batch was required, which usually resulted in either incomplete exchange or (at least partial) conversion to the stable trirutile-type polymorph.

Fig. 1 XRD patterns of the MSb₂O₆ samples prepared via ion exchange. (a) NiSb₂O₆, (b) CuSb₂O₆, (c) MgSb₂O₆, (d) ZnSb₂O₆, (e) CoSb₂O₆ (sample I), (f) CoSb₂O₆ (sample II), and (g) CdSb₂O₆ (sample I). Inset shows the expanded low-angle part for CuSb₂O₆. The arrows point to the reflections from foreign phases.

Table 1 Crystallographic and microprobe analytical data of the new metastable MSb₂O₆ phases in comparison with the known trirutile-type polymorphs (standard deviations in the last decimal digit are given in parentheses)

M	^VI R, Å ^26	Metastable trigonal layered polymorphs (stable for M = Cd)						Trirutile^27
		a, Å	c, Å	c/a	V/Z	M/2Sb	Na/2Sb	V/Z	ΔV, %
a Treated with aqueous acetic acid to remove free MgO before analysis. b Sodium content could not be estimated due to overlap of its strongest line with the line from Zn. c Extremely inhomogeneous distribution of Na: only found in 2–4 points of 10 or 11.
Ni	0.83	5.076(4)	4.5329(16)	0.893	101.2	1.02(6)	0	99.35	1.9
Cu	0.87	5.054(4)	4.5881(10)	0.908	101.5	1.00(12)	0	99.81	1.9
Mg^a	0.86	5.116(5)	4.538(8)	0.887	102.8	1.07(15)	0.11(3)	99.86	3.0
Zn	0.88	5.114(3)	4.5679(16)	0.893	103.4	0.93(4)	?^b	100.88	2.5
Co(I)	0.885	5.1318(3)	4.5520(3)	0.887	103.8	0.99(5)	0	100.53	3.3
Same, calcined at 950°						1.00(5)	0.02(5)^c
Co(II)		5.164(2)	4.503(2)	0.872	104.0	0.96(3)	0.04(8)^c
Same, calcined at 950°						0.99(3)	0.06(8)^c
Cd(I)	1.09	5.2405(20)	4.796(3)	0.915	114.1	1.03(3)	0.06(3)
Same, calcined at 950°						1.02(2)	0.03(3)
Cd(II)		5.2403(16)	4.803(3)	0.917	114.2	0.99(2)	0.08(3)
Cd^3		5.2399(2)	4.8045(4)	0.917	114.2

---

The same approach was applied to the preparation of CdSb₂O₆, for which a rosiate-type structure is the stable form. Thus, the limitations of reaction temperature and time were unnecessary, and the exchange was performed at 500 °C for 2 h. This resulted in the formation of single-phase products with both 2- and 5-fold excess of CdSO₄, marked I and II, respectively. Both have much better crystallinity than others (Fig. 1g) and the lattice parameters are in good agreement with literature data (Table 1).

In contrast to the samples prepared from sulfates, our MgSb₂O₆ contained admixtures of foreign crystalline phases including MgO (Fig. 1c). This is because we failed to avoid hydrolysis while drying the starting hydrous MgCl₂.

The analytical data, as shown in Table 1, despite considerable scattering from point to point, confirm that obtained NiSb₂O₆ and CuSb₂O₆ are sufficiently pure: the M/Sb ratio is stoichiometric within the experimental accuracy and the Na content is essentially zero. On the other hand, the MgSb₂O₆ contained foreign phase(s) even after the removal of MgO via acid leaching. In addition to XRD, this is evident from the microprobe data showing the elevated average Mg/Sb ratio and especially high scatter.

With other three compounds, the situation was less obvious. The single analyzed sample of ZnSb₂O₆ and one of the two CoSb₂O₆ samples (labelled II) showed somewhat reduced M/Sb ratio (although within the experimental accuracy) associated with a non-zero sodium content in both Co samples (in the presence of Zn, determination of Na was unreliable). This suggests the possibility of sodium substitution for M²⁺ and correlates with variations in the XRD data. A comparison of the XRD patterns of CoSb₂O₆ I (Fig. 1e) and CoSb₂O₆ II (Fig. 1f) shows that the less pure sample CoSb₂O₆ II, in contrast to CoSb₂O₆ I, does not show splitting of the pairs 001 + 100 and 002 + 111, indicating a considerably lower c/a ratio. Similar variations were observed with the ZnSb₂O₆ samples, but those with unresolved 001 + 100 reflections have not been reported herein. The different behaviours of Zn and Co compounds compared to those of Ni and Cu might be tentatively attributed to the somewhat larger ionic radii of the former pair of cations, which is favourable for sodium substitution. However, ionic radius of Cd²⁺ is much larger and closer to that of Na⁺, but no Cd deficiency indicating sodium substitution can be seen in Table 1, especially with sample I, where a lower excess of the Cd salt might favour incomplete ion exchange. Therefore, we hypothesized that the elevated sodium content in the CdSb₂O₆ samples might be due to the adsorbed or occluded salts rather than ionic substitutions. Note that the sodium content in CdSb₂O₆(I) diminishes on calcination, probably due to volatilization of the salt impurity. The role of Na in MSb₂O₆ has been further discussed in Section 3.2.

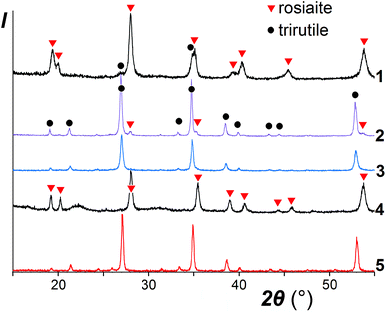
It was noticed that the transformation to the stable polymorph was markedly enhanced in the presence of a salt melt, obviously due to the dissolution-precipitation mechanism. As illustrated in the XRD patterns in Fig. 2, for ZnSb₂O₆, taken as a typical example, prolonged treatment with the molten salt at 420–500 °C resulted in the conversion of the metastable trigonal layered rosiaite-type phase into the stable trirutile-type polymorph. On the other hand, this conversion was not observed at considerably higher temperature of 750 °C if ZnSb₂O₆ was free of the salt mixture. Note that exchange reaction of NaSbO₃ with ZnCl₂ under hydrothermal conditions yielded stable ZnSb₂O₆ at even lower temperature of 230 °C (for 4 days), whereas phase-pure products with M = Pb, Cu, Ni, and Mn could not be obtained via this method.¹⁴

Fig. 2 XRD patterns of ZnSb₂O₆ samples with different thermal history: 1, prepared by ion exchange for 6 h at 420 °C: rosiaite type with only a trace of the stable trirutile-type phase; 2, same after an additional 10 h treatment with the salt mixture at 420 °C: trirutile type with only trace of the starting rosiaite; 3, prepared for 5 h at 500 °C: only trirutile type; 4, rosiaite-type phase prepared under the optimal conditions, washed, and annealed for 2 h at 750 °C: no trirutile; 5, same annealed for an hour at 950 °C: only trirutile type. Red triangles, reflections from rosiaite; black circles, reflections from trirutile.

A comparison of the patterns 1 and 4 depicted in Fig. 2 shows that annealing of ZnSb₂O₆ at 750 °C resulted in an increased axial ratio c/a and the appearance of large broad halos in the XRD pattern, which are characteristic of an amorphous phase. Similar halos are also visible in the patterns of CuSb₂O₆ and NiSb₂O₆ in Fig. 1a and b. Annealing at 950 °C resulted in complete transformation of trigonal MSb₂O₆ (M = Co, Ni, Cu, and Zn) to stable trirutile-type polymorphs (Fig. 3 and pattern 5 in Fig. 2). No additional phases were found within the sensitivity of the XRD. This means that the amorphous phases have the same composition as the crystalline products, being intermediates in the transformation between the trigonal and tetragonal phases. This is different from the previously studied case of MnSb₂O₆, where the stable phase was structurally related to the metastable phase and the transformation might have proceeded within an intact crystal.¹

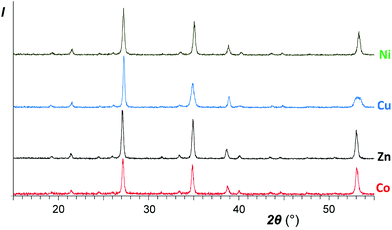Fig. 3 XRD patterns of the same samples as abovementioned in Fig. 1 after calcinations for an hour at 950 °C. Top to bottom: NiSb₂O₆, CuSb₂O₆, ZnSb₂O₆, and CoSb₂O₆ (sample I).

3.2. Structural characterization

As shown in Table 1 and Fig. 4, the formula volumes of trigonal MSb₂O₆ (except for M = Cu) have an excellent correlation with the ionic radii of M²⁺, and for the five new phases, they are 2–3% larger than those for the stable trirutile-type phases although all coordination numbers are the same. Fig. 4 presents an additional example of a morphotropic series where substitution of a larger cation (herein, Co²⁺ in CoSb₂O₆) by an even larger cation (herein, Mn²⁺ or Cd²⁺) leads to less dense structure types,²⁸ opposite to the widely assumed homology rule.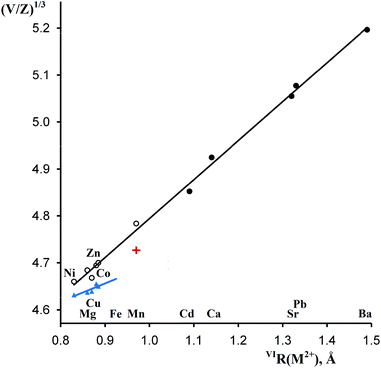

Fig. 4 Correlations between the octahedral ionic radii²⁶ of M²⁺ and reduced cell parameters (V/Z)^1/3 of MSb₂O₆. Empty and filled circles, rosiaite type, metastable and stable phases, respectively; blue triangles, stable phases of the trirutile type; red cross, stable MnSb₂O₆, P321.

As discussed earlier,¹ the ilmenite-type structure of NaSbO₃ and rosiaite-type structure of MSb₂O₆ (M = Ca, Cd, Sr, Pb, and Ba) are based on the same octahedral SbO_6/2 layers. Therefore, M²⁺ substitution for 2Na⁺ may occur by mere gliding of the layers to avoid the face sharing of MO₆ and SbO₆ octahedra. This gliding may result in stacking faults. Therefore, it is not surprising that XRD peaks in the powder patterns (Fig. 1) are considerably broader than those of starting NaSbO₃. Largest broadening is observed with M = Cu. This, together with the deviation seen in Fig. 4, may be an indication of lowered symmetry due to the Jahn–Teller effect characteristic of Cu²⁺. Inset in Fig. 1 shows that the reflection 100 that may split upon transition from the trigonal to any lower crystal system is markedly broader than 001, which does not split in any case. However, the quality of the powder pattern precludes a detailed structural investigation.

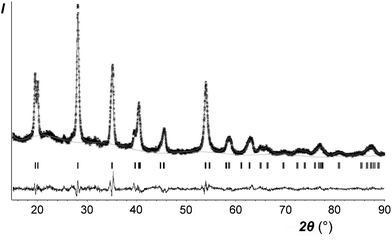
Only the crystal structure of CoSb₂O₆ (the sample I with minimum sodium impurity, if any, see Table 1) was refined using the Rietveld method. The main results are listed in Tables 2–4 and in the ESI† (cif). Fig. 5 compares the experimental and calculated XRD profiles, whereas Table 4 and Fig. 6 compare the new and previously known structures of CoSb₂O₆.

Fig. 5 Rietveld refinement results for CoSb₂O₆. Stars, experimental data; line, calculated profile; line at the bottom, difference profile; vertical bars, calculated positions of the Bragg reflections.

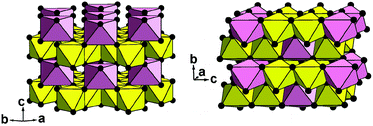Fig. 6 Two crystal structures of CoSb₂O₆ in a polyhedral presentation: new trigonal form (left) and known tetragonal form⁵ (right). Yellow octahedra, SbO₆; pink octahedra, CoO₆; and black balls, oxygen anions.

Table 2 Refinement details for trigonal CoSb₂O₆ (sample I, see Table 1)

Crystal system		Trigonal	Density (calc.), g cm^−3		6.372
Space group		P3̄1m (no. 162)	Texture parameters (March–Dollase)		Axis 001
					Ratio 0.9873
Lattice constants, Å	a	5.13183(25)	2Θ range, °		15.00–89.96
	c	4.55202(34)	Step width, °		0.02
Cell volume, Å^3		103.820(11)	No. of data points		3748
Formula weight		398.4	No. of reflections
			Calc. (α1 only)		39
Z		1	No. of variables		44 (6 – of structure)
Wavelengths, Å	α 1	1.54056	Agreement factors	R(F^2)	0.05085
	α 2	1.54439		R p	0.0611
	Ratio	0.5		R wp	0.0776
				χ ^2	2.166

---

Table 3 Atomic positions and thermal parameters in trigonal CoSb₂O₆

Atom	Wyckoff position	Site symmetry	Occup.	x/a	y/b	z/c	U iso
Mn	1a	3̄m	1	0	0	0	0.01 fixed
Sb	2d	32	1	1/3	2/3	1/2	0.01958 equi.
O	6k	m	1	0.3721(18)	0	0.2518(13)	0.03 fixed

---

	U 11	U 22 = U11	U 33	U 12 = U11/2	U 13	U 23
Sb	0.0156(4)	0.0156	0.0276(8)	0.00779	0	0

---

Table 4 Principal interatomic distances (Å) and bond angles (°) in trigonal CoSb₂O₆ in comparison to the stable tetragonal polymorph⁵ and corresponding sums of ionic radii²⁶

Bonds, angles	Rosiaite type, P3̄1m	Trirutile type, P42/mnm	Sum of radii
Co–O	2.227(8) × 6	2.054 (average of six)	2.105
Sb–O	1.975(4) × 6	1.985 (average of six)	1.96
O–Co–O	84.1–95.9	77.7–102.3
O–Sb–O	82.8–97.0	79.2–99.6
Co–O1–Sb	125.40 × 2	129.62 × 2
Sb–O1–Sb	97.17	100.75
Sum of the three	348.0	360.0
Co–O2–Sb		126.36 × 2
Sb–O2–Sb		133.29
Sum of the three		360.0

---

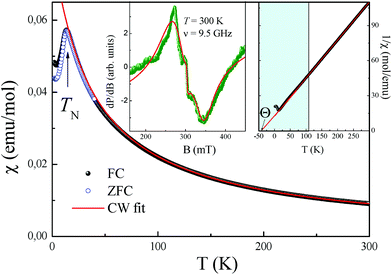
A comparison of the bond lengths and bond angles in the two polymorphs (Table 4) shows that both the CoO₆ and SbO₆ octahedra, especially the former, are much more regular in the new phase than in the stable trirutile-type counterpart. The same was noticed for MnSb₂O₆ ¹ although its stable form is not of the trirutile type.

The trigonal structure of CoSb₂O₆ is based on the distorted hexagonal close packing (better to say, 2H eutaxy) of oxygen anions, where cations fill half octahedral voids. Each oxygen atom has 10 oxygen neighbours at the distances of 2.61–2.98 Å plus two oxygen neighbours more distant at 3.31 Å. Although the rutile and trirutile structure types are also often described as 2H derivatives, it is actually incorrect.² Indeed, the two independent anions in tetragonal CoSb₂O₆ ⁵ have oxygen environments of 11 + 2 and 10 + 1 + 2; thus, the tetragonal close packing with 11 (rather than 12) neighbours is a more adequate term in this case.² The cation arrangements in the two polymorphs also significantly differ. In the trirutile-structure type, each metal–oxygen octahedron shares two edges with other octahedra, and higher-valence cations have only one common edge. In the rosiaite-structure type, the number of shared edges is the same only as an arithmetic mean. Octahedra populated with lower-valence cations have no shared edges at all, whereas those populated with higher-valence cations share three edges each (Fig. 6). In addition, the trigonal form, despite the larger formula volume, exhibits shorter Sb–Sb distances across the shared edges: 2.96 Å in contrast to 3.05 and 3.11 Å for Sb–Sb and Sb–Co, respectively, in the tetragonal form. All this leads to stronger cation–cation repulsion in the rosiaite type and explains its instability with respect to the trirutile type. For large M²⁺ (Cd⋯Ba), size disparity with Sb⁵⁺ precludes the formation of the trirutile type; then, the rosiate type becomes stable.

The crystal-chemistry role of the sodium impurity remains unclear. Previously,¹ we suggested the existence of small non-exchanged ilmenite-type fragments as stacking faults in the main MnSb₂O₆ phase. However, this disagrees with the lattice parameter changes. Pure NaSbO₃ has a c/a ratio of 3.011 for the three-layered rhombohedral packing.²⁹ For the primitive one-layered packing, it should be 3.011/3 = 1.004. These admixtures must increase the c/a ratio of our products. However, a comparison of the samples I and II of CoSb₂O₆ in Table 1 shows the opposite.

As discussed in Section 3.1, sodium substitution for M²⁺ was most probable with M = Cd but could not be supported by the analytical data and lattice parameters (Table 1). In addition, the introduction of large Na⁺ cations in the interlayer is also expected to increase the c/a. Moreover, to provide charge balance, there should be either additional Na⁺ ions (for which we do not see available sites) or holes that can be easily interpreted as Co³⁺; however, this is hardly applicable for zinc or cadmium. The problem could not be solved by powder XRD owing to the very small content of sodium, its relatively small X-ray scattering factor, and diffuse nature of the diffraction patterns. The crystal structure refinement reported herein is based on the ideal composition CoSb₂O₆.

3.3. Special case of FeSb₂O₆

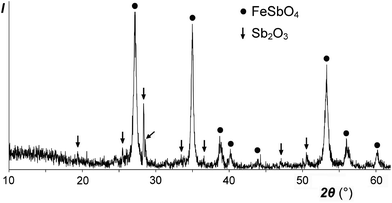
Our low-temperature preparation of FeSb₂O₆ in an inert atmosphere differs from the preceding high-temperature preparation in air:²⁰ instead of the mixture FeSbO₄ + 0.5Sb₂O₄, we obtained FeSbO₄ + 0.5Sb₂O₃ (Fig. 7), due to the reducing power of the excess FeSO₄. In any case, FeSb₂O₆ could not be prepared, due to incompatible oxidation states, reacting according to the following scheme: 2Fe²⁺ + Sb⁵⁺ → 2Fe³⁺ + Sb³⁺.

Fig. 7 XRD pattern of the reaction product between a NaSbO₃ and FeSO₄–KCl melt in a CO₂ atmosphere at 500 °C. Filled circles, reflections from FeSbO₄ (rutile type); arrows, reflections from Sb₂O₃ (valentinite).

This electron transfer from Fe²⁺ (3d⁶) to Sb⁵⁺ (4d¹⁰) creates an additional 5s² shell for Sb and thus should result in an increase in the total volume. The formula volume of the hypothetical trirutile-type FeSb₂O₆ was estimated to be approximately 101.4 ų by extrapolation using the plot in Fig. 4 and Shannon's ionic radius for high-spin Fe²⁺. The volume of the equivalent stable mixture FeSbO₄ + 0.5Sb₂O₄ is considerably higher, 103.9 or 104.4 ų, obtained using the data for monoclinic or orthorhombic Sb₂O₄,³⁰ respectively. Therefore, trirutile-type FeSb₂O₆, which is unstable at normal pressure, may be stabilized at high pressures although this may be complicated by high-spin-to-low-spin transitions.

3.4. Magnetic properties

3.4.1. NiSb₂O₆. The temperature-dependence of the magnetic susceptibility χ = M/B of NiSb₂O₆, measured at B = 0.1 T, is shown in Fig. 8(a). In both the field-cooled (FC) and zero-field cooled (ZFC) measurement protocols, it passes through smooth maximum at ∼19.5 K, indicating an onset of antiferromagnetic long-range ordering. The Néel temperature, as estimated from the first derivative dχ/dT(T), is noticeably lower, T_N = 15 K, than the maximum on χ(T), which is characteristic of low-dimensional magnets with strong short-range correlations. Below T_N, the χ_ZFC(T) and χ_FC(T) dependencies demonstrate clear divergence and additional growth of the magnetic susceptibility, signalling the presence of non-negligible spin-glass and/or impurity effects. This is also confirmed from the ESR data, which reveal the superposition of two resonance modes, which are most probably related to the main signal (broad signal) and impurity line (narrow signal) as shown in the left inset in Fig. 8(a). The fit of the experimental χ(T) data in the high-temperature range with the Curie–Weiss law χ = χ₀ + C/(T − Θ) allows an estimation of the temperature-independent term as χ₀ = 4.87 × 10⁻⁵ emu mol⁻¹, Curie constant C = 1.3 emu K mol⁻¹, and Weiss temperature Θ = −33 K. The temperature-independent term χ₀ takes a positive value, indicating the predominance of the van Vleck contribution of Ni²⁺ ions over the sum of the Pascal constant of the individual ions χ_dia = −1.12 × 10⁻⁴ emu mol⁻¹.³¹

Fig. 8 (a) Temperature-dependence of the magnetic susceptibility of NiSb₂O₆ measured at B = 0.1 T. (b) Magnetization isotherms of NiSb₂O₆ at various temperatures. Insets in (a): ESR spectrum at room temperature (left side) and inverse value of the magnetic susceptibility 1/χ, emphasizing the predominance of the antiferromagnetic correlations (right side).

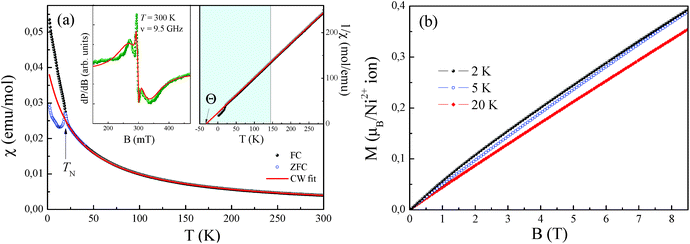
The effective magnetic moment calculated from the obtained Curie constant takes μ_eff = 3.2μ_B/Ni²⁺. This value is in reasonable agreement with the theoretical estimation according to 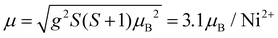, where the average effective g-factor was directly measured via electron spin resonance (ESR) g = 2.21, which is well consistent with typical for Ni²⁺ values.

The negative sign of the Weiss temperature indicates the predominance of antiferromagnetic exchange interactions in the system, in agreement with the long-range antiferromagnetic ordering. The field dependence of the magnetization of NiSb₂O₆ (Fig. 8b) demonstrates characteristic S-type behaviour at low temperatures, which indicates the competing exchange interactions of both the ferro- and antiferromagnetic nature.

Interestingly, note that the magnetic properties observed herein for this novel phase possessing the trigonal layered rosiaite-type structure are essentially different from those reported for its stable polymorph with the tetragonal trirutile-type structure (space group P4₂/mnm). The magnetic behaviour of all the trirutile-type compounds MSb₂O₆ (M = Ni, Co, and Cu) is quite similar. Their low-dimensional magnetic behaviour was confirmed from the magnetic susceptibility, specific heat and thermal expansion measurements, ESR and NMR/NQR techniques, etc. as well as by electronic structure calculations. A characteristic feature is the presence of a wide temperature range, where all MSb₂O₆ with a trirutile structure exhibit short-range antiferromagnetic order. For the case of trirutile NiSb₂O₆, it was found that the χ(T) demonstrates a clear low-dimensional broad maximum at T_max ∼ 40 K followed by long-range antiferromagnetic order below T_N = 2.5 K.⁴ Despite the almost perfect 2D square Ni²⁺ sublattice, the data were well described within the formalism of antiferromagnetic S = 1 1D spin chain via Ni–O–O–Ni superexchange pathways with the main exchange parameter J/k_B ∼ −45 K.

3.4.2. CoSb₂O₆. Similar to NiSb₂O₆, both CoSb₂O₆ samples revealed an onset of antiferromagnetic long-range order at low temperatures with approximately the same Néel temperature, as high as 11 K (Fig. 9), although sample II shows a somewhat larger discrepancy between the ZFC and FC results, which is in agreement with the higher Na impurity level. Once again, similar to the nickel sample, the new rosiaite-type CoSb₂O₆ polymorph does not show any sign of a low-dimensional maximum on χ(T) in contrast to the tetragonal trirutile phase with short-range ordering at T_max ∼ 35 K, preceding the antiferromagnetic ordering at T_N = 13.5 K.^5–7 Opposite to the known trirutile phase, which was treated in the frame of the Ising dimers model with J/k_B ∼ −10 K and spin-gap Δ ≈ 34 K,⁷ the magnetic susceptibility of the new rosiaite-type CoSb₂O₆ nicely follows the Curie–Weiss law over the wide temperature range above T_N (Fig. 9). On the other hand, the main parameters of the magnetic subsystem, obtained from the experimental data, are comparable for both structure types. In particular, the temperature-independent term χ₀ = 7.3 × 10⁻⁵ emu mol⁻¹ for the new sample indicates a prevailing van Vleck contribution of Co²⁺ over the diamagnetic counterpart of ions constituting CoSb₂O₆; the Weiss temperature Θ ≈ −38 K is consistent with the predominance of antiferromagnetic exchange interactions and very close to the value ∼−32 K reported for the trirutile sample.⁷ The effective magnetic moment μ_eff ≈ 4.9μ_B/Co²⁺ is in reasonable agreement with the theoretical estimations using the average effective g-factor g_av = 2.3 ± 0.1 obtained from the anisotropic ESR absorption line (left inset of Fig. 9). Detailed investigations of the magnetic properties of the new rosiaite-type CoSb₂O₆ polymorph have been planned to be reported later together with its magnetic structure, which is now under study via low-temperature neutron diffraction.

Fig. 9 Temperature-dependence of the magnetic susceptibility of CoSb₂O₆-II measured at B = 0.1 T. Insets: ESR spectrum at room temperature (left side) and inverse value of magnetic susceptibility 1/χ, emphasizing the predominance of the antiferromagnetic correlations (right side).

3.4.3. CuSb₂O₆. On comparing the magnetic behaviour of the trirutile- and rosiaite-type MSb₂O₆ families, the most drastic difference was observed for M = Cu. The trirutile counterpart undergoes a structural phase transition from the high-temperature tetragonal phase (space group P4₂/mnm) to the low-temperature monoclinic phase (space group P2₁/n) at T_ph = 380 K.^8,9 However, it has close similarity to its trirutile-type relatives, NiSb₂O₆ and CoSb₂O₆: 1D short-range order was observed with T_max = 60 K followed by the long-range ordering at T_N = 8.5 K.^9,10 Susceptibility measurements performed on both the powder and single crystal samples of CuSb₂O₆ fit extremely well over a wide temperature range to a nearest-neighbour-only S = 1/2 uniform Heisenberg 1D chain model with an exchange constant ranging from −86 K to −98 K (see ref. 11 and references therein).

Moreover, the latter low-temperature phase transition has attracted significant interest because it was suggested to be possible spin-Peierls-like phase transition.^9,12 The octahedral oxygen environment of the magnetic Cu²⁺ ions gives rise to the dominant Cu–O–O–Cu superexchange pathway, which forms magnetic chains along the (a + b) direction at z = 0, and (a − b) direction at z = 0.5 ¹³ with the main intrachain exchange integral J_∥/k_B ∼ −94 K (ref. 13) and remarkably small ratio J_∥/J_⊥ = 120.⁶

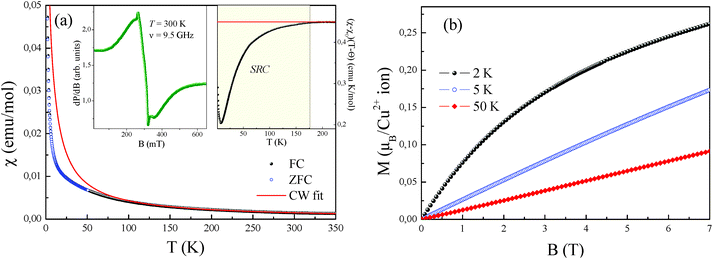
The temperature-dependence of the magnetic susceptibility χ = M/B of new rosiaite-type CuSb₂O₆, measured at B = 0.1 T, is shown in Fig. 10(a). This follows the Curie–Weiss behaviour at elevated temperatures and does not show clear signature of any long-range order transition down to 2 K. However, left-side bending at low temperatures and a clear deviation from the Curie–Weiss law at T < 100 K can be observed, indicating rather strong short-range exchange interactions in this compound. The dependencies of magnetic susceptibility measured in the field-cooled (FC) and zero-field cooled (ZFC) regimes do not demonstrate any divergence, confirming the absence of any spin disorder effects. The fit of the experimental data in the high-temperature range with the function χ = χ₀ + C/(T − Θ) allows an estimation of the temperature-independent term χ₀ = 1.46 × 10⁻⁵ emu mol⁻¹, Curie constant C = 0.447 emu K mol⁻¹, and Weiss temperature Θ = −4 K.

Fig. 10 (a) Temperature-dependence of the magnetic susceptibility of CuSb₂O₆ measured at B = 0.1 T. (b) Magnetization isotherms of CuSb₂O₆ at various temperatures. Insets: ESR spectrum at room temperature (left side) and special scale of magnetic susceptibility (χ − χ₀)(T − Θ), emphasizing the nature of the magnetic exchange interactions (right side).

Similar to the NiSb₂O₆ and CoSb₂O₆ samples, the temperature-independent term χ₀ comprises diamagnetic Pascal and paramagnetic van Vleck contributions. The positive value of χ₀ indicates the predominance of the van Vleck term χ_vV = 7.18 × 10⁻⁴ emu mol⁻¹ over the sum of the Pascal constant of individual ions χ_dia = −1.12 × 10⁻⁴ emu mol⁻¹.³¹ The van Vleck contribution is defined by the splitting of the d-shell of Cu²⁺ ions in a distorted octahedral environment.

The effective magnetic moment calculated from the obtained Curie constant takes μ_eff = 1.9μ_B/Cu²⁺. This value is in excellent agreement with the theoretical estimation according to 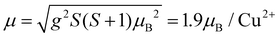, where the average effective g-factor was directly measured by electron spin resonance (ESR). As depicted in the left inset in Fig. 10(a), the ESR spectrum shows relatively broad anisotropic absorption line, which is typical of the powder pattern of the Cu²⁺ compounds. The estimated values of the principal components of g-tensor are g_∥ = 2.20 and g_⊥ = 2.19, providing an average g_av = 2.196.

The negative sign of the Weiss temperature indicated the predominance of antiferromagnetic exchange interactions in the system. This is also confirmed by the temperature-dependence of the scaled product (χ − χ₀)(T − Θ) shown in the right inset of Fig. 10(a). At high temperatures, this product follows a horizontal line, obeying the Curie–Weiss law, whereas below approximately 175 K, it deviates downward, indicating the predominance of the antiferromagnetic short-range correlations. Despite the wide range of correlations, the system does not reach ordered state, which probably relates to frustration and competing exchange interactions. The presence of exchange interactions of both the ferro- and antiferromagnetic nature follows from the field dependence of the magnetization (Fig. 10(b)), which demonstrates characteristic S-type behaviour at 2 K, which is similar to those for the isostructural compound with Ni²⁺. However, at higher temperature, magnetization shows ordinary linear trend, typical of antiferro- or paramagnets. This behaviour is completely different from the trirutile-type CuSb₂O₆, which demonstrated clear spin-flop transition with H_SF ∼ 1.3 T at 5 K below the Néel temperature T_N = 8.5 K.^6,9 Interestingly, the relatively high Néel temperature for trirutile-type CuSb₂O₆ has not been confirmed from theoretical calculations due to the tiny balance in the energy levels of d_x²−y² and d_3z²−r² electronic shells of Cu²⁺ ions in the octahedral oxygen environments and hence is related to large intrinsic magnetic anisotropy.¹¹ The value predicted from this theoretical analysis is less than 1.5 K.¹¹ Consequently, the structural changes for the new polymorph lead to more regular octahedral parameters, reducing the magnetic anisotropy for rosiaite-type compound, which in turn results in an essential decrease in the ordering temperature.

The parallel and independent low-temperature neutron diffraction study of CuSb₂O₆ confirmed the absence of long-range magnetic order down to 1.5 K. Fig. 11 only shows the same reflections that were observed by XRD at room temperature although their relative intensities are entirely different. In particular, the first pair of reflections 001 + 100 is practically invisible. Good agreement between the experimental and calculated profiles confirmed the rosiaite-type structure; however, full-scale structure refinement was not attempted due to the scarce experimental data.

Fig. 11 Rietveld refinement results of the powder neutron diffraction pattern of CuSb₂O₆ at 1.5 K. Red filled circles, experimental data; black line, calculated profile; blue line at the bottom, difference profile; and green vertical bars, calculated positions of the Bragg reflections.

The diffuse maximum between 33 and 39°, as shown in Fig. 11, coincides, in terms of the interplanar spacings d, with that observed in the XRD pattern of Fig. 1b between 21 and 24°. Therefore, it is not related to short-range magnetic ordering.

4. Conclusions

Herein, five new metastable trigonal layered MSb₂O₆ phases (M = Co, Ni, Cu, Zn, and Mg) were prepared by the low-temperature ion-exchange reactions, together with previously known CdSb₂O₆. FeSb₂O₆ could not be prepared due to the incompatible oxidation states but is predicted to stabilize at high pressures. CoSb₂O₆ and NiSb₂O₆ antiferromagnetically order at 11 and 15 K, respectively. In contrast to their stable trirutile-type polymorphs, they do not show any signs of low-dimensional magnetic behaviour at higher temperatures. CuSb₂O₆ does not exhibit long-range magnetic order down to 1.5 K but shows antiferromagnetic short-range correlations.

Acknowledgements

The work was supported by the Russian Foundation for Basic Research under the grant 14-03-01122. A. N. V. acknowledges the support in part from the Ministry of Education and Science of the Russian Federation in the framework of Increase Competitiveness Program of NUST <MISiS> (no. K2-2016-066) and by Act 211 of the Government of Russian Federation, contract no. 02.A03.21.0006.

References

1. V. B. Nalbandyan, E. A. Zvereva, A.Yu. Nikulin, I. L. Shukaev, M.-H. Whangbo, H.-J. Koo, M. Abdel-Hafiez, X.-J. Chen, C. Koo, A. N. Vasiliev and R. Klingeler, Inorg. Chem., 2015, 54, 1705–1711.
2. W. H. Baur, Crystallogr. Rev., 2007, 13, 65–113.
3. A. Castro, I. Rasines, M. C. Sanchez-Martos and P. Garcia-Casado, Powder Diffr., 1988, 3, 219–221.
4. E. Ramos, F. Fernandez, A. Jerez, C. Pico, J. Rodriguez-Carvajal, R. Saez-Puche and M. L. Veiga, Mater. Res. Bull., 1992, 27, 1041–1047.
5. J. N. Reimers, J. E. Greedan, C. V. Stager and R. Kremer, J. Solid State Chem., 1989, 83, 20–30.
6. A. B. Christian, S. H. Masunaga, A. T. Schye, A. Rebello and J. J. Neumeier, Phys. Rev. B: Condens. Matter, 2014, 90, 224423.
7. A. B. Christian, A. Rebello, M. G. Smith and J. J. Neumeier, Phys. Rev. B: Condens. Matter, 2015, 92, 174425.
8. E.-O. Giere, A. Brahimi, H. J. Deiseroth and D. Reinen, J. Solid State Chem., 1997, 131, 263–274.
9. A. Rebello, M. G. Smith, J. J. Neumeier, B. D. White and Yi.-K. Yu, Phys. Rev. B: Condens. Matter, 2013, 87, 224427.
10. A. M. Nakua and J. E. Greedan, J. Solid State Chem., 1995, 118, 199–201.
11. D. Kasinathan, K. Koepernik and H. Rosner, Phys. Rev. Lett., 2008, 100, 237202.
12. M. Kato, A. Hatazaki, K. Yoshimura and K. Kosuge, Physica B, 2000, 281&282, 663–664.
13. M. Herak, D. Žilić, D. Matković-Calogović and H. Berger, Phys. Rev. B: Condens. Matter, 2015, 91, 174436.
14. J. Singh, N. Bhardwaj and S. Uma, Bull. Mater. Sci., 2013, 36, 287–291.
15. D. P. Dutta, A. Ballal, A. Singh, M. H. Fulekarc and A. K. Tyagi, Dalton Trans., 2013, 42, 16887–16897.
16. H. Mizoguchi and P. M. Woodward, Chem. Mater., 2004, 16, 5233–5248.
17. J. Tamaki, Y. Yamada, Y. Yamamoto, M. Matsuoka and I. Ota, Sens. Actuators, B, 2000, 66, 70–73.
18. C. R. Michel, N. L. L. Contreras, M. A. López-Alvarez and A. H. Martinez-Preciado, Sens. Actuators, B, 2012, 171-172, 686–690.
19. H. Guillen-Bonilla, V.-M. Rodriguez-Betancourtt, J.-T. Guillen-Bonilla, J. Reyes-Gomez, L. Gildo-Ortiz, M. Flores-Martinez, M. de la L. Olvera-Amador and J. Santoyo-Salazar, J. Nanomater., 2015, 979543.
20. A. R. Basso, R. Cabella, G. Lucchetti, P. Marescotti and A. Martinelli, Neues Jahrb. Mineral., Monatsh., 2003, 9, 407–420.
21. V. B. Nalbandyan, M. Avdeev and A. A. Pospelov, Solid State Sci., 2006, 8, 1430–1437.
22. A. G. Bergman and M. S. Golubeva, Dokl. Akad. Nauk SSSR, 1953, 89, 471–473.
23. A. C. Larson and R. B. Von Dreele, General Structure Analysis System (GSAS), Los Alamos National Laboratory Report LAUR 86-748, Los Alamos National Laboratory, Los Alamos, NM, 2004.
24. B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210–213.
25. J. Rodrigues-Carvajal, FullProf_suite. http://www.ill.eu/sites/fullprof/.
26. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Cryst., 1976, 32, 751–767.
27. Powder Diffraction File. International Centre for Diffraction Data, Newtown Square, Pennsylvania, USA, 2006. Cards 00-17-284, 00-18-403, 00-37-1470, 00-38-453, 00-38-1083.
28. A. A. Novikova and V. B. Nalbandyan, Crystallogr. Rev., 2013, 19, 125–148.
29. B. Wang, S. C. Chen and M. Greenblatt, J. Solid State Chem., 1994, 108, 184–188.
30. J. Amador, E. G. Puebla, M. A. Monge, I. Rasines and C. R. Valero, Inorg. Chem., 1988, 27, 1367–1370.
31. G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532–536.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6dt04859e

---