Open Access Article
Open Access ArticlePhotonics and spectroscopy in nanojunctions: a theoretical insight
Michael
Galperin

Department of Chemistry & Biochemistry, University of California San Diego, 9500 Gilman Dr., La Jolla, CA 92093, USA. E-mail: migalperin@ucsd.edu; Tel: +1 858 246 0511
First published on 11th April 2017
Abstract
The progress of experimental techniques at the nanoscale in the last decade made optical measurements in current-carrying nanojunctions a reality, thus indicating the emergence of a new field of research coined optoelectronics. Optical spectroscopy of open nonequilibrium systems is a natural meeting point for (at least) two research areas: nonlinear optical spectroscopy and quantum transport, each with its own theoretical toolbox. We review recent progress in the field comparing theoretical treatments of optical response in nanojunctions as is accepted in nonlinear spectroscopy and quantum transport communities. A unified theoretical description of spectroscopy in nanojunctions is presented. We argue that theoretical approaches of the quantum transport community (and in particular, the Green function based considerations) yield a convenient tool for optoelectronics when the radiation field is treated classically, and that differences between the toolboxes may become critical when studying the quantum radiation field in junctions.
1 Introduction
Optical spectroscopy is an important diagnostic tool routinely applied to study molecules (either in gas or condensed phases, or adsorbed on surfaces). In nanojunctions spectroscopic applications range from characterization of molecular structures and junction interfaces, to introducing nanoscale thermometry, to inducing and controlling molecular dynamics and chemistry. A wide range of spectroscopic techniques are utilized in the studies including (to name a few) infrared,1–4 X-ray,5,6 sum frequency generation (SFG),7–10 as well as surface (SERS)11–15 and tip-enhanced (TERS)16–22 Raman spectroscopy.In recent years optical experiments in current-carrying single-molecule junctions have become a reality.23–30 Combination of the fields of optical spectroscopy and molecular electronics indicates the emergence of a new field of research, coined molecular optoelectronics.31 In particular, multiple experiments reported detection of current-induced photon emission (electroluminescence).32–51 Among them vibrationally39,50 and spatially42 resolved photo-emission and electroluminescence as a measure of multi-electron processes41,43,46,49 and noise44–46 in junctions, and also as indicators of vibronic motion48 and real space energy transfer,51 were reported. Alternatively, external illumination was utilized as a means to control electron transfer and transport.52–62 Measurements of light induced magnetization in chiral molecules were also reported in the literature.63–68
For molecules chemisorbed on metallic surfaces or encapsulated in nanocavities molecular excitations are coupled with plasmons. This interaction leads to enhancement of molecular signals,69–72 which yields the possibility to measure the optical response of single molecules.73–76 Thus engineering effective plasmonic structures is crucially important, and nanoplamonics becomes an inherent part in the construction and operation of any molecular optoelectronic device.3,40,43,45,57,58,77–86 Note that while usually construction of nanometer scale gaps is the way to form areas of high electromagnetic field (hot spots),77 the possibility of surface enhanced spectroscopy without nanogaps was also reported.82
As already mentioned surface enhanced Raman (SERS)87–90 and tip-enhanced Raman (TERS)91,92 spectroscopy techniques are utilized as indicators of structural changes and dynamics in junctions. Simultaneous measurements of SERS and conductivity93–101 provide information on dynamical correlations between the two signals95,102 serve as a measure of current-induced heating,94,96 and characterize charging states of molecules in junctions.99,101,103
While initially most of the optical experiments in junctions were focused on steady-state response, lately time-dependent and transient characteristics started to attract attention. Optical pump–probe type measurements in junctions were realized in the form of time-dependent voltage induced plasmonic luminescence.47 Laser pulse induced transport measurements as a tool to assess the intramolecular dynamics on a sub-picosecond time scale were also suggested.104,105 Recently multidimensional spectroscopy measurements in the presence of current (although not yet in junctions) were reported in the literature.106–108
The observation of quantum effects in light–matter interactions is another recent development. For example, quantum effects in nanoplasmonics (such as transition of entanglement between photons and plasmons) recently started to attract attention indicating the emergence of quantum plasmonics as a new field of research.109–121 Similarly, strong light–molecule coupling in nanocavities,122–126 when states of light and matter cannot be separately distinguished and a hybrid state (polariton) is formed, reveals the quantum nature of the external electromagnetic field. Finally, very recently, an ultra-strong coupling regime (the regime where the coupling between light and matter becomes the largest energy scale in the system) was achieved experimentally.127
Experimental advancements in nanojunction spectroscopy posed a challenge for adequate theoretical description.31,128,129 In particular, these advancements resulted in the necessity to combine theoretical tools of optical spectroscopy with those of quantum transport. Corresponding formulations were developed and applied to the description of absorption and current-induced light emission,51,130–143 as well as light-induced current in junctions.60,104,105,130,144–150 In these studies light–matter interactions were mostly treated by combining classical electrodynamics of radiation field with quantum mechanical description of the molecule.129,150–162 Similarly, theoretical approaches to (yet to be measured in junctions) multidimensional spectroscopy were proposed.108,163–166
Significant theoretical efforts were devoted to development of theory of Raman spectroscopy in current-carrying junctions167–172 and its application to modeling of current induced heating,103,167,168,173,174 dynamics and conformational changes,84,175,176 chemistry,177 control of charging states of the molecule,99,101,103,178 study of time-dependent correlations between conductance and Raman response,179–181 and elucidation of chemical enhancement in SERS.102,179,180,182–186 Here the radiation field was mostly treated quantum mechanically. Also strong light–matter (plasmon–molecule) couplings were treated theoretically with the radiation field described quantum mechanically.165,187–199 Finally, quantum treatment of the field was required to describe optically measured noise characteristics of junctions.200,201 Quantum effects in photonics and optical spectroscopy have been discussed in recent reviews.202,203
From a theoretical perspective, optical spectroscopy in nanojunctions (optoelectronics) is a field where theoretical approaches of nonlinear optical spectroscopy meet those of quantum transport theory. Theoretical toolboxes of the two research communities are slightly different and sometimes also utilize a bit different language. For example, traditionally optical spectroscopy relies on bare perturbation theory (PT) in light-matter interaction formulated within the Liouville space for classification of optical response of isolated molecular systems. Optical transitions in the latter are considered between many-body states of the molecule. This type of treatment became standard in the spectroscopy community. Naturally, this same approach is sometimes applied to open systems and/or when the radiation field is treated quantum mechanically. Theoretical methods of quantum transport community are numerous. The common (and probably most developed) is the nonequilibrium Green's functions (NEGF) approach. It is formulated in the Hilbert space and in its canonical form utilizes quasiparticles (or elementary excitations, or molecular orbitals) as a basis.
This review compares theoretical approaches of the two communities in their treatment of spectroscopy in nanojunctions. We discuss their strong and weak sides and indicate limitations in the applicability of the approaches. The structure of the review is as follows. Section 2 discusses theoretical approaches to optical spectroscopy. To make the review self-contained, in Section 2.1 we give a short introduction to theoretical methodology standard in the nonlinear optical spectroscopy community. Section 2.2 discusses photonics in nanojunctions from the perspective of Green function methods. First we briefly introduce canonical NEGF in Section 2.2.1 and then follow with its two many-body flavors: the pseudoparticle NEGF (PP-NEGF) in Section 2.2.2 and Hubbard NEGF in Section 2.2.3. We compare the theoretical approaches and argue that the latter two formulations can be a convenient choice for optoelectonics. Theoretical considerations of spectroscopy in junctions with the radiation field treated classically are presented in Section 3. Quantum treatment of the radiation field in junctions is discussed in Section 4. Section 5 concludes.
2 Theoretical methodology
A distinct feature of junction spectroscopy is interdependence of optical and electronic characteristics of an optoelectronic device. Indeed, optical spectroscopy of isolated systems is focused on photon flux; this flux is the only channel of communication between the system and environments (measuring devices). In contrast, in nanojunctions, where the electron participating in the optical scattering process is free to leave contributing to electron and energy fluxes, combined theoretical consideration of all the constituents is crucial. In this case one does not have optical signal independent of electric current, rather one has to deal with a comprehensive description.Let us consider junctions under external illumination.† The Hamiltonian of the total system is
Ĥ = ĤM + ĤK + Ĥp + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) MK + MK + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) MP MP | (1) |
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) MK and
MK and ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) MP describe coupling to contacts and light–matter interaction. In general, part or all of the contributions can be time-dependent due to external driving. Contacts and radiation field Hamiltonians are assumed to be reservoirs of free carriers (electrons and photons, respectively):
MP describe coupling to contacts and light–matter interaction. In general, part or all of the contributions can be time-dependent due to external driving. Contacts and radiation field Hamiltonians are assumed to be reservoirs of free carriers (electrons and photons, respectively): 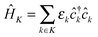 and
and 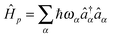 , where
, where 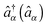 and
and 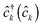 are creation (annihilation) operators for photons in mode α and electrons in state k of contact K. For simplicity below we specialize to bilinear coupling to contacts and rotating wave approximation in light–matter interactions‡
are creation (annihilation) operators for photons in mode α and electrons in state k of contact K. For simplicity below we specialize to bilinear coupling to contacts and rotating wave approximation in light–matter interactions‡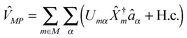 | (2) |
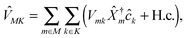 | (3) |
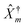 are matter excitation operators due to electron transfer from state k in contacts or optical excitation by the radiation field.
are matter excitation operators due to electron transfer from state k in contacts or optical excitation by the radiation field.
Most theoretical studies of optical spectroscopy and quantum transport are focused on evaluation of fluxes (photon, p, and electron, e, respectively), which are defined as rates of change of carrier populations in baths (respectively, photon population of radiation field modes and electron density in contacts)204,205
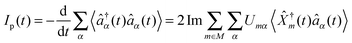 | (4) |
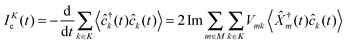 | (5) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (t0)] is quantum mechanical and statistical averaging with respect to the initial density operator (usually assumed to be the direct product of radiation field and electronic components
(t0)] is quantum mechanical and statistical averaging with respect to the initial density operator (usually assumed to be the direct product of radiation field and electronic components ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (t0) =
(t0) = ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) p(t0) ⊗
p(t0) ⊗ ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) e(t0)). Energy fluxes, Jp(t) and JKe(t), are defined in a similar way as rates of change of energy in the baths.§ The fluxes can be expressed in terms of single-particle Green functions (two time correlation functions; see below). Note that index m in eqn (2) and (4) has a meaning of optical transfer in the system, that is total number of electrons in M does not change. In contrast, m in eqn (3) and (5) indicates electron transfer between M and K; such transfer results in change of electron population in the system.
e(t0)). Energy fluxes, Jp(t) and JKe(t), are defined in a similar way as rates of change of energy in the baths.§ The fluxes can be expressed in terms of single-particle Green functions (two time correlation functions; see below). Note that index m in eqn (2) and (4) has a meaning of optical transfer in the system, that is total number of electrons in M does not change. In contrast, m in eqn (3) and (5) indicates electron transfer between M and K; such transfer results in change of electron population in the system.
Other quantities of interest are related to statistics of photon208–211 and electron212–214 transport as well as cross-correlations between the two. Measurements of fluctuations of particle fluxes were reported in junction studies for photon215,216 and electron transport.49,217–219 A number of experiments demonstrated cross-correlation effects.41,46,220 Theoretically fluctuations are characterized within the full counting statistics (for time-local cumulants of transfer distribution)221 or via the two-particle Green function (e.g., g(2)222,223 or current–current224–227 correlation functions). Higher order correlation functions were also considered in the literature.228
Evaluation of the correlation functions is performed within either Liouville or Hilbert spaces with the former being the standard choice in the nonlinear spectroscopy community. While the two representations differ only in the way the correlation function is evaluated, and ideally one expects the same result from both considerations, approximations involved in real-life calculations are quite different, so that the results depend on the way (and level) of treatment. Below we give a short pedagogical introduction to different approaches and indicate their strong and weak sides.
2.1 Liouville space formulation
We start from a very short introduction to the Liouville space formulation – an accepted standard approach in the field of nonlinear optical spectroscopy. A comprehensive formulation can be found in ref. 204, which became a standard reference for classification and interpretation of optical experiments.Expressing photon flux, eqn (4), in the interaction picture with respect to the light–matter coupling (2) yields 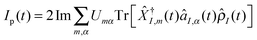 , where subscript I indicates the interaction picture. The integral form of the Liouville–von Neumann equation for the total density matrix is
, where subscript I indicates the interaction picture. The integral form of the Liouville–von Neumann equation for the total density matrix is
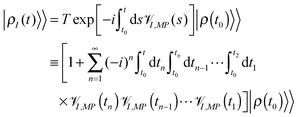 | (6) |
![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) I,MP is the interaction picture form of the Liouville space superoperator corresponding to the Hilbert space operator
I,MP is the interaction picture form of the Liouville space superoperator corresponding to the Hilbert space operator ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) MP of (2). Expansion of the evolution operator (T ordered exponent in the first row of eqn (6)) in the Taylor series (second and third rows of (6)) yields bare perturbation theory (PT) in
MP of (2). Expansion of the evolution operator (T ordered exponent in the first row of eqn (6)) in the Taylor series (second and third rows of (6)) yields bare perturbation theory (PT) in ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) MP, which presents evolution of the total density matrix as a sum of time-ordered (t ≥ tn ≥ tn−1 ≥ ⋯ ≥ t1 ≥ t0) sets of light–matter interactions. Taking into account that any Liouville space superoperator is expressed in Hilbert space as a commutator of the corresponding operator, every
MP, which presents evolution of the total density matrix as a sum of time-ordered (t ≥ tn ≥ tn−1 ≥ ⋯ ≥ t1 ≥ t0) sets of light–matter interactions. Taking into account that any Liouville space superoperator is expressed in Hilbert space as a commutator of the corresponding operator, every ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) I,MP(ti) in (6) acts on either bra or ket of the result of prior evolution,
I,MP(ti) in (6) acts on either bra or ket of the result of prior evolution, 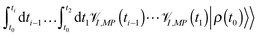 . Thus, the Liouville space expression for photon flux (4),
. Thus, the Liouville space expression for photon flux (4),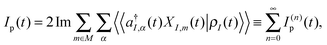 | (7) |
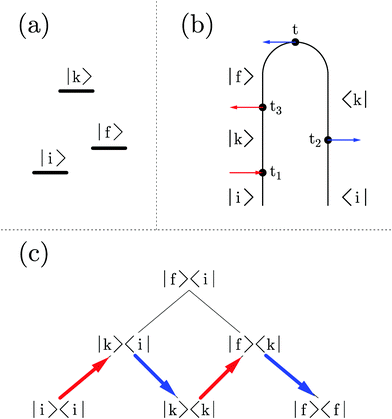
 , pointing to left) or annihilation (âα, pointing to right) photon operators for the quantum radiation field, or the corresponding negative and positive components when the radiation field is treated classically. Graphical representations of the type (see, e.g., Fig. 1b), coined double-sided Feynman diagrams,¶ are widely utilized in the spectroscopy community to classify optical processes. Time ordered sequences of changes in the state of the system (changes in its bra and ket with time) are known as pathways in Liouville space (see Fig. 1c); they are instrumental in discussing propagation of coherences and populations in the system resulting from optical scattering processes. Similarly, one can expand electron flux IKe(t), eqn (5), in orders of light–matter interaction
, pointing to left) or annihilation (âα, pointing to right) photon operators for the quantum radiation field, or the corresponding negative and positive components when the radiation field is treated classically. Graphical representations of the type (see, e.g., Fig. 1b), coined double-sided Feynman diagrams,¶ are widely utilized in the spectroscopy community to classify optical processes. Time ordered sequences of changes in the state of the system (changes in its bra and ket with time) are known as pathways in Liouville space (see Fig. 1c); they are instrumental in discussing propagation of coherences and populations in the system resulting from optical scattering processes. Similarly, one can expand electron flux IKe(t), eqn (5), in orders of light–matter interaction ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) MP, eqn (2). Expansions in coupling to contacts
MP, eqn (2). Expansions in coupling to contacts ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) MK, eqn (3), were also considered in the literature.139
MK, eqn (3), were also considered in the literature.139
Bare PT (6) in ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) MP decouples light and matter degrees of freedom, i.e. each contribution is a product of two correlation functions (electron and photon), which have to be evaluated independently. Often after completing the derivation the incoming field is assumed to be in a coherent state, and transfer to classical representation is performed. Thus, optical response to the classical field only requires evaluation of the electronic multi-time correlation function. Even contributions in the expansion (7) usually drop out because of the odd number of photon creation/annihilation operators in the correlation function (for classical field these terms drop out by symmetry in the case of isotropic medium204). Sometimes quantum description is used for a subset of modes, while the rest of the field is treated classically.231 Note that application of bare PT to description of quantum fields (or to molecule–contacts coupling
MP decouples light and matter degrees of freedom, i.e. each contribution is a product of two correlation functions (electron and photon), which have to be evaluated independently. Often after completing the derivation the incoming field is assumed to be in a coherent state, and transfer to classical representation is performed. Thus, optical response to the classical field only requires evaluation of the electronic multi-time correlation function. Even contributions in the expansion (7) usually drop out because of the odd number of photon creation/annihilation operators in the correlation function (for classical field these terms drop out by symmetry in the case of isotropic medium204). Sometimes quantum description is used for a subset of modes, while the rest of the field is treated classically.231 Note that application of bare PT to description of quantum fields (or to molecule–contacts coupling ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) MP) may be problematic even when perturbation theory is applicable (e.g., when the ratio of light–matter coupling is small compared with the system coupling to electronic baths). The reason is the ability of photons to serve as intermediates inducing effective non-Markov interactions within the electron system. The latter enters theoretical description via electron self-energies, which cannot be properly described within bare PT (see discussion in Section 2.2.1).
MP) may be problematic even when perturbation theory is applicable (e.g., when the ratio of light–matter coupling is small compared with the system coupling to electronic baths). The reason is the ability of photons to serve as intermediates inducing effective non-Markov interactions within the electron system. The latter enters theoretical description via electron self-energies, which cannot be properly described within bare PT (see discussion in Section 2.2.1).
In contrast to isolated systems, in junctions electron correlation is averaged over both system (molecule) and bath (contacts) degrees of freedom. As long as light–matter interaction is assumed to be confined to the system (molecule) only (i.e. electron operators in the correlation function are those of the system only), the multi-time correlation function can be evaluated by employing the regression formula. This procedure is often utilized and is exact when system evolution is Markovian.232 Note that while formally a time-local quantum master equation can always be derived, in practice evaluation of the time-convolutionless propagator is a complicated task.233 Thus, most practical applications so far utilize effective Markovian propagators, which (when employed with the regression formula) may be problematic. In particular, within the approach every interaction with the optical field results in the destruction of the molecule–contacts coherence. The latter is an artifact of the formulation, which may lead to qualitative failures (see discussion in Section 3).
To summarize, the Liouville space superoperator formulation of nonlinear optical spectroscopy has several important advantages. First, the formulation follows evolution of the density matrix in real time, which allows for an intuitive graphical representation of optical processes in the form of double sided Feynman diagrams. Second, system's response can be described within the basis of its many-body states (eigenbasis of the Hamiltonian ĤM), which allows one to account for all the intra-system interactions exactly and paves a way to incorporate the results of standard quantum-chemistry simulations (usually performed for isolated molecules) into numerical modelling of optoelectronic devices. These advantages were mentioned in many works on optical spectroscopy.132,139,164,165,169,204,234,235 At the same time the bare PT and utilization of the regression formula may be problematic. The former fails to adequately describe open systems when the radiation field is treated quantum mechanically. The latter leads to qualitative mistakes due to the approximate nature of effective Markovian propagators employed in practical simulations (This is true for both classical and quantum radiation field treatments). Note that multi-time correlation functions in principle can be evaluated numerically exactly (i.e. without employing the regression formula).236–239 However, the significant cost of such approaches so far limits their applicability to simple models. Note also that, the standard approach (e.g., Redfield quantum master equation), which employs many-body states of the system as a basis, does not properly account for the system (molecule)–electronic baths (contacts) couplings.240,241
Below we show that Hilbert space Green function formulations are capable of yielding (within similar level of theory) the same advantages while avoiding the pitfalls of the Liouville space superoperator methods.
2.2 Hilbert space formulations
While theoretical treatments of quantum transport utilize both Hilbert and Liouville space formulations, the former is the choice of the nonequilibrium Green function (NEGF) technique. Below we focus on the NEGF (and its generalizations) and discuss application of the technique to description of optical spectroscopy in nanojunctions.Evolution of a nonequilibrium system in the Hilbert space relies on contour (rather than real time as in Liouville space) ordering. A particular ordering of contour variables, which we will denote by Greek index τ in contrast to t indicating real time, defines the projection of a correlation function. These projections are equivalent to double sided Feynman diagrams of the Liouville space formulation, although the number of contour projections is smaller (requirement of real time ordering in the Liouville space formulation results in bigger number of such projections, i.e. one contour projection includes several double sided Feynman diagrams). Note that projections and diagrams (in their original meaning) are different things. For example, Fig. 2 demonstrates two different fourth order Feynman diagrams representing two-particle scattering and virtual photon exchange processes, respectively; both diagrams will have the same set of projections (or double sided Feynman diagrams).
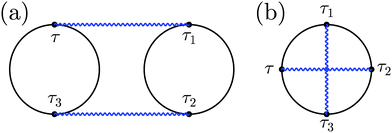 | ||
| Fig. 2 Feynman diagrams for (a) two-particle scattering and (b) virtual photon exchange. Solid (black) and wavy (blue) lines represent the electron and photon Green function, respectively. | ||
Historically introduction of the contour is the consequence of an attempt to build an analog of Feynman diagrams for nonequilibrium systems. The Feynman diagrammatic technique relies on the Gell-Mann and Low theorem242 which (for equilibrium systems at zero temperature) allows one to establish connection between initial (t0 → −∞) and final (t0 → +∞) ground states of the system. Absence of such connection in a nonequilibrium situation necessitates using bra and ket of the starting state as initial and final states of the process (i.e. starting state density matrix is utilized for quantum mechanical and statistical averaging).||Ref. 244 presents a beautiful and thorough discussion about relations between the Feynman (zero temperature equilibrium), Matsubara (finite temperature equilibrium), and Keldysh (nonequilibrium) theories.
Fluxes (4) and (5) can be exactly expressed in terms of Green functions as205,247–249
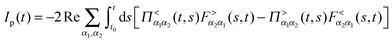 | (8) |
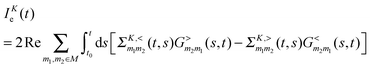 | (9) |
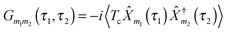 | (10) |
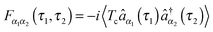 | (11) |
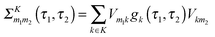 | (12) |
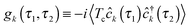 is the Green function of a free electron in state k of contact K. The explicit expression for the photon self-energy, Πα1,α2(τ1,τ2), depends on the level of treatment (e.g., order of diagrammatic perturbation theory employed – see below). While analytical forms of the self-energy ΣK are known, other constituents of the fluxes (8) and (9) have to be evaluated by solving a set of coupled equations.
is the Green function of a free electron in state k of contact K. The explicit expression for the photon self-energy, Πα1,α2(τ1,τ2), depends on the level of treatment (e.g., order of diagrammatic perturbation theory employed – see below). While analytical forms of the self-energy ΣK are known, other constituents of the fluxes (8) and (9) have to be evaluated by solving a set of coupled equations.
Note that the expression for photon flux, eqn (8), is relevant only when the radiation field is treated quantum mechanically. For the classical field one has to either evaluate multi-time correlation functions as discussed in Section 2.1 or solve the time-dependent problem for a system (molecule) coupled to the external classical field. The latter situation was considered in many works,146,151–153,155–158 where the radiation field was treated classically propagating Maxwell equations along with quantum mechanical treatment of electron dynamics. The expression for electron flux, eqn (9), is always correct. Note also that in junctions where formation of the local field is affected by both plasmon excitations in the contacts and molecular response, bare perturbation theory (which for a particular optical process discards back action of the matter on the field) may be not enough. This was shown in studies considering radiation field both classically155,157 and quantum mechanically.193 Finally, the fact that, e.g., the electron Green function G enters expressions for both fluxes,**eqn (8) and (9), indicates inter-dependence of the fluxes and demonstrates the necessity of consistent (i.e. within the same level of theory) description of optoelectronic device responses.
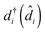 are the usual operators of the second quantization which create (annihilate) an electron in orbital i of the system M. The approach is most convenient when intra-system interactions are small compared with the coupling to electronic baths, so that the former can be treated within diagrammatic perturbation theory. In this case, one can utilize, e.g., set of molecular (or Kohn–Sham) orbitals to represent the electronic structure of the molecule. The latter are (de)populated by electron transfer between electronic reservoirs and molecule. Thus index m in eqn (9) stands for such an orbital, so that electron flux is exactly expressed in terms of single particle Green functions
are the usual operators of the second quantization which create (annihilate) an electron in orbital i of the system M. The approach is most convenient when intra-system interactions are small compared with the coupling to electronic baths, so that the former can be treated within diagrammatic perturbation theory. In this case, one can utilize, e.g., set of molecular (or Kohn–Sham) orbitals to represent the electronic structure of the molecule. The latter are (de)populated by electron transfer between electronic reservoirs and molecule. Thus index m in eqn (9) stands for such an orbital, so that electron flux is exactly expressed in terms of single particle Green functions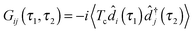 | (13) |
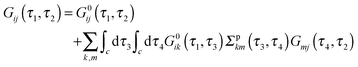 | (14) |
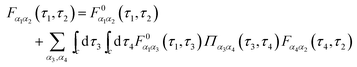 | (15) |
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) MP, Σp is the electronic self-energy due to coupling to radiation field, and Π is photon self-energy due to coupling to electrons. The latter two quantities can be derived only approximately; the approximations should satisfy conservation laws for physical quantities. A way to formulate conserving approximations was formulated in the works by Kadanoff and Baym.250,251 The interested reader is encouraged to consult the book by Stefanucci and van Leeuwen252 for a detailed consideration of the issue.
MP, Σp is the electronic self-energy due to coupling to radiation field, and Π is photon self-energy due to coupling to electrons. The latter two quantities can be derived only approximately; the approximations should satisfy conservation laws for physical quantities. A way to formulate conserving approximations was formulated in the works by Kadanoff and Baym.250,251 The interested reader is encouraged to consult the book by Stefanucci and van Leeuwen252 for a detailed consideration of the issue.
Diagrammatic perturbation theory is built by constructing the Luttinger–Ward functional, Φ. The latter is a collection of all dressed connected skeleton diagrams (i.e., connected combinations of Green functions G and F that have no self-energy insertions).253,254 Expressions for self-energies are obtained as functional derivatives252,255
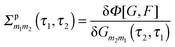 | (16) |
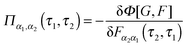 | (17) |
It is important to note that in contrast to bare PT (an expansion to a particular order), diagrammatic PT sums a particular type of diagrams (the type corresponding to a particular order) to infinity. Indeed, Luttinger–Ward functional Φ is expressed in terms of full Green functions G and F rather than their zero order analogs G0 and F0.†† This summation is central for conserving character of an approximation. Note also that the necessity (for quantum radiation field) to solve simultaneously two coupled (via their self-energies) Dyson equations (eqn (14) and (15)) corresponds to formation of the local field due to both external source and system response. The situation is relevant for, e.g., molecules in nanocavities or in the vicinity of metal surfaces. However, even if one can assume independence of the radiation field with respect to molecular response,‡‡ still for an approximation to be conserving one has to sum a subset of diagrams to infinity – via dependence of electron self-energy Σp on full Green function G and structure of Dyson equation (14). Bare PT does not take into account these resummations and thus will violate conservation laws. As a result traditional classification of optical processes (and utilization of the double sided Feynman diagrams as is standard in optical spectroscopy community) becomes questionable in comprehensive treatments of open systems.
To summarize, an important advantage of the NEGF is existence of established set of rules (the nonequilibrium diagrammatic technique) to treat interactions in the system (in particular, light–matter interactions) in an organized perturbative way preserving physical conservation laws. The approach is able to exactly account for system (molecule) coupling to electronic baths (contacts). It is also instrumental in studying counting statistics of transport in both steady-state256 and transient257,258 regimes. NEGF is the direct successor to original (Feynman and Matsubara) Green function formulations244 and as such allows physically motivated choice of relevant diagrams in the same way as does the Feynman diagrammatic technique. The main drawback of the method with respect to optoelectronic problems is its quasiparticle formulation. This significantly complicates treatment of strong intra-system interactions and makes (TD)DFT (also formulated in the basis of effective single particle orbitals) a method of choice for electronic structure simulations.259–261 The latter does not connect well with the traditional optical spectroscopy language and has some limitations related to both foundations of (TD)DFT (e.g., utilization of Kohn–Sham orbitals as physical objects) and in terms of its application to transport.262
We now turn to many-body flavors of the NEGF which to some extent are capable of overcoming these limitations.
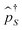 to unphysical vacuum |vac〉. Pseudoparticle operators satisfy the usual commutation or anticommutation relations depending on the Bose (e.g., even number of electrons) or Fermi (e.g., odd number of electrons) character of the corresponding many-body state. Any full set of many-body states should fulfill the normalization condition (sum over many-body states probabilities should be one). This condition is not automatically satisfied by the second quantization in the space of many-body states of the system, and should be imposed to restrict the so called extended Hilbert space to its physical subspace
to unphysical vacuum |vac〉. Pseudoparticle operators satisfy the usual commutation or anticommutation relations depending on the Bose (e.g., even number of electrons) or Fermi (e.g., odd number of electrons) character of the corresponding many-body state. Any full set of many-body states should fulfill the normalization condition (sum over many-body states probabilities should be one). This condition is not automatically satisfied by the second quantization in the space of many-body states of the system, and should be imposed to restrict the so called extended Hilbert space to its physical subspace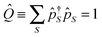 | (18) |
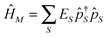 . However, it makes
. However, it makes ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) MK non-quadratic: index m in eqn (3) indicates transition (S1,S2) between a pair of states which differ by a single electron, so the interaction becomes
MK non-quadratic: index m in eqn (3) indicates transition (S1,S2) between a pair of states which differ by a single electron, so the interaction becomes 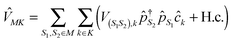 . Similarly, index m in eqn (2) stands for a transition between a pair of states with the same number of electrons. A simplified version of the pseudoparticle methodology is already well known for a long time as the slave-boson technique (see, e.g., ref. 263 and 264 – classics of quantum transport in junctions). Recently, development of the dynamical mean field theory renewed interest in the methodology.265
. Similarly, index m in eqn (2) stands for a transition between a pair of states with the same number of electrons. A simplified version of the pseudoparticle methodology is already well known for a long time as the slave-boson technique (see, e.g., ref. 263 and 264 – classics of quantum transport in junctions). Recently, development of the dynamical mean field theory renewed interest in the methodology.265
In PP-NEGF the central object of interest is the single pseudoparticle Green function
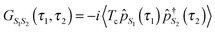 | (19) |
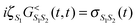 (here ζS = +1 (−1) for Bose (Fermi) state |S〉).
(here ζS = +1 (−1) for Bose (Fermi) state |S〉).
The main technical difference between NEGF and PP-NEGF comes from the necessity to impose restriction (18). This results in several unusual properties of pseudoparticle Green functions. For example, NEGF fluctuation–dissipation relation, G>ij(t1,t2) − G<ij(t1,t2) = Grij(t1,t2) − Gaij(t1,t2), becomes for the PP-NEGF in the ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) = 0 subspace
= 0 subspace 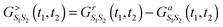 because
because 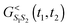 does not have contributions in
does not have contributions in ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) = 0; Dyson equations for retarded (
= 0; Dyson equations for retarded (![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) = 0 subspace) and lesser (
= 0 subspace) and lesser (![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) = 1 subspace) projections are decoupled in the PP-NEGF; to reflect physical reality any projection in the diagrammatic expansion should contain only one lesser Green function (sum of charges
= 1 subspace) projections are decoupled in the PP-NEGF; to reflect physical reality any projection in the diagrammatic expansion should contain only one lesser Green function (sum of charges ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) from different contributions in any diagram should be 1 – this is contribution from any lesser Green function, then the diagram as a whole belongs to physical subspace of the extended Hilbert space); etc. An interested reader is encouraged to consult ref. 265–268. In particular, ref. 266 is a beautiful introduction to the methodology; ref. 268 contains explicit expressions for self-energies due to coupling to fermionic (e.g., contacts) and bosonic (e.g., radiation field or thermal environment) baths.
from different contributions in any diagram should be 1 – this is contribution from any lesser Green function, then the diagram as a whole belongs to physical subspace of the extended Hilbert space); etc. An interested reader is encouraged to consult ref. 265–268. In particular, ref. 266 is a beautiful introduction to the methodology; ref. 268 contains explicit expressions for self-energies due to coupling to fermionic (e.g., contacts) and bosonic (e.g., radiation field or thermal environment) baths.
To summarize, PP-NEGF has several important advantages: (1) the method is conceptually simple; (2) standard diagrammatic perturbation theory can be applied (in particular, this means that physical conservation laws are preserved within the methodology); (3) already in its lowest (second) order in system–baths interactions, the non-crossing approximation (NCA), the pseudoparticle NEGF goes beyond standard QME approaches by accounting for both non-Markovian effects and hybridization of molecular states; (4) the method is capable of treating transport in the language of many-body states of the isolated molecule, exactly accounting for all intra-molecular interactions. We stress that while (similar to the Liouville space formulation) PP-NEGF describes a system utilizing its many-body states (eigenstates of ĤM) and accounts (albeit perturbatively) for hybridization between states of the system and baths, it avoids the two main problems of the Liouville space superoperator method (as discussed at the end of Section 2.1). As any approximate scheme the pseudoparticle NEGF has its own limitations;269 however those are important mostly at low temperatures (below Kondo temperature). Also, the lowest order of the method (NCA) was recently shown to be sensitive to details of accompanying approximations.270 Finally, an important deficiency of the methodology is related to its inability to yield information on full counting statistics. Presumably, the problem comes from its formulation within extended (unphysical) Hilbert space. We now turn to a methodology which allows one to overcome the difficulty.
The Hubbard NEGF is capable of describing the physics of open current carrying nanojunctions starting from the atomic limit (system and baths are decoupled) with all intra-system interactions taken into account exactly; system–baths couplings are used as small parameters in perturbative expansion. In this sense it is similar to PP-NEGF discussed above with the important difference that the methodology is formulated solely in physical Hilbert space. In contrast to PP-NEGF, which studies temporal correlations between pairs of many-body states of the system, eqn (19), Hubbard NEGF focuses on similar correlations between transitions from one many-body state to another. The latter are described by Hubbard (or projection) operators
![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) S1S2 = |S1〉〈S2| S1S2 = |S1〉〈S2| | (20) |
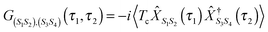 | (21) |
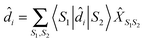 , immediately shows connection between (13) and (21). Indices m in eqn (2)–(5) are such transitions between many-body states, m = (S1S2): Bose type transitions in eqn (2) and (4) and Fermi in eqn (3) and (5).
, immediately shows connection between (13) and (21). Indices m in eqn (2)–(5) are such transitions between many-body states, m = (S1S2): Bose type transitions in eqn (2) and (4) and Fermi in eqn (3) and (5).
The cornerstone for both NEGF and PP-NEGF diagrammatic techniques is Wick's theorem242,243 which relies on (anti)commutation relations for creation and annihilation (Fermi) Bose operators: 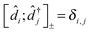 and
and 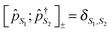 , respectively. It is crucial that the result of (anti)commutation is a number. This is not so for Hubbard operators (20):
, respectively. It is crucial that the result of (anti)commutation is a number. This is not so for Hubbard operators (20): 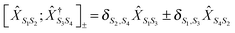 . Nevertheless, a variant of Wick's theorem for Hubbard operators was developed for equilibrium systems.272–274 The consideration was based on commutation properties of the equilibrium density matrix with Hubbard operators. In junctions one has to deal with a mixture of quasiparticle excitations in the baths and Hubbard operators describing eigenstates of the system Hamiltonian ĤM. Moreover, the system is in a nonequilibrium state. To build a nonequilibrium diagrammatic technique for Hubbard Green functions we made two assumptions: (1) originally (at t0 → −∞) the system and baths were decoupled and the system (molecule) was in thermal equilibrium and (2) after coupling was established the system reached steady-state defined solely by bath induced boundary conditions (i.e. memory of the initial state was lost). The latter is a usual assumption within the NEGF, and thus the former is unimportant for long time behavior of the system. The choice of thermal equilibrium as the initial condition allows one to employ Wick's theorem of ref. 272–274 for Hubbard operators, while the standard Wick's theorem242,243 is utilized to decouple quasiparticle correlation functions in perturbative expansion. The latter introduce boundary conditions imposed by baths on the system. After expansion to desired order in the coupling is finished, the diagrams are dressed in complete analogy with the standard diagrammatic technique. This results in a modified version of the Dyson type equation
. Nevertheless, a variant of Wick's theorem for Hubbard operators was developed for equilibrium systems.272–274 The consideration was based on commutation properties of the equilibrium density matrix with Hubbard operators. In junctions one has to deal with a mixture of quasiparticle excitations in the baths and Hubbard operators describing eigenstates of the system Hamiltonian ĤM. Moreover, the system is in a nonequilibrium state. To build a nonequilibrium diagrammatic technique for Hubbard Green functions we made two assumptions: (1) originally (at t0 → −∞) the system and baths were decoupled and the system (molecule) was in thermal equilibrium and (2) after coupling was established the system reached steady-state defined solely by bath induced boundary conditions (i.e. memory of the initial state was lost). The latter is a usual assumption within the NEGF, and thus the former is unimportant for long time behavior of the system. The choice of thermal equilibrium as the initial condition allows one to employ Wick's theorem of ref. 272–274 for Hubbard operators, while the standard Wick's theorem242,243 is utilized to decouple quasiparticle correlation functions in perturbative expansion. The latter introduce boundary conditions imposed by baths on the system. After expansion to desired order in the coupling is finished, the diagrams are dressed in complete analogy with the standard diagrammatic technique. This results in a modified version of the Dyson type equation
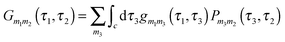 | (22) |
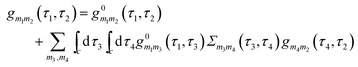 | (23) |
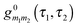 is the locator in the absence of coupling to the baths, and Pm1m2(τ1,τ2) is the strength operator. Eqn (22) and (23) are exact in the same sense as the usual Dyson equation. For details of derivation and rules of the nonequilibrium diagrammatic technique, the interested reader is encouraged to consult ref. 275 and references therein.
is the locator in the absence of coupling to the baths, and Pm1m2(τ1,τ2) is the strength operator. Eqn (22) and (23) are exact in the same sense as the usual Dyson equation. For details of derivation and rules of the nonequilibrium diagrammatic technique, the interested reader is encouraged to consult ref. 275 and references therein.
It is important to note that the nonequilibrium diagrammatic technique for Hubbard Green functions is a generalization of the Liouville superoperator formulation described in Section 2.1. On-the-contour diagrams are directly related to NEGF Feynman diagrams and account for both projections (as is the case in the double sided Feynman diagrams) and contractions between Hubbard operators of the system, quasiparticle operators representing electrons in contacts, and radiation field operators – respectively, Green functions (21), (12), and (11) (compare Fig. 3 with Fig. 1b). Note that the Hubbard NEGF can also be considered as a Green function generalization of the real-time perturbation theory developed for density matrices276–279 and as an extension of the auxiliary fields Hubbard Green function approach280–285 (as it yields an organized diagrammatic procedure to account for the system–baths couplings and allows evaluation of multi-time correlation functions). In contrast to the PP-NEGF, the Hubbard NEGF is formulated solely in the physical Hilbert space. As a result it can be utilized to study full counting statistics of transport (see preliminary data in Section 4). However, the approach (at the current level of development) has an important formal limitation: no clear way of constructing the Luttinger–Ward functional Φ has been proposed so far. Thus, while model simulations which we performed in ref. 275 show close correspondence with exact results, at the moment one cannot formally guarantee conserving character of the Hubbard NEGF diagrammatic expansions. A way to overcome the difficulty may be in constructing path integral formulation for the Hubbard NEGF utilizing generalized coherent states.286 This direction requires further research.
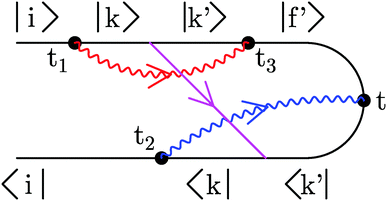 | ||
| Fig. 3 An example of an optical scattering process in junction. |i〉 and |k〉 are eigenstates of a neutral molecule, and |k′〉 and |f′〉 are eigenstates of a cation. Wavy lines (red and blue) represent photon Green functions (11), and the straight line (magenta) indicates electron self-energy due to coupling to contacts (12). | ||
3 Classical light
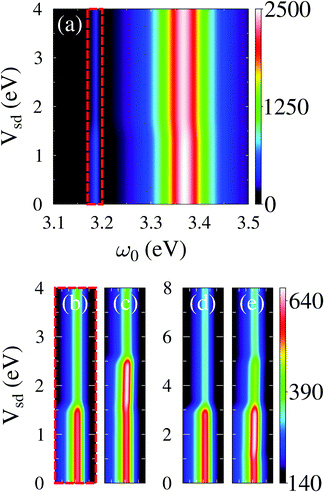
Until recently most simulations of optical properties in junctions were performed utilizing classical radiation fields. Roughly one can separate these studies into two groups: steady-state and time-dependent considerations. In the latter group (and for harmonic driving) either transition to Floquet space149,287–289 or transformation into the rotating frame of the field allow one to formulate the effective time-independent problem.147,249If light–matter coupling is relatively weak so that perturbative expansion in the interaction can be performed, bare PT expansion (as discussed in Section 2.1) is justified, and standard tools of nonlinear optical spectroscopy can be used in the studies of junctions. These studies are often performed for the steady-state regime (in the frequency domain). For example, ref. 132 and 139 utilized the Liouville space formulation to discuss current induced fluorescence in molecular junctions. Ref. 169 studied stimulated and spontaneous light emission. Multidimensional optical spectroscopy in junctions was considered in ref. 163 and 164. Evaluation of the resulting multi-time electronic correlation functions, eqn (6), was performed either by employing the quasiparticle language and utilizing the standard Wick's theorem,132,163 or by relying on the quantum regression formula.139,164,169 The former way is exact; the price to pay is the necessity to work in the quasiparticle (orbital) basis assuming noninteracting (quadratic) character of the molecular Hamiltonian. Such assumptions are quite common in DFT based simulations; however one has to be cautious when taking Kohn–Sham orbitals as suitable representations for molecular orbitals. In particular, in junctions the approach may lead to qualitative failures in predicting junction responses to external perturbations.262 Possible pitfalls of the regression formula are discussed in Section 2.1. For example, in ref. 290 we used a three level model to demonstrate that the regression formula (when the quantum master equation utilizes second order to account for system–baths couplings) fails to reproduce coherent 2D optical response of a junction. At the same time the PP-NEGF methodology (within the same, second order, level of treatment of system–baths couplings) yields qualitatively correct signals (see Fig. 4).
Explicit time-dependent simulations with respect to spectroscopy in nanojunctions are often employed to simulate plasmon excitations induced in metallic contacts by an external time-dependent radiation field. A numerical scheme propagates Maxwell equations (e.g., the finite-difference time domain approach291 is a popular choice) with the quantum system response entering the calculation via polarization current density.157 Junction dynamics is usually simulated within the quantum master equation or Green function approaches. A clear advantage of the former is time-locality of the density matrix; however, low order treatments of system–contacts couplings may result in qualitative failures.241,292 An easy heuristic workaround is introduction of buffer zones, which while being part of the dynamical calculation provide smooth connection between the nonequilibrium system and equilibrium baths.293,294 More rigorous (yet still not too heavy to remain practical) methodology is the hierarchical equation of motion approach;295–297 its main limitation is restriction to high temperatures. Dynamical simulations employing Green functions are naturally more demanding,245,246,248,266 and usually (when going beyond the adiabatic regime) approximations are required to make the approach practical.298 An interesting development is a representation which maps time-nonlocal interacting Dyson equation onto a noninteracting auxiliary Hamiltonian with additional bath degrees of freedom; the latter problem can be efficiently solved.299 We employed NEGF within the wide-band approximation to simulate transport and optical response of molecular junctions driven by time-dependent plasmonic field.146,153,157 Among other things we demonstrated the importance of molecular response in the formation of the local field (see Fig. 5) and hence also in junction responses. The latter indicates that due to the crucial role of plasmonic enhancement in junction spectroscopy one has to be careful when applying bare PT treatments to study optics in nanojunctions even with classical fields.
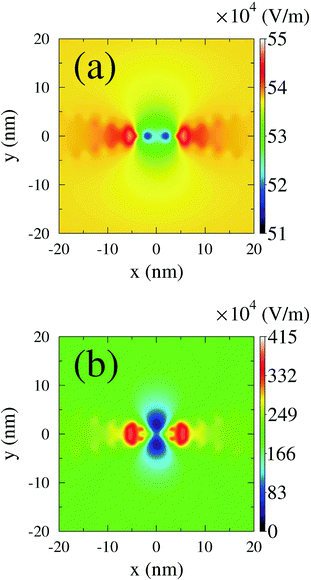 | ||
| Fig. 5 Instantaneous near field strength in a junction calculated (a) without and (b) with the molecular response. Reprinted (figure) with permission from [A. J. White, M. Sukharev, and M. Galperin, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 205324.] Copyright (2012) by the American Physical Society. http://dx.doi.org/10.1103/PhysRevB.86.205324. | ||
Another case where working in the time-domain may be preferable is pump–probe type spectroscopy. Quantitative mapping of fast voltage pulse by plasmonic luminescence (probe) was demonstrated in STM junction measurements.47 An opposite proposal of pumping by light (laser pulse pair sequences) and probing dc current104 and noise105 was put forward as a way to access intra-molecular dynamics on the sub-picosecond time scale.§§ Theoretical simulations were performed utilizing the quantum master equation104 and NEGF105 (see Fig. 6); experimental verification of the proposed approach is an ongoing research in the group of Prof. Yoram Selzer.
Finally, a distinct feature of spectroscopy in open systems (nanojunctions) is the fact that photons and electrons participate in the same scattering process but contribute to different separately measured signals (e.g., photon flux and electron current). This simple idea is behind all the suggestions of measuring transport characteristics of one agent to describe the properties of the other. In terms of theoretical treatment this is an indication of the necessity to treat both photon and electron fluxes, eqn (4) and (5), at the same level of theory. Technically this is seen from the fact that both fluxes can be expressed in terms of the same correlation (Green) functions, which has to be evaluated at the same level of theory in both cases. For example, ref. 179 and 180 consider temporal correlations between Raman signal and conductance for a model of junction driven by time-dependent classical field (see Fig. 7). The electron Green function, which enters expressions for both fluxes, was evaluated exactly with respect to light–matter coupling.
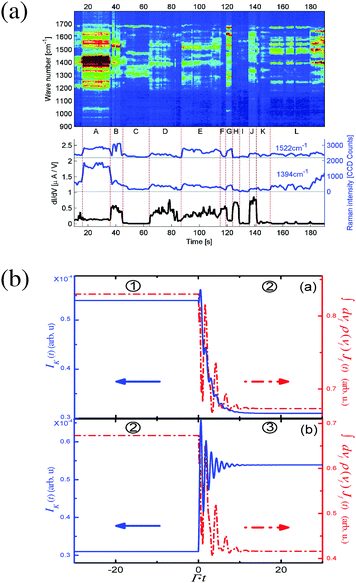 | ||
| Fig. 7 Time-dependent fluctuations in simultaneously measured electronic conductance and Raman response in molecular junctions. Shown are (a) experimental data and (b) a theoretical analysis. (a) Reprinted with permission from D. R. Ward, N. J. Halas, J. W. Ciszek, J. M. Tour, Y. Wu, P. Nordlander and D. Natelson, Nano Lett., 2008, 8, 919–924. Copyright (2008) American Chemical Society. (b) Reprinted with permission from [T.-H. Park and M. Galperin, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075447.] Copyright (2011) by the American Physical Society. http://dx.doi.org/10.1103/PhysRevB.84.075447. | ||
4 Quantum light
Quantum treatment of radiation field is required when purely quantum effects are pronounced in the light–matter interaction. These effects include photons in entangled and squeezed states, measurements of counting statistics of photon flux, interactions induced by quantum light in an electron subsystem, etc. Note that the latter are present even in the absence of an external field.301Turning to theoretical treatment of Raman spectroscopy in nanojunctions, it is worth mentioning that any spontaneous light emission (SLE) has to be considered quantum mechanically.204 Thus, corresponding theoretical derivations always start from quantum treatment of the field, eqn (4). After the derivation is completed, one can switch to classical description. Then bare PT and the corresponding multi-time correlation functions, eqn (6), become a safe way for description of optical response in junctions. Alternatively one may decide to stay with quantum treatment of the field. This is what was done in our NEGF and PP-NEGF theoretical studies of Raman spectroscopy in junctions.103,167,168,171–174,183 Following the standard nonlinear optical spectroscopy formulation, they rely on bare PT expansion in the light–matter interaction. Resulting treatment is to some extent similar to that of ref. 132 and 163 for NEGF treatments and is better than state-based formulations of ref. 139, 164 and 169 in treating molecule–contacts coupling for PP-NEGF treatments; the only difference is that Green function approaches make it easier to separate specifically Raman diagrams from other SLE contributions.170 The central point is that these are bare PT (in light–matter coupling) considerations, and as such they describe light scattering from broadened (due to molecule–contacts hybridization) nonequilibrium current-carrying states (or levels) of the molecule. This is not a comprehensive treatment of responses of an optoelectronic device. Nevertheless, such approaches are still useful for qualitative understanding of Raman scattering in nanojunctions.
We now give a short overview of recent theoretical studies of Raman scattering in current carrying junctions. After first simultaneous measurements of Raman and conductance in molecular junctions were reported,94,95 a theory of Raman scattering from current carrying molecular states was developed (along the lines discussed above) in ref. 167 and 168 and utilized to discuss estimation of a ‘nonequilibrium temperature’ of molecular vibrations (extent of heating of the vibrations by electron flux) from the ratio of Stokes and anti-Stokes peak intensities. Ref. 173 and 174 extended the latter analysis to electronic heating in molecular junctions in an attempt to interpret measurements presented in ref. 96. It was found that in contrast to vibrational heating in junctions, data on electronic heating are much less reliable except at very low biases. In particular, modeling showed that the main contribution observed in the experiments as electronic heating may result from non-equilibrium electronic distribution in the molecule, while contribution from actual electronic heating is negligible.
Charge transfer (chemical) contribution to surface enhanced Raman was discussed in ref. 183. Here quantum bare PT treatment of light–matter interaction was compared with the quasi-classical approach. The latter was shown to be inadequate at biases beyond threshold defined by characteristic frequencies of molecular vibrations (i.e. when inelastic effects become pronounced).
Experimentally observed bending of Stokes lines under bias in an OPV3 junction27 was explained by dependence of molecular vibrational normal modes on the charging state of the molecule in ref. 300. Charging induced frequency renormalization was studied in ref. 300 using a model where molecule–phonon coupling was taken into account up to the quadratic term in shift of nuclear coordinates (from their equilibrium positions in neutral molecule) on charging (this quadratic term yields anharmonic effects in the model). Estimating model parameters from first principle simulations resulted in shift of vibrational frequency similar to experimental data on Stokes line bending (see Fig. 8). Utilization of the state-based approach (the PP-NEGF) in first principles simulation103 provided an easy way to simulate the Raman spectrum. Studies of charge-induced renormalization of vibrational frequencies were later reported also in ref. 99 and 101.
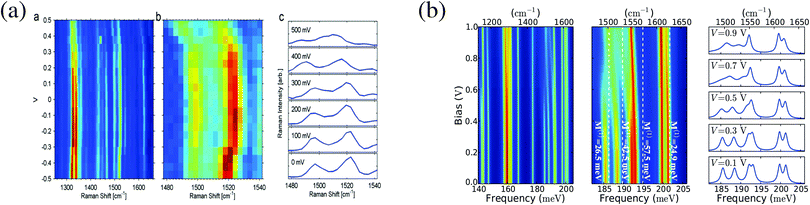 | ||
| Fig. 8 Bias dependence of Raman shift in OPV3 junction. Shown are (a) experimental data and (b) a theoretical analysis. (a) Reprinted with permission from Macmillan Publishers Ltd: [Nat. Nanotechnol.] (ref. 96), Copyright (2011). (b) Reprinted with permission from [K. Kaasbjerg, T. Novotný, and A. Nitzan, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 201405.] Copyright (2013) by the American Physical Society. http://dx.doi.org/10.1103/PhysRevB.88.201405. | ||
Besides Raman shift and intensity of Stokes and anti-Stokes lines, widths and shapes of Raman peaks may also be a source of information on junction structure. The width of the Stokes line and its dependence on junction characteristics (relaxation rates, proximity of the electronic level to Fermi energy, and bias) were discussed within a generic HOMO–LUMO model in ref. 171. Experimental observation and theoretical analysis of Fano-like lineshapes in the Raman spectra are presented in ref. 172 (see Fig. 9). The study found that the observed Fano-like features in principle can be explained by interference between vibrational and electronic Raman scattering amplitudes (the Fano resonance); however model calculations suggested that the observed lineshape asymmetry was dominated by purely electronic scattering sidebands that dress vibrational Stokes peaks.
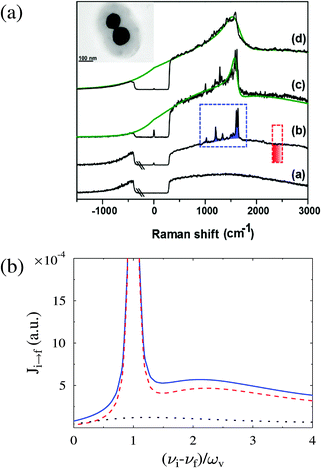 | ||
| Fig. 9 Fano-like lineshapes in the Raman spectra of molecules adsorbed at metal interfaces: (a) experimental data and (b) a theoretical analysis. Plotted in (b) are pure electronic (black dotted line), electronic-dressed vibrational Raman (red dashed line), and their sum (full blue line). Figure reprinted with permission from [S. Dey, M. Banik, E. Hulkko, K. Rodriguez, V. A. Apkarian, M. Galperin, and A. Nitzan, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 035411.] Copyright (2016) by the American Physical Society. http://dx.doi.org/10.1103/PhysRevB.93.035411. | ||
As stated above a comprehensive treatment of an optoelectronic device should account for all the fluxes (photon and electron) at the same level of theory. When considering quantum fields such comprehensive consideration requires special care. In particular (as was discussed in Section 2.2.1), for the consideration to satisfy physical conservation laws, one is forced to abandon the bare PT approach. The latter is well known to be a non-conserving approximation which may fail qualitatively when vertical flow (redistribution of electronic population in energy) is present.250–252,255,302 For example, in the theory of inelastic transport, which is technically equivalent to electron–photon interactions, second order bare PT (Born approximation) is non-conserving, and one has to employ the self-consistent Born approximation to get meaningful results.303 The same situation holds for any other interaction which causes vertical flow in the system (see, e.g., ref. 304). Thus, e.g., it is not surprising that any consideration of current-induced fluorescence with radiation field being treated quantum mechanically leads to a self-consistent treatment.130,131
The main difference between classical and quantum fields (with respect to conserving character of approximation) is the ability of the latter to mediate the photon supported effective electron–electron interaction. Technically this interaction comes in the form of electronic self-energy due to coupling to radiation field, which being approximated in an inappropriate way (e.g., within bare PT) leads to violation of charge and energy conservation laws. A suitable way to derive conserving approximations is discussed in Section 2.2.1 (see eqn (16) and (17)). We note that the restrictions on application of standard tools of nonlinear optical spectroscopy to nanojunctions are relevant only for radiation fields treated quantum mechanically, because classical fields do not induce time-nonlocal interactions in an electronic subsystem (i.e. technically they do not produce self-energies). To illustrate the point in ref. 249 we utilized NEGF to consider optical and electronic responses (fluxes) of a nanojunction within the bare PT (as accepted in the nonlinear spectroscopy community) and diagrammatic PT (as is usual in quantum transport considerations) approaches (see Fig. 10).
Quantum treatment of radiation field is also required for strong light–matter interactions. Here light and matter degrees of freedom cannot be separately distinguished, and thus theoretical treatment should be performed in the basis of eigenstates of the Hamiltonian ĤM + Ĥp + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) MP, eqn (1), accounting for the matter, the light, and interaction between them. We note that Green function methods presented in Sections 2.2.2 and 2.2.3 are ideally suited for the task. Note that also here conserving character of resulting approximation should be satisfied; however this time self-energies due to coupling to other baths (e.g., contacts or thermal environment, etc.) rather than self-energies coming from accounting for the light–matter interaction are to be built properly. In ref. 193 we utilized the PP-NEGF to study strong molecule–plasmon interactions in nanojunctions. Fig. 11 shows sensitivity of a molecule–plasmon Fano resonance to junction bias and intra-molecular interactions.
MP, eqn (1), accounting for the matter, the light, and interaction between them. We note that Green function methods presented in Sections 2.2.2 and 2.2.3 are ideally suited for the task. Note that also here conserving character of resulting approximation should be satisfied; however this time self-energies due to coupling to other baths (e.g., contacts or thermal environment, etc.) rather than self-energies coming from accounting for the light–matter interaction are to be built properly. In ref. 193 we utilized the PP-NEGF to study strong molecule–plasmon interactions in nanojunctions. Fig. 11 shows sensitivity of a molecule–plasmon Fano resonance to junction bias and intra-molecular interactions.
Finally, theoretical treatments related to statistics of photon flux also require quantum description of the radiation field. Note that an accurate (conserving, as discussed above) treatment in this case is even more important: while in ref. 249 we demonstrated sensitivity of flux (first cumulant of the full counting statistics, FCS) higher order cumulants of the FCS are much more sensitive to details of theoretical modeling.207,292 Participation of photons and electrons in the same process reveals itself in inter-dependence of optical and transport characteristics of an optoelectronic device. For example, the ability of the plasmon emission spectrum to characterize finite frequency quantum noise of electron transport was demonstrated experimentally46 and discussed theoretically201 (see eqn (10) and (12) in ref. 201 for formal connection between plasmonic light emission and the quantum noise). Similarly, optical spectra as a source of information on multielectron processes in junctions were measured40 and studied theoretically200 (see Fig. 12). Ref. 306 and 307 considered noise of photon and electron fluxes as well as cross-correlation counting statistics. The consideration utilized the quantum master equation within the Born–Markov approximation, which is known to be problematic for description of relatively strong (compared to kBT) system–bath couplings Γ.240,241,292 For a molecule chemisorbed on metallic surface Γ ∼ 0.01–0.5 eV308,309 while energy scale corresponding to room temperature is kBT ∼ 0.03 eV. Thus Green function approaches, which are not limited by high temperature restriction, are preferable for treatment of counting statistics in molecular junctions. From the two state-based Green function methodologies introduced above (Sections 2.2.2 and 2.2.3) only the Hubbard NEGF provides possibility to simulate FCS (see Fig. 13). Application of the Hubbard NEGF to description of optoelectronic devices is a direction for future research.
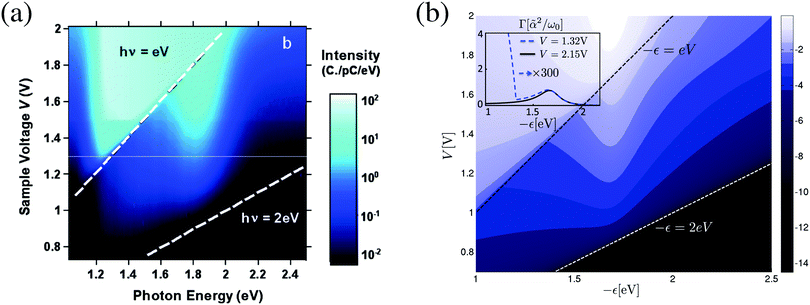 | ||
| Fig. 12 Bias induced light emission as a source of information on electron–electron and electron–plasmon interactions in junctions. Emission spectrum vs. applied bias: (a) experimental data and (b) a theoretical analysis. (a) Reprinted with permission from [G. Schull, N. Neel, P. Johansson, and R. Berndt, Phys. Rev. Lett., 2009, 102, 057401.] Copyright (2014) by the American Physical Society. http://dx.doi.org/10.1103/PhysRevLett.102.057401. (b) Reprinted with permission from [F. Xu, C. Holmqvist, and W. Belzig, Phys. Rev. Lett., 2014, 113, 066801.] Copyright (2014) by the American Physical Society. http://dx.doi.org/10.1103/PhysRevLett.113.066801. | ||
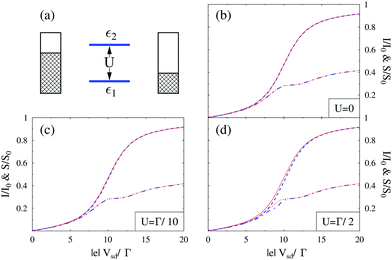 | ||
Fig. 13 Full counting statistics of electron transport in junctions. Simulation is performed for Hubbard model (a), 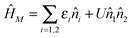 , with parameters ε2 = −ε1 = 5Γ. Shown are current (I0 = eΓ/ℏ, solid red and dashed blue lines) and zero frequency noise (S0 = e2Γ/ℏ, dotted red and dash-dotted blue lines) calculated, respectively, within NEGF (red) and Hubbard NEGF (blue) methodologies for (b) U = 0 (NEGF is exact here), (c) U = Γ/10, and (d) U = Γ/2. In (c) and (d) NEGF utilizes second order diagrammatic perturbation theory in U; Hubbard NEGF is second order in system–baths coupling (i.e. first order in Γ).305 , with parameters ε2 = −ε1 = 5Γ. Shown are current (I0 = eΓ/ℏ, solid red and dashed blue lines) and zero frequency noise (S0 = e2Γ/ℏ, dotted red and dash-dotted blue lines) calculated, respectively, within NEGF (red) and Hubbard NEGF (blue) methodologies for (b) U = 0 (NEGF is exact here), (c) U = Γ/10, and (d) U = Γ/2. In (c) and (d) NEGF utilizes second order diagrammatic perturbation theory in U; Hubbard NEGF is second order in system–baths coupling (i.e. first order in Γ).305 | ||
5 Conclusions
In recent years optical experiments in current-carrying nanojunctions have become a reality indicating the emergence of a new field of research coined optoelectronics. Experimental advances challenged theory to develop adequate approaches to characterize responses of open nonequilibrium systems to external drivings. The field of optoelectronics is a natural meeting point of (at least) two research communities: nonlinear optical spectroscopy and quantum transport. Each of the communities has its own theoretical toolbox. We reviewed the recent progress in the field comparing theoretical treatments of optical spectroscopy in nanojunctions. In particular, bare perturbation theory usually performed in the Liouville space and formulated in the language of superoperators (a standard theoretical tool in spectroscopic studies of isolated systems) was compared with theoretical approaches accepted in the quantum transport community. With respect to the latter we focus on the Hilbert space Green function based considerations. The standard nonequilibrium Green function (NEGF) was discussed together with its state-based flavors: pseudoparticle and Hubbard NEGF. We argued that the Green function considerations yield a convenient tool for optoelectronics when the radiation field is treated either classically or quantum mechanically. We showed that bare perturbation theory becomes inapplicable, when a comprehensive treatment of nanojunction responses to bias and quantized radiation field is the goal of the study. We conclude that the Hubbard NEGF is a promising methodology which generalizes the standard tools of nonlinear optical spectroscopy and is capable of comprehensive studies of optoelectronic devices. Further development of the methodology and its applications to nanojunction spectroscopy are directions for future research.Acknowledgements
This review is based upon work supported by the National Science Foundation under grant no. CHE-1565939 and the U.S. Department of Energy under grant no. DE-SC0006422.References
- Y. Jun and X.-Y. Zhu, J. Am. Chem. Soc., 2004, 126, 13224–13225 CrossRef CAS PubMed.
- V. Burtman, A. Ndobe and Z. Vardeny, Solid State Commun., 2005, 135, 563–573 CrossRef CAS.
- L. Bernard, Y. Kamdzhilov, M. Calame, S. J. van der Molen, J. Liao and C. Schönenberger, J. Phys. Chem. C, 2007, 111, 18445–18450 CAS.
- A. Scott, C. A. Hacker and D. B. Janes, J. Phys. Chem. C, 2008, 112, 14021–14026 CAS.
- M. Lefenfeld, J. Baumert, E. Sloutskin, I. Kuzmenko, P. Pershan, M. Deutsch, C. Nuckolls and B. M. Ocko, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 2541–2545 CrossRef CAS PubMed.
- S. Conoci, S. Petralia, P. Samorí, F. Raymo, S. Di Bella and S. Sortino, Adv. Funct. Mater., 2006, 16, 1425–1432 CrossRef CAS.
- Z. Wang, J. A. Carter, A. Lagutchev, Y. K. Koh, N.-H. Seong, D. G. Cahill and D. D. Dlott, Science, 2007, 317, 787–790 CrossRef CAS PubMed.
- J. A. Carter, Z. Wang and D. D. Dlott, Acc. Chem. Res., 2009, 42, 1343–1351 CrossRef CAS PubMed.
- H. Asanuma, H. Noguchi, Y. Huang, K. Uosaki and H.-Z. Yu, J. Phys. Chem. C, 2009, 113, 21139–21146 CAS.
- P. J. N. Kett, M. T. L. Casford and P. B. Davies, J. Phys. Chem. Lett., 2012, 3, 3276–3280 CrossRef CAS.
- A. Nitzan, Science, 2007, 317, 759–760 CrossRef CAS PubMed.
- G.-K. Liu, J. Hu, P.-C. Zheng, G.-L. Shen, J.-H. Jiang, R.-Q. Yu, Y. Cui and B. Ren, J. Phys. Chem. C, 2008, 112, 6499–6508 CAS.
- B. Liu, A. Blaszczyk, M. Mayor and T. Wandlowski, ACS Nano, 2011, 5, 5662–5672 CrossRef CAS PubMed.
- S. L. Kleinman, R. R. Frontiera, A.-I. Henry, J. A. Dieringer and R. P. Van Duyne, Phys. Chem. Chem. Phys., 2013, 15, 21–36 RSC.
- E. A. Pozzi, A. B. Zrimsek, C. M. Lethiec, G. C. Schatz, M. C. Hersam and R. P. Van Duyne, J. Phys. Chem. C, 2015, 119, 21116–21124 CAS.
- N. Jiang, E. T. Foley, J. M. Klingsporn, M. D. Sonntag, N. A. Valley, J. A. Dieringer, T. Seideman, G. C. Schatz, M. C. Hersam and R. P. Van Duyne, Nano Lett., 2012, 12, 5061–5067 CrossRef CAS PubMed.
- M. D. Sonntag, J. M. Klingsporn, L. K. Garibay, J. M. Roberts, J. A. Dieringer, T. Seideman, K. A. Scheidt, L. Jensen, G. C. Schatz and R. P. Van Duyne, J. Phys. Chem. C, 2012, 116, 478–483 CAS.
- J. M. Klingsporn, M. D. Sonntag, T. Seideman and R. P. Van Duyne, J. Phys. Chem. Lett., 2014, 5, 106–110 CrossRef CAS PubMed.
- J. M. Klingsporn, N. Jiang, E. A. Pozzi, M. D. Sonntag, D. Chulhai, T. Seideman, L. Jensen, M. C. Hersam and R. P. V. Duyne, J. Am. Chem. Soc., 2014, 136, 3881–3887 CrossRef CAS PubMed.
- N. Chiang, N. Jiang, D. V. Chulhai, E. A. Pozzi, M. C. Hersam, L. Jensen, T. Seideman and R. P. Van Duyne, Nano Lett., 2015, 15, 4114–4120 CrossRef CAS PubMed.
- X. Wang, J.-H. Zhong, M. Zhang, Z. Liu, D.-Y. Wu and B. Ren, Anal. Chem., 2016, 88, 915–921 CrossRef CAS PubMed.
- C. Toccafondi, G. Picardi and R. Ossikovski, J. Phys. Chem. C, 2016, 120, 18209–18219 CAS.
- J.-H. Tian, B. Liu, X. Li, Z.-L. Yang, B. Ren, S.-T. Wu, N. Tao and Z.-Q. Tian, J. Am. Chem. Soc., 2006, 128, 14748–14749 CrossRef CAS PubMed.
- D. R. Ward, G. D. Scott, Z. K. Keane, N. J. Halas and D. Natelson, J. Phys.: Condens. Matter, 2008, 20, 374118 CrossRef CAS PubMed.
- F. Rossel, M. Pivetta and W.-D. Schneider, Surf. Sci. Rep., 2010, 65, 129–144 CrossRef CAS.
- T. Shamai and Y. Selzer, Chem. Soc. Rev., 2011, 40, 2293–2305 RSC.
- D. Natelson, Y. Li and J. B. Herzog, Phys. Chem. Chem. Phys., 2013, 15, 5262–5275 RSC.
- S. V. Aradhya and L. Venkataraman, Nat. Nanotechnol., 2013, 8, 399–410 CrossRef CAS PubMed.
- Z. H. Kim, Front. Phys., 2014, 9, 25–30 CrossRef.
- R. Matsushita and M. Kiguchi, Phys. Chem. Chem. Phys., 2015, 17, 21254–21260 RSC.
- M. Galperin and A. Nitzan, Phys. Chem. Chem. Phys., 2012, 14, 9421–9438 RSC.
- F. Touhari, E. J. A. J. Stoffels, J. W. Gerritsen, H. van Kempen and P. Callant, Appl. Phys. Lett., 2001, 79, 527–529 CrossRef CAS.
- G. Hoffmann, L. Libioulle and R. Berndt, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 212107 CrossRef.
- G. Hoffmann, R. Berndt and P. Johansson, Phys. Rev. Lett., 2003, 90, 046803 CrossRef PubMed.
- E. Ćavar, M.-C. Blüm, M. Pivetta, F. m. c. Patthey, M. Chergui and W.-D. Schneider, Phys. Rev. Lett., 2005, 95, 196102 CrossRef PubMed.
- H. Yanagi, H. Mukai and M. Nair, Thin Solid Films, 2006, 499, 123–128 CrossRef CAS.
- W.-J. Li, K. L. Kavanagh, A. A. Talin, W. M. Clift, C. M. Matzke and J. W. P. Hsu, J. Appl. Phys., 2007, 102, 013703 CrossRef.
- P. Brodard, Chimia, 2007, 61, 613–616 CrossRef CAS.
- S. W. Wu, G. V. Nazin and W. Ho, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 205430 CrossRef.
- G. Schull, N. Neel, P. Johansson and R. Berndt, Phys. Rev. Lett., 2009, 102, 057401 CrossRef PubMed.
- N. L. Schneider, G. Schull and R. Berndt, Phys. Rev. Lett., 2010, 105, 026601 CrossRef PubMed.
- C. Chen, P. Chu, C. A. Bobisch, D. L. Mills and W. Ho, Phys. Rev. Lett., 2010, 105, 217402 CrossRef PubMed.
- Z. C. Dong, X. L. Zhang, H. Y. Gao, Y. Luo, C. Zhang, L. G. Chen, R. Zhang, X. Tao, Y. Zhang, J. L. Yang and J. G. Hou, Nat. Photonics, 2010, 4, 50–54 CrossRef CAS.
- N. L. Schneider, F. Matino, G. Schull, S. Gabutti, M. Mayor and R. Berndt, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 153403 CrossRef.
- N. L. Schneider and R. Berndt, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 035445 CrossRef.
- N. L. Schneider, J. T. Lü, M. Brandbyge and R. Berndt, Phys. Rev. Lett., 2012, 109, 186601 CrossRef CAS PubMed.
- C. Grosse, M. Etzkorn, K. Kuhnke, S. Loth and K. Kern, Appl. Phys. Lett., 2013, 103, 183108 CrossRef.
- J. Lee, S. M. Perdue, A. R. Perez and V. A. Apkarian, ACS Nano, 2014, 8, 54–63 CrossRef CAS PubMed.
- A. Burtzlaff, N. L. Schneider, A. Weismann and R. Berndt, Surf. Sci., 2016, 643, 10–12 CrossRef CAS.
- A. Yu, S. Li, B. Dhital, H. P. Lu and W. Ho, J. Phys. Chem. C, 2016, 120, 21099–21103 CAS.
- H. Imada, K. Miwa, M. Imai-Imada, S. Kawahara, K. Kimura and Y. Kim, Nature, 2016, 538, 364–367 CrossRef CAS PubMed.
- S. J. van der Molen, J. Liao, T. Kudernac, J. S. Agustsson, L. Bernard, M. Calame, B. J. van Wees, B. L. Feringa and C. Schönenberger, Nano Lett., 2009, 9, 76–80 CrossRef CAS PubMed.
- G. Noy, A. Ophir and Y. Selzer, Angew. Chem., Int. Ed., 2010, 49, 5734–5736 CrossRef CAS PubMed.
- E. S. Tam, J. J. Parks, W. W. Shum, Y.-W. Zhong, M. B. Santiago-Berríos, X. Zheng, W. Yang, G. K.-L. Chan, H. D. Abruña and D. C. Ralph, ACS Nano, 2011, 5, 5115–5123 CrossRef CAS PubMed.
- S. Battacharyya, A. Kibel, G. Kodis, P. A. Liddell, M. Gervaldo, D. Gust and S. Lindsay, Nano Lett., 2011, 11, 2709–2714 CrossRef CAS PubMed.
- I. Rattalino, V. Cauda, P. Motto, T. Limongi, G. Das, L. Razzari, F. Parenti, E. Di Fabrizio, A. Mucci, L. Schenetti, G. Piccinini and D. Demarchi, RSC Adv., 2012, 2, 10985–10993 RSC.
- M. Vadai, N. Nachman, M. Ben-Zion, M. Bürkle, F. Pauly, J. C. Cuevas and Y. Selzer, J. Phys. Chem. Lett., 2013, 4, 2811–2816 CrossRef CAS.
- P. P. Pal, N. Jiang, M. D. Sonntag, N. Chiang, E. T. Foley, M. C. Hersam, R. P. Van Duyne and T. Seideman, J. Phys. Chem. Lett., 2015, 6, 4210–4218 CrossRef CAS PubMed.
- T. Sendler, K. Luka-Guth, M. Wieser, Lokamani, J. Wolf, M. Helm, S. Gemming, J. Kerbusch, E. Scheer, T. Huhn and A. Erbe, Adv. Sci., 2015, 2, 1500017 CrossRef PubMed.
- D. Cvetko, G. Fratesi, G. Kladnik, A. Cossaro, G. P. Brivio, L. Venkataraman and A. Morgante, Phys. Chem. Chem. Phys., 2016, 18, 22140–22145 RSC.
- D. Taherinia and C. D. Frisbie, J. Phys. Chem. C, 2016, 120, 6442–6449 CAS.
- H. Y. He, S. T. Pi, Z. Q. Bai, M. Banik, V. A. Apkarian and R. Q. Wu, J. Phys. Chem. C, 2016, 120, 20914–20921 CAS.
- Y. Paltiel, G. Jung, T. Aqua, D. Mocatta, U. Banin and R. Naaman, Phys. Rev. Lett., 2010, 104, 016804 CrossRef CAS PubMed.
- B. Göhler, V. Hamelbeck, T. Z. Markus, M. Kettner, G. F. Hanne, Z. Vager, R. Naaman and H. Zacharias, Science, 2011, 331, 894–897 CrossRef PubMed.
- R. Naaman and D. H. Waldeck, J. Phys. Chem. Lett., 2012, 3, 2178–2187 CrossRef CAS PubMed.
- O. Ben Dor, N. Morali, S. Yochelis, L. T. Baczewski and Y. Paltiel, Nano Lett., 2014, 14, 6042–6049 CrossRef CAS PubMed.
- H. Einati, D. Mishra, N. Friedman, M. Sheves and R. Naaman, Nano Lett., 2015, 15, 1052–1056 CrossRef CAS PubMed.
- P. C. Mondal, P. Roy, D. Kim, E. E. Fullerton, H. Cohen and R. Naaman, Nano Lett., 2016, 16, 2806–2811 CrossRef CAS PubMed.
- D. L. Jeanmaire and R. P. Van Duyne, J. Electroanal. Chem. Interfacial Electrochem., 1977, 84, 1–20 CrossRef CAS.
- S. Nie and S. R. Emory, Science, 1997, 275, 1102–1106 CrossRef CAS PubMed.
- K. Kneipp, Y. Wang, H. Kneipp, L. T. Perelman, I. Itzkan, R. R. Dasari and M. S. Feld, Phys. Rev. Lett., 1997, 78, 1667–1670 CrossRef CAS.
- J.-F. Li, S.-Y. Ding, Z.-L. Yang, M.-L. Bai, J. R. Anema, X. Wang, A. Wang, D.-Y. Wu, B. Ren, S.-M. Hou, T. Wandlowski and Z.-Q. Tian, J. Am. Chem. Soc., 2011, 133, 15922–15925 CrossRef CAS PubMed.
- J. I. Gersten, R. L. Birke and J. R. Lombardi, Phys. Rev. Lett., 1979, 43, 147–150 CrossRef CAS.
- J. Gersten and A. Nitzan, J. Chem. Phys., 1980, 73, 3023–3037 CrossRef CAS.
- B. N. J. Persson, Chem. Phys. Lett., 1981, 82, 561–565 CrossRef CAS.
- K. A. Willets and R. P. Van Duyne, Annu. Rev. Phys. Chem., 2007, 58, 267–297 CrossRef CAS PubMed.
- D. R. Ward, N. K. Grady, C. S. Levin, N. J. Halas, Y. Wu, P. Nordlander and D. Natelson, Nano Lett., 2007, 7, 1396–1400 CrossRef CAS PubMed.
- J. B. Lassiter, J. Aizpurua, L. I. Hernandez, D. W. Brandl, I. Romero, S. Lal, J. H. Hafner, P. Nordlander and N. J. Halas, Nano Lett., 2008, 8, 1212–1218 CrossRef CAS PubMed.
- O. Pérez-González, N. Zabala, A. G. Borisov, N. J. Halas, P. Nordlander and J. Aizpurua, Nano Lett., 2010, 10, 3090–3095 CrossRef PubMed.
- R. Arielly, A. Ofarim, G. Noy and Y. Selzer, Nano Lett., 2011, 11, 2968–2972 CrossRef CAS PubMed.
- J. B. Herzog, M. W. Knight, Y. Li, K. M. Evans, N. J. Halas and D. Natelson, Nano Lett., 2013, 13, 1359–1364 CrossRef CAS PubMed.
- A. B. Zrimsek, A.-I. Henry and R. P. Van Duyne, J. Phys. Chem. Lett., 2013, 4, 3206–3210 CrossRef CAS.
- Y. Zhang, Y.-R. Zhen, O. Neumann, J. K. Day, P. Nordlander and N. J. Halas, Nat. Commun., 2014, 5, 4424 CAS.
- F. Benz, C. Tserkezis, L. O. Herrmann, B. de Nijs, A. Sanders, D. O. Sigle, L. Pukenas, S. D. Evans, J. Aizpurua and J. J. Baumberg, Nano Lett., 2015, 15, 669–674 CrossRef CAS PubMed.
- Y. Li, M. L. Simeral and D. Natelson, J. Phys. Chem. C, 2016, 120, 22558–22564 CAS.
- K. T. Crampton, A. Zeytunyan, A. S. Fast, F. T. Ladani, A. Alfonso-Garcia, M. Banik, S. Yampolsky, D. A. Fishman, E. O. Potma and V. A. Apkarian, J. Phys. Chem. C, 2016, 120, 20943–20953 CAS.
- B. Vlčková, M. Moskovits, I. Pavel, K. Šišková, M. Sládková and M. Šlouf, Chem. Phys. Lett., 2008, 455, 131–134 CrossRef.
- J.-F. Li, Y.-F. Huang, S. Duan, R. Pang, D.-Y. Wu, B. Ren, X. Xu and Z.-Q. Tian, Phys. Chem. Chem. Phys., 2010, 12, 2493–2502 RSC.
- J. F. Li, Y. F. Huang, Y. Ding, Z. L. Yang, S. B. Li, X. S. Zhou, F. R. Fan, W. Zhang, Z. Y. Zhou, W. Yin, B. Ren, Z. L. Wang and Z. Q. Tian, Nature, 2010, 464, 392–395 CrossRef CAS PubMed.
- M. Moskovits, Phys. Chem. Chem. Phys., 2013, 15, 5301–5311 RSC.
- M. D. Sonntag, E. A. Pozzi, N. Jiang, M. C. Hersam and R. P. V. Duyne, J. Phys. Chem. Lett., 2014, 5, 3125–3130 CrossRef CAS PubMed.
- S.-Y. Ding, J. Yi, J.-F. Li, B. Ren, D.-Y. Wu, R. Panneerselvam and Z.-Q. Tian, Nat. Rev. Mater., 2016, 1, 16021 CrossRef CAS.
- A. Jaiswal, K. G. Tavakoli and S. Zou, Anal. Chem., 2006, 78, 120–124 CrossRef CAS PubMed.
- Z. Ioffe, T. Shamai, A. Ophir, G. Noy, I. Yutsis, K. Kfir, O. Cheshnovsky and Y. Selzer, Nat. Nanotechnol., 2008, 3, 727–732 CrossRef CAS PubMed.
- D. R. Ward, N. J. Halas, J. W. Ciszek, J. M. Tour, Y. Wu, P. Nordlander and D. Natelson, Nano Lett., 2008, 8, 919–924 CrossRef CAS PubMed.
- D. R. Ward, D. A. Corley, J. M. Tour and D. Natelson, Nat. Nanotechnol., 2011, 6, 33–38 CrossRef CAS PubMed.
- A. L. Schmucker, G. Barin, K. A. Brown, M. Rycenga, A. Coskun, O. Buyukcakir, K. D. Osberg, J. F. Stoddart and C. A. Mirkin, Small, 2013, 9, 1900–1903 CrossRef CAS PubMed.
- R. Matsuhita, M. Horikawa, Y. Naitoh, H. Nakamura and M. Kiguchi, J. Phys. Chem. C, 2013, 117, 1791–1795 CAS.
- Y. Li, P. Doak, L. Kronik, J. B. Neaton and D. Natelson, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 1282–1287 CrossRef CAS PubMed.
- S. Kaneko, D. Murai, S. Fujii and M. Kiguchi, Int. J. Mod. Phys. B, 2016, 30, 1642010 CrossRef CAS.
- Y. Li, P. Zolotavin, P. Doak, L. Kronik, J. B. Neaton and D. Natelson, Nano Lett., 2016, 16, 1104–1109 CrossRef CAS PubMed.
- M. Banik, V. A. Apkarian, T.-H. Park and M. Galperin, J. Phys. Chem. Lett., 2013, 4, 88–92 CrossRef CAS PubMed.
- A. J. White, S. Tretiak and M. Galperin, Nano Lett., 2014, 14, 699–703 CrossRef CAS PubMed.
- Y. Selzer and U. Peskin, J. Phys. Chem. C, 2013, 117, 22369–22376 CAS.
- M. A. Ochoa, Y. Selzer, U. Peskin and M. Galperin, J. Phys. Chem. Lett., 2015, 6, 470–476 CrossRef CAS PubMed.
- G. Nardin, T. M. Autry, K. L. Silverman and S. T. Cundiff, Opt. Express, 2013, 21, 28617–28627 CrossRef PubMed.
- K. J. Karki, J. R. Widom, J. Seibt, I. Moody, M. C. Lonergan, T. Pullerits and A. H. Marcus, Nat. Commun., 2014, 5, 5869 CrossRef CAS PubMed.
- E. Vella, H. Li, P. Grégoire, S. M. Tuladhar, M. S. Vezie, S. Few, C. M. Bazán, J. Nelson, C. Silva-Acuña and E. R. Bittner, Sci. Rep., 2016, 6, 29437 CrossRef CAS PubMed.
- M. I. Stockman, Opt. Express, 2011, 19, 22029–22106 CrossRef PubMed.
- M. S. Tame, K. R. McEnery, S. K. Ozdemir, J. Lee, S. A. Maier and M. S. Kim, Nat. Phys., 2013, 9, 329–340 CrossRef CAS.
- B. Luk'yanchuk, N. I. Zheludev, S. A. Maier, N. J. Halas, P. Nordlander, H. Giessen and C. T. Chong, Nat. Mater., 2010, 9, 707–715 CrossRef PubMed.
- F. J. G. de Abajo, Nature, 2012, 483, 417–418 CrossRef CAS PubMed.
- J. A. Scholl, A. L. Koh and J. A. Dionne, Nature, 2012, 483, 421–427 CrossRef CAS PubMed.
- K. J. Savage, M. M. Hawkeye, R. Esteban, A. G. Borisov, J. Aizpurua and J. J. Baumberg, Nature, 2012, 491, 574–577 CrossRef CAS PubMed.
- P. Nordlander, Science, 2014, 343, 1444–1445 CrossRef PubMed.
- P. Z. El-Khoury and W. P. Hess, Nano Lett., 2014, 14, 4114–4118 CrossRef CAS PubMed.
- S. F. Tan, L. Wu, J. K. Yang, P. Bai, M. Bosman and C. A. Nijhuis, Science, 2014, 343, 1496–1499 CrossRef CAS PubMed.
- W. Zhu, R. Esteban, A. G. Borisov, J. J. Baumberg, P. Nordlander, H. J. Lezec, J. Aizpurua and K. B. Crozier, Nat. Commun., 2016, 7, 11495 CrossRef CAS PubMed.
- F. Benz, M. K. Schmidt, A. Dreismann, R. Chikkaraddy, Y. Zhang, A. Demetriadou, C. Carnegie, H. Ohadi, B. de Nijs, R. Esteban, J. Aizpurua and J. J. Baumberg, Science, 2016, 354, 726–729 CrossRef CAS PubMed.
- S. Lerch and B. M. Reinhard, Adv. Mater., 2016, 28, 2030–2036 CrossRef CAS PubMed.
- T. Wang and C. A. Nijhuis, Appl. Mater. Today, 2016, 3, 73–86 CrossRef.
- T. Schwartz, J. A. Hutchison, C. Genet and T. W. Ebbesen, Phys. Rev. Lett., 2011, 106, 196405 CrossRef CAS PubMed.
- J. A. Hutchison, T. Schwartz, C. Genet, E. Devaux and T. W. Ebbesen, Angew. Chem., Int. Ed., 2012, 51, 1592–1596 CrossRef CAS PubMed.
- J. A. Hutchison, A. Liscio, T. Schwartz, A. Canaguier-Durand, C. Genet, V. Palermo, P. Samorí and T. W. Ebbesen, Adv. Mater., 2013, 25, 2481–2485 CrossRef CAS PubMed.
- T. Schwartz, J. A. Hutchison, J. Léonard, C. Genet, S. Haacke and T. W. Ebbesen, ChemPhysChem, 2013, 14, 125–131 CrossRef CAS PubMed.
- A. Canaguier-Durand, E. Devaux, J. George, Y. Pang, J. A. Hutchison, T. Schwartz, C. Genet, N. Wilhelms, J.-M. Lehn and T. W. Ebbesen, Angew. Chem., Int. Ed., 2013, 52, 10533–10536 CrossRef CAS PubMed.
- K. Murch, Nat. Phys., 2017, 13, 11–12 CrossRef CAS.
- C. R. Kagan and M. A. Ratner, MRS Bull., 2004, 29, 376–384 CrossRef CAS.
- H. Chen, G. C. Schatz and M. A. Ratner, Rep. Prog. Phys., 2012, 75, 096402 CrossRef PubMed.
- M. Galperin and A. Nitzan, Phys. Rev. Lett., 2005, 95, 206802 CrossRef PubMed.
- M. Galperin and A. Nitzan, J. Chem. Phys., 2006, 124, 234709 CrossRef PubMed.
- U. Harbola, J. B. Maddox and S. Mukamel, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 075211 CrossRef.
- M. Galperin and S. Tretiak, J. Chem. Phys., 2008, 128, 124705 CrossRef PubMed.
- K. Miwa, M. Sakaue and H. Kasai, J. Phys. Soc. Jpn., 2013, 82, 063715 CrossRef.
- K. Miwa, M. Sakaue and H. Kasai, J. Phys. Soc. Jpn., 2013, 82, 124707 CrossRef.
- K. Miwa, M. Sakaue and H. Kasai, Nanoscale Res. Lett., 2013, 8, 204 CrossRef PubMed.
- K. Miwa, H. Imada, M. Sakaue, H. Kasai and Y. Kim, e-J. Surf. Sci. Nanotechnol., 2015, 13, 385–390 CrossRef CAS.
- S. Ajisaka, B. Žunkovič and Y. Dubi, Sci. Rep., 2015, 5, 8312 CrossRef CAS PubMed.
- H. P. Goswami, W. Hua, Y. Zhang, S. Mukamel and U. Harbola, J. Chem. Theory Comput., 2015, 11, 4304–4315 CrossRef CAS PubMed.
- G. Chenkn, X.-g. Li and Z.-c. Dong, Chin. J. Chem. Phys., 2015, 28, 552–556 CrossRef.
- T. A. Niehaus, T. Frauenheim and B. Korff, J. Phys. Chem. C, 2016, 120, 3699–3704 CAS.
- R. Wang, Y. Zhang, F. Bi, T. Frauenheim, G. Chen and C. Yam, Nanoscale, 2016, 8, 13168–13173 RSC.
- A. Dasgupta, D. Singh, R. P. N. Tripathi and G. V. P. Kumar, J. Phys. Chem. C, 2016, 120, 17692–17698 CAS.
- B. D. Fainberg, M. Jouravlev and A. Nitzan, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 245329 CrossRef.
- G. Li, S. Welack, M. Schreiber and U. Kleinekathöfer, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 075321 CrossRef.
- B. D. Fainberg, M. Sukharev, T.-H. Park and M. Galperin, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 205425 CrossRef.
- U. Peskin and M. Galperin, J. Chem. Phys., 2012, 136, 044107 CrossRef PubMed.
- A. J. White, U. Peskin and M. Galperin, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 205424 CrossRef.
- L.-Y. Hsu, D. Xie and H. Rabitz, J. Chem. Phys., 2014, 141, 124703 CrossRef PubMed.
- Z. Hu, M. A. Ratner and T. Seideman, J. Chem. Phys., 2014, 141, 224104 CrossRef PubMed.
- K. Lopata and D. Neuhauser, J. Chem. Phys., 2009, 131, 014701 CrossRef PubMed.
- K. Lopata and D. Neuhauser, J. Chem. Phys., 2009, 130, 104707 CrossRef PubMed.
- M. Sukharev and M. Galperin, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 165307 CrossRef.
- H. Chen, J. M. McMahon, M. A. Ratner and G. C. Schatz, J. Phys. Chem. C, 2010, 114, 14384–14392 CAS.
- C. Arntsen, K. Lopata, M. R. Wall, L. Bartell and D. Neuhauser, J. Chem. Phys., 2011, 134, 084101 CrossRef PubMed.
- M. Sukharev and A. Nitzan, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 043802 CrossRef.
- A. J. White, M. Sukharev and M. Galperin, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 205324 CrossRef.
- Y. Gao and D. Neuhauser, J. Chem. Phys., 2012, 137, 074113 CrossRef PubMed.
- J. Mullin and G. C. Schatz, J. Phys. Chem. A, 2012, 116, 1931–1938 CrossRef CAS PubMed.
- M. Kornbluth, A. Nitzan and T. Seideman, J. Chem. Phys., 2013, 138, 174707 CrossRef PubMed.
- S. M. Parker, M. Smeu, I. Franco, M. A. Ratner and T. Seideman, Nano Lett., 2014, 14, 4587–4591 CrossRef CAS PubMed.
- G. Chen, X.-G. Li, Z.-Y. Zhang and Z.-C. Dong, Nanoscale, 2015, 7, 2442–2449 RSC.
- S. Rahav and S. Mukamel, J. Chem. Phys., 2010, 133, 244106 CrossRef CAS PubMed.
- B. K. Agarwalla, U. Harbola, W. Hua, Y. Zhang and S. Mukamel, J. Chem. Phys., 2015, 142, 212445 CrossRef PubMed.
- P. Saurabh and S. Mukamel, J. Chem. Phys., 2016, 144, 124115 CrossRef PubMed.
- H. Li, A. Gauthier-Houle, P. Grégoire, E. Vella, C. Silva-Acuña and E. R. Bittner, Chem. Phys., 2016, 481, 281–286 CrossRef CAS.
- M. Galperin, M. A. Ratner and A. Nitzan, Nano Lett., 2009, 9, 758–762 CrossRef CAS PubMed.
- M. Galperin, M. A. Ratner and A. Nitzan, J. Chem. Phys., 2009, 130, 144109 CrossRef PubMed.
- U. Harbola, B. K. Agarwalla and S. Mukamel, J. Chem. Phys., 2014, 141, 074107 CrossRef PubMed.
- M. Galperin, M. A. Ratner and A. Nitzan, J. Chem. Phys., 2015, 142, 137101 CrossRef PubMed.
- Y. Gao, M. Galperin and A. Nitzan, J. Chem. Phys., 2016, 144, 244114 CrossRef PubMed.
- S. Dey, M. Banik, E. Hulkko, K. Rodriguez, V. A. Apkarian, M. Galperin and A. Nitzan, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 035411 CrossRef.
- M. Galperin and A. Nitzan, J. Phys. Chem. Lett., 2011, 2, 2110–2113 CrossRef CAS.
- M. Galperin and A. Nitzan, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 195325 CrossRef.
- J.-T. Lü, M. Brandbyge, P. Hedegård, T. N. Todorov and D. Dundas, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 245444 CrossRef.
- X.-F. Lang, P.-G. Yin, E.-Z. Tan, T.-T. You and L. Guo, J. Raman Spectrosc., 2013, 44, 425–432 CrossRef CAS.
- D.-Y. Wu, L.-B. Zhao, X.-M. Liu, R. Huang, Y.-F. Huang, B. Ren and Z.-Q. Tian, Chem. Commun., 2011, 47, 2520–2522 RSC.
- F. Mirjani, J. M. Thijssen and M. A. Ratner, J. Phys. Chem. C, 2012, 116, 23120–23129 CAS.
- T.-H. Park and M. Galperin, Europhys. Lett., 2011, 95, 27001 CrossRef.
- T.-H. Park and M. Galperin, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075447 CrossRef.
- T.-H. Park and M. Galperin, Phys. Scr., T, 2012, 151, 014038 CrossRef.
- L. L. Zhao, L. Jensen and G. C. Schatz, Nano Lett., 2006, 6, 1229–1234 CrossRef CAS PubMed.
- M. Oren, M. Galperin and A. Nitzan, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 115435 CrossRef.
- M. Banik, A. Nag, P. Z. El-Khoury, A. Rodriguez Perez, N. Guarrotxena, G. C. Bazan and V. A. Apkarian, J. Phys. Chem. C, 2012, 116, 10415–10423 CAS.
- N. Valley, N. Greeneltch, R. P. Van Duyne and G. C. Schatz, J. Phys. Chem. Lett., 2013, 4, 2599–2604 CrossRef CAS.
- P. Tarakeshwar, J. L. Palma, D. Finkelstein-Shapiro, A. Keller, I. Urdaneta, M. Calatayud, O. Atabek and V. Mujica, J. Phys. Chem. C, 2014, 118, 3774–3782 CAS.
- J. Zuloaga, E. Prodan and P. Nordlander, Nano Lett., 2009, 9, 887–891 CrossRef CAS PubMed.
- A. Ridolfo, O. Di Stefano, N. Fina, R. Saija and S. Savasta, Phys. Rev. Lett., 2010, 105, 263601 CrossRef CAS PubMed.
- A. Manjavacas, F. J. G. d. Abajo and P. Nordlander, Nano Lett., 2011, 11, 2318–2323 CrossRef CAS PubMed.
- P. Song, P. Nordlander and S. Gao, J. Chem. Phys., 2011, 134, 074701 CrossRef PubMed.
- R. Esteban, A. G. Borisov, P. Nordlander and J. Aizpurua, Nat. Commun., 2012, 3, 825 CrossRef PubMed.
- D. Marinica, A. Kazansky, P. Nordlander, J. Aizpurua and A. G. Borisov, Nano Lett., 2012, 12, 1333–1339 CrossRef CAS PubMed.
- A. J. White, B. D. Fainberg and M. Galperin, J. Phys. Chem. Lett., 2012, 3, 2738–2743 CrossRef CAS.
- P. Song, S. Meng, P. Nordlander and S. Gao, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 121410 CrossRef.
- O. Pérez-González, J. Aizpurua and N. Zabala, Opt. Express, 2013, 21, 15847–15858 CrossRef PubMed.
- F. Schlawin, K. E. Dorfman, B. P. Fingerhut and S. Mukamel, Nat. Commun., 2013, 4, 1782 Search PubMed.
- J. C. L. Carreño and F. P. Laussy, Phys. Rev. A: At., Mol., Opt. Phys., 2016, 94, 063825 Search PubMed.
- J. C. L. Carreño, C. Sánchez Muñoz, E. del Valle and F. P. Laussy, Phys. Rev. A: At., Mol., Opt. Phys., 2016, 94, 063826 Search PubMed.
- M. Kowalewski, K. Bennett and S. Mukamel, J. Chem. Phys., 2016, 144, 054309 Search PubMed.
- F. Xu, C. Holmqvist and W. Belzig, Phys. Rev. Lett., 2014, 113, 066801 Search PubMed.
- K. Kaasbjerg and A. Nitzan, Phys. Rev. Lett., 2015, 114, 126803 Search PubMed.
- P. Lodahl, S. Mahmoodian and S. Stobbe, Rev. Mod. Phys., 2015, 87, 347–400 CrossRef CAS.
- K. E. Dorfman, F. Schlawin and S. Mukamel, Rev. Mod. Phys., 2016, 88, 045008 CrossRef.
- S. Mukamel, Principles of Nonlinear Optical Spectroscopy, Oxford University Press, 1995, vol. 6 Search PubMed.
- H. Haug and A.-P. Jauho, Quantum Kinetics in Transport and Optics of Semiconductors, Springer, Berlin, Heidelberg, Second, substantially revised edn, 2008 Search PubMed.
- M. Esposito, M. A. Ochoa and M. Galperin, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 235440 CrossRef.
- M. A. Ochoa, A. Bruch and A. Nitzan, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 035420 CrossRef.
- R. J. Glauber, Phys. Rev. Lett., 1963, 10, 84–86 CrossRef.
- R. J. Glauber, Phys. Rev., 1963, 131, 2766–2788 CrossRef.
- P. L. Kelley and W. H. Kleiner, Phys. Rev., 1964, 136, A316–A334 CrossRef.
- M. O. Scully and W. E. Lamb, Phys. Rev., 1969, 179, 368–374 CrossRef.
- L. S. Levitov and G. B. Lesovik, JETP Lett., 1993, 58, 230–235 Search PubMed.
- L. S. Levitov, H. Lee and G. B. Lesovik, J. Math. Phys., 1996, 37, 4845–4866 CrossRef.
- Y. M. Blanter and M. Buttiker, Phys. Rep., 2000, 336, 1–166 CrossRef CAS.
- J. Kim, O. Benson, H. Kan and Y. Yamamoto, Nature, 1999, 397, 500–503 CrossRef CAS.
- E. Zakka-Bajjani, J. Dufouleur, N. Coulombel, P. Roche, D. C. Glattli and F. Portier, Phys. Rev. Lett., 2010, 104, 206802 CrossRef PubMed.
- D. Djukic and J. M. van Ruitenbeek, Nano Lett., 2006, 6, 789–793 CrossRef CAS PubMed.
- O. Tal, M. Krieger, B. Leerink and J. M. van Ruitenbeek, Phys. Rev. Lett., 2008, 100, 196804 CrossRef CAS PubMed.
- J.-C. Forgues, F. B. Sane, S. Blanchard, L. Spietz, C. Lupien and B. Reulet, Sci. Rep., 2013, 3, 2869 CrossRef PubMed.
- T. Fujisawa, T. Hayashi, R. Tomita and Y. Hirayama, Science, 2006, 312, 1634 CrossRef CAS PubMed.
- M. Esposito, U. Harbola and S. Mukamel, Rev. Mod. Phys., 2009, 81, 1665–1702 CrossRef CAS.
- C. Emary, C. Pöltl, A. Carmele, J. Kabuss, A. Knorr and T. Brandes, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 165417 CrossRef.
- S. Dambach, B. Kubala, V. Gramich and J. Ankerhold, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 054508 CrossRef.
- O. L. Bo and Y. Galperin, J. Phys.: Condens. Matter, 1996, 8, 3033–3045 CrossRef.
- U. Gavish, Y. Levinson and Y. Imry, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, R10637–R10640 CrossRef CAS.
- U. Gavish, Y. Imry and Y. Levinson, Quantum noise, detailed balance and Kubo formula in nonequilibrium quantum systems, 2002, arXiv: 0211681.
- F. M. Souza, A. P. Jauho and J. C. Egues, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 155303 CrossRef.
- K. E. Dorfman and S. Mukamel, Phys. Scr., 2016, 91, 083004 CrossRef.
- J. Schwinger, J. Math. Phys., 1961, 2, 407–432 CrossRef.
- L. V. Keldysh, Sov. Phys. JETP, 1965, 20, 1018–1026 Search PubMed.
- K. E. Dorfman, F. Schlawin and S. Mukamel, J. Phys. Chem. Lett., 2014, 5, 2843–2849 CrossRef CAS PubMed.
- H.-P. Breuer and F. Petruccione, The Theory of Open Quantum Systems, Oxford University Press, 2003 Search PubMed.
- L. Kidon, E. Y. Wilner and E. Rabani, J. Chem. Phys., 2015, 143, 234110 CrossRef PubMed.
- S. Mukamel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 021111 CrossRef PubMed.
- U. Harbola and S. Mukamel, Phys. Rep., 2008, 465, 191–222 CrossRef.
- L. Mühlbacher and E. Rabani, Phys. Rev. Lett., 2008, 100, 176403 CrossRef PubMed.
- R. B. Saptsov and M. R. Wegewijs, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 235432 CrossRef.
- R. B. Saptsov and M. R. Wegewijs, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 045407 CrossRef.
- G. Cohen, E. Gull, D. R. Reichman and A. J. Millis, Phys. Rev. Lett., 2015, 115, 266802 CrossRef PubMed.
- M. Esposito and M. Galperin, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 205303 CrossRef.
- M. Esposito and M. Galperin, J. Phys. Chem. C, 2010, 114, 20362–20369 CAS.
- A. L. Fetter and J. D. Walecka, Quantum Theory of Many-Particle Systems, McGraw-Hill Book Company, 1971 Search PubMed.
- P. Danielewicz, Ann. Phys., 1984, 152, 239–304 CAS.
- M. Wagner, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 6104–6117 CrossRef.
- A. Stan, N. E. Dahlen and R. van Leeuwen, J. Chem. Phys., 2009, 130, 224101 CrossRef PubMed.
- P. Myöhänen, A. Stan, G. Stefanucci and R. van Leeuwen, J. Phys.: Conf. Ser., 2010, 220, 012017 CrossRef.
- Y. Meir and N. S. Wingreen, Phys. Rev. Lett., 1992, 68, 2512–2515 CrossRef PubMed.
- A.-P. Jauho, N. S. Wingreen and Y. Meir, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 5528–5544 CrossRef CAS.
- Y. Gao and M. Galperin, J. Chem. Phys., 2016, 144, 174113 CrossRef PubMed.
- G. Baym and L. P. Kadanoff, Phys. Rev., 1961, 124, 287–299 CrossRef.
- G. Baym, Phys. Rev., 1962, 127, 1391–1401 CrossRef.
- G. Stefanucci and R. van Leeuwen, Nonequilibrium Many-Body Theory of Quantum Systems. A Modern Introduction, Cambridge University Press, 2013 Search PubMed.
- J. M. Luttinger and J. C. Ward, Phys. Rev., 1960, 118, 1417–1427 CrossRef.
- C. De Dominicis and P. C. Martin, J. Math. Phys., 1964, 5, 14–30 CrossRef.
- R. Haussmann, Self-consistent Quantum-Field Theory and Bosonization for Strongly Correlated Electron Systems, Springer-Verlag, Berlin, Heidelberg, 1999 Search PubMed.
- A. O. Gogolin and A. Komnik, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195301 CrossRef.
- G.-M. Tang and J. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 195422 CrossRef.
- Z. Yu, G.-M. Tang and J. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 195419 CrossRef.
- P. Damle, A. W. Ghosh and S. Datta, Chem. Phys., 2002, 281, 171–187 CrossRef CAS.
- Y. Xue, S. Datta and M. A. Ratner, Chem. Phys., 2002, 281, 151–170 CrossRef CAS.
- M. Brandbyge, J.-L. Mozos, P. Ordejón, J. Taylor and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165401 CrossRef.
- A. Baratz, M. Galperin and R. Baer, J. Phys. Chem. C, 2013, 117, 10257–10263 CAS.
- N. S. Wingreen and Y. Meir, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 11040–11052 CrossRef CAS.
- N. Sivan and N. S. Wingreen, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11622–11629 CrossRef CAS.
- H. Aoki, N. Tsuji, M. Eckstein, M. Kollar, T. Oka and P. Werner, Rev. Mod. Phys., 2014, 86, 779–837 CrossRef.
- M. Eckstein and P. Werner, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 115115 CrossRef.
- J. H. Oh, D. Ahn and V. Bubanja, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 205302 CrossRef.
- A. J. White and M. Galperin, Phys. Chem. Chem. Phys., 2012, 14, 13809–13819 RSC.
- G. Kotliar, S. Y. Savrasov, K. Haule, V. S. Oudovenko, O. Parcollet and C. A. Marianetti, Rev. Mod. Phys., 2006, 78, 865–951 CrossRef CAS.
- H.-T. Chen, G. Cohen, A. J. Millis and D. R. Reichman, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 174309 CrossRef.
- J. Hubbard, Proc. R. Soc. London, Ser. A, 1967, 296, 82–99 CrossRef CAS.
- Y. A. Izyumov and Y. N. Skryabin, Statistical Mechanics of Magentically Ordered Systems, Consultants Bureau, New York and London, 1988 Search PubMed.
- Y. A. Izyumov, M. I. Katsnelson and Y. N. Skryabin, Itinerant Electron Magnetism (in Russian), Nauka, Moscow, 1994 Search PubMed.
- S. G. Ovchinnikov and V. V. Val'kov, Systems Operators in the Theory of Strongly Correlated Electrons, Imperial College Press, 2004 Search PubMed.
- F. Chen, M. A. Ochoa and M. Galperin, J. Chem. Phys., 2017, 146, 092301 CrossRef.
- H. Schoeller and G. Schön, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 18436–18452 CrossRef CAS.
- J. König, J. Schmid, H. Schoeller and G. Schön, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16820–16837 CrossRef.
- H. Schoeller, Lect. Notes Phys., 2000, 544, 137–166 CAS.
- M. Leijnse and M. R. Wegewijs, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 235424 CrossRef.
- I. Sandalov, B. Johansson and O. Eriksson, Int. J. Quantum Chem., 2003, 94, 113–143 CrossRef CAS.
- J. Fransson, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 075314 CrossRef.
- I. Sandalov and R. G. Nazmitdinov, J. Phys.: Condens. Matter, 2006, 18, L55–L61 CrossRef CAS.
- I. Sandalov and R. G. Nazmitdinov, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 075315 CrossRef.
- M. Galperin, A. Nitzan and M. A. Ratner, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 125320 CrossRef.
- J. Fransson, Non-Equilibrium Nano-Physics. A Many-Body Approach, Springer, 2010 Search PubMed.
- A. Perelomov, Generalized Coherent States and Their Applications, Springer, 1986 Search PubMed.
- T.-S. Ho, K. Wang and S.-I. Chu, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 1798–1816 CrossRef CAS.
- G. Stefanucci, S. Kurth, A. Rubio and E. K. U. Gross, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 075339 CrossRef.
- D. Rai and M. Galperin, J. Phys. Chem. C, 2013, 117, 13730–13737 CAS.
- Y. Gao and M. Galperin, J. Chem. Phys., 2016, 144, 244106 CrossRef PubMed.
- S. D. Gedney, Introduction to the finite-difference time-domain (FDTD) method for electromagnetics, Morgan & Claypool, 2011 Search PubMed.
- M. Esposito, M. A. Ochoa and M. Galperin, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 115417 CrossRef.
- T. Zelovich, L. Kronik and O. Hod, J. Chem. Theory Comput., 2014, 10, 2927–2941 CrossRef CAS PubMed.
- L. Chen, T. Hansen and I. Franco, J. Phys. Chem. C, 2014, 118, 20009–20017 CAS.
- J. Jin, X. Zheng and Y. Yan, J. Chem. Phys., 2008, 128, 234703 CrossRef PubMed.
- R. Härtle, G. Cohen, D. R. Reichman and A. J. Millis, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 235426 CrossRef.
- Y. Yan, J. Chem. Phys., 2014, 140, 054105 CrossRef PubMed.
- S. Latini, E. Perfetto, A.-M. Uimonen, R. van Leeuwen and G. Stefanucci, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 075306 CrossRef.
- K. Balzer and M. Eckstein, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 035148 CrossRef.
- K. Kaasbjerg, T. Novotný and A. Nitzan, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 201405 CrossRef.
- A. Baratz, A. J. White, M. Galperin and R. Baer, J. Phys. Chem. Lett., 2014, 5, 3545–3550 CrossRef CAS PubMed.
- L. P. Kadanoff and G. Baym, Quantum Statistical Mechanics, W. A. Benjamin, Inc., New York, 1962 Search PubMed.
- T.-H. Park and M. Galperin, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 205450 CrossRef.
- P. Myöhänen, A. Stan, G. Stefanucci and R. van Leeuwen, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 115107 CrossRef.
- F. Chen, K. Miwa and M. Galperin, to be published.
- R. Sánchez, G. Platero and T. Brandes, Phys. Rev. Lett., 2007, 98, 146805 CrossRef PubMed.
- R. Sánchez, G. Platero and T. Brandes, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 125308 CrossRef.
- I. Kinoshita, A. Misu and T. Munakata, J. Chem. Phys., 1995, 102, 2970–2976 CrossRef.
- W. Tian, S. Datta, S. Hong, R. Reifenberger, J. I. Henderson and C. P. Kubiak, J. Chem. Phys., 1998, 109, 2874–2882 CrossRef CAS.
Footnotes |
| † For future reference we write down a quantized radiation field. |
| ‡ Note that more general couplings can be considered as well.130,146 |
| § However, note recent discussion on inconsistency of this definition with thermodynamic laws.206,207 |
| ¶ Note that the name is a bit misleading, because for quantum radiation field a diagram is characterized also by contractions (Green functions) of the corresponding field operators (see Fig. 3). |
| || Note that if initial correlations are to be taken into account one needs to consider a combination of the Keldysh and Matsubara contours. We do not discuss this possibility here; the interested reader is encouraged to consult ref. 243–246. |
| ** Electron Green function enters expression for photon flux, eqn (8), via photon self-energy Π. |
| †† Note that also structure of the Dyson equations, eqn (14) and (15), implies resumming which accounts for reducible diagrams. |
| ‡‡ One has to use F0 everywhere in this case and disregard eqn (15). |
| §§ DC transport measurements are an important part of the suggestion, because electronic components are too slow to directly measure dynamics with picosecond resolution. |
| This journal is © The Royal Society of Chemistry 2017 |