Self-assembled uracil complexes containing tautomeric uracils: an IRMPD spectroscopic and computation study of the structures of gaseous uracil_nCa²⁺ (n = 4, 5, or 6) complexes

Abstract

The structures of doubly-charged uracil (U) complexes with Ca²⁺, U_nCa²⁺ (n = 4, 5, 6), were studied by infrared multiple photon dissociation (IRMPD) spectroscopy and computational methods. The ions were produced by electrospray ionization (ESI) and were isolated in the gas phase in a Fourier-transform ion cyclotron resonance mass spectrometer (FT-ICR-MS). The recorded IRMPD spectra in both the fingerprint and the C–H/N–H/O–H stretching regions, combined with computed vibrational spectra, reveal that the structures present in the greatest abundance consist of both canonical uracil as well as the lactam (or colloquially “enol”) tautomer of uracil. U₄Ca²⁺ consists of two hydrogen-bonded dimers of uracil, one canonical and one tautomer, with each uracil interacting with Ca²⁺ through a carbonyl oxygen. The structures most consistent with the vibrational spectrum of U₆Ca²⁺ consist of two hydrogen-bonded uracil trimers, each composed of two canonical and one enolic uracil, with each uracil also interacting with Ca²⁺ through carbonyl oxygen. U₅Ca²⁺ consists of one of the aforementioned trimers and dimers, each containing one enol tautomerized uracil. The computed structures whose vibrational spectra best agree with the experimental vibrational spectra are also the lowest-energy structures for all three complexes. This study clearly shows that some uracils adopt the normally very high energy enol tautomer in the lowest energy gas phase complexes of uracil with a doubly-charged ion like Ca²⁺.

---

1. Introduction

Adenine, guanine, thymine, cytosine, and uracil are nucleobases comprising deoxyribonucleic acid (DNA) and/or ribonucleic acid (RNA). During the process of DNA and RNA replication, metal cations exhibit different effects depending on their concentrations. At high concentration, they can interact with the nucleobases and disrupt normal hydrogen bonding patterns between base pairs. Their presence at high concentrations, therefore, can cause the mismatching of the nucleobases which is considered to be the main reason for mutations as they interfere with the native conformations of the nucleic acid polymers.^1,2 However, at lower concentrations, metal cations interact with the phosphate groups of the nucleic acids, stabilizing the double helix of DNA.³ In the 1960s, guanosine 5′-monophosphate was found to form planar G-tetrad complexes that exhibit Hoogsteen paired motifs.⁴ Further research in the 1980s revealed that these structures could form in DNA, stabilized by monovalent cations.^5,6 Studies of G-tetrads are of interest due to their biological relevance as they are found within the guanine-rich telomeric regions near the ends of chromosomes^1,5,7 and within the promoter regions of oncogenes.⁸ Therefore, the G-tetrad has been investigated as a potential target for cancer therapies.⁹ Whether these structures exist in vivo was controversial; there is evidence that they are formed in living cells, as proteins that recognize the G-tetrad have been found.^10,11 More recently, there has been evidence found that telomere end-binding proteins (TEBPs) regulate G-quadruplex DNA formation in vivo.¹²

Cation-bound self-assembled nucleobase complexes have attracted the attention of scientists not only in biological fields, but also materials chemistry. Specific knowledge of self-assembled nucleobase structures bound to metal cations can be applied in the fields of supramolecular chemistry and nanotechnologies where the ability to selectively produce molecular-scale structures is pivotal. It is necessary to better understand how non-covalent interactions such as hydrogen bonds, ion–dipole interactions and π–π interactions affect the structures of complexes containing nucleobases and metal cations. This knowledge can be applied to self-assembly and molecular recognition processes to form supramolecular polymers,¹³ nanofibres,¹⁴ and nano-scale electronics.¹⁵ Stable uracil tetramers containing metal cations at their centers, with Hoogsteen-bonding patterns analogous to the guanine quartets, have been found to exist in four-stranded RNA molecules.¹⁶

Uracil complexes in the gas phase have been studied by density functional theory (DFT) and electrospray ionization-mass spectrometry (ESI-MS) by Zins et al.¹⁷ Lithium, sodium, and calcium cations (Li⁺, Na⁺, Ca²⁺) were found to bond to uracil producing a series of different adducts; notable among these was a decameric complex that appeared to have unusual stability for such a complex structure. The decamer was identified as a magic number cluster, which have a high relative intensity compared to the other ions present. Potassium was not capable of forming the uracil decamer, but the calcium cation led to the formation of particularly large clusters such as 18-mers (U₁₈Ca²⁺) and even 24-mers (U₂₄Ca²⁺). These results indicate that both the size and the charge of the metal cation affect uracil aggregation. Theoretical calculations showed that a low energy decamer structure of Na⁺ and Ca²⁺ were the same, with two quasiplanar uracil pentamers on two sides with cations in the center. The uracil pentamer is stabilized by ten NH–O hydrogen bonds between uracil molecules. The metal cation interacts with two uracil pentamers by cation dipole interactions. These calculations also showed that the lithium cation may be too small to form sufficient ion–dipole interactions to occupy the space between two uracil pentamers so the Li⁺ ion forms octameric complexes with the cation existing between two uracil tetramers. Of course, these mass spectral observations did not provide evidence to support the theoretically determined structures.

Further research into the structure of uracil pentamer complex [U₅M]⁺ (M = K⁺, Na⁺, Cs⁺) was conducted using electrospray ionization mass spectrometry (ESI-MS).¹⁸ The proposed structure for these pentamers contains two hydrogen bonds between two neighboring uracils forming a cyclic structure with the metal cation in the middle. The uracil pentamer system has a non-planar geometry with K⁺ in the center while Na⁺ bonded complex is not exactly a metal-centered structure. The U₅Na⁺ is not as thermodynamically stable as U₅K⁺ because there are fewer interactions with Na⁺ as a result of its off-center structure. The results also indicated that the suitable size of the metal cation is vital for stabilizing such a complex. Work by Gillis et al.¹⁹ investigated the energetics of dissociation of trapped gas phase uracil cluster ions consisting of 4–14 uracil units and a divalent calcium ion center (U_nCa²⁺ where n = 4–14) by blackbody infrared radiative dissociation (BIRD) kinetics and theoretical methods. It was determined that the energy of dissociation for U₆Ca²⁺ is significantly greater than that for the larger clusters (n = 7–14) consistent with collision induced dissociation (CID) studies by Zins et al.²⁰ and indicates that the clusters are composed of an inner solvent shell of six uracil molecules bound directly to the Ca²⁺, with additional uracils bound in a second solvation shell through hydrogen bonding to the inner shell uracil molecules. Theoretical and experimental results also revealed an odd–even alternation of dissociation threshold energies for the larger clusters, where complexes with an even number of uracil molecules were found to be more stable to dissociation, indicating that the large clusters of uracil, beyond n = 6, may be composed of hydrogen-bonded dimeric units of uracil bound to the inner U₆Ca²⁺ core. In this work, plausible structures were suggested, but only those containing canonical uracil were contemplated, and no spectroscopic evidence for the structures was available.

The present work aims to provide more direct experimental insight into the previously proposed structures of the U_nCa²⁺ (n = 4–6), using infrared multiple photon dissociation (IRMPD) spectroscopy in the 1000–1900 cm⁻¹ and 2800–3800 cm⁻¹ regions. The experimental IRMPD spectra are compared to theoretical infrared (IR) spectra from electronic structure calculations. Different computation methods and basis sets are used to compare the energies of isomeric structures. By comparing theoretical and experimental results, the precise structures of uracil complexes are determined.

2. Methods

2.1 Computational methods

Geometry optimizations and frequency calculations were performed using the Gaussian 09 suite of programs using B3LYP density functional theory and the 6-31+G(d,p) split-valance basis set for all atoms from which the relative 298 K Gibbs energies and enthalpies of various different isomers were compared. The computed IR spectra were scaled by 0.97 and 0.95 in the lower (900–2000 cm⁻¹) and higher (2700–4000 cm⁻¹) energy regions, respectively, to compare with the experimental IRMPD spectra. The single point energies for all lowest energy structures were performed using B3LYP/6-311+G(3df,3pd) for comparison. For all calculations, an empirical dispersion correction was done using Grimme's D3 version with the original D3 damping function, B3LYPD3.²¹

2.2 Experimental methods

For the IRMPD spectroscopy, two different instruments were used, one for each of the fingerprint and C–H/N–H/O–H stretching region. For both, a Bruker Apex-Qe 7 Fourier-transform ion cyclotron resonance mass spectrometer (FT-ICR-MS) with an Apollo II electrospray ion source was used. Uracil and calcium chloride were purchased from Sigma-Aldrich and used without further purification. The solution producing the uracil tetramer (U₄Ca²⁺) was 1.7 mmol L⁻¹ uracil in 50/50 water and methanol and 5–10 drops of 10 mmol L⁻¹ in CaCl₂. U₅Ca²⁺ and U₆Ca²⁺ were prepared to concentrations of 2.5 mmol L⁻¹ uracil in a 50/50 mixture of water and acetonitrile and contained 130 μmol L⁻¹ CaCl₂. Solutions were injected using a 1 mL syringe at a flow rate of 112 μL h⁻¹. The temperature of the dry gas was set as 90 °C. Prior to IRMPD, ions were isolated by standard FT-ICR isolation techniques.

For IRMPD experiments in the fingerprint region, the FT-ICR-MS was coupled to a free electron laser (FEL) at the Centre Laser Infrarouge d’Orsay.^22,23 Irradiation times were between 1 and 2 s and the FEL was scanned at 5 cm⁻¹ intervals. In the C–H/N–H/O–H stretch region isolated ions were irradiated with an optical parametric oscillator/amplifier (OPO/A) in the Laboratory for the Study of Energetics, Structures, and Reactions of Gaseous Ions at Memorial University.²⁴ The ions were irradiated by the laser for 1 s, and the scan step was set as 2 cm⁻¹. The IRMPD efficiencies (intensities) are the negative of the logarithm of the product ion intensities divided by the sum of the total ion intensities.

3. Results and discussion

3.1 Infrared multiple photon dissociation of U_nCa²⁺

Mass spectra following 3420 cm⁻¹ irradiation of the isolated U₄Ca²⁺, U₅Ca²⁺, and U₆Ca²⁺ complexes are displayed in Fig. S10A–C (ESI†), respectively. U₄Ca²⁺ (m/z 244) undergoes charge separation to UH⁺ (m/z 113) and (U₃Ca-H)⁺ (m/z 375), the latter of which loses uracil to form (U₂Ca-H)⁺ (m/z 263). U₅Ca²⁺ (m/z 300) undergoes loss of uracil (m/z 244) which undergoes the same fragmentation as just described for U₄Ca²⁺.

U₅Ca²⁺ also undergoes charge separation forming UH⁺ and (U₄Ca-H)⁺ (m/z 487) the latter of which undergoes successive losses of uracil forming m/z 375, 263 and 151.

U₆Ca²⁺ (m/z 356) presumably underwent loss of uracil to form m/z 300 exclusively as no (U₅Ca-H)⁺ (m/z 599) was observed. The U₅Ca²⁺ then underwent charge separation and loss of uracil as just described.

All parent and fragment ions were accounted for when determining the IRMPD efficiency to construct the IRMPD spectra which will be discussed below.

3.2 IRMPD spectra for U_nCa²⁺

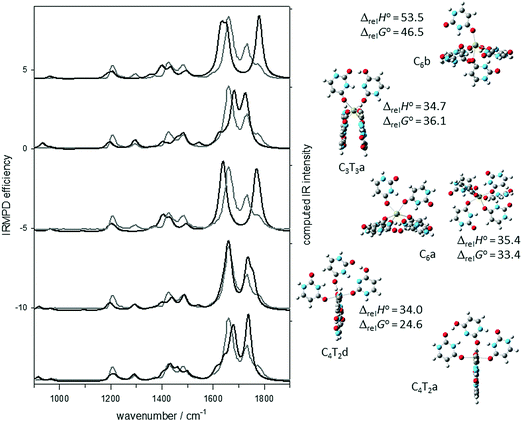
In Fig. 1, the IRMPD spectra in the fingerprint and C–H/N–H/O–H stretching region for U₄Ca²⁺, U₅Ca²⁺, and U₆Ca²⁺ are presented. Clearly, in both regions, the spectra of each complex are quite similar to one another, so similar structures might be expected. In the high energy region, sharp N–H stretching bands are observed at about 3420 cm⁻¹ and broad hydrogen bonded N–H (or O–H—vide infra) are observed between about 3400 and 2800 cm⁻¹. In the fingerprint region, the most intense bands are observed between about 1575 cm⁻¹ and 1800 cm⁻¹ correspond to strong C=O stretching for uracil. These bands are quite indicative of the structure of the complex and can be broken down into three regions. The first, indicated by ‘A’ in Fig. 1, is the most red-shifted of the three regions and the band centred at about 1635 cm⁻¹ is the stretching of the C=O bound to the metal cation. The second region, B, has absorptions centred around 1730 cm⁻¹ and the third, C, weak shoulders are observed at about 1775 cm⁻¹. Region C is where strong free C=O stretching vibrations would be expected and just to the red, region B, C=O stretching that has been slightly red shifted by an interaction such as a hydrogen bond is expected.

Fig. 1 Comparison of the experimental IRMPD spectra for U_nCa²⁺ (n = 4, 5, 6) in the fingerprint and the CH/NH/OH stretching regions.

In previous work,^17,19,20 only canonical (or diketo) uracil was considered when trying to obtain lowest energy structures of Ca²⁺/uracil complexes. The lowest energy structure found for U₄Ca²⁺ (Scheme 1A) had each of the uracils bound to Ca²⁺ through O4 and a hydrogen bond between N3H and O4 of the neighbouring uracil. This structure is called C₄a, where C₄ indicates four canonical uracils and ‘a’ represents the lowest energy structure. While this structure is consistent with the spectra in the higher energy region—a free N–H group and hydrogen bonding N–H stretching—the four free C=O groups would be expected to produce intense features in region C at about 1800 cm⁻¹ in the fingerprint region of the infrared spectrum. The structures of the U₄Ca²⁺, U₅Ca²⁺, and U₆Ca²⁺ complexes will be discussed in more detail below.

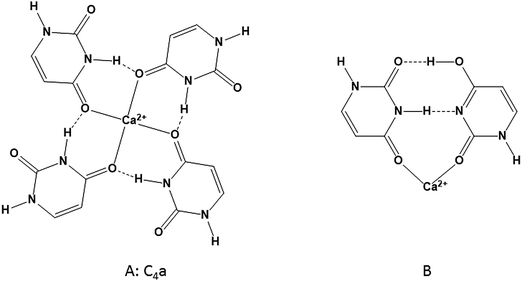Scheme 1 (A) The lowest energy U₄Ca²⁺ composed of all diketo uracils determined in previous works.^17,19,20 (B) Dimeric Ca²⁺/uracil structure composed of one diketo and one N3O4 tautomer comprising another U₄Ca²⁺ isomer.

3.3 U₄Ca²⁺

In some recent studies, it was shown that in the presence of ions uracil^25–30 and thymine³¹ tautomerize preferentially where the N3 hydrogen is instead on O4 (N3O4 tautomer) and the ion interacts with O2 and N3. While the canonical structure for uracil and thymine is significantly lower in energy than any of the enol tautomers, the N3O4 tautomer of thymine bound to a dication can be lower in energy by some 100 kJ mol⁻¹ than the canonical tautomer bound to a dication.³¹ Therefore, the normally high energy tautomers of uracil, seen in Scheme 2 need to be considered.

Scheme 2 Four tautomers of uracil including the numbering convention for pyrimidine bases such as uracil.

Based on this previous work and armed with the spectroscopy in Fig. 1, a structure for U₄Ca²⁺ composed of two dimers of uracil, each with one canonical and one N3O4 tautomer, both bound to Ca²⁺ (see Scheme 1B) was constructed. In this structure, canonical uracil is bound to Ca²⁺ through O4 and the N3O4 tautomer is bound to Ca²⁺ through O2 providing the strong band in region A. There is a hydrogen bonded N–H group and a hydrogen bonded O–H group, as well as two free N–H groups, consistent with the spectra in the high energy region. There is a hydrogen bonded carbonyl providing the strong band in region B and no free carbonyl group, again consistent with the infrared spectrum. The U₄Ca²⁺ complex based on these dimers is named C₂T₂a (T for tautomeric uracil) is calculated to be lower in 298 K Gibbs energy by 51.3 kJ mol⁻¹ (see Fig. 2) than the lowest energy structure determined with all canonical uracils.

Fig. 2 Comparison of the experimental IRMPD spectrum (grey trace) for U₄Ca²⁺ and the B3LYP/6-31+G(d,p) computed IR spectra (black traces) for four different isomers. The 298 K enthalpies and Gibbs energies relative to structure C₂T₂a are also shown (also computed using B3LYP/6-31+G(d,p)).

In Fig. 2, the experimental IRMPD spectra (grey traces) are compared with the computed IR spectra (black traces) for the structures depicted in the centre of the figure. It is clear that the computed spectrum for the lowest energy structure, C₂T₂a, compares very well with the entirety of the recorded IRMPD spectrum. It is equally apparent that the computed infrared spectrum for the C₄a structure, discussed above, is not consistent with the C=O stretching region of the experimental IRMPD spectrum. The obvious disagreement is the absence of a strong free C=O stretch in the experimental IRMPD spectrum, which is predicted by the calculations, and the presence of the hydrogen bonded C=O stretch in the IRMPD spectrum, which is not predicted by the calculations. Fig. 2 also shows the second and third lowest energy structures from Gillis et al.,¹⁹ which are also high in energy compared to C₂T₂a, and have similar inconsistencies with the IRMPD spectrum mainly in the 1700–1800 cm⁻¹ region.

There are other isomers of U₄Ca²⁺ consisting of two dimers composed of one canonical and one tautomeric uracil. C₂T₂b is similar to C₂T₂a except the tautomeric uracil has the N3 hydrogen shifted to O4 and this uracil is bound to Ca²⁺ through O2, see Fig. S1 (ESI†). This results in a structure that is only 8.0 kJ mol⁻¹ higher in 298 K Gibbs energy than C₂T₂a. The IRMPD spectrum in the fingerprint region is also consistent with the computed IR spectrum for C₂T₂b. In the higher energy region, there is a pronounced red-shift computed for the hydrogen bonded O–H stretch, however this is not enough to rule out a contribution to the experimental spectrum from C₂T₂b. C₂T₂a/b contains one dimer each as the ones in C₂T₂a and C₂T₂b and results in a structure that is computed to be only 3.9 kJ mol⁻¹ higher in 298 K Gibbs energy than the lowest energy C₂T₂a isomer. Assuming a thermal distribution, it would be expected that C₂T₂a/b contributes about 20% of the mixture of ions. It is clear that C₂T₂a/b also reproduces the experimental spectrum quite well and unlike C₂T₂a predicts the weak band observed at about 1530 cm⁻¹.

C₂T₂c and C₂T₂d both have the canonical uracil bound to Ca²⁺ through O2 and differ from each in the same way that C₂T₂a and C₂T₂b differ from one another. C₂T₂c and C₂T₂d are more than 20 kJ mol⁻¹ higher in energy than C₂T₂a and their computed spectra do not compare as well with the experimental IRMPD spectrum. It is concluded from these experiments and calculations that the main contributor to the experimental IRMPD spectrum is the C₂T₂a structure with a tetrahedral arrangement of two uracil hydrogen bonded dimers with one member of the dimer canonical and one which is a keto–enol tautomer.

Some other higher energy structures for U₄Ca²⁺ are shown in Fig. S7 (ESI†) along with their computed energies and a comparison of the computed and experimental vibrational spectra. These include structures based on four N3O4 or N1O4 tautomeric uracils whose computed vibrational spectra do not reproduce the experimental spectra.

3.4 U₆Ca²⁺

To construct a structure for U₆Ca²⁺, like U₄Ca²⁺, that is consistent with its experimental vibrational spectrum, a third dimer as in Scheme 1B is added to U₄Ca²⁺ to form an octahedral structure. The complex optimizes to the octahedral structure labeled C₃T₃a in Fig. 3. This isomer, based on the three dimers, “collapses” such that two of the dimers have a B–B stacking interaction. The agreement between the computed IR spectrum for this structure and the IRMPD spectrum is certainly not poor enough to rule the structure out.

Fig. 3 A comparison of the experimental IRMPD spectrum (grey trace) for U₆Ca²⁺ and the B3LYP/6-31+G(d,p) computed IR spectra (black traces) for five different isomers. The 298 K enthalpies and Gibbs energies relative to structure C₄T₂a are also shown (also computed using B3LYP/6-31+G(d,p)).

Another way to form the U₆Ca²⁺ is to add canonical uracil to each of the dimers, constructing two trimers with two canonical uracils and one of the tautomers in each, as in Scheme 3, where both canonical uracils are hydrogen bonded to the tautomeric uracil. The added uracil in this trimer (iii in Scheme 3) is also bound to Ca²⁺ through O4. The addition of this third uracil to each of the dimers in the lowest energy tetramer structure, C₂T₂a, results in a structure where the two trimers are perpendicular to each other, forming a roughly octahedral complex, and is lower in 298 K Gibbs energy than C₄T₂f by 36.1 kJ mol⁻¹. Distortion of the complexes from an octahedral structure is due to the inter-trimer uracil hydrogen bonding. The computed infrared spectrum for this lowest-energy structure, C₄T₂a, can be seen in Fig. 3 and compares very well—better than C₄T₂f—with the experimental spectrum in the fingerprint region and the higher energy region (see Fig. S2, ESI†). This structure, along with C₄T₂b, C₄T₂c, and C₄T₂e, compared in Fig. S3 (ESI†), maximize the number of hydrogen bonds with two N–H to O=C, one O–H to O=C, and one N–H to N. However, C₂T₂a matches the IRMPD spectrum in the fingerprint region much better. C₄T₂b differs in that one canonical uracil (iii in Scheme 3) is bound through O2 rather than O4 and is 13 kJ mol⁻¹ higher in energy. C₄T₂c and C₄T₂e have the two canonical uracils hydrogen bonded together and are higher in energy by 16 and 30 kJ mol⁻¹, respectively.

Scheme 3 Lowest energy trimeric Ca²⁺/uracil structure composed of two canonical uracils and one N3O4 tautomer comprising the lowest energy U₆Ca²⁺ isomer.

Another structure that has a computed IR spectrum that compares favourably with the IRMPD spectrum is C₄T₂d (Fig. 3 and Fig. S2, ESI†). This structure, like C₄T₂c and C₄T₂e, differs from C₄T₂a in that the two canonical uracils in each of the trimers is hydrogen bonded together, in the case of C₄T₂d via an N3–H to O4 hydrogen bond and a C5–H to O2 interaction. While this structure is consistent with the IRMPD spectrum, it is 24.6 kJ mol⁻¹ higher in 298 K Gibbs energy which makes it unlikely to be observed.

As was the case for the tetramers, the previously determined hexameric structures based solely upon canonical uracils,¹⁹i.e. C₆a and C₆b in Fig. 3 and Fig. S2 (ESI†), are higher in energy than C₄T₂a and their computed IR spectra do not compare well with the IRMPD spectra. The main problem with the computed spectra is that they contain a free C=O stretch (region C) and do not predict the hydrogen bonded C=O stretch (region B) which is observed experimentally. Some other higher energy structures and their computed spectra are shown in Fig. S9 (ESI†), including those where the two trimers are mixed in that they contain a trimer of C₄T₂a and one of either C₄T₂b, c, or e. These ‘mixed’ complexes are intermediate in energy; for example, C₄T₂a/b is higher in energy than C₄T₂a, but lower in energy than C₄T₂b. They are not nearly as good a fit to the IRMPD spectra in comparison to C₄T₂a (Fig. S9, ESI†).

3.5 U₅Ca²⁺

The IRMPD spectrum of U₅Ca²⁺ is compared to the computed IR spectra of several isomers in Fig. 4 and Fig. S4–S6, S8 (ESI†). Removal of one of the canonical uracils (iii in Scheme 3) from the lowest energy U₆Ca²⁺ structure results in two very similar structures, C₃T₂a and C₃T₂b (in Fig. 4 and Fig. S4, respectively, ESI†) which only differ in 298 K Gibbs energy by 0.6 kJ mol⁻¹. They do not differ significantly in structure, simply whether tautomeric or canonical uracil in the remaining dimer is closest to the trimer. The IR spectrum of C₃T₂a is consistent with the experimental IRMPD spectrum but certainly C₃T₂b cannot be ruled out spectroscopically or energetically. C₃T₂c and C₃T₂d differ from C₃T₂a and C₃T₂b in that uracil iii in the trimer is bound through O2 rather than O4 and results in structures that are a little less than 8 kJ mol⁻¹, higher in 298 K Gibbs energy. While neither of these structures can be ruled out spectroscopically, they do not agree as well as the two lower energy structures in the C=O stretching region. C₃T₂e and C₃T₂f differ in that the trimeric moiety is composed of tautomeric uracil bound to a canonical uracil bound to Ca²⁺via O2 and the second canonical uracil is bound through O4, but hydrogen bonded to canonical uracil. This results in structures just slightly higher than the previously discussed structure and their computed IR spectra are not as good a match to the experimental vibrational spectrum in the fingerprint region. Other computed IR spectra for higher energy structures are compared in Fig. 4 and the ESI.†

Fig. 4 Comparison of the experimental IRMPD spectrum (grey trace) for U₅Ca²⁺ and the B3LYP/6-31+G(d,p) computed IR spectra (black traces) for five different isomers. The 298 K enthalpies and Gibbs energies relative to structure C₃T₂a are also shown (also computed using B3LYP/6-31+G(d,p)).

In Fig. S6 (ESI†), the computed IR spectra for the three lowest energy C5-based structures that were determined previously¹⁹ are compared to the experimental IRMPD spectrum. Besides being between 23 and 33 kJ mol⁻¹ higher in energy than C₂T₃a, spectroscopically these isomers can be ruled out based on the poor agreement in the C=O stretching region as discussed previously for the U₄Ca²⁺ and U₆Ca²⁺ complexes.

3.6 Other observed U_5,6Ca²⁺ structures

In the IRMPD spectra for U₅Ca²⁺ and U₆Ca²⁺, there is a weak but pronounced shoulder observed in region C of Fig. 1, just to the red of 1800 cm⁻¹. The band can only be attributed to a free C=O stretch which is not present in any of the lowest energy structures. The only structures found that contain a free C=O stretch are those not based on the dimer or trimer containing an N3O4 tautomer. Because the lowest energy structures of pentamer and hexamer clusters lack the free C=O stretch, the existence of higher energy clusters is likely due to the presence of this shoulder peak at 1800 cm⁻¹ observed in the experimental spectrum. For example, the lowest energy isomer containing a free C=O stretch for U₆Ca²⁺, is C₆a. This isomer is also some 33 kJ mol⁻¹ higher in 298 K Gibbs energy than C₄T₂a, and if present, it must be kinetically trapped, probably during the electrospray process. Tautomerization of the all keto tautomer of uracil to the enol–keto tautomer proceeds with a very high activation energy, some 200 kJ mol⁻¹ for neutral uracil.³² The tautomerization barrier is computed to be lower, but still considerable (70 kJ mol⁻¹, 298 K Gibbs energy barrier) for both the protonated and water-assisted tautomerization³³ and an intramolecularly assisted uracil tautomerization in (U₂-H)Cu⁺.²⁸

3.7 Computed energies

The B3LYPD3/6-31+G(d,p) lowest energy structures for U₄Ca²⁺ as well as for the lowest energy C₃T₁ and C₄ structures, were submitted to a single point calculation at the same level of theory but with the larger 6-311+G(3df,3pd) basis. The calculations are compared in Table 1, using the thermal corrections to the 298 K enthalpy and Gibbs energy from the vibrational calculations with the smaller basis. Clearly, there is very little difference between the computed energies using the smaller or larger basis sets. A similar set of calculations were performed on various U₅Ca²⁺ and U₆Ca²⁺ isomers with the same conclusion (see Tables S2 and S3, ESI†).

Table 1 Comparison of basis set on the 298 K energetics (top relative enthalpies, bottom relative Gibbs energies) in kJ mol⁻¹ of some U₄Ca²⁺ structures

Structure	B3LYPD3/6-31+G(d,p)	B3LYPD3/6-311+G(3df,3pd)
C2T2a	0.0	0.0
	0.0	0.0
C2T2b	7.3	6.8
	8.0	7.5
C2T2c	21.7	21.7
	22.4	22.3
C2T2d	24.6	24.3
	25.6	25.4
C3T1a	35.9	35.2
	31.8	31.2
C4a	54.8	58.0
	51.3	54.5

---

4. Conclusions

A combination of IRMPD spectroscopy and computational chemistry was used to show that the structures of three doubly charged uracil/calcium clusters: U₄Ca²⁺, U₅Ca²⁺, and U₆Ca²⁺, all contain two N3O4 enol-tautomerized uracils. The lowest energy structure for the U₄Ca²⁺ complex consists of two uracil dimers, each consisting of one canonical and one tautomeric uracil, with two hydrogen bonds between them. The lowest energy U₆Ca²⁺ complex consists of two uracil trimers, the same dimeric structure as in U₄Ca²⁺ but a second canonical uracil doubly hydrogen bonded to the other side of the tautomeric uracil. The lowest energy U₅Ca²⁺ consists of one dimer and one trimer as in the U₄Ca²⁺ and U₆Ca²⁺, respectively. The computed IR spectra for the lowest energy structures for each of the complexes were consistent with the experimental IRMPD spectra in all cases.

For U₄Ca²⁺ a second structure, only a few kJ mol⁻¹ higher than the lowest energy structure, with an IR spectrum also consistent with the IRMPD spectrum also accounts for a small absorption at about 1530 cm⁻¹. A weak shoulder observed in the free C=O stretch region for both U₄Ca²⁺ and U₄Ca²⁺ are thought to be due to a small amount of higher energy, kinetically trapped complexes with only canonical uracils, as these are the only ones with predicted absorptions in these regions.

The structures determined for U₄Ca²⁺, U₅Ca²⁺, and U₆Ca²⁺ are vastly different than those previously determined and only composed of canonical uracils.^17,19,20 This is easily seen in the C=O stretch region where there is the absence of a strong absorption in the IRMPD spectra due to a free C=O group which is predicted for canonical uracil based structures and the presence of a hydrogen bonded C=O stretch in the IRMPD spectrum which is not predicted for the canonical uracil based structures.

In previous experiments¹⁹ the BIRD dissociation kinetics of U_nCa²⁺ were observed where n = 5–14. The thermochemistries of dissociation led to the conclusion that U₁₄Ca²⁺ was composed of a U₆Ca²⁺ core surrounded by four hydrogen bonded dimers of uracil in the second solvation shell, each hydrogen bonded to the core. This conclusion was based on the even uracil (n = 14, 12, 10, 8) containing complexes being more strongly bound than the odd uracil containing complexes (n = 13, 11, 9, 7), the difference between the successive dissociations, i.e. n = 14 and 13 being about the strength of a hydrogen bond, 10 kJ mol⁻¹. While a detailed computational study of these larger complexes is beyond the scope of this study, it is interesting to contemplate a structure for the U₁₄Ca²⁺ complex that also explains this even-odd dissociation energy observation. One such structure is proposed in Scheme 4 (only showing half the uracils in the complex) based on a core containing the T₄C₂a isomer of U₆Ca²⁺. In this structure, each uracil dimer is bound to the complex via three interactions. The uracil labeled ‘a’ in Scheme 4 is bound by three hydrogen bonds, one to the other dimer, and might be the first to be lost, leaving the uracil labeled ‘b’ bound by only two hydrogen bonds and the second to be lost. Uracil ‘c’ is bound by three interactions and would be the third uracil lost followed by ‘d’ which is only bound to the core by two hydrogen bonds.

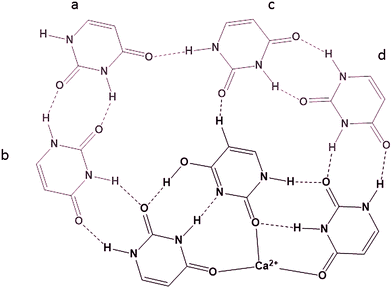Scheme 4 Possible structure of one half of U₁₄Ca²⁺ with the 6 mer core composed of two trimeric structures.

Conflicts of interest

There are no conflicts to declare.

References

1. B. Lippert, J. Chem. Soc., Dalton Trans., 1997, 21, 3971–3976.
2. J. E. Reed, A. A. Arnal and S. Neidle, J. Am. Chem. Soc., 2006, 128(18), 5992–5993.
3. G. L. Eichhorn; N. A. Berger; J. J. Butzow; P. Clark; J. Heim; J. Pitha; C. Richardson; J. M. Rifkind; Y. Shin and E. Tarien, in Metal Ions in Biological Systems: Studies of Some Biochemical and Environmental Problems, ed. S. K. Dhar, Springer US, Boston, MA, 1973, pp. 43–66.
4. M. Gellert, M. N. Lipsett and D. R. Davies, Proc. Natl. Acad. Sci. U. S. A., 1962, 48(12), 2013–2018.
5. W. I. Sundquist and A. Klug, Nature, 1989, 342, 825–829.
6. J. R. Williamson, M. K. Raghuraman and T. R. Cech, Cell, 1989, 59, 871–880.
7. J. R. Williamson, Annu. Rev. Biophys. Biomol. Struct., 1994, 23, 703–730.
8. L. Yuan, T. Tian, Y. Chen, S. Yan, X. Xing, Z. Zhang, Q. Zhai, L. Xu, S. Wang, X. Weng, B. Yuan, Y. Feng and X. Zhou, Sci. Rep., 2013, 3, 01811.
9. L. R. Kelland, Eur. J. Cancer, 2005, 41, 971–979.
10. R. Erlitzki and M. Fry, J. Biol. Chem., 1997, 272(25), 15881–15890.
11. M. P. Horvath and S. C. Schultz, J. Mol. Biol., 2001, 310, 367–377.
12. K. Paeschke, T. Simonsson, J. Postberg, D. Rhodes and H. J. Lipps, Nat. Struct. Mol. Biol., 2005, 12(10), 847–854.
13. S. J. Rowan, P. Suwanmala and S. Sivakova, J. Polym. Sci., Part A: Polym. Chem., 2003, 41, 3589–3596.
14. T. Shimizu, R. Iwaura, M. Masuda and T. Hanada, J. Am. Chem. Soc., 2001, 123(8), 5947–5955.
15. Y. Eichen, E. Braun and U. Sivan, Acta Polym., 1998, 49, 663–670.
16. C. Cheong and P. B. Moore, Biochemistry, 1992, 31, 8406–8414.
17. E. Zins, S. Rochut and C. Pepe, J. Mass Spectrom., 2009, 2008(2008), 40–49.
18. B. Qiu, J. Liu, Z. Qin, G. Wang and H. Luo, Chem. Commun., 2009, 2863.
19. E. A. L. Gillis, M. Demireva, K. Nanda, G. Beran, E. R. Williams and T. D. Fridgen, Phys. Chem. Chem. Phys., 2012, 14(10), 3304–3315.
20. E. Zins, S. Rochut and C. Pepe, J. Mass Spectrom., 2009, 2009(2008), 813–820.
21. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 15.
22. J. M. Bakker, T. Besson, D. Scuderi and P. Maı, J. Phys. Chem. A, 2007, 111, 13415–13424.
23. R. Prazeres, F. Glotin, C. Insa, D. A. Jaroszynski and J. M. Ortega, Eur. Phys. J. D, 1998, 3, 87–93.
24. M. Azargun, Y. Jami-Alahmadi and T. D. Fridgen, Phys. Chem. Chem. Phys., 2017, 19, 1281–1287.
25. B. Power, V. Haldys, J. Y. Salpin and T. D. Fridgen, Int. J. Mass Spectrom., 2015, 378, 328–335.
26. A. A. Power, O. Y. Ali, M. Burt and T. D. Fridgen, Interna, 2012, 330, 233–240.
27. O. Y. Ali, N. M. Randell and T. D. Fridgen, ChemPhysChem, 2012, 13, 1507–1513.
28. O. Y. Ali and T. D. Fridgen, ChemPhysChem, 2012, 13, 588–596.
29. B. Power, S. Rowe and T. D. Fridgen, J. Phys. Chem. B, 2017, 121, 58–65.
30. T. E. Akinyemi, R. R. Wu, Y.-W. Nei, N. A. Cunningham, H. A. Roy, J. D. Steill, G. Berden, J. Oomens and M. T. Rodgers, J. Am. Soc. Mass Spectrom, 2017, 28(11), 2438–2453.
31. M. Kabeláč and P. Hobza, J. Phys. Chem. B, 2006, 110(29), 14515–14523.
32. X. Hu, H. Li, W. Liang and S. Han, J. Phys. Chem. B, 2005, 109(12), 5935–5944.
33. J. M. Bakker, R. K. Sinha, T. Besson, M. Brugnara, P. Tosi, J. Salpin and P. Maitre, J. Phys. Chem. A, 2008, 112, 12393–12400.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp07128k

---