Open Access Article
Open Access ArticleAb initio thermodynamic properties and their uncertainties for crystalline α-methanol†
Ctirad
Červinka
 *a and
Gregory J. O.
Beran
*a and
Gregory J. O.
Beran
 b
b
aDepartment of Physical Chemistry, University of Chemistry and Technology Prague, Technická 5, CZ-166 28 Prague 6, Czech Republic. E-mail: cervinkc@vscht.cz
bDepartment of Chemistry, University of California, Riverside, California 92521, USA
First published on 24th October 2017
Abstract
To investigate the performance of quasi-harmonic electronic structure methods for modeling molecular crystals at finite temperatures and pressures, thermodynamic properties are calculated for the low-temperature α polymorph of crystalline methanol. Both density functional theory (DFT) and ab initio wavefunction techniques up to coupled cluster theory with singles, doubles, and perturbative triples (CCSD(T)) are combined with the quasi-harmonic approximation to predict energies, structures, and properties. The accuracy, reliability, and uncertainties of the individual quantum-chemical methods are assessed via detailed comparison of calculated and experimental data on structural properties (density) and thermodynamic properties (isobaric heat capacity). Performance of individual methods is also studied in context of the hierarchy of the quantum-chemical methods. The results indicate that while some properties such as the sublimation enthalpy and thermal expansivity can be modeled fairly well, other properties such as the molar volume and isobaric heat capacities are harder to predict reliably. The errors among the energies, structures, and phonons are closely coupled, and most accurate predictions here appear to arise from fortuitous error compensation among the different contributions. This study highlights how sensitive molecular crystal property predictions can be to the underlying model approximations and the significant challenges inherent in first-principles predictions of solid state structures and thermochemistry.
1. Introduction
Molecular crystals are ubiquitous, and knowledge of their thermodynamic properties is indispensable in many technological applications. Performing calorimetric experiments is typically straightforward at ordinary pressures and most temperatures. However, thermodynamic data is much scarcer at high pressures due to the complexity of the experiments and the associated uncertainties. Therefore, a reliable computational methodology capable of generating thermodynamic data for molecular crystals, even at extreme conditions,1 would help to generate potentially useful data or to explain experimentally observed phenomena from the structural or molecular point of view. Most computational studies of molecular crystals neglect thermal contributions to thermochemical properties at finite temperatures and pressures, since calculating static cohesive electronic energies is much simpler than rigorously accounting for all relevant vibrational and thermal terms. However, predicting the most stable phase or polymorph under certain thermodynamic conditions can require sub-kJ mol−1 accuracy,2,3 in which case factors such as thermal expansion of the crystal and the temperature dependence of the isobaric heat capacity can play a key role. These effects can be captured only if the anharmonicity of the unit cell vibrations is included in the computational model.Dynamical strategies, based mainly on molecular dynamics, represent perhaps the best way of calculating temperature- and pressure-dependent thermodynamic properties, but in practice the accuracy of such approaches is frequently limited by the quality of the potential used to drive the dynamics. Due to a prohibitively high computational cost of ab initio molecular dynamics for most molecular crystal systems, such works generally use force-field-based classical molecular dynamics or metadynamics, although pioneering studies using ab initio molecular dynamics4,5 or path integral methods6 in this context have been published recently. Recent examples of molecular dynamics-based studies include investigations of polymorphism,7–9 solubility10 and nucleation.11
Another option for computing thermodynamic properties from first principles is to combine static electronic structure computations with a statistical-thermodynamic model. The quasi-harmonic approximation12–14 has emerged as a versatile and often reliable protocol, though some attempts have also been made to capture the anharmonicity more realistically.15,16 The quasi-harmonic approximation typically employs a standard harmonic description of the crystal vibrations at a given unit cell volume with a simple model for estimating how those vibrational frequencies vary with changes in the cell volume. These changes in the phonon frequencies incorporate some anharmonicity into the harmonic model. On the other hand, the simple quasi-harmonic model cannot necessarily describe systems with highly anharmonic vibrational modes or systems at high temperatures well, and the isotropic form of the quasi-harmonic model does not always work well for crystal structures exhibiting considerable anisotropy.
Several recent studies and reviews employ the quasi-harmonic approximation to calculate the thermodynamic properties of molecular crystals and emphasize the importance of the thermal terms for phenomena such as the thermal expansivity or polymorphism.2,3,17–19 The results of those studies indicate that the quasi-harmonic approximation sometimes enables calculation of temperature-dependent trends in properties such as molar volumes, sublimation enthalpies, or Gibbs energies for various molecular crystals with a semi-quantitative accuracy or better. This sometimes translates to sub-kJ mol−1 accuracy, which is important for polymorph stability ranking18–20 and predicting of phase change properties.3,12,21 Quasi-harmonic models are also capable of capturing anomalous behavior such as the negative thermal expansion of some systems2,4 or non-monotonic sublimation enthalpy trends,3,12 although several cases have been reported where the computational methodology fails to reproduce experimental data.22 Other limitations of the quasi-harmonic approximation arise from the high computational cost for large molecules/unit cells, flexible molecules, and other cases where such high accuracy cannot practically be achieved.17 To date, most quasi-harmonic calculations in molecular crystals have relied on DFT,18,19,22–26 or they have not examined the uncertainty and sensitivity of the calculated thermodynamic properties in detail.12,13 A thorough study investigating the computational uncertainty and sensitivity of wavefunction-based ab initio quasi-harmonic calculations for molecular crystals is still missing.
Calculations of thermodynamic properties depend strongly on the quality of the vibrational properties used, particularly the lattice vibrational mode frequencies. Several recent works investigate the calculations of spectral and vibrational properties of molecular crystals from first principles, aiming to estimate the uncertainty of such calculations.22,27–30 These studies suggest that dispersion-corrected DFT calculations are capable of predicting the vibrational frequencies semi-quantitatively. There are crystals for which the calculated and experimental data are in a good agreement, as well as cases for which the differences of experiment and theory range up to a few tens of cm−1.22 Moreover, harmonic DFT calculations with commonly-used density functionals systematically overestimate the intramolecular vibrational frequencies for most organic molecules, due to both the neglect of anharmonicity and errors inherent in the chosen functional/basis set.31–33 This means that dispersion-corrected DFT calculations of phonons can impart considerable uncertainty to the evaluation of the thermal contributions to thermodynamic properties. Therefore, the reliability of ab initio wavefunction-based phonon calculations and practical implementations for them need to be examined further.
In this work, we investigate the low-temperature crystalline polymorph of methanol, which is commonly referred to as α-methanol, in detail. The orthorhombic α-methanol crystal structure (space group P212121, Z = 4, Fig. 1)34 is fully ordered and stable at low temperatures below 157.34 K,35 and up to medium pressures roughly below 3.5 GPa.36 For this test case of α-methanol crystal, we compare the performance of dispersion-corrected DFT and more sophisticated ab initio wavefunction methods up to coupled cluster singles, doubles and perturbative triples (CCSD(T)). Properties such as molar volume (Vm) and isobaric heat capacities (Cp) are calculated as functions of both temperature and pressure. We examine the interplay among the unit cell energy model, its geometry optimization, and phonons, and we quantify the sensitivity of predicted structural and thermodynamic properties to errors in the models. The results highlight the challenges in predicting molecular crystal properties quantitatively from first principles.
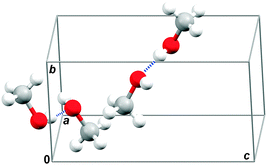 | ||
| Fig. 1 Unit cell structure of orthorhombic α-methanol with marked two antiparallel hydrogen bond chains passing through a unit cell. | ||
2. Computational methods
The electronic structure and energy of the unit cells and related properties were calculated in parallel within the periodic DFT-D3 framework37 as implemented in VASP (version 5.4.1),38 and the hybrid many-body interaction (HMBI) model39 using Molpro (2012.1)40 for ab initio calculations and Tinker (6.2)41 for Amoeba force-field42 calculations. All calculations initiated from the experimental unit cell structure and atomic coordinates, reference code METHOL04 from the Cambridge Crystal Structure Database.43 Both atomic positions and unit cell vectors were optimized subject to space group symmetry constraints. Having found the unit cell structure corresponding to a minimum on the energy hypersurface, the electronic energies of the optimized unit cells [Eel(V)] were calculated as a function of volume, usually for 15 discrete volume points around the energy minimum.14,22 The specific manner in which the volume expansion occurs differs depending on the software package used. In VASP, the volumes were scaled by a given factor and then the system was relaxed subject to a fixed total unit cell volume, which allows relaxation of the individual lattice constants. Data produced from these VASP DFT geometries are labeled with a dagger (†). Fixed volume optimizations with variable lattice constants have not been implemented in HMBI. Instead, two different strategies were employed. For most of the calculations, the cohesive energy curves Eel(V) were mapped out by relaxing the crystal structures under fixed external pressure (circle-labeled data sets, ˙), applying positive pressures for compression and negative pressures for expansion. For comparison purposes, calculations which scale the lattice constants isotropically and hold them fixed while the atomic positions were relaxed were also considered (star-labeled data sets, *). Allowing the unit cell dimensions to vary independently (instead of simply scaling the lattice parameters) when determining the electronic cohesive energy incorporates some anisotropy into the quasi-harmonic model.2.1 Periodic DFT calculations
Electronic structure of the unit cells was calculated using the projector-augmented wave (PAW)44 formalism, PBE functional45 and the semiempirical DFT-D3 dispersion correction,37 including the Becke–Johnson dumping (BJ).46–48 A plane wave energy cutoff of 700 eV was used for the periodic DFT calculations, along with the so-called hard PAW potentials49 and the Monkhorst–Pack sampling of the k-space.50 Phonon properties were calculated for supercells (larger than 10 Å in all directions) created by replication of the optimized unit cells using a finite displacement method51 and the program Phonopy.52 The phonon density of states was calculated for each of five unit cell volumes, which enabled the construction of the Helmholtz vibrational energy [Avib(T,V)] as a function of both temperature and volume as needed by the quasi-harmonic approximation. Mode-specific Grüneisen parameters were evaluated from the five sets of frequencies to determine each vibrational frequency at an arbitrary volume. Separately, analytical Avib(V) forms were obtained by fitting the calculated Avib(V) values from the five discrete volume points to a linear function.142.2 HMBI calculations
The HMBI model39,53–56 represents the total energy of the crystal in terms of individual molecules (monomers) and their interactions with other monomers via the many-body expansion.57–63 The energies of monomers and spatially proximal dimers are computed via electronic structure theory, while long-range dimers and clusters consisting of larger numbers of molecules (many-body effects) are treated with a computationally inexpensive classical polarizable force field. In this work, the treatment of individual dimers (molecular pairs) was smoothly switched from quantum to classical over the intermolecular distance separation of 9 and 10 Å. Exploitation of space group symmetry reduces the number of fragments that need to be calculated significantly, further reducing the computation cost.64Ab initio calculations were performed using counterpoise correction65 and second-order Møller–Plesset perturbation theory (MP2) and CCSD(T)66 in the aug-cc-pVXZ correlation-consistent basis sets (abbreviated avxz below).67 Unit cell optimizations and calculations of the Γ-point vibrational frequencies were performed only at the MP2/avdz and MP2/avtz levels. In addition, single-point energies were evaluated at the MP2/avqz level, extrapolated complete basis set (cbs) limit MP2,68 and the CCSD(T)/avtz level using the MP2/avtz unit cell geometries. CCSD(T)/cbs energies were estimated using MP2/cbs, MP2/avtz and CCSD(T)/avtz energies.69 As with the DFT calculations, phonon frequencies were evaluated at five different unit cell volumes to enable evaluation of mode-specific Grüneisen parameters and the Helmholtz vibrational energy.
2.3 Quasi-harmonic approximation
Summation of Eel(V) with Avib(T,V)14 yields total Helmholtz energy profiles [Acr(T,V)] for the unit cell.14 Analytic volume-dependent Helmholtz energy profiles were subsequently obtained by fitting Acr(T,V) to the Murnaghan equation of state70 separately for each temperature. The molar volume is found by differentiating the fitted Helmholtz energy Acr(T,V) with respect to volume at constant temperature and solving the standard thermodynamic relationship for V at the desired temperature and pressure: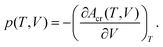 | (1) |
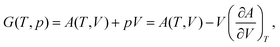 | (2) |
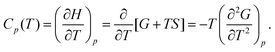 | (3) |
3. Results and discussion
The first two sections describe the prediction of the basic ingredients for the quasi-harmonic approximation: the energy–volume curves and the phonon frequencies. The subsequent sections use these properties to predict thermodynamic observables—the sublimation enthalpy, the molar volume, and the isobaric heat capacity—that are compared against experiment.3.1 Electronic energy–volume curves
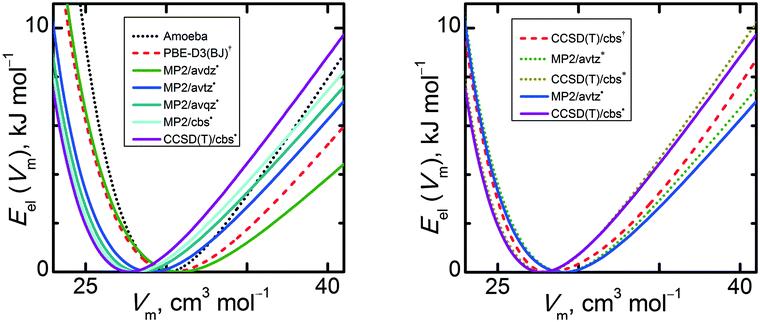
Optimization of the unit cells retains the experimental crystal packing of the methanol molecules, as can be seen in the structure overlays (Fig. S1, ESI†) and tabulated coordinates (Table S1, ESI†). Fig. 2 compares the electronic cohesive energies for α-methanol as functions of unit cell volume. The Eel(V) curve calculated solely with the classical Amoeba force field differs considerably from those predicted with electronic structure methods. It exhibits the steepest expansion branch, while its compression branch is less steep than expected. The shapes of the HMBI Eel(V) curves obtained using MP2 or CCSD(T) are qualitatively similar to one another. However, several important details should be noted as they can considerably affect the final thermodynamic properties. The MP2/avdz˙ Eel(V) curves from fixed-pressure optimizations are very close to the constant-volume optimized PBE-D3(BJ)† ones. Increasing the basis set from avdz to the cbs limit decreases the optimal volume by 9% (or by 12% if using the fully isotropic HMBI model). Similar basis set behavior is observed in other crystals such as carbon dioxide and ice.2,12 When counterpoise-corrections are employed (as they are here), larger basis sets typically lead to stronger intermolecular binding, which translates to smaller unit cell volumes. For a given basis set, switching from MP2 to CCSD(T) reduces the optimal volume of Eel(V) by 1.5%. If one shifts the various Eel(V) curves laterally such that they share a common minimum volume, it can be seen that increasing the basis set/level of theory also leads to slightly steeper compression and expansion branches about the minimum. Compared to MP2/avdz˙, the slope of the CCSD(T)/cbs˙ Eel(V) curve is 1.9 times larger in the compression branch and 1.6 times larger in the expansion branch.Fig. 2 also contains valuable information about the dependence of the Eel(V) curve shape on the source of the optimized unit cell geometry. The HMBI MP2/avtz curves obtained using isotropic (*) and anisotropic (˙) geometries are similar, with the anisotropic curve exhibiting a slightly softer expansion slope (by 6%) due to the additional unit cell relaxation that model allows. The differences between the isotropic and anisotropic Eel(V) curves is even smaller at the CCSD(T)/cbs level, with slopes differing by only 5%. As will be discussed in Section 3.4, the experimentally observed thermal expansion of α-methanol is only moderately anisotropic, so it is not too surprising that the difference between these two modeling approaches on Eel(V) is small.
In contrast, performing CCSD(T)/cbs single-point energies on the periodic PBE-D3(BJ) geometries (labeled CCSD(T)/cbs†) yields appreciably different energy curves and minima than the other two CCSD(T)/cbs (˙ and *) data sets. Using the PBE-D3(BJ) geometries shifts the CCSD(T) minimum to larger volume, makes the compression branch steeper, and alters the expansion branch such that the energy well is flatter near the minimum but steeper for larger expansions. Visually, the CCSD(T)/cbs† curve on the PBE-D3(BJ) geometry roughly mimics the average of the PBE-D3(BJ)† curve and the CCSD(T)/cbs˙ one. This shape for Eel(V) means that calculations based on the DFT-optimized unit cell geometries will produce larger molar volumes than those using the MP2-optimized unit cells.
The contrast between the results obtained from the MP2 and DFT geometry optimizations raises the question of what the CCSD(T)-optimized Eel(V) curve would look like if it were practical to compute. Some insight can be gained by examining the performance of PBE-D3(BJ) and MP2 on the methanol dimer from the S66x8 test set. Comparing against complete-basis-set CCSD(T) benchmarks, both MP2 and PBE-D3(BJ) overbind the dimer, but the overbinding is larger with DFT (root-mean-square error 0.7 kJ mol−1 for MP2/cbs, 0.9 kJ mol−1 for PBE-D3(BJ)/avqz, and 1.5 kJ mol−1 for PBE-D3(BJ)/PAW over the eight intermolecular separations; see Table S2, ESI†). Notably, the PBE-D3(BJ) interaction energy weakens much more slowly as one moves away from equilibrium toward either shorter or longer intermolecular separations. This erroneously flatter energy basin around the dimer equilibrium geometry contributes to the softer compression and expansion branches seen in the crystal.
Further insight can be found in the predicted lattice energies, calculated for the optimized geometries obtained by minimizing the electronic energy only, which are summarized in Table 1. In the small aug-cc-pVDZ basis set, the MP2 lattice energy (in absolute value) is 45.4 kJ mol−1, and it increases to 52.9 kJ mol−1 at the cbs limit. CCSD(T)/cbs increases it further, to 54.7 kJ mol−1. This contrasts the S66x8 dimer geometry, for which the CCSD(T)/cbs interaction energies are always weaker than the MP2/cbs ones (a reminder that analysis of dimer interactions alone has limitations in the context of the crystal71). Regardless, PBE-D3(BJ) binds even stronger, at 57.4 kJ mol−1, while CCSD(T)/cbs† on those DFT geometries binds more weakly at 51.5 kJ mol−1. The same holds true across the entire expansion and compression curves—the CCSD(T)/cbs energies are more strongly bound for the MP2 geometries than for the PBE-D3(BJ) ones. So while actual CCSD(T)/cbs energy optimizations are computationally impractical, this data suggests that the MP2/avtz optimized structures are closer to the optimal CCSD(T) structures than the PBE-D3(BJ) geometries, though it is unclear if that also translates to the MP2 geometries producing a more reliable Eel(V) curvature.
| Level of theory | E coh | ΔZPVEsubEa | ΔsubHa | E coh | ΔZPVEsubEb | ΔsubHb |
|---|---|---|---|---|---|---|
| a Values calculated for the unit cell geometries obtained by optimization of electronic energy. b Values calculated for the unit cell volumes obtained by the quasi-anisotropic quasi-harmonic model. | ||||||
| MP2/avdz˙ | −45.44 | −6.72 | 38.72 | −45.13 | −6.31 | 38.82 |
| MP2/avtz˙ | −50.00 | −6.77 | 43.23 | −49.62 | −6.29 | 43.33 |
| MP2/avqz˙ | −51.68 | — | 44.82 | −51.34 | −6.47 | 44.87 |
| MP2/cbs˙ | −52.93 | — | 46.16 | −52.61 | −6.60 | 46.01 |
| CCSD(T)/avtz˙ | −51.77 | — | 45.00 | −51.47 | −6.46 | 45.02 |
| CCSD(T)/cbs˙ | −54.63 | — | 47.86 | −54.37 | −6.77 | 47.59 |
| PBE-D3(BJ)† | −57.42 | −6.96 | 50.46 | −57.01 | −6.65 | 50.36 |
| CCSD(T)/cbs† | −50.21 | — | 43.25 | −49.80 | −6.83 | 42.97 |
| Experiment3 | — | — | 45.7 | — | — | 45.7 |
Based on these Eel(V) curves, it can be concluded that MP2 and CCSD(T) yield smaller equilibrium unit cell volumes, predict less thermal expansion will occur (due to the steeper expansion branch), and exhibit lower compressibility for α-methanol crystals compared to the DFT calculations here.
3.2 Vibrational frequencies
The temperature dependence of properties in quasi-harmonic crystalline solids arises through the phonon contributions. Fundamental vibrational frequencies of α-methanol were calculated using both many body expansion (HMBI coupled with MP2) and periodic DFT (PBE-D3(BJ)) calculations. This section compares results obtained from these calculations against each other and experimental data. Vibrational frequencies calculated in ref. 22 using periodic optPBE-vdW72 calculations are also included for comparison.Several experimental low-temperature spectroscopic studies for α-methanol can be found in the literature.73–81 Most of them agree on the vibrational assignment and fundamental frequencies of the intramolecular modes within the reported experimental uncertainty – a few cm−1 for sharp strong peaks and up to 20 cm−1 for weak broad peaks. The main exceptions are the frequencies of the internal methyl rotation modes, which exhibit scatter on the order of several tens of cm−1. Several studies focus on the intermolecular (lattice) vibrational modes,76,82,83 though, a complete experimental assignment of individual modes has not been performed to our knowledge.
Fig. 3 shows the relative percentage deviations between the calculated intramolecular frequencies and the experimental data from the most complete work.74 Both DFT functionals yield more accurate O–H and C–H stretching mode frequencies (deviations below 5%) than MP2 (deviations ranging from 5 to 10%). Using the larger avtz basis set instead of avdz for the MP2 calculations leads to a slight improvement for the stretching modes (deviation decreases by 2 percentage points). All methods overestimate the frequencies of the stretching modes, except DFT results for O–H stretches. Predicted harmonic frequencies are often larger than the anharmonic experimental values. Similar trends can be observed for the intramolecular deformation and C–O stretching modes for which all deviations are lower than 5% in absolute value. Concerning the internal methyl rotation modes, both DFT functionals significantly overestimate the frequencies (PBE-D3(BJ) by 25%), while MP2 exhibits smaller deviations (5–10%). However, shifting to the larger avtz basis set increases the MP2 errors. Detailed comparison of calculated and experimental vibrational frequencies can be found in Table S3 in the ESI.†
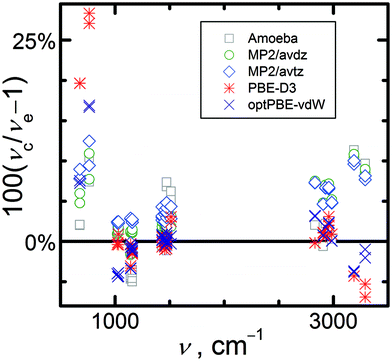 | ||
| Fig. 3 Relative percentage deviations of calculated (νc) fundamental intramolecular vibrational frequencies calculated at selected levels of theory from experimental frequencies (νe). | ||
To enable investigations of the sensitivity of the computational model on the uncertainty of vibrational frequencies in Sections 3.4 and 3.5, we evaluated empirical scale factors for the MP2/avtz intramolecular frequency set. The intramolecular frequencies were scaled separately for the low (below 2000 cm−1) and high (above 2000 cm−1) wavelength regions, as is common when computing ideal gas properties.31,84 The multiplicative scale factors are intended to shift the calculated harmonic frequencies to be in closer agreement with the anharmonic experimental data. By comparing the calculated and experimental74 frequencies of the intramolecular vibrational modes and averaging over all modes of the unit cell, scale factors of 0.9682 below 2000 cm−1 and 0.9302 above 2000 cm−1 were obtained for this crystal. Such values lie within the typical range for MP2 or DFT calculations of intramolecular fundamental frequencies.31–33,84 Scaling reduces the mean and absolute percentage deviations of the calculated intramolecular frequencies versus experiment from 4.8% and 5.8% to 0.1% and 2.5%, respectively. These intramolecular vibrational frequency scaling parameters will be used further in Sections 3.4 and 3.5.
Next, consider the intermolecular vibrational modes. Fig. 4 illustrates the agreement of the calculated fundamental frequencies of the lattice modes of α-methanol with experimental data measured in ref. 82 and further analyzed in ref. 76. Again, data from ref. 22 calculated using the optPBE-vdW functional72 are included for comparison. In general, the calculated frequencies of the lattice modes exhibit percentage deviations that are one order of magnitude higher than the intramolecular modes, which could be expected in context of the results from ref. 22. For nearly all the lattice modes, pure Amoeba calculations yield significantly higher frequencies than the quantum chemical calculations do. Among the electronic structure methods, the periodic PBE-D3(BJ) calculations give the highest frequency values. Methanol crystals contain strong hydrogen bond chains whose vibrational modes occur at relatively high wavelengths (above 300 cm−1). Their values are overestimated by all of the computational methods used by up to 25%. Librational lattice modes are expected to be found in the middle wavelength region. The frequencies of these modes are mostly underestimated by the quantum chemical methods used here. Translational lattice modes should be found in the lowest wavelength region, and most of the predicted frequencies in this region are overestimated by up to 40%, while others are underestimated by almost 80%. Together, prevailing overestimation of the low-frequency lattice modes translates to considerable underestimation of calculated thermodynamic properties such as entropy or heat capacity for this crystal with either PBE-D3(BJ) or MP2-based vibrational properties.
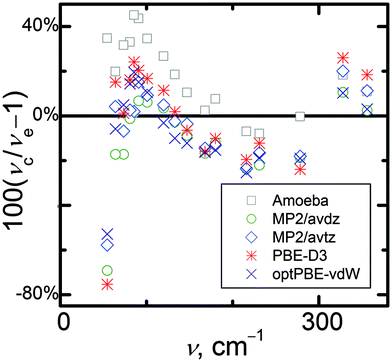 | ||
| Fig. 4 Relative percentage deviations of calculated (νc) fundamental lattice vibrational frequencies calculated at selected levels of theory from experimental frequencies (νe). | ||
One might note that the experimental vibrational frequencies were obtained at 20 K,82 while the predicted phonons were obtained for the unit cell structure corresponding to the electronic energy minimum. The latter neglects expansion due to zero-point vibrational motion and the small amount of thermal expansion between 0 and 20 K, which can lead to misleading comparisons.27 To estimate the thermal and vibrational effects on the lattice-mode frequencies, the frequencies were reevaluated using the calculated MP2 or PBE-D3(BJ) quasi-harmonic unit cell volumes at 20 K and Grüneisen parameters for the individual modes. In this way, temperature-dependent quasi-harmonic frequencies of the lattice modes can be approximated. The resulting frequency values are listed in Table S4 (ESI†). With this correction, the mean absolute percentage deviations of the lattice-mode frequencies changed from 13% to 16% and from 19% to 14% for HMBI MP2/avtz* and periodic PBE-D3(BJ)† frequencies, respectively. So while such expansion effects do impact the comparison between theory and experiment, they do not appear to be the principal source of error in the predicted frequencies.
Next, these calculated phonon properties were employed to compute vibrational Helmholtz energy profiles for α-methanol at various temperatures as a function of unit cell volume and interpolated via linear functions. Fig. 5 compares these Avib(V) profiles at 0 K. Clearly, pure Amoeba calculations yield an Avib(V) line whose slope differs considerably from the other models. In contrast, the MP2 and PBE-D3(BJ) Avib(V) lines differ primarily in their absolute values (by about 6 kJ mol−1), rather than in their slopes. The PBE-D3(BJ)†Avib(V) lines exhibit slopes that are 8% steeper than the MP2/avdz* ones and 2% steeper than the MP2/avtz* ones. Including the anisotropy in MP2 HMBI calculations changes the slopes of Avib(V) by 9%, making them less steep for MP2/avdz˙ and more steep for MP2/avtz˙. The basis set size clearly impacts the vibrational properties appreciably, which will translate to observable differences in phenomena such as the thermal expansion. Unlike the slopes, absolute values of Avib(V) do not impact thermodynamic properties such as the density or heat capacity of a single phase. However, absolute values of Avib(V) become extremely important when comparing properties between different phases, e.g. Gibbs energies and related phase equilibria.
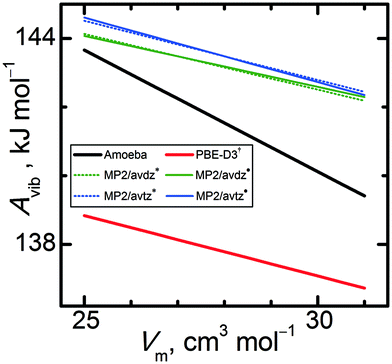 | ||
| Fig. 5 Vibrational Helmholtz energies of α-methanol at 0 K as a function of unit cell volume, as by selected quantum chemical levels of theory. | ||
3.3 Sublimation enthalpy
Now consider the sublimation enthalpy at 0 K. The differences in the zero-point vibrational energy (ΔZPVEsubE) between the crystal and ideal gas phase were calculated within the harmonic approximation by combining the phonon results obtained using the HMBI MP2/avdz, MP2/avtz and PAW/PBE-D3(BJ) levels of theory with the fundamental vibrational frequencies of an isolated gas-phase methanol molecule whose geometry was optimized at the same levels of theory. No scaling factors were applied to the calculated vibrational frequencies for this purpose. Sublimation energies (ΔsubH) were evaluated at 0 K coupling the cohesive energies and ΔZPVEsubE terms, both evaluated either using a “static” model based on the geometries corresponding to the minimum of the electronic energy (described in Section 3.1), or a quasi-harmonic model based on the unit cell volumes corresponding to the minima of the Helmholtz energy profiles at 0 K and zero pressure (using the quasi-anisotropic MP2/avtz˙ phonon data). Table 1 lists the respective cohesive energies, ΔZPVEsubE terms and ΔsubH values. It compares them against the reference experimental value of 45.7 ± 0.3 kJ mol−1, which was extrapolated to 0 K and whose uncertainty was critically evaluated in ref. 3. Both the static and quasi-harmonic models yield comparable ΔZPVEsubE values. The ΔsubH values exhibit larger scatter due to variations in the underlying cohesive energies. Smaller basis set HMBI MP2 calculations underestimate ΔsubH, and increasing the basis set size in the MP2 calculations converges the calculated ΔsubH towards the experimental value. The static MP2/cbs ΔsubH value matches experiment extremely well, overestimating it by only 0.5 kJ mol−1, which is comparable to the experimental uncertainty. However, switching from MP2 to CCSD(T) increases the α-methanol cohesive energy further, and the CCSD(T)/cbs ΔsubH value is 2.2 kJ mol−1 larger than experiment. On the other hand, the CCSD(T)/cbs† ΔsubH value from the DFT geometry underestimates the experimental value by 2.4 kJ mol−1. In contrast, PBE-D3(BJ)† overestimates the sublimation enthalpy by an even larger 5 kJ mol−1.Comparing the static and quasi-harmonic ΔsubH results, one observes that the larger unit cell volume of the quasi-harmonic model (due to expansion from zero-point vibrational energy) slightly destabilizes the cohesive energy of the crystal (by 0.2–0.4 kJ mol−1 depending on the curvature of given Eel(V) curves). However, the larger volume also decreases the ZPVE in the crystal, leading to a less negative ΔZPVEsubE term. Thus, the two contributions counteract one another and the static and quasi-harmonic models yield ΔsubH values for α-methanol that differ by less than 0.3 kJ mol−1 at 0 K.
3.4 Molar volume
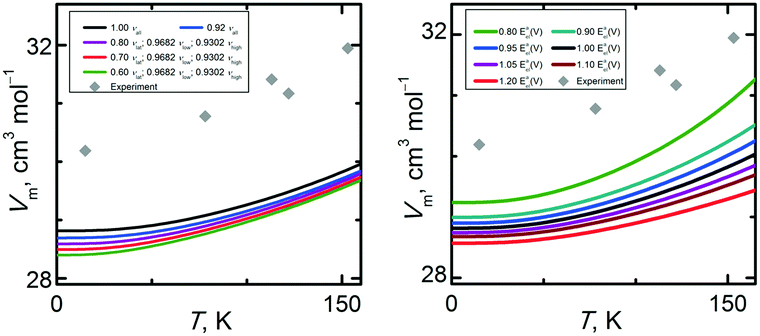
Directly measurable thermodynamic properties such as density or isobaric heat capacity can be obtained from the calculated Eel(V) and Avib(V) curves. The appropriateness of the computational model for calculation of the structural properties can be assessed by comparing the calculated and experimental molar volumes at the standard pressure. The quasi-harmonic approximation enables quantification of the thermal expansion, meaning that the temperature-dependence of the molar volume can be discussed as well.To our knowledge, only five references report information on experimental molar volumes at standard pressure.34,85–88 In Fig. 6, it can be seen that these points exhibit a non-negligible scatter which obscures the actual extent of thermal expansion and hinders drawing strong conclusions about the accuracy of the calculated thermal expansivity. Qualitatively, the calculated Vm(T) trends are generally in reasonable agreement with the experimental data. Fig. 6 illustrates the performance of the same hierarchy of quantum chemistry levels of theory for predicting the molar volume. The trends in the molar volume of α-methanol mimic those seen above for the Eel(V) curves. Switching from DFT or small-basis MP2 to larger basis sets and/or CCSD(T) yields smaller equilibrium molar volumes. Compared to experimental data near 0 K, the MP2/avdz˙ molar volume is overestimated by 8%, while the CCSD(T)/cbs˙ molar volume is underestimated by 3.9% (by 4.3% for the fully isotropic CCSD(T)/cbs* model). Increasing the basis set systematically decreases the molar volume, as seen previously.2,12 At the complete basis set limit, MP2 already underestimates the experimental molar volume, and switching to CCSD(T) reduces the molar volume further in this system.
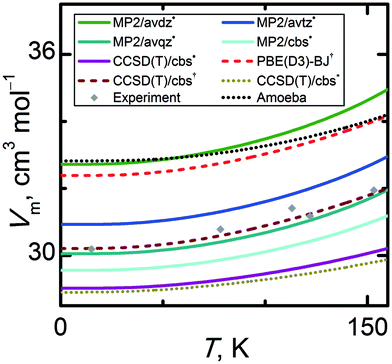 | ||
| Fig. 6 Comparison of temperature-dependent molar volumes of α-methanol at standard pressure calculated by various quantum chemical levels of theory. | ||
The closest agreement between theory and experiment in the low temperature region is observed for MP2/avqz˙ and CCSD(T)/cbs†, which differ from the experimental data by less than 0.5% and 0.2%, respectively. Of course, the good agreement with experiment for these two particular levels of theory represents a fortuitous compensation of errors: MP2/avqz˙ uses a large but still incomplete basis, while the CCSD(T)/cbs† result is based on a geometry that is further from the true CCSD(T)/cbs minimum (as measured by energy and discussed in Section 3.1). Including the anisotropy in the computational model (through unit cell geometry optimizations) increases the molar volume by 0.4% at the vicinity of 0 K and by 1.7% around the α–β phase transition temperature 157.34 K.35 Though these changes are small, the rate of thermal expansion from the anisotropic model appears slightly closer to the experimentally observed result.
Since the MP2/avtz, MP2/avqz, MP2/cbs, and CCSD(T)/cbs data sets all utilize the MP2/avtz phonons, the differences among the molar volumes obtained at these levels of theory arise solely from the differences in the Eel(V) curves. The slope of the CCSD(T)/cbs˙ Vm(T) curve for α-methanol is 36% less steep than those of the MP2/avtz˙ curve (47% less steep for CCSD(T)/cbs*), as a result of a steeper (by 22% and 29%) expansion branches of the Eel(V) curve, respectively. Clearly, a compensation of errors in the calculated Eel(V) and Avib(V) functions can result in a very good agreement of theory and experiment, e.g. too a steep Eel(V) can be compensated for by a slower decline of Avib(V) or vice versa. This phenomenon can also be observed when comparing the Amoeba and MP2/avdz˙ data sets in Fig. 2, 5 and 6. Despite predicting much steeper potential energy curves, Amoeba yields a molar volume that is comparable to the MP2/avdz one. Closer inspection reveals that the MP2/avtz level of theory best reproduces the experimental slope of the Vm(T) curve. Higher levels of theory damp the thermal expansivity and yield less realistic Vm(T) slopes. Notably, the Vm(T) slope of the CCSD(T)/cbs*, CCSD(T)/cbs˙ and CCSD(T)/cbs† data sets are 49%, 38% and 10% underestimated when compared to experimental data, respectively.
Table 2 summarizes the experimental and calculated lattice parameters for the temperatures of the experimental determination. Experimental unit cell parameters of α-methanol at 15 K and 122 K were determined in two literature studies.34,88 Note that both this study and ref. 34 align the hydrogen bonds along cell vector a, while ref. 88 aligns them along cell vector b. The experimental data suggests that α-methanol undergoes moderately anisotropic thermal expansion between 15 K and 122 K, expanding 0.1%, 1.1%, and 2.0% in the a, b, and c directions, respectively. The anisotropy reflects the fact that the thermal expansion preferentially occurs in directions orthogonal to the hydrogen bonds (i.e. along the b and c vectors).
| Data set | T (K) | a | b | c | V |
|---|---|---|---|---|---|
| a Ref. 88 uses a different system of axes where a and b vectors are interchanged. b Fully isotropic expansion quasi-harmonic model used (star labeled in text). c Anisotropy of the electronic cohesive energy included in the quasi-harmonic model (circle labeled in text). | |||||
| Experiment88 | 15 | 4.6411a | 4.8728a | 8.8671 | 200.53 |
| PAW/PBE-D3(BJ) | 4.45 | 5.21 | 9.26 | 215.13 | |
| PAW/optPBE-vdW22 | 4.60 | 5.15 | 9.33 | 221.23 | |
| HMBI MP2/avtzb | 4.58 | 4.91 | 9.06 | 203.68 | |
| HMBI MP2/avtzc | 4.55 | 4.95 | 9.12 | 205.45 | |
| Experiment34 | 122 | 4.6469 | 4.9285 | 9.0403 | 207.04 |
| PAW/PBE-D3(BJ) | 4.47 | 5.33 | 9.30 | 221.73 | |
| PAW/optPBE-vdW22 | 4.61 | 5.22 | 9.43 | 227.29 | |
| HMBI MP2/avtzb | 4.64 | 4.97 | 9.17 | 211.39 | |
| HMBI MP2/avtzc | 4.56 | 5.09 | 9.17 | 212.55 | |
Obviously, the fully isotropic model employed here (star labeled data sets from HMBI calculations on isotropic MP2/avtz geometries), fails to capture the anisotropic expansion, and it predicts comparable elongation of all three unit cell vectors during the thermal expansion (see Table 2). In contrast, both quasi-anisotropic models (dagger and circle labeled data sets) correctly predict larger expansion along the b and c vectors and less expansion along the a vector. However, both the HMBI and DFT quasi-anisotropic models incorrectly predict larger expansion along the b vector instead of the c vector.
Although it neglects the anisotropic expansion, the isotropic MP2/avtz* model fortuitously predicts the overall unit cell volume the most accurately. The quasi-anisotropic MP2/avtz˙ model produces flatter Eel(V) and steeper Avib(V) curves, which translates to larger unit cell volumes than those from MP2/avtz*. On the other hand, counterpoise-corrected MP2/avtz typically overestimates unit cell volumes due to basis set incompleteness2,12 (see Fig. 6). Using a larger basis set would decrease the volume, moving it in the direction of improved agreement with experiment. Of course, the molar volumes computed with larger-basis MP2 and CCSD(T) single points hint that the molar volume may well become too small if full optimizations were performed at higher levels of theory.
While the thermal expansivity derives from the expansion branch of the Eel(V) curve, the compressibility of the crystal involves both branches of Eel(V). Therefore, the comparison of a calculated Vm(p) trend at a given temperature with experimental data should provide more insight into the consistency and accuracy of the theoretical model. Fig. 7 illustrates a comparison of Vm(p) trends for the various computational models against experimental data from ref. 86 at 153.2 K. Unfortunately, experimental thermodynamic data in the high-pressure region are rather scarce, and the comparison has to be limited to the sub GPa range. In Fig. 7, all calculated Vm(p) curves qualitatively capture the convex decline of the volume with increasing pressure. Again, improving the basis set and correlation treatment leads to lower molar volumes. MP2/avdz˙ yields molar volumes overestimated by 6.0%, while CCSD(T)/cbs* and CCSD(T)/cbs˙ underestimate the volume by 6.2% and 5.7%, respectively. The best agreement in terms of slopes of the calculated Vm(p) curves is achieved for the quasi-anisotropic CCSD(T)/cbs† and CCSD(T)/cbs˙ data sets, with slopes differing from the experimental data by only 10% and 4% on average, respectively. The isotropic CCSD(T)/cbs* data set underestimates the slope by 16% relative to the experimental data. At higher pressures around 1 GPa, both CCSD(T)/cbs* and CCSD(T)/cbs˙ predict similar Vm(p) curves, indicating that the anisotropy plays a smaller role in the compression of α-methanol than it does in the thermal expansion. Fig. S2 (ESI†) illustrates calculated molar volumes at selected temperatures in the high pressure region. Because the curvature of the isotropic Eel(V) curve is flatter, lower molar volumes are obtained with CCSD(T)/cbs* for the compression regime at pressures above 2 GPa at 0 K (this pressure threshold increases with rising temperature).
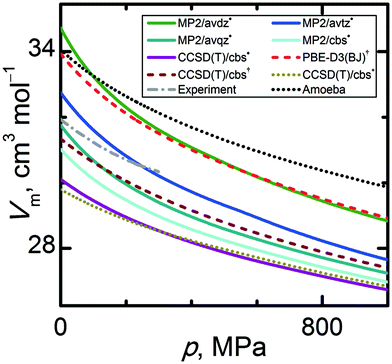 | ||
| Fig. 7 Comparison of pressure-dependent molar volumes of α-methanol at 153.2 K calculated by various quantum chemical levels of theory. | ||
Given that errors exist in both the predicted Eel(V) curves and quasi-harmonic phonon frequencies, it is interesting to investigate how uncertainty in those fundamental quantities translates into uncertainties in the predicted molar volumes and thermal expansivity. To study the sensitivity of these cell volume properties to the uncertainty in the phonon frequencies, we used the CCSD(T)/cbs* data set and scaled the MP2/avtz* fundamental vibrational frequencies. Two cases were considered: (1) scaling all modes by 0.92, or (2) scaling lattice modes with values ranging from 0.8 to 0.6, low-frequency intramolecular modes (below 2000 cm−1) by 0.9682, and high-frequency intramolecular modes (above 2000 cm−1) by 0.9302 (the scaling parameters obtained in Section 3.2). These multiple scale factors were developed in the same way as in ref. 31: by comparing calculated and experimental fundamental vibrational frequencies for individual modes and aiming to bring the scaled calculated frequencies into as close agreement with their experimental counterparts as possible. As expected, down-scaling the phonon frequencies leads to a steeper decline of the Avib(V) functions, which translates to decreased molar volumes that underestimate the experimental values even more. In other words, scaling the phonon frequencies down shifts the molar volumes in the wrong direction, even though the intramolecular harmonic frequencies of are obviously overestimated relative to the anharmonic experimental values and scale factors lower than unity are appropriate. On the other hand, frequency scaling does partially correct the slopes of the Vm(T) curves relative to experiment. Without a complete experimental assignment of the lattice vibrational modes, it is difficult to assess the appropriate scaling of those modes more carefully. Illustration of how the frequency scaling affects the calculated molar volumes is given in Fig. 8 (left column). Notably, the frequency scalings considered here affect the molar volumes by less than 2%, which is considerably less than the difference between theory and experiment.
An analogous procedure was performed to study the sensitivity of molar volumes on the steepness of the Eel(V) curve. A single scale factor ranging from 0.8 to 1.2 was used to scale the whole Eel(V) curve, adjusting the slopes of its branches without altering its shape. Fig. 8 (right column) shows that modifying the steepness of the Eel(V) curve affects the molar volume more significantly than frequency scaling, namely up to 5%, which is already comparable with the percentage deviation of the CCSD(T)/cbs* molar volume results from experimental data. As expected, making the Eel(V) curve less steep amplifies the thermal expansivity of the crystal and vice versa. Making the Eel(V) curve 20% less steep almost fully corrects the slope of the Vm(T) curves to the experimental value although it does not correct the volume offset at zero temperature. Making the energy well even flatter will result in unnaturally steep V(T) curves pointing to strongly overestimated thermal expansivity. It means that the correct volume trends cannot be simply reached by scaling the energy well only, since the volume is affected by a complex interplay of both the shape/position of the electronic energy well and the phonon properties.
Another potential source of computational uncertainty lies in the fitting procedure which is used to interpolate the discrete points of the Helmholtz energy profiles to obtain Helmholtz energy as a function of volume in an analytical form. Recent works14,22 have used the simple model Murnaghan equation70 which, however, was not developed or optimized for molecular crystals. Therefore, imperfect fits can occur for more complex shapes of Eel(V) curves, and those fitting errors would impact the Helmholtz energy. This can subsequently introduce considerable uncertainty into the resulting thermodynamic properties. It should be noted that even small root-mean-square errors (RMSE) ranging in the order of tenths of kJ mol−1 can be problematic when sub-kJ mol−1 accuracy is required. For details on a comparison of selected functional forms used for fitting of total Helmholtz energy, such as Birch–Murnaghan equation, empirical equations or splines, see Fig. S3 and Table S5 in ESI.† The Vm(T) curves differ by a few percentage units depending on the functional forms used in the fit. Although splines can fit the Eel(V) data perfectly in terms of RMSE, their use cannot be recommended for this purpose because they usually do not smooth any numerical noise in the discrete energy points obtained from the quantum calculations. This noise can lead to sudden, artificial changes of trends or even peaks in the final thermodynamic properties. Such computational artifacts occur mostly in the vicinity of the nodal points where a transformation between two spline functions occurs.
To summarize, the quasi-harmonic calculations predict the rate of thermal expansion with decent accuracy, especially when quasi-anisotropic models are used for the energy–volume curves. However, predicting the actual molar volume is more difficult, with the nominally best models of theory underestimating it by several percent. Sensitivity analysis suggests that the shape of the Eel(V) curve has a larger impact on the thermal expansivity than the magnitudes of the phonon frequencies. However, simple scaling of either the energy–volume curve or the phonons does not bring the predicted molar volume curves into quantitative agreement with experiment.
3.5 Heat capacity
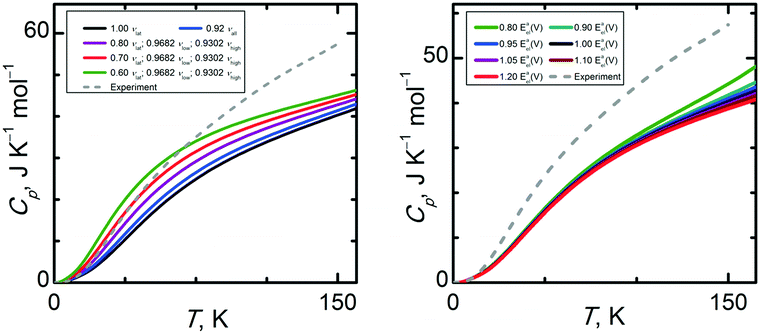
Structural properties of condensed phase systems (like molar volumes) are usually easier to predict theoretically than thermodynamic properties. This proves to be the case for α-methanol and its isobaric heat capacities. Experimental Cp(T) data were taken from ref. 35, which reports Cp uncertainties not exceeding 0.5 J K−1 mol−1. There are also older works89,90 reporting data on Cp which agree very well with ref. 35.Fig. 9 shows that CCSD(T)/cbs† calculations yield a Cp(T) trend being in the closest agreement to the experimental data. Still, the relative percentage deviation of this data set amounts to 12%, equivalent to 7 J K−1 mol−1 at 150 K. In case of the quasi-anisotropic HMBI based Cp(T) results, using larger basis sets and CCSD(T) instead of MP2 only worsens the agreement between theory and experiment. For example, MP2/avdz˙ and CCSD(T)/cbs˙ underestimate Cp(T) by 21% and 29% at higher temperatures, respectively (isotropic CCSD(T)/cbs* Cp(T) even by 32%). Such deviations largely exceed the tolerable uncertainty threshold for calculated Cp(T) for applications requiring sub-kJ mol−1 accuracy. The fact that all calculated Cp(T) are significantly underestimated suggests that the calculated vibrational frequencies, especially the lattice modes, are significantly overestimated by theory. To analyze the sensitivity of Cp(T) on the uncertainty of vibrational frequencies and the shape of the Eel(V) curve, the same procedure consisting in scaling the intermediate properties was performed as in the case of the molar volumes.
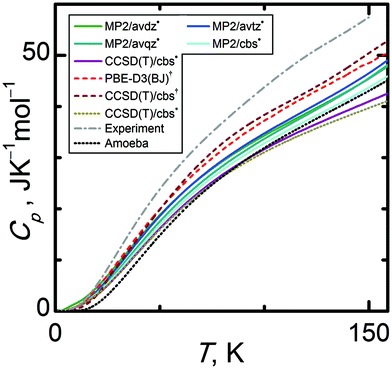 | ||
| Fig. 9 Comparison of isobaric heat capacities (Cp) of α-methanol at standard pressure calculated by various quantum chemical levels of theory. | ||
Fig. 10 (left column) reveals that heat capacities are significantly more sensitive to the uncertainty of the vibrational frequencies than the molar volumes were. By varying the scale factor used for the lattice modes, we found that an optimal value around 0.70 is capable of bringing the Cp(T) trend obtained at the CCSD(T)/cbs* level to close agreement with the experimental data in temperature region below 60 K. This result suggests a substantial computational uncertainty in the vibrational frequencies of the lattice modes of α-methanol. At higher temperatures, other uncertainty sources prevail since further lowering the scale factor below 0.70 does not improve the quality of the calculated Cp(T). Obviously, higher-frequency modes, especially methyl rotations, become important above 60 K. Thermal expansion also contributes more appreciably to the isobaric heat capacity at higher temperatures.
Sensitivity trends for Cp(T) are reversed compared to those for the molar volume, since Cp(T) depends much more on the uncertainty of the vibrational frequencies than the uncertainty of the Eel(V) curve. As can be seen in Fig. 10 (right column), the shape of the Eel(V) curve becomes relevant in the temperature region above 60 K. However, scaling the Eel(V) curve by a factor 0.80 causes a 10% change in Cp at 150 K, corresponding to 4 J K−1 mol−1. Fig. S4 (ESI†) illustrates calculated Cp at selected temperatures in the high pressure region.
Because CCSD(T)/cbs˙ is assumed to be the highest level of theory used in this work, its massive underestimation of Cp merits closer analysis. As Cp is significantly affected by both vibrational frequencies and the thermal expansivity, errors in both parameters accumulate to give a 30% underestimation of Cp. Anisotropic CCSD(T)/cbs˙ data on both Cp(T) and Vm(T) are in closer agreement with experiment than the corresponding isotropic CCSD(T)/cbs* data sets. The quasi-anisotropic model softens the overly steep CCSD(T)/cbs* expansion branch, improving the quality of the calculated thermal expansivity. Still, the CCSD(T)/cbs˙ Eel(V) curve is burdened with some uncertainty as it is constructed only using single point CCSD(T)/cbs calculations on MP2/avtz˙ geometries, not on CCSD(T)/cbs geometries. When combined with the errors in the MP2/avtz˙ phonon frequencies, the resulting CCSD(T)/cbs˙ Cp exhibits one of the largest deviations from the experimental data among all of the levels of theory employed here (larger than lower-level MP2 providing less steep Eel(V) curves). Using higher-level methods makes the Eel(V) well steeper and attenuates the already underestimated thermal expansion, causing the higher-level methods to yield Cp in worse agreement with experiment. In contrast, CCSD(T)/cbs† predicts Cp much better (percentage deviation more than halved related to CCSD(T)/cbs˙), possibly due to partial compensation of errors of the phonons and thermal expansivity. This result contradicts the methanol dimer benchmarks described earlier, where MP2 provided a much better description of both the binding energy and the shape of the potential energy well. In other words, it once again appears that error cancellation between the calculated lattice energy, unit cell volume, and phonons plays a significant role in the quality of the thermodynamic and structural predictions.
4. Conclusions
We calculated vibrational, structural and thermodynamic properties of α-methanol using wavefunction-based ab initio methods in the HMBI formalism and periodic DFT calculations, both coupled with the quasi-harmonic approximation. The results of this study provide a mixed picture. On the one hand, experimental properties such as the sublimation enthalpy at 0 K and the thermal expansivity are reproduced fairly well by the higher levels of theory. On the other hand, other properties prove more problematic to be predicted reliably. The intramolecular vibrational frequencies are often significantly overestimated, as one might expect from a harmonic vibrational model. The intramolecular modes can be corrected somewhat through frequency scaling. However, the errors in the lattice phonons are proportionally much larger and vary more in sign and magnitude, which is particularly troublesome given the large impact these modes have on many finite-temperature properties. Using MP2/avtz instead of DFT does not provide appreciable improvements in the predicted phonons for α-methanol. Although the models predict the rate of thermal expansion reasonably, the best calculations underestimate the unit cell volume appreciably, suggesting that the models overbind the crystal somewhat (which is also supported by the sublimation enthalpies). The isobaric heat capacity is substantially underestimated as well.Sensitivity analysis was performed to investigate how errors in the fundamental computed quantities affect the observed properties. We find that crystal phase densities are more sensitive to the shape of Eel(V) curve, while isobaric heat capacities depend more on the quality of the vibrational frequencies. The shapes of the Eel(V) curves do converge with increasing basis set/level of theory. The assumption of isotropic crystal expansion in the model, leading to artificially steep walls on the CCSD(T)/cbs* curve, can impact the resulting structural thermodynamic properties by attenuating the thermal expansion. This can be partially corrected by allowing the unit cell to expand anisotropically, though the quasi-anisotropic model used for the CCSD(T)/cbs˙ and CCSD(T)/cbs† data sets is not capable of capturing the anisotropic effects completely (because the phonons depend only on the cell volume, rather than the specific cell shape). Even though the quasi-anisotropic results are always in a closer agreement with experimental data than the isotropic data are, the magnitude of the computational errors observed here cannot be fully explained by the crystal anisotropy. Nevertheless, anisotropy affects both the cohesive energy and vibrational frequencies and is a non-negligible source of the computational uncertainty for the structural and thermodynamic properties for molecular crystals. A three-dimensional extension of the quasi-harmonic approximation which would allow a rigorous treatment of the anisotropic expansion would provide an interesting topic for future work.
For the heat capacities, uncertainties in the frequencies are particularly apparent at low temperatures (below 60 K for methanol). At higher temperatures, uncertainty in the thermal expansivity contributes appreciably to the errors in Cp as well. These issues cause an underestimation of the calculated isobaric heat capacities that reaches 30% for the CCSD(T)/cbs˙ level of theory, easily exceeding the acceptable levels of uncertainty for applications requiring sub-kJ mol−1 accuracy. Reducing the uncertainty in Cp would require simultaneously improving the quality of the vibrational frequencies and the thermal expansivity trends which are dominated by Eel(V) as well as accounting for the anisotropy of all such contributions properly.
One of the interesting observations here is how much compensation of errors among the different electronic energy, geometry, and phonon properties impacts the final results. Despite evidence that the CCSD(T) results based on the MP2 geometries are probably superior to those on the DFT geometries, properties such as the heat capacities predicted from the DFT geometries actually agree more closely with experiment. Ideally, one would compute all properties at the large-basis CCSD(T) limit, but of course that is computationally infeasible in practice. Employing single-point energies with the higher electronic structure methods did clearly improve the quality of the predicted sublimation energies and are probably worthwhile. In contrast, MP2 phonons did not appear to provide significant improvements over the DFT ones, so one might reduce the computational effort required by computing phonons with DFT (potentially on unit cells predicted with either DFT or MP2) instead of MP2. That said, the limited accuracy of the harmonic phonons from either method remains a significant issue. The fact that one can compute thermodynamic properties in molecular crystals at such high levels of theory represents how much theoretical progress has been made in recent years. Nevertheless, it is clear that additional theoretical advances are needed before crystal properties can consistently be predicted quantitatively at finite-temperature and pressure properties. The errors among energies, volumes, and frequencies are all closely coupled, and improving the treatment of the phonons and the crystal expansion could significantly impact all of the predicted properties.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
C. Č. acknowledges financial support from the Czech Science Foundation (GACR No. 17-03875S) and the Fulbright Commission. G. B. gratefully acknowledges financial support from the U.S. National Science Foundation (CHE-1665212) and supercomputer time from XSEDE (TG-CHE110064). Access to the computing and storage facilities owned by parties and projects contributing to the National Grid Infrastructure MetaCentrum, provided under the program “Projects of Large Infrastructure for Research, Development, and Innovations” (LM2010005) and the CERIT-SC under the program Centre CERIT Scientific Cloud, part of the Operational Program Research and Development for Innovations, Reg. no. CZ.1.05/3.2.00/08.0144 is highly appreciated.References
- B. Schatschneider, S. Monaco, A. Tkatchenko and J. J. Liang, J. Phys. Chem. A, 2013, 117, 8323–8331 CrossRef CAS PubMed.
- Y. N. Heit and G. J. O. Beran, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 514–529 CAS.
- C. Červinka and M. Fulem, J. Chem. Theory Comput., 2017, 13, 2840–2850 CrossRef PubMed.
- M. A. Salim, S. Y. Willow and S. Hirata, J. Chem. Phys., 2016, 144, 204503 CrossRef PubMed.
- S. Y. Willow, M. A. Salim, K. S. Kim and S. Hirata, Sci. Rep., 2015, 5, 14358 CrossRef CAS PubMed.
- C. P. Herrero and R. Ramirez, J. Phys.: Condens. Matter, 2014, 26, 233201 CrossRef CAS PubMed.
- E. Schneider, L. Vogt and M. E. Tuckerman, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 542–550 CAS.
- E. C. Dybeck, N. S. Abraham, N. P. Schieber and M. R. Shirts, Cryst. Growth Des., 2017, 17, 1775–1787 CAS.
- R. Ramirez, N. Neuerburg and C. P. Herrero, J. Chem. Phys., 2012, 137, 134503 CrossRef CAS PubMed.
- J. Park, I. Nessler, B. McClain, D. Macikenas, J. Baltrusaitis and M. J. Schnieders, J. Chem. Theory Comput., 2014, 10, 2781–2791 CrossRef CAS PubMed.
- F. Giberti, M. Salvalaglio and M. Parrinello, IUCrJ, 2015, 2, 256–266 CrossRef CAS PubMed.
- Y. N. Heit, K. D. Nanda and G. J. O. Beran, Chem. Sci., 2016, 7, 246–255 RSC.
- S. Hirata, K. Gilliard, X. He, J. Li and O. Sode, Acc. Chem. Res., 2014, 47, 2721–2730 CrossRef CAS PubMed.
- R. P. Stoffel, C. Wessel, M.-W. Lumey and R. Dronskowski, Angew. Chem., Int. Ed., 2010, 49, 5242–5266 CrossRef CAS PubMed.
- P. B. Allen, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 064106 CrossRef.
- O. Hellman, I. A. Abrikosov and S. I. Simak, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 180301 CrossRef.
- J. Hoja, A. M. Reilly and A. Tkatchenko, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1294 CrossRef.
- J. G. Brandenburg and S. Grimme, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 502–513 CAS.
- S. R. Whittleton, A. Otero-de-la-Roza and E. R. Johnson, J. Chem. Theory Comput., 2017, 13, 441–450 CrossRef CAS PubMed.
- S. L. Price, D. E. Braun and S. M. Reutzel-Edens, Chem. Commun., 2016, 52, 7065–7077 RSC.
- A. Otero-de-la-Roza and E. R. Johnson, J. Chem. Phys., 2012, 137, 054103 CrossRef CAS PubMed.
- C. Červinka, M. Fulem, R. P. Stoffel and R. Dronskowski, J. Phys. Chem. A, 2016, 120, 2022–2034 CrossRef PubMed.
- V. L. Deringer, J. George, R. Dronskowski and U. Englert, Acc. Chem. Res., 2017, 50, 1231–1239 CrossRef CAS PubMed.
- J. George, V. L. Deringer, A. Wang, P. Muller, U. Englert and R. Dronskowski, J. Chem. Phys., 2016, 145, 234512 CrossRef PubMed.
- J. Hermann, R. A. DiStasio and A. Tkatchenko, Chem. Rev., 2017, 117, 4714–4758 CrossRef CAS PubMed.
- B. Santra, J. Klimeš, A. Tkatchenko, D. Alfe, B. Slater, A. Michaelides, R. Car and M. Scheffler, J. Chem. Phys., 2013, 139, 154702 CrossRef PubMed.
- M. T. Ruggiero, J. A. Zeitler and A. Erba, Chem. Commun., 2017, 53, 3781–3784 RSC.
- T. Fang, Y. Z. Li and S. H. Li, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1297 CrossRef.
- T. Fang, J. T. Jia and S. H. Li, J. Phys. Chem. A, 2016, 120, 2700–2711 CrossRef CAS PubMed.
- A. M. Reilly and A. Tkatchenko, J. Chem. Phys., 2013, 139, 024705 CrossRef PubMed.
- C. Červinka, M. Fulem and K. Růžička, J. Chem. Eng. Data, 2012, 57, 227–232 CrossRef.
- M. L. Laury, M. J. Carlson and A. K. Wilson, J. Comput. Chem., 2012, 33, 2380–2387 CrossRef CAS PubMed.
- J. P. Merrick, D. Moran and L. Radom, J. Phys. Chem. A, 2007, 111, 11683–11700 CrossRef CAS PubMed.
- M. T. Kirchner, D. Das and R. Boese, Cryst. Growth Des., 2008, 8, 763–765 CAS.
- H. G. Carlson and E. F. Westrum, J. Chem. Phys., 1971, 54, 1464–1471 CrossRef CAS.
- M. V. Kondrin, A. A. Pronin, Y. B. Lebed and V. V. Brazhkin, J. Chem. Phys., 2013, 139, 084510 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- J. Hafner, G. Kresse, D. Vogtenhuber and M. Marsman, Vienna Ab-initio Simulation Package 5.4.1, 2014 Search PubMed.
- G. J. O. Beran, S. Wen, K. Nanda, Y. Huang and Y. Heit, Top. Curr. Chem., 2014, 345, 59–93 CrossRef CAS PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CrossRef CAS.
- J. W. Ponder, Tinker 6.2, 2013 Search PubMed.
- J. W. Ponder, C. Wu, P. Ren, V. S. Pande, J. D. Chodera, M. J. Schnieders, I. Haque, D. L. Mobley, D. S. Lambrecht, R. A. DiStasio, M. Head-Gordon, G. N. I. Clark, M. E. Johnson and T. Head-Gordon, J. Phys. Chem. B, 2010, 114, 2549–2564 CrossRef CAS PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., 2016, 72, 171–179 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- E. R. Johnson and A. D. Becke, J. Chem. Phys., 2006, 124, 174104 CrossRef PubMed.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 123, 154101 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- K. Parlinski, Z. Q. Li and Y. Kawazoe, Phys. Rev. Lett., 1997, 78, 4063–4066 CrossRef CAS.
- A. Togo, Phonopy 1.9.7, 2009 Search PubMed.
- G. J. O. Beran and K. Nanda, J. Phys. Chem. Lett., 2010, 1, 3480–3487 CrossRef CAS.
- Y. H. Huang, Y. H. Shao and G. J. O. Beran, J. Chem. Phys., 2013, 138, 224112 CrossRef PubMed.
- K. D. Nanda and G. J. O. Beran, J. Chem. Phys., 2012, 137, 174106 CrossRef PubMed.
- S. Wen and G. J. O. Beran, J. Chem. Theory Comput., 2011, 7, 3733–3742 CrossRef CAS PubMed.
- P. J. Bygrave, N. L. Allan and F. R. Manby, J. Chem. Phys., 2012, 137, 164102 CrossRef CAS PubMed.
- C. Červinka, M. Fulem and K. Růžička, J. Chem. Phys., 2016, 144, 064505 CrossRef PubMed.
- S. J. Nolan, P. J. Bygrave, N. L. Allan and F. R. Manby, J. Phys.: Condens. Matter, 2010, 22, 074201 CrossRef CAS PubMed.
- A. L. Ringer and C. D. Sherrill, Chem. – Eur. J., 2008, 14, 2542–2547 CrossRef CAS PubMed.
- K. Rosciszewski, B. Paulus, P. Fulde and H. Stoll, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 5482–5488 CrossRef CAS.
- O. Sode and S. Hirata, J. Phys. Chem. A, 2010, 114, 8873–8877 CrossRef CAS PubMed.
- J. Yang, W. F. Hu, D. Usvyat, D. Matthews, M. Schutz and G. K. L. Chan, Science, 2014, 345, 640–643 CrossRef CAS PubMed.
- Y. Heit and G. J. O. Beran, J. Comput. Chem., 2014, 35, 2205–2214 CrossRef CAS PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- J. Paldus, I. Shavitt and J. Čížek, Phys. Rev. A: At., Mol., Opt. Phys., 1972, 5, 50–66 CrossRef.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- A. Halkier, T. Helgaker, P. Jorgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243–252 CrossRef CAS.
- J. Řezáč and P. Hobza, J. Chem. Theory Comput., 2013, 9, 2151–2155 CrossRef PubMed.
- F. D. Murnaghan, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 244–247 CrossRef CAS.
- A. M. Reilly and A. Tkatchenko, Chem. Sci., 2015, 6, 3289–3301 RSC.
- J. Klimeš, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2010, 22, 022201 CrossRef PubMed.
- J. R. Durig, C. B. Pate, Y. S. Li and D. J. Antion, J. Chem. Phys., 1971, 54, 4863–4870 CrossRef CAS.
- M. Falk and E. Whalley, J. Chem. Phys., 1961, 34, 1554–1568 CrossRef CAS.
- O. Galvez, B. Mate, B. Martin-Llorente, V. J. Herrero and R. Escribano, J. Phys. Chem. A, 2009, 113, 3321–3329 CrossRef CAS PubMed.
- S. X. Weng and A. Anderson, Phys. Status Solidi B, 1992, 172, 545–555 CrossRef CAS.
- C. J. Bennett, S. H. Chen, B. J. Sun, A. H. H. Chang and R. I. Kaiser, Astrophys. J., 2007, 660, 1588–1608 CrossRef CAS.
- A. T. Wen, M. Michaud and L. Sanche, J. Electron Spectrosc. Relat. Phenom., 1998, 94, 23–32 CrossRef CAS.
- A. B. Dempster and G. Zerbi, J. Chem. Phys., 1971, 54, 3600–3609 CrossRef CAS.
- D. M. Hudgins, S. A. Sandford, L. J. Allamandola and A. Tielens, Astrophys. J., Suppl. Ser., 1993, 86, 713–870 CrossRef CAS PubMed.
- A. Pellegrini, D. R. Ferro and G. Zerbi, Mol. Phys., 1973, 26, 577–594 CrossRef CAS.
- A. Anderson, B. Andrews, E. M. Meiering and B. H. Torrie, J. Raman Spectrosc., 1988, 19, 85–89 CrossRef CAS.
- P. T. T. Wong and E. Whalley, J. Chem. Phys., 1971, 55, 1830–1845 CrossRef CAS.
- C. Červinka, M. Fulem and K. Růžička, J. Chem. Eng. Data, 2013, 58, 1382–1390 CrossRef.
- W. Biltz, W. Fischer and E. Wunnenberg, Z. Phys. Chem., Abt. A, 1930, 151, 13–55 CAS.
- M. Riembauer, L. Schulte and A. Wurflinger, Z. Phys. Chem. Neue Fol., 1990, 166, 53–61 CrossRef CAS.
- K. J. Tauer and W. N. Lipscomb, Acta Crystallogr., 1952, 5, 606–612 CrossRef CAS.
- B. H. Torrie, S. X. Weng and B. M. Powell, Mol. Phys., 1989, 67, 575–581 CrossRef CAS.
- J. E. Ahlberg, E. R. Blanchard and W. O. Lundberg, J. Chem. Phys., 1937, 5, 539–551 CrossRef CAS.
- L. A. K. Staveley and A. K. Gupta, Trans. Faraday Soc., 1949, 45, 50–61 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Optimized unit cell structures and overlays with the experimental structure. Methanol dimer benchmarks. Comparison of calculated and experimental vibrational frequencies along with the quasi-harmonic estimates of the frequencies at 20 K. Calculated molar volumes and isobaric heat capacities of α-methanol in the high-pressure region. Analysis of the quality of Helmholtz energy fits. See DOI: 10.1039/c7cp06605h |
| This journal is © the Owner Societies 2017 |