The anharmonic quartic force field infrared spectra of hydrogenated and methylated PAHs

Abstract

Polycyclic aromatic hydrocarbons (PAHs) have been shown to be ubiquitous in a large variety of distinct astrophysical environments and are therefore of great interest to astronomers. The majority of these findings are based on theoretically predicted spectra, which make use of scaled DFT harmonic frequencies for band positions and the double harmonic approximation for intensities. However, these approximations have been shown to fail at predicting high-resolution gas-phase infrared spectra accurately, especially in the CH-stretching region (2950–3150 cm⁻¹, 3 μm). This is particularly worrying for the subset of hydrogenated or methylated PAHs to which astronomers attribute the observed non-aromatic features that appear in the CH-stretching region of spectral observations of the interstellar medium (ISM). In our previous work, we presented the anharmonic theoretical spectra of three linear PAHs and five non-linear PAHs, demonstrating the importance of including anharmonicities into theoretical calculations. In this work we extend these techniques to two methylated PAHs (9-methylanthracene, and 9,10-dimethylanthracene) and four hydrogenated PAHs (9,10-dihydroanthracene, 9,10-dihydrophenanthrene, 1,2,3,4-tetrahydronaphthalene, and 1,2,3,6,7,8-hexahydropyrene) in order to better understand the aliphatic IR features of substituted PAHs. The theoretical spectra are compared with the spectra obtained under matrix isolation low-temperature conditions for the full vibrational fundamental range and under high-resolution, low-temperature gas-phase conditions for the CH-stretching region. Excellent agreement is observed between the theoretical and high-resolution experimental spectra with a deviation of 0.00% ± 0.17%, and changes to the spectra of PAHs upon methylation and hydrogenated are tracked accurately and explained.

---

1 Introduction

Due to their remarkable stability, polycyclic aromatic hydrocarbon (PAH) molecules are widely used in everyday life. They are a major component of soot, created during combustion processes¹ and due to their biological activity, they pollute water and the atmosphere. In the terrestrial atmosphere, several reactions² lead to functionalised PAHs–PAHs with chemical side groups and/or heteroatom substitution. These functionalisations have an impact on the properties of the molecules, for example, methylation can increase or decrease the carcinogenicity level of PAHs depending on the substitution position.³

Functionalised PAHs are also of interest from a materials science perspective. For example, hydrogenation of PAHs changes the local molecule hybridization from sp² to sp³, and therefore they can be used as a model system for studies of hydrogenated graphene, which is a promising successor of silicon in the electronic industry thanks to the tunability of the graphene band gap depending on the location of the additional hydrogens.⁴

Several studies indicate that PAHs are also of high importance in astrophysical environments. PAHs have been detected in interplanetary dust particles and meteorites,^5,6 and are most certainly the carriers of aromatic infrared bands (AIBs),^7,8 a family of IR emission features spanning the 3–20 μm (3300–500 cm⁻¹) region, observed in a variety of astrophysical environments. In particular, hydrogenated and methylated PAHs are considered to be responsible for additional features at 3.40, 3.46, 3.51, 3.56 μm and 6.9 μm,^9–13 which can be particularly strong in evolved stars.¹⁴ Also, hydrogenated PAHs have gained interest as potential catalysts for H₂ formation in astrophysical regions dominated by visible-ultraviolet photons.¹⁵

The IR spectra of methylated and hydrogenated PAHs have been explored both experimentally,^16,17 mostly in a matrix environment,¹⁸ and computationally using DFT and the double harmonic approximation.¹⁹ For normal PAHs, previous experiments have shown that the theoretical double harmonic spectra compare poorly, especially in the 3.1–3.5 μm (3200–2900 cm⁻¹)²⁰ and 5–6 μm (2000–1600 cm⁻¹) regions.²¹ This is due to the inability of the harmonic approximation to account for combination bands, overtones, mode couplings and resonances.

In our previous work,^20–23 we showed that good agreement between theoretical and experimental spectra can be obtained when an anharmonic theoretical approach is used; specifically, a second-order vibrational perturbation treatment that accounts for large numbers of mutually resonating modes and combination bands. This work extends these studies in order to address the high-resolution spectra of hydrogenated and methylated PAHs. Anharmonic treatment is applied to six “decorated” PAH species: 9-methylanthracene, 9,10-dimethylanthracene, 9,10-dihydroanthracene, 9,10-dihydrophenanthrene, 1,2,3,4-tetrahydronaphthalene, and 1,2,3,6,7,8-hexahydropyrene (see Fig. 1). The goal is two-fold: to further expand and test the anharmonic methods outlined in our previous work to include hydrogenated and methylated species, and to explain how and why PAH spectra change with the introduction of aliphatic groups. A robust theoretical understanding of the IR spectral features and the role of anharmonicities is key to analyzing and interpreting astronomical observations. This is particularly important because of the upcoming launch of the James Webb Space Telescope in 2018, as astronomers will record for the first time astronomical spectra at high spectral resolution and high sensitivity.

Fig. 1 From top to bottom: 9-methylanthracene, 9,10-dimethylanthracene, 9,10-dihydroanthracene, 9,10-dihydrophenanthrene, 1,2,3,4-tetrahydronaphthalene, and 1,2,3,6,7,8-hexahydropyrene. Symmetries from top to bottom: C_s, C_2h, C₂, C₂, C₂, and C_2v.

Of particular interest is the behavior of aliphatic vibrational modes in resonance with the CH-stretching region of around 3 μm. For this, we compare the low-temperature high-resolution gas-phase IR absorption spectra of the six decorated species, which allows direct comparisons to the theoretical methods, further validating our approach. Full peak analyses are performed for the bands in the CH-stretching region. The remaining IR range is also compared to the available matrix isolation spectra (MIS) and high-temperature gas-phase spectra to confirm accuracy in the full IR range.

2 Theoretical methods

The theoretical methods of this work follow similar techniques to our previous work.^21,23,24 The software package Gaussian09²⁵ is used to optimize the geometry of the molecules, as well as to calculate the quartic force fields (QFFs) and IR intensities. In order to handle the large number of mutually resonating modes (polyads²⁶), we use a locally modified version of the SPECTRO²⁷ software package to perform second order vibrational perturbation theory treatment (VPT2) after transforming the QFF constants from normal to Cartesian coordinates.²⁴ We use the resulting eigenvalues of the VPT2 polyad treatment for the final line positions and the square of the eigenvectors to distribute intensities over resonating modes (see ref. 21 and 23 for more details).

Recently, problems with the stability of the quartic force field of PAHs using a combination of the B97-1 functional²⁸ and TZ2P basis set²⁹ have been discovered. Therefore, a switch has been made in this work to the B3LYP hybrid functional,^30,31 and the polarized double-ζ basis set N07D,³² a combination developed specifically with the anharmonic calculations of medium-size molecules in mind.³³

Known issues arise in the anharmonic analysis involving the low barrier “free-rotor” vibrational modes of methyl groups.³⁴ To circumvent this issue, cubic and quartic force constant terms involving the free-rotor modes were set to zero, essentially treating these vibrational modes at the harmonic level.

3 Results

Comparisons between the theoretical anharmonic spectra and experimental spectra obtained under the two experimental conditions were performed. To aid comparison, the theoretical spectra have been convolved³⁷ with Lorentzian profiles to best match the experimental band-widths. Band assignments are made between theory and experiment based on the position, intensity, and local trends of the convolved spectra. The values given for the experiment and theory are obtained through fitting Lorentzian profiles using the software package Fityk.³⁸ Vibrational mode descriptions were obtained through visualization of the atomic motions of each of the normal modes.

Fig. 2 shows a comparison between the convolved theoretical spectra (blue, HWHM = 1.6 cm⁻¹) and the high-resolution low-temperature gas-phase spectra (black), both normalized to their highest peak in this spectral range. See the ESI† for similar comparisons for the remaining molecules. Detailed band assignments are also given in the ESI† for each PAH. Due to strong resonances in the CH-stretching region, assignment to a single unique fundamental or combination band is not possible; instead, the dominant resonant components (typically over 10% contribution) are given. The intensity source is given as a separate column since a small resonance component (<10%) can be the dominant source of intensity if the related fundamental band is very intense (see the Theory section of ref. 21 for more details). Vibrational mode descriptions are also given for each PAH in the corresponding tables (see the ESI†).

Fig. 2 Theoretical anharmonic IR spectrum of this work of 9,10-dihydrophenanthrene compared with the high-resolution gas-phase IR absorption spectrum of this work.

High-resolution low-temperature gas-phase experimental data do not exist for the full infrared range, so comparisons are performed between the anharmonic spectra and the available MIS^18,39 spectra for the remaining IR range. Fig. 3 shows a comparison between the convolved theoretical spectra (blue, HWHM = 1 cm⁻¹) and the MIS spectra (green). See the ESI† for similar comparisons for the remaining molecules. Three ranges are shown for each molecule, 2000–1600 cm⁻¹, 1600–1100 cm⁻¹, and 1100–500 cm⁻¹. No significant features appear between 3000 and 2000 cm⁻¹. No data are available below 500 cm⁻¹. All intensities, both theoretical and experimental, are scaled to their maximum intensity in the spectral range (2000–500 cm⁻¹). Assignments between the MIS data and the anharmonic data of this work are also presented in the ESI.†

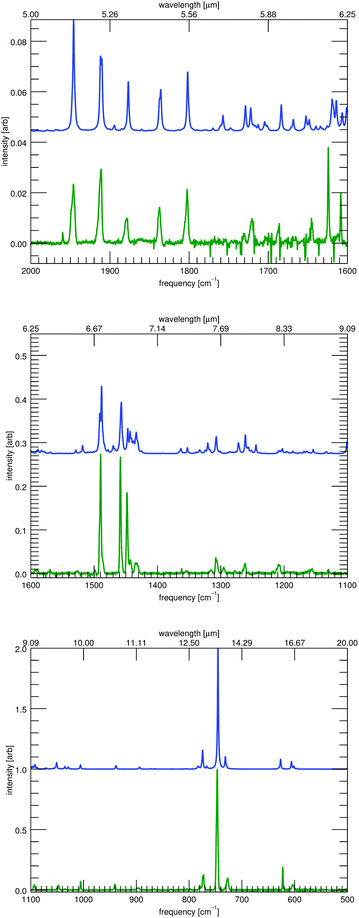Fig. 3 The matrix-isolation infrared spectrum^35,36 of 9,10-dihydrophenanthrene (green, bottom of each panel) compared to the convolved (FWHM 2 cm⁻¹) theoretical anharmonic calculations of this work (blue, top each panel). Three spectral ranges are shown.

When changing from B97-1/TZ2P to B3LYP/N07D, the improvement in agreement between theory and experiment was found to be significant; from an error of 1% down to 0.1% (30 cm⁻¹ to 3 cm⁻¹ in the CH-stretching region). Further functional/basis set benchmark studies on the anharmonic spectra of PAHs are warranted and are currently underway.

4 Discussion

4.1 Overall comparison to the low-temperature high-resolution gas-phase spectra

The low-temperature high-resolution gas-phase spectra and the corresponding convolved theoretical spectra (see the ESI†) show excellent agreement. Fig. 4 shows a histogram of the percent differences between the theoretical and experimental line positions for the six PAHs combined. A fitted Gaussian gives an average deviation of 0.00% ± 0.17%. The aliphatic contributions to the histogram have been highlighted in green. For each of the theoretical CH-stretching region spectra, there appears to be a tendency to shift the aliphatic modes too far down when compared to experiment, with the lowest energy aliphatic modes being the largest outliers. The push to lower energies indicates an overcorrection of the anharmonic effects. Whether this is due to the anharmonic correction of the bands, or due to the resonance terms themselves is not clear. The freezing of the methyl rotors could also be a factor; however the appearance of the same shift in the hydrogenated PAHs points away from this explanation. Future benchmark studies including the decorated PAHs could address this issue. The level of agreement between theory and experiment of the aromatic modes does not appear to be altered upon functionalization of the PAHs.

Fig. 4 Histogram showing the percent differences between the line positions of the anharmonic theory (this work) and the low-temperature high-resolution gas-phase experiments for all six PAH species combined. The aliphatic contributions to the histogram have been highlighted in green.

Relative intensity agreement is moderate with an average deviation of −12% ± 50%. The major source of error in calculating the intensities of the CH-stretching region is the reliance on the distribution of harmonic intensities through the polyads rather than anharmonic intensities.^21,23 The calculation and redistribution of “true” anharmonic intensities should improve the fits. The discrepancies between the theoretical and experimental intensities did not hamper reliable band identifications.

4.2 Overall comparison to MIS

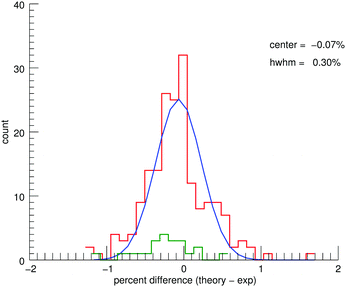
The MIS spectra and the corresponding convolved theoretical spectra (see ESI†) show good agreement. Fig. 5 shows a histogram of the percent differences between the theoretical and experimental line positions for five of the PAHs combined (no MIS data exist for 9,10-dimethylanthracene). A fitted Gaussian gives an average deviation of −0.07% ± 0.30%. Previous work⁴⁰ has shown the unpredictable shifts due to matrix interactions to be 0.21% ± 0.63%. Therefore, the theoretical spectra are accurate within the limitations of MIS spectroscopy. The aliphatic contributions to the histogram have been highlighted in green. As in the CH-stretching region, there appears to be an overcorrection of the aliphatic bands compared to the aromatic bands. The overall agreement between theory and experiment for the aromatic modes is not impacted for the functionalized PAHs.

Fig. 5 Histogram showing the percent differences between the line positions of the anharmonic theory (this work) and the MIS experiments for the five (no MIS data exist for 9,10-dimethylanthracene) PAH species combined. The aliphatic contributions to the histogram are highlighted in green.

Relative intensity agreement is moderate with an average deviation of −18% ± 62%. It was possible to make use of anharmonic intensities in this region; however, MIS experiments are notorious for affecting the intensities of bands. Therefore, confirmation of the reliability of the anharmonic intensity calculations requires high-resolution low-temperature gas-phase spectra in this region.

4.3 Anthracene series

Three anthracene-based PAHs have been considered: 9-methylanthracene; 9,10-dimethylanthracene; and 9,10-dihydroanthracene. Fig. 6 shows the theoretical IR spectra of these three molecules in comparison with the theoretical spectrum of anthracene. Absolute intensities have been doubled, with the main peaks truncated to show details of the smaller peaks.

Fig. 6 Comparison between anthracene-containing PAHs from the anharmonic theoretical spectra.

The most prominent change when moving from anthracene to the methylated and hydrogenated versions occurs in the CH-stretching region, with both methylated species bearing a strong resemblance to one another and to a lesser extent to the hydrogenated version. While anthracene shows one dominant peak, the decorated PAHs show five prominent features. These five features can be split into three regions based on the vibrational modes involved in the Fermi resonances.

(1) Combinational aromatic states of CC-stretching modes paired with CH-in-plane-bending modes in Fermi resonances with aromatic CH-stretching modes. The behavior of this region is comparable to the “regular” CH-stretching region of a typical PAH. In anthracene, this produces one main feature centered around 3055 cm⁻¹, while for the decorated anthracenes, this feature is centered around 3085 cm⁻¹. The push to higher energies likely reflects steric interactions between the native anthracene hydrogens and the additional hydrogens. For the methylated anthracenes, this region spans approximately 30 cm⁻¹, while for the hydrogenated anthracene, it spans approximately 60 cm⁻¹. In regular anthracene, this region spans the whole CH-stretching region (approximately 200 cm⁻¹).

(2) Combinational aromatic/aliphatic states of CC-stretching modes paired with CH-in-plane-bending modes in Fermi resonances with aliphatic CH-stretching modes. For the methylated anthracenes, this region is centered around 3055 cm⁻¹ with a width of 30 cm⁻¹ and is characterized by one dominant peak, while for the hydrogenated anthracene it is centered around 2960 cm⁻¹ with a width of 160 cm⁻¹ and is characterized by two dominant peaks.

(3) Combinational aliphatic states of CH-in-plane-bending modes paired with CH-in-plane-bending modes in Fermi resonances with aliphatic CH-stretching modes. For the methylated anthracenes, this region is centered around 2960 cm⁻¹ with a width of 150 cm⁻¹ and is characterized by two dominant peaks, while for the hydrogenated anthracene it is centered around 2849 cm⁻¹ with a width of 50 cm⁻¹ and is again characterized by two dominant peaks. The additional feature observed in the theoretical spectra of both methylated anthracenes around 2760 cm⁻¹ is not observed in the experimental spectra.

One could argue that the region between 1000 and 600 cm⁻¹ shows more variation between the anthracene-like species than the CH-stretching region around 3000 cm⁻¹. However, this is misleading. The differences are not directly due to methylation and hydrogenation, but rather indirectly due to the disruption of the types of CH bonds present in the molecule. As has been shown previously,⁴¹ the position of the bands in this region is sensitive to the number of hydrogen atoms on a given aromatic ring involved in out-of-plane CH-bending modes. For example, anthracene has two features in this region: one at 885 cm⁻¹ from the out-of-plane CH-bendings of the hydrogens on the middle ring, or solo hydrogens (no adjacent hydrogens); and one at 730 cm⁻¹ from the out-of-plane CH-bendings of the hydrogens on the terminal rings, or quarto hydrogens (four adjacent hydrogens). Similar characteristic features exist at distinct frequencies for other aromatic ring types; duo (two adjacent hydrogens) out-of-plane CH-bendings and trio (three adjacent hydrogens) out-of-plane CH-bendings. The intensity ratios of these bands have also been shown to correlate with the ratios of the edge structure of PAHs. Therefore, when moving from anthracene to 9-methylanthracene, the intensity of the solo CH-bending mode is observed to be reduced by a factor of two because one of the solo hydrogens has been replaced with the methyl group. This trend continues for 9,10-dimethylanthracene with the elimination of the solo CH-bending mode as both solo hydrogens have been replaced with methyl groups. Similarly, with 9,10-dihydroanthracene, both solo hydrogens are eliminated with the hydrogenation resulting in the loss of the solo CH-bending mode feature. Other subtle differences exist as well. When moving from anthracene to 9-methylanthracene to 9,10-dimethylanthracene, two sets of bands appear and disappear around 840 cm⁻¹ and 775 cm⁻¹. These bands are again due to solo and quarto hydrogen bending modes. The appearance and disappearance of these bands are likely due to symmetry effects. These modes are weak or inactive in the higher symmetric anthracene, gain considerable intensity with the breaking of symmetry from the addition of one methyl group, and lose intensity again with the near symmetry restoration from the addition of the second methyl group. The splitting of the quarto feature of 9,10-dihydroanthracene is due to interference from the hydrogenated groups.

The final region that shows significant change in the methylated and hydrogenated versions of anthracene is from 1600 to 1300 cm⁻¹. The intensity in this region is doubled or even tripled compared to normal anthracene. This region is dominated by out-of-plane combination bands including CH-bends paired with CH-bends, CH-bends paired with CC-bends, and CC-bends paired with CC-bends. The enhancement of this region is likely due to the disruption of the planarity of the molecules, leading to stronger dipoles for the out-of-plane combination bands.

4.4 Hydrogenated series

Four hydrogenated PAHs have been considered: 9,10-dihydroanthracene; 9,10-dihydrophenanthrene; 1,2,3,4-tetrahydronaphthalene; and 1,2,3,6,7,8-hexahydropyrene. Fig. 7 shows the theoretical IR spectra of these four molecules in comparison with their non-hydrogenated counterparts from our previous work.^20,21 Absolute intensities have been doubled, with the main peaks truncated, to show details of the smaller peaks. 9,10-Dihydroanthracene is absent from Fig. 7, see Fig. 6 for its comparison.

Fig. 7 Comparison between normal and hydrogenated versions of PAHs from the anharmonic theoretical spectra.

As stated previously, the most dramatic change to the spectra occurs in the CH-stretching region of the PAHs upon hydrogenation. The features centered around 3080 cm⁻¹ of all four hydrogenated PAHs behave in a similar manner to their normal PAH counterparts in that they are aromatic CH-stretching modes in resonance with the combination bands of CC-stretching with in-plane CH-bending modes. Spreading of intensity over a larger region is also observed in each of the hydro-PAHs when compared to their normal counterparts, especially for lower energy modes down to 3020 cm⁻¹. A break occurs before a sharp rise in aliphatic features beginning at 2950 cm⁻¹ for all four hydro-PAHs. Three aliphatic regions then exist for each hydro-PAH: the features centered around 2950 cm⁻¹ are due to in-plane CH-stretching modes of the aliphatic CH bonds that do not participate strongly in resonance; the features centered around 2900 cm⁻¹ are due to out-of-plane CH-stretching modes of the aliphatic CH bonds in resonance; and the features centered near 2850 cm⁻¹ are due to less sterically hindered out-of-plane CH-stretching modes of the aliphatic CH bonds in resonance. Notable changes can also be observed in the CH-stretching region as hydrogenation increases. In the slightly hydrogenated PAHs (9,10-dihydroanthracene and 9,10-dihydrophenanthrene), the aromatic region contains many closely spaced features, while the aliphatic region has fewer and more widely spaced features. In the highly hydrogenated PAHs (1,2,3,4-tetrahydronaphthalene and 1,2,3,6,7,8-hexahydropyrene), the opposite is true, the aliphatic region contains many closely spaced features, while the aromatic region has fewer and more widely spaced features. As shown in our previous work,^21,23 and confirmed here, the large number of closely spaced features in the CH-stretching region is due to strong Fermi resonances. As such, there is not only the obvious loss of aromatic CH-stretching fundamentals and a gain in the aliphatic CH-stretching fundamentals as expected upon hydrogenation, but there is also a Fermi resonance shift from aromatic fundamentals and aromatic combination bands to between aliphatic fundamentals and aliphatic combination bands. This results in the dense number of features moving from the aromatic region to the aliphatic region, as observed in the highly hydrogenated species.

As in the methyl-anthracene series, significant changes occur in the 1000 to 600 cm⁻¹ region. Again, these changes are not unique to hydrogenation, but rather reflect the loss of solo, duo, trio and quarto hydrogen edges. In 9,10-dihydroanthracene, the solo CH-bending mode near 900 cm⁻¹ is lost as both solo sites are hydrogenated. In 9,10-dihydrophenanthrene, the duo CH-bending mode near 800 cm⁻¹ is lost upon hydrogenation. In 1,2,3,4-tetrahydronaphthalene, significant intensity is lost in the quarto CH-bending mode near 780 cm⁻¹ as four out of eight quarto sites are hydrogenated, and a slight shift of the quarto bending mode to lower energy occurs as the aromaticity is disrupted. In 1,2,3,6,7,8-hexahydropyrene, the trio CH-bending modes near 780 cm⁻¹ are lost upon hydrogenation of the six trio hydrogens, and a slight shift of the duo bending mode to lower energy occurs as the aromaticity is disrupted.

A significant increase in intensity is also observed in the bands near 1500 cm⁻¹ for all of the hydrogenated PAHs. However, unlike the methylated species, these features are more localized and are due to CH₂ bending modes of the hydrogenated sites.

4.5 Astrophysical implications

Determination of the carriers of the minor features observed at 3.40, 3.46, 3.51, and 3.56 μm (2941, 2890, 2849, and 2809 cm⁻¹) in the CH-stretching region of the AIBs is important to understand the chemical populations in various physical environments. The lack of, or abundance of, these features in environments can point to chemical- or photo-processing of PAHs in space. It is generally believed that these bands are due to aliphatic substitutions to PAHs, either through hydrogenation or alkylation.¹² It has been shown previously¹⁸ that the aliphatic groups of hydrogenated PAHs can indeed reproduce most of these features. Our work here confirms these findings. All four hydrogenated PAHs studied are able to contribute to the features observed at 3.40, 3.46, and 3.51 μm. For 9,10-dihydroanthracene and 9,10-dihydrophenanthrene, the features are distinct and easily classified. The feature at 3.40 μm is due to in-plane CH-stretching modes of the hydrogenated sites with little contribution from resonances. The two features at 3.46, and 3.51 μm are due to out-of-plane CH-stretching modes of the hydrogenated sites in strong resonance with combination bands of paired CH-bending modes. The splitting of the out-of-plane CH-stretching modes into the two distinct features is due to the particular modes that are involved in the resonance. Moving up in the degree of hydrogenation with 1,2,3,4-tetrahydronaphthalene and 1,2,3,6,7,8-hexahydropyrene, the previously distinct vibrational regions are now blurred into one. While both highly hydrogenated PAHs show many features centered near 3.40, 3.46, and 3.51 μm, they are less separated in the spectra. This region is now dominated by Fermi resonances, resulting in many more aliphatic spectral features than observed for the dihydrogenated PAHs. This leads to the possibility that astronomical PAHs with only a few hydrogenated sites would show sharp distinct features around 3.40, 3.46, and 3.51 μm, while PAHs with a majority of hydrogenated sites would show wide blended features around 3.40, 3.46, and 3.51 μm. The feature at 3.56 μm is unaccounted for in all of the theoretical spectra. Both the methylated PAHs 9-methylanthracene and 9,10-dimethylanthracene show contributions to the 3.40 and 3.46 μm features. Here, these features arise from the CH-stretching modes of the methyl groups in resonance with a wide variety of combination bands. This region is again dominated by Fermi resonances, spreading a large number of features over a wide range. No contributions to the 3.51 and 3.56 μm features are predicted for the two methylated PAHs.

The aromatic CH-stretching region is also affected by the inclusion of additional hydrogens or substitution of methyl groups. For the methylated PAHs, the typical aromatic CH-stretching bands are pushed to higher energies (as high as 3100 cm⁻¹); however, they also now begin to resonate with lower energy combination bands involving methyl CH-bending modes (down to 3050 cm⁻¹) resulting in a wider, more even distribution of intensity over the aromatic region than a normal PAH. The aromatic CH-stretching region of the hydrogenated PAHs shows similar behavior in that the intensity is distributed over a wider range than a normal PAH. However, there is no shift to higher energies, and the intensity is more concentrated in the lower energy aromatic modes and resonances. At higher temperatures, as lines broaden and blend, these behaviors will affect the apparent line widths and positions.

It has also been proposed¹⁸ that the feature at 6.9 μm (1450 cm⁻¹) is likely due to HCH-bending modes (or so-called methylene scissoring modes) of hydrogenated PAHs, and could be used as a tracer for hydrogenated PAHs in astronomical observations. The HCH-bending modes are indeed stronger around 6.9 μm, but regular in-plane CH-bending modes also gain significant intensity in this region. Complicating matters further, enhancements in intensities in this region are now also observed for the methylated PAHs. For the methylated PAHs, this enhanced region extends from 6.9 μm down to 7.4 μm (1450 cm⁻¹) consisting of combination bands of both CC and CH out-of-plane bending modes.

5 Conclusions

This work presented the anharmonic spectra of six CH-bond-containing PAHs: 9-methylanthracene, 9,10-dimethylanthracene, 9,10-dihydroanthracene, 9,10-dihydrophenanthrene, 1,2,3,4-tetrahydronaphthalene, and 1,2,3,6,7,8-hexahydropyrene. The choice of these PAHs was motivated largely by the need to accurately describe the CH-stretching region (3100–2800 cm⁻¹) to aid the analysis of astronomical observations of the AIBs. In particular, to explain the source of the 3.40, 3.46, 3.51, and 3.56 μm (2941, 2890, 2849, and 2809 cm⁻¹) IR features observed in a variety of astronomical objects. We have shown that hydrogenated PAHs can contribute to the 3.40, 3.46, and 3.51, μm features, and methylated PAHs can contribute to the 3.40 and 3.46 μm features. No experimental bands were found to explain the 3.56 μm feature. In conjunction with the low-temperature high-resolution gas-phase spectra presented here, the vibrational sources of the dominant features in the CH-stretching region have been identified and characterized. As in our previous work,^21,23 Fermi resonances are shown to dominate the aromatic CH-stretching region. Without proper treatment of resonances (i.e., polyad treatment), this region cannot be reproduced accurately. Fermi resonances are now shown to affect not only aromatic CH-stretching modes but also aliphatic CH-stretching modes. This results in many more strong aliphatic bands than would be predicted at the harmonic level. The CH-stretching region has been shown to be the most sensitive upon hydrogenation or methylation; with the gradual loss of aromatic features centered around 3050 cm⁻¹ and the rise of the aliphatic features around 2900 cm⁻¹. Not only is there a loss of aromatic fundamental features, but the ability for the remaining aromatic fundamentals to engage in resonances is found to diminish as the molecule becomes more aliphatic. Conversely, as the aliphatic fundamental features become stronger, their tendency to engage in strong resonances increases.

IR features have also been characterized in conjunction with MIS data for the range of 2000 to 500 cm⁻¹. The changes in the IR spectra of the hydrogenated and methylated PAHs in this region can be attributed mainly to changes in which IR modes are active (i.e., molecular symmetry considerations), or changes in the edge structure (i.e., solo, duo, trio, quarto out-of-plane CH-bending modes). These changes are not unique to hydrogenation or methylation of PAHs, but are seen across various PAH species and derivatives. The only significant changes that correlate with hydrogenation or methylation (save for the CH-stretching region discussed above) are the features between 1450 and 1350 cm⁻¹. The hydrogenated PAHs show a significant enhancement in intensity of the features near 1450 cm⁻¹ compared to their non-hydrogenated counterparts. These features are confirmed as being due to CH₂ bending modes. The methylated PAHs also show enhanced features near 1450 cm⁻¹, but these are less localized and extend down to 1350 cm⁻¹. The features here consist of combination bands of both CC and CH out-of-plane bending modes.

Line position agreement between the anharmonic treatment of this work and the low-temperature high-resolution gas-phase is excellent, agreeing with an average deviation of 0.00% ± 0.18%. The MIS line positions agree with an average deviation of −0.07% ± 0.30%, well within expected experimental limitations. As stated previously, the improvement in accuracy compared to our previous work is due to the improved basis/functional combination (B3LYP/N07D) in the anharmonic approach. The issues observed in the previously recommended basis/functional for anharmonic calculations of PAHs (B97-1/TZ2P) lead to the need for a more in-depth benchmark study.

With the current anharmonic analysis of our collection of PAH families, extensions into temperature dependent spectra and full emission spectra are both feasible and currently underway.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank Scott Sandford (NASA Ames) for providing the MIS data. The authors would also like to thank the two reviewers for providing feedback, which was used to improve the manuscript. The spectroscopic study of interstellar PAHs at Leiden Observatory was supported by the Advanced European Research Council Grant 246976, a Spinoza award, and by the Dutch Astrochemistry Network funded by the Netherlands Organization for Scientific Research, NWO. We acknowledge the European Union (EU) and Horizon 2020 funding awarded under the Marie Sklodowska-Curie action to the EUROPAH consortium, grant number 722346. Calculations were carried out on the Dutch national e-infrastructure (Cartesius) with the support of SURF Cooperative, under NWO EW project SH-362-15. AC acknowledges NWO for a VENI grant (639.041.543). AP acknowledges NWO for a VIDI grant (723.014.007). XH and TJL gratefully acknowledge support from the NASA 12-APRA12-0107 grant, and NAI funding 13-13NAI17_2-0039. XH acknowledges the support from NASA/SETI Co-op Agreement NNX15AF45A. This material is based on work supported by the National Aeronautics and Space Administration through the NASA Astrobiology Institute under Cooperative Agreement Notice NNH13ZDA017C issued through the Science Mission Directorate.

References

1. A. L. C. Lima, J. W. Farrington and C. M. Reddy, Environ. Forensics, 2005, 6, 109–131.
2. D. Vione, S. Barra, G. de Gennaro, M. de Rienzo, S. Gilardoni, M. G. Perrone and L. Pozzoli, Ann. Chim., 2004, 94, 257–268.
3. S. Hecht, S. Amin, A. Melikian, E. La Voie, D. Hoffmann and R. Harvey, ACS Monograph No. 283, American Chemical Society, Washington, DC, 1985, pp. 85–106.
4. D. C. Elias, R. R. Nair, T. M. G. Mohiuddin, S. V. Morozov, P. Blake, M. P. Halsall, A. C. Ferrari, D. W. Boukhvalov, M. I. Katsnelson, A. K. Geim and K. S. Novoselov, Science, 2009, 323, 610–613.
5. I. Allamandola, S. Sandford and B. Wopenka, Science, 1987, 237, 56–60.
6. F. L. Plows, J. E. Elsila, R. N. Zare and P. R. Buseck, Geochim. Cosmochim. Acta, 2003, 67, 1429–1436.
7. A. Leger and J. L. Puget, Astron. Astrophys., 1984, 137, L5–L8.
8. L. J. Allamandola, A. G. G. M. Tielens and J. R. Barker, Astrophys. J., 1985, 290, L25–L28.
9. L. J. Allamandola, A. G. G. M. Tielens and J. R. Barker, Astrophys. J., Suppl. Ser., 1989, 71, 733–775.
10. A. Moorhouse, T. R. Geballe, L. J. Allamandola, A. G. G. M. Tielens and P. W. J. L. Brand, Interstellar Dust, 1989, p. 107.
11. C. Joblin, A. G. G. M. Tielens, L. J. Allamandola and T. R. Geballe, Astrophys. J., 1996, 458, 610.
12. D. Wagner, H. Kim and R. Saykally, Astrophys. J., 2000, 545, 854.
13. K. V. Bruce, J. Hrivnak and S. Kwok, Astrophys. J., 2000, 535, 275–292.
14. T. R. Geballe and W. E. C. J. van der Veen, Astron. Astrophys., 1990, 235, L9–L12.
15. E. Rauls and L. Hornekær, Astrophys. J., 2008, 679, 531.
16. J. Semmler, P. W. Yang and G. E. Crawford, Vib. Spectrosc., 1991, 2, 189–203.
17. M. Steglich, C. Jäger, F. Huisken, M. Friedrich, W. Plass, H.-J. Räder, K. Müllen and T. Henning, Astrophys. J., Suppl. Ser., 2013, 208, 26.
18. S. A. Sandford, M. P. Bernstein and C. K. Materese, Astrophys. J., Suppl. Ser., 2013, 205, 8.
19. S. R. Langhoff, J. Phys. Chem., 1996, 100, 2819–2841.
20. E. Maltseva, A. Petrignani, A. Candian, C. J. Mackie, X. Huang, T. J. Lee, A. G. G. M. Tielens, J. Oomens and W. J. Buma, Astrophys. J., 2015, 814, 23.
21. C. J. Mackie, A. Candian, X. Huang, E. Maltseva, A. Petrignani, J. Oomens, W. J. Buma, T. J. Lee and A. G. G. M. Tielens, J. Chem. Phys., 2015, 143, 224314.
22. E. Maltseva, A. Petrignani, A. Candian, C. J. Mackie, X. Huang, T. J. Lee, A. G. Tielens, J. Oomens and W. J. Buma, Astrophys. J., 2016, 831, 58.
23. C. J. Mackie, A. Candian, X. Huang, E. Maltseva, A. Petrignani, J. Oomens, A. L. Mattioda, W. J. Buma, T. J. Lee and A. G. Tielens, J. Chem. Phys., 2016, 145, 084313.
24. C. J. Mackie, A. Candian, X. Huang, T. J. Lee and A. G. G. M. Tielens, J. Chem. Phys., 2015, 142, 244107.
25. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ã. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian Inc., Wallingford CT, 2009.
26. J. M. Martin, T. J. Lee, P. R. Taylor and J.-P. François, J. Chem. Phys., 1995, 103, 2589–2602.
27. J. F. Gaw, A. Willets, W. H. Green and N. C. Handy, Advances in Molecular Vibrations and Collision Dynamics, ed. J. M. Bowman and M. A. Ratner, JAI Press, Inc., Greenwich, Connecticut, 1991, 170–185.
28. F. A. Hamprecht, A. J. Cohen, D. J. Tozer and N. C. Handy, J. Chem. Phys., 1998, 109, 6264–6271.
29. T. Dunning, et al. , J. Chem. Phys., 1971, 55, 716–723.
30. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
31. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
32. V. Barone, P. Cimino and E. Stendardo, J. Chem. Theory Comput., 2008, 4, 751–764.
33. V. Barone, M. Biczysko and J. Bloino, Phys. Chem. Chem. Phys., 2014, 16, 1759–1787.
34. J. Bloino, M. Biczysko and V. Barone, J. Chem. Theory Comput., 2012, 8, 1015–1036.
35. D. M. Hudgins and S. A. Sandford, J. Phys. Chem. A, 1998, 102, 329–343.
36. C. Boersma, C. W. Bauschlicher, Jr., A. Ricca, A. L. Mattioda, J. Cami, E. Peeters, F. Sánchez de Armas, G. Puerta Saborido, D. M. Hudgins and L. J. Allamandola, Astrophys. J., 2014, 211, 8.
37. A.-R. Allouche, J. Comput. Chem., 2011, 32, 174–182.
38. M. Wojdyr, J. Appl. Crystallogr., 2010, 43, 1126–1128.
39. S. R. Langhoff, C. W. Bauschlicher, D. M. Hudgins, S. A. Sandford and L. J. Allamandola, J. Phys. Chem. A, 1998, 102, 1632–1646.
40. M. E. Jacox, Chem. Soc. Rev., 2002, 31, 108–115.
41. S. Hony, C. Van Kerckhoven, E. Peeters, A. Tielens, D. Hudgins and L. Allamandola, Astron. Astrophys., 2001, 370, 1030–1043.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp06546a

---