Raman spectroscopy studies of the terahertz vibrational modes of a DUT-8 (Ni) metal–organic framework

Abstract

Low-frequency lattice vibrational modes have been discussed to play a crucial role in the phase transformation process of flexible metal–organic frameworks (MOFs). Therefore, Raman spectroscopy was applied to study the lattice dynamics of a pillared layer DUT-8(Ni) framework (DUT – Dresden University of Technology), existing in rigid and flexible forms. Both the open and the close pore phases could be unambiguously identified by breathing mode bands at 23 cm⁻¹ and 60 cm⁻¹ in the corresponding Raman spectra, showing the efficiency of the technique for monitoring the flexibility of MOF materials as well as the differences in the lattice vibrations of the two phases. Born–Oppenheimer Molecular Dynamics simulations showed that observed low-frequency bands indeed correspond to the oscillation of the breathing mode along the diagonals of the pore channels. Moreover, the directional character of low-frequency vibrations in the flexible version of DUT-8(Ni) could be visualized by the orientation dependent Raman spectroscopy experiment.

---

1. Introduction

Switchable Metal–Organic Frameworks (MOFs) or soft porous crystals are unique materials, which are able to transform their crystal structure from a dense, nonporous to a highly porous, open state and vice versa as a response to external stimuli.^1,2 Despite the high potential of these novel materials as promising adsorbents in gas storage, gas separation and sensor technologies, the mechanism behind switching and factors influencing switchability are not fully understood yet.

Low-frequency vibrations typically appearing below 100 cm⁻¹ (terahertz region) contribute considerably to the heat energy transport and consequently to the physical properties of the materials. Moreover, terahertz vibrations reveal significant biological functions in dynamic biological systems (cell and tissue components such as DNA, proteins, amino-acids, etc.), and are the fingerprints of them.³ For example, collective vibrational modes of proteins are highly sensitive to conformational changes.⁴ Also the low-frequency radial “breathing” mode of carbon nanotubes is unique and is not observed in other carbon systems.^5,6

Recently, Tan and co-workers reported lattice vibrations including soft modes (breathing modes of the framework) to be critical for understanding the adsorption induced structural transition in zeolitic imidazole frameworks ZIF-4, ZIF-7, and ZIF-8.^7,8 The authors claim that THz modes are intrinsically linked not only to anomalous elasticity underpinning gate-opening and pore-breathing mechanisms, but also to shear-induced phase transitions and the onset of structural instability.

However, to the best of our knowledge, so far only a few investigations have addressed the experimental observation of THz vibrations of flexible MOFs, mainly due to the technical challenges involved in low-frequency vibrational spectroscopy. To date, low-frequency vibrations have been investigated for ZIF-4, ZIF-7, ZIF-8 ⁷ using inelastic neutron scattering and synchrotron radiation, far-infrared absorption spectroscopy and for HKUST-1 ⁹ using Raman (down to 50 cm⁻¹) and synchrotron far-infrared spectroscopy.

Even though Raman spectroscopy has been successfully applied for characterization of diverse MOF structures,^10–15 it is usually used for investigation of the spectral region above 200 cm⁻¹ (in the case of IR spectroscopy above 600 cm⁻¹) which is responsible for the fingerprint vibrations. Thus, for example, the interactions of guest molecules with the framework^16–20 or the coupling reaction of acetylene side groups within a layer in a MOF²¹ were monitored using Raman spectroscopy.

In the present contribution, Raman spectroscopy and Born–Oppenheimer Molecular Dynamics simulations were used to study the soft-mode low-frequency Raman vibrations in the pillared layer MOF Ni₂(ndc)₂(dabco) (ndc – 2,6-naphthalenedicarboxylate, dabco – 1,4-diazabicyclo[2.2.2]octane), also known as DUT-8(Ni).^22,23 The peculiarity of this MOF is that it can be synthesized in “rigid” and “flexible” forms, depending on the synthetic conditions.²⁴ The rigid version (DUT-8(Ni)_rigid), consisting of nano sized crystallites, can be desolvated without any phase transition and shows a typical “Type Ia” nitrogen physisorption isotherm at 77 K. In contrast, the flexible form (DUT-8(Ni)_flex), crystalized as macro crystals, undergoes a transformation into a closed phase (cp) upon desolvation and can be reversibly transformed into the open phase (op) by adsorption of gases or liquids. Both modifications were investigated in their “as made” as well as desolvated forms to probe the terahertz vibrational modes which are jointly responsible for flexibility.

2. Experimental

2.1 Methods

The Raman spectra in the 180° geometry were recorded on a Horiba Jobin Yvon T64000 spectrometer equipped with a liquid nitrogen cooled charge coupled device detection system in the subtractive dispersion mode at room temperature. An Ar⁺ ion laser (Spectra Physics Stabilite 2017) with λ = 514.5 nm and a power of 5 mW was used as an excitation light source. The angular experiments were carried out using the incident laser beam focused on the sample by a 50× Olympus objective lens with a numerical aperture of 0.75. The scattered light was collected by the same objective lens in the backscattering geometry and analyzed through a polarizer and a λ-plate. Spectroscopic measurements were performed in the subtractive dispersion mode, which attained a low-frequency limit of 10 cm⁻¹ in the present setup to investigate the low-frequency spectra. The deformation of the low-frequency spectral edge by an optical slit, which sometimes smears the true features of the low-frequency spectra, was carefully eliminated by rigorous optical alignment.

Since anisotropy is an essential property of any crystal, Raman spectra are dependent on the crystal orientation with respect to polarizations of the electric fields of an incident and scattered light. Unfortunately, it was not possible to mount the single crystal under the microscope for an appropriate crystal axis orientation. Therefore the assignment was performed later on a single crystal diffractometer (Fig. S3, ESI†). Two experiment series were conducted with parallel and crossed polarizations of incident and scattered beams to study the angular dependence of intensities of Raman spectral lines on the polarization direction of the incident and scattered radiation. The shift of the incidence point of exciting radiation was not more than 2 μm in the complete resolution by 2π.

DUT-8(Ni) (open phase) crystalizes in space group P4/n.²² The atoms are located in the 8g Wyckoff position. The Raman mode representation in the hexagonal phase at the Brillouin zone center is as follows: Γ_R = 81A_g + 81B_g + 81¹E_g + 81²E_g. Polarization selection rules are presented in Table S1 (ESI†). The angular dependent Raman spectra of the open state should contain only A_g and B_g modes in our experimental geometry. DUT-8(Ni) (closed phase) crystalizes in space group P1²³ with 66 atoms in the unit cell. Γ_R in the hexagonal phase at the Brillouin zone center is 195A. Polarization selection rules are presented in Table S2 (ESI†). The number of observed modes in the Raman spectrum of the closed phase (195) is expected to be larger in comparison with the open phase (162).

2.2 Computational details

The Born–Oppenheimer molecular dynamics (BOMD) simulations of periodic models of the DUT-8(Ni) MOF were carried out using the QUICKSTEP^25,26 module of CP2K²⁷ with a mixed Gaussian and plane waves basis.²⁸ Three-dimensional periodic boundary conditions were applied. The PBE exchange–correlation functional was used²⁹ with Goedecker–Teter–Hutter (GTH) pseudopotentials^30,31 incorporating scalar-relativistic core corrections. The orbital transformation method³² was employed for an efficient wave function optimization. Contracted Gaussian basis sets of DZVP quality were used with a grid cutoff of 300 Hartree.^33,34 In all calculations Grimme's DFT-D3 dispersion correction was applied. BOMD simulations were performed in fully flexible cells within the NPT ensemble at 300 K, 1.0 bar, and the equations of motion were integrated with a time step of 1.0 fs. The temperature and pressure were controlled via canonical sampling through a velocity rescaling thermostat as implemented in the CP2K code. The crystal structure of the model for the BOMD simulations of the flexible DUT-8(Ni) MOF was taken from the ESI in ref. 23. The geometry of the crystal structure of the open pore form of DUT-8(Ni) was first optimized using the method mentioned above. After geometry optimization, a BOMD simulation of the open pore form was performed without the presence of any solvent molecules. After 15 ps simulation in a fully flexible NPT ensemble the open form transforms into its closed pore form. The closed pore form was simulated again in the fully flexible NPT ensemble for ca. 9 ps and the analysis of the diagonal distances in the pore was made for the last 6 ps. In order to estimate the frequency of the breathing motion in the open and closed form, respectively, the diagonal distances corresponding to the distances between two opposite Ni ions (Fig. 5) were measured at every femtosecond. The two diagonal distances in the rectangular pore were plotted vs. simulation time and averaged over every 200 fs in order to reduce the computational noise. The periods in the oscillatory behaviour per fs for the diagonal distances were counted and the corresponding frequency was estimated.

2.3 Samples

DUT-8(Ni)_flex and DUT-8(Ni)_rigid were synthesized and activated according to a previously published procedure.²⁴ X-ray powder diffraction patterns were measured to prove the sample's phase purity (Fig. S4, ESI†). The samples are denoted as follows (Fig. S1, ESI†): S1 – as made DUT-8(Ni)_flex; S2 – as made DUT-8(Ni)_rigid; S3 – desolvated DUT-8(Ni)_flex; S4 – desolvated DUT-8(Ni)_rigid.

3. Results and discussion

Low-frequency lattice modes have been discussed to have a major impact for triggering a range of lattice phase transformations such as gate opening and breathing phenomena. The terahertz region (<3 THz) corresponding to a low wavenumber region in Raman spectroscopy was marked as an area of high interest as ab initio quantum mechanical calculations predicted a number of soft modes, pore breathing, and gate-opening motions for different MOFs.^7,9

Since Raman spectroscopy is an ideal technique to analyze normal modes of lattice vibrations, we applied it for investigation of the THz vibration region of the switchable metal–organic framework DUT-8, existing in two modifications: rigid and flexible with the aim of analyzing the potential differences and similarities in the lattice vibrations of the latter.

Four different samples of DUT-8 series were investigated: as made and desolvated DUT-8(Ni) in its rigid and flexible form, respectively.

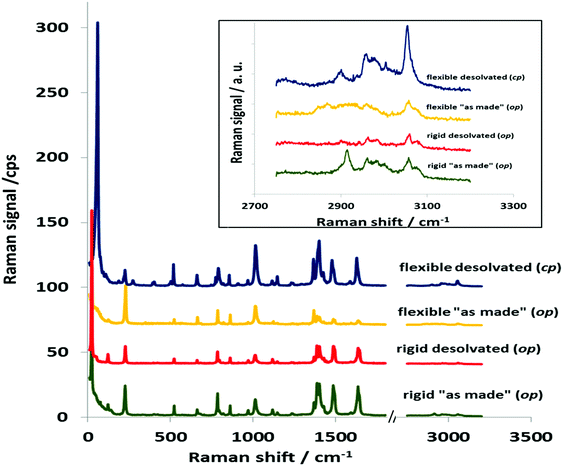
The full Raman spectra of DUT-8 compounds can be divided into three main regions (Fig. 1): (i) a high-frequency region between 3200 and 2750 cm⁻¹; (ii) a fingerprint region which includes lines from 300 to 1700 cm⁻¹ and from 2750 to 3250 cm⁻¹; (iii) a low wavenumber region up to 300 cm⁻¹.

Fig. 1 Raman spectra of samples in a wide spectral range.

The lines in region (i) correspond to the vibrations of the functional molecular groups. The positions of the lines in fingerprint regions are similar for all investigated DUT-8(Ni) samples. The Raman spectral analysis of the fingerprint region provides information about vibrations of functional groups (for example, the lines at 1014 cm⁻¹ are associated with the aromatic ring breathing vibrations and phenyl ring angular vibrations, the lines at 2800–3100 cm⁻¹ to –CH stretching, and the –NH asymmetry stretching bonds).

Recently, this region was analyzed in detail for DUT-8(Ni)_flex and DUT-8(Ni)_rigid, but only minor differences could be found because of the same bonding situation in these two materials.²⁴

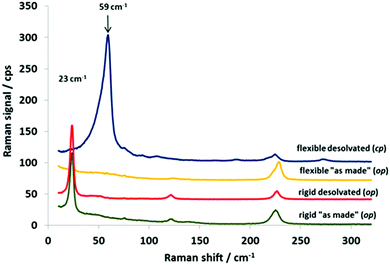
In contrast, despite the fact that desolvated DUT-8(Ni)_rigid and DUT-8(Ni)_flex are compositionally equal, the low-frequency regions up to 300 cm⁻¹ (iii), corresponding mostly to the lattice vibrations, are remarkably different (Fig. 2). Often this region is overlooked in the characterization of MOF materials, due to the high experimental demand of the setup required. It should be noted that the intensity of low-frequency lines is several times stronger than the lines in other regions of the spectrum (Table S3, ESI†). Both the “as made” materials investigated, independent of the flexibility degree, show a strong band in the THz region at around 23 cm⁻¹. This band persists unchanged in the spectrum after desolvation of DUT-8(Ni)_rigid. Structural switching of DUT-8(Ni)_flex from the op to cp phase leads to the pronounced evolution in the low-wavenumber area, in general.

Fig. 2 Low-frequency Raman spectra of DUT-8(Ni) samples.

The strongest line around 23 cm⁻¹ characteristic for the open structure disappears and a new band at 59.8 cm⁻¹ is observed in the spectrum of desolvated DUT-8(Ni). Thus, this characteristic band can unambiguously characterize the state of the system (open/closed). The open system shows the typical line at ca. 23 cm⁻¹, the closed system – at ca. 60 cm⁻¹.

The Raman spectrum of desolvated, DUT-8(Ni)_flex has low-energy bands that are much broader compared to those of the open DUT-8(Ni) framework. The width of the low-energy Raman bands can be attributed to intermolecular interactions (π–π interactions) within the crystal in its closed pore form (Fig. 4).

Moreover, considering the range from 200 to 650 cm⁻¹, we found lines at 115, 398 and 571 cm⁻¹, which are present only in the spectrum of DUT-8(Ni)_flex. Thus, consideration of the spectral region up to 700 cm⁻¹ (Table S3, ESI†) shows that the experimental results are in agreement with the group theoretical analysis prediction (discussed in Section 2.1).

Since the lattice vibrations in soft porous crystals are connected with framework flexibility, they may be reflected in the local elastic properties and reveal a signature of the structural flexibility of the soft porous crystals.

Coudert and co-workers studied the elastic properties including the Young's modulus and shear modulus for the typical representative of pillared layer MOFs, DMOF-1,³⁵ with the composition Zn₂(bdc)₂(dabco) (bdc – terephthalate) and revealed the presence of high anisotropy of the Young's modulus (Fig. 3).³⁶ Since DUT-8 is isoreticular to DMOF-1, where the terephthalates are replaced by 2,6-napthalenedicarboxylates, similar anisotropy and the presence of similar directions of very low Young's modulus are expected.

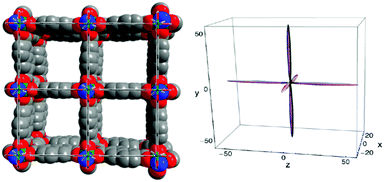Fig. 3 Left: View of the crystal structure of as made DUT-8(Ni) along channels (along crystallographic c axis); right: the directional Young's modulus for DMOF-1 represented as 3D surfaces, with axes tick labels in GPa ³⁶ (Copyright©2012 American Physical Society).

The stiff directions correspond to the positions of naphthylene dicarboxylate linkers in the structure, along [110] and [−110], and Ni₂(dabco)-chains along [001] in the open phase of DUT-8(Ni).²³ The soft directions in DUT-8(Ni) op, corresponding to the breathing mode along a and b axes, should coincide with the directions of strong collective lattice vibrations (Fig. 4).

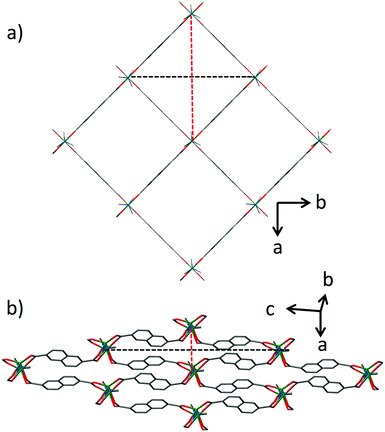Fig. 4 Crystal structure of DUT-8(Ni): (a) the open pore phase; (b) the close pore phase. The soft directions are indicated as dashed lines.

BOMD simulations performed on the open pore form of DUT-8(Ni) indeed show the oscillation of the breathing mode along the soft directions mentioned above (Fig. 5).

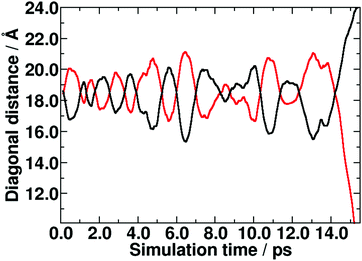Fig. 5 Oscillation of the breathing mode in the open pore form of DUT-8(Ni) during the MD simulation. The colors of the lines correspond to the diagonals indicated in Fig. 4a.

Seven periods in the breathing mode for ca. 12.3 picoseconds correspond to the frequency of 0.57 THz or approximately 18 cm⁻¹. This value is in good agreement with the value of 23 cm⁻¹ obtained from the Raman spectrum.

BOMD calculations performed for the close pore structure show that the directions of oscillation are not equivalent, i.e. oscillations along the short diagonal have a lower frequency compared to those along the long diagonal (Fig. 6). Ten periods in the breathing mode of the long diagonal for ca. 6 picoseconds correspond to 1.5 THz or approximately 50 cm⁻¹, confirming the experimental shift of the peak to the higher wave numbers (59 cm⁻¹).

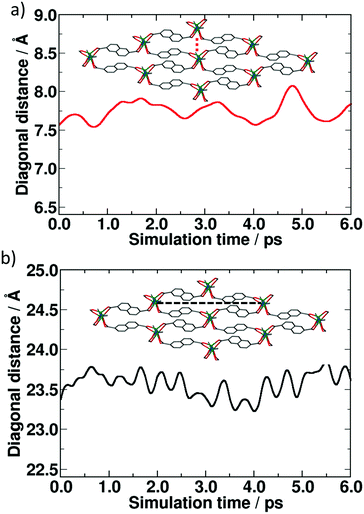Fig. 6 Oscillation of the breathing mode in the closed form of DUT-8(Ni) during the MD simulation: (a) short diagonal, (b) long diagonal.

In order to confirm the directional character of low-frequency vibrations in DUT-8, we investigated the orientation dependence of the Raman spectra. Symmetry types of vibrations are attributed to polarization measurements of the spectra obtained on oriented samples. The lines corresponding to vibrations of different symmetry should manifest at different polarizations of incident and scattered radiation.^37–45

A clear angular dependence of the Raman signal (Fig. 7) was observed for single crystals of DUT-8(Ni)_flexible in its open as well as closed state. The characteristic signal at 23.4 cm⁻¹ for as made DUT-8(Ni)_flex reaches the highest intensity at ca. 90 and 270° of rotation as it would be expected from the changed crystal orientation (a, b vs. c axis) with respect to the incident light beam (see Fig. S2 and S3 ESI†).

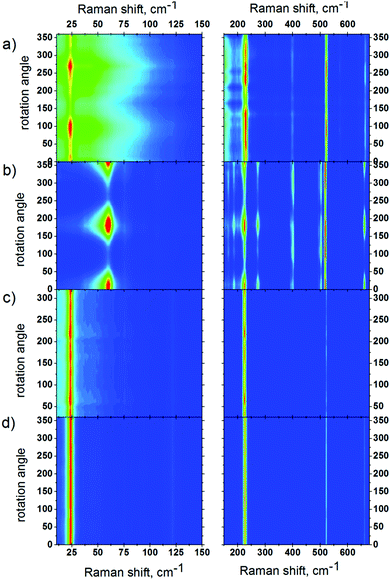Fig. 7 Rotation maps of VV polarization for as made DUT-8(Ni)_flex (a); desolvated DUT-8(Ni)_flex (b); as made DUT-8(Ni)_rigid (c); desolvated DUT-8(Ni)_rigid (d) samples.

This signal shifts to 59.8 cm⁻¹ after structure closing, maintaining, as expected, a similar angular dependence for open and closed pore structures.

The angular dependence confirms the directional character of low frequency vibrations, whereas in the c direction no signal is observed, and the signal is most intense perpendicular to c.

For the polycrystalline DUT-8(Ni)_rigid sample such an angular dependence could not be observed, due to the statistical orientation of the crystallites of the powdered sample in the beam. (The size of DUT-8(Ni)_rigid crystals is below 1 μm, therefore it was not possible to investigate a single crystal.)

4. Conclusions

The present Raman scattering study on the DUT-8 (Ni) metal–organic framework system shows a significant difference in the low-frequency region for open (23 cm⁻¹ line) and closed (60 cm⁻¹ line) pore forms of DUT-8(Ni). The results of BOMD simulations are in good agreement with experimental findings and support the assignment of the soft breathing modes, and thus characterize the two otherwise very similar forms of DUT-8(Ni). The applied technique can be further established for monitoring the phase transitions in flexible MOF materials. The clear polarization anisotropy of Raman lines for DUT-8(Ni) samples opens up new horizons for using this technique for the precise determination of the “breathing” direction in the MOF crystals. These low-frequency vibrations seem to be highly suited to distinguishing rigid vs. flexible and open vs. closed samples as well as to studying switching phenomena in metal–organic frameworks.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the DFG for financial support (FOR 2433). ZIH Dresden is thanked for access to its high performance computing facilities. The authors are grateful to Dr S. N. Krylova for valuable symmetry analysis discussion.

Notes and references

1. S. Horike, S. Shimomura and S. Kitagawa, Nat. Chem., 2009, 1, 695.
2. A. Schneemann, V. Bon, I. Schwedler, I. Senkovska, S. Kaskel and R. A. Fischer, Chem. Soc. Rev., 2014, 43, 6062.
3. Handbook of Photonics for Biomedical Science, ed. V. V. Tuchin, CRC Press, 2010, p. 868.
4. S. E. Dobbins, V. I. Lesk and M. J. E. Sternberg, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 10390.
5. R. C. Batra and S. S. Gupta, J. Appl. Mech., 2008, 75, 061010.
6. M. Milnera, J. Kürti, M. Hulman and H. Kuzmany, Phys. Rev. Lett., 2000, 84, 1324.
7. M. R. Ryder, B. Civalleri, T. D. Bennett, S. Henke, S. Rudić, G. Cinque, F. Fernandez-Alonso and J.-C. Tan, Phys. Rev. Lett., 2014, 113, 215502.
8. N. Y. Tan, M. T. Ruggiero, C. Orellana-Tavra, T. Tian, A. D. Bond, T. M. Korter, D. Fairen-Jimenez and J. A. Zeitler, Chem. Commun., 2015, 51, 16037.
9. M. R. Ryder, B. Civalleri, G. Cinque and J.-C. Tan, CrystEngComm, 2016, 18, 4303.
10. Y. H. Hu and L. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 174103.
11. N. R. Dhumal, M. P. Singh, J. A. Anderson, J. Kiefer and H. J. Kim, J. Phys. Chem. C, 2016, 120, 3295.
12. Y. Chen, J. Zhang, J. Li and J. V. Lockard, J. Phys. Chem. C, 2013, 117, 20068.
13. H. C. Garcia, R. Diniz, M. I. Yoshida and L. F. C. de Oliveira, J. Mol. Struct., 2010, 978, 79.
14. M.-H. Zeng, Z. Yin, Y.-X. Tan, W.-X. Zhang, Y.-P. He and M. Kurmoo, J. Am. Chem. Soc., 2014, 136, 4680.
15. T. D. Petersen, G. Balakrishnan and C. L. Weeks, Dalton Trans., 2015, 44, 12824.
16. K. Tan, N. Nijem, Y. Gao, S. Zuluaga, J. Li, T. Thonhauser and Y. J. Chabal, CrystEngComm, 2015, 17, 247.
17. A. Centrone, D. Y. Siberio-Pérez, A. R. Millward, O. M. Yaghi, A. J. Matzger and G. Zerbi, Chem. Phys. Lett., 2005, 411, 516.
18. N. Nijem, P. Canepa, L. Kong, H. Wu, J. Li, T. Thonhauser and Y. J. Chabal, J. Phys.: Condens. Matter, 2012, 24, 424203.
19. N. Nijem, P. Thissen, Y. Yao, R. C. Longo, K. Roodenko, H. Wu, Y. Zhao, K. Cho, J. Li, D. C. Langreth and Y. J. Chabal, J. Am. Chem. Soc., 2011, 133, 12849.
20. D. Y. Siberio-Perez, A. G. Wong-Foy, O. M. Yaghi and A. J. Matzger, Chem. Mater., 2007, 19, 3681.
21. Z. Wang, A. Błaszczyk, O. Fuhr, S. Heissler, C. Wöll and M. Mayor, Nat. Commun., 2017, 8, 1.
22. N. Klein, C. Herzog, M. Sabo, I. Senkovska, J. Getzschmann, S. Paasch, M. R. Lohe, E. Brunner and S. Kaskel, Phys. Chem. Chem. Phys., 2010, 12, 11778.
23. V. Bon, N. Klein, I. Senkovska, A. Heerwig, J. Getzschmann, D. Wallacher, I. Zizak, M. Brzhezinskaya, U. Mueller and S. Kaskel, Phys. Chem. Chem. Phys., 2015, 17, 17471.
24. N. Kavoosi, V. Bon, I. Senkovska, S. Krause, C. Atzori, F. Bonino, J. Pallmann, S. Paasch, E. Brunner and S. Kaskel, Dalton Trans., 2017, 46, 4685.
25. M. Krack and M. Parrinello, Quickstep: make the atoms dance NIC, Jülich, 2004.
26. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167(2), 103.
27. CP2K. http://https://www.cp2k.org.
28. G. Lippert, J. Hutter and M. Parrinello, Mol. Phys., 1997, 92(3), 477.
29. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77(18), 3865.
30. S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(3), 1703.
31. C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58(7), 3641.
32. M. Krack, Theor. Chem. Acc., 2005, 114(1-3), 145.
33. J. VandeVondele and J. Hutter, J. Chem. Phys., 2003, 118(10), 4365.
34. J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127(11), 114105.
35. D. N. Dybtsev, H. Chun and K. Kim, Angew. Chem., Int. Ed., 2004, 43, 5033.
36. A. U. Ortiz, A. Boutin, A. H. Fuchs and F.-X. Coudert, Phys. Rev. Lett., 2012, 109, 195502.
37. A. S. Oreshonkov, J. V. Gerasimova, A. A. Ershov, A. S. Krylov, K. A. Shaykhutdinov, A. N. Vtyurin, M. S. Molokeev, K. Y. Terent’ev and N. V. Mihashenok, J. Raman Spectrosc., 2016, 47, 531.
38. M. C. Munisso, W. Zhu and G. Pezzotti, Phys. Status Solidi B, 2009, 246, 1893.
39. K. Fukatsu, W. Zhu and G. Pezzotti, Phys. Status Solidi B, 2010, 247, 278.
40. Y. Fujii, M. Noju, T. Shimizu, H. Taniguchi, M. Itoh and I. Nishio, Ferroelectrics, 2014, 462, 8.
41. G. Pezzotti, H. Sueoka, A. A. Porporati, M. Manghnani and W. Zhu, J. Appl. Phys., 2011, 110, 013527.
42. L. Puppulin, M. Kotaki, M. Nakamura, D. Iba, I. Moriwakic and G. Pezzotti, J. Raman Spectrosc., 2012, 43, 1957.
43. A. Ahlawat, D. K. Mishra, V. G. Sathe, R. Kumar and T. K. Sharma, J. Phys.: Condens. Matter, 2013, 25, 025902.
44. T. Sander, S. Eisermann, B. K. Meyer and P. Klar, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 165208.
45. M. A. Rafiq, P. Supancic, M. E. Costa, P. M. Vilarinho and M. Deluca, Appl. Phys. Lett., 2014, 104, 011902.

---

Footnote

† Electronic supplementary information (ESI) available: Photographs of the crystals investigated and powder XRD patterns. See DOI: 10.1039/c7cp06225g

---