Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
LK peptide side chain dynamics at interfaces are independent of secondary structure†
Michael A.
Donovan
 a,
Helmut
Lutz
a,
Yeneneh Y.
Yimer
b,
Jim
Pfaendtner
a,
Helmut
Lutz
a,
Yeneneh Y.
Yimer
b,
Jim
Pfaendtner
 b,
Mischa
Bonn
b,
Mischa
Bonn
 a and
Tobias
Weidner
a and
Tobias
Weidner
 *abc
*abc
aMax Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany
bDepartment of Chemical Engineering, University of Washington, 105 Benson Hall, Seattle, WA 98195, USA
cDepartment of Chemistry, Aarhus University, Langelandsgade 140, 8000 Aarhus C, Denmark. E-mail: weidner@chem.au.dk
First published on 9th October 2017
Abstract
Protein side chain dynamics are critical for specific protein binding to surfaces and protein-driven surface manipulation. At the same time, it is highly challenging to probe side chain motions specifically at interfaces. One important open question is the degree to which the motions of side chains are dictated by local protein folding or by interactions with the surface. Here, we present a real-time measurement of the orientational dynamics of leucine side chains within leucine–lysine (LK) model peptides at the water–air interface, with three representative peptide folds: α-helix, 310-helix and β-strand. The results, modeled and supported by molecular dynamics simulations, show that the different peptide folds exhibit remarkably similar sub-picosecond orientational side chain dynamics at the air/water interface. This demonstrates that the side chain motional dynamics is decoupled from the local secondary structure.
Proteins are highly dynamic entities, and protein dynamics have direct implications for protein structure and function.1,2 Side chains play a role in protein driven surface manipulation,3 enzymatic catalysis,4,5 and in protein-protein interactions.6 In addition, they undergo rotameric transitions7 and perform torsional motions on pico- to nanosecond timescales.1,8–10 Protein side chain dynamics are typically determined via NMR spectroscopy through linewidth measurements where changes in conformational entropy can be inferred.1,11–19 NMR can track changes in a protein's chemical environment upon complexation and has been used to show that, in solution, side chain dynamics of methyl containing residues can provide insights about different local environments within a protein.6 The dynamics are not monitored directly in real time, however, but they are inferred from spectral line shapes.11,20
An advantage of electronic22–24 and vibrational25,26 spectroscopic methods is that they can directly resolve sub-picosecond events and thereby provide direct insight into how protein side chains move.
Specifically at interfaces, information about protein side chain dynamics on pico-second timescales has been lacking. Yet side chain motions are particularly important here, since they mediate the contact to the interface and play a role in the recognition of hard and soft tissue.13,27,28 The understanding of these dynamic interactions can help unravel key biological processes from biomineralization,11,21 protein membrane interactions,29 host–guest interactions,6,30 to the specific protein recognition of mineral surfaces.31
One important question is the impact of local folding within proteins on the dynamics of side chains when interacting with surfaces. Here, leucine–lysine (LK) peptides provide an ideal model system. LK peptides are known to form well-defined secondary structures at hydrophobic, hydrophilic and aqueous interfaces based on their hydrophobic periodicity (Scheme 1).13,21,32,33 At the air/water interface, hydrophobic leucine side chains point toward the vapor phase whereas hydrophilic lysines are oriented towards the aqueous phase.21 In this study, we probe leucine dynamics of LKs folding into α helices (LKα14: Ac-LKKLLKLLKKLLKL-OH), β strands (LKβ15: Ac-LKLKLKLKLKLKLKL-OH), and 310 helices (LK310: Ac-LLKLLKLLKLLKL-OH). These peptides have been studied extensively as model systems for protein–surface interactions and therefore provide an ideal starting point to explore interfacial protein dynamics.13,21,27,33–35
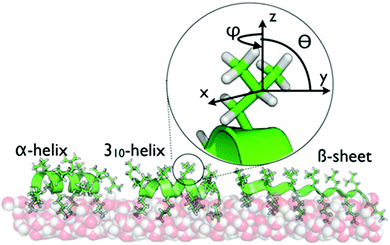 | ||
| Scheme 1 The secondary structures of LKα14, LK310, and LKβ15 at the air/water interface are dictated by the hydrophobic periodicity of the amino acid sequence. The peptides have been previously shown to bind with the indicated foldings.21 Hydrophobic leucine side chains are exposed to the vapor phase while the hydrophilic lysines remain hydrated in the water phase. The inset shows the geometry of the leucine sites used in this study. | ||
Previously, interface-specific time-resolved vibrational spectroscopy has helped unveil the orientational dynamics of a monomeric leucine amino acid at the air/water interface. It was shown that the methyl units reoriented diffusively on a time scale of 20 ps with diffusivities of Dφ = 0.07 rad2 ps−1 in the plane of the surface and Dθ = 0.05 rad2 ps−1 out of plane36 (see Scheme 1 for definition of angles). Here we report on how the folding of the peptide backbone affects ultrafast motions by following the dynamics of leucine side chains in LK peptides with different folds at the air/water interface using time-and polarization-resolved sum-frequency generation spectroscopy (TPSFG).37–39 We quantify the results through the help of numerical modelling and molecular dynamics (MD) simulations.
TPSFG is a time resolved variant of surface-sensitive SFG.40–46 In TPSFG, an intense, linearly polarized IR pump pulse partially depletes the vibrational ground state within a sub-ensemble of molecules whose vibrational transition moment is oriented preferentially along the pump polarization direction. Orientational motion and vibrational energy transfer can be followed while the excited vibrational group relaxes back to equilibrium.37–39 When the pump polarization is parallel (||) to that of the probe, the signal decays due to both intramolecular vibrational relaxation (IVR) and orientational motions back into the plane (ip) of the surface, whereas when the pump direction is orthogonal (⊥), IVR and out of plane motions (oop) are most efficiently sampled.
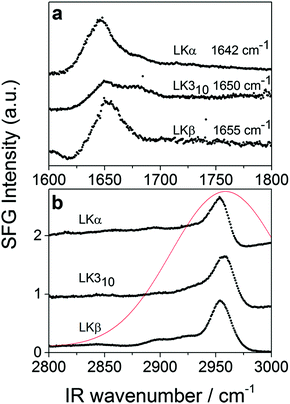
To verify the interfacial secondary structure for the LK peptides, we have first recorded static ssp (s polarized SF, s polarized Vis, p polarized IR) SFG spectra in the amide-I region. The spectra are shown in Fig. 1a, and display intense resonances ranging from 1642 cm−1 for LKα14 to 1655 cm−1 for LKβ15. These resonance positions are in agreement with published values47 for the target folds.
The time-resolved experiments focus on the leucine methyl C–H resonances. Representative static sps (s polarized SF, p polarized VIS, s polarized IR probe) spectra of the C–H region are shown in Fig. 1b for 0.1 mg mL−1 solutions of three different folds of LK peptide adsorbed to the air/D2O interface. This polarization combination is chosen based on our previous study with leucine.36 Qualitatively, all three spectra show an intense resonance at 2958 cm−1 which is assigned to the methyl in-plane asymmetric (AS) stretch.21 It is this AS stretching mode we are predominantly exciting with an intense mid-IR pump pulse which spans the entire aliphatic stretching region (Fig. 1b). The pump polarization is alternated between s (||) and p (⊥) to generate the traces for the signal near 2958 cm−1 shown in Fig. 2. The data in Fig. 2 show the ground state bleach of the methyl AS stretch mode around zero delay between pump and probe followed by subsequent recovery of the signal. The solid lines which follow the recovery of the signal are numerically simulated according to reference37 and will be discussed later in the text.
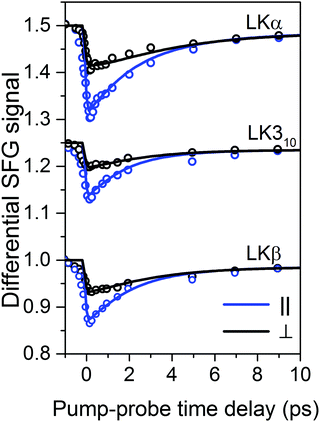 | ||
| Fig. 2 Transient SFG traces of LKα14, LK310, and LKβ15 adsorbed to the air/D2O interface: experimental pump–probe transients of LK peptides adsorbed to the air/D2O interface (open circles) along with numerically simulated orientation-dependent dynamic response (solid lines). The corresponding inferred diffusion coefficients Dθ and Dφ are summarized in Table 1. Traces are offset for clarity. | ||
For a first approximation of the relaxation times, we can fit the signal recovery rates k(‖,⊥) = 1/τ(‖,⊥) with exponential kinetics (see ESI† for fits and further discussion). The results are summarized in Table 1. Importantly, the fits show that the parallel relaxation is significantly faster compared to the perpendicular dynamics, which shows that reorientation must contribute to the measured signals.39
| Peptide | τ 1,‖ (ps) | τ 1,⊥ (ps) | T sim1 (ps) | D φ (rad2 ps−1) | D θ (rad2 ps−1) | θ 0 (degree) |
|---|---|---|---|---|---|---|
| LKα14 |
2.99
(0.24) |
4.89
(0.71) |
3.3 |
0.12
(0.04) |
0.06
(0.01) |
62 |
| LKβ15 |
2.43
(0.29) |
5.57
(0.59) |
2.5 |
0.13
(0.02) |
0.04
(0.01) |
62 |
| LK310 |
2.08
(0.27) |
3.63
(0.58) |
2.2 |
0.13
(0.02) |
0.05
(0.01) |
63 |
The polarized excitation pulse temporarily changes the symmetry at the surface and transient tensor elements add to the signal.37 This complicates the direct quantitative analysis.
In addition, the experimentally measured traces are underdetermined since the signal recovery of the transient data depends on three time constants: the vibrational relaxation time T1, the in-plane diffusivity Dφ, and the out-of-plane diffusivity Dθ.
In the limiting case for small angular spread Δθ (i.e. Δθ ≪ sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ0) and negligible out of plane motion, a convenient way to determine the molecular diffusion directly is to analyze the anisotropy decay (see ESI† for details).37,48 The in plane diffusivity Dφ can, in this limiting case, be determined directly by plotting the anisotropy decay between the parallel and perpendicularly pumped traces.37 However, since the present peptide systems allow a broad distribution of side chain conformations and out-of-plane motion it is not a priori apparent that this would be a reliable approach here.
θ0) and negligible out of plane motion, a convenient way to determine the molecular diffusion directly is to analyze the anisotropy decay (see ESI† for details).37,48 The in plane diffusivity Dφ can, in this limiting case, be determined directly by plotting the anisotropy decay between the parallel and perpendicularly pumped traces.37 However, since the present peptide systems allow a broad distribution of side chain conformations and out-of-plane motion it is not a priori apparent that this would be a reliable approach here.
We therefore performed molecular dynamics (MD) simulations to track the peptide dynamics and to combine the experimental data with theoretical transients calculated from the MD data.
The combination of MD and time resolved SFG has recently been successfully applied to monomeric leucine adsorbed at the air–water interface.36 The method uses MD simulation of the interfacial LK peptide dynamics as a basis for a numerical model37 to calculate the time-resolved SFG response. The numerical model requires information about (i) the static molecular orientation, defined by the mean tilt angle θ0 and the angular spread Δθ; (ii) the orientational in plane and out of plane diffusivities (Dφ, Dθ); and (iii) the vibrational relaxation time T1.
To computationally determine the molecular orientation and the reorientational diffusion of the methyl groups of leucine at the vacuum/water interface, we performed all-atom MD simulations at 298 K. Three separate simulations were performed for a layer of 23 molecules of LKα14, LKβ15, and LK310. Further details about the simulations are presented in the ESI.† Briefly, the peptides were packed as a layer on 8 by 8 nm in between a 6.8 nm thick slab of water and 7 nm of vacuum. To approximate experimental conditions, phosphate ions were added, and the box was neutralized by adding chloride ions. Note that while the simulations can provide, θ0, Δθ, Dφ and Dθ, it cannot provide T1. Table 1 lists guessed values of T1 defined as T1sim which are arrived at by finding the best visual fit to the data (see ESI† Section IV). T1 values determined experimentally are labelled T1 and found in ESI† Table S1.
After an equilibration period of 100 ns, 5 ns were simulated with coordinates being written to a trajectory file with a frequency of 4 fs for analysis. As expected for a peptide layer with random in-plane orientation, the azimuthal φ angles showed no predominant orientation for all peptides (see ESI†). The mean tilt angle θ0 and the angular spread Δθ were obtained from a Gaussian fit (see ESI† for details) to the methyl group distributions shown in Fig. 3. The mean tilt angles θ0 for the respective α, β, and 310 folds where 62°, 62°, and 63° with angular spreads Δθ of 32°, 39°, and 29°, respectively. This shows that the assumption of the limiting case of only in-plane reorientation is not applicable. The in- and out-of-plane methyl reorientational diffusion coefficients Dφ and Dθ were determined by first numerically solving the two-dimensional rotational diffusion equation for a specific set of (Dφ, Dθ). Then the square of residuals, χ2, between the thus calculated results and the simulation derived time-dependent methyl group angle dependent (i.e. f(θ, φ)) population distributions was calculated (Fig. 3b see ESI† for details). We determined that χ2 for α, and β, and 310 peptides exhibit minima for the out-of-plane diffusion Dθ at respectively 0.06 ± 0.01, 0.04 ± 0.01, and 0.05 ± 0.01 rad2 ps−1 and for the in-plane diffusion Dφ at 0.12 ± 0.04, 0.13 ± 0.02, and 0.13 ± 0.02 rad2 ps−1 (Fig. 3a–c). The simulations thus indicate that leucine methyl groups reorient – on average – at twice the rate in-plane than out-of-plane, but with no significant differences between the respective folds.
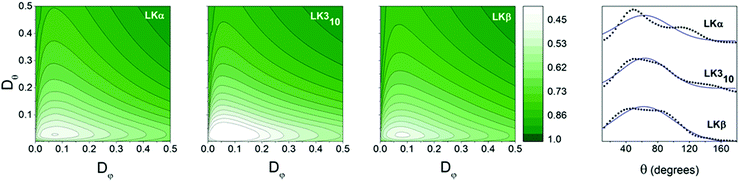 | ||
| Fig. 3 Orientational information: contour plots: variation of χ2 with Dφ and Dθ for methyl groups of LK peptides at the air–water interface. Dφ and Dθ are inferred from the point for which the variance χ2 is at a minimum. Values for all three peptides may be found in Table 1. Far right: Orientation distributions of leucine methyl groups in LK peptides at the air/water interface in black. Gaussian fits are shown with blue line. | ||
The vibrational relaxation times Tsim1 used for the numerical simulation37 to produce the traces in Fig. 2 were initially approximated to be close to previously reported values of ∼3 ps for methyl stretching vibrations of long aliphatic chains;26,38,49 precise values were subsequently obtained by choosing vibrational relaxation times which give the best visual fit to the experimental data. It is interesting to note, that the α-helix motif showed a slower vibrational relaxation compared to the β-strand and 310-helix. This is, in line with reports by Backus and Stock et al., who have shown that structural flexibility within peptides in solution enhances vibrational energy transfer.50,51 Plotting the number of peptide–peptide hydrogen bonds (see ESI†) showed that LKα14 has indeed the largest number of H-bonds.
The simulated transient SFG responses for the different peptide folds with orientational parameters obtained from MD are shown as solid lines in Fig. 2. The obtained theoretical traces capture the signal depletion and recovery in the experimental data very well. The close match between theory and experiment confirms the peptide side chain dynamics obtained from simulation and shows that the methyl reorientation dynamics are, within the error margins, independent of the folding of the peptide backbone.
It is interesting to compare dynamics of the leucine side chains within peptides monomeric leucines at the air–water interface. The out of plane dynamics are very similar for the peptide-bound leucine as compared to monomeric leucine, with a diffusivity of ca. 0.06 rad2 ps−1 for the peptides and 0.05 rad2 ps−1 for the monomers. The in plane diffusivity, however, is sped up by a factor of two with an average diffusivity of 0.12 rad2 ps−1 for the peptides and 0.07 rad2 ps−1 for the isolated leucine. Likely, the binding geometry and lateral proximity between neighbouring leucines enforced by the peptide backbone leads to more rapid motion within the surface plane. Going to much larger proteins, the reorientational time scales found for the LKs are comparable with methyl groups within the hydrophobic core of globular proteins (5–80 ps) as determined with NMR.12
Conclusions
Our data show that at the interface the side chain orientational dynamics are independent of the backbone folding. This is surprising in view of the diversity of steric environments side chain groups experience within helical and strand-like folding motifs within peptide monolayers. This independence of backbone structure also means that large, complex proteins with unknown interfacial folding can be studied using time-resolved SFG. While the present study uses model peptides and can only provide a first view of the role of folding for side chain dynamics, the study is a first step understanding this aspect of functional dynamics beyond the traditional structure-function paradigm.Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. D. acknowledges financial support from the International Max Planck Research School, Cho-Shuen Hsieh, Johannes Franz, and Ruth Livingstone for discussion and for providing the Matlab code to analyze experimental data. T. W. thanks the Deutsche Forschungsgemeinschaft (WE 4478/4-1) and the Aarhus University Research Foundation (AUFF). J. P. acknowledges support from NSF award CBET-1264459 and the Hyak supercomputer system supported in part by UW-IT. Open Access funding provided by the Max Planck Society.Notes and references
- J. R. Lewandowski, M. E. Halse, M. Blackledge and L. Emsley, Science, 2015, 348, 578–581 CrossRef CAS PubMed
.
- A. B. Law, P. J. Sapienza, J. Zhang, X. Zuo and C. M. Petit, J. Am. Chem. Soc., 2017, 139, 3599–3602 CrossRef CAS PubMed
.
- T. Weidner, M. Dubey, N. F. Breen, J. Ash, J. E. Baio, C. Jaye, D. A. Fischer, G. P. Drobny and D. G. Castner, J. Am. Chem. Soc., 2012, 134, 8750–8753 CrossRef CAS PubMed
.
- K. E. Bowers and C. A. Fierke, Biochemistry, 2004, 43, 5256–5265 CrossRef CAS PubMed
.
- Z. Wang, C. E. Bertrand, W.-S. Chiang, E. Fratini, P. Baglioni, A. Alatas, E. E. Alp and S.-H. Chen, J. Phys. Chem. B, 2013, 117, 1186–1195 CrossRef CAS PubMed
.
- A. L. Lee, S. A. Kinnear and A. J. Wand, Nat. Struct. Mol. Biol., 2000, 7, 72–77 CAS
.
- P. Schanda, M. Huber, J. Boisbouvier, B. H. Meier and M. Ernst, Angew. Chem., Int. Ed., 2011, 50, 11005–11009 CrossRef CAS PubMed
.
- K. A. Henzler-Wildman, M. Lei, V. Thai, S. J. Kerns, M. Karplus and D. Kern, Nature, 2007, 450, 913–916 CrossRef CAS PubMed
.
- O. F. Lange, N.-A. Lakomek, C. Farès, G. F. Schröder, K. F. A. Walter, S. Becker, J. Meiler, H. Grubmüller, C. Griesinger and B. L. de Groot, Science, 2008, 320, 1471 CrossRef CAS PubMed
.
- R. G. Smock and L. M. Gierasch, Science, 2009, 324, 198 CrossRef CAS PubMed
.
-
R. Adrienne, A. Jason, Z. Ariel, L. M. David, J. G. Jeffrey, G. Gil and D. Gary, Proteins at Interfaces III State of the Art, American Chemical Society, 2012, vol. 1120, ch. 4, pp. 77–96 Search PubMed
.
- L. K. Nicholson, L. E. Kay, D. M. Baldisseri, J. Arango, P. E. Young, A. Bax and D. A. Torchia, Biochemistry, 1992, 31, 5253–5263 CrossRef CAS PubMed
.
- T. Weidner, N. F. Breen, K. Li, G. P. Drobny and D. G. Castner, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 13288–13293 CrossRef CAS PubMed
.
- L. Vugmeyster, D. Ostrovsky, T. Villafranca, J. Sharp, W. Xu, A. S. Lipton, G. L. Hoatson and R. L. Vold, J. Phys. Chem. B, 2015, 119, 14892–14904 CrossRef CAS PubMed
.
- Y. Fu, V. Kasinath, V. R. Moorman, N. V. Nucci, V. J. Hilser and A. J. Wand, J. Am. Chem. Soc., 2012, 134, 8543–8550 CrossRef CAS PubMed
.
- T. Rajitha Rajeshwar, J. C. Smith and M. Krishnan, J. Am. Chem. Soc., 2014, 136, 8590–8605 CrossRef PubMed
.
- G. P. Lisi and J. P. Loria, Chem. Rev., 2016, 116, 6323–6369 CrossRef CAS PubMed
.
- T. I. Igumenova, K. K. Frederick and A. J. Wand, Chem. Rev., 2006, 106, 1672–1699 CrossRef CAS PubMed
.
- L. Vugmeyster, D. Ostrovsky, M. A. Clark, I. B. Falconer, G. L. Hoatson and W. Qiang, Biophys. J., 2016, 111, 2135–2148 CrossRef CAS PubMed
.
- L. Columbus and W. L. Hubbell, Trends Biochem. Sci., 2002, 27, 288–295 CrossRef CAS PubMed
.
- H. Lutz, V. Jaeger, R. Berger, M. Bonn, J. Pfaendtner and T. Weidner, Adv. Mater. Interfaces, 2015, 2, 1500282 CrossRef
.
- J. Bredenbeck, J. Helbing, J. R. Kumita, G. A. Woolley and P. Hamm, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 2379–2384 CrossRef CAS PubMed
.
- Y. Qin, L. Wang and D. Zhong, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 8424–8429 CrossRef CAS PubMed
.
- G. Zhang, J. Li, P. Cui, T. Wang, J. Jiang and O. V. Prezhdo, J. Phys. Chem. Lett., 2017, 1031–1037, DOI:10.1021/acs.jpclett.7b00311
.
- Y. S. Kim and R. M. Hochstrasser, J. Phys. Chem. B, 2009, 113, 8231–8251 CrossRef CAS PubMed
.
- A. Ghosh, M. Smits, J. Bredenbeck, N. Dijkhuizen and M. Bonn, Rev. Sci. Instrum., 2008, 79, 093907 CrossRef PubMed
.
- T. Weidner, N. F. Breen, G. P. Drobny and D. G. Castner, J. Phys. Chem. B, 2009, 113, 15423–15426 CrossRef CAS PubMed
.
- J. L. Lorieau, L. A. Day and A. E. McDermott, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 10366–10371 CrossRef CAS PubMed
.
- D. K. Schach, W. Rock, J. Franz, M. Bonn, S. H. Parekh and T. Weidner, J. Am. Chem. Soc., 2015, 137, 12199–12202 CrossRef CAS PubMed
.
- P. T. Corbett, J. Leclaire, L. Vial, K. R. West, J.-L. Wietor, J. K. M. Sanders and S. Otto, Chem. Rev., 2006, 106, 3652–3711 CrossRef CAS PubMed
.
-
Proteins at Interfaces III State of the Art, ed. T. Horbett, J. L. Brash and W. Norde, American Chemical Society, 2012, vol. 1120 Search PubMed
.
- G. Guiffo-Soh, B. Hernández, Y.-M. Coïc, F.-Z. Boukhalfa-Heniche and M. Ghomi, J. Phys. Chem. B, 2007, 111, 12563–12572 CrossRef CAS PubMed
.
- S. Roy, T. L. Naka and D. K. Hore, J. Phys. Chem. C, 2013, 117, 24955–24966 CAS
.
- G. J. Holinga, R. L. York, R. M. Onorato, C. M. Thompson, N. E. Webb, A. P. Yoon and G. A. Somorjai, J. Am. Chem. Soc., 2011, 133, 6243–6253 CrossRef CAS PubMed
.
- D. C. Phillips, R. L. York, O. Mermut, K. R. McCrea, R. S. Ward and G. A. Somorjai, J. Phys. Chem. C, 2007, 111, 255–261 CAS
.
- M. A. Donovan, Y. Y. Yimer, J. Pfaendtner, E. H. G. Backus, M. Bonn and T. Weidner, J. Am. Chem. Soc., 2016, 138, 5226–5229 CrossRef CAS PubMed
.
- H.-K. Nienhuys and M. Bonn, J. Phys. Chem. B, 2009, 113, 7564–7573 CrossRef CAS PubMed
.
- S. Yamamoto, A. Ghosh, H.-K. Nienhuys and M. Bonn, Phys. Chem. Chem. Phys., 2010, 12, 12909–12918 RSC
.
- C.-S. Hsieh, R. K. Campen, A. C. Vila Verde, P. Bolhuis, H.-K. Nienhuys and M. Bonn, Phys. Rev. Lett., 2011, 107, 116102 CrossRef PubMed
.
- X. D. Zhu, H. Suhr and Y. R. Shen, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 3047–3050 CrossRef CAS
.
- R. Lu, W. Gan, B.-H. Wu, H. Chen and H.-F. Wang, J. Phys. Chem. B, 2004, 108, 7297–7306 CrossRef CAS
.
- M. Fang and S. Baldelli, J. Phys. Chem. Lett., 2015, 6, 1454–1460 CrossRef CAS PubMed
.
- M. R. Watry and G. L. Richmond, J. Phys. Chem. B, 2002, 106, 12517–12523 CrossRef CAS
.
- N. Ji and Y.-R. Shen, J. Chem. Phys., 2004, 120, 7107–7112 CrossRef CAS PubMed
.
- M. Sovago, R. K. Campen, G. W. H. Wurpel, M. Müller, H. J. Bakker and M. Bonn, Phys. Rev. Lett., 2008, 100, 173901 CrossRef PubMed
.
- M. Vinaykin and A. V. Benderskii, J. Phys. Chem. B, 2013, 117, 15833–15842 CrossRef CAS PubMed
.
- A. Barth and C. Zscherp, Q. Rev. Biophys., 2003, 35, 369–430 CrossRef
.
- D. Zimdars, J. I. Dadap, K. B. Eisenthal and T. F. Heinz, J. Phys. Chem. B, 1999, 103, 3425–3433 CrossRef CAS
.
- M. Smits, A. Ghosh, J. Bredenbeck, S. Yamamoto, M. Müller and M. Bonn, New J. Phys., 2007, 9, 390 CrossRef
.
- E. H. G. Backus, R. Bloem, R. Pfister, A. Moretto, M. Crisma, C. Toniolo and P. Hamm, J. Phys. Chem. B, 2009, 113, 13405–13409 CrossRef CAS PubMed
.
- S. Buchenberg, N. Schaudinnus and S. Gerhard, J. Chem. Theory Comput., 2015, 11, 1330–1336 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details, simulation details, and additional modelling. See DOI: 10.1039/c7cp05897g |
| This journal is © the Owner Societies 2017 |