Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Interplay between the folding mechanism and binding modes in folding coupled to binding processes†
Rajendra
Sharma
 ab,
David
De Sancho
ab,
David
De Sancho
 *cd and
Victor
Muñoz
*cd and
Victor
Muñoz
 *abe
*abe
aNational Biotechnology Center, CSIC, Madrid 28049, Spain
bIMDEA Nanoscience, Madrid 28049, Spain
cIKERBASQUE, Basque Foundation for Science, Bilbao, 48013, Spain
dCIC nanoGUNE, San Sebastian 20018, Spain. E-mail: d.desancho@nanogune.eu
eDepartment of Bioengineering, University of California Merced, Merced, CA 95340, USA. E-mail: vmunoz3@ucmerced.edu
First published on 18th October 2017
Abstract
Proteins that fold upon binding to their partners exhibit complex binding behavior such as induced-fit. But the connections between the folding mechanism and the binding mode remain unknown. Here we focus on the high affinity complex between the physiologically and marginally unstable, fast folder PSBD and the E1 subunit of pyruvate dehydrogenase. Using coarse-grained simulations we investigate the binding to E1 of a partially disordered PSBD under two folding scenarios: two-state and downhill. Our simulations show that induced-fit binding requires that PSBD folds–unfolds in the downhill folding regime. In contrast, a two-state folding PSBD must fold completely before it binds. The reason is that effective coupling between folding and binding involves partially folded conformations, which are only sufficiently populated under the downhill folding regime. Our results establish a direct mechanistic link between complex binding and downhill folding, supporting the idea that PSBD operates functionally as a conformational rheostat.
Recent developments are unveiling a plethora of exceptions to the classical paradigm by which proteins fold into unique 3D structures in a single stroke (two-state folding) and bind to their partners in a lock-and-key fashion. The experimental identification of proteins that fold downhill1 confirmed a key prediction of the energy landscape theory2 and expanded the palette of folding behaviors. Downhill proteins lose/gain the native structure gradually, eventually leading to one-state folding when the barrier disappears altogether.3 Such gradual disorder has been characterized at atomic resolution by NMR,4,5 kinetically using ultrafast methods,6 and in individual molecules.7 On the binding front, we now know that intrinsically disordered proteins (IDPs) can fold upon binding8 in a process that may provide kinetic advantages (“fly-casting”)9 and result in complex binding phenomena such as induced-fit and conformational selection.10 Some IDPs morph upon binding to structurally diverse partners,11–13 and others exhibit sophisticated allosteric behavior.14 Interestingly, there is a direct connection between fast, non-cooperative folding and the marginal stability of the native fold that leads to intrinsic disorder.15 Downhill folding and IDPs thus seem to be two sides of the same coin. It has been in fact proposed that the structural malleability and complex binding modes found on IDPs may require that the protein folds downhill, in which case IDPs could be operating as conformational rheostats rather than conventional switches.16
Here we focus on the case of the pyruvate dehydrogenase complex (PDC),17 a large macromolecular assembly composed of multiple copies of three types of subunits. In this complex a small domain from the central flexible region of E2 (PSBD) binds to both E1 and E3, and it is key to the swinging arm mechanism that channels substrates.17 Folding studies have shown that PSBDs are marginally stable downhill folders that have been tuned by natural selection to be partially unfolded (disordered) at the living temperature of the host organism.18,19 In parallel, the binding processes of E1 and E3 to PSBD occur with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
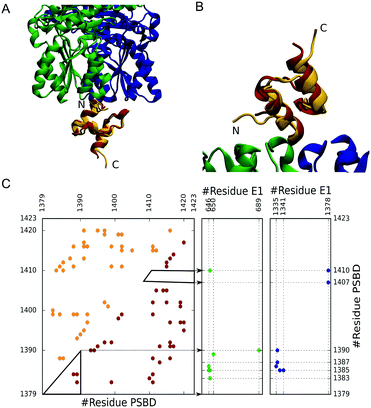
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry, are mutually exclusive, and are of very high affinity (sub-nanomolar KD).20 Yet, the structures of PSBD bound to E1 and E3 reveal strikingly superficial binding interfaces (Fig. 1A and B) with few intermolecular contacts (Fig. 1C). In these complexes PSBD exhibits very high B-factors that hint at the presence of conformational heterogeneity in the bound state.21,22 Here we are interested in the role that downhill folding may play in the binding properties of PSBD. In particular, we focus on the E1–PSBD complex (Fig. 1).
1 stoichiometry, are mutually exclusive, and are of very high affinity (sub-nanomolar KD).20 Yet, the structures of PSBD bound to E1 and E3 reveal strikingly superficial binding interfaces (Fig. 1A and B) with few intermolecular contacts (Fig. 1C). In these complexes PSBD exhibits very high B-factors that hint at the presence of conformational heterogeneity in the bound state.21,22 Here we are interested in the role that downhill folding may play in the binding properties of PSBD. In particular, we focus on the E1–PSBD complex (Fig. 1).
To investigate the coupling between PSBD folding and binding to E1, we used coarse-grained simulations, which allow us to control the folding scenario of PSBD and thus investigate the link between folding properties and binding modes. We model the PSBD folding using the Karanicolas and Brooks (KB) model, which is Gō-like, represents the protein geometry using the Cα trace (with harmonic potentials for angles and bonds), and contains statistical energy terms for torsions as well as a native-centric pairwise contact potential23 (see the ESI† for details). We parameterized the KB model from the contacts derived from a high-quality NMR structure of PSBD obtained at 293 K (1w3d,24 gold in Fig. 1) using a 4.5 Å cutoff distance for contacts between heavy atoms, as originally prescribed.23 The X-ray structure does not include the N- and C-terminal residues of PSBD because they were unstructured in the crystal. To define the interactions in the complex, we added the missing residues without incorporating additional contacts to avoid non-physiological protein end effects (total length of 45 residues). In Fig. 1C we show the contact map that forms the basis of the Gō potential for PSBD folding together with the intermolecular contacts with E1 derived from the complex structure (1w85).22 Because the binding to E1 also involves multiple charged residues, we added a description of electrostatic interactions using a simple Debye–Hückel term calibrated against experiments25 and used before in the context of IDP binding.26
We adjusted the intramolecular PSBD interaction energy to the folding temperature to mimic the physiological conditions of the host organism (B. stearothermophilus lives around 333–343 K, and the experimental denaturation temperature of PSBD is ∼340 K).19 Under these conditions PSBD is partially disordered, favoring the coupling of folding and binding. To investigate the role played by PSBD's folding scenario on binding, we fine-tuned the model to modify the free energy barrier at the folding temperature. This procedure involved extensive equilibrium simulations at multiple temperatures for every version of the model using Langevin dynamics within the Gromacs 4.0.5 package,27 and analyzing the trajectories with histogram methods.28 From this exercise we found that the PSBD folding free energy barrier could be modulated by: (1) making the repulsive radii of the Cα beads all the same, in contrast to the original KB implementation in which the repulsive radius for each bead is set to the distance to the closest residue in the native structure that is not in a direct contact23 and (2) scaling down the magnitude of the angular and dihedral contributions to the force-field (see technical details in the ESI†). In contrast, changes in the contact interaction energies had negligible effects on the folding free energy barrier.
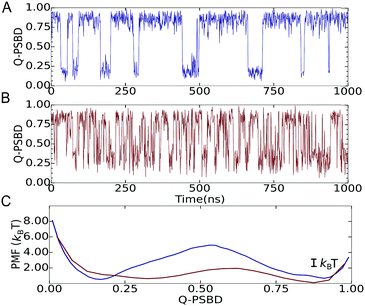
We then focused on two folding scenarios. In the first one, PSBD folding–unfolding is two-state-like, as manifested by trajectories projected as a function of the fraction of native PSBD contacts (QPSBD; see the ESI† for definitions) showing a binary switching pattern (Fig. 2A). The corresponding potential of mean force (PMF) for this model shows two defined basins at QPSBD ≈ 0.2 and 0.85 separated by a ∼4.7 kBT free energy barrier (blue in Fig. 2C). For the downhill folding scenario, the modified model reproduced the marginal thermodynamic folding barrier (∼1 kBT) obtained experimentally from differential scanning calorimetry29 and multi-probe thermodynamic analysis.19 The downhill version of the model resulted in faster dynamics and more complex folding–unfolding trajectories projected as a function of QPSBD (Fig. 2B), and a PMF with a free energy barrier of ∼1.2 kBT (red in Fig. 2C). Here we note that the behavior shown in Fig. 2B and C lies well within the downhill scenario, but it does not reach the one-state (global downhill) limit.3 It is also worth noting that lowering the barrier is accompanied by displacement of the unfolded well to higher QPSBD, consistent with the observation of the residual structure in the unfolded states of fast folding proteins.30
To investigate the coupling between PSBD folding and binding to E1, we parameterized the binding component of the Gō-like force-field using intermolecular contacts derived from the original X-ray structure of the E1–PSBD complex (1w85, Fig. 1C). In this structure, the coordinates for the PSBD are not well resolved (low electron density and very high B factors) and several E1 residues and/or atoms are missing.22 We added all the missing parts using the Modeller software package31 with a limited number of optimization steps to minimize deviations from the experimental structure. In a second step we grafted the PSBD structure from NMR (1w3d) onto the E1 docking site and fitted its exact position to the crystallographic PSBD model by minimizing the RMSD of select Cα atoms (i.e. final RMSD = 0.38 Å, see Fig. 1A and B). This exercise, which was necessary to build a complete model for binding, did not change the intermolecular contacts that define the binding interface in the X-ray structure. The final intra-PSBD and inter-molecular interactions used for all the calculations are shown in Fig. 1C.
We then calibrated the strength of intermolecular interactions on both folding scenarios so that binding simulations reproduced the experimental dissociation constant of the complex, KD = 3.2 × 10−10 M32 (we used a 600 Å per side cubic simulation box, resulting in 7.7 μM protein concentration). Binding coupled to folding was then investigated by performing long replica exchange simulations keeping the E1 coordinates frozen. The simulations sampled well both the bound and unbound states, resulting in an aggregate simulation time of 96 microseconds (see the ESI† for additional details).
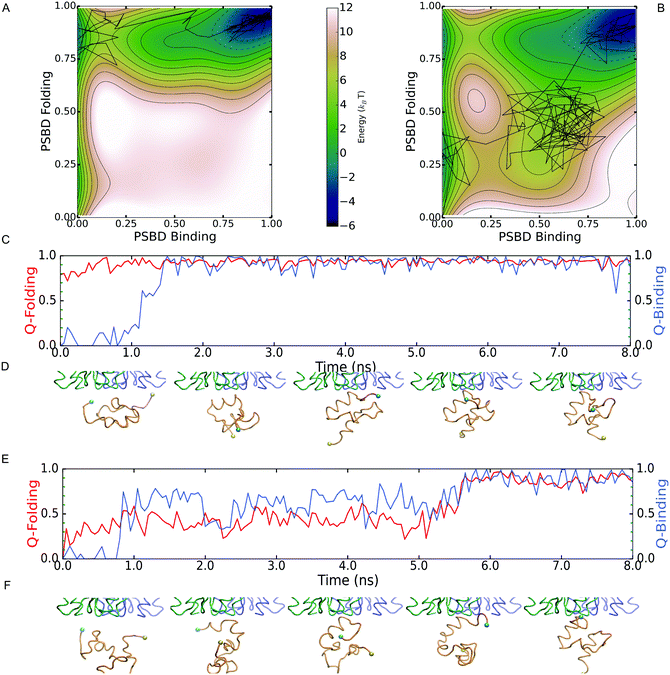
Although the two scenarios are identical in terms of the degree of PSBD unfolding and the binding affinity to E1, the simulations revealed important differences in binding behavior. Such differences are readily apparent in Fig. 3A and B, which show the 2D PMFs calculated as a function of folding and binding order parameters. The PMF for the two-state scenario (Fig. 3A) shows that in the unbound state (low QPSBD-E1) the protein fluctuates between the equally populated folded and unfolded basins (midpoint conditions). However, the binding to E1 only takes place when PSBD is fully folded (QPSBD > 0.7) and thus folding and binding are decoupled. The entire process can be described with the simple linear three state model: UU ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) FU
FU ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) FB, in which the first letter indicates the PSBD folding status (U-unfolded and F-folded) and the second its binding status (U-unbound and B-bound). E1 thus selects the folded conformation of PSBD from an ensemble with equal populations of folded and unfolded species, and hence the binding process can be described as following a conformational selection mechanism.33 In contrast, the PMF for the downhill folding scenario (Fig. 3B) demonstrates an effective coupling between folding and binding that results in richer behavior. Fig. 3B shows two alternative mechanisms. The first one is the UU
FB, in which the first letter indicates the PSBD folding status (U-unfolded and F-folded) and the second its binding status (U-unbound and B-bound). E1 thus selects the folded conformation of PSBD from an ensemble with equal populations of folded and unfolded species, and hence the binding process can be described as following a conformational selection mechanism.33 In contrast, the PMF for the downhill folding scenario (Fig. 3B) demonstrates an effective coupling between folding and binding that results in richer behavior. Fig. 3B shows two alternative mechanisms. The first one is the UU ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) FU
FU ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) FB found in the two-state scenario. The second one involves binding of unfolded PSBD (UB), manifested by a significant population of microstates with low to intermediate values of QPSBD (0.2–0.5) and intermediate to high values of QPSBD-E1 (0.5–0.6). This alternative mechanism can be described with the scheme: UU
FB found in the two-state scenario. The second one involves binding of unfolded PSBD (UB), manifested by a significant population of microstates with low to intermediate values of QPSBD (0.2–0.5) and intermediate to high values of QPSBD-E1 (0.5–0.6). This alternative mechanism can be described with the scheme: UU ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) UB
UB ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) FB, where a partially unfolded PSBD molecule first binds and then folds while being bound, thus following an induced fit mechanism.
FB, where a partially unfolded PSBD molecule first binds and then folds while being bound, thus following an induced fit mechanism.
Analysis of the binding transition paths provides additional information. Transition paths are the reactive segments of a trajectory, which comprise all the mechanistic information about the binding process. Examples of binding transition paths are provided in Fig. 3C–F. The binding transition path for the two-state scenario (Fig. 3C and D) shows how PSBD is already folded before approaching its docking site in E1. Upon contact with E1, folded PSBD binds via a lock-and-key mechanism that results in a sharp transition and the subsequent freezing of PSBD's conformational ensemble in the bound state (i.e. FB experiences minimal QPSBD fluctuations). All the observed transition paths for the two-state scenario adhere to this behavior. Therefore, there are no structural correlations between binding and folding in the two-state scenario.
The transition path shown for the downhill folding scenario (Fig. 3E and F) corresponds to the folding–binding diagonal path in the 2D PMF (Fig. 3B). Binding takes place from the unfolded state resulting in concerted folding and binding via an induced-fit mechanism. The transition path is accordingly much longer (over an order of magnitude difference) and permits the reconfiguration of PSBD while it remains loosely bound to E1 (QPSBD-E1 ∼ 0.50). Binding and folding exhibit correlated fluctuations during which PSBD populates partially unfolded conformations for significant fractions of the time. These conformations are in fact part of the PSBD folding barrier (0.55 < QPSBD < 0.75) and become effectively coupled to binding because their basal population is significant (marginal barrier). Additional examples of induced-fit binding transition paths are provided in the ESI.† Overall, roughly 50% of the binding transition paths observed under the downhill scenario were induced-fit, whereas the remainder involved complete folding followed by binding (i.e. conformational selection).
Conclusions
In this work we have used a coarse grained computational model to explore how the folding mechanism of PSBD (i.e. two-state vs. downhill) influences its binding to E1. We find that the two-state version of PSBD must fold before binding to E1. Binding occurs via a conformational selection mechanism where PSBD remains structurally rigid while bound. In contrast, the downhill PSBD version populates myriads of partially folded conformations that are able to bind to E1, resulting in induced-fit binding. We can thus conclude that effective coupling between folding of PSBD and binding to E1 requires: (1) a downhill folding scenario and (2) a structurally localized binding interface that facilitates binding of partially folded conformations. Therefore, the presence of intrinsic disorder is not sufficient per se to produce complex binding behavior such as induced-fit.Our results provide a practical demonstration of a conformational rheostat, in which the conformational flexibility of a downhill folding ensemble makes it possible to implement complex functions in single-domain proteins.1 The possibility that PSBD operates as a conformational rheostat sheds some light onto the role that this small domain plays in the swinging arm of PDC. Particularly, it hints at how a partially disordered, downhill folding PSBD could adapt its folding ensemble to bind to the structurally distinct E1 and E3 and result in the effective coupling of both binding events. Such coupling could result in the alternating binding cycles that are required for efficiently channeling substrates during PDC catalysis.17 Moreover, the changes in the microenvironment (reactants, products, and cofactors) that take place during this complex reaction could further tune the PSBD folding ensemble to trigger binding to (or dissociation from) E1 or E3, thus synchronizing catalysis and binding throughout the entire reaction.
More generally, the connection that we observe between the folding scenario of PSBD and its binding behavior originates from fundamental physical principles and is not specific of the molecular system studied. Hence, the same connection between the folding mechanism and binding should apply to the binding modes of many other proteins that fold in the downhill regime. Downhill folding proteins share certain features, including a small size, a primarily helical secondary structure and a loosely knit network of contacts in the hydrophobic core,30 which are also often associated with some IDPs. These commonalities lead us to hypothesize that the complex binding modes and allosteric behavior that are being reported in the folding upon binding of IDPs16 do not simply emerge from the protein being unstructured, but require the IDP to fold downhill. In other words, we hypothesize that a conformational rheostat (i.e. a partly disordered downhill folder) is the molecular mechanism behind the functioning of IDPs.16
Conflicts of interest
There are no conflicts to declare.Acknowledgements
RS acknowledges an FPI fellowship from the Spanish Ministry of Economy and Competitiveness. DDS was supported by an Ikerbasque Research Fellowship and acknowledges Robert B. Best for useful discussions and the kind donation of computational tools. This research was supported by grants BIO 2011-28092 (Spanish Ministry of Economy and Competitiveness), ERC-2012-ADG-323059 (European Research Council) and MCB-1616759 (National Science Foundation) to VM, and grant CTQ2015-65320-R (MINECO/FEDER) to DDS.References
- M. M. Garcia-Mira, M. Sadqi, N. Fischer, J. M. Sanchez-Ruiz and V. Munoz, Science, 2002, 298, 2191–2195 CrossRef CAS PubMed.
- J. D. Bryngelson, J. N. Onuchic, N. D. Socci and P. G. Wolynes, Proteins, 1995, 21, 167–195 CrossRef CAS PubMed.
- V. Muñoz, Annu. Rev. Biophys. Biomol. Struct., 2007, 36, 395–412 CrossRef PubMed.
- M. Sadqi, D. Fushman and V. Munoz, Nature, 2006, 442, 317–321 CrossRef CAS PubMed.
- L. Sborgi, A. Verma, S. Piana, K. Lindorff-Larsen, M. Cerminara, C. M. Santiveri, D. E. Shaw, E. de Alba and V. Muñoz, J. Am. Chem. Soc., 2015, 137, 6506–6516 CrossRef CAS PubMed.
- P. Li, F. Y. Oliva, A. N. Naganathan and V. Muñoz, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 103–108 CrossRef CAS PubMed.
- J. Liu, L. A. Campos, M. Cerminara, X. Wang, R. Ramanathan, D. S. English and V. Muñoz, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 179–184 CrossRef CAS PubMed.
- V. N. Uversky, Chem. Rev., 2014, 114, 6557–6560 CrossRef CAS PubMed.
- B. A. Shoemaker, J. Portman and P. G. Wolynes, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 8868–8873 CrossRef CAS PubMed.
- R. B. Berlow, H. J. Dyson and P. E. Wright, FEBS Lett., 2015, 589, 2433–2440 CrossRef CAS PubMed.
- B. Y. Qin, C. Liu, H. Srinath, S. S. Lam, J. J. Correia, R. Derynck and K. Lin, Structure, 2005, 13, 1269–1277 CrossRef CAS PubMed.
- J. C. Ferreon, C. W. Lee, M. Arai, M. A. Martinez-Yamout, H. J. Dyson and P. E. Wright, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 6591–6596 CrossRef CAS PubMed.
- M. Kjaergaard, K. Teilum and F. M. Poulsen, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 12535–12540 CrossRef CAS PubMed.
- A. C. Ferreon, J. C. Ferreon, P. E. Wright and A. A. Deniz, Nature, 2013, 498, 390–394 CrossRef CAS PubMed.
- A. N. Naganathan, U. Doshi and V. Muñoz, J. Am. Chem. Soc., 2007, 129, 5673–5682 CrossRef CAS PubMed.
- V. Muñoz, L. A. Campos and M. Sadqi, Curr. Opin. Struct. Biol., 2016, 36, 58–66 CrossRef PubMed.
- R. N. Perham, Annu. Rev. Biochem., 2000, 69, 961–1004 CrossRef CAS PubMed.
- A. N. Naganathan, P. Li, R. Perez-Jimenez, J. M. Sanchez-Ruiz and V. Muñoz, J. Am. Chem. Soc., 2010, 132, 11183–11190 CrossRef CAS PubMed.
- A. N. Naganathan and V. Munoz, J. Phys. Chem. B, 2014, 118, 8982–8994 CrossRef CAS PubMed.
- I. A. Lessard and R. N. Perham, Biochem. J., 1995, 306(Pt 3), 727–733 CrossRef CAS PubMed.
- S. S. Mande, S. Sarfaty, M. D. Allen, R. N. Perham and W. G. Hol, Structure, 1996, 4, 277–286 CrossRef CAS PubMed.
- R. A. Frank, J. V. Pratap, X. Y. Pei, R. N. Perham and B. F. Luisi, Structure, 2005, 13, 1119–1130 CrossRef CAS PubMed.
- J. Karanicolas and C. L. Brooks, Protein Sci., 2002, 11, 2351–2361 CrossRef CAS PubMed.
- M. D. Allen, R. W. Broadhurst, R. G. Solomon and R. N. Perham, FEBS J., 2005, 272, 259–268 CrossRef CAS PubMed.
- Y. C. Kim and G. Hummer, J. Mol. Biol., 2008, 375, 1416–1433 CrossRef CAS PubMed.
- D. De Sancho and R. B. Best, Mol. BioSyst., 2012, 8, 256–267 RSC.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS.
- A. N. Naganathan, R. Perez-Jimenez, V. Muñoz and J. M. Sanchez-Ruiz, Phys. Chem. Chem. Phys., 2011, 13, 17064–17076 RSC.
- D. De Sancho, U. Doshi and V. Munoz, J. Am. Chem. Soc., 2009, 131, 2074–2075 CrossRef CAS PubMed.
- N. Eswar, B. Webb, M. A. Marti-Renom, M. S. Madhusudhan, D. Eramian, M.-y. Shen, U. Pieper and A. Sali, Current protocols in bioinformatics, ed. Andreas D. Baxevaniset al., 2006, ch. 5, unit-5.6 Search PubMed.
- H.-I. Jung, S. J. Bowden, A. Cooper and R. N. Perham, Protein Sci., 2002, 11, 1091–1100 CrossRef CAS PubMed.
- D. D. Boehr, R. Nussinov and P. E. Wright, Nat. Chem. Biol., 2009, 5, 789–796 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details on simulation methods and additional examples of transition paths. See DOI: 10.1039/c7cp04748g |
| This journal is © the Owner Societies 2017 |