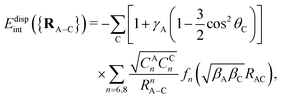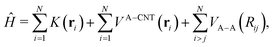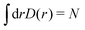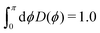Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantum confinement of molecular deuterium clusters in carbon nanotubes: ab initio evidence for hexagonal close packing†
María Pilar
de Lara-Castells
 *a,
Andreas W.
Hauser
*a,
Andreas W.
Hauser
 *b,
Alexander O.
Mitrushchenkov
*b,
Alexander O.
Mitrushchenkov
 c and
Ricardo
Fernández-Perea
c and
Ricardo
Fernández-Perea
 d
d
aInstituto de Fsica Fundamental (C.S.I.C.), Serrano 123, E-28006, Madrid, Spain. E-mail: Pilar.deLara.Castells@csic.es
bInstitute of Experimental Physics, Graz University of Technology, Petersgasse 16, A-8010 Graz, Austria. E-mail: andreas.w.hauser@gmail.com
cUniversité Paris-Est, Laboratoire Modélisation et Simulation Multi Echelle, MSME UMR 8208 CNRS, 5 bd Descartes, 77454 Marne-la-Vallée, France
dInstituto de Estructura de la Materia (C.S.I.C.), Serrano 123, E-28006, Madrid, Spain
First published on 17th October 2017
Abstract
An ab initio study of quantum confinement of deuterium clusters in carbon nanotubes is presented. First, density functional theory (DFT)-based symmetry-adapted perturbation theory is used to derive parameters for a pairwise potential model describing the adsorbate–nanotube interaction. Next, we analyze the quantum nuclear motion of N D2 molecules (N < 4) confined in carbon nanotubes using a highly accurate adsorbate-wave-function-based approach, and compare it with the motion of molecular hydrogen. We further apply an embedding approach and study zero-point energy effects on larger hexagonal and heptagonal structures of 7–8 D2 molecules. Our results show a preference for crystalline hexagonal close packing hcp of D2 molecules inside carbon nanotubes even at the cost of a reduced volumetric density within the cylindrical confinement.
1 Introduction
Clean sources of energy and efficient energy storage are at the core of the current research in nanoscience and nanotechnology. Hydrogen is being actively pursued as a substitute for fossil fuels since its combustion produces only heat and water, and it can be efficiently combined with oxygen in a fuel cell to produce electricity. However, realizing the promise of hydrogen as a widely used fuel still requires a substantial development of efficient storage materials,1,2 including metal organic frameworks3 and carbon-based nanoporous materials.4,5The general goal in hydrogen storage methods is to pack hydrogen molecules as close as possible. There exists direct experimental evidence for solid-like packing of hydrogen at supercritical temperatures.6 Moreover, recent low-temperature (11–22 K) neutron-diffraction-based experimental measurements by Cabrillo et al. have provided evidence for the formation of a crystalline hcp structure of molecular deuterium clusters inside carbon nanotubes (CNTs).7,8 This work has raised the fundamental question of the role of nuclear quantum effects for hydrogen adsorption and confinement at low temperatures. Provided that the inter-adsorbate interactions are strong, the crystal formation of the adsorbate inside CNTs has been observed with a symmetry reflecting that of the adsorbate bulk crystal since a long time ago.9 In stark contrast, when the inter-adsorbate interactions are weak, both experimental observations and theoretical calculations have revealed that the structures associated to the confined (solid) adsorbate depart largely from those corresponding to the bulk crystal (for instance, considering ice10,11). In this sense, the experimental observation of hcp structures for adsorbates characterized by very weak interactions such as D2–D2 is relevant and needs a fundamental understanding.
Very recent studies have addressed the possible existence of either a superfluid12 or a crystalline phase13,14 for parahydrogen molecules inside carbon nanotubes at zero temperature12,14 or temperatures below 4 K,13 revealing the impact of quantum nuclear effects (see also ref. 15 for a recent review). Motivated by active experimental research, the last few years have seen marked progress in the development of methods to describe the quantum nuclear motion of H2 and D2 isotopes encapsulated by carbon nanotubes, including diffusion dynamics (see, e.g., ref. 16 and 17 and references therein). These theoretical studies have provided explanations of relevant confinement effects such as the quantum-induced reversed trend in H2 and D2 diffusion rates upon lowering the temperature,17 confirming the experimental observations,18 and have revealed a strong influence of the adsorbate–nanotube interaction potential on the rate values.
Modern intermolecular interaction theory allows an ab initio characterization of van der Waals-dominated interactions of molecular or atomic adsorbates with carbon surfaces such as the D2–CNT interaction. For example, recent options include density functional theory (DFT)-based symmetry-adapted perturbation theory [SAPT(DFT)],19–31 the incremental method32 applied at coupled-cluster level,33–37 and mixed schemes combining non-periodic ab initio treatments and the dispersionless density functional approach38–40 including periodic boundary conditions.23–37 For the specific case of molecule-CNT interaction, an accurate treatment by Patkowski and collaborators includes the benchmarking of dispersion-including DFT functionals with composite second-order Möller–Plesset perturbation theory and the coupled-cluster approach applied on models of carbon nanotubes.41,42
This work presents an ab initio study of the quantum nuclear motion of deuterium clusters in carbon nanotubes at zero temperature. For this purpose, we propose an additive pairwise potential model for the D2–nanotube interaction which relies on high-level ab initio calculations using the SAPT(DFT) approach.19,20 The latter technique assumes that the zero-order wavefunction of the total system is a product of the wavefunction of each isolated subsystem, with antisymmetry being taken into account at each order of the perturbation expansion. It is worth noting that the SAPT(DFT) approach has been previously applied to describe molecular hydrogen adsorption on planar carbon surfaces,23,25 achieving a remarkable agreement with experimental measurements of bound state energies. The additive pairwise potential model uses the partition of van der Waals interaction into dispersion and dispersionless contributions. Specifically, the parameters of analytical dispersionless and dispersion terms are tuned up for a small representative CNT using SAPT(DFT)-based dispersionless and dispersion energies. As discussed in ref. 31, the potential model relies on two basic conclusions from accurate studies of van der Waals-dominated adsorbate/surface systems (see, e.g., ref. 37 and 43) (1) the short-range nature of the dispersionless contribution allows an appropriate tuning of model parameters using ab initio energies on small representative cluster models; (2) the dispersion is long-range, but dispersion parameters show excellent transferability properties upon increasing the size of the surface cluster models.
To describe the molecular motion of D2 clusters, we apply a highly accurate adsorbate wave-function-based approach, an embedding scheme as well as a vibrational model to present evidence of the hcp structure observed in the experiment.7,8 The adsorbate wave-function-based approach consists in explicitly solving the nuclear Schrödinger equation in the real space, using the the Discrete Variable Representation (DVR) method44 for the discretization, and treating the molecular adsorbate as a pseudo-atom. Recent studies23,25 have shown that the behaviour of the H2/coronene system is not affected by the relative orientation of the molecule, suggesting that it can be treated as a pseudo-atom. Within the selected model (adiabatic formulation, reduced dimension space for D2, and pairwise interaction approximation), the method provides an exact solution if convergence with the DVR basis is achieved. Appealing features of the method are the absence of phenomenological terms, the inclusion of bosonic symmetry, and the possibility of calculating excited states. The main disadvantage is in the limited number of adsorbates (up to three) that can be included in well-converged solutions. It has been very recently applied to describe the quantum nuclear motion of helium and molecular nitrogen clusters in carbon nanotubes,31 revealing very different quantum confinement effects depending on the CNT diameter, and agreeing very well with experimental measurements.45 In the next section, we briefly present the methods used in this study. Our results are reported in Section 3. Finally, the main conclusions are provided in Section 4.
2 Method
2.1 Adsorbate-nanotube interaction
The adsorbate/CNT interaction VA−CNT is introduced by applying an additive pairwise potential model.31 As mentioned above, our model uses different functions for the dispersionless and dispersion energy contributions. It accounts for the typical exponential growth of the dominant dispersionless contribution, the exchange-repulsion but also including a Gaussian-type ‘cushion’ to describe weakly attractive tails stemming from other dispersionless termswhere Rc is a cut-off distance, RA–C stands for the distance between the adsorbate center-of-mass and one carbon atom of the nanotube, and θC is the angle between the radial vector going from the nanotube center to one carbon atom and the vector RA–C pointing from the adsorbate center-of-mass to the same C atom. The dimensionless factor γA in the first term accounts for the anisotropy of the C–C bonds. The sum in the second term runs over all carbon atoms of the nanotube. For the dispersion part, we apply the typical C6/C8 expansion with the damping functions of Tang and Toennies fn (n = 6, 8)46
where γR is also a dimensionless anisotropy parameter. The inclusion of γA and γR anisotropy terms has been found to be important when modelling potential corrugation effects on both curved carbon and metal surfaces.30,31,47
Model parameters are derived by fitting the dispersionless and dispersion SAPT(DFT) terms, as calculated for the interaction between a single H2 and a hydrogen-saturated nanotube CNT(5,5) tube made of 62 atoms, considering two transverse sections of the tube. Using the SAPT(DFT) MOLPRO21,48 implementation, we followed the same computational setup as reported in ref. 31, using the Perdew–Burke–Ernzerhof (PBE) density functional49 and the augmented polarized correlation-consistent triple-zeta basis50 for all atoms but the hydrogen atoms saturating the dangling bonds, for which the correlation-consistent double-zeta basis was used (see ref. 31 and ESI† for further details).
2.2 Adsorbate wave-function treatment
In order to calculate the adsorbate wave-functions, we have applied the same method proposed in our previous work.31 Very briefly, adsorbate molecules A are described as structureless bosonic particles. However, note that the potential felt by them is derived from the interactions of H2 molecules in arrangements where their intramolecular axes are parallel to tube (i.e., the z) axis. The parallel orientation to the tube long axis has been chosen because it is mostly favorable energetically. Indeed any averaging over rotational motion of H2 would lead to a less deep well due to the repulsive wall while practically leaving the potential close to the tube center unmodified. Thus, as can be seen in Fig. S2 of the ESI,† the adsorbate/nanotube potential for the parallel orientation differs only minimally from the one obtained by averaging over the J = 0 rotational state of molecular hydrogen.Using cylindric coordinates ri ≡ (ri, ϕi, zi) for the adsorbate center-of-mass position (see Fig. 1), the total Hamiltonian is written as a sum of one-particle kinetic energy terms and effective pairwise additive adsorbate/CNT (VA−CNT) and inter-adsorbate (VA–A) interactions
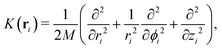 | (1) |
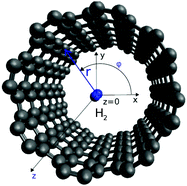 | ||
| Fig. 1 Figure illustrating the atomic structural models for the H2/CNT system. Gray spheres represent carbon atoms while blue spheres stand for one H2 molecule inside a carbon nanotube with diameter of helicity index (10,10). Cylindrical coordinates (r, ϕ, z) of the H2 center-of-mass are also indicated. The H–H bond is oriented along the z axis, with the bond length fixed to the vibrationally averaged rigid rotor value, req = 0.7508 Å from ref. 23. | ||
To model the adsorbate–adsorbate interaction, we have used the ab initio potential energy surface reported by Hinde,52 as restricted to our one-dimensional model. The values of the equilibrium distance (3.46 Å) and well-depth (24.72 cm−1) are very close to those of the well-known Silvera–Goldman potential53 for the H2 molecule in the J = 0 rotational state (3.41 Å and 23.84 cm−1, respectively).
2.3 Embedding approach
To confirm that the hcp structure is preferred over a face-centered cubic fcc structure, we have applied an embedding approach as follows: first, we choose a nanotube with a length of 23.36 Å (10 cell units). Next, we define an embedding region comprising 14 D2 molecules in two C6 hexagonal structures with circumradius of value a as well as two D2 molecules located at their centers (see TOC graphics). The two C6 hexagonal structures are located in a plane perpendicular to the tube axis, separated by a distance of c/2 from z = 0. Then, the embedding potential acting on a D2 molecule is simply| Vemb(r,z) = 6 × VD2–D2(R+) + 6 × VD2–D2(R−) + VD2–D2(Z+) + VD2–D2(Z−) |
with r and z denoting the cylindric coordinates of a reference molecule (i.e., center-of-mass position) and VD2–D2 as the interaction potential between two isolated D2 molecules. Note that the cylindrical symmetry of the problem is preserved. Finally, we obtain the adsorbate wave-functions of the embedded molecule as described in the previous section, but after adding the embedding potential to the adsorbate–nanotube interaction potential. In this case, however, the z-dependence of the adsorbate–nanotube potential is also included. Explicitly, the Schrödinger equation of a single embedded D2 molecule,
| Ĥembψemb(r) = εembψemb(r), | (2) |
 | (3) |
2.4 Vibrational model
To further test whether the hcp structure is preferred for larger clusters, we have applied a vibrational model to single layers of D2 molecules with either C6 or C7 symmetries inside the CNT(10,10) nanotube. We reduce our analysis to radial motions of the D2 molecules in a plane perpendicular to the tube axis. Using our additive pairwise potential model, an analytical expression of the Hessian matrix is obtained by calculating the second derivatives. This matrix is diagonalized to obtain 2N eigenvalues. Three of them are zero, corresponding to the two planar translations and one in-plane rotation. The remaining eigenvalues are converted into vibrational frequencies ωi and the zero-point energy (ZPE) is determined via a summation,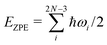 | (4) |
3 Results and discussion
3.1 Adsorbate/nanotube interaction
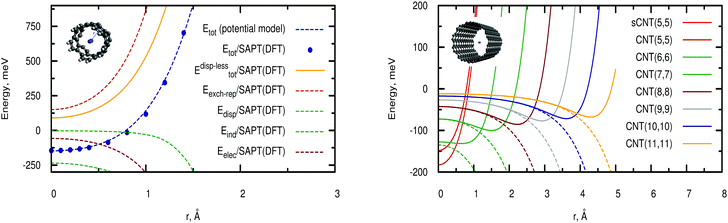
The left-hand panel of Fig. 2 shows the total D2/CNT interaction potential as a function of the radial distance r between the molecule center-of-mass and the nanotube center, along with the electrostatic Eelec, exchange-repulsion Eexch-rep, induction Eind, and dispersion contributions Edisp. Upon applying our pairwise potential model, we obtain the radial scans of interaction energies presented in the right-hand panel of Fig. 2 for nanotubes of increasing diameter (see also Table 1).| CNT | (5,5) | (6,6) | (7,7) | (8,8) | (9,9) | (10,10) |
|---|---|---|---|---|---|---|
| d CNT | 6.74 | 8.14 | 9.47 | 10.85 | 12.18 | 13.56 |
| E min | −183 | −131 | −100 | −85 | −77 | −72 |
| r min | 0.0 | 0.65 | 1.50 | 2.23 | 2.93 | 3.60 |
As can be observed in Fig. 2 (left-hand panel), the D2/CNT attractive interaction is dispersion-dominated, with the net repulsive dispersionless contribution mainly determined by the exchange-repulsion term. As typically found, the exchange-repulsion grows exponentially as the molecule-surface distance decreases although such behaviour is somewhat smoothed out by the attractive electrostatic contribution. The induction term contributes very little at the potential minimum but considerably at the carbon cage. The potential minimum is located at the center of the narrow nanotube (diameter of 6.74 Å), where the adsorbates benefit from the dispersion interaction with carbon atoms at both sides of the carbon cage. However, upon increasing the nanotube diameter (see right-hand panel of Fig. 2), the dispersion becomes very small at the nanotube center and the potential minima shift towards the carbon cage (see also Table 2). For a nanotube of diameter of 27.21 Å, the value of the well-depth (−56 meV) is already close to that obtained for a graphene sheet and measured for the H2 molecule adsorbed onto graphite (−51.7 meV from ref. 54). For a (5,5) nanotube, the energy at the potential minimum (−183) is about 15% larger than the well-depth of the potential proposed by Gordillo et al.55 as a sum of Lennard-Jones-type C–H2 interactions. From Fig. 2 it can also be observed that the potential model closely reproduces the ab initio results.
| D2/CNT | (D2)2/CNT | (D2)3/CNT | H2/CNT | (H2)2/CNT | (H2)3/CNT | |
|---|---|---|---|---|---|---|
| E tot, meV | –64.89 | −130.76 | −196.80 | −62.24 | −124.96 | −187.27 |
| 〈VA–A〉, meV | — | −0.98 (−0.86) | −2.13 | −6.63 | −0.48 (−0.37) | −1.00 |
3.2 Adsorbate wave-functions
As a model system in previous studies12,13,56 and to simulate realistic experimental conditions,7,8 we have performed adsorbate wave-function calculations considering a long carbon nanotube of helicity index (10,10) and diameter of 13.56 Å. Moreover, this diameter fits very well with the expected distance in the hcp structure of the bulk crystal. We focus here on the lowest-energy adsorbate (bosonic) wave-function with Λ = 0.The adsorption energies of (D2)N and (H2)N clusters to the CNT(10,10) nanotube are shown in Table 2. The one-particle density distributions D(r) are plotted in Fig. 3 as functions of the radial r distance from the adsorbate to the tube center.
As previously found for helium and molecular parahydrogen clusters confined by either an attractive dopant57–59 or carbon nanotubes,31 the total energy (see Table 2) can be expressed as N times the energy of the ground-state wave-function ε0 plus a small term 〈VA–A〉 accounting for the weak inter-adsorbate attractive interaction
| EN = N × ε0 + 〈VA–A〉. |
A strong confinement at the adsorbate–nanotube potential minimum is also found in classical descriptions of molecular adsorption. This is consistent with the small zero-point energy for the adsorbate–nanotube vibration (about 7 meV) as compared with the well-depth (about −72.5 meV). In contrast, the D2–D2 vibrational motion is characterized by an extremely large zero-point energy (2.20 meV for the pure D2 dimer) as compared with the corresponding potential minimum (−3.065 meV), with an even larger value for the lighter H2 dimer (2.70 meV). The associated pair density distribution is very delocalized and extends over more than 8 Å.
This is clearly seen in Fig. 4 which presents plots of the pair densities D(R12) as a function of the adsorbate–adsorbate distance for (D2)2 and (H2)2 dimers considering both isolated as well as confined clusters. We observe that the pair densities become more localized when going from isolated to confined clusters, and upon augmenting the mass of the hydrogen isotope. However, the carbon cage is barely affecting the adsorbate–adsorbate interaction of the confined dimers (by about −0.1 meV only, see Table 2).
Let us now consider the adsorbate wave-function dependence on relative inter-adsorbate degrees of freedom. Fig. 5 plots the density distributions of the (D2)2 and (H2)2 dimers as a function of the relative angle ϕ12 = ϕ2 − ϕ1 (left-hand panel) as well as the relative inter-adsorbate distance along the tube axis z12 = z2 − z1 (right-hand panel). The peak at ϕ12 = 60° in the angular distribution of the (D2)2 dimer (left-hand panel) corresponds to a C6-type arrangement of the two molecules at the plane with a zero value of z12 (right-hand panel), which is obviously consistent with the hcp structure in the extended system (see TOC graphics). Notice that the pair distribution for the lighter (H2)2 dimer is more extended and delocalized due to the larger zero-point energy.
From the right-hand panel of Fig. 5, it can be observed that the pair density distribution D(z12) for the (D2)2 dimer is very broad and develops a shoulder at about the position of the potential minimum for the adsorbate–adsorbate interaction. The bimodal structure of the D(z12) distribution also reflects the multi-configurational character of the adsorbate wave-function and a strong coupling between inter-adsorbate radial and angular vibrational modes due to the two-dimensional confinement induced by the carbon cage. Interestingly, the double-peaked distribution in the (D2)2 dimer becomes disentangled in two pair distributions peaked at zero and 3.6 Å. Clearly, the density profiles along the tube axis are being shaped by the inter-adsorbate interaction. Similarly, notice that the angular distribution peaked at about 60° become more localized for the (D2)3 trimer (see left-hand panel of Fig. 5), with average of the relative angles equal to 55° and 27°. These values are close to those in the extended hcp structure (60° and 30°). The adsorbate wave-function dependence on relative angles is also determined by the inter-adsorbate interaction.
Taken together, our adsorbate wave-function results show that the structuring of molecular deuterium clusters inside CNTs is determined by a delicate balance between attractive adsorbate–nanotube and inter-adsorbate interactions, with the extremely large zero-point energy corrections of the latter in a key role. This structuring is such that the attractive adsorbate–adsorbate interaction is optimized, avoiding an increase of the zero-point energy cost for the adsorbate–adsorbate vibrational mode, but also taking advantage of the attractive adsorbate–nanotube potential minimum. On one hand, the magnitude of the adsorbate–nanotube potential minimum (about −80 meV) is much larger than the inter-adsorbate counterpart (about −3 meV). On the other hand, as in doped helium and molecular hydrogen clusters,58,59,62 the average adsorbate–adsorbate contribution to the total energy (about −1 meV, see Table 2) scales approximately with the number of adsorbate pairs (i.e., as N(N − 1)/2), while the one-particle term (about −65 meV) scales linearly with N. Therefore, a significant influence of the two-body term would have been expected for larger clusters than those considered here. Moreover, accurate adsorbate wave-function calculations of small doped clusters have indicated a cyclic arrangement of N (N < 6) hydrogen molecules around the dopant center-of-mass58 which depart largely from the structuring under confinement by the carbon walls here revealed.
We notice that the findings in this work are consistent with our previous results on two-dimensional confinement of helium clusters,31 where the main peak of the pair correlation function was located at a position very close to that measured for superfluid liquid helium63 when considering two or three 4He atoms.31 Thus, carbon nanotubes seem to enhance nuclear quantum effects in cold few-atom clusters at the nanoscale such as, for example, signaling the transition to a two-dimensional quantum fluid with just a few 4He atoms. Very intriguing quantum phenomena have also been revealed when immersing carbon nanotubes in helium droplets such as an incomplete flooding of the quantum fluid.29
3.3 Embedding approach
As illustrated in the TOC graphics, the hcp structure contains alternating C6 and C3 symmetry arrangements. To provide an evidence of the C3 structure, let us now consider how the radial density distribution of a D2 molecule is modified by two C6 symmetry arrangements of D2 molecules. For this purpose, as described in the second section, we calculate the wavefunction of a single D2 in an effective potential incorporating the effect of the two hexagonal D2 shells. As shown in Fig. 6, the addition of these shells as an embedding potential causes the shift of radial density peak from the lateral region at r = 3.6 Å to about r = 1.8 Å. The reasons of this behaviour is revealed in Fig. 6: at the tube center (z = 0), the repulsive barrier of the embedding potential is located at r = 3.6 Å as the peaks of the radial densities for the D2 molecules from the hexagonal shells, while the largest attractive interaction between the embedded and the D2 shells occurs at about r = 1.8 Å. This value differs from that of the exact hcp structure (for a = 3.6 Å) by 0.2 Å only for the C3 symmetry arrangement. This deviation is small when considering that the D2 molecules from the hexagonal shells are not fixed particles but display density distributions which, along r, extend by about 1 Å.The effect of the embedding potential is also manifested in the binding energy of an embedded D2 molecule (−53.21 meV). Remarkably, this value differs by just 18% from the “unembedded” counterpart (−64.89, see Table 2). Hence, the reduced attractive D2–nanotube interaction upon getting further from the carbon cage in the C3 symmetry structure is almost compensated by the attractive interaction with D2 molecules in the adjacent C6 shells. Once again, this is in contrast with the expected classical behaviour, i.e., the adhesion of D2 molecules to the carbon walls whatever its number be, and highlights a delicate balance between D2–D2 and D2–nanotube interactions.
To close our adsorbate wave-function analysis, we note that the packing of D2 molecules on the triangular-type arrangement is also consistent with the central column of D2 molecules distributed along the z axis is in the hcp structure (see TOC graphics). The existence of the central column has been reported by Rossi and Ancilotto12 as well as Del Maestro and Boninsegni.13 As detailed in the ESI,† an effective model explains that the state of the dimer formed along the tube axis is extremelly weakly bound (by about −0.03 meV) for a D2 molecule at a C6-type arrangement with r = 3.6 Å (i.e., the average position for a single D2 inside the (10,10) nanotube). However, the formation of a cluster of three D2 molecules in a C3 arrangement inside the same nanotube makes the effective inter-adsorbate interaction much deeper, supporting much more strongly bound vibrational states.
3.4 Vibrational model
This section is dedicated to the vibrational analysis of single layers of D2 molecules with either C6 or C7 symmetries inside a CNT(10,10) nanotube. Following the outline discussed in Section 2.4, we first build a total PES model by combining our pairwise potential model for the interaction between D2 molecules and the carbon structure with an analytical expression for the D2–D2 potential reported by Hinde.52 A convenient one-dimensional cut through this still complicated potential energy surface, a function of 2N − 3 vibrational degrees of freedom with N = 7, is obtained by scans over the energy with respect to the “breathing mode” of the deuterium cluster. Results are presented in Fig. 7. | ||
| Fig. 7 Potential energy scans for the breathing mode of D2 arrangements inside (10,10) carbon nanotubes. | ||
We use these energy curves to derive an approximate analytical potential surface for planar motions of the D2 molecules inside the tube and determine the zero-point energy in the corresponding modes from the Hessian matrix of this potential. Zero energy is set to the geometry where all D2 molecules are at infinite distance from the tube and from each other. As can be seen, the confinement leads to approximately harmonic shapes of both potentials. The curves become steeper at larger distances, indicating that size extension is more costly than a compression of the D2 arrangement due to the stronger repulsion effects from the wall of the carbon nanotubes than from inter-adsorbate interactions. The different packing of the D2 molecules in either C6 or C7 symmetric structures has a significant impact on the curvature of the potential: adding an extra D2 molecule to the hcp structure leads to a much steeper curvature. However, note that the minimum of energy is barely affected by the addition of an extra D2 molecule, which shows that the total gain and costs of a particle addition are comparable to each other. A better overview is obtained if we compare electronic binding energies per D2 molecule as presented in Table 3, which provides almost the same electronic energies per particle in both geometries. However, zero point effects need to be taken into consideration in the low energy regime (Fig. 7).
| System | E | ZPE | E corr |
|---|---|---|---|
| 7 D2 in (10,10) | −559 | 91 | −468 |
| 8 D2 in (10,10) | −558 | 118 | −440 |
Assuming a simple model of interconnected springs (see ESI†), the potential energy of the confined D2 molecules is fully defined by only two parameters, a spring constant f and a minimum distance rmin between the interconnected D2 molecules. Within this approach of coupled harmonic oscillators, justified by the small deviations from the optimum intermolecular distance, we obtain a force constant f = 798 cm−1 Å−2 and an equilibrium distance of 3.578 Å in the C6 symmetry for CNT(10,10). In C7 symmetry we obtain a force constant f = 1311 cm−1 Å−2 and an equilibrium spring distance of 3.627 Å. Diagonalization of the analytical Hessian with these parameters yields a set of vibrational frequencies ωi, from which the total zero point energy of each system can be derived. For convenience, these zero point energies are then divided by the number of D2 molecules and added to the corresponding electronic energies per particle listed in Table 3 for each symmetry. Such a comparison reveals that the C6 symmetric arrangement, which emulates the hcp structure in the extended tube, is now clearly preferred over a C7 symmetric arrangement due to its lower zero point energy.
4 Conclusions
In summary, a new potential model for the hydrogen-nanotube interaction has been proposed which is based on accurate ab initio determinations through DFT-based symmetry adapted perturbation theory. This potential model is used in adsorbate wave-function calculations of molecular deuterium clusters confined by the CNT(10,10) nanotube, considering up to three molecules. Our results show a preference of hcp over other structural arrangements. They highlight that the intermolecular structuring is ultimately determined by a subtle balance between attractive adsorbate–nanotube and adsorbate–adsorbate interactions, with a prominent role played by the extremely large zero-point energy associated to the latter. An embedding approach shows that the C3 symmetry arrangement in the hcp structure can also be explained. Finally, a vibrational model demonstrates that the hcp structure is preferred over an heptagonal geometry due to quantum nuclear effects stemming from zero-point energy corrections.The pairwise additive potential model applied in this work allows for an efficient treatment of molecular hydrogen physisorption on carbon-based materials, which is of special interest to researchers in the field of hydrogen storage and other applications concerning gas storage or gas separation. Moreover, as has been demonstrated, the accuracy of this potential model is high enough to even allow the discussion of quantum motion at very low temperatures within the frameworks of adsorbate wavefunction theory, which might become relevant in future studies of neutral molecules in weak confinement potentials for new technologies such as quantum information processing and molecular data storage.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been partly supported by the Spanish Agencia Estatal de Investigación (AEI) and the Fondo Europeo de Desarrollo Regional (FEDER, UE) under Grant no. MAT2016-75354-P and COST Action CM1405 “Molecules in Motion” (MOLIM). MPdLC is greatly thankful to Carlos Cabrillo for having provided details of his experimental measurements prior to publication and very helpful discussions, as well as the CTI (CSIC) and CESGA super-computer facilities (Spain) for the provided resources.References
- L. Schlapbach and A. Züttel, Nature, 2001, 414, 353–358 CrossRef CAS PubMed.
- A. Züttel, Mater. Today, 2003, 6, 24–33 CrossRef.
- N. Rosi, J. Eckert, M. Eddaoudi, D. Vodak, J. Kim, M. O'Keeffe and O. Yaghi, Science, 2003, 300, 1127–1129 CrossRef CAS PubMed.
- H. M. Cheng, Q. H. Yang and C. Liu, Carbon, 2001, 39, 1447–1454 CrossRef CAS.
- C. Liu, Y. Chen, C.-Z. Wu, S.-T. Xu and H.-M. Cheng, Carbon, 2010, 48, 452–455 CrossRef CAS.
- V. P. Ting, A. J. Ramirez-Cuesta, N. Bimbo, J. E. Sharpe, A. Noguera-Diaz, V. Presser, S. Rudic and T. J. Mays, ACS Nano, 2015, 9, 8249–8254 CrossRef CAS PubMed.
- C. Cabrillo, private communication, publication in preparation.
- C. Cabrillo, R. Fernández Perea, C. Mondelli, M. A. González and L. Chico, Molecular Deuterion Crystallisation Under Quasi-1D Confinement, ECNS2015 VI European Conference on Neutron Scattering, http://ecns2015.unizar.es/images/posters_list.pdf.
- R. R. Meyer, J. Sloan, R. E. Dunin-Borkowski, A. I. Kirkland, M. C. Novotny, S. R. Bailey, J. L. Hutchison and M. L. H. Green, Science, 2000, 289, 1324–1326 CrossRef CAS PubMed.
- Y. Maniwa, H. Kataura, M. Abe, A. Udaka, S. Suzuki, Y. Achiba, H. Kira, K. Matsuda, H. Kadowaki and Y. Okabe, Chem. Phys. Lett., 2005, 401, 534–538 CrossRef CAS.
- K. Koga, G. T. Gao, H. Tanaka and X. C. Zeng, Nature, 2001, 421, 802–805 CrossRef PubMed.
- M. Rossi and F. Ancilotto, Phys. Rev. B, 2016, 94, 100502 CrossRef.
- A. Del Maestro and M. Boninsegni, Phys. Rev. B, 2017, 95, 054517 CrossRef.
- G. Ferré, M. C. Gordillo and J. Boronat, Phys. Rev. B, 2017, 95, 064502 CrossRef.
- C. Cazorla and J. Boronat, Rev. Mod. Phys., 2017, 89, 035003 CrossRef.
- T. Lu, E. M. Goldfield and S. K. Gray, J. Phys. Chem. B, 2006, 110, 1742–1751 CrossRef CAS PubMed.
- M. Mondelo-Martell and F. Huarte-Larrañaga, J. Phys. Chem. A, 2016, 120, 6501–6512 CrossRef CAS PubMed.
- T. X. Nguyen, H. Jobic and S. K. Bhatia, Phys. Rev. Lett., 2010, 105, 085901 CrossRef CAS PubMed.
- A. J. Misquitta, B. Jeziorski and K. Szalewicz, Phys. Rev. Lett., 2003, 91, 033201 CrossRef PubMed.
- A. Heßelmann and G. Jansen, Chem. Phys. Lett., 2003, 367, 778–784 CrossRef.
- A. Heßelmann, G. Jansen and M. Schütz, J. Chem. Phys., 2005, 122, 014103 CrossRef PubMed.
- D. E. Taylor, J. G. Ángyán, G. Galli, C. Zhang, F. Gygi, K. Hirao, J. W. Song, K. Rahul, O. A. von Lilienfeld, R. Podeszwa, I. W. Bulik, T. M. Henderson, G. E. Scuseria, J. Toulouse, R. Peverati, D. G. Truhlar and K. Szalewicz, J. Chem. Phys., 2016, 145, 124105 CrossRef PubMed.
- M. P. de Lara-Castells and A. O. Mitrushchenkov, J. Phys. Chem. A, 2015, 119, 11022–11032 CrossRef CAS PubMed.
- M. d. R. Cuevas-Flores, M. A. Garca Revilla and M. Bartolomei, J. Comput. Chem., 2017 DOI:10.1002/jcc.24920.
- M. Bartolomei, R. Perez de Tudela, K. Arteaga, T. González Lezana, M. I. Hernandez, J. Campos-Martnez, P. Villarreal, J. Hernández Rojas, J. Breton and F. Pirani, Phys. Chem. Chem. Phys., 2017, 19, 26358–26368 RSC.
- M. Bartolomei, E. Carmona-Novillo, M. I. Hernández, J. Campos-Martnez and F. Pirani, J. Phys. Chem. C, 2013, 117, 10512–10522 CAS.
- A. Hesselmann and T. Korona, Phys. Chem. Chem. Phys., 2011, 13, 732–743 RSC.
- E. Munusamy, R. Sedlak and P. Hobza, ChemPhysChem, 2011, 12, 3253–3261 CrossRef CAS PubMed.
- A. W. Hauser and M. P. de Lara-Castells, J. Phys. Chem. Lett., 2016, 7, 4929–4935 CrossRef CAS PubMed.
- A. W. Hauser and M. P. de Lara-Castells, Phys. Chem. Chem. Phys., 2017, 19, 1342–1351 RSC.
- A. W. Hauser, A. O. Mitrushchenkov and M. P. de Lara-Castells, J. Phys. Chem. C, 2017, 121, 3807–3821 CAS.
- H. Stoll, J. Chem. Phys., 1992, 97, 8449–8454 CrossRef CAS.
- E. Voloshina, D. Usvyat, M. Schütz, Y. Dedkov and B. Paulus, Phys. Chem. Chem. Phys., 2011, 13, 12041–12047 RSC.
- M. P. de Lara-Castells, H. Stoll, B. Civalleri, M. Causà, E. Voloshina, A. O. Mitrushchenkov and M. Pi, J. Chem. Phys., 2014, 141, 151102 Search PubMed.
- M. P. de Lara-Castells, A. O. Mitrushchenkov and H. Stoll, J. Chem. Phys., 2015, 143, 102804 CrossRef PubMed.
- M. P. de Lara-Castells, N. F. Aguirre, H. Stoll, A. O. Mitrushchenkov, D. Mateo and M. Pi, J. Chem. Phys., 2015, 142, 131101 Search PubMed.
- M. P. de Lara-Castells, M. Bartolomei, A. O. Mitrushchenkov and H. Stoll, J. Chem. Phys., 2015, 143, 194701 CrossRef PubMed.
- K. Pernal, R. Podeszwa, K. Patkowski and K. Szalewicz, Phys. Rev. Lett., 2009, 103, 263201 CrossRef PubMed.
- R. Podeszwa and K. Szalewicz, J. Chem. Phys., 2012, 136, 161102 CrossRef PubMed.
- R. Podeszwa, K. Pernal, K. Patkowski and K. Szalewicz, J. Phys. Chem. Lett., 2010, 1, 550–555 CrossRef CAS.
- D. G. A. Smith and K. Patkowski, J. Phys. Chem. C, 2014, 118, 544–550 CAS.
- D. G. A. Smith and K. Patkowski, J. Phys. Chem. C, 2015, 119, 4934–4948 CAS.
- M. P. de Lara-Castells, H. Stoll and A. O. Mitrushchenkov, J. Phys. Chem. A, 2014, 118, 6367–6384 CrossRef CAS PubMed.
- Z. Bačič and J. C. Light, Annu. Rev. Phys. Chem., 1989, 40, 469–498 CrossRef.
- T. Ohba, Sci. Rep., 2016, 6, 28992 CrossRef CAS PubMed.
- K. T. Tang and J. P. Toennies, J. Chem. Phys., 1984, 80, 3726–3741 CrossRef CAS.
- M. P. de Lara-Castells, R. Fernández-Perea, F. Madzharova and E. Voloshina, J. Chem. Phys., 2016, 144, 244707 CrossRef PubMed.
- H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. O. Mitrushchenkov and G. Rauhut, et al., MOLPRO, version 2012.1, a package of ab initio programs, see http://www.molpro.net.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- D. E. Woon and T. H. Dunning, Jr., J. Chem. Phys., 1994, 100, 2975–2988 CrossRef CAS.
- J. Echave and D. C. Clary, Chem. Phys. Lett., 1992, 190, 225–230 CrossRef CAS.
- R. J. Hinde, J. Chem. Phys., 2008, 128, 154308 CrossRef PubMed.
- I. F. Silvera and V. V. Goldman, J. Chem. Phys., 1978, 69, 4209–4213 CrossRef CAS.
- L. Mattera, F. Rosatelli, C. Salvo, F. Tommasini, U. Valbusa and G. Vidali, Surf. Sci., 1980, 93, 515–525 CrossRef CAS.
- M. C. Gordillo, J. Boronat and J. Casulleras, Phys. Rev. Lett., 2000, 85, 2348–2351 CrossRef CAS PubMed.
- M. Ying, Y. Xia, X. Liu, F. Li, B. Huang and Z. Tan, Appl. Phys. A: Mater. Sci. Process., 2004, 78, 771–775 CrossRef CAS.
- M. P. de Lara-Castells, G. Delgado-Barrio, P. Villarreal and A. O. Mitrushchenkov, J. Chem. Phys., 2009, 131, 194101 CrossRef CAS PubMed.
- M. P. de Lara-Castells and A. O. Mitrushchenkov, J. Phys. Chem. Lett., 2011, 2, 2145–2151 CrossRef CAS.
- N. F. Aguirre, P. Villarreal, G. Delgado-Barrio, A. O. Mitrushchenkov and M. P. de Lara-Castells, Phys. Chem. Chem. Phys., 2013, 15, 10126–10140 RSC.
- A. F. Schuch and R. L. Mills, Phys. Rev. Lett., 1966, 16, 616–618 CrossRef.
- C. S. Barrett, L. Meyer and J. Wasserman, J. Chem. Phys., 1966, 45, 834–837 CrossRef CAS.
- M. P. de Lara-Castells, G. Delgado-Barrio, P. Villarreal and A. O. Mitrushchenkov, Int. J. Quantum Chem., 2011, 111, 406–415 CrossRef.
- E. C. Svenson, V. F. Sears, A. D. Woods and P. Martel, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 21, 3638–3651 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the SAPT(DFT) calculations, the pairwise potential model, the grid basis used in adsorbate wave-function calculations, an effective model of the inter-adsorbate interaction along the tube axis, and expressions of the analytical spring model potentials used within the vibrational model. See DOI: 10.1039/c7cp05869a |
| This journal is © the Owner Societies 2017 |