Conformational structures of the tetrahydrofuran cation determined using one-photon mass-analyzed threshold ionization spectroscopy†
Sung Man
Park
,
Yu Ran
Lee
,
Do Won
Kang
,
Hong Lae
Kim
* and
Chan Ho
Kwon
 *
*
Department of Chemistry, College of Natural Sciences and Institute for Molecular Science and Fusion Technology, Kangwon National University, Chuncheon 24341, Korea. E-mail: chkwon@kangwon.ac.kr; hlkim@kangwon.ac.kr
First published on 25th October 2017
Abstract
One-photon vacuum ultraviolet mass-analyzed threshold ionization (VUV-MATI) spectroscopy was used to characterize the essential conformations of tetrahydrofuran (THF) and thus determine the stereochemistry of the furanose ring constituting the backbones of DNA and RNA. Since the VUV-MATI spectrum of THF exactly corresponds to the vibrational spectrum of the gas-phase THF cation, the above cation was detected using time-of-flight mass spectrometry featuring the delayed pulsed-field ionization of the target in high Rydberg states by scanning the wavelength of the VUV pulse across the region of the vibrational spectrum. The position of the 0-0 band in the recorded VUV-MATI spectrum was extrapolated to the zero-field limit, allowing the adiabatic ionization energy of THF to be accurately estimated to be 9.4256 ± 0.0004 eV. The above ionization was assigned to a transition between C2-symmetric neutral (S0) and cationic (D0) ground states. The potential energy surfaces associated with molecular pseudorotation in the above states were constructed at the B3LYP/aug-cc-pVDZ level, being in good agreement with experimental observations. The twisted (C2-symmetric) and bent (CS-symmetric) conformers of the S0 state were predicted to be separated by a small interconversion barrier, whereas the D0 state exclusively existed in the C2 conformation. Based on the above, the peaks in the MATI spectrum were successfully assigned based on the Franck–Condon factors and vibrational frequencies calculated by varying the geometrical parameters of the C2 conformation, which determines the precise molecular structure of the THF cation.
Introduction
The conformations of saturated four-membered rings generally reflect the balance between ring strain and torsional forces arising from non-tetrahedral methylene groups, which affects ring-puckering vibrations.1 These low-frequency vibrations feature a large transition dipole moment and can thus be observed in the far infrared region. Comparative studies of cyclobutane and oxetane conformations revealed that the former exhibits a larger puckering angle due to considerable methylene torsional forces, whereas the latter experiences reduced torsional forces and thus shows a smaller planarization barrier.2–5 Importantly, the conformational changes of cyclic compounds experiencing large torsional forces can be viewed as ring-puckering vibrational motion with the puckering phase rotating around the ring, which is denoted as pseudorotation. As an example, pseudorotation in cyclopentane has been well documented by thorough investigations of its low-frequency vibrational modes in the far infrared and microwave regions.6,7The precise conformation of tetrahydrofuran (THF), which can be viewed as an oxygen-substituted cyclopentane, is of fundamental importance for biological studies, since this molecule constitutes the furanose ring in the backbone of certain carbohydrates and DNA/RNA. Thus, investigations of the biological activities and deformation of such large biomolecules should include conformational studies on basic structural units such as THF. THF has two possible conformations, namely twisted (C2-symmetric) and bent (CS-symmetric) ones, with their interconversion expected to occur along the pseudorotational coordinate, i.e., without going through the flat C2v conformation at the highest point of potential energy surfaces describing general conformational changes.8 In view of the above, the pseudorotation of THF was investigated using experimental and theoretical methods and was shown to arise from consecutive small-barrier interconversions between conformations exhibiting CS, C1, C2, C1, and CS symmetries. Generally, pseudorotation can be described as coupled twisting and bending motions associated with ring-puckering vibrations. Consequently, assuming that these low-frequency modes do not significantly interact with other vibrational motions, the potential energy surface for pseudorotation can be described using two-dimensional coordinates.9–15 Engerholm et al. revealed that the microwave spectrum of THF exhibits a strong vibration–rotation interaction, which was interpreted as restricted low-barrier pseudorotation, with the results of dipole moment measurements suggesting that the twisted configuration of THF exhibits a lower energy than the bent one.9 Moreover, the rotational spectrum of THF recorded under supersonic jet conditions employing Fourier transform microwave spectroscopy confirmed that the twisted conformation corresponds to the potential minimum with the improved potential parameters in the four-fold pseudorotational potential function.12 Most previous experimental studies predicted that the C2 and CS conformations should correspond to global and local minima, respectively, with the energy difference between them being very small (∼30 meV). Conversely, electron momentum measurements performed by Yang et al. suggested that the CS conformation corresponds to the most populated structure of THF at ambient temperature,14 whereas subsequent absorption, electron energy loss, and photoelectron spectroscopy measurements along with theoretical calculations questioned the above conclusion and suggested that the ground electronic states of the above conformers should have almost equal energies.15 Unluckily, extensive theoretical investigations of the equilibrium conformation of THF afforded controversial results, being influenced by the applied theory and even the size of the same-level basis sets. Recently, Rayón and Sordo performed high-level ab initio calculations to show that the global minimum structure corresponds to the CS conformation, pointing out the difficulty of precisely characterizing the equilibrium ground-state conformation of THF due to the nearly flat potential energy surface along the pseudorotational coordinate.
In some favourable cases, e.g., for molecules with UV- and visible region-active chromophores, high-resolution spectra of low-frequency vibrational modes could be recorded using laser-induced fluorescence and/or resonance-enhanced multiphoton ionization techniques.16 Moreover, the ring-puckering vibrations and the corresponding potential energy surfaces and conformations of excited electronic states have been investigated for selected cyclic ketones.17,18 However, the vibrational spectra of gas-phase molecular ions are difficult to obtain using conventional absorption or emission spectroscopy, especially in the low-frequency region. In the present study, the vibrational spectrum of the THF cation was recorded using mass-analyzed threshold ionization (MATI) spectroscopy utilizing a vacuum ultraviolet laser.19–22 MATI inherently allows the vibrational spectrum of a selected molecular ion to be recorded from the zero-point vibrational energy level up to the point of interest, achieving higher resolution than ordinary photoelectron spectroscopy.23
The removal of an electron from the highest occupied molecular orbital (HOMO) of THF, which corresponds to the oxygen lone-pair orbitals, 9b and 12a’ for C2 and CS conformers, respectively, affords cations in the ground electronic state. In these cations, the increased ring angle strain is expected to lower the planarization barrier and thus favour more planar conformations, as demonstrated in a study of thietane and its cation.22,24,25 The ionization energies of THF previously obtained using VUV absorption and photoelectron spectroscopy equal 9.433 and 9.427 eV, respectively, with poor spectral resolution hindering unambiguous assignments to C2 or CS conformers.15,26 Therefore, we decided to figure out whether the above-mentioned conformational interconversion still occurs in the ground-electronic-state THF cation and determine the equilibrium conformation of this species. Since MATI can discriminate between the above conformers and provide the corresponding ionization energies by recording 0–0 bands at different positions of the MATI spectrum, we attempted to identify the above bands of individual conformers using quantum chemical calculations. The spectroscopic data obtained in the present study extended beyond the potential energy surfaces and could provide accurate vibrational energy levels and unambiguous conformational structures of the THF cation, allowing the vibrational potential energy function that defines the energetics of the conformational change to be precisely determined.
Experimental
A. VUV-MATI spectroscopy
Experiments were performed using an in-house-built VUV-MATI spectrometer described in previous reports.20,22 Briefly, a pulsed molecular beam of a gas-phase sample in equilibrium with the corresponding liquid in a reservoir was introduced into the ionization chamber through a skimmer (Beam Dynamics, diameter = 1 mm) located 3 cm downstream of the pulse nozzle orifice (Parker Valve, diameter = 500 μm). The concentration of the sample was controlled by keeping the sample reservoir at a temperature of 0 °C (ice bath) and an Ar stagnation pressure of 3 atm. The background pressure inside the chamber was maintained below 10−7 Torr. THF was purchased from TCI (>99.5%) and used without further purification.Coherent VUV light (126–132 nm) was generated by four-wave difference-frequency mixing (2ω1 − ω2) in Kr. Specifically, the employed ω1 = 216.667 nm for the resonant 5p[5/2]2–4p6 transition in Kr was generated by mixing after doubling in a BBO crystal the output of a dye laser (Continuum, ND6000) pumped by a Nd:YAG laser (Continuum, Surelite III). The tunable visible-light with ω2 = 595–760 nm was generated by another dye laser (Lambda Physik, ScanMate 2E) pumped by a separate Nd:YAG laser (Spectra-Physics, Quanta-Ray INDI). The pressure in the Kr gas cell required for obtaining the best VUV conversion efficiency equalled 3–5 Torr. VUV light, overlapping with the molecular beam in a counterpropagating manner, was introduced into the ionization chamber at an off-center position through a MgF2 lens (that also acted as an entrance window of the chamber) to separate VUV light in the ionization zone from residual UV and visible light. The dye laser output was calibrated using a wavelength meter (HighFinesse, WS-5). A spoil field of 0–0.2 V cm−1 was applied for ∼20 μs to remove the direct ions and electrons produced by the VUV laser pulse, with molecules in the zero kinetic energy (ZEKE) state subsequently ionized by a pulsed electric field of ∼12 V cm−1. The thus generated MATI ions were extracted and detected using a flight tube with a dual-channel MCP detector, with the resolution of the MATI spectrum equalling ∼8 cm−1.
B. Quantum chemical calculations
All quantum chemical calculations were carried out employing the Gaussian program package.27 The optimized geometries and vibrational frequencies of C2- and CS-symmetric THF conformers were calculated for neutral and cationic ground states, respectively. Various density functionals such as B3LYP, B3PW91, B971, ωB97XD, and m062x were attempted up to the aug-cc-pVTZ basis set, but the B3LYP/aug-cc-pVDZ level was mostly employed to analyze the MATI spectra in view of its accuracy and convenience. Scaling factors of 0.9859 and 0.9874 were used for the calculated vibrational frequencies of neutral and cationic THF states, respectively, to compensate for the uncertainties arising from vibrational anharmonicity and the incomplete treatment of electron correlation.28,29 Franck–Condon factors for individual vibrational transitions were calculated by varying the geometrical parameters of the cation to obtain the best fit of the experimental spectrum. The potential energy surfaces describing conformational transitions between neutral/cationic THF conformers with C2, CS, and C2v symmetries were constructed along dihedral angles representing twisting and bending vibrational motions.Results and discussion
Fig. 1 shows a MATI spectrum of THF, with the peak at 76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 019 cm−1 identified as the 0–0 band of a THF conformer based on the onset of its photoionization efficiency curve. The dominance of the above band implied the absence of significant structural differences between neutral THF and the corresponding cation. The ion internal energy provided at the top of the horizontal axis represents the vibrational energy of the THF cation measured relative to the 0–0 band position, ensuring that the observed MATI spectrum of THF is the vibrational spectrum of the THF cation. Since the ionization energy of a given molecule can be lowered by perturbation of the applied electric field,30 the corresponding measurements need to be performed under field-free conditions, which can be achieved by measuring the 0–0 band positions at different field strengths and extrapolating them to the zero-field limit (Supplement 1, ESI†). Accordingly, the first adiabatic ionization energy of THF was precisely determined as 76
019 cm−1 identified as the 0–0 band of a THF conformer based on the onset of its photoionization efficiency curve. The dominance of the above band implied the absence of significant structural differences between neutral THF and the corresponding cation. The ion internal energy provided at the top of the horizontal axis represents the vibrational energy of the THF cation measured relative to the 0–0 band position, ensuring that the observed MATI spectrum of THF is the vibrational spectrum of the THF cation. Since the ionization energy of a given molecule can be lowered by perturbation of the applied electric field,30 the corresponding measurements need to be performed under field-free conditions, which can be achieved by measuring the 0–0 band positions at different field strengths and extrapolating them to the zero-field limit (Supplement 1, ESI†). Accordingly, the first adiabatic ionization energy of THF was precisely determined as 76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 026 ± 3 cm−1 (9.4256 ± 4 eV), which was close to the value of 9.427 eV previously obtained for the C2 conformer.26 Based on the adiabatic ionization energy of 9.372 eV estimated from the vertical ionization energy of 9.73 eV of the CS conformer,26 the MATI signal of this conformer was expected to be located at frequencies below the observed 0–0 band. However, no MATI signals of appreciable intensity were found, including those corresponding to C2 conformer hot bands that could be discriminated under cold-molecular-beam conditions to avoid confusion. It was therefore suggested that the observed 0-0 band originates from the C2 (twisted) conformer of the THF cation, with the calculation results discussed in the next section strongly supporting this assignment.
026 ± 3 cm−1 (9.4256 ± 4 eV), which was close to the value of 9.427 eV previously obtained for the C2 conformer.26 Based on the adiabatic ionization energy of 9.372 eV estimated from the vertical ionization energy of 9.73 eV of the CS conformer,26 the MATI signal of this conformer was expected to be located at frequencies below the observed 0–0 band. However, no MATI signals of appreciable intensity were found, including those corresponding to C2 conformer hot bands that could be discriminated under cold-molecular-beam conditions to avoid confusion. It was therefore suggested that the observed 0-0 band originates from the C2 (twisted) conformer of the THF cation, with the calculation results discussed in the next section strongly supporting this assignment.
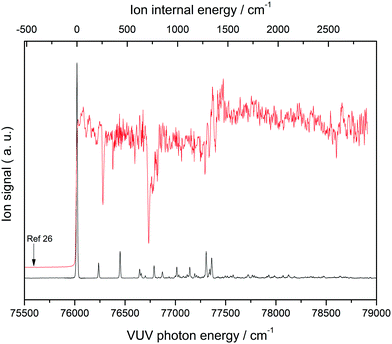 | ||
| Fig. 1 One-photon vacuum ultraviolet mass-analyzed threshold ionization (VUV-MATI) spectrum of THF and the corresponding photoionization efficiency curve. Arrow shows the ionization onset of the CS conformer predicted in ref. 26. | ||
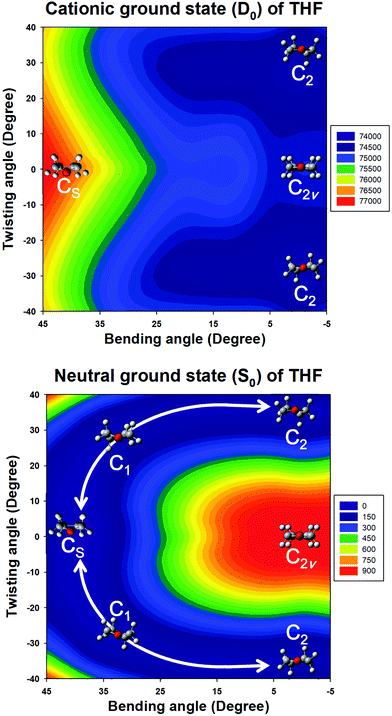
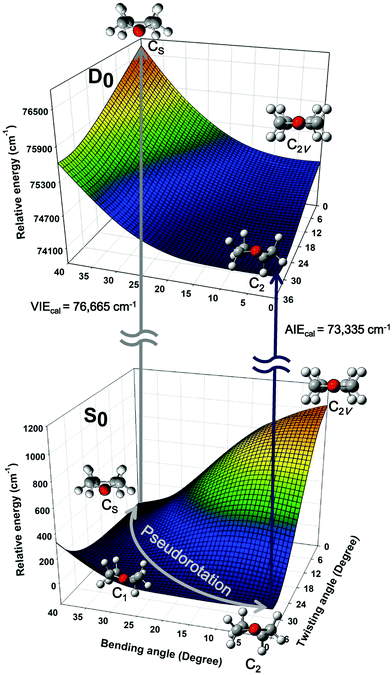
Quantum chemical calculations were performed to clarify the electronic transitions and ionization energies of the C2 and CS conformers of THF, with the corresponding geometry optimization (S0 neutral ground electronic state and D0 cationic ground state) performed at the B3LYP/aug-cc-pVDZ level of theory. Subsequently, conformational changes along the pseudorotational coordinates of the S0 and D0 states were determined by constructing a two-dimensional potential energy surface as a function of dihedral angles representing ring bending and twisting motions describing the conformational interconversion of THF performed with optimization of the remaining geometrical parameters as shown in Fig. 2. The constructed potential energy surface (PES) showed that the global minimum of the S0 state corresponded to the CS conformation, with the C2 conformation lying 38 cm−1 higher and the corresponding interconversion barrier equalling 57 cm−1. As previously pointed out, the calculated PES of the S0 state predicted the co-existence of both THF conformers at ambient temperature. However, the CS conformer of the D0 state could not be optimized due to being located on an unbound PES at a much higher energy than the C2 conformer, implying that the cationic state existed exclusively in the C2 conformation (Fig. 3). The zero-point energy-corrected adiabatic ionization energy calculated for the C2 conformer equalled 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 335 cm−1, whereas it could not be calculated for the unbound CS conformer, allowing only its vertical ionization energy to be determined (76
335 cm−1, whereas it could not be calculated for the unbound CS conformer, allowing only its vertical ionization energy to be determined (76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 665 cm−1). Table 1 compares the measured and calculated ionization energies reported herein to those reported previously. Although the ion signal of the CS conformer was expected to appear in the high-energy region of the MATI spectrum, it could not be detected due to the unbound nature of this species, resulting in the exclusive observation of the MATI spectrum of the C2 conformer. Therefore, it was concluded that the peak at ∼76
665 cm−1). Table 1 compares the measured and calculated ionization energies reported herein to those reported previously. Although the ion signal of the CS conformer was expected to appear in the high-energy region of the MATI spectrum, it could not be detected due to the unbound nature of this species, resulting in the exclusive observation of the MATI spectrum of the C2 conformer. Therefore, it was concluded that the peak at ∼76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 019 cm−1 represented the 0–0 band of the C2 conformer, with almost all other peak assignments performed based on the vibrational modes of the cationic C2 conformer. The geometrical parameters, bond lengths, and angles of optimized C2 structures are listed in Table 2, which shows that the calculated results for neutral THF were in remarkably good agreement with the X-ray crystallography data listed together for comparison.10
019 cm−1 represented the 0–0 band of the C2 conformer, with almost all other peak assignments performed based on the vibrational modes of the cationic C2 conformer. The geometrical parameters, bond lengths, and angles of optimized C2 structures are listed in Table 2, which shows that the calculated results for neutral THF were in remarkably good agreement with the X-ray crystallography data listed together for comparison.10
| VUV spectroscopya | Threshold PESc | Calculatione | This work | |
|---|---|---|---|---|
a
Ref. 15.
b Ionization onsets for C2 and CS conformers were superimposed and undistinguishable.
c
Ref. 26.
d The adiabatic ionization energy of the CS conformer was estimated from the measured vertical ionization energy of 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 478 cm−1.
e Ionization energies after zero-point energy correction at the B3LYP/aug-cc-pVDZ level.
f Calculated vertical ionization energy of the CS conformer at the B3LYP/aug-cc-pVDZ level. 478 cm−1.
e Ionization energies after zero-point energy correction at the B3LYP/aug-cc-pVDZ level.
f Calculated vertical ionization energy of the CS conformer at the B3LYP/aug-cc-pVDZ level.
|
||||
| C 2 symmetry | 76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 082b 082b |
76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 034 034 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 335 335 |
76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 026 ± 3 026 ± 3 |
| C S symmetry | 76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 082b 082b |
75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590 (78 590 (78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 478)d 478)d |
76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 665f 665f |
Not observed |
| C 2 symmetry | S0 (1A) | D0 (2B) | ||
|---|---|---|---|---|
| X-raya | Cal.b | Opt.c | Fittingd | |
| a Geometrical parameters reported using X-ray crystallography (ref. 10). b Equilibrium geometries calculated for the neutral C2 conformer. c Equilibrium geometries for the cationic C2 conformer. Values in parentheses reflect ionization-induced geometrical changes with respect to the calculated neutral species. d Geometries of the THF cation providing quantitative agreement between calculated and experimental results. | ||||
| Bond length [Å] | ||||
| O1–C2 | 1.435 | 1.439 | 1.428(0.011) | 1.432(−0.007) |
| C2–C4 | 1.531 | 1.533 | 1.524(−0.009) | 1.526(−0.007) |
| C4–C5 | 1.531 | 1.537 | 1.544(−0.007) | 1.544(−0.007) |
| C2–H6 | 1.090 | 1.099 | 1.103(−0.094) | 1.117(−0.018) |
| C2–H7 | 1.090 | 1.103 | 1.118(−0.015) | 1.102(−0.001) |
| C4–H8 | 1.090 | 1.099 | 1.098(0.001) | 1.095(−0.004) |
| C4–H9 | 1.090 | 1.097 | 1.095(−0.002) | 1.098(0.001) |
| Bond angle [°] | ||||
| C2–O1–C3 | 109.8 | 110.1 | 110.7(−0.6) | 110.8(0.7) |
| O1–C2–C4 | 106.7 | 106.3 | 107.0(0.7) | 106.6(0.3) |
| C2–C4–C5 | 101.9 | 101.9 | 102.6(0.7) | 102.5(0.6) |
| H6–C2–H7 | 108.4 | 105.1(−3.3) | 108.0(−0.4) | |
| H9–C4–H8 | 108.3 | 108.3(−0.0) | 108.4(0.1) | |
| O1–C2–C4–C5 | 29.6 | 30.1 | 26.0(−4.1) | 27.1(−3.0) |
| C2–C4–C5–C3 | −35.2 | −35.9 | −30.9(−5.0) | −32.4(3.5) |
| H6–C2–O1–C3 | 108.2 | 110.1(1.9) | 108.1(−0.1) | |
| H7–C2–O1–C3 | −133.9 | −139.8(−5.9) | −138.9(−5.0) | |
| H8–C4–C2–O1 | 151.8 | 147.1(−4.7) | 148.2(−3.6) | |
| H9–C4–C2–O1 | −87.1 | −92.8(−5.7) | −91.7(−4.6) | |
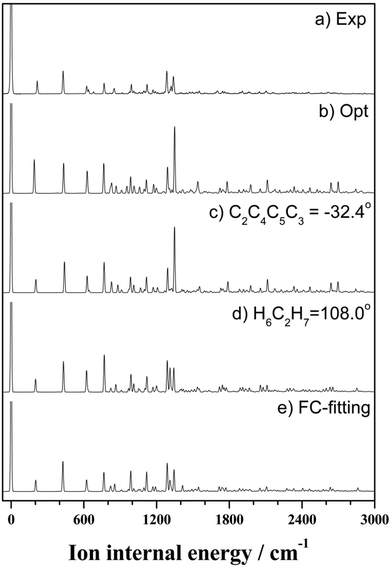
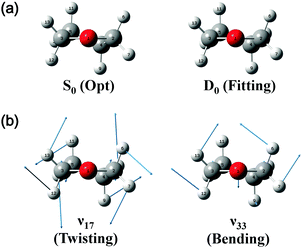
On the basis of the above discussion, the observed MATI peaks could be assigned based on the dipole selection rules for the S0 → D0 transitions of the C2 conformer. The above rules allow vibrational transitions from the ground vibrational state of neutral THF to the totally symmetric a modes of the cationic ground state due to the cooling of molecules in the molecular beam.25 The corresponding vibrational frequencies were determined utilizing the geometries of the neutral and cationic C2 conformer optimized at the B3LYP/aug-cc-pVDZ level. Franck–Condon (FC) factors for individual vibrational transitions were determined based on the calculated vibrational wave vectors of S0 and D0 states and used for spectral simulations together with the calculated frequencies. Fig. 4 shows the thus simulated spectrum along with the experimental MATI spectrum, revealing their good agreement except for the relative intensities. The calculated intensity of a given spectral peak should be sensitive to the transition-induced molecular structure change and hence depend on the FC factors. The well-established geometry of the ground-state C2 conformer allowed the FC factors (and hence, the simulated spectrum) to be determined by varying the cation geometrical parameters of bond lengths/angles to obtain the best fit to the experimental spectrum. This procedure, known as Franck–Condon fitting, has successfully been used to analyze the experimental MATI spectra of molecules such as pyrimidine or pyridine and determine the structures of the corresponding cations.19,20 As shown in Table 2, the ionization-induced structural change mainly involved motions associated with vibrational modes 17 and 33 (twisting and bending vibrational motions), as depicted in Fig. 5, resulting in significant changes in C2–C4–C5–C3 and H7–C2–O1–C3 dihedral angles and the H6–C2–H7 bond angle. Thus, the VUV-MATI spectrum was expected to show prominent overtone and combination bands related to the abovementioned low-frequency modes 17 and 33 (mode numbering was performed according to the Mulliken notation).
The FC fitting was carried out starting from changes in the dihedral angles of the ring and the out-of-plane angles of the H atoms, with bond lengths determined to be less sensitive to the calculated spectral change. First, the vibrational frequencies and wavefunctions of the cation were calculated with the above mentioned angle parameters changed a little and optimization of the remaining structural parameters, from which the FC factors were calculated to simulate the spectrum. Then, this process was iterated by changing the angle parameters in the cation step by step from the equilibrium values until the best-fit spectrum was obtained. The refined geometrical parameters of the cationic C2 conformer (Table 2) were obtained from the best-fit spectrum presented in Fig. 4. The high quality of the obtained fit allowed the structure of the above cation to be precisely determined, as shown in Fig. 5.
Almost all peaks observed in the MATI spectrum could be unambiguously assigned by comparison with the best-fit spectrum. As expected, the prominent peak at 215 cm−1 was assigned to mode 171 (a-symmetric twisting vibrational mode). Moreover, the peak at 428 cm−1 was assigned to mode 332, which is an overtone of the b-symmetric bending vibrational mode, allowing peaks at 849 and 1270 cm−1 to be assigned as 334 and 336, respectively. Thus, considering the anharmonic oscillator levels for 332, 334, and 336 overtones, the wavenumber of the corresponding fundamental mode (331) was determined as 217 cm−1. Subsequently, peaks at 640, 1053, 1190, 1242, 1403, 1448, 1552, 1597, 1701, 1743, and 1761 cm−1 were ascribed to combination bands with 332, i.e., 332171, 332161, 332151, 332141, 33212n, 332111, 332101, 33291, 33281, 33271, and 33261, respectively. The fundamental frequencies of modes 161–61 corresponded to 623, 767, 813, 916, 992, 1012, 1121, 1170, 1284, 1312, and 1339 cm−1, respectively, with the assignment of mode 131 based on the best-fit spectrum, since the 332131 combination band was superimposed on the prominent peak of 61. Peaks at 786, 1053, 1096, 1162, and 1321 cm−1 represented the combinations of 331 with b-symmetric modes 321, 301, 291, 281, and 271, respectively. Peaks at 838, 978, 1025, 1211, 1495, 1526, and 1552 cm−1 were attributed to combinations of mode 171 with a-symmetric modes 161, 151, 141, 111, 81, 71, and 61, respectively. In addition, peaks at 1906, 2049, 2271, 2402, and 2615 cm−1 represented the combinations of mode 81 with a-symmetric modes 161, 151, 121, 101, and 61, respectively, and those at 1962, 2104, 2324, 2349, 2454, and 2653 cm−1 were combinations of mode 61 with a-symmetric modes 161, 151, 121, 111, 101, and 71, respectively. Thus, most of the MATI peaks could be assigned to combination bands of modes 332, 17, 8, and 6. The distinct peaks at 569 and 945 cm−1 were assigned to the non-totally symmetric 321 and 281 bands, respectively, based on the combinations of mode 331, which requires further explanation and investigation. As previously mentioned, all peaks observed in the MATI spectrum of THF could be assigned to the cationic ground state C2 conformers. Detailed information on assigned peaks (Fig. 6) is provided in Table 3, which also lists the corresponding intensities normalized with respect to that of the 0–0 band.
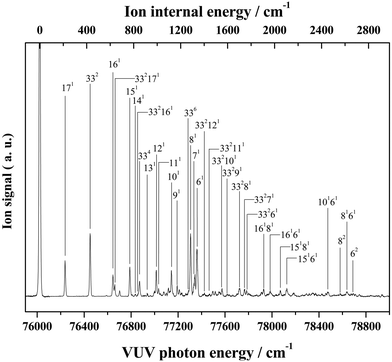 | ||
| Fig. 6 VUV-MATI spectrum of THF shown in Fig. 1 with vibrational assignments based on the Franck–Condon fit (see the text). The spectrum is magnified two times to show the details. | ||
| Modea | Symm. (C2) | S0(1A)b | VUV-MATI (2B) | Opt.d | Fittinge | |||
|---|---|---|---|---|---|---|---|---|
| Freq. | Int.c | Freq. | Int.c | Freq. | Int.c | |||
| a Vibrational assignments in Mulliken notation. b Ref. 10. c Normalized to the intensity of the 0–0 band. d Frequencies and Franck–Condon factors calculated for the geometries of neutral and cationic C2 conformers optimized at the B3LYP/aug-cc-pVDZ level. e Frequencies and Franck–Condon factors resulting in quantitative agreement between calculated and experimental results obtained by adjusting the geometrical parameters of the cationic C2 conformer. f The fundamental frequency of mode 33 was estimated considering the anharmonic oscillator levels of overtones 332, 334, and 336. g Fundamental frequencies of non-totally symmetric (b) modes were estimated using the fundamental frequency of mode 33 for combination bands with 331. | ||||||||
| Fundamentals | ||||||||
| 171 | a | 260 | 215 | 0.0714 | 191 | 0.0184 | 203 | 0.0620 |
| 161 | a | 644 | 623 | 0.0433 | 629 | 0.1007 | 623 | 0.0617 |
| 151 | a | 836 | 767 | 0.0587 | 765 | 0.1626 | 766 | 0.1035 |
| 141 | a | 896 | 813 | 0.0039 | 830 | 0.0543 | 820 | 0.0242 |
| 131 | a | 932 | 916 | 0.0063 | 912 | 0.0178 | 911 | 0.0092 |
| 121 | a | 1031 | 992 | 0.0522 | 988 | 0.0903 | 989 | 0.1118 |
| 111 | a | 1142 | 1012 | 0.0166 | 1016 | 0.0374 | 1014 | 0.0156 |
| 101 | a | 1176 | 1121 | 0.0518 | 1118 | 0.0744 | 1120 | 0.1061 |
| 91 | a | 1240 | 1170 | 0.0020 | 1127 | 0.0300 | 1171 | 0.0260 |
| 81 | a | 1360 | 1284 | 0.1249 | 1292 | 0.1373 | 1290 | 0.1503 |
| 71 | a | 1368 | 1312 | 0.0267 | 1310 | 0.0124 | 1312 | 0.0604 |
| 61 | a | 1464 | 1339 | 0.0847 | 1351 | 0.3615 | 1346 | 0.1187 |
| 331 | b | 217f | 217 | 214 | ||||
| 321 | b | 569g | 0.0025 | 580 | 576 | |||
| 301 | b | 839g | 845 | 852 | ||||
| 291 | b | 879g | 881 | 883 | ||||
| 281 | b | 945 | 0.0021 | 948 | 946 | |||
| 271 | b | 1107 | 1112 | 1108 | ||||
| 251 | b | 1259 | 1254 | 1250 | ||||
| Overtone and combination | ||||||||
| 332 | a | 428 | 0.1252 | 434 | 0.1637 | 428 | 0.1635 | |
| 332171 | a | 640 | 0.0241 | 625 | 0.0301 | 631 | 0.0101 | |
| 331321 | a | 786 | 0.0034 | 796 | 0.0026 | 789 | 0.0034 | |
| 171161 | a | 838 | sh | 820 | 0.0310 | 826 | 0.0122 | |
| 334 | a | 849 | 0.0304 | 867 | 0.0402 | 855 | 0.0401 | |
| 171151 | a | 978 | 0.0116 | 956 | 0.0391 | 969 | 0.0117 | |
| 171141 | a | 1025 | 0.0062 | 1022 | 0.0058 | 1024 | 0.0002 | |
| 332161 | a | 1053 | 0.0130 | 1062 | 0.0165 | 1051 | 0.0101 | |
| 331301 | a | 1056 | 0.0080 | 1063 | 0.0129 | 1066 | 0.0111 | |
| 331291 | a | 1096 | 0.0174 | 1099 | 0.0195 | 1098 | 0.0201 | |
| 331281 | a | 1162 | sh | 1166 | 0.0002 | 1160 | 0.0002 | |
| 332151 | a | 1190 | 0.0141 | 1199 | 0.0266 | 1194 | 0.0169 | |
| 171111 | a | 1211 | 0.0064 | 1230 | 0.0013 | 1217 | 0.0032 | |
| 332141 | a | 1242 | 0.0067 | 1264 | 0.0089 | 1248 | 0.0040 | |
| 336 | a | 1270 | 0.0123 | 1300 | 0.0110 | 1284 | 0.0109 | |
| 331271 | a | 1321 | 0.0439 | 1329 | 0.0194 | 1322 | 0.0166 | |
| 332121 | a | 1403 | 0.0057 | 1421 | 0.0148 | 1416 | 0.0183 | |
| 334161 | a | 1473 | 0.0108 | 1496 | 0.0041 | 1479 | 0.0025 | |
| 17181 | a | 1495 | 0.0105 | 1483 | 0.0200 | 1493 | 0.0064 | |
| 17171 | a | 1526 | 0.0101 | 1501 | 0.0037 | 1515 | 0.0058 | |
| 17161 | a | 1552 | 0.0154 | 1542 | 0.0578 | 1549 | 0.0049 | |
| 33291 | a | 1597 | 0.0055 | 1610 | 0.0049 | 1598 | 0.0042 | |
| 161121 | a | 1611 | 0.0045 | 1616 | 0.0023 | 1621 | 0.0041 | |
| 151131 | a | 1680 | 0.0044 | 1678 | 0.0026 | 1678 | 0.0008 | |
| 333301171 | a | 1701 | 0.0163 | 1687 | 0.0012 | 1697 | 0.0003 | |
| 161101 | a | 1743 | 0.0120 | 1747 | 0.0120 | 1743 | 0.0108 | |
| 33261 | a | 1761 | 0.0129 | 1785 | 0.0592 | 1774 | 0.0194 | |
| 151111 | a | 1778 | 0.0073 | 1782 | 0.0042 | 1780 | 0.0008 | |
| 16191 | a | 1790 | 0.0055 | 1806 | 0.0031 | 1794 | 0.0017 | |
| 151101 | a | 1890 | 0.0079 | 1883 | 0.0155 | 1886 | 0.0145 | |
| 16181 | a | 1906 | 0.0158 | 1921 | 0.0179 | 1914 | 0.0127 | |
| 16161 | a | 1962 | 0.0090 | 1980 | 0.0378 | 1969 | 0.0081 | |
| 15181 | a | 2049 | 0.0104 | 2058 | 0.0226 | 2056 | 0.0166 | |
| 15161 | a | 2104 | 0.0169 | 2117 | 0.0640 | 2112 | 0.0148 | |
| 12191 | a | 2162 | 0.0076 | 2164 | 0.0020 | 2158 | 0.0022 | |
| 12181 | a | 2271 | 0.0060 | 2279 | 0.0101 | 2278 | 0.0141 | |
| 10191 | a | 2294 | 0.0068 | 2294 | 0.0018 | 2290 | 0.0022 | |
| 12161 | a | 2324 | 0.0061 | 2339 | 0.0338 | 2335 | 0.0140 | |
| 11161 | a | 2349 | 0.0074 | 2368 | 0.0120 | 2360 | 0.0015 | |
| 10181 | a | 2402 | 0.0039 | 2410 | 0.0073 | 2410 | 0.0122 | |
| 10171 | a | 2438 | 0.0045 | 2428 | 0.0009 | 2432 | 0.0063 | |
| 10161 | a | 2454 | 0.0098 | 2469 | 0.0235 | 2466 | 0.0105 | |
| 82 | a | 2558 | 0.0047 | 2584 | 0.0066 | 2581 | 0.0085 | |
| 8161 | a | 2615 | 0.0090 | 2643 | 0.0540 | 2637 | 0.0202 | |
| 7161 | a | 2653 | 0.0056 | 2661 | 0.0080 | 2658 | 0.0012 | |
| 62 | a | 2669 | 0.0063 | 2702 | 0.0590 | 2692 | 0.0048 | |
| 33329191 | a | 2689 | 0.0049 | 2709 | 0.0003 | 2696 | 0.0003 | |
| 33211181 | a | 2722 | 0.0030 | 2741 | 0.0007 | 2732 | 0.0003 | |
| 15114161 | a | 2915 | 0.0041 | 2946 | 0.0029 | 2932 | 0.0019 | |
Conclusions
Herein, one-photon vacuum ultraviolet mass-analyzed threshold ionization was used to record the vibrational spectrum of the THF cation and thus determine the first (adiabatic) ionization energy of THF as 76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 026 ± 3 cm−1 (9.4256 ± 0.0004 eV), which is more accurate than those obtained previously. Analysis of the above MATI spectrum and quantum chemical density functional theory calculations allowed the structure of THF in the ground electronic state (S0) to be assigned to the bent CS conformation, with the twisted C2 conformer located at a slightly higher energy and the corresponding interconversion barrier equalling 57 cm−1. However, the most probable structure of the ground-state (D0) THF cation corresponded to the twisted C2 conformer, whereas the CS conformer was located at a much higher energy on the unbound potential energy surface. The observed ionization energy and vibrational spectrum could be explained assuming that both neutral THF and its cation exhibit C2 conformations in their ground electronic states. The observed spectrum was fitted to the simulated one using Franck–Condon fitting, and the thus obtained best fit was used to precisely determine the structure of the THF cation.
026 ± 3 cm−1 (9.4256 ± 0.0004 eV), which is more accurate than those obtained previously. Analysis of the above MATI spectrum and quantum chemical density functional theory calculations allowed the structure of THF in the ground electronic state (S0) to be assigned to the bent CS conformation, with the twisted C2 conformer located at a slightly higher energy and the corresponding interconversion barrier equalling 57 cm−1. However, the most probable structure of the ground-state (D0) THF cation corresponded to the twisted C2 conformer, whereas the CS conformer was located at a much higher energy on the unbound potential energy surface. The observed ionization energy and vibrational spectrum could be explained assuming that both neutral THF and its cation exhibit C2 conformations in their ground electronic states. The observed spectrum was fitted to the simulated one using Franck–Condon fitting, and the thus obtained best fit was used to precisely determine the structure of the THF cation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the National Research Foundation of Korea (2016R1D1A3B03935921 and 2017R1A4A1015405).References
- J. Laane, Annu. Rev. Phys. Chem., 1994, 45, 179–211 CrossRef CAS.
- T. Ueda and T. Shimanouchi, J. Chem. Phys., 1968, 49, 470–471 CrossRef CAS.
- T. B. Malloy Jr. and W. J. Lafferty, J. Mol. Spectrosc., 1975, 54, 20–38 CrossRef.
- R. A. Creswell and I. M. Mills, J. Mol. Spectrosc., 1974, 52, 392–412 CrossRef CAS.
- R. A. Kydd, H. Wieser and M. Danyluk, J. Mol. Spectrosc., 1972, 44, 14–17 CrossRef CAS.
- J. R. Durig and D. W. Wertz, J. Chem. Phys., 1968, 49, 2118–2121 CrossRef CAS.
- L. E. Bauman and J. Laane, J. Phys. Chem., 1988, 92, 1040–1051 CrossRef CAS.
- V. M. Rayón and J. A. Sordo, J. Chem. Phys., 2005, 112, 204303 CrossRef PubMed.
- G. G. Engerholm, A. C. Luntz and W. D. Gwinn, J. Chem. Phys., 1969, 50, 2446–2457 CrossRef CAS.
- B. Cadioli, E. Gallinella, C. Coulombeau, H. Jobic and G. Berthier, J. Phys. Chem., 1993, 97, 7844–7856 CrossRef CAS.
- S. J. Han and Y. K. Kang, J. Mol. Struct.: THEOCHEM, 1996, 369, 157–165 CrossRef CAS.
- R. Meyer, J. C. Lopez, J. L. Alonso, S. Melandri, P. G. Favero and W. Caminati, J. Chem. Phys., 1999, 111, 7871–7880 CrossRef CAS.
- D. G. Melnik, S. Gopalakrishnan, T. A. Miller and F. C. De Lucia, J. Chem. Phys., 2003, 118, 3589–3599 CrossRef CAS.
- T. Yang, G. Su, C. Ning, J. Deng, F. Wang, S. Zhang, X. Ren and Y. Huang, J. Phys. Chem. A, 2007, 111, 4927–4933 CrossRef CAS PubMed.
- A. Giuliani, P. Limao-Vieira, D. Duflot, A. R. Milosavljevic, B. P. Marinkovic, S. V. Hoffmann, N. Mason, J. Delwiche and M.-J. Hubin-Franskin, Eur. Phys. J. D, 2009, 51, 97–108 CrossRef CAS.
- A. R. Potts and T. Baer, J. Phys. Chem. A, 1997, 101, 8970–8978 CrossRef CAS.
- J. Zhang, W. Y. Chiang and J. Laane, J. Chem. Phys., 1993, 98, 6129–6137 CrossRef CAS.
- C. M. Cheatham and J. Laane, J. Chem. Phys., 1991, 94, 7734–7743 CrossRef CAS.
- J. H. Kim, J. H. Lee, H. Hwang, H. L. Kim and C. H. Kwon, Phys. Chem. Chem. Phys., 2014, 16, 1590–1596 RSC.
- Y. R. Lee, D. W. Kang, H. L. Kim and C. H. Kwon, J. Chem. Phys., 2014, 141, 174303 CrossRef PubMed.
- D. W. Kang, H. L. Kim and C. H. Kwon, Int. J. Mass Spectrom., 2016, 397-398, 52–57 CrossRef CAS.
- Y. R. Lee, C. B. Park, J. Hwang, B. J. Sung, H. L. Kim and C. H. Kwon, J. Phys. Chem. A, 2017, 121, 1163–1167 CrossRef CAS PubMed.
- (a) L. Zhu and P. Johnson, J. Chem. Phys., 1991, 94, 5769–5771 CrossRef CAS; (b) H. Dietrich, R. Lindner and K. Müller-Dethlefs, J. Chem. Phys., 1994, 101, 3399–3402 CrossRef CAS.
- D. O. Harris, H. W. Harrington, A. C. Luntz and W. D. Gwinn, J. Chem. Phys., 1966, 44, 3467–3480 CrossRef CAS.
- H. J. Chun, E. Ocola and J. Laane, J. Phys. Chem. A, 2017, 121, 2798–2803 CrossRef PubMed.
- M. Dampc, B. Mielewska, M. R. F. Siggel-King, G. C. King and M. Zubek, Chem. Phys., 2009, 359, 77–81 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. F. Zakrzewski, J. A. Montgometry, R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, J. L. Andres, M. Head-Gordon, E. S. Replogle and J. A. Pople, Gaussian 09, Gaussian Inc., Pittsburgh, PA, 2009 Search PubMed.
- J. P. Merrick, D. Moran and L. Radom, J. Phys. Chem. A, 2007, 111, 11683 CrossRef CAS PubMed.
- P. Sinha, S. E. Boesch, C. Gu, R. A. Wheeler and A. K. Wilson, J. Phys. Chem. A, 2004, 108, 9213 CrossRef CAS.
- E. W. Schlag, ZEKE Spectroscopy, Cambridge University Press, Cambridge, 1998 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp05646j |
| This journal is © the Owner Societies 2017 |