Proton mobility in aqueous systems: combining ab initio accuracy with millisecond timescales†
Gabriel
Kabbe
 ,
Christian
Dreßler
and
Daniel
Sebastiani
,
Christian
Dreßler
and
Daniel
Sebastiani
 *
*
Institute of Chemistry, Martin-Luther-University Halle-Wittenberg, von-Danckelmann-Platz 4, 06120 Halle, Germany. E-mail: daniel.sebastiani@chemie.uni-halle.de
First published on 10th October 2017
Abstract
We present a multiscale simulation of proton transport in liquid water, combining ab initio molecular dynamics simulations with force-field ensemble averaging and kinetic Monte-Carlo simulations. This unique Ansatz allows for ab initio accuracy incorporating the femtosecond dielectric relaxation dynamics of the aqueous hydrogen bonding network, and bridges the time-scale gap towards the explicit simulation of millisecond diffusion dynamics.
1 Introduction
Proton transfer in water plays an important role in many chemical and biological processes.1–3 Especially with regard to Proton Exchange Membrane (PEM) fuel cells, the high conductivity of water is a desirable property and the reason for the efficiency of Nafion-based membranes.4–8 These membranes enclose water channels, in which proton conduction is possible. In this context, a lot of research has been conducted to further clarify the proton conduction mechanisms both experimentally and theoretically.A model picture of the underlying mechanisms which explain the anomalously high proton conduction in water was actually first proposed by Grotthuss more than 200 years ago.9 It comprises two main elements: a hopping step, which is later followed by reorientation. The hopping step can actually happen as a series of proton transfers along a chain of water molecules, or rather “water wire”,10,11 which leads to the propagation of the excess charge along the chain without any diffusive motion of the molecules themselves, and a simultaneous reversal of the chain's dipole moment. Consequently, the subsequent rotation of the water molecules is necessary in order to enable further proton transfer along the same “water wire”.
In recent years, this idealized model picture has been refined further. In particular, the water reorientation by rotation is believed to be an oversimplification as a water molecule in bulk water is hydrogen-bonded to four neighbor molecules, which hinders free rotation. Instead, the breaking of a hydrogen bond, which is necessary to reduce the hydrogen-bond coordination number of an accepting H2O from four to three, is considered the rate-determining step.12,13
With the continuously increasing computing capabilities, ab initio calculations of proton transfer in water have become feasible. It is now possible to investigate proton transfer on the atomistic level.13–19 However, while offering a high accuracy, these methods are still computationally expensive and give only access to timescales of tens to hundreds of picoseconds. Especially with regard to the simulation of macroscopic properties of proton exchange membranes, they often do not allow statistically relevant sampling of the excess proton movement in a reasonable amount of time. Similarly, the adequate incorporation of co-solvents, geometric confinement, effects, or the influence of functional interfaces is computationally challenging.
In this work, we present a coupled Molecular Dynamics/Lattice Monte Carlo (cMD/LMC) approach, which aims at simulating large-scale excess charge diffusion in aqueous systems. This combined method has already been applied successfully to PEM materials20,21 and solid acids.22 Based on structural dynamics calculated from molecular dynamics (MD), it builds a time-dependent excess charge transition matrix for the Lattice Monte Carlo (LMC) scheme. The mapping between the topology of the system and the resulting excess charge transfer rate is determined with statistical analysis from ab initio MD.
On the basis of a neutral classical MD trajectory of water, we show that our cMD/LMC scheme is able to determine dynamical quantities of the excess charge in best agreement with ab initio methods over large time scales.
2 Method
For the propagation of an excess proton through a liquid water system, we have developed a hybrid scheme which combines aspects from molecular dynamics (MD), and lattice/kinetic Monte Carlo methods.23–25 Protons can jump between lattice sites with transfer rates which are extracted on-the-fly from an underlying MD simulation (see also ref. 20–22). Each lattice site represents an oxygen atom of the considered system and can be in one of two states: occupied or unoccupied. The trajectory-based evolution of the pairwise oxygen distances in the MD results in a change of the proton transition rate in the LMC scheme. This scheme has been shown to yield a realistic picture of condensed-phase systems.In order to take the characteristic hydrogen-bond network of H3O+ in liquid water into account, we construct the LMC topology such that each oxygen site is connected to its closest three neighbors.
2.1 Lattice Monte Carlo scheme
The LMC system consists of a discrete range of states and is described by a master equation with time-dependent transition rates: | (1) |
The scheme first translates the transfer rate 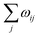 from a lattice site i into a “lifetime” of this very site. In this context, the lifetime is defined as the duration τ, after which the excess charge at lattice site i is transferred to an adjacent site. In our specific algorithm, this lifetime is calculated by drawing a random number x in the interval (0, 1] and solving the equation
from a lattice site i into a “lifetime” of this very site. In this context, the lifetime is defined as the duration τ, after which the excess charge at lattice site i is transferred to an adjacent site. In our specific algorithm, this lifetime is calculated by drawing a random number x in the interval (0, 1] and solving the equation
 | (2) |
Once this specific lifetime has passed, the algorithm determines the target site for the excess charge by drawing another random number x from the interval  and choosing the second oxygen site with index j0 such that
and choosing the second oxygen site with index j0 such that
 | (3) |
2.2 Determination of the excess charge diffusion
The challenge in determining the excess charge motion from an atomic trajectory is the fact that there is no “labeled” excess charge particle whose position can be tracked. Instead, similar to the Grotthuss picture, a multitude of protons are involved during a (long-range) excess charge transfer.Within the ab initio molecular dynamics (AIMD) simulations, the excess charge diffusion is therefore determined by means of a collective variable specifically designed for this task, with an effective coordinate given by:
 | (4) |
In contrast to MD, the cMD/LMC scheme represents the excess charge position explicitly as an overprotonated molecular state that is assigned to a water molecule at each time step. It is therefore trivial to follow the excess charge over time and determine its diffusion.
Unlike MD, the proton motion in the cMD/LMC scheme is not continuous: when a water molecule transfers its excess charge to another nearby molecule, the excess charge position changes instantaneously from the position of the donor molecule to the position of the acceptor molecule. As a consequence, the mean squared displacement function is discontinuous and changes stepwise by the full oxygen–oxygen distance.
2.3 Excess charge transfer rate determination
In order to obtain a realistic transfer rate matrix between individual lattice sites for the cMD/LMC scheme, the instantaneous atomic geometry around a protonated water molecule must be mapped onto the probability of an excess charge transfer for a given constellation of the H3O+'s surroundings. We determine this mapping by statistically analysing the excess charge transfer events within the ab initio MD trajectory and determining the transfer rate as a function of the oxygen–oxygen distance between H3O+ and the surrounding H2O molecules by means of the following algorithm for each time step t:(1) Determine the distance distribution ρOO(dOO,t) of potential H+ acceptor water molecules around the H3O+.
(2) Lookup the distance distribution ρjump(dOO,t) of actual H+ acceptor molecules, i.e. consider only those waters to which a proton jump has actually occurred in the next MD step at t + Δt.
(3) The proton jump rate at time t is determined via
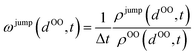 | (5) |
| ωjump(dOO) = 〈ωjump(dOO,t)〉t | (6) |
 | (7) |
3 Results
3.1 Analysis of ab initio molecular dynamics of protonated water
While the ab initio trajectories are used both as a reference system and for analysis of the dynamical properties of H3O+, the classical trajectory provides the underlying topology for calculating the excess charge jump rates of the cMD/LMC scheme.
AIMD trajectories of 100 water molecules and an excess proton in a periodic box of length 14.405 × 14.405 × 14.405 Å3 were used to determine the proton jump rates and analyze the radial distribution function (RDF) between hydronium and neutral water. In order to investigate the temperature dependence of the observables, three trajectories at 300 K, 350 K and 400 K were run. We used the BLYP functional32,33 with a DZVP-MOLOPT-SR-GTH basis and the GTH pseudopotential.34 The DFT-D3 dispersion correction was used.35 The molecular dynamics simulation was run with a timestep of 0.5 fs using the Nosé–Hoover thermostat.36
At the force field level, an MD trajectory consisting of 216 water molecules in a periodic box of length 18.626 × 18.626 × 18.626 Å3 was run on a simulation time scale of 10 ns at 350 K. For the classical MD, we used the TIP4P water model with the Amber force field.37
3.2 Dielectrical relaxation following an elementary proton hopping step
The presence of an excess proton in water leads to considerable electrostatic forces, which influence the structure of water molecules in the vicinity of the H3O+ ion. This effect is incorporated automatically by AIMD, which is known to yield a precise description of both structure and femto/picosecond dynamics around a solvated charge,15,16,38 but is missing within the cMD/LMC scheme, as the excess charge state within the LMC is not returned as feedback to the MD simulation. As a result, the acceptor–donor distances in the LMC scheme are overestimated, which leads to a diminished proton hopping rate and therefore an underestimation of the overall excess charge diffusion.We propose a scheme which adjusts the trajectory data to take into account this dielectric response of the water upon protonation changes. Specifically, we analyze how the presence of an excess charge in the AIMD influences the RDF of the first solvation shell. This change is subsequently used to construct a conversion function that provides a mapping between the pairwise oxygen distances of an uncharged water system and those of a protonated system within the first solvation shell.
To address this issue, we construct a conversion function which maps the distance distribution of an uncharged water and its first solvation shell to the distance distribution of a hydronium ion and its first solvation shell. This allows us to take the structural effect of a charged particle within the LMC scheme into account by effectively rescaling the distances between an occupied oxygen site and its neighbors.
For the construction of the conversion function, we use the integrated RDF, which yields the number of particles within a radius r. It is defined as
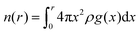 | (8) |
We also define nhydronium(r) as the integrated RDF of the desired distribution (i.e. the hydronium–H2O distribution), and nneutral(r) as the integrated RDF of the original distribution in the neutral H2O system.
The conversion function c(d) is then defined as:
| c(d) = nhydronium−1(nneutral(d)) | (9) |
In our implementation, we calculate the conversion function at discrete points, and use a linear interpolation scheme to provide a continuous mapping.
Note that the conversion function effectively shortens the donor hydrogen bonds by around 0.25 Å in the range between 2.5 Å and 3 Å. This agrees well with the distance of the peaks of the H3O+–H2O versus the H2O–H2O (see Fig. 2).
 | (10) |
The choice of the dielectric relaxation time parameter trelax determines the time span, in which the linear rescaling takes place. It turns out that an adequate range for trelax is found between 2 and 10 ps.
3.3 Proton dynamics in the cMD/LMC approach
In the following, we investigate how the cMD/LMC scheme reproduces dynamical quantities such as MSD and the excess charge autocorrelation. For this, we compare the dynamical properties of the LMC scheme with the reference AIMD calculation and experimental results.| Method | D/Å2 ps−1 |
|---|---|
| LMC (w/rescaling, trelax = 0 ps) | 10.5(3) |
| LMC (w/rescaling, trelax = 4 ps) | 1.69(6) |
| LMC (w/rescaling, trelax = 6 ps) | 1.72(5) |
| LMC (w/o rescaling, (trelax → ∞)) | 1.01(3) |
| Reference AIMD (this work) | 1.48(1) |
| Experimental | 0.86539 |
Next, we compare the results of the cMD/LMC scheme, and ab initio results. Fig. 4 shows the variation of the excess charge diffusion coefficient with respect to the relaxation time parameter. We see that the diffusion coefficient is in best agreement with the reference AIMD for values trelax between 4 and around 12 ps. Values of trelax below 2 ps, on the other hand, lead to unrealistically high diffusion coefficients which differ by an order of magnitude. Using the oxygen distances of the neutral water system yields a lower diffusion coefficient (around 1 Å2 ps−1) than our reference AIMD. The reason for this behavior can be seen from Fig. 2: the neutral oxygen–oxygen distances lie around a distance of 1.7 Å, which corresponds to a proton jump rate of less than one jump per ps. It should be noted that the lowest possible diffusion rate in our scheme occurs, if the excess charge does not jump at all. In this case, only the oxygen diffusion contributes with D = 0.6 Å2 ps−1.
While the concept of the relaxation time parameter trelax is physically motivated, the range of 4 to 12 ps obtained by comparison of the final diffusion coefficient to the reference AIMD simulation may appear a quasi-empirical choice. However, this range can also be derived from an analytical consideration: assuming an activation energy of 2.6 kcal mol−1 for the cleavage and reformation of two hydrogen bonds,42 and using a wavenumber of 170 cm−1 for the hydrogen bond stretching frequency,43 application of the Arrhenius equation yields an average time of around five picoseconds before a hydrogen bond breaks. This quantitative agreement validates the choice of trelax = 5 ps as a universal value (for liquid water).
| η(t) = 〈δi+(t0),i+(t0+t)〉t0 | (11) |
Fig. 5 shows the results for the reference AIMD and LMC the scheme for a range of values for trelax. Qualitatively, the results are similar to the diffusion coefficients: the best agreement with the reference ab initio trajectory is found for values of trelax between 2 and 8 ps. The LMC scheme with unrescaled distances shows the lowest decline of η, caused by the larger oxygen–oxygen distances and the resulting decreased excess charge transfer rates. The LMC scheme with instantaneous relaxation, on the other hand, shows the fastest decline.
4 Conclusion
We have investigated proton dynamics in liquid water on extended time scales using a multiscale scheme which combines ab initio and classical molecular dynamics with kinetic Monte-Carlo. By virtue of deriving all relevant energetic/kinetic parameters needed for the KMC part from ab initio calculations, we are able to reach an accuracy comparable to quantum chemical methods on mesoscopic time scales.The diffusion constants and the excess state lifetimes obtained from our multiscale Ansatz agree quantitatively with reference AIMD simulations. Our studies show that the dielectrical relaxation of the immediate surroundings of the hydronium ion needs to be explicitly incorporated into the scheme for a realistic description of the excess proton diffusion process. The typical relaxation time in our scheme agrees well with hydrogen bond lifetimes, which we see as a confirmation of the importance of hydrogen bond cleavage as the rate determining step for excess proton transfer.
Our approach is easily applicable to more complex multi-component systems such as Nafion, water channels in proteins, and other nano structured molecular systems.
Conflicts of interest
There are no conflicts to declare.References
- M. Rini, B.-Z. Magnes, E. Pines and E. T. J. Nibbering, Science, 2003, 301, 349–352 CrossRef CAS PubMed.
- O. F. Mohammed, D. Pines, J. Dreyer, E. Pines and E. T. J. Nibbering, Science, 2005, 310, 83–86 CrossRef CAS PubMed.
- S. Meiboom, J. Chem. Phys., 1961, 34, 375–388 CrossRef CAS.
- S. Dokmaisrijan and E. Spohr, J. Mol. Liq., 2006, 129, 92 CrossRef CAS.
- M. K. Petersen and G. A. Voth, J. Phys. Chem. B, 2006, 110, 18594–18600 CrossRef CAS PubMed.
- D. Seeliger, C. Hartnig and E. Spohr, Electrochim. Acta, 2005, 50, 4234–4240 CrossRef CAS.
- S. Feng and G. A. Voth, J. Phys. Chem. B, 2011, 115, 5903–5912 CrossRef CAS PubMed.
- M. Cappadonia, Solid State Ionics, 1995, 77, 65–69 CrossRef CAS.
- C. J. T. De Grotthuss, Mémoire sur la décomposition de l'eau et des corps qu'elle tient en dissolution à l'aide de l'électricité galvanique, 1805 Search PubMed.
- G. Bekçioğlu, C. Allolio and D. Sebastiani, J. Phys. Chem. B, 2015, 119, 4053–4060 CrossRef PubMed.
- G. Bekçioğlu, C. Allolio, M. Ekimova, E. T. J. Nibbering and D. Sebastiani, Phys. Chem. Chem. Phys., 2014, 16, 13047–13051 RSC.
- N. Agmon, Chem. Phys. Lett., 1995, 244, 456–462 CrossRef CAS.
- D. Marx, ChemPhysChem, 2006, 7, 1848–1870 CrossRef CAS PubMed.
- L. Vilčiauskas, M. E. Tuckerman, J. P. Melchior, G. Bester and K.-D. Kreuer, Solid State Ionics, 2013, 252, 34–39 CrossRef.
- M. Tuckerman, K. Laasonen, M. Sprik and M. Parrinello, J. Chem. Phys., 1995, 103, 150–161 CrossRef CAS.
- M. Tuckerman, K. Laasonen, M. Sprik and M. Parrinello, J. Phys. Chem., 1995, 99, 5749–5752 CrossRef CAS.
- M. E. Tuckerman, D. Marx and M. Parrinello, Nature, 2002, 417, 925–929 CrossRef CAS PubMed.
- D. Marx, M. E. Tuckerman, J. Hutter and M. Parrinello, Nature, 1999, 397, 601–604 CrossRef CAS.
- P. Intharathep, A. Tongraar and K. Sagarik, J. Comput. Chem., 2006, 27, 1723–1732 CrossRef CAS PubMed.
- G. Kabbe, C. Wehmeyer and D. Sebastiani, J. Chem. Theory Comput., 2014, 10, 4221–4228 CrossRef CAS PubMed.
- G. Kabbe, C. Dreßler and D. Sebastiani, J. Phys. Chem. C, 2016, 120, 19905–19912 CAS.
- C. Dreßler, G. Kabbe and D. Sebastiani, J. Phys. Chem. C, 2016, 120, 19913–19922 Search PubMed.
- A. Prados, J. J. Brey and B. Sánchez-Rey, J. Stat. Phys., 1997, 89, 709–734 CrossRef.
- Y. Cao, H. Li and L. Petzold, J. Chem. Phys., 2004, 121, 4059–4067 CrossRef CAS PubMed.
- D. T. Gillespie, J. Phys. Chem., 1977, 81, 2340–2361 CrossRef CAS.
- G. A. Ludueña, T. D. Kühne and D. Sebastiani, Chem. Mater., 2011, 23, 1424–1429 CrossRef.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25 CrossRef CAS.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed.
- D. van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- H. J. C. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- D. J. Evans and B. L. Holian, J. Chem. Phys., 1985, 83, 4069–4074 CrossRef CAS.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- C. Allolio and D. Sebastiani, Phys. Chem. Chem. Phys., 2011, 13, 16395–16403 RSC.
- J. H. Simpson and H. Y. Carr, Phys. Rev., 1958, 111, 1201–1202 CrossRef CAS.
- J. C. Grossman, E. Schwegler, E. W. Draeger, F. Gygi and G. Galli, J. Chem. Phys., 2004, 120, 300–311 CrossRef CAS PubMed.
- E. Schwegler, J. C. Grossman, F. Gygi and G. Galli, J. Chem. Phys., 2004, 121, 5400–5409 CrossRef CAS PubMed.
- S. Cukierman, Biophys. J., 2000, 78, 1825–1834 CrossRef CAS PubMed.
- W. B. Bosma, L. E. Fried and S. Mukamel, J. Chem. Phys., 1993, 98, 4413–4421 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Proton jump rate functions determined from AIMD, illustration of the linear distance rescaling. See DOI: 10.1039/c7cp05632j |
| This journal is © the Owner Societies 2017 |





