Explicit description of complexation between oppositely charged polyelectrolytes as an advantage of the random phase approximation over the scaling approach
Received
4th August 2017
, Accepted 15th September 2017
First published on 15th September 2017
Abstract
A polyelectrolyte complex (PEC) of oppositely charged linear chains is considered within the Random Phase Approximation (RPA). We study the salt-free case and use the continuous model assuming a homogeneous distribution of the charges throughout the polyions. The RPA correction to the PEC free energy is renormalized via subtraction of polyion self-energy in order to find the correlation free energy of the complex. An analogous procedure is usually carried out in the case of the Debye–Hückel (DH) plasma (a gas of point-like ions), where the infinite self-energy of point-like charges is subtracted from the diverging RPA correction. The only distinction is that in the PEC both the RPA correction and chain self-energy of connected like charges are convergent. This renormalization allows us to demonstrate that the correlation free energy of the PEC is negative, as could be expected, while the scaling approach postulates rather than proving the negative sign of the energy of interactions between the blobs. We also demonstrate that the increasing concentration of oppositely charged polyions in the solution first results in the formation of neutral globules of the PEC consisting of two polyions as soon as the concentration reaches a certain threshold value, cgl, whereas solution macroscopic phase separation (precipitation of globules) occurs at a much higher concentration, ccoac, ccoac ≫ cgl. Partitioning of polyions between different states is calculated and analytical dependencies of cgl and ccoac on the polyion length, degree of ionization and solvent polarity are found.
1 Introduction
Correlation effects are of major importance in many charged systems, especially if they comprise macro- and/or multivalent co- and counterions,1 which control the strength and character of electrostatic interactions. In addition to the valency of the ions, phase behavior of charged liquids (solutions of colloidal particles, polyelectrolytes (PEs), etc.) depends on relative “asymmetry” of co- and counterions. For example, bulky macroions (like charged colloidal particles, microgels2,3 or linear PEs4) with small (point-like) monovalent counterions can be attributed to strongly “asymmetric” charged solutions where high entropic mobility of the counterions protects complete local neutralization of the system and formation of a condensed phase. Therefore, the presence of charged groups in such asymmetric systems can promote solubility of the macroions. In contrast, in charge “symmetric” systems, like solutions of oppositely charged PEs,5–9 condensation of the macroions occurs in the isoelectric point (total charge of the macrions is equal to zero). Therefore, the electrostatic attraction decreases the solubility of the macroions in the “symmetric” system.10–12 In the intermediate cases of the asymmetry or beyond the isoelectric point, the interplay between attractive and repulsive electrostatic interactions is responsible for the clustering of the macroions in soluble aggregates. In many cases, solubility of the aggregates is provided by the effect of overcharging (charge inversion):13–16 the total charge of the complex becomes opposite to the bare charge of the macroions.
The spatial charge distribution in the “asymmetric” systems is essentially inhomogeneous. It allows developing mean-field theories (Poison–Boltzmann or multi-zone approximation) like for dilute solutions of PE micelles17–20 or microgels.21 On the other hand, the inhomogeneous charge distribution means strong spatial charge fluctuations which are equivalent to the strong charge fluctuations at a certain spatial coordinate evolving over time as long as the ergodic hypothesis is valid. Therefore, calculations of the fluctuation contribution to the free energy in such systems are sophisticated. In contrast, charge fluctuations are much smaller in the “symmetric” solutions and the mean-field treatment is not able to describe the Coulomb interactions properly (they are equal to zero at this level). The electrostatics due to the small charge fluctuations can be taken into account within the framework of the Random Phase Approximation (RPA), which is a linear response approximation analogous to the one-loop approximation used in quantum field theory.
Over 90 years ago, Debye and Hückel (DH) have considered the problem of electrolyte solutions (the simplest “symmetric” system) demonstrating deviations from the ideal gas behaviour.22 Using the Poison–Boltzmann equation linearization, they have calculated corrections to the osmotic pressure and to the free energy of the ideal gas, both are negative. However, independently of the valency of the ions, their condensation or ion pair formation cannot be described within such an approach. The condition for linearization is that the energy of the electrostatic interactions between the ions is much smaller than the energy of their thermal motion. Three decades later, the first theoretical attempt to describe saline solutions of oppositely charged PEs was undertaken by Overbeek and Voorn.23 They have treated non-electrostatic interactions within the Flory–Huggins lattice theory, while Coulomb interactions between all charges of the system (mobile low-molecular-weight ions and charged groups of the chains) have been described using the DH expression. Thus, connectivity of the charged groups into the chains was neglected.
In the late 1980s in pioneer works of Borue and Erukhimovich, the RPA was applied to semidilute PE solutions and complexes, where the charge connectivity into the chain was taken into consideration by the addition of the polyion conformational entropy term to the free energy functional.24,25 The beauty of the RPA for the oppositely charged PEs is that the condensation of the chains (complex formation) can properly be described at this level because polymer chains are known to be “poor in entropy”: even small attraction between charged groups is able to overcome the entropic penalty due to the complex formation. Possibility of microphase separation in semidilute PE solutions and mixtures of oppositely charged polyions was predicted within the framework of this approach.24,26–28 Later on, similar theory was applied for the description of PE multilayers,29 polyampholytes30 and overcharged interpolyelectrolyte complexes.31,32 Further development of the RPA included consideration of ion pairing,28,33,34 short wavelength integration cutoff,33,35 hard-core and finite-size ion effects.33,34,36,37 In our group, fluctuations of polymer and charge densities were examined independently (discrete charge distribution), which allowed getting a general expression for the free energy unifying different limiting cases.38 The RPA theory for rod-like polymer chains capable of liquid-crystalline ordering was developed in ref. 39–42. Treatment of single PE chain trapping own counterions as one-component plasma (i.e. point-like charges immersed into homogeneously and oppositely charged background) is also based on the RPA.35,43–46 Castelnovo and Joanny,47 and then Fredrickson and co-workers48 extended the fluctuation theory of complexation beyond the RPA.
Recently account for fluctuations by means of liquid state theory approaches allowed describing solutions49 and complexes50 of highly charged PEs. In the framework of this method it was theoretically shown that low-molecular-weight salt ions prefer a supernatant rather than a coacervate,50 in contrast to predictions of Vroon–Overbeek theory that neglects both connectivity of PE charges and excluded volume interactions.37,51,52 This finding on salt ion partitioning being in principal agreement with experiment was later confirmed using computer simulations.53,54
In the present paper, we propose a procedure of physically motivated renormalization of the RPA results for the symmetric PEC allowing us to distinguish the correlation (free) energy of the PEC and self-energy of polyions in the salt-free case. Proper renormalization makes possible to find partitioning of polyions between different states (non-aggregated chains, neutral PEC globules and coacervates) in a stoichiometric mixture of polyanions and polycations. Threshold concentrations of globule formation and macroscopic phase separation are found analytically.
The model with a charge continuously smeared throughout the flexible chain is used for the theoretical treatment of the PEC.24,55 The RPA correction to the free energy is known to be convergent within the framework of this model.29–32 However, the knowledge of this positive expression, which allows us to find the electrostatic contribution to the osmotic pressure and the polymer volume fraction in the complex properly, is not enough for calculation of the correlation (free) energy. Nonzero self-energy of the chains caused by connectivity of the charged groups has to be calculated and subtracted from the RPA results. The self-energy takes into account repulsive interactions of the charges in each individual chain. Due to the subtraction procedure, the correlation energy, which corresponds to the attraction between oppositely charged chains, occurs to be negative as one would expect. In contrast to the scaling approach, where the interaction energy between the blobs was postulated to be negative,56 the RPA proposes a straightforward way for calculation of the correlation free energy defining the numerical factor as soon as one deals with the polymers in a Θ-solvent. In particular, the knowledge of the self-energy allows quantifying the association of single chains into a complex (calculation of the critical concentration of association).
Here it is necessary to mention that initially a renormalization procedure of the RPA results for PE solutions based on the subtraction of chains self-energy was proposed by Mahdi and Olvera de la Cruz who motivated it primarily by mathematical convenience.36 Lately Shen and Wang have explicitly distinguished self-energy of polyions in PE solution and found solution correlation energy via subtraction of the chain self-energy from the formal field-theoretic result.57 In the present paper, we apply the same renormalization procedure to the case of the PEC. It makes possible to argue for the first time the negative sign of the complex correlation energy within the RPA.
In order to make the calculation of the correlation free energy in the case of PECs more lucid and clear, we use analogy with well-known DH plasma wherein subtraction of infinite self-energy of point-like ions from the diverging RPA result is necessary to get a finite negative expression for the correlation free energy. An analogy between correlation functions in the case of the PE complex and the DH plasma also occurs to be very useful.
The paper is organized as follows. In the next section the DH plasma is discussed in detail, first without and then with volume interactions, and well-known results for ion–ion correlation functions and correlation free energy of plasma are reproduced. In Section 3, we move on to the case of the PEC and propose a renormalization procedure of the RPA free energy correction. It allows us to obtain the correlation free energy of the complex. Section 4 deals with the calculation of the critical concentrations of PEC formation and coacervation. Closed-form expressions for these concentrations are found.
2 Debye–Hückel plasma
We consider a neutral plasma consisting of oppositely charged ions, each of the size a and volume a3. Let the average volume fractions of positively and negatively charged ions are equal: 〈n+〉 = 〈n−〉 = n0. Here n0 is dimensionless, so that the concentration of each type of the ions equals n0/a3. Neglecting short-range interactions between the ions under the condition of a small concentration, n0 ≪ 1, one gets the classical case of the DH plasma of point-like charges. The total free energy is a sum of two terms:| | | Ftot{n+(r), n−(r)} = Ftr + Fel-st | (1) |
the ideal gas entropy| | 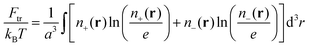 | (2) |
and the energy of long-range Coulomb interactions between the ions| | 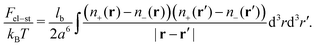 | (3) |
Here, lb = e2/(εkBT) is the Bjerrum length.
Correlated electrostatic attraction makes the osmotic pressure of the DH plasma lower than that of the ideal gas. The RPA can be used in order to find the free energy correction to the ideal gas term and to calculate the density–density correlation functions of the DH plasma. The concentration fluctuations are defined as δnk(r) = nk(r) − n0, and Fourier transforms are given by
| | 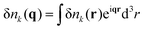 | (4) |
| | 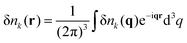 | (5) |
where
k = +, −. Deviation of the free energy functional from the mean-field value,
FMF/
kBT = 2
Vn0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
ln(
n0/
e)/
a3, in the Gaussian (square) approximation reads:
| | 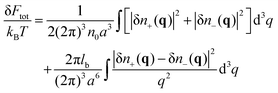 | (6) |
where
V is the total system volume. Owing to the following representation of the free energy fluctuations
| | 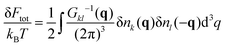 | (7) |
and introducing the Debye radius
rD2 =
a3/(8π
lbn0), one can obtain the direct matrix of the plasma correlation functions in the Fourier space:
| | 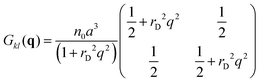 | (8) |
The spherically symmetric density–density correlation functions
Gkl(
r) = 〈δ
nk(0)·δ
nl(
r)〉 are calculated using the inverse Fourier transforms and take the form
| | 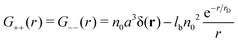 | (9) |
| | 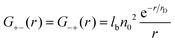 | (10) |
The second set of the correlation functions,
G+− =
G−+, is caused only by the electrostatic attraction between the oppositely charged ions: it is equal to zero at
lb = 0. For this reason it can be designated as
G+− =
Gcorr. The first set of correlation functions,
G++ =
G−−, should be divided into two parts:
G++ =
Gself −
Gcorr. The first nonvanishing at the
lb = 0 part,
Gself =
n0a3δ(
r) is known as a correlation function of the neutral ideal gas while the second part, −
Gcorr, should be ascribed to the repulsion of like charges. Note that both
Gcorr and
Gself are positive at any values of
r.
The correction to the electrostatic energy caused by ion–ion correlations (density fluctuations) can be calculated as follows:
| | 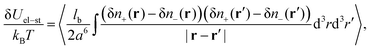 | (11) |
where the angle brackets denote the thermodynamic averaging. Owing to the expression 〈δ
nk(
r)δ
nl(
r′)〉 =
Gkl(|
r −
r′|) and denoting
R = |
R| = |
r −
r′|, one can calculate
| | 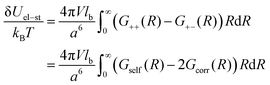 | (12) |
Thus, the self-energy of point-like ions and the energy of interaction between the ions are given by
| | 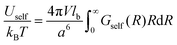 | (13) |
| | 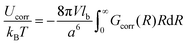 | (14) |
It is well-known that the self-energy of point-like charge diverges:
| | 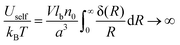 | (15) |
where the delta function in the spherical coordinates was substituted, δ(
R) = δ(
R)/(4π
R2). On the other hand, the correlation internal energy is finite:
| | 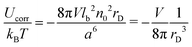 | (16) |
The energy is negative and decreases with the increase of the concentration
n0. It means that the electrostatic interactions are attractive. To pass to the Helmholtz free energy correction, one can apply the relation between thermodynamic potentials
| | 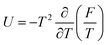 | (17) |
As a result, the free energy density correction reads
| | 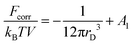 | (18) |
and constant
A1 = 0 because the condition
Fcorr = (
Ftot −
Fid) → 0 at
T → ∞ should be satisfied,
Fid being the free energy of neutral ideal gas equal to
FMF.
58
Another way to get the correlation free energy correction is based on the calculation of Gaussian functional integrals
| | 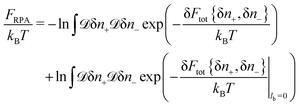 | (19) |
In order to calculate the integrals, quadratic form
| | 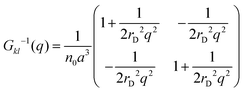 | (20) |
should be diagonalized. After transformations, one gets the following expression
| | 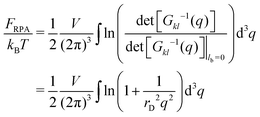 | (21) |
diverging at
q → ∞,
i.e. at
r → 0. This divergence is a consequence of infinite self-energy of point-like charges.
FRPA includes both the self- and the interaction energies,
FRPA =
Fself +
Fcorr. The self-energy is given by
eqn (15) and can be rewritten using Fourier transform:
| | 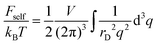 | (22) |
Finally, the converging result for the correlation free energy
| | 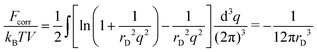 | (23) |
coincides with one deduced above. It is also worth noting that considering ions of non-zero radius and finite charge density function instead of point-like ions with
δ-function type charge distribution, one can avoid all energy divergences.
59
As we mentioned in Introduction, the above calculations of the correlation (free) energy are valid when this correction is small as compared to the energy of thermal motion, |Fcorr| ≪ |Ftr|. This condition is fulfilled at a low concentration of the ions, n0 ≪ (a/lb)3.
2.1 Debye–Hückel plasma with volume interactions
In order to take into account volume interactions of the plasma ions, we can use the virial expansion and the following term should be added to the total free energy| | 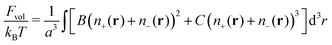 | (24) |
Here B and C are the second and the third dimensionless virial coefficients. After expansion of the total free energy functional into the series in powers of the density fluctuations, the Fourier transforms of the correlation functions take the form:| | 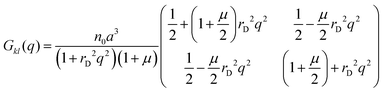 | (25) |
were μ = 4n0(B + 6Cn0). The value μ = 0 corresponds to the case without volume interactions, and the matrix coincides with the matrix 8. The correlation functions read| | 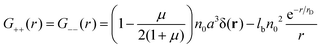 | (26) |
| | 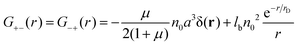 | (27) |
Due to the RPA linearity, the correlation functions can be represented as a sum of (i) the ideal gas self-correlation function, Gself = n0a3δ(r), (ii) the term caused by the volume interactions, Gvol = −μn0a3δ(r)/(2 + 2μ), and (iii) the term Gcorr = lbn02e−r/rD/r induced by the electrostatic interactions:| | | G++ = Gself + Gvol − Gcorr | (28) |
The terms Gself and Gcorr coincide with those defined above for the DH plasma without volume interactions. Gvol term vanishes when the triple repulsion compensates pairwise attraction, B = −6Cn0. Following eqn (19), one can calculate the RPA correction to the free energy caused by the Coulomb interaction. Despite the presence of the volume interactions, the result for FRPA coincides with eqn (21). Thus, the self-energy given by eqn (13) should be subtracted from FRPA to find the correlation energy, and the latter coincides with correlation energy for the DH plasma without volume interactions, Fcorr/kBTV = −1/(12πrD3). Independence of FRPA and Fcorr of the volume interactions should be attributed to the linearity of the RPA.
Note that eqn (11)–(14) remain valid in the case of non-zero volume interactions as well, so that definitions of the self-energy and the correlation energy are the same. Indeed, relationship G++ − G+− = Gself − 2Gcorr is satisfied despite Gvol ≠ 0. In the general case, the term caused purely by the electrostatic interactions should be defined as
In the next section we apply the proposed approach to describe complex formation between oppositely charged PE chains.
3 Interpolyelectrolyte complex
Let us consider a complex of two oppositely charged linear PEs in a salt-free, Θ-solvent. For the sake of simplicity, we study the case of a symmetric complex, i.e. f+ = f− = f are the fractions of charged groups in these polyions, and Φ+ and Φ− are their average polymer volume fractions in complex, respectively. The complex electric neutrality is provided by condition Φ+ = Φ− = Φtot/2, where Φtot is the total polymer volume fraction within the complex. The lengths of polycations and polyanions are also assumed to be equal, N+ = N− = N (see ref. 60 for the asymmetric case). We study the classical model proposed by Borue and Erukhimovich which assumes that electric charge is continuously smeared throughout the chains.24,25
The total free energy in kBT units takes the form:
| | | Ftot{Φ+(r), Φ−(r)} = Ftr + Fconf + Fel-st + Fvol | (31) |
The first term is responsible for the translational entropy of polymer chains:
| | 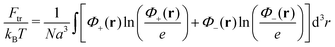 | (32) |
The second term is the conformational entropy of polyions
61,62| | 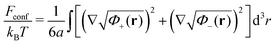 | (33) |
with
a being the length of the statistical segment. Deduced independently by Edwards and later by Lifshitz, it takes into account the entropy cost of the polymer non-uniform distribution. The case of flexible polymer chains is under consideration, so that
a3 is of the order of the segment volume. The Coulomb energy is given by
| | 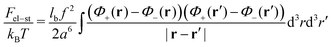 | (34) |
We restrict our consideration to the case of weakly charged PEs,
f ≪ 1, and a rather polar solvent,
u ∼ 1, so that effects of cross-chain ion pairing
63–65 and attraction of resultant dipoles
66–68 can be neglected. Finally, the volume interactions, namely triple repulsive interactions between the segments in the Θ-solvent, are taken into account within the last term of the total free energy
| | 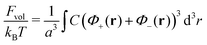 | (35) |
with
C being the dimensionless third virial coefficient. The mean-field value of the total free energy of the neutral complex takes the form:
| | 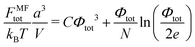 | (36) |
where the second term is negligible at high
N,
i.e. the volume interactions dominate over the chain translational entropy. Thus, the repulsive interactions make the complex unstable. The complex formation cannot be described at the mean-field level because the latter neglects the electrostatic attractions between charged chains. At the same time, the complex formed by oppositely charged PEs is globular, and weak fluctuation within the globule provides applicability of the RPA (see
ref. 25 for detailed discussion).
Expansion of the free energy functional into the series in powers of the polymer density fluctuations allows calculating the inverse matrix of correlation functions
| | 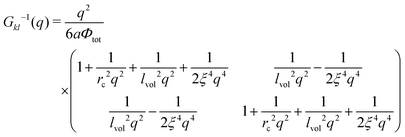 | (37) |
with
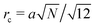
being the correlation radius of the ideal polymer chain (
i.e. the Gaussian chain size),
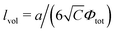
being the correlation radius of infinite neutral chain caused solely by the volume interactions and
ξ =
a/(48π
uf2Φtot)
1/4 being the screening radius of the electrostatic interactions in PE complex;
u =
lb/
a is the dimensionless Bjerrum length. The RPA correction to the free energy of the PEC can be found in a similar way to that for the DH plasma (see
eqn (19) and (21)):
| | 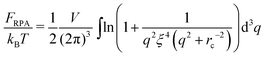 | (38) |
and this integral converges at any
rc and any finite
ξ (infinite
ξ corresponds to the case of neutral polymers,
f = 0). Thus, one gets
| | 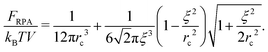 | (39) |
FRPA is always positive as soon as the complex is formed (
ξ <
rc). In order to get the correlation free energy of the PEC, the self-energy of polyions should be subtracted from the RPA results. Following an analogy between the PEC and the DH plasma, the correlation functions should be divided into the parts related to connectivity of monomer units into the chain,
Gself, electrostatic,
Gcorr, and volume,
Gvol, interactions:
| | | G++ = Gself + Gvol − Gcorr | (40) |
The term
Gself appears only in the correlation functions of like charges as a consequence of their connectivity into a chain. Indeed, the charges of opposite signs belong to different chains and are not linked with each other by the covalent bonds.
In order to find the correlation free energy and the self-energy, one should explicitly calculate these components of the correlation functions:
| | 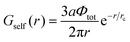 | (42) |
| | 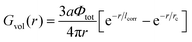 | (43) |
| | 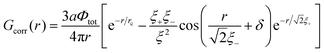 | (44) |
Here
lcorr is known to be the correlation radius of neutral polymer solution
| | 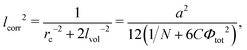 | (45) |
with the radii
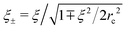
and dimensionless
δ = arctan(
ξ+ξ−/2
rc2). Note that the electrostatic interactions vanish at
lb = 0, and
Gcorr = 0. Similarly,
Gvol = 0 in the absence of volume interactions,
i.e. at
C = 0.
Gself is known to be the Ornstein–Zernike type correlation function of a single Gaussian chain and is equal to the correlation function in the solution of the ideal chains.
69
Using relationship similar to eqn (13) and introducing additional multiplier f2 for the transition from the polymer–polymer to charge–charge correlation function, one obtains
| |  | (46) |
where
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) chains
chains =
VΦtot/(
a3N) is the total number of polymer chains (both polycations and polyanions) in the system.
Since u ∼ 1/T, the free and the internal electrostatic energies coincide, Fself = Uself, and the density of the self-energy can be represented as follows:
| | 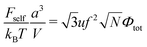 | (47) |
It is necessary to emphasize that the self-energy term is not a mean-field energy of the charged chains with Gaussian statistics but the correction term caused by Gaussian correlations in the location of charges (see Appendix A for a detailed discussion). The value of the self-energy term is defined by the choice of the reference polymer system: it is the system without volume and electrostatic interactions, C = 0 and lb = 0. Therefore, the chains in the reference system possess Gaussian statistics at any length scales owing to the conformational entropy term Fconf in the total free energy.
Thus, similar to the case of the DH plasma (eqn (23)), the correlation energy can be written as follows:
| | 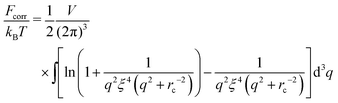 | (48) |
The correlation energy
(48) is always negative owing to the negative integrand, and this result fully coincides with common comprehension of correlation energy as negative energy taking into account the correlation attraction of opposite charges. In the case of an infinitely long chain,
N → ∞, the second term in square brackets diverges at
q → 0,
i.e. at large distances. Indeed, the Coulomb correlation energy of an infinitely long PE chain with the Gaussian statistics at any length scales is infinite and grows with increasing chain length proportional to
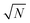
, see
eqn (47). For this reason the term accounting for the chain translational entropy cannot be neglected in the total free energy.
Result similar to eqn (48) has been used earlier by Mahdi and Olvera de la Cruz who calculated the phase diagram of semidilute PE solution in the presence of salt.36 The authors justified subtraction of the second term in square brackets by mathematical convenience: this “… irrelevant subtracted term only facilitates the algebra and gives an electrostatic contribution that reduces to the simple Debye–Hückel electrostatic free energy in the correct limit.”36 In fact, subtraction of the self-energy does not influence results for PE solution since it is a constant term and can be omitted: the self free energy density is proportional to the polymer volume fraction Φ and does not contribute to the osmotic pressure.70 However, if we would like to calculate the correlation energy of the PEC or to compare two states of the PE chains – aggregated into PEC and free – it is necessary to properly calculate and comprehend calculation of the free energy of the system. Subtraction of the self-energy of the chains is very important for distinguishing the reference state of the system and, hence, proper calculation of energy of Coulomb interactions. Application of the renormalization procedure to the case of the PEC and the proof of the negative sign of the correlation free energy are the novelties of the above part of the present work.
The self-energy is proportional to the number of PE subchains in the system ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) chains, like the self-energy is proportional to the number of charges in the DH plasma. The difference between these two systems is the following: point-like charges are structureless and their self-energy is unchanged under any conditions, while the PE chain can adopt different conformations resulting in different mutual spatial locations of charges and different self-energy.
chains, like the self-energy is proportional to the number of charges in the DH plasma. The difference between these two systems is the following: point-like charges are structureless and their self-energy is unchanged under any conditions, while the PE chain can adopt different conformations resulting in different mutual spatial locations of charges and different self-energy.
The same identification of the PE chain self-energy as the energy necessary to connect charges onto a single chain has been recently used by Shen and Wang, and our choice of the reference state coincides with theirs: “the zero energy of the electrostatics is taken to be the state where charges are dispersed into infinitesimal bits at infinity.”57 The dependence of the chain self-energy on its conformation was discussed in ref. 57 as well. The authors introduced chain self-energy in order to find correlation free energy of PE solution, and we use very similar renormalization with the same chain self-energy definition. The only difference is that we apply it to the case of the interpolyelectrolyte complexes rather than solution of similarly charged chains.
The positive value of the PRA correction (39) means that the number of like charges surrounding any selected charge on the chain in the PEC is more than the number of opposite charges, despite repulsion of like charges and attraction of opposite charges. This fact is caused by the binding of like charges into the chain. Since these bonds exist before complex formation, their impact on the charge–charge correlations was separated from the correlations induced by purely Coulomb attraction. The Coulomb energies caused by these correlations were treated as the self-energy and the correlation energy, respectively.
3.1 Equilibrium density of the PEC
In order to find the equilibrium polymer volume fraction within the complex, the sum of the mean-field and the correlation free energies should be minimized. The minimization is equivalent to the equating of the osmotic pressure of the complex to zero:| | 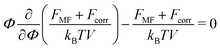 | (49) |
Here we neglect the translational entropy of polyions within the complex and the nonzero concentration of free polyions in the outer solution since their concentration is exponentially small (see Section 4). The RPA correction FRPA can be used instead of Fcorr in order to find the PEC density because the self-energy does not contribute to the osmotic pressure. At that, FRPA represents the total electrostatic energy of the system, i.e. the energy with respect to the state when all infinitesimal (not elementary) charges are moved away from each other at infinite distances. This choice of the reference state assumes that polymer chains are broken, and the energy required to gather them back into a single chain and provide the chain with the Gaussian conformation ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) G,chel-st equals mean-field electrostatic chain energy
G,chel-st equals mean-field electrostatic chain energy ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) G,chMF plus the self-energy of a chain
G,chMF plus the self-energy of a chain ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) G,chcorr, see Appendix A.
G,chcorr, see Appendix A.
In the case of infinitely long chains (N → ∞), we get 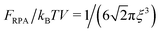 , so that the polymer volume fraction within the complex reads
, so that the polymer volume fraction within the complex reads
| | 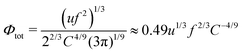 | (50) |
and the free energy of the PEC per unit volume equals
| | 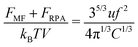 | (51) |
Thus, the free energy per chain within the macroscopic PEC phase takes the form:
| | 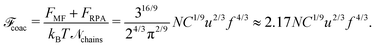 | (52) |
Scaling analysis of the chain free energy within the PEC performed in
ref. 56 predicts
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) coac
coac ≈ −
Nu2/3f4/3. The sign minus in the scaling result was justified by attraction of oppositely charged blobs within the complex.
56 However, the negative energy of correlation attraction between oppositely charged blobs is of the order of the blob self-energy. So the scaling consideration does not allow us to define the sign (plus or minus) of the free energy within the complex,
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) coac
coac. It is necessary to mention here that properly defined correlation energy of the PEC given by
eqn (48) is indeed negative, but the free energy of the complex being the sum of the correlation free energy and the self-energy of the chains is positive. Moreover, scaling treats polyions as a set of disrupted blobs resulting in a linear dependence of the chain correlation energy on its length
N, while RPA accounts for correlations within the chain on all length scales and yields asymptotically
N3/2.
4 Equilibrium between non-aggregated charged chains and their complex
In order to calculate the critical concentration of PEC formation properly, one should take into account correlation corrections to the mean-field energy of both neutral stoichiometric complex and single charged chains. Below we propose a way of calculation of the self-energy of free PE chains in the solution.
4.1 Self-energy of a single polyelectrolyte chain
It is well-known that the PE chain in dilute solution adopts elongated (swollen) rather than Gaussian coil conformation, Fig. 1. Owing to the small concentration of PE, all counterions are assumed to abandon the chain and distribute homogeneously throughout the solution. On the length scales r < ξel-st ∼ au−1/3f−2/3, where the electrostatic interactions do not play a role, the chain is an unperturbed Gaussian coil, while on larger scales, r > ξel-st, it resembles a string of the characteristic length L ∼ Na2/ξel-st ∼ aNu1/3f2/3, Fig. 1. Thus, the intra-chain correlations are different on different length scales. Calculations of the Coulomb energy of the swollen PE chain based on the correlations predicted by scaling are performed in Appendix B.
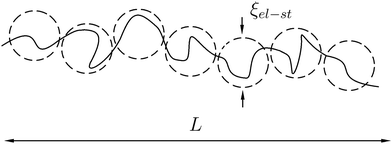 |
| | Fig. 1 Schematic representation of polyelectrolyte chain as a sequence of electrostatic blobs. | |
A more rigorous method to derive the similar result for chain electrostatic energy is not to adopt a priori assumption on the blob size, ξblob = ξel-st. Indeed, let ξblob be the size of the blob, and correlations inside it are Gaussian. The number of monomer units in the blob g ∼ (ξblob/a)2 and the average distance between i-th and j-th units 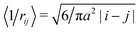 . The electrostatic energy of a single blob is given by
. The electrostatic energy of a single blob is given by
| | 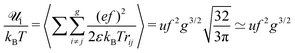 | (53) |
The number of the blobs in the chain
Nblob =
N/
g =
Na2/
ξblob2. Since the PE chain is stretched, the average distance between two blobs,
k-th and
l-th, is given by 〈
rkl〉 =
ξblob|
k −
l|, 1 ≤
k,
l ≤
Nblob. The charge of each blob equals
q =
efg and the total electrostatic energy of interactions between all blobs reads
| | 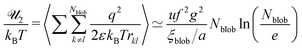 | (54) |
Thus, the total electrostatic energy is given by
| | 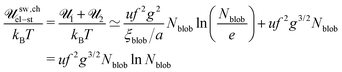 | (55) |
while the elastic energy of deformation reads
| | 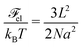 | (56) |
and
L =
ξblobNblob =
Na2/
ξblob. The total free energy of the chain can be expressed as a function of
ξblob which has to be minimized with respect to
ξblob:
| | 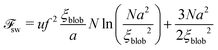 | (57) |
The exact value of
ξblob is determined by the equation:
| | 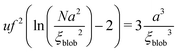 | (58) |
Taking into account
Na2 ≫
ξblob2 and
N ≫ 1, one gets
71| | 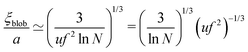 | (59) |
and the total free energy can be estimated as
| | 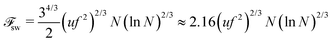 | (60) |
This final result, which takes into account not only the mean-field free energy of a chain
31,32 but also contribution due to the correlation of charges (see Appendix B), should be used in calculations of the critical concentration of PEC formation. The scaling estimations for the single PE chain free energy coincide with the above results up to the logarithmic and numerical factors, which are usually omitted in scaling estimations.
56 However, it will be shown below that account for these corrections, 2.16(ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N
N)
2/3, is crucial for equilibrium between the free chains and the PEC.
A more common procedure for the self-energy calculation of a swollen PE chain in both dilute and semidilute salt solutions can be found in the recent work of Shen and Wang, where the authors took into account coupling between the chain conformation and the screening of Coulomb interactions in the solution.57 Owing to the low polyion ionization degree, f ≪ 1, we have also neglected chain entanglements (knots), which are known to be localized, adopt a tight configuration and relax very slowly (or even remain frozen) in the case of highly charged polyelectrolytes.72
4.2 Critical concentration of PEC formation
In this section, we discuss the state of oppositely charged polyions in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solution. One can expect that in extremely dilute solutions polyions exist as single chains, while their increasing concentration should result in complexation and formation of either single globules on the basis of one polycation and one polyanion or a macroscopic condensed phase (coacervate). For the sake of simplicity, the equilibrium between the three states of the polyions, namely (i) single chains, (ii) neutral globules and (iii) macroscopic liquid coacervates will be considered, though formation of a solid precipitate is also possible in some cases,73e.g. for oppositely charged chiral polypeptides extra capable of hydrogen bonding.73,74 Here we neglect formation of globules consisting of several couples of oppositely charged polyions assuming that their fraction will be smaller in comparison with the globules on the basis of one couple. In other words, we assume that the size distribution function of the globules has a narrow maximum for the one couple.
1 solution. One can expect that in extremely dilute solutions polyions exist as single chains, while their increasing concentration should result in complexation and formation of either single globules on the basis of one polycation and one polyanion or a macroscopic condensed phase (coacervate). For the sake of simplicity, the equilibrium between the three states of the polyions, namely (i) single chains, (ii) neutral globules and (iii) macroscopic liquid coacervates will be considered, though formation of a solid precipitate is also possible in some cases,73e.g. for oppositely charged chiral polypeptides extra capable of hydrogen bonding.73,74 Here we neglect formation of globules consisting of several couples of oppositely charged polyions assuming that their fraction will be smaller in comparison with the globules on the basis of one couple. In other words, we assume that the size distribution function of the globules has a narrow maximum for the one couple.
Let us assume that the chains are pretty long, N(uf2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N/3)2/3 ≫ 1, i.e. the number of the electrostatic blobs within the chain exceeds unity by far. Free energy of the chains in each state can be divided into concentration-dependent entropic and concentration-independent energy contributions. The latter has the form:
N/3)2/3 ≫ 1, i.e. the number of the electrostatic blobs within the chain exceeds unity by far. Free energy of the chains in each state can be divided into concentration-dependent entropic and concentration-independent energy contributions. The latter has the form:
| | ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) sw = 2.16(uf2)2/3N(ln sw = 2.16(uf2)2/3N(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N)2/3 N)2/3 | (61) |
| | ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) coac = 2.17(uf2)2/3NC1/9 coac = 2.17(uf2)2/3NC1/9 | (62) |
for the single swollen and complexed chains, respectively. Here we assume that the single PE chains do not retain counterions since energy gain provided by the trapping of one counterions is
N times lower than that as a consequence of PE complex formation. We also neglect the DH-type correlation attraction of these chains at an extremely small polymer concentration, which is negligible in comparison with their translational entropy,
cch ≪ (
a/
lb)
3(
fN)
−6. This estimation follows from the treatment of the solution as the DH plasma with ion charges equal to
Q =
efN. Since the critical concentration of complex formation depends on the chain length
N exponentially (see below), this condition is fulfilled for long enough chains. It is also assumed that inequality
ξ ≪
rc is fulfilled owing to the long enough PE chains.
The energy contribution for the case of the globule includes the energy per chain of the complex coacervate and the excess surface energy per chain, 2πRgl2γ. Here γa2/(kBT) = 0.11(uf2)2/3C−7/18 is the surface tension coefficient of the globule.32,75 This result takes into consideration connectivity of PE charges32 and for this reason differs from that found in ref. 76, where combination of Vroon–Overbeek and Cahn–Hilliard theories neglecting polymer specificity of the system was used. Thus, free energy per chain in globule reads
| | ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) gl = 2.17(uf2)2/3NC1/9 + 0.68(uf2)4/9N2/3C−5/54. gl = 2.17(uf2)2/3NC1/9 + 0.68(uf2)4/9N2/3C−5/54. | (63) |
Denoted by Mtot the total number of polycations (polyanions) in the solution of volume V. Let the fraction (1 − s) of polyions forms coacervate, and the total number of single polycations and polycations in the globules (i.e. in supernatant) equals M = sMtot. If all polyions in the supernatant are single chains, their free energy reads
| | 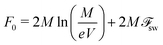 | (64) |
Formation of the globules can be treated as a reversible process of dimerization. Let us assume that fraction
p of the supernatant polyions are involved in the globules. The free energy of the supernatant can be calculated
via calculation of the partition function of the system, following the approach proposed in
ref. 77. The state when all chains in the supernatant are free is the reference state with the corresponding partition function
Z0,
F0 = −
kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z0
Z0. The partition function of the supernatant
Z with
pM globules reads
| | Zsn = Z0PcombWvole2Mp(![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) sw− sw−![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) gl). gl). | (65) |
Wvol is the probability to find
Mp polycations in the vicinity of corresponding
Mp polyanions, namely, the center of mass of polyanions and polycations located within the volume of the order of the globule volume
vgl:
| | 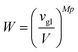 | (66) |
with
vglob = 2
Na3/
Φtot. The combinatorial factor
Pcomb is the total number of ways to select
Mp cations, and assemble
Mp globules:
| | 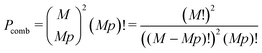 | (67) |
Thus, the free energy of the supernatant
Fsn = −
kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z
Z reads
| | 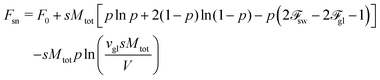 | (68) |
Finally, free energy of chains in the coacervate can be written as follows:
| | 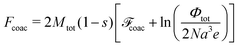 | (69) |
The equilibrium distribution of the polyions between three states can be found
via minimization of the total free energy
Ftot(
s,
p) =
Fsn +
Fcoac with respect to
p and
s. It has to be noted that minimization with respect to
p results in the law of mass action connecting concentrations of single chains and globules:
| | 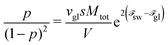 | (70) |
The fractions of polyions in the coacervate, globules and non-aggregated state are shown in Fig. 2. In Fig. 3 we plot corresponding concentrations of polyions and globules in the supernatant. It is seen that increasing the polyion concentration first results in the formation of single globules. The single chains do not aggregate only at extremely small polymer concentrations. Their coexistence with the globules is observed also at extremely small polymer concentrations. The single globules dominate in the solution in a very wide concentration range, c = 10−20–10−6, above which the macroscopic coacervate is formed. These numerical results coincide well with analytical estimations of the critical concentrations of the globules cgl and coacervate ccoac formation, which can be found from eqn (68)–(70):
| | 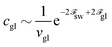 | (71) |
| | 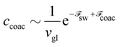 | (72) |
Indeed, for long enough chains
cgl ≪
ccoac as long as 2
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) gl
gl −
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) coac
coac −
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) sw
sw < 0, and the formation of the globules starts at much lower concentrations than their precipitation in the solution. At chosen values of the numerical parameters, all assumptions adopted above are valid. Namely, polyions are long enough to contain a large number of the electrostatic blobs and they exist in the non-aggregated state only at extremely small concentrations. In the concentration range shown in
Fig. 2 and 3, the coacervate volume is much smaller than the total volume of the system, so that disregard of the supernatant volume diminution in the course of precipitation is justified.
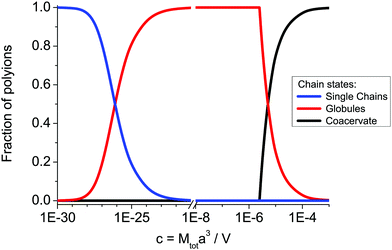 |
| | Fig. 2 Fractions of the single polyions, s(1 − p), complexed polyions in the globules, sp, and polyions in the coacervate, (1 − s), vs. total dimensionless concentration of polycations (polyanions) in the solution c = Mtota3/V at N = 150, f = 0.1, u = 1, C = 1. | |
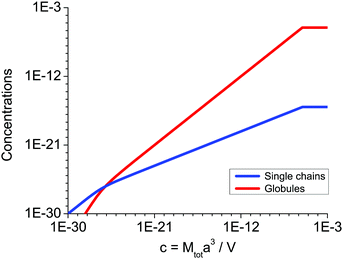 |
| | Fig. 3 Concentrations of the single polycations, s(1 − p)c, and single globules, spc, in the supernatant vs. total concentration of polycations in the solution c = Mtota3/V at N = 150, f = 0.1, u = 1, C = 1. | |
Our principal result on the formation of single neutral interpolyelectrolyte globules prior to the macroscopic phase separation at increasing concentration of polyions in solution coincides with that recently reported by Delaney and Fredrickson.78 They proved this fact by means of both scaling analysis and theoretical-field methods. At that, analytical expressions for threshold concentrations, cgl and ccoac, found in the present paper seem to be more precise as compared to scaling estimations78 where both the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N correction as well as the surface effects were neglected, while strict theoretical-field analysis performed in their work did not allow finding analytical formulas.
N correction as well as the surface effects were neglected, while strict theoretical-field analysis performed in their work did not allow finding analytical formulas.
5 Conclusion
Attraction of oppositely charged PEs within the complex is caused by fluctuation of charges and local deviation from electric neutrality. This correlation-induced attraction is opposed by repulsive volume interactions, and the equilibrium polymer volume fraction within the complex is defined from their balance. It is natural to expect that the correlation electrostatic free energy of the complex, Fcorr, should be negative, similar to the case of the DH plasma. However, direct calculations of the RPA contribution, FRPA, within the framework of a continuous model of charge distribution lead to the positive expression. This result is explained as follows. The formal calculations of the RPA Gaussian integrals take into account not only electrostatically induced correlations but also correlations caused by initial connectivity of like charges into the chain. The latter are caused by the structure of the polymer chain and should be included not into the correlation energy but into the self-energy of PE chains, Fself.
The self-energy of polyions depends on the conformation of the chain, and different chain conformations can be used as a reference state. However, in the framework of the Borue–Erukhimovich model25 which was widely used in the past few decades, the reference state is the Gaussian coil. This choice of the reference state is caused not only by mathematical (the structure of the free energy functional containing the conformational entropy term) but also by physical reasons. Indeed, a PEC in a Θ-solvent is known to be a polymer globule, so that polyions within the globular complex/in coacervate adopt the conformation of a Gaussian coil on any length scales.
The self-energy of a PE chain within the complex equal to 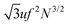 is the Coulomb energy due to the correlations of charges along the polyion in ideal coil conformation. It is important to stress that the mean-field free energy of charged polyions with Gaussian coil statistics should not be included into their self-energy because of the overall complex electric neutrality (see Appendix A). The physical meaning of the chain self-energy can be defined as follows. It is the work which is necessary to simultaneously assemble an equal number of polycations and polyanions in the same volume (volume of PEC) providing them conformations of Gaussian coil. This work is required not to get non-zero overall charge of this volume (as in the case of single polyions, eqn (60)), since the complex is electrically neutral, but to achieve connectivity of charges into Gaussian coils. In turn, energy of fluctuation-induced attraction between these already assembled polyions is the true correlation energy, Fcorr.
is the Coulomb energy due to the correlations of charges along the polyion in ideal coil conformation. It is important to stress that the mean-field free energy of charged polyions with Gaussian coil statistics should not be included into their self-energy because of the overall complex electric neutrality (see Appendix A). The physical meaning of the chain self-energy can be defined as follows. It is the work which is necessary to simultaneously assemble an equal number of polycations and polyanions in the same volume (volume of PEC) providing them conformations of Gaussian coil. This work is required not to get non-zero overall charge of this volume (as in the case of single polyions, eqn (60)), since the complex is electrically neutral, but to achieve connectivity of charges into Gaussian coils. In turn, energy of fluctuation-induced attraction between these already assembled polyions is the true correlation energy, Fcorr.
For the first time within Borue–Erukhimovich polyelectrolyte complex model we split the RPA result for the energy of Coulomb interactions within the complex, FRPA, into two parts: self-energy of the chains, Fself, and correlation energy of the complex, Fcorr. We demonstrate that the correlation free energy of the complex within the framework of this model considering continuous charge distribution, Fcorr = FRPA − Fself, is negative, in accordance with general expectations. The proposed procedure for the RPA result renormalization (subtraction of the chain self-energy) is based on physical arguments and uniquely defined. This procedure and PE chain self-energy definition are akin to those used formerly by Mahdi and Olvera de la Cruz36 and later by Shen and Wang in the case of PE solutions.57
Accounting for not only the mean-field term but also the correlation electrostatic free energy of the swollen single chain allows us to find the critical concentration cgl of the single-globule PEC formation and concentration of precipitation of these globules, ccoac. Analytical expressions for these concentrations are found for the case of pretty long chains providing a large number of electrostatic blobs. It is shown that the single globules of the PEC exist in a wide range of polyion concentrations, cgl ≪ ccoac, when complexation is already favourable owing to a high energy gain in the course of polyion neutralization, while precipitation is still unfavourable because of entropic reasons.
Appendix A. Mean-field and correlation energies of polyions with Gaussian statistics
Consider a bare charged PE chain with Gaussian statistics on any length scales assuming that all counterions leave the chain. Electrostatic energy of the chain can be calculated as follows:| | 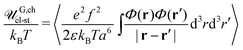 | (73) |
After substitution 〈Φ(r)Φ(r′)〉 = 〈Φ(r)〉〈Φ(r′)〉 + gchain(|r − r′|), the chain electrostatic energy can be represented as a sum of two terms:| | ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) G,chel-st = G,chel-st = ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) G,chMF + G,chMF + ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) G,chcorr G,chcorr | (74) |
Note that the correlation function of a single Gaussian chain gG,ch(|r − r′|) = gG,ch(R), R = |r − r′| coincides with Gself(R) obtained earlier in eqn (42). This fact is a consequence of identical statistics of the single Gaussian chain and the chain in the solution of ideal (i.e. non-interacting) chains. The mean-field electrostatic energy written in the conventional form reads| | 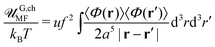 | (75) |
and omitting numerical factor one gets uQ2/rc with Q = Nf being the chain charge in the elementary charge e units and 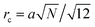 being the characteristic Gaussian size of the chain. On the other hand,
being the characteristic Gaussian size of the chain. On the other hand, ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) G,chel-st,MF = 0 within the complex since the excess charge of the PE molecule is compensated by the oppositely charged counterpart. The correlation term can be easily calculated:
G,chel-st,MF = 0 within the complex since the excess charge of the PE molecule is compensated by the oppositely charged counterpart. The correlation term can be easily calculated:| | 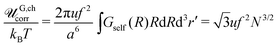 | (76) |
This result coincides with the RPA self-energy calculations, eqn (46), and supports the proposed interpretation for the self-energy being excess Coulomb energy caused by Gaussian correlations of linked chain charges. Account for the correlations is of great importance since both the mean-field self-energy of the Gaussian chain, ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) G,chMF, and the self-energy correction caused by correlations,
G,chMF, and the self-energy correction caused by correlations, ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) G,chcorr, depend on the parameters in similar ways, both ∼uf2N3/2. They differ only by numerical coefficients.
G,chcorr, depend on the parameters in similar ways, both ∼uf2N3/2. They differ only by numerical coefficients.
Appendix B. Mean-field and correlation energies of the swollen polyion
Let Φ0 be the average polymer volume fraction within the sphere of the diameter ∼L circumscribed around the swollen PE chain (see Fig. 1), Φ0 = Na3/L3 = ξel-st3/(Na3) = u−1f−2N−2 where ξel-st ∼ au−1/3f−2/3 is the electrostatic blob. To calculate the Coulomb energy of the swollen PE chain, we use the method similar to that presented in Appendix A in the case of the Gaussian charged chain. The electrostatic energy of the chain is given by| | 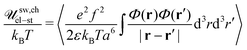 | (77) |
and Φ(r) = Φ0 + δΦ(r). Owing to 〈Φ(r)Φ(r′)〉 = 〈Φ(r)〉〈Φ(r′)〉 + 〈δΦ(r)δΦ(r′)〉 = Φ02 + Gsw,ch(r, r′), one can find| | 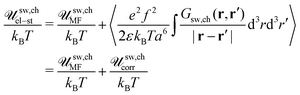 | (78) |
Here mean-field electrostatic energy of the chain ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) sw,chMF is defined as
sw,chMF is defined as| | 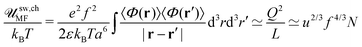 | (79) |
since 〈Φ(r)〉 = Φ0 within the sphere circumscribed around the chain. The correlation electrostatic energy of the chain, ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) sw,chcorr, can be found owing to its known (within the scaling consideration) correlation function, Gsw,ch(R). The intra-chain correlation function is given by
sw,chcorr, can be found owing to its known (within the scaling consideration) correlation function, Gsw,ch(R). The intra-chain correlation function is given by| | 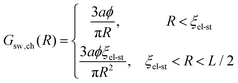 | (80) |
since the chain is Gaussian at R < ξel-st and linear at R > ξel-st, and ϕ ∼ u1/3f2/3 is the polymer volume fraction inside the blob. Then| | 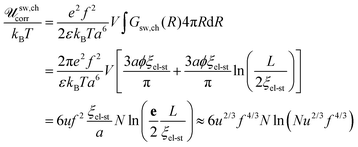 | (81) |
and e is the Euler's number. Thus, correlation electrostatic energy ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) sw,chcorr exceeds the mean-field term
sw,chcorr exceeds the mean-field term ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) sw,chMF by a factor of ln
sw,chMF by a factor of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N. For this reason account for the correlation term is requisite when charge of the chain is considered to be smeared throughout the sphere of diameter L.
N. For this reason account for the correlation term is requisite when charge of the chain is considered to be smeared throughout the sphere of diameter L.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
A. M. R. is grateful to Prof. E. Yu. Kramarenko and Prof. I. Ya. Erukhimovich for fruitful discussions. The authors acknowledge financial support from the Russian Science Foundation, project #15-13-00124, and the Government of the Russian Federation within Act 211, contract #02.A03.21.0011.
References
- A. Y. Grosberg, T. T. Nguyen and I. B. I. Shklovski, Rev. Mod. Phys., 2002, 74, 329–345 CrossRef CAS.
- W. Richtering and A. Pich, Soft Matter, 2012, 8, 11423–11430 RSC.
- R. Schroeder, A. A. Rudov, L. A. Lyon, W. Richtering, A. Pich and I. I. Potemkin, Macromolecules, 2015, 48, 5914–5927 CrossRef CAS.
- A. R. Khokhlov, J. Phys. A: Math. Gen., 1980, 13, 979–987 CrossRef CAS.
- K. N. Bakeev, V. A. Izumrudov, S. I. Kuchanov, A. B. Zezin and V. A. Kabanov, Macromolecules, 1992, 25, 4249–4254 CrossRef CAS.
- E. Spruijt, A. H. Westphal, J. W. Borst, M. A. Cohen Stuart and J. van der Gucht, Macromolecules, 2010, 43, 6476–6484 CrossRef CAS.
- Q. Wang and J. B. Schlenoff, Macromolecules, 2014, 47, 3108–3116 CrossRef CAS.
- M. Boustta, L. Leclercq, M. Vert and V. V. Vasilevskaya, Macromolecules, 2014, 47, 3574–3581 CrossRef CAS.
- J. Fu and J. B. Schlenoff, J. Am. Chem. Soc., 2016, 138, 980–990 CrossRef CAS PubMed.
- A. B. Kayitmazer, D. Seeman, B. B. Minsky, P. L. Dubin and Y. Xu, Soft Matter, 2013, 9, 2552–2583 RSC.
- F. Comert, A. J. Malanowski, F. Azarikia and P. L. Dubin, Soft Matter, 2016, 12, 4154–4161 RSC.
- F. Comert, D. Nguyen, M. Rushanan, P. Milas, A. Y. Xu and P. L. Dubin, J. Phys. Chem. B, 2017, 121, 4466–4473 CrossRef CAS PubMed.
- E. M. Mateescu, C. Jeppesen and P. Pincus, Europhys. Lett., 1999, 46, 493–498 CrossRef CAS.
- S. Y. Park, R. F. Bruinsma and W. M. Gelbart, Europhys. Lett., 1999, 46, 454–460 CrossRef CAS.
- I. I. Potemkin, Europhys. Lett., 2004, 68, 487–493 CrossRef CAS.
- O. Lenz and C. Holm, Eur. Phys. J. E: Soft Matter Biol. Phys., 2008, 26, 191–195 CrossRef CAS PubMed.
- N. P. Shusharina, P. Linse and A. R. Khokhlov, Macromolecules, 2000, 33, 3892–3901 CrossRef CAS.
- O. V. Borisov and E. B. Zhulina, Macromolecules, 2003, 36, 10029–10036 CrossRef CAS.
- S. V. Venev, P. Reineker and I. I. Potemkin, Macromolecules, 2010, 43, 10735–10742 CrossRef CAS.
- E. A. Lysenko, A. I. Kulebyakina, P. S. Chelushkin, A. M. Rumyantsev, E. Y. Kramarenko and A. B. Zezin, Langmuir, 2012, 28, 17108–17117 CrossRef CAS PubMed.
- A. M. Rumyantsev, A. A. Rudov and I. I. Potemkin, J. Chem. Phys., 2015, 142, 171105 CrossRef PubMed.
- P. Debye and E. Hückel, Phys. Z., 1923, 24, 185–206 CAS.
- J. T. G. Overbeek and M. J. Voorn, J. Cell. Comp. Physiol., 1957, 49, 7–26 CrossRef CAS.
- V. Y. Borue and I. Y. Erukhimovich, Macromolecules, 1988, 21, 3240–3249 CrossRef.
- V. Y. Borue and I. Y. Erukhimovich, Macromolecules, 1990, 23, 3625–3632 CrossRef CAS.
- J.-F. Joanny and L. Leibler, J. Phys., 1990, 51, 545–557 CAS.
- A. R. Khokhlov and I. A. Nyrkova, Macromolecules, 1992, 25, 1493–1502 CrossRef CAS.
- A. M. Rumyantsev and E. Kramarenko, Soft Matter, 2017 10.1039/C7SM01340J.
- M. Castelnovo and J.-F. Joanny, Langmuir, 2000, 16, 7524–7532 CrossRef CAS.
- M. Castelnovo and J.-F. Joanny, Macromolecules, 2002, 35, 4531–4538 CrossRef CAS.
- N. N. Oskolkov and I. I. Potemkin, Macromolecules, 2006, 39, 3648–3654 CrossRef CAS.
- N. N. Oskolkov and I. I. Potemkin, Macromolecules, 2007, 40, 8423–8429 CrossRef CAS.
- A. V. Ermoshkin and M. Olvera de la Cruz, Macromolecules, 2003, 36, 7824–7832 CrossRef CAS.
- A. Kudlay, A. V. Ermoshkin and M. Olvera de la Cruz, Macromolecules, 2004, 37, 9231–9241 CrossRef CAS.
- N. V. Brilliantov, Contrib. Plasma Phys., 1998, 38, 489–499 CrossRef CAS.
- K. A. Mahdi and M. Olvera de la Cruz, Macromolecules, 2000, 33, 8870–8881 CrossRef.
- A. Kudlay and M. Olvera de la Cruz, J. Chem. Phys., 2004, 120, 154902 CrossRef PubMed.
- I. I. Potemkin and V. V. Palyulin, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 041802 CrossRef PubMed.
- I. I. Potemkin, R. E. Limberger, A. N. Kudlay and A. R. Khokhlov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 011802 CrossRef PubMed.
- I. I. Potemkin and A. R. Khokhlov, J. Chem. Phys., 2004, 120, 10848 CrossRef CAS PubMed.
- I. I. Potemkin, N. N. Oskolkov, A. R. Khokhlov and P. Reineker, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 021804 CrossRef PubMed.
- D. Yang, S. V. Venev, V. V. Palyulin and I. I. Potemkin, J. Chem. Phys., 2011, 34, 074901 CrossRef PubMed.
- N. V. Brilliantov, D. V. Kuznetsov and R. Klein, Phys. Rev. Lett., 1998, 81, 1433–1436 CrossRef CAS.
- N. V. Brilliantov, V. V. Malinin and R. R. Netz, Eur. Phys. J. D, 2002, 18, 339–345 CAS.
- A. M. Tom, S. Vemparala, R. Rajesh and N. V. Brilliantov, Phys. Rev. Lett., 2016, 117, 147801 CrossRef PubMed.
- Y. A. Budkov, A. L. Kolesnikov, N. Georgi, E. A. Nogovitsyn and M. G. Kiselev, J. Chem. Phys., 2015, 142, 174901 CrossRef PubMed.
- M. Castelnovo and J.-F. Joanny, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 6, 377–386 CrossRef CAS.
- J. Lee, Y. O. Popov and G. H. Fredrickson, J. Chem. Phys., 2008, 128, 224908 CrossRef PubMed.
- C. E. Sing, J. W. Zwanikken and M. Olvera de la Cruz, Macromolecules, 2013, 46, 5053–5056 CrossRef CAS.
- S. L. Perry and C. Sing, Macromolecules, 2015, 48, 5040–5053 CrossRef CAS.
- S. Srivastava and M. V. Tirrel, Adv. Chem. Phys., 2016, 161, 499–544 CrossRef.
- C. E. Sing, Adv. Colloid Interface Sci., 2017, 239, 2–16 CrossRef CAS PubMed.
- T. Lytle, M. Radhakrishna and C. Sing, Macromolecules, 2016, 49, 9693–9705 CrossRef CAS.
- M. Radhakrishna, K. Basu, Y. Liu, R. Shamsi, S. L. Perry and C. E. Sing, Macromolecules, 2017, 50, 3030–3037 CrossRef CAS.
- I. Borukhov, D. Andelman and H. Orland, Eur. Phys. J. B, 1998, 5, 869–880 CrossRef CAS.
- N. P. Shusharina, E. B. Zhulina, A. V. Dobrynin and M. Rubinstein, Macromolecules, 2005, 38, 8870–8881 CrossRef CAS.
- K. Shen and Z.-G. Wang, J. Chem. Phys., 2017, 146, 084901 CrossRef PubMed.
-
L. D. Landau and E. M. Lifshitz, Statistical Physics, Part 1, Pergamon Press, New York, 1970 Search PubMed.
- Z.-G. Wang, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 021501 CrossRef PubMed.
- R. Zhang and B. I. Shklovskii, Phys. A, 2005, 352, 216–238 CrossRef CAS.
- S. F. Edwards, Proc. Phys. Soc., 1966, 88, 265–280 CrossRef CAS.
- I. M. Lifshitz, Sov. Phys. – JETP, 1969, 28, 1280–1286 Search PubMed.
- S. B. Moldakarimov, E. Y. Kramarenko, A. R. Khokhlov and S. E. Kudaibergenov, Macromol. Theory Simul., 2001, 10, 780–788 CrossRef CAS.
- Z. Ou and M. Muthukumar, J. Chem. Phys., 2006, 124, 154902 CrossRef PubMed.
- A. Salehi and R. G. Larson, Macromolecules, 2016, 49, 9706–9719 CrossRef CAS.
- A. R. Khokhlov and E. Y. Kramarenko, Macromol. Theory Simul., 1994, 3, 45–59 CrossRef CAS.
- A. G. Cherstvy, J. Phys. Chem. B, 2010, 114, 5241–5249 CrossRef CAS PubMed.
- O. E. Philippova, A. M. Rumyantsev, E. Y. Kramarenko and A. R. Khokhlov, Macromolecules, 2013, 46, 9359–9367 CrossRef CAS.
-
A. Y. Grosberg and A. R. Khokhlov, Statistical Physics of Macromolecules, AIP Press, New York, 1994 Search PubMed.
- J. Qin and J. J. de Pablo, Macromolecules, 2016, 49, 8789–8800 CrossRef.
- P. G. de Gennes, P. Pincus, R. M. Velasco and E. J. Brochard, J. Phys., 1976, 37, 1461–1473 CAS.
- P. G. Dommersnes, Y. Kantor and M. Kardar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 031802 CrossRef PubMed.
- J. van der Gucht, E. Spruijt, M. Lemmers and M. A. Cohen Stuart, J. Colloid Interface Sci., 2011, 361, 407–422 CrossRef CAS PubMed.
- S. L. Perry, L. Leon, K. Q. Hoffmann, M. J. Kade, D. Priftis, K. A. Black, D. Wong, R. A. Klein, C. F. I. Piercell, K. O. Margossian, J. K. Whitmer, J. Qin, J. J. de Pablo and M. Tirrel, Nat. Commun., 2015, 14, 6052 CrossRef PubMed.
- A. S. Bodrova, E. Y. Kramarenko and I. I. Potemkin, Macromolecules, 2010, 43, 2622–2629 CrossRef CAS.
- J. Qin, D. Priftis, R. Farina, S. L. Perry, L. Leon, J. Whitmer, K. Hoffman, M. Tirrel and J. J. de Pablo, ACS Macro Lett., 2014, 3, 565–568 CrossRef CAS.
- A. N. Semenov and M. Rubinstein, Macromolecules, 1998, 31, 1373–1385 CrossRef CAS.
- K. T. Delaney and G. H. Fredrickson, J. Chem. Phys., 2017, 146, 224902 CrossRef.
|
| This journal is © the Owner Societies 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab and
Igor I.
Potemkin
ab and
Igor I.
Potemkin
 *abc
*abc
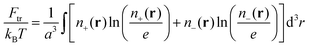
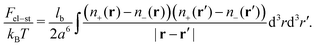
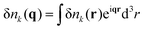
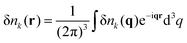
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(n0/e)/a3, in the Gaussian (square) approximation reads:
ln(n0/e)/a3, in the Gaussian (square) approximation reads: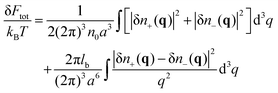
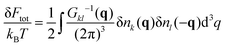
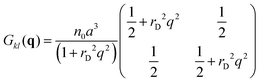
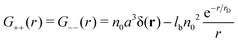
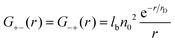
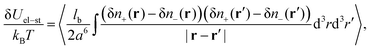
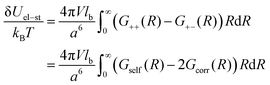
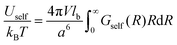
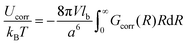
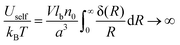
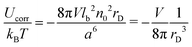
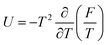
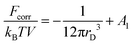
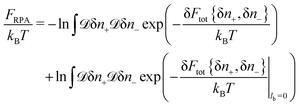
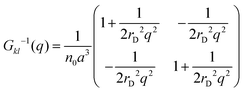
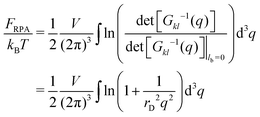
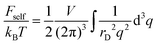
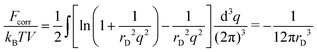
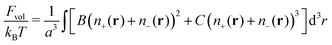
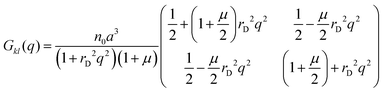
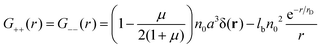
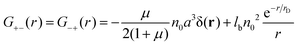
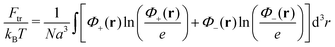
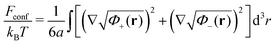
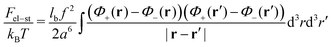
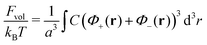
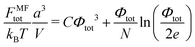
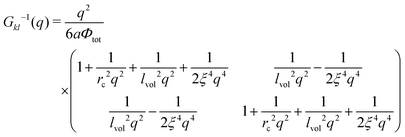
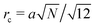 being the correlation radius of the ideal polymer chain (i.e. the Gaussian chain size),
being the correlation radius of the ideal polymer chain (i.e. the Gaussian chain size), 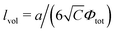 being the correlation radius of infinite neutral chain caused solely by the volume interactions and ξ = a/(48πuf2Φtot)1/4 being the screening radius of the electrostatic interactions in PE complex; u = lb/a is the dimensionless Bjerrum length. The RPA correction to the free energy of the PEC can be found in a similar way to that for the DH plasma (see eqn (19) and (21)):
being the correlation radius of infinite neutral chain caused solely by the volume interactions and ξ = a/(48πuf2Φtot)1/4 being the screening radius of the electrostatic interactions in PE complex; u = lb/a is the dimensionless Bjerrum length. The RPA correction to the free energy of the PEC can be found in a similar way to that for the DH plasma (see eqn (19) and (21)):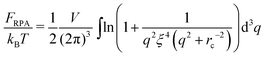
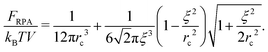
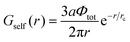
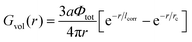
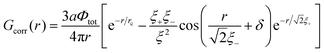
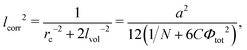
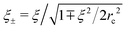 and dimensionless δ = arctan(ξ+ξ−/2rc2). Note that the electrostatic interactions vanish at lb = 0, and Gcorr = 0. Similarly, Gvol = 0 in the absence of volume interactions, i.e. at C = 0. Gself is known to be the Ornstein–Zernike type correlation function of a single Gaussian chain and is equal to the correlation function in the solution of the ideal chains.69
and dimensionless δ = arctan(ξ+ξ−/2rc2). Note that the electrostatic interactions vanish at lb = 0, and Gcorr = 0. Similarly, Gvol = 0 in the absence of volume interactions, i.e. at C = 0. Gself is known to be the Ornstein–Zernike type correlation function of a single Gaussian chain and is equal to the correlation function in the solution of the ideal chains.69

![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) chains = VΦtot/(a3N) is the total number of polymer chains (both polycations and polyanions) in the system.
chains = VΦtot/(a3N) is the total number of polymer chains (both polycations and polyanions) in the system.
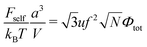
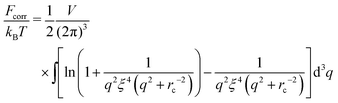
 , see eqn (47). For this reason the term accounting for the chain translational entropy cannot be neglected in the total free energy.
, see eqn (47). For this reason the term accounting for the chain translational entropy cannot be neglected in the total free energy.
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) chains, like the self-energy is proportional to the number of charges in the DH plasma. The difference between these two systems is the following: point-like charges are structureless and their self-energy is unchanged under any conditions, while the PE chain can adopt different conformations resulting in different mutual spatial locations of charges and different self-energy.
chains, like the self-energy is proportional to the number of charges in the DH plasma. The difference between these two systems is the following: point-like charges are structureless and their self-energy is unchanged under any conditions, while the PE chain can adopt different conformations resulting in different mutual spatial locations of charges and different self-energy.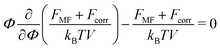
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) G,chel-st equals mean-field electrostatic chain energy
G,chel-st equals mean-field electrostatic chain energy ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) G,chMF plus the self-energy of a chain
G,chMF plus the self-energy of a chain ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) G,chcorr, see Appendix A.
G,chcorr, see Appendix A.
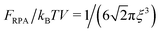 , so that the polymer volume fraction within the complex reads
, so that the polymer volume fraction within the complex reads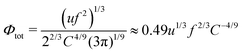
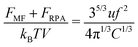
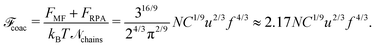
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) coac ≈ −Nu2/3f4/3. The sign minus in the scaling result was justified by attraction of oppositely charged blobs within the complex.56 However, the negative energy of correlation attraction between oppositely charged blobs is of the order of the blob self-energy. So the scaling consideration does not allow us to define the sign (plus or minus) of the free energy within the complex,
coac ≈ −Nu2/3f4/3. The sign minus in the scaling result was justified by attraction of oppositely charged blobs within the complex.56 However, the negative energy of correlation attraction between oppositely charged blobs is of the order of the blob self-energy. So the scaling consideration does not allow us to define the sign (plus or minus) of the free energy within the complex, ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) coac. It is necessary to mention here that properly defined correlation energy of the PEC given by eqn (48) is indeed negative, but the free energy of the complex being the sum of the correlation free energy and the self-energy of the chains is positive. Moreover, scaling treats polyions as a set of disrupted blobs resulting in a linear dependence of the chain correlation energy on its length N, while RPA accounts for correlations within the chain on all length scales and yields asymptotically N3/2.
coac. It is necessary to mention here that properly defined correlation energy of the PEC given by eqn (48) is indeed negative, but the free energy of the complex being the sum of the correlation free energy and the self-energy of the chains is positive. Moreover, scaling treats polyions as a set of disrupted blobs resulting in a linear dependence of the chain correlation energy on its length N, while RPA accounts for correlations within the chain on all length scales and yields asymptotically N3/2.
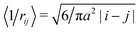 . The electrostatic energy of a single blob is given by
. The electrostatic energy of a single blob is given by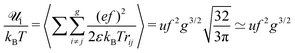
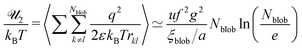
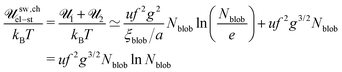
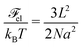
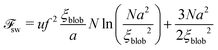
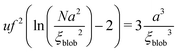
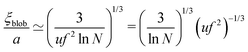
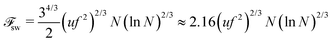
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N)2/3, is crucial for equilibrium between the free chains and the PEC.
N)2/3, is crucial for equilibrium between the free chains and the PEC.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solution. One can expect that in extremely dilute solutions polyions exist as single chains, while their increasing concentration should result in complexation and formation of either single globules on the basis of one polycation and one polyanion or a macroscopic condensed phase (coacervate). For the sake of simplicity, the equilibrium between the three states of the polyions, namely (i) single chains, (ii) neutral globules and (iii) macroscopic liquid coacervates will be considered, though formation of a solid precipitate is also possible in some cases,73e.g. for oppositely charged chiral polypeptides extra capable of hydrogen bonding.73,74 Here we neglect formation of globules consisting of several couples of oppositely charged polyions assuming that their fraction will be smaller in comparison with the globules on the basis of one couple. In other words, we assume that the size distribution function of the globules has a narrow maximum for the one couple.
1 solution. One can expect that in extremely dilute solutions polyions exist as single chains, while their increasing concentration should result in complexation and formation of either single globules on the basis of one polycation and one polyanion or a macroscopic condensed phase (coacervate). For the sake of simplicity, the equilibrium between the three states of the polyions, namely (i) single chains, (ii) neutral globules and (iii) macroscopic liquid coacervates will be considered, though formation of a solid precipitate is also possible in some cases,73e.g. for oppositely charged chiral polypeptides extra capable of hydrogen bonding.73,74 Here we neglect formation of globules consisting of several couples of oppositely charged polyions assuming that their fraction will be smaller in comparison with the globules on the basis of one couple. In other words, we assume that the size distribution function of the globules has a narrow maximum for the one couple.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N/3)2/3 ≫ 1, i.e. the number of the electrostatic blobs within the chain exceeds unity by far. Free energy of the chains in each state can be divided into concentration-dependent entropic and concentration-independent energy contributions. The latter has the form:
N/3)2/3 ≫ 1, i.e. the number of the electrostatic blobs within the chain exceeds unity by far. Free energy of the chains in each state can be divided into concentration-dependent entropic and concentration-independent energy contributions. The latter has the form:![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) sw = 2.16(uf2)2/3N(ln
sw = 2.16(uf2)2/3N(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N)2/3
N)2/3![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) coac = 2.17(uf2)2/3NC1/9
coac = 2.17(uf2)2/3NC1/9![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) gl = 2.17(uf2)2/3NC1/9 + 0.68(uf2)4/9N2/3C−5/54.
gl = 2.17(uf2)2/3NC1/9 + 0.68(uf2)4/9N2/3C−5/54.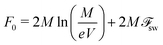
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z0. The partition function of the supernatant Z with pM globules reads
Z0. The partition function of the supernatant Z with pM globules reads![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) sw−
sw−![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) gl).
gl).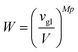
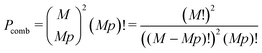
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z reads
Z reads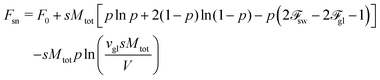
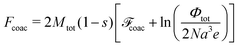
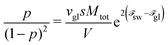
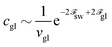
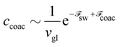
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) gl −
gl − ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) coac −
coac − ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) sw < 0, and the formation of the globules starts at much lower concentrations than their precipitation in the solution. At chosen values of the numerical parameters, all assumptions adopted above are valid. Namely, polyions are long enough to contain a large number of the electrostatic blobs and they exist in the non-aggregated state only at extremely small concentrations. In the concentration range shown in Fig. 2 and 3, the coacervate volume is much smaller than the total volume of the system, so that disregard of the supernatant volume diminution in the course of precipitation is justified.
sw < 0, and the formation of the globules starts at much lower concentrations than their precipitation in the solution. At chosen values of the numerical parameters, all assumptions adopted above are valid. Namely, polyions are long enough to contain a large number of the electrostatic blobs and they exist in the non-aggregated state only at extremely small concentrations. In the concentration range shown in Fig. 2 and 3, the coacervate volume is much smaller than the total volume of the system, so that disregard of the supernatant volume diminution in the course of precipitation is justified.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N correction as well as the surface effects were neglected, while strict theoretical-field analysis performed in their work did not allow finding analytical formulas.
N correction as well as the surface effects were neglected, while strict theoretical-field analysis performed in their work did not allow finding analytical formulas.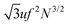 is the Coulomb energy due to the correlations of charges along the polyion in ideal coil conformation. It is important to stress that the mean-field free energy of charged polyions with Gaussian coil statistics should not be included into their self-energy because of the overall complex electric neutrality (see Appendix A). The physical meaning of the chain self-energy can be defined as follows. It is the work which is necessary to simultaneously assemble an equal number of polycations and polyanions in the same volume (volume of PEC) providing them conformations of Gaussian coil. This work is required not to get non-zero overall charge of this volume (as in the case of single polyions, eqn (60)), since the complex is electrically neutral, but to achieve connectivity of charges into Gaussian coils. In turn, energy of fluctuation-induced attraction between these already assembled polyions is the true correlation energy, Fcorr.
is the Coulomb energy due to the correlations of charges along the polyion in ideal coil conformation. It is important to stress that the mean-field free energy of charged polyions with Gaussian coil statistics should not be included into their self-energy because of the overall complex electric neutrality (see Appendix A). The physical meaning of the chain self-energy can be defined as follows. It is the work which is necessary to simultaneously assemble an equal number of polycations and polyanions in the same volume (volume of PEC) providing them conformations of Gaussian coil. This work is required not to get non-zero overall charge of this volume (as in the case of single polyions, eqn (60)), since the complex is electrically neutral, but to achieve connectivity of charges into Gaussian coils. In turn, energy of fluctuation-induced attraction between these already assembled polyions is the true correlation energy, Fcorr.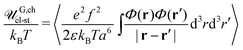
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) G,chel-st =
G,chel-st = ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) G,chMF +
G,chMF + ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) G,chcorr
G,chcorr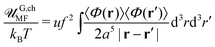
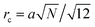 being the characteristic Gaussian size of the chain. On the other hand,
being the characteristic Gaussian size of the chain. On the other hand, ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) G,chel-st,MF = 0 within the complex since the excess charge of the PE molecule is compensated by the oppositely charged counterpart. The correlation term can be easily calculated:
G,chel-st,MF = 0 within the complex since the excess charge of the PE molecule is compensated by the oppositely charged counterpart. The correlation term can be easily calculated: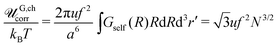
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) G,chMF, and the self-energy correction caused by correlations,
G,chMF, and the self-energy correction caused by correlations, ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) G,chcorr, depend on the parameters in similar ways, both ∼uf2N3/2. They differ only by numerical coefficients.
G,chcorr, depend on the parameters in similar ways, both ∼uf2N3/2. They differ only by numerical coefficients.
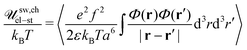
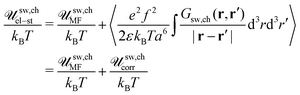
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) sw,chMF is defined as
sw,chMF is defined as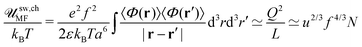
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) sw,chcorr, can be found owing to its known (within the scaling consideration) correlation function, Gsw,ch(R). The intra-chain correlation function is given by
sw,chcorr, can be found owing to its known (within the scaling consideration) correlation function, Gsw,ch(R). The intra-chain correlation function is given by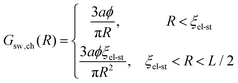
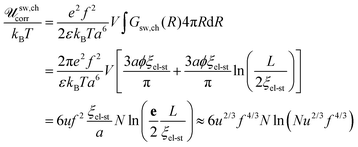
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) sw,chcorr exceeds the mean-field term
sw,chcorr exceeds the mean-field term ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) sw,chMF by a factor of ln
sw,chMF by a factor of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N. For this reason account for the correlation term is requisite when charge of the chain is considered to be smeared throughout the sphere of diameter L.
N. For this reason account for the correlation term is requisite when charge of the chain is considered to be smeared throughout the sphere of diameter L.



