 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Vibrational nonlinear optical properties of spatially confined weakly bound complexes†
Robert
Zaleśny
 *a,
Marta
Chołuj
a,
Justyna
Kozłowska
*a,
Marta
Chołuj
a,
Justyna
Kozłowska
 a,
Wojciech
Bartkowiak
*a and
Josep M.
Luis
a,
Wojciech
Bartkowiak
*a and
Josep M.
Luis
 *b
*b
aDepartment of Physical and Quantum Chemistry, Faculty of Chemistry, Wrocław University of Science and Technology, Wybrzeże Wyspiańskiego 27, 50-370 Wrocław, Poland. E-mail: robert.zalesny@pwr.edu.pl; wojciech.bartkowiak@pwr.edu.pl
bInstitute of Computational Chemistry and Catalysis and Department of Chemistry, University of Girona, Campus de Montilivi, 17071 Girona, Catalonia, Spain. E-mail: josepm.luis@udg.edu
First published on 14th August 2017
Abstract
This study focuses on the theoretical description of the influence of spatial confinement on the electronic and vibrational contributions to (hyper)polarizabilities of two dimeric hydrogen bonded systems, namely HCN⋯HCN and HCN⋯HNC. A two-dimensional analytical potential is employed to render the confining environment (e.g. carbon nanotube). Based on the results of the state-of-the-art calculations, performed at the CCSD(T)/aug-cc-pVTZ level of theory, we established that: (i) the influence of spatial confinement increases with increasing order of the electrical properties, (ii) the effect of spatial confinement is much larger in the case of the electronic than vibrational contribution (this holds for each order of the electrical properties) and (iii) the decrease in the static nuclear relaxation first hyperpolarizability upon the increase of confinement strength is mainly due to changes in the harmonic term, however, in the case of nuclear relaxation second hyperpolarizability the anharmonic terms contribute more to the drop of this property.
1 Introduction
The interaction between the electric field and spatially confined quantum objects is intensively investigated in recent years, due to its importance for both fundamental science and the prospects of applications. Great achievements in new technologies for the synthesis of low-dimensional semiconductor structures (e.g. quantum dots, quantum wires or more complicated nanometric semiconductors like quantum rings), whose properties seem to be suitable for optoelectronic devices,1–3 can be considered as some of the important motivating factors for the development of theoretical models able to cope with the spatial confinement phenomena. The reports from experimental studies on more extended molecular systems, which indicate the possibility of tuning the optical response of molecules encapsulated in different chemical cages, might also be considered as encouraging. For instance, it has been shown quite recently that the second harmonic generation (SHG) efficiencies of push–pull aminopyridine derivatives intercalated into inorganic layered materials are larger than those measured for the pure chromophores.4 Likewise, the materials consisting of a dye encapsulated inside metal–organic-framework (MOF) structures are also promising to exhibit large SHG activity.5 Last but not least, the confinement of organic molecules in two-dimensional nanospace has been reported as an effective strategy to enlarge their two-photon absorption strength.6–8The promising conclusions from experimental works are accompanied by the growing interest in theoretical analyses of the linear and nonlinear optical (L&NLO) properties of confined quantum objects. Usually, in order to describe the behaviour of such systems, the various kinds of analytical potentials are employed. One of the simplest and earliest ideas dates back to 1937, when Michels et al. proposed an enclosing of the hydrogen atom inside an impenetrable sphere in order to explore the pressure influence on hydrogen dipole polarizability.9 Over the years this methodology has been reported in a number of studies allowing us to gain insights into the effect of the confining environment on the dipole moment (μ), polarizability (α), first and second hyperpolarizability (β and γ) of various molecular systems (e.g. H, He, Li, Be, B, C, N, O, F, Ne, Br, H−, F−, Cl−, O2−, S2−, H2+, H2, HeH, LiH, LiF, HCl, HF, HArF, OCS, HCN, CO2, HCCCl, HCCCN, HCN⋯HCNn, CO, BF).10–26
Even though the list of spatially restricted quantum objects whose L&NLO response has already been investigated is quite long, it is mainly limited to atoms or simple molecules. Besides, in the vast majority of cases, only the purely electronic contributions to the static electric properties of these systems were analysed. In contrast, the studies on vibrational (hyper)polarizabilities of the spatially limited molecular systems are rare,23,24 although the prominent role of molecular vibrations in various NLO processes is quite well recognized for the unconfined molecules (see for example ref. 27–30). The importance of this issue has been revealed only recently, in our study performed on the model linear molecules (HCN, HCCH and CO2).24 As has been demonstrated the electronic contributions can prevail over the vibrational terms for unconfined molecules. However, the spatial confinement modifies the electronic contribution to hyperpolarizabilities to a larger extent than the vibrational one. Thus both counterparts should be considered in the interpretation of the nonlinear optical properties of spatially confined molecules.
Aiming at verifying this conclusion for molecular complexes, in this work we report on the effect of orbital compression on the electronic and vibrational contributions to α, β and γ of two dimeric hydrogen bonded (HB) systems, composed of the HCN molecule or its tautomeric form, i.e. HCN⋯HCN and HCN⋯HNC. Due to the presence of hydrogen bonds, these systems are expected to exhibit significant vibrational hyperpolarizabilities. Hence, it is interesting to shed light on confinement-induced relative changes in the electronic and vibrational properties. Until now, the confinement of HB complexes inside chemical cages was studied mostly in a broader context of physical chemistry, as it allows for temporary isolation (from milliseconds to hours) of the complexes by mechanical barriers in very small spaces,31–34 providing a ‘snapshot’ of what goes on with the individual donor and acceptor hydrogen bond pairs. Simultaneously, the influence of the confining environments on the structural and energetic properties of HB complexes exposed to the high pressure or encapsulated inside various chemical cages has also been widely studied.25,34–44 Among others, based on the results of NMR measurements obtained for the hydrogen bonded carboxylic acid dimers embedded in different molecular capsules it was shown that the orbital compression leads to the shortening of the hydrogen bond length.34,37 Likewise, the data obtained from the Raman scattering study performed on the crystalline deuterated formic acid indicate that under the influence of high pressure the strength of deuterium bonds has been enhanced.38 Similar findings emerged from the recent theoretical studies concerning the impact of spatial restriction, represented by the cylindrical harmonic potential, on the properties of linear hydrogen bonded complexes.25,43 It should be highlighted that previous studies on the L&NLO properties of the spatially limited hydrogen bonded complexes are scarce in the literature. In fact, the only report analysing the influence of the orbital compression on the electric properties of HB molecular complexes is that by Roztoczyńska et al.,25 who found that the effect of the analytical confining potential leads to the decrease of both the dipole moment and dipole polarizability of the linear HCN chains. Thus, to the best of our knowledge, the present study is a pioneering exploration of confinement-induced changes in the electronic and vibrational nonlinear optical properties for weakly bound systems. It is also worth mentioning that this is a significant extension of our earlier systematic research focusing on the influence of a chemical confining environment on the vibrational contributions to molecular polarizabilities.23,24
2 Computational methods
Under the assumption of the validity of the clamped nuclei approximation, the molecular (non)linear optical properties (P = α, β, γ) may be separated into pure electronic, nuclear relaxation (Pnr) and curvature (Pcurv) contributions:45,46| P = Pe + Pnr + Pcurv | (1) |
| αnr(0;0) = [μ2](0,0)ω=0 | (2) |
| βnr(0;0,0) = [μα](0,0)ω=0 + [μ3](1,0)ω=0 + [μ3](0,1)ω=0 | (3) |
| γnr(0;0,0,0) = [α2](0,0)ω=0 + [μβ](0,0)ω=0 + [μ2α](1,0)ω=0 + [μ2α](0,1)ω=0 + [μ4](2,0)ω=0 + [μ4](0,2)ω=0 + [μ4](1,1)ω=0 | (4) |
Alternatively, the nuclear relaxation contributions can be calculated from finite-field derivatives of the electronic properties computed at the field-relaxed equilibrium geometries (FF-NR method).49,50 In general, during FF-NR calculations it should be ensured that the geometry relaxation must not result from rotations of the molecule through alignment of the permanent and/or induced dipole moment in the field direction. For that reason, the field-dependent optimization should be performed while strictly maintaining the Eckart conditions.51 Such optimizations can be carried out with the aid of the procedure developed by Luis et al.50
Moreover, in order to reduce the numerical differentiation error in the FF-NR approach, in this study we follow the Romberg–Rutishauser scheme.52,53 The correction of order p to the derivative P is determined iteratively according to the formula:
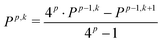 | (5) |
The double harmonic square bracket terms are sufficient to compute the nuclear relaxation contribution to some dynamic NLO properties within the infinite optical frequency approximation. These include, inter alia, the electro-optical Pockels effect (EOPE), the intensity-dependent refractive index (IDRI) and electric field induced second harmonic generation (ESHG). In square bracket notation the properties were determined as:30
 | (6) |
 | (7) |
 | (8) |
In this work, the effect of spatial confinement was modelled by applying the harmonic oscillator potential of cylindrical symmetry, centred at the nucleus and represented by the sum of one-electron contributions:
 | (9) |
| ΔEHFint ≈ E(ϕ) − E(ϕ = 0.0) |
In the present study we employed the CCSD(T) method combined with the aug-cc-pVTZ basis set. As demonstrated in our earlier study this basis set delivers 1% accuracy in electronic and nuclear relaxation (hyper)polarizabilities of small molecules.55 Tight convergence criteria during the optimization of coupled cluster wavefunction were imposed (energy convergence criterion was set to 10−12 hartree). The latter and the large number of electric field amplitudes are the main factors contributing to very high computational expenses of the BKPT and FF-NR calculations performed in this study. The state-of-the-art results presented herein encouraged us to carry out the assessment of the MP2 method in computing both electronic and vibrational hyperpolarizabilities of confined molecules. The results are presented in the ESI† and show that the MP2 method reproduces the correct trends, although the errors may reach up to 15%.
FF-NR and BKPT calculations were performed using custom computer routines based on the energies computed using the GAUSSIAN 2009 package.56
3 Results and discussion
In order to analyze the confinement-induced changes in the electric properties of molecular aggregates, two model hydrogen-bonded systems were chosen, namely: HCN⋯HCN and HCN⋯HNC. For the sake of brevity, in what follows we will also refer to these systems as A and B, respectively. These strongly bonded bimolecular complexes were studied by Heikkilä and Lundell57 who determined the interaction energy. The results of calculations, performed at the CCSD(T)/6-311++G(2d,2p) level of theory, indicate that HCN⋯HNC is much more strongly bonded than HCN⋯HCN and the corresponding interaction energies are −17.947 and −27.650 kJ mol−1. This is reflected in shortening of the N⋯H bond length from 2.207 Å to 1.946 Å (results obtained at the MP2/6-311++G(2d,2p) level by Heikkilä and Lundell).57 This is in line with the results of calculations obtained in this work, i.e. the shortening of the N⋯H bond length from 2.204 Å to 1.967 Å on passing from HCN⋯HCN to HCN⋯HNC. Despite these significant differences in the equilibrium structure and interaction strength for isolated complexes, the patterns of confinement-induced changes in geometrical parameters for both systems are similar (see Fig. 1). For ϕ = 0.1 a.u. one observes the shortening of all covalent bonds in A and B roughly by 0.006 Å, while the N⋯H bond length is shorter by 0.011 Å. Larger strength of confinement, i.e. ϕ = 0.2 a.u., leads to further shortening of covalent bonds in both complexes (from 0.020 to 0.022 Å with respect to the unconfined systems) and yet there is a significant decrease in the N⋯H bond length ranging from 0.035 Å (HCN⋯HCN) to 0.039 Å (HCN⋯HNC). The results presented herein for molecular complexes are consistent with what was reported for molecules, e.g. the confinement-induced shortening of covalent bonds was also observed for CO2, C2H2, HCN and HCCCN.23,24 An analogous behavior has also been noted for the hydrogen bond length in several theoretical as well as experimental works concerning the effect of spatial confinement on the HB complexes.25,37,43,58 As pointed out by Cammi et al. the shortening of the interatomic distances upon confinement is directly connected with the deformation of the molecular electronic charge density, due to the Pauli repulsive interaction with the environment.59,60 According to the authors, such an interaction causes an increase of electron density in the interatomic regions of the molecule, which leads to a reduction of bond lengths. In some measure, these findings are in line with those emerging from the extensive quantum-chemical calculations conducted for the spatially limited HB dimers.43 In particular, based on the results obtained using quantum theory of atoms in molecules, it has been shown that upon increasing the strength of the orbital compression the electron density at the hydrogen bond critical point becomes larger, which might be directly related to the shortening of the hydrogen bond length. | ||
| Fig. 1 Bond-length changes (given in Å) in the presence of confining potential (ϕ, given in a.u.). Shown is also the orientation of studied complexes in the Cartesian coordinate system. | ||
The significant difference in the N⋯H bond length for both complexes is expected to have an impact on the electric dipole properties. Indeed, the data presented in Table 1 for unconfined complexes demonstrate that, by and large, (hyper)polarizabilities of HCN⋯HNC are higher than those for HCN⋯HCN. Similar observation has been made by Brandão et al., who studied how the isomeric change affects the magnitude of electronic contributions to the electric properties.61 As has been demonstrated such an effect has a notable influence on the values of μ, α and, in particular, β of linear chains of HCN and HNC molecules.
| ϕ | α e | α nr | β e | β nrEOPE | β nr | γ e | γ nrIDRI | γ nrESHG | γ nr |
|---|---|---|---|---|---|---|---|---|---|
| HCN⋯HCN | |||||||||
| 0.0 | 49.88 | 4.75 | −28 | −56 | −225 | 6.5 × 103 | 2.6 × 103 | 0.2 × 103 | 11.3 × 103 |
| 0.1 | 47.65 | 4.59 | −25 | −52 | −211 | 5.2 × 103 | 2.3 × 103 | 0.2 × 103 | 10.0 × 103 |
| 0.2 | 43.25 | 4.19 | −23 | −46 | −185 | 3.6 × 103 | 1.8 × 103 | 0.1 × 103 | 7.5 × 103 |
| HCN⋯HNC | |||||||||
| 0.0 | 52.39 | 8.12 | −74 | −61 | −301 | 9.0 × 103 | 2.8 × 103 | <0.1 × 103 | 22.2 × 103 |
| 0.1 | 50.01 | 7.79 | −62 | −56 | −282 | 6.8 × 103 | 2.5 × 103 | <0.1 × 103 | 19.6 × 103 |
| 0.2 | 45.48 | 7.15 | −53 | −49 | −250 | 4.5 × 103 | 2.0 × 103 | <−0.1 × 103 | 16.2 × 103 |
We will now turn to the discussion of confinement-induced changes in the diagonal electronic contributions to α, β and γ based on the data compiled in Table 1 and Fig. 2. Note that all the NLO properties were calculated using geometries optimized for the indicated amplitudes of the confining potential (ϕ). In the case of electronic polarizability there is a similar decrease upon increasing the confinement strength from ϕ = 0.0 to ϕ = 0.2 a.u. (13.29% for A and 13.19% for B). This result was quite expected, as a direct consequence of the electron density compression due to the presence of the confinement effect.18,19,21,22 The corresponding changes in electronic first hyperpolarizability are more pronounced, i.e. there is a 17.86% and 28.38% drop in this property for A and B, respectively. The largest effect of spatial confinement is observed in the case of γe: when increasing the confinement strength from ϕ = 0.0 to ϕ = 0.2 a.u. there is an accompanying decrease in this property as large as 44.62% and 50.00%, for A and B, respectively. Based on these results one can conclude that even moderate changes in the strength of confinement can lead to quite large changes in electronic hyperpolarizabilities. Moreover, as it can be noticed, the influence of orbital compression on the magnitude of (hyper)polarizabilities increases with the increasing order of the electrical properties. A similar remark has been made previously in several theoretical studies concerning the electric properties of molecular systems embedded in the model confining potentials.19,21–23 Note that the electronic properties discussed thus far were calculated at geometries optimized for the indicated amplitudes of confining potential (ϕ). In order to address the importance of the effect of confinement-induced structural relaxation on αe, βe and γe we have performed property calculations at a set of frozen geometries (for ϕ = 0 and ϕ ≠ 0). Based on the results shown in Table S2 in the ESI,† it can be concluded that the geometry relaxation makes only a minor contribution to the overall confinement-induced changes in electronic (hyper)polarizabilities.
 | ||
| Fig. 2 Relative percentage changes of electronic (EL) and nuclear-relaxation (NR) (hyper)polarizabilities as a function of the confinement strength (ϕ, given in a.u.). | ||
In what follows we will seek to establish if the conclusion presented above also holds for the vibrational nonlinear optical properties of weakly bound HCN isomers. In doing so, we will analyse the confinement-induced changes in the vibrational properties of both complexes. The relevant data are presented in Table 1 and Fig. 2. As above, we will discuss the percentage changes between the properties computed for unconfined and confined complexes (where ϕ = 0.2 a.u.). Similar to electronic polarizability, a drop in the αnr value occurs for both systems upon increasing confinement and the corresponding change equals to 11.79% (A) and 11.95% (B). Note that the obtained decrease in the αnr values is slightly smaller than the corresponding changes in αe. The orbital compression has, again, almost an identical influence on nuclear-relaxation static first hyperpolarizability of both complexes and reduces its magnitude by 17.78% and 16.94% for A and B, respectively. As one can notice, in the case of the HCN⋯HCN complex the degree of the confinement-induced change in βnr is virtually the same as for βe. In contrast, β of HCN⋯HNC behaves differently and the drop in the nuclear relaxation contribution is roughly 10% smaller than that for βe. Finally, we find that γnr for both systems is much less susceptible to spatial confinement and the corresponding changes are 33.63% (A) and 27.03% (B). It should not be overlooked that these changes are much smaller than those observed for electronic second hyperpolarizability. Table 1 also contains the values of dynamic vibrational hyperpolarizabilities. The confinement-induced change in βnrEOPE(−ω;ω,0), on passing from ϕ = 0.0 to ϕ = 0.2 a.u., is 17.86% and 19.67% for A and B, respectively. However, a much larger effect is found for γnrIDRI, i.e. the change in this property is 30.77% (A) and 28.57% (B). We may thus conclude that in terms of magnitude the effect of confinement is similar for the static and dynamic vibrational properties.
In order to rationalize the changes in the static nuclear-relaxation hyperpolarizabilities upon confinement, we performed their breakdown into harmonic and net anharmonic contributions. The results are presented in Fig. 3 and 4 and all numerical data are presented in the ESI.† As shown by the latter figure, the above discussed confinement-induced changes in βnr can be mainly associated with the decrease of the harmonic contribution (75.00% and 68.63% of total βnr drop for A and B, respectively). However, in the case of γnr the anharmonic terms become far more important and they are responsible for the confinement-induced decrease of this property, i.e. the drop in γnr is 65.78% and 73.33% due to a decrease of anharmonic terms for A and B, respectively.
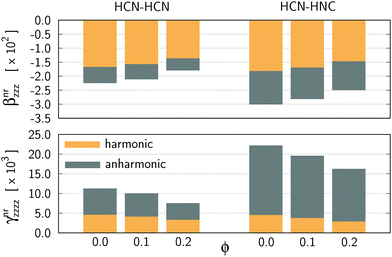 | ||
| Fig. 3 Breakdown of nuclear-relaxation hyperpolarizabilities into harmonic and anharmonic contributions as a function of the confinement strength (ϕ). All values are given in atomic units. | ||
 | ||
| Fig. 4 Percentage contributions of harmonic and anharmonic terms to the total confinement-induced change (ϕ = 0 → ϕ = 0.2) in βnr and γnr for HCN⋯HCN (A) and HCN⋯HNC (B). | ||
In an attempt to shed more light on the confinement-induced changes in the vibrational properties, we employed the BKPT formalism which allows for the analysis of the normal mode contributions to individual square bracket terms appearing in eqn (3) and (4). In order to unravel the connection between the changes in harmonic terms and the changes in the vibrational structure, we performed an exemplary analysis of individual normal modes contributing to the harmonic part of βnr. The results for the [μα](0,0) term are presented in Fig. 5 (for other terms we refer to the ESI†). The plots present the individual normal mode contributions (vertical bars) together with the total value (bold dotted line). As seen, in the case of studied molecular systems, only two modes have major contribution to the confinement-induced decrease in [μα](0,0). For both complexes these two modes correspond to: (i) the intermolecular stretching vibration (n = 1), (ii) the stretching vibration of hydrogen involved in the hydrogen bond (n = 12 (A) and n = 13 (B)). The same conclusions hold for [μ2](0,0) and [μβ](0,0) terms. Besides the modes n = 1 and n = 12 (n = 13), the modes n = 10 and n = 11, which correspond to C–N stretching and play a minor role in the BK terms that contain a normal mode derivative of μ, also have a major contribution to [α2](0,0).
 | ||
| Fig. 5 The convergence of the [μα](0,0)zzz term as a function of normal modes for ϕ = 0.1 a.u. and ϕ = 0.2 a.u. All values are given in atomic units. | ||
In the case of γnr, as shown in Fig. 4, the anharmonic terms play a major role in confinement-induced changes of this property. In order to connect these changes with a particular mode of vibration, we evaluated the  term, up to n = 4 for each normal mode i (the data are presented in the ESI†). Anharmonic contributions to βnr and γnr are proportional to the second ([μ3](1,0), [μ2α](1,0), [μ2α](0,1)), third ([μ3](1,0), [μ4](1,1), [μ4](2,0)) and fourth ([μ4](0,2)) power of this term.62 Based on the data presented in the ESI† it is possible to link, albeit with some uncertainty, the pivotal role of intermolecular stretching vibration (n = 1) with confinement-induced changes in anharmonic contributions.
term, up to n = 4 for each normal mode i (the data are presented in the ESI†). Anharmonic contributions to βnr and γnr are proportional to the second ([μ3](1,0), [μ2α](1,0), [μ2α](0,1)), third ([μ3](1,0), [μ4](1,1), [μ4](2,0)) and fourth ([μ4](0,2)) power of this term.62 Based on the data presented in the ESI† it is possible to link, albeit with some uncertainty, the pivotal role of intermolecular stretching vibration (n = 1) with confinement-induced changes in anharmonic contributions.
4 Conclusions
In this theoretical study we presented the analysis of the effect of spatial confinement on the electronic and vibrational contributions to longitudinal (hyper)polarizabilities of two dimeric hydrogen bonded systems, namely HCN⋯HCN and HCN⋯HNC. All the properties in question were calculated at the CCSD(T)/aug-cc-pVTZ level of theory. A two-dimensional analytical potential of cylindrical symmetry was applied to model the effect of the confining environment (e.g. carbon nanotube). The vibrational contributions to the static and dynamic properties were evaluated employing the perturbation method of Bishop and Kirtman together with the finite-field nuclear relaxation method. The results obtained in this study made possible drawing several new observations regarding the effect of confinement on the properties of molecular complexes. The most important ones can be summarized as follows:– The influence of spatial confinement increases with increasing order of the electrical properties, both for electronic and vibrational contributions.
– The effect of spatial confinement is much larger in the case of electronic than vibrational contributions and this holds for each order of the electrical properties.
– The decrease in the static βnr upon the increase of confinement strength is mainly due to changes in the harmonic term, however, in the case of γnr the anharmonic terms contribute more to the drop of this property.
Finally, it should be underlined that this is the first study analysing the effect of spatial confinement on static and dynamic (hyper)polarizabilities of weakly-bound systems. Authors would like to express their hope that more studies will follow, so it will be possible to generalize the conclusions presented herein.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Polish National Science Centre (Grant No. 2015/19/B/ST4/01881). J. M. L. is grateful for financial support from the Spanish MINECO CTQ2014-52525-P and the Catalan DIUE 2014SGR931. Authors gratefully acknowledge Wroclaw Centre for Networking and Supercomputing for the generous allotment of computer time.References
- A. Radu, A. A. Kirakosyan, D. Laroze, H. M. Baghramyan and M. G. Barseghyan, J. Appl. Phys., 2014, 116, 093101 CrossRef.
- V. A. Fonoberov and A. A. Balandin, Appl. Phys. Lett., 2004, 85, 5971 CrossRef CAS.
- T. Feldtmann, L. Schneebeli, M. Kira and S. W. Koch, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 155319 CrossRef.
- F. Bureš, D. Cvejn, K. Melánová, L. Beneš, J. Svoboda, V. Zima, O. Pytela, T. Mikysek, Z. Ržičková, I. V. Kityk, A. Wojciechowski and N. AlZayedf, J. Mater. Chem. C, 2016, 4, 468–478 RSC.
- T. Song, J. Yu, Y. Cui, Y. Yanga and G. Qian, Dalton Trans., 2016, 45, 4218–4223 RSC.
- K. Kamada, Y. Tanamura, K. Ueno, K. Ohta and H. Misawa, J. Phys. Chem. C, 2007, 111, 11193–11198 CAS.
- J. Yu, Y. Cui, C. Wu, Y. Yang, Z. Wang, M. O'Keeffe, B. Chen and G. Qian, Angew. Chem., Int. Ed., 2012, 51, 10542–10545 CrossRef CAS PubMed.
- J. Yu, Y. Cui, H. Xu, Y. Yang, Z. Wang, B. Chen and G. Qian, Nat. Commun., 2013, 4, 2719 Search PubMed.
- A. Michels, J. de Boer and A. Bjil, Physica, 1937, 4, 981–994 CrossRef CAS.
- H. E. Montgomery, Chem. Phys. Lett., 2002, 352, 529–532 CrossRef CAS.
- P. Chattaraj and U. Sarkar, Chem. Phys. Lett., 2003, 372, 805–809 CrossRef CAS.
- T. Sako and G. H. F. Diercksen, J. Phys. B: At., Mol. Opt. Phys., 2003, 36, 743–759 Search PubMed.
- K. Strasburger and P. Naciążek, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 025002 CrossRef.
- F. Holka, M. Urban, P. Neogrády and J. Paldus, J. Chem. Phys., 2014, 141, 214303 CrossRef CAS PubMed.
- S. Mateos-Cortés, E. Ley-Koo and S. A. Cruz, Int. J. Quantum Chem., 2002, 86, 376–389 CrossRef.
- J. Marin and G. Muñoz, THEOCHEM, 1993, 287, 281–285 CrossRef.
- J. M. H. Lo, M. Klobukowski, D. Bielińska-Wąż, E. W. S. Schreiner and G. H. F. Diercksen, J. Phys. B: At., Mol. Opt. Phys., 2006, 39, 2385–2402 CrossRef CAS.
- J. M. H. Lo and M. Klobukowski, Chem. Phys., 2006, 328, 132–138 CrossRef CAS.
- W. Bartkowiak and K. Strasburger, THEOCHEM, 2010, 960, 93–97 CrossRef CAS.
- J. Kozłowska, R. Zaleśny and W. Bartkowiak, Chem. Phys., 2014, 428, 19–28 CrossRef.
- J. Kozłowska and W. Bartkowiak, Chem. Phys., 2014, 441, 83–92 CrossRef.
- J. Kozłowska, A. Roztoczyńska and W. Bartkowiak, Chem. Phys., 2015, 456, 98–105 CrossRef.
- R. Zaleśny, R. W. Góra, J. Kozłowska, J. M. Luis, H. Ågren and W. Bartkowiak, J. Chem. Theory Comput., 2013, 9, 3463–3472 CrossRef PubMed.
- R. Zaleśny, R. Góra, J. M. Luis and W. Bartkowiak, Phys. Chem. Chem. Phys., 2015, 17, 21782–21786 RSC.
- A. Roztoczyńska, J. Kozłowska, P. Lipkowski and W. Bartkowiak, Chem. Phys. Lett., 2014, 608, 264–268 CrossRef.
- M. Chołuj and W. Bartkowiak, Chem. Phys. Lett., 2016, 663, 84–89 CrossRef.
- P. Macak, Y. Luo, P. Norman and H. Ågren, J. Chem. Phys., 2000, 113, 7055–7061 CrossRef CAS.
- D. M. Bishop, J. M. Luis and B. Kirtman, J. Chem. Phys., 2002, 116, 9729–9739 CrossRef CAS.
- E. Kamarchik and A. I. Krylov, J. Phys. Chem. Lett., 2011, 2, 488–492 CrossRef CAS.
- B. Kirtman, B. Champagne and J. M. Luis, J. Comput. Chem., 2000, 21, 1572–1588 CrossRef CAS.
- D. Tzeli, G. Theodorakopoulos, I. D. Petsalakis, D. Ajami and J. Rebek, Jr, J. Am. Chem. Soc., 2011, 133, 16977–16985 CrossRef CAS PubMed.
- W. Jiang, K. Tiefenbacher, D. Ajami and J. Rebek, Jr., Chem. Sci., 2012, 3, 3022–3025 RSC.
- D. Tzeli, I. D. Petsalakis, G. Theodorakopoulos, D. Ajami, W. Jiang and J. Rebek, Jr, Chem. Phys. Lett., 2012, 548, 55–59 CrossRef CAS.
- D. Ajami, H. Dube and J. Rebek, Jr, J. Am. Chem. Soc., 2011, 133, 9689–9691 CrossRef CAS PubMed.
- A. J. Sadlej and M. Jabłoński, Chem. Phys. Lett., 2008, 436, 322–326 Search PubMed.
- M. Jabłoński and M. Sola, J. Phys. Chem. A, 2012, 114, 10253–10260 CrossRef PubMed.
- D. Ajami, P. M. Tolstoy, H. Dube, S. Odermatt, B. Koeppe, J. Guo, H.-H. Limbach and J. Rebek Jr., Angew. Chem., Int. Ed., 2011, 50, 528–531 CrossRef CAS PubMed.
- H. Shimizu, Physica, 1986, 139, 479–481 Search PubMed.
- W. Wang, D. Wang, Y. Zhang, B. Ji and A. Tian, J. Chem. Phys., 2011, 134, 054317 CrossRef PubMed.
- Y. J. Wang and L. Y. Wang, Int. J. Quantum Chem., 2011, 111, 4465–4471 CrossRef CAS.
- C. N. Ramachandran and N. Sathyamurthy, Chem. Phys. Lett., 2005, 410, 348–351 CrossRef CAS.
- M. Khatua, S. Pan and P. K. Chattaraj, Chem. Phys. Lett., 2014, 616–617, 49–54 CrossRef CAS.
- P. Lipkowski, J. Kozłowska, A. Roztoczyńska and W. Bartkowiak, Phys. Chem. Chem. Phys., 2014, 16, 1430–1440 RSC.
- A. Roztoczyńska, J. Kozłowska, P. Lipkowski and W. Bartkowiak, Phys. Chem. Chem. Phys., 2016, 18, 2417–2427 RSC.
- D. Bishop, Adv. Chem. Phys., 1998, 104, 1–40 CrossRef CAS.
- B. Kirtman, J. M. Luis and D. M. Bishop, J. Chem. Phys., 1998, 108, 10008–10012 CrossRef CAS.
- D. M. Bishop and B. Kirtman, J. Chem. Phys., 1991, 95, 2646 CrossRef CAS.
- D. M. Bishop, J. M. Luis and B. Kirtman, J. Chem. Phys., 1998, 108, 10008–10012 CrossRef.
- D. M. Bishop, M. Hasan and B. Kirtman, J. Chem. Phys., 1995, 103, 4157–4159 CrossRef CAS.
- J. M. Luis, M. Duran, J. L. Andrés, B. Champagne and B. Kirtman, J. Chem. Phys., 1999, 111, 875–884 CrossRef CAS.
- C. Eckart, Phys. Rev., 1926, 28, 711 CrossRef.
- H. Rutishauser, Numerische Mathematik, 1963, 5, 48 CrossRef.
- M. Medved, M. Stachová, D. Jacquemin, J.-M. André and E. A. Perpète, THEOCHEM, 2007, 847, 39–46 CrossRef CAS.
- J. Kongsted and O. Christiansen, J. Chem. Phys., 2007, 127, 154315 CrossRef PubMed.
- R. Zaleśny, A. Baranowska-Łączkowska, M. Medveď and J. M. Luis, J. Chem. Theory Comput., 2015, 11, 4119–4128 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN 09 Revision D.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- A. Heikkilä and J. Lundell, J. Phys. Chem. A, 2000, 104, 6637–6643 CrossRef.
- R. C. Dougherty, J. Chem. Phys., 1998, 109, 7372–7378 CrossRef CAS.
- R. Cammi, V. Verdolino, B. Mennucci and J. Tomasi, Chem. Phys., 2008, 344, 135–141 CrossRef CAS.
- R. Cammi, C. Cappelli, B. Mennucci and J. Tomasi, J. Chem. Phys., 2012, 137, 154112 CrossRef CAS PubMed.
- I. Brandão, R. Rivelino, T. L. Fonseca and M. A. Castro, Chem. Phys. Lett., 2013, 580, 9–13 CrossRef.
- J. M. L. J. Martí, M. Duran, J. L. Andrés and B. Kirtman, J. Chem. Phys., 1998, 108, 4123–4130 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp04259k |
| This journal is © the Owner Societies 2017 |
