Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Low-lying, Rydberg states of polycyclic aromatic hydrocarbons (PAHs) and cyclic alkanes†
E.
Bohl‡
a,
B.
Mignolet‡
 b,
J. O.
Johansson
b,
J. O.
Johansson
 a,
F.
Remacle
a,
F.
Remacle
 b and
E. E. B.
Campbell
b and
E. E. B.
Campbell
 *ac
*ac
aEaStCHEM, School of Chemistry, University of Edinburgh, Edinburgh, EH9 3FJ, UK. E-mail: eleanor.campbell@ed.ac.uk
bTheoretical Physical Chemistry, UR MolSYS, B6c, University of Liège, B4000, Liège, Belgium
cDivision of Quantum Phases & Devices, School of Physics, Konkuk University, Seoul, 05029, Korea
First published on 24th August 2017
Abstract
TD-DFT calculations of low-lying, Rydberg states of a series of polycyclic hydrocarbons and cyclic alkanes are presented. Systematic variations in binding energies and photoelectron angular distributions for the first members of the s, p and d Rydberg series are predicted for increasing molecular complexity. Calculated binding energies are found to be in very good agreement with literature values where they exist for comparison. Experimental angle-resolved photoelectron spectroscopy results are presented for coronene, again showing very good agreement with theoretical predictions of binding energies and also for photoelectron angular distributions. The Dyson orbitals for the small “hollow” carbon structures, cubane, adamantane and dodecahedrane, are shown to have close similarities to atomic s, p and d orbitals, similar to the superatom molecular orbitals (SAMOs) reported for fullerenes, indicating that these low-lying, diffuse states are not restricted to π-conjugated molecules.
1. Introduction
Highly diffuse atomic-like molecular orbitals, with electron binding energies close to the lowest excited valence states, have been the subject of recent interest since the report of spectacular images of such states in low-temperature scanning tunnel spectroscopy studies of C60.1 These orbitals were given the name “superatom molecular orbital” (SAMO) due to their similarity with hydrogenic atomic orbitals. Evidence was also found for the existence of excited fullerene SAMO states in fs laser photoelectron spectroscopy experiments.2–5 Theoretical studies have confirmed the unusual nature of these lowest-lying members of Rydberg series in fullerenes, showing a deviation in the binding energies extrapolated from higher-lying, more conventional Rydberg states due to the proximity to the molecular core and also having a significant component of the electron density inside the hollow cage.6 SAMO states have also been predicted in theoretical calculations of fullerene anions.7 Interest in these exotic, excited electronic states has been sparked by their predicted ability to form highly diffuse nearly-free electron bands in the solid state,8 making them potentially interesting for applications within molecular electronics. They are also of fundamental interest due to their intrinsic beauty and their potential role in astrochemistry.9An understanding of the photophysics of excited electronic states of polycyclic aromatic hydrocarbons (PAH) is also of considerable interest for both molecular electronics10 and astrochemistry.11 Although the spectroscopy of these systems has been extensively studied for many years, relatively little is known about the low-lying Rydberg states of PAHs. Due to the proximity of the lowest members of Rydberg series to the molecular core, they can deviate from pure Rydberg states and be mixed with valence states of similar energy. A number of transitions observed in UV absorption spectroscopy and electron energy loss spectroscopy have been assigned to these states.12 Bréchignac et al. have recently reported photoelectron–photoion coincidence measurements on coronene that provide information on autoionising resonances that have been attributed to a p-like Rydberg series converging on an excited cation state.13 Weber and co-workers identified peak structure in fs photoelectron spectroscopy (Rydberg Fingerprint Spectroscopy) experiments of a number of PAHs that was attributed to low-lying Rydberg states. In these studies, the angular momenta of the states were assigned on the basis of the measured quantum defect that was indicative of the molecular structure. The photoelectron spectra were proposed as a means of “molecular fingerprinting”.14 TD-DFT studies have concentrated on individual valence transitions15 or on reproducing experimental spectra16 without focusing specifically on the molecular orbital nature of the excited states. A G0W0 theoretical study has predicted diffuse low-lying Rydberg states in corannulene and other “bowl-shaped” molecules and considered the potential for formation of nearly-free electron bands in the solid state, similar to the fullerene SAMOs, but with a much lower excitation energy, making them potentially more attractive for molecular electronics applications.17
In this paper we use a combination of TD-DFT and fs laser photoelectron spectroscopy to explore the properties of low-lying Rydberg states of PAH molecules and cyclic alkanes. We predict that all these molecules exhibit highly diffuse low angular momentum Rydberg states that extend across the entire molecule and have beautifully simple orbital geometries, showing close similarities with the fullerene SAMOs. We show that the calculations can reproduce the experimental binding energies of these states and we provide a detailed comparison with experimental photoelectron angular distributions obtained for coronene. The results show that these intriguing and beautiful excited states are not restricted to curved systems17 or even to conjugated molecules. The photoelectron angular distributions and electron density distributions of the lowest members of the Rydberg series of small cage alkanes such as cubane, adamantine and dodecahedrane, indicate that the use of the term SAMO, coined for fullerenes, could be an appropriate description also for these hollow, non-conjugated molecules.
2. Methods
2.1. Computational
The quantum chemistry Kohn–Sham DFT implementation was used as included in Gaussian 09 with the CAM-B3LYP functional.18 This functional gives relatively accurate excitation energies for local, charge transfer and Rydberg states19 and the Dyson orbitals computed with this functional are in reasonable agreement with Dyson orbitals computed at the EOM-CC level.20 A large basis set including diffuse basis functions was used to describe the PAH excited electronic states. Since the binding energies of the electronic states of interest are expected to lie within a range of 0–3 eV, TD-DFT computations for large bands of up to 100 excited states were carried out at the TD-DFT/CAM-B3LYP level with the 6-31++G(d,p) basis set augmented with a set of diffuse s and p functions on each carbon atom (with an exponent of 0.01095).21 The ionisation energies (I.E.) of the PAHs and binding energies (B.E.) of the low-lying Rydberg states of naphthalene and coronene computed at this level of theory are in good agreement with experimental data (Table 1 and ESI†).| Molecule | Theor. B.E./eV | Theor. I.E./eV | Exp I.E./eV | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| s | pz | px | py | d | Vert. | Adiab. | Vert. | Adiab. | ||
| Experimental values:a Recommended value of the adiabatic I.E. from the NIST Chemistry WebBook.34b Schmidt.35c Zhang et al.36d Clar et al.37e Akiyama et al.38f Clar and Schmidt.39g Bréchignac et al.13h Bishof et al.40i Worrell et al.41 | ||||||||||
| Benzene | C6H6 | 2.90 | 2.42 | 2.33 | 2.33 | 1.48–1.74 | 9.27 | 9.12 | 9.24 ± 0.02b | 9.24378 ± 0.00007a |
| Naphthalene | C10H8 | 2.50 | 2.14 | 2.12 | 2.11 | 1.36–1.58 | 8.05 | 7.94 | 8.14b | 8.144 ± 0.001a |
| Anthracene | C14H10 | 2.23 | 1.97 | 1.92 | 1.90 | 1.25–1.50 | 7.26 | 7.16 | 7.41b | 7.439 ± 0.006a |
| Tetracene | C18H12 | 2.05 | 1.85 | 1.76 | 1.75 | 1.07–1.46 | 6.72 | 6.64 | 6.97b | 6.93c |
| Pentacene | C22H14 | 1.92 | 1.76 | 1.64 | 1.63 | 0.88–1.39 | 6.34 | 6.26 | 6.61 ± 0.02b | 6.63 ± 0.05a |
| Hexacene | C26H16 | 1.83 | 1.68 | 1.55 | 1.55 | 0.97–1.33 | 6.05 | 5.98 | 6.36 ± 0.02b | 6.36d |
| Phenanthrene | C14H10 | 2.00 | 1.60 | 1.68 | 1.62 | 1.19–1.47 | 7.84 | 7.69 | 7.86 ± 0.02b | 7.891 ± 0.001a |
| Pyrene | C16H10 | 2.19 | 1.86 | 1.80 | 1.90 | 1.04–1.49 | 7.31 | 7.20 | 7.42e | 7.426 ± 0.001a |
| Coronene | C24H12 | 1.98 | 1.67 | 1.80 | 1.72 | 1.09–1.40 | 7.29 | 7.20 | 7.29f | 7.310 ± 0.005g |
| Cubane | C8H8 | 2.74 | 2.62 | 2.62 | 2.62 | 1.56–1.67 | 9.50 | 8.78 | 9.00h | 8.6 ± 0.1a |
| Adamantane | C10H16 | 2.68 | 2.09 | 2.13 | 2.08 | 1.52–1.66 | 9.75 | 9.52 | 9.75 ± 0.02i | 9.25 ± 0.04a |
| Dodecahedrane | C20H20 | 2.70 | 2.19 | 2.13 | 2.13 | 1.44–1.58 | 9.31 | 9.12 | — | — |
| Dodecahedrene | C20 | 2.77 | 2.46 | 2.56 | 2.56 | 1.34–1.36 | 7.35 | 7.12 | — | — |
The photoelectron angular distributions of the neutral PAHs are computed from their Dyson orbitals,22–24 which are defined as the overlap between the wavefunction of a neutral electronic state with a cationic electronic state. We computed the Dyson orbital of each TD-DFT excited state corresponding to its photoionisation to the cationic ground state. Since the excited states are often composed of several orbital excitations, the Dyson orbitals are a linear combination of molecular orbitals, which can give them a complex shape24,25 that is different from the DFT Kohn–Sham orbitals used to build the excitations in TDDFT. For the Rydberg states the Dyson orbitals are typically composed of several Rydberg orbitals, corresponding to HOMO-Rydberg orbital transitions of the same symmetry, with the lower excited states often containing some significant contribution from excited valence molecular orbitals.26
A central quantity in the computation of the photoelectron angular distributions and photoionisation widths (proportional to the photoionisation cross-sections) is the photoionisation matrix element,24,25 which is the dipolar coupling element between the neutral wavefunction and the wavefunction of an ionised state. This matrix element can be rewritten as the dipolar coupling of the Dyson orbital (i.e. the orbital from which the electron is ionised) with the wavefunction of the ionised electron, which is taken here as a plane wave. The photoionisation widths and photoelectron angular distributions were computed from the photoionisation matrix elements at the equilibrium geometry of an oriented molecule for several orientations of the electric field using an in-house code.6 Then we randomly select 600 orientations of the electric field and use Euler rotations to rotate the oriented molecule and its angular distribution for each electric field polarisation so that we obtain a set of randomly oriented molecules with an electric field polarised in a single direction. The photoionisation widths and photoelectron angular distributions reported below take into account the averaging over molecular orientation. From the photoelectron angular distributions we can determine the anisotropy parameter as outlined in Section 3.2 of the paper. Additional information can be found in the ESI† and in a previous study of the SAMO excited states of C60.6
2.2. Experimental
The experimental apparatus consists of a velocity map imaging photoelectron spectrometer and a time-of-flight mass spectrometer, which has been explained in more detail previously.3 Coronene was purchased from Sigma-Aldrich (97% purity) and was used without further purification. The coronene sample was heated in an oven to about 180–195 °C to create an effusive molecular beam. The output from an amplified Ti:Sapphire laser system (800 nm, 120 fs pulse duration, 1 kHz repetition rate) was frequency doubled using a BBO crystal to provide pulses at a wavelength of 400 nm. A fused silica lens (50 cm focal length) was used to focus the laser beam into the spectrometer chamber. The laser intensity was adjusted by using a continuously variable neutral density filter.The effusive molecular beam was intersected at right angles by the laser and the photoelectrons or ions extracted perpendicular to both the laser beam and the molecular beam. The photoelectrons were imaged onto a position sensitive, velocity map imaging detector as described in detail previously.3 Centroiding was applied27 while recording the images which were integrated over 107 laser pulses. The recorded images were inverted using a modified POP inversion algorithm28 which included Legendre polynomials up to the 10th order.29 The inversion was checked for consistency by ensuring that the same peak structure was obtained in the photoelectron spectra when the data were inverted using BASEX.30 The calibration of the energy scale was achieved by recording the multiphoton ionisation of xenon, resulting in well-known peaks.31 A detailed description of the data analysis is given by Johansson et al.3
The technique used to probe the low-lying Rydberg structure has been called Rydberg Fingerprint Spectroscopy.5,14 By using fs laser pulses, multiphoton excitation leads to an incoherent population of a series of Rydberg states that can be single-photon ionised within the same laser pulse. The technique can be used to obtain resolved peak structure even for vibrationally hot molecules since the final, ionising transition conserves the vibrational quantum number. Rydberg structure is preferentially seen in the photoelectron spectra due to the much higher probability for ionising the Rydberg states within the timescale of the laser pulse compared to the more densely populated excited valence states.6
3. Results and discussions
3.1. TD-DFT calculations
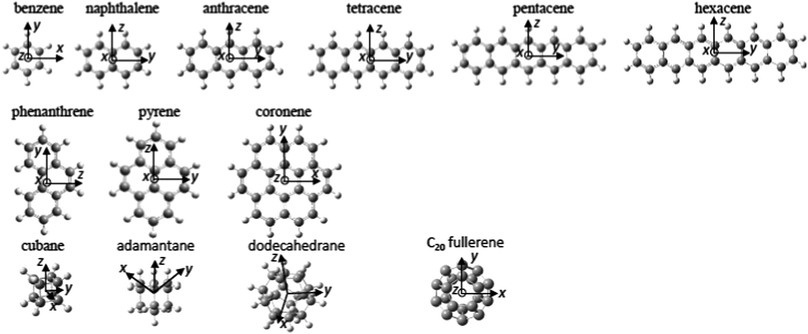
The structures of the molecules investigated in this study are shown in Fig. 1. Three families were investigated: the “1D” PAH family consisting of benzene to hexacene, the “2D” PAH family of phenanthrene to coronene and the “3D” family consisting of the cyclic alkanes, cubane, adamantine, and dodecahedrane as well as the C20 fullerene, dodecahedrene. Table 1 displays the excited Rydberg binding energies (determined from the difference between the calculated values for the relevant Dyson orbitals and the vertical ionisation energies) calculated at the TD-DFT/CAM-B3LYP/6-31(2+)+G(d,p) level for all investigated molecules, along with experimental values from the literature. The binding energy data for the first s, p and d Rydberg bands is also shown graphically in Fig. 2a where the development of the binding energies with increasing molecular complexity can be easily seen. The “1D” and “2D” PAH families have very similar binding energies for the same number of carbon atoms with the binding energy generally decreasing with increasing molecular size. The binding energies for the “3D” series are slightly higher with an almost constant binding energy for the s Rydberg state for the range of investigated molecules. The s and d binding energies are very close for the hydrogenated dodecahedrane and the “bare” fullerene dodecahedrene but the p-Rydberg binding energy appears significantly lower for dodecahedrane. Since the ionisation energies differ by 2 eV, this implies that the excitation energies needed to access the Rydberg states in the “bare” fullerene are ca. 2 eV lower than for C20H20. The “error bars” indicate the calculated or experimentally determined energy spread of the corresponding Rydberg band. The agreement between experimental and calculated binding energies is very good. Fig. 2a also shows the previously reported theoretical and experimental values for the SAMOs of C60, C70, C82 and C84 fullerenes for comparison.6 The theoretical values for C60 and above were calculated at the TD-DFT/B3LYP/6-31+G(d) level (triangles)3 and also TD-DFT/CAM-B3LYP 6-31+G(d)-Bq(6-31(6+)G(d)) level for C60 (diamonds).6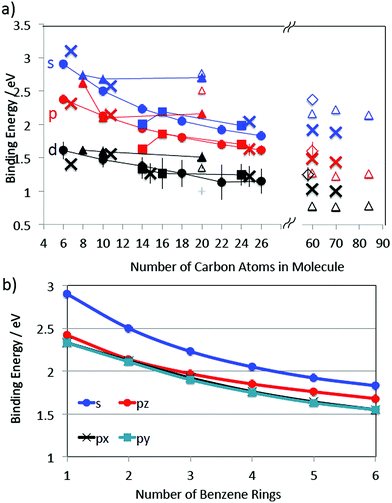 | ||
| Fig. 2 (a) Binding energies of the lowest-lying s, p and d Rydberg states as a function of molecular size. The straight lines connect molecules from the same “family” (Fig. 1) and are to guide the eye. Circles: Benzene to hexacene, filled squares: phenanthrene to coronene, filled triangles: cubane to dodecahedrane, empty triangles and empty diamonds: “bare” fullerenes, crosses: experimental data. The experimental PAH values have been shifted slightly along the x-axis for clarity. The vertical lines indicate the spread in binding energies for the given Rydberg band. Experimental values: benzene,12 naphthalene,14 anthracene,33 coronene from this study. Previously reported values for fullerenes are included for comparison.3 (b) Computed binding energies of the s, px, py and pz Rydberg states of the 1D PAH family (px values are almost identical to py). | ||
The Dyson orbitals of the lowest s and p Rydberg states are shown in Fig. 3 for some of the investigated molecules. They all show diffuse, hydrogenic character, with, for most of them, two nodal surfaces corresponding to quantum numbers n = 3, 4 and 5 for s, p and d bands respectively, similar to the previously investigated SAMO states of the fullerenes.6 Experimental data on the binding energies of the lowest s, p and d Rydberg states of naphthalene is available from Rydberg Fingerprint Spectroscopy studies,14 shown in Fig. 2, and is in good agreement with the calculated values (2.57 eV, 2.14 eV and 1.55 eV respectively for the s, p and d bands). There is also information available from absorption spectroscopy assigning broad bands at 2.55 ± 0.09 eV and 2.35 ± 0.09 eV to the s and p Rydberg states, respectively.32 Rydberg structure was observed in fs photoionisation studies of anthracene at binding energies of 1.15 eV and 1.38 eV33 that we attribute to the lowest-lying d Rydberg state due to the good agreement with the calculations.
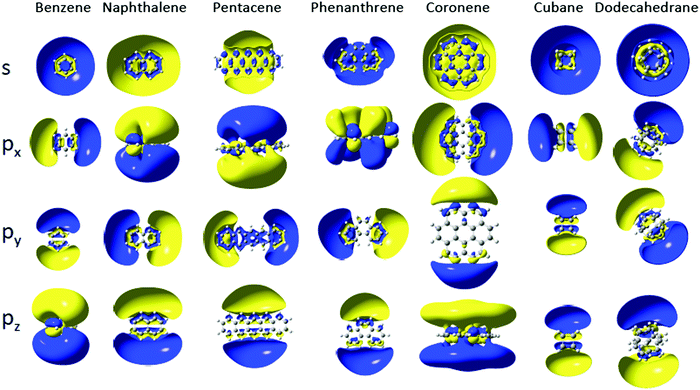 | ||
| Fig. 3 Cut in the Dyson orbitals of s and p Rydberg states of selected molecules (isocontour of 0.005 |e|/a03). | ||
For the 1D PAH series from naphthalene to hexacene, the binding energies of the s and p Rydberg states decrease smoothly as the number of benzene rings present in the molecule increases, Fig. 2b.
The py and px Rydberg states, which are oriented respectively along the molecular plane and perpendicular to it, have very close binding energies (within 0.02 eV) and the gap with the s Rydberg state is constant within 0.1 eV (Fig. 2b and Table 1) in the series. The py and px Rydberg states are not degenerate by symmetry as they belong to different irreducible representation of the D2h point group (B2u for py and B3u for px). The third component of the p Rydberg, pz (B1u), has a binding energy that does not decrease as quickly as for the px and py components of the p Rydberg band, suggesting it is less affected by the growing size of the PAH. The spatial delocalization of the pz orbital along the molecule increases as the PAH becomes larger but the distance between the positive and negative lobes remains similar unlike for the py Rydberg for example (Fig. 3). The benzene molecule is also categorized in the 1D PAH family but the binding energy of the s and p Rydberg states are larger than for the other PAHs and the two p components in the plane are degenerate by symmetry. Overall all the s and p Rydberg states shown in Fig. 3 exhibit a mixed character with binding σ or π valence orbitals, which is characteristic for low-lying molecular Rydberg states.26
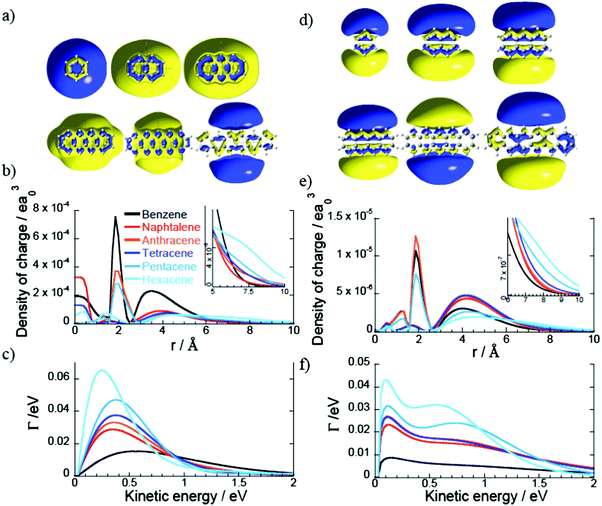
The Dyson orbitals of the PAH Rydberg states strongly vary as the number of benzene rings increases for the 1D family. For instance the benzene molecule has an almost spherical s Dyson orbital while for the naphthalene, anthracene and tetracene molecules (respectively two, three and four benzene rings) the s orbital exhibits an elliptical shape and for the larger PAHs, the Dyson orbital has a doughnut shape (or two lobes) centred at the centre of mass (Fig. 4a). As the number of benzene rings increases in the molecule, the s Rydberg orbital becomes more diffuse (Fig. 4b) and so its binding energy decreases. The breaking of the spherical symmetry could also destabilize the states. A similar trend is observed for the pz Rydberg state where the binding energy decreases as the size of the PAH increases (Fig. 4e and f). It should also be pointed out that the pz orbital is not delocalized over the whole molecule, it spreads at most over four benzene rings.
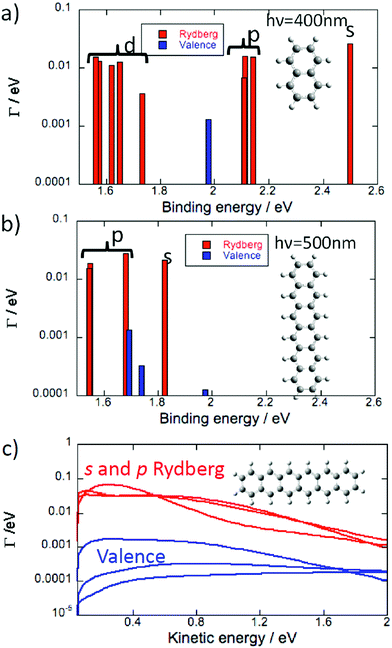
Rydberg fingerprint spectroscopy, the experimental technique used here to probe the binding energies and photoelectron angular distributions of the low-lying Rydberg states, relies on the photoionisation lifetimes of the Rydberg states being much shorter than those of excited valence states.6,42 When this is the case, the peak structure due to population and ionisation of Rydberg states dominates over the lower signal from the high density of populated valence excited states that can also contribute to a thermal emission background. The photoionisation widths, Γ, that are proportional to the photoionisation cross sections and inversely proportional to the photoionisation lifetimes, were computed for the excited states of naphthalene and hexacene (Fig. 5a and b) for photon energies appropriate for fs laser studies and a laser intensity of 1012 W cm−2. Since the widths vary with the kinetic energy of the ionised electron, they have been computed for ionisation by a 400 nm photon for naphthalene and a 500 nm photon for hexacene so that the kinetic energy of the electron ionised from the s Rydberg is around 0.6 eV in both cases. The widths of the Rydberg states are between one and three orders of magnitude larger than those of the valence states lying in the vicinity of these Rydberg states. This is less than for C606 but is still sufficient to provide confidence that the Rydberg states will be clearly visible in the fs laser photoelectron spectrum. The photoionisation widths for the Rydberg states are around one order of magnitude smaller in magnitude to those of the fullerene SAMOs while the widths of the valence states are of the same order of magnitude. Unlike in fullerenes, the density of valence states between the Rydberg bands is smaller for the PAHs, probably because of the smaller size of the PAHs.
The photoionisation widths of the Rydberg states quickly decrease when the ionised electron kinetic energy increases (Fig. 5c), unlike the valence state widths that are more or less constant in the energy domain 0–2 eV. Therefore the gap between the widths of the Rydberg and valence states decreases when the photon energy increases. This indicates that the underlying signal from photoionised valence states could obscure the Rydberg structure as the electron kinetic energy increases.
For the 1D PAH family, we observe an increase of the photoionisation widths of the s and pz Rydberg states with the size of the molecule (Fig. 4c). For instance the widths of the Rydberg states of hexacene are three times larger than the ones of benzene because the Dyson orbitals of the hexacene Rydberg states are more diffuse than the ones of benzene.
3.2. Photoelectron spectra and angular distributions: coronene comparison
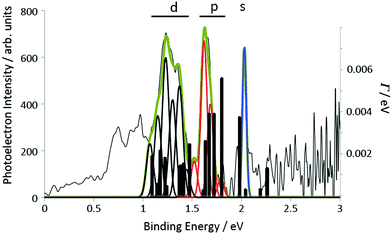
On the basis of the calculations discussed in the previous section, coronene was chosen as an example of a relatively large PAH molecule where one could expect the Rydberg structure to be visible in the fs photoelectron spectra. The experimental photoelectron angular distributions (PAD) provide a stringent test of the theoretical predictions. Fig. 6a provides two examples of photoelectron spectra obtained for 400 nm excitation at two different laser intensities, 7 × 1011 W cm−2 and 4.6 × 1012 W cm−2. Both spectra show simple peak structure superimposed on a featureless, decreasing background spectrum. The featureless background spectrum was observed previously for 800 nm, >3 × 1012 W cm−2, 150 fs photoionisation and attributed to the emission of thermal electrons prior to equilibration between the electronic and vibrational degrees of freedom,43 similar to what is observed for fullerenes.5 No Rydberg structure was resolved in these earlier coronene fs laser experiments.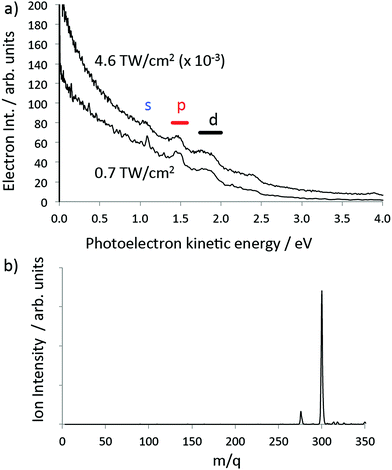 | ||
| Fig. 6 Experimental data for coronene obtained with a 120 fs, 400 nm laser pulse (a) angle-integrated photoelectron spectra for two values of the laser intensity. The structure due to photoionisation of the s, p and d lowest Rydberg bands is indicated. (b) Mass spectrum obtained for 7 × 1011 W cm−2. The small peak at 276u is due to 1,12-benzoperylene impurity.13 | ||
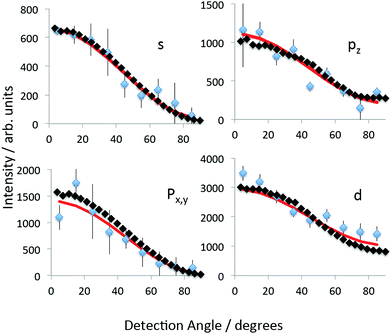
Three peaks can be clearly seen in the photoelectron spectra that are assigned to the s, p and d Rydberg bands due to the good agreement with the calculated binding energies (Fig. 2a and Table 1). In order to ensure that there is no influence in the photoelectron spectra from multiple ionisation and to minimise the thermal background and effect of high laser intensities, all further analysis was carried out for the lower laser intensity data (7 × 1011 W cm−2). A mass spectrum obtained under identical laser conditions is shown in Fig. 6b, clearly showing that only the parent molecular ion and a small impurity ion peak are present. The experimental binding energies are obtained from the photoelectron kinetic energies (ε) by assuming that the Rydberg states are single-photon ionised: B.E. = hν − ε, where ν is the laser frequency. The peaks are fitted with Gaussian functions. Fig. 7 illustrates the peak fitting for the angle-integrated spectrum that has had the background thermal distribution subtracted along with an additional featureless background for photoelectron energies <3.1 eV, attributed to ionisation from excited valence states (see ESI† for more details on the background subtraction). A single Gaussian function is used to fit the s-peak while multiple functions are used for the p and d bands. The narrow s-peak is found at a binding energy of 2.04 ± 0.02 eV. The quoted error accounts for errors in the calibration of the kinetic energy scale and peak fitting errors (±0.01 eV) and the bandwidth of the 120 fs laser pulse (±0.012 eV). The central p-band peak at a binding energy of 1.63 ± 0.02 eV is assigned to the pz Rydberg state while the peaks on either side at 1.53 ± 0.02 eV, 1.71 ± 0.02 eV and 1.79 ± 0.02 eV are assigned to py, mixed px–py and px, based on comparison with the calculations. Although six peaks have been used to fit the d-band, we have refrained from assigning these peaks to different d-states and report only the range of binding energies, 1.08 eV to 1.44 eV, and the angular distributions from the sum of these fitted peaks.
In order to extract the PADs, the inverted VMI image is divided into 10° segments. The background is subtracted from each segment and the peak structure is fitted using the Gaussian functions shown in Fig. 7. The peak widths were constrained to be constant but the central position was allowed to vary. The extracted integrated intensities of the relevant Gaussians are plotted as a function of the angle, θ, with respect to the laser polarisation direction, in Fig. 8. The sum of px and py and of all six fitted d-peaks has been plotted.
Since the excited states are incoherently populated, the final step in the photoionisation process can simply be considered to be a single-photon ionisation from the excited states. For a single pulse of linearly polarized light interacting with a randomly oriented target this results in a PAD, I(θ, ε), for a specific photoelectron kinetic energy, ε, according to44
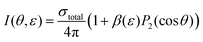 | (1) |
| Rydberg state | Expt. B.E./eV | Theor. B.E./eV | ε/eV | β exp | β theor |
|---|---|---|---|---|---|
| s | 2.04 ± 0.02 | 1.98 | 1.06 ± 0.01 | 1.7 ± 0.2 | 1.71 |
| pz | 1.63 ± 0.02 | 1.66 | 1.47 ± 0.01 | 1.2 ± 0.2 | 0.96 |
| px | 1.79 ± 0.02 | 1.79 | 1.31 ± 0.01 | 1.9 ± 0.4 | 1.81 |
| py | 1.53 ± 0.02 | 1.63 | 1.57 ± 0.01 | 2.3 ± 0.4 | 1.84 |
| px, py mix | 1.71 ± 0.02 | 1.72 | 1.39 ± 0.01 | 2.0 ± 0.5 | |
| Σpx, py | 1.66 ± 0.09 | 1.63–1.79 | 1.44 ± 0.08 | 1.8 ± 0.3 | 1.83 |
| Σd | 1.22 ± 0.19 | 1.09–1.47 | 1.88 ± 0.18 | 0.8 ± 0.15 | 0.94 |
3.3. Asymmetry parameters
The theoretical asymmetry parameters are plotted for the 1D, 2D and 3D PAH molecules (Fig. 1) in Fig. 9. The crosses indicate the experimental values for coronene, also given in Table 2. The left hand plots are for the quasi-linear series from benzene to hexacene. The almost spherical s-state of benzene has a β = 2, independent of ε, which is the value expected for single photon ionisation of an atomic s-state. The other 1D PAHs do not have a spherical symmetry and the β value clearly deviates from the value of β = 2. This is indicative of the lower D2h symmetry of these molecules. There is a systematic shift in the predicted minimum in β towards lower photoelectron kinetic energies as the molecular size increases and the shape of the Dyson orbitals clearly deviates from a spherical atomic s orbital (see Fig. 4a). The calculated and experimental values for C60 are consistent with β ≈ 26 as is the calculated β for the s-states of cubane, adamantane and dodecahedrane (right hand plot). The low-lying Rydberg states of the hollow “3D” carbon molecules have an electron density distribution that is more purely atomic-like, thus perhaps justifying the introduction of the term SAMO (superatom molecular orbital)1 to describe them. However, for cubane and adamantane, the molecules are too small to allow for significant electron density inside the cage which is a distinguishing feature of the fullerene SAMOs.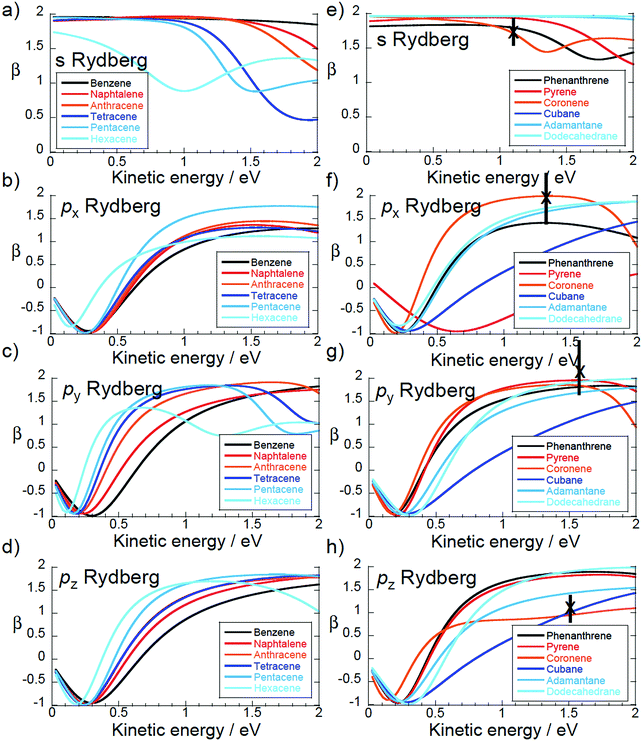 | ||
| Fig. 9 Calculated β. Left: “1D” series benzene to hexacene. Right: “2D” series phenanthrene to coronene plus “3D” cubane to dodecahedrane. Crosses: experimental values for coronene. | ||
The asymmetry parameter for the px states of the quasi-linear series approaches a similar kinetic energy dependence, β(ε), as the molecular size increases. This is understandable since the x-axis is perpendicular to the molecular plane. The variation of the asymmetry parameter for the px states is similar to that of the pz and py states except that it reaches a plateau around β ≈ 1 while the pz and py states reach plateaus around β ≈ 2 (in the energy range 1–2 eV). This is also the case for the px state of phenanthrene and pz state of coronene that are perpendicular to the molecular plane. In the case of coronene, it is this difference in the behaviour of the asymmetry parameter that allows the px, py and pz peaks to be clearly assigned in the measured spectrum.
In the quasi-two-dimensional series (phenanthrene to coronene) there is a systematic variation in both the px and the pyβ values, as one might expect from the molecular structures (Fig. 1). Note that for this series the arrangement of the x, y and z axes changes depending on the molecular symmetry (Fig. 1).
4. Conclusions
We report TD-DFT/CAM-B3LYP/6-31(2+)+G(d,p) calculations on a wide range of PAH molecules and cubic alkanes in order to probe the properties of the lowest members of diffuse molecular Rydberg states. We show the occurrence of diffuse atomic-like molecular orbitals with similarities to the “SAMOs” reported for fullerenes6,8 and corannulene.17 The calculations are compared to fs photoelectron spectroscopy studies of coronene, showing excellent agreement with both the electron binding energies and the photoelectron angular distributions. The predictive nature of the calculations could help identify molecules with promising properties for electronic applications and also contribute to elucidating the role of PAHs in astrochemistry.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors thank A. V. Bulgakov for helpful discussions. E. B., J. O. J. and E. E. B. C. gratefully acknowledge financial support from the Leverhulme Foundation (RPF-298 “PES of hollow nanomaterials”). JOJ is a Royal Society of Edinburgh/BP Trust Research Fellow. BM and FR acknowledge support from the Fonds National de la Recherche Scientifique (FNRS), Belgium and from the Consortium des Equipements de Calcul Intensif (CECI) for computational resources (FNRS 2.5020.11) and of the FNRS research project T.0132.16.References
- M. Feng, J. Zhao and H. Petek, Science, 2008, 320, 359–362 CrossRef CAS PubMed.
- J. O. Johansson, G. G. Henderson, F. Remacle and E. E. B. Campbell, Phys. Rev. Lett., 2012, 108, 173401 CrossRef PubMed.
- J. O. Johansson, E. Bohl, G. G. Henderson, B. Mignolet, T. J. S. Dennis and F. Remacle, et al. , J. Chem. Phys., 2013, 139, 084309 CrossRef PubMed.
- H. Li, B. Mignolet, Z. Wang, K. J. Betsch, K. D. Carnes and I. Ben-Itzhak, et al. , J. Phys. Chem. Lett., 2016, 7, 4677–4682 CrossRef CAS PubMed.
- J. O. Johansson and E. E. B. Campbell, Chem. Soc. Rev., 2013, 42, 5661–5671 RSC.
- B. Mignolet, J. O. Johansson, E. E. B. Campbell and F. Remacle, ChemPhysChem, 2013, 14, 3332–3340 CrossRef CAS PubMed.
- V. K. Voora, L. S. Cederbaum and K. D. Jordan, J. Phys. Chem. Lett., 2013, 4, 849–853 CrossRef CAS PubMed.
- J. Zhao, M. Feng, J. L. Yang and H. Petek, ACS Nano, 2009, 3, 853–864 CrossRef CAS PubMed.
- A. Omont, Astron. Astrophys., 2016, 590, A52 CrossRef.
- X. Feng, W. Pisula and K. Müllen, Pure Appl. Chem., 2009, 81, 2203–2224 CrossRef CAS.
- A. G. G. M. Tielens, Annu. Rev. Astron. Astrophys., 2008, 46, 289–337 CrossRef CAS.
- M. B. Robin, Higher Excited States of Polyatomic Molecules, Academic Press, New York, 1974 Search PubMed.
- P. Bréchignac, G. A. Garcia, C. Falvo, C. Joblin, D. Kokkin and A. Bonnamy, et al. , J. Chem. Phys., 2014, 141, 164325 CrossRef PubMed.
- N. Kuthirummal and P. M. Weber, Chem. Phys. Lett., 2003, 378, 647–653 CrossRef CAS.
- M. Hammonds, A. Pathak and P. J. Sarre, Phys. Chem. Chem. Phys., 2009, 11, 4458–4464 RSC.
- G. Malloci, G. Mulas and C. Joblin, Astron. Astrophys., 2004, 426, 105–117 CrossRef CAS.
- L. Zoppi, L. Martin-Samos and K. K. Baldridge, Phys. Chem. Chem. Phys., 2015, 17, 6114–6121 RSC.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- M. J. G. Peach, P. Benfield, T. Helgaker and D. J. Tozer, J. Chem. Phys., 2008, 128, 44118 CrossRef PubMed.
- A. O. Gunina and A. I. Krylov, J. Phys. Chem. A, 2016, 120, 9841–9856 CrossRef CAS PubMed.
- J. A. Sonk and H. B. Schlegel, J. Phys. Chem. A, 2011, 115, 11832–11840 CrossRef CAS PubMed.
- B. T. Pickup, Chem. Phys., 1977, 19, 193–208 CrossRef CAS.
- G. M. Seabra, I. G. Kaplan, V. G. Zakrzewski and J. V. Ortiz, J. Chem. Phys., 2004, 121, 4143–4155 CrossRef CAS PubMed.
- C. M. Oana and A. I. Krylov, J. Chem. Phys., 2007, 127, 234106 CrossRef PubMed.
- C. M. Oana and A. I. Kryov, J. Chem. Phys., 2009, 131, 124114 CrossRef PubMed.
- H. Reisler and A. I. Krylov, Int. Rev. Phys. Chem., 2009, 28, 267–308 CrossRef CAS.
- B.-Y. Chang, R. C. Hoetzlein, J. A. Mueller, J. D. Geiser and P. I. Houston, Rev. Sci. Instrum., 1998, 69, 1665–1670 CrossRef CAS.
- G. M. Roberts, J. L. Nixon, J. Lecointre, E. Wrede and J. R. Verlet, Rev. Sci. Instrum., 2009, 80, 053104 CrossRef CAS PubMed.
- G. G. Henderson, Femtosecond Laser Studies of Fullerenes and Nanotubes, PhD thesis, University of Edinburgh, 2012 Search PubMed.
- V. Dribinski, A. Ossadtchi, V. A. Mandelshtam and H. Reisler, Rev. Sci. Instrum., 2002, 73, 2634–2642 CrossRef CAS.
- V. Schyja, T. Lang and H. Helm, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 57, 3692–3697 CrossRef CAS.
- G. A. George and G. C. Morris, J. Mol. Spectrosc., 1968, 26, 67–71 CrossRef CAS.
- M. Goto and K. Hansen, J. Chem. Phys., 2011, 135, 214310 CrossRef CAS PubMed.
- [12/05/2017]. Available from: http://webbook.nist.gov/chemistry/.
- W. Schmidt, J. Chem. Phys., 1977, 66, 828–845 CrossRef CAS.
- J. Zhang, L. Pei and W. Kong, J. Chem. Phys., 2008, 128, 104301 CrossRef PubMed.
- E. Clar, J. M. Robertson, R. Schlogl and W. Scmidt, J. Am. Chem. Soc., 1981, 103, 1320–1328 CrossRef CAS.
- I. Akiyama, K. C. Li, P. R. leBreton, P. P. Fu and R. G. Harvey, Tetrahedron, 1976, 32, 2563 CrossRef.
- E. Clar and W. Schmidt, Tetrahedron, 1977, 33, 2093 CrossRef CAS.
- P. Bishof, P. E. Eaton, R. Gleiter, E. Heilbronner, T. B. Jones and H. Musso, et al. , Helv. Chim. Acta, 1978, 61, 547–557 CrossRef.
- C. Worrell, J. W. CVerhoeven and W. N. Speckamp, Tetrahedron, 1974, 30, 3525–3531 CrossRef CAS.
- E. Bohl, K. P. Sokół, B. Mignolet, J. O. F. Thompson, J. O. Johansson and F. Remacle, et al. , J. Phys. Chem. A, 2015, 119, 11504–11508 CrossRef CAS PubMed.
- M. Kjellberg, A. V. Bulgakov, M. Goto, O. Johansson and K. Hansen, J. Chem. Phys., 2010, 133, 074308 CrossRef CAS PubMed.
- J. Cooper and R. N. Zare, J. Chem. Phys., 1968, 48, 942–943 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp03913a |
| ‡ These authors contributed equally to the work. |
| This journal is © the Owner Societies 2017 |